Известия РАН. Механика твердого тела, 2020, № 6, стр. 33-39

НЕОДНОРОДНАЯ ЗАДАЧА ТЕОРИИ УПРУГОСТИ В ПОЛУПОЛОСЕ. ТОЧНОЕ РЕШЕНИЕ

М. Д. Коваленко^a, b, *, И. В. Меньшова^a, c, **, А. П. Кержаев^a, ***, G. Yu^d, e, ****

^a Институт теории прогноза землетрясений и математической геофизики РАН
Москва, Россия

^b Институт прикладной механики РАН
Москва, Россия

^c Московский государственный технический университет им. Н.Э. Баумана
Москва, Россия

^d School of Civil Engineering, Qingdao University of Technology
Qingdao, China

^e Cooperative Innovation Center of Engineering Construction and Safety in Shandong Blue Economic Zone, Qingdao University of Technology
Qingdao, China

^* E-mail: kov08@inbox.ru
^** E-mail: menshovairina@yandex.ru
^*** E-mail: alex_kerg@mail.ru
^**** E-mail: yu-guangming@263.net

Поступила в редакцию 10.07.2020
После доработки 25.07.2020
Принята к публикации 15.08.2020

DOI: 10.31857/S0572329920060094

Полный текст (PDF)

Аннотация

В статье в виде рядов по собственным функциям Папковича–Фадля построены точные решения двух неоднородных краевых задач теории упругости для полуполосы со свободными длинными сторонами: 1) торец полуполосы свободен, 2) торец полуполосы жестко защемлен. Для решения неоднородной задачи в свободной полосе используется соотношение ортогональности Папковича. К нему потом добавляется точное решение для полуполосы.

Ключевые слова: полуполоса, неоднородная краевая задача, собственные функции Папковича–Фадля, соотношение ортогональности Папковича, точное решение

1. Введение. В статье получены точные решения для полуполосы со свободными длинными сторонами. Внешняя нагрузка действует внутри полуполосы вдоль ее оси (четно-симметричная деформация). Торец полуполосы свободен (напряжения равны нулю) или жестко защемлен (перемещения равны нулю). Вначале решается соответствующая неоднородная задача для бесконечной полосы. Затем с помощью точных решений для полуполосы [1, 2] удовлетворяются граничные условия на торце.

Решение неоднородной задачи в бесконечной полосе строится с использованием соотношения ортогональности Папковича. Это позволяет существенно упростить процесс решения, а окончательные формулы представить в виде рядов по собственным функциям Папковича–Фадля, коэффициенты которых записываются в простом явном виде.

В 1940 П.Ф. Папковичем в статье [3] было получено соотношение биортогональности для собственных функций, возникающих при решении краевой задачи в полуполосе со свободными длинными сторонами. В работе [1] отмечалось, что соотношение ортогональности Папковича можно использовать для бесконечной полосы с разрывами перемещений или напряжений. Известно [4], что задачи с разрывами эквивалентны неоднородным краевым задачам теории упругости. Основываясь на этом, с помощью соотношения ортогональности Папковича можно быстро получить решение неоднородной задачи для свободной полосы.

2. Решение неоднородной задачи в бесконечной полосе. Простой путь решения неоднородной задачи для свободной полосы основан на соотношении ортогональности Папковича. В этом случае результат получается в виде рядов $(\operatorname{Re} {{\lambda }_{k}} < 0)$

${{\sigma }_{x}}(x,y) = C\operatorname{sign} (x) + \operatorname{sign} (x)\sum\limits_{k = 1}^\infty {2\operatorname{Re} [{{A}_{k}}{{s}_{x}}({{\lambda }_{k}},y){{e}^{{{{\lambda }_{k}}|x|}}}]} $

${{\sigma }_{y}}(x,y) = \operatorname{sign} (x)\sum\limits_{k = 1}^\infty {2\operatorname{Re} [{{A}_{k}}{{s}_{y}}({{\lambda }_{k}},y){{e}^{{{{\lambda }_{k}}|x|}}}]} $

(2.1)

${{\tau }_{{xy}}}(x,y) = \sum\limits_{k = 1}^\infty {2\operatorname{Re} [{{A}_{k}}{{t}_{{xy}}}({{\lambda }_{k}},y){{e}^{{{{\lambda }_{k}}|x|}}}]} $

$U(x,y) = \frac{{C{\text{|}}x{\text{|}}}}{{2(1 + \nu )}} + \sum\limits_{k = 1}^\infty {2\operatorname{Re} [{{A}_{k}}\xi ({{\lambda }_{k}},y){{e}^{{{{\lambda }_{k}}|x|}}}]} $

$V(x,y) = - \operatorname{sign} (x)\frac{{C\nu y}}{{2(1 + \nu )}} + \operatorname{sign} (x)\sum\limits_{k = 1}^\infty {2\operatorname{Re} [{{A}_{k}}\chi ({{\lambda }_{k}},y){{e}^{{{{\lambda }_{k}}|x|}}}]} $

по собственным функциям Папковича–Фадля

${{s}_{x}}({{\lambda }_{k}},y) = (1 + \nu ){{\lambda }_{k}}\{ (\sin {{\lambda }_{k}} - {{\lambda }_{k}}\cos {{\lambda }_{k}})\cos {{\lambda }_{k}}y - {{\lambda }_{k}}y\sin {{\lambda }_{k}}\sin {{\lambda }_{k}}y\} $

${{s}_{y}}({{\lambda }_{k}},y) = (1 + \nu ){{\lambda }_{k}}\{ (\sin {{\lambda }_{k}} + {{\lambda }_{k}}\cos {{\lambda }_{k}})\cos {{\lambda }_{k}}y + {{\lambda }_{k}}y\sin {{\lambda }_{k}}\sin {{\lambda }_{k}}y\} $

(2.2)

${{t}_{{xy}}}({{\lambda }_{k}},y) = (1 + \nu )\lambda _{k}^{2}(\cos {{\lambda }_{k}}\sin {{\lambda }_{k}}y - y\sin {{\lambda }_{k}}\cos {{\lambda }_{k}}y)$

$\xi ({{\lambda }_{k}},y) = \left( {\frac{{1 - \nu }}{2}\sin {{\lambda }_{k}} - \frac{{1 + \nu }}{2}{{\lambda }_{k}}\cos {{\lambda }_{k}}} \right)\cos {{\lambda }_{k}}y - \frac{{1 + \nu }}{2}{{\lambda }_{k}}y\sin {{\lambda }_{k}}\sin {{\lambda }_{k}}y$

$\chi ({{\lambda }_{k}},y) = \left( {\frac{{1 + \nu }}{2}{{\lambda }_{k}}\cos {{\lambda }_{k}} + \sin {{\lambda }_{k}}} \right)\sin {{\lambda }_{k}}y - \frac{{1 + \nu }}{2}{{\lambda }_{k}}y\sin {{\lambda }_{k}}\cos {{\lambda }_{k}}$

где λ_k – комплексные корни трансцендентного уравнения $\lambda + \sin \lambda \cos \lambda = 0$ [1, 2].

Известны различные формы записи соотношения ортогональности Папковича. Воспользуемся той, что приведена в статье [1]:

(2.3)

$\int\limits_{ - 1}^1 {\left[ {{{s}_{x}}({{\lambda }_{k}},y)\xi ({{\lambda }_{m}},y) - \chi ({{\lambda }_{k}},y){{t}_{{xy}}}({{\lambda }_{m}},y)} \right]dy} = \left\{ \begin{gathered} 2(1 + \nu )\lambda _{k}^{3}\quad {\text{(}}k = m) \hfill \\ 0\quad (k \ne m) \hfill \\ \end{gathered} \right.$

Если на торце правой полуполосы $\{ \Pi {\kern 1pt} :\;{\text{|}}x{\text{|}} \geqslant 0,\;{\text{|}}y{\text{|}} \leqslant 1\} $ со свободными длинными сторонами заданы продольные нормальные напряжения X(y) и поперечные перемещения V(y), то коэффициенты A_k рядов (2.1) легко найти с помощью (2.3):

(2.4)

${{A}_{k}} = \frac{1}{{2(1 + \nu )\lambda _{k}^{3}}}\int\limits_{ - 1}^1 {\left[ {X(y)\xi ({{\lambda }_{k}},y) - V(y){{t}_{{xy}}}({{\lambda }_{k}},y)} \right]dy} \quad (k \geqslant 1)$

Продолжая решение из правой полуполосы в левую как нечетно-симметричное и полагая в (2.4) $V(y) = 0$ (в силу нечетности продолжения), получим формулы (2.1), описывающие решение задачи в свободной бесконечной полосе с разрывами нормальных напряжений. В этих формулах

(2.5)

${{A}_{k}} = \frac{1}{{2(1 + \nu )\lambda _{k}^{3}}}\int\limits_{ - 1}^1 {X(y)\xi ({{\lambda }_{k}},y)dy} $

Если подставить (2.5) в первые две формулы (2.1), то с помощью теоремы о вычетах получим

(2.6)

${{\sigma }_{x}}(0,y) = X(y),\quad {{\sigma }_{y}}(0,y) = \nu X(y)$

Проверим выполнение уравнений равновесия и совместности деформаций для решения (2.1). Используя равенства, которым удовлетворяют собственные функции Папковича–Фадля:

(2.7)

$\frac{d}{{dy}}{{t}_{{xy}}}({{\lambda }_{k}},y) = - {{\lambda }_{k}}{{s}_{x}}({{\lambda }_{k}},y),\quad \frac{d}{{dy}}{{s}_{y}}({{\lambda }_{k}},y) = - {{\lambda }_{k}}{{t}_{{xy}}}({{\lambda }_{k}},y)$

а также следующие свойства обобщенных функций [5] (штрихом обозначена производная дельта-функции):

(2.8)

$\frac{d}{{dx}}\operatorname{sign} (x) = 2\delta (x),\quad \delta (x){{e}^{{{{\lambda }_{k}}|x|}}} = \delta (x),\quad \delta {\kern 1pt} '(x){{e}^{{{{\lambda }_{k}}|x|}}} = \delta {\kern 1pt} '(x),\quad \delta (x)\operatorname{sign} (x) = 0$

с учетом формул (2.6) получим

(2.9)

$\begin{gathered} \frac{\partial }{{\partial x}}{{\sigma }_{x}}(x,y) + \frac{\partial }{{\partial y}}\tau _{{xy}}^{{}}(x,y) = 2X(y)\delta (x),\quad \frac{\partial }{{\partial y}}\sigma _{y}^{{}}(x,y) + \frac{\partial }{{\partial x}}\tau _{{xy}}^{{}}(x,y) = 0 \\ \left( {\frac{{{{\partial }^{2}}}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}}}{{\partial {{y}^{2}}}}} \right)(\sigma _{x}^{{}}(x,y) + \sigma _{y}^{{}}(x,y)) = 2(1 + \nu )X(y)\delta '(x) \\ \end{gathered} $

Как известно, уравнения (2.9) соответствуют неоднородной задаче [6]. Следовательно, решение (2.1) с разрывами нормальных напряжений эквивалентно решению неоднородной задачи для свободной полосы.

Если в формулах (2.1) заменить x на x – β, то получим

$\sigma _{x}^{{}}(x,y) = C\operatorname{sign} (x - \beta ) + \operatorname{sign} (x - \beta )\sum\limits_{k = 1}^\infty {2\operatorname{Re} [{{A}_{k}}{{s}_{x}}({{\lambda }_{k}},y){{e}^{{{{\lambda }_{k}}|x - \beta |}}}]} $

$\sigma _{y}^{{}}(x,y) = \operatorname{sign} (x - \beta )\sum\limits_{k = 1}^\infty {2\operatorname{Re} [{{A}_{k}}{{s}_{y}}({{\lambda }_{k}},y){{e}^{{{{\lambda }_{k}}|x\, - \,\beta |}}}]} $

(2.10)

$\tau _{{xy}}^{{}}(x,y) = \sum\limits_{k = 1}^\infty {2\operatorname{Re} [{{A}_{k}}{{t}_{{xy}}}({{\lambda }_{k}},y){{e}^{{{{\lambda }_{k}}|x - \beta |}}}]} $

$U(x,y) = \frac{{C{\text{|}}x - \beta {\text{|}}}}{{2(1 + \nu )}} + \sum\limits_{k = 1}^\infty {2\operatorname{Re} [{{A}_{k}}\xi ({{\lambda }_{k}},y){{e}^{{{{\lambda }_{k}}|x - \beta |}}}]} $

$V(x,y) = - \operatorname{sign} (x - \beta )\frac{{C\nu y}}{{2(1 + \nu )}} + \operatorname{sign} (x - \beta )\sum\limits_{k = 1}^\infty {2\operatorname{Re} [{{A}_{k}}\chi ({{\lambda }_{k}},y){{e}^{{{{\lambda }_{k}}|x - \beta |}}}]} $

3. Решение неоднородной задачи для полуполосы со свободными длинными сторонами. Решение неоднородной задачи для полуполосы Π со свободными длинными сторонами и какими-либо граничными условиями на торце получается как сумма решений неоднородной задачи для свободной полосы (2.10) и однородной задачи для полуполосы Π.

Последнее имеет вид [7] ($x \geqslant 0,\,\,\operatorname{Re} {{\lambda }_{k}} > 0$)¹ ¹:

a) если на торце полуполосы заданы нормальные напряжения, то

$\sigma _{x}^{{hs}}\left( {x,y} \right) = {{C}_{0}} + \sum\limits_{k = 1}^\infty {2\operatorname{Re} \left\{ {{{\sigma }_{k}}\frac{{{{s}_{x}}\left( {{{\lambda }_{k}},y} \right)}}{{{{M}_{k}}}}\frac{{\operatorname{Im} ( - \overline {{{\lambda }_{k}}} {{e}^{{{{\lambda }_{k}}x}}})}}{{\operatorname{Im} ({{\lambda }_{k}})}}} \right\}} $

$\sigma _{y}^{{hs}}\left( {x,y} \right) = \sum\limits_{k = 1}^\infty {2\operatorname{Re} \left\{ {{{\sigma }_{k}}\frac{{{{s}_{y}}\left( {{{\lambda }_{k}},y} \right)}}{{{{M}_{k}}\lambda _{k}^{2}}}{{\lambda }_{k}}\overline {{{\lambda }_{k}}} \frac{{\operatorname{Im} ( - {{\lambda }_{k}}{{e}^{{{{\lambda }_{k}}x}}})}}{{\operatorname{Im} ({{\lambda }_{k}})}}} \right\}} $

(3.1)

$\tau _{{xy}}^{{hs}}\left( {x,y} \right) = \sum\limits_{k = 1}^\infty {2\operatorname{Re} \left\{ {{{\sigma }_{k}}\frac{{{{t}_{{xy}}}\left( {{{\lambda }_{k}},y} \right)}}{{{{\lambda }_{k}}{{M}_{k}}}}{{\lambda }_{k}}\overline {{{\lambda }_{k}}} \frac{{\operatorname{Im} ( - {{e}^{{{{\lambda }_{k}}x}}})}}{{\operatorname{Im} ({{\lambda }_{k}})}}} \right\}} $

${{U}^{{hs}}}\left( {x,y} \right) = {{B}_{0}} + \frac{{{{C}_{0}}x}}{{2(1 + \nu )}} + \sum\limits_{k = 1}^\infty {2\operatorname{Re} \left\{ {{{\lambda }_{k}}{{\sigma }_{k}}\frac{{\xi \left( {{{\lambda }_{k}},y} \right)}}{{{{\lambda }_{k}}{{M}_{k}}}}\frac{{\operatorname{Im} ( - \overline {{{\lambda }_{k}}} {{e}^{{{{\lambda }_{k}}x}}})}}{{\operatorname{Im} ({{\lambda }_{k}})}}} \right\}} $

${{V}^{{hs}}}\left( {x,y} \right) = - \frac{{{{C}_{0}}\nu y}}{{2(1 + \nu )}} + \sum\limits_{k = 1}^\infty {2\operatorname{Re} \left\{ {{{\sigma }_{k}}\frac{{\chi \left( {{{\lambda }_{k}},y} \right)}}{{{{M}_{k}}}}\frac{{\operatorname{Im} (\overline {{{\lambda }_{k}}} {{e}^{{{{\lambda }_{k}}x}}})}}{{\operatorname{Im} ({{\lambda }_{k}})}}} \right\}} $

b) если на торце полуполосы заданы касательные напряжения, то

$\sigma _{x}^{{hs}}\left( {x,y} \right) = \sum\limits_{k = 1}^\infty {2\operatorname{Re} \left\{ {{{\tau }_{k}}\frac{{{{s}_{x}}\left( {{{\lambda }_{k}},y} \right)}}{{{{M}_{k}}}}\frac{{\operatorname{Im} ({{e}^{{{{\lambda }_{k}}x}}})}}{{\operatorname{Im} ({{\lambda }_{k}})}}} \right\}} $

$\sigma _{y}^{{hs}}\left( {x,y} \right) = \sum\limits_{k = 1}^\infty {2\operatorname{Re} \left\{ {{{\tau }_{k}}\frac{{{{s}_{y}}\left( {{{\lambda }_{k}},y} \right)}}{{\lambda _{k}^{2}{{M}_{k}}}}\frac{{\operatorname{Im} (\lambda _{k}^{2}{{e}^{{{{\lambda }_{k}}x}}})}}{{\operatorname{Im} ({{\lambda }_{k}})}}} \right\}} $

(3.2)

$\tau _{{xy}}^{{hs}}\left( {x,y} \right) = \sum\limits_{k = 1}^\infty {2\operatorname{Re} \left\{ {{{\tau }_{k}}\frac{{{{t}_{{xy}}}\left( {{{\lambda }_{k}},y} \right)}}{{{{\lambda }_{k}}{{M}_{k}}}}\frac{{\operatorname{Im} ({{\lambda }_{k}}{{e}^{{{{\lambda }_{k}}x}}})}}{{\operatorname{Im} ({{\lambda }_{k}})}}} \right\}} $

${{U}^{{hs}}}\left( {x,y} \right) = - \sum\limits_{k = 1}^\infty {2\operatorname{Re} \left\{ {{{\tau }_{k}}\frac{{\xi \left( {{{\lambda }_{k}},y} \right)}}{{{{\lambda }_{k}}{{M}_{k}}}}\frac{{\operatorname{Im} ({{\lambda }_{k}}{{e}^{{{{\lambda }_{k}}x}}})}}{{\operatorname{Im} ({{\lambda }_{k}})}}} \right\}} $

${{V}^{{hs}}}\left( {x,y} \right) = \sum\limits_{k = 1}^\infty {2\operatorname{Re} \left\{ {\frac{{{{\tau }_{k}}}}{{{{\lambda }_{k}}}}\frac{{\chi \left( {{{\lambda }_{k}},y} \right)}}{{{{M}_{k}}}}\frac{{\operatorname{Im} ({{\lambda }_{k}}{{e}^{{{{\lambda }_{k}}x}}})}}{{\operatorname{Im} ({{\lambda }_{k}})}}} \right\}} $

Здесь ${{M}_{k}} = {{\cos }^{2}}({{\lambda }_{k}})$ – нормирующий множитель, а ${{\sigma }_{k}},\;{{\tau }_{k}}$ – коэффициенты Лагранжа [1, 2], которые нужно найти из граничных условий на торце полуполосы. Постоянным B₀, C₀ соответствует элементарное решение.

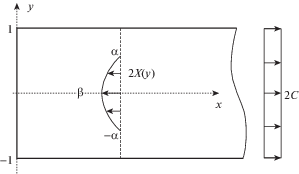
3.1. Решение неоднородной задачи для полуполосы со свободным торцом. Рассмотрим неоднородную задачу для полуполосы $\Pi $ со свободным торцом (рис. 1).

Рис. 1

Воспользуемся формулами (2.10), (3.1), (3.2) и будем считать, что при x = 0

(3.3)

$\sigma _{x}^{{hs}}\left( {0,y} \right) = - \sigma _{x}^{{}}(0,y),\quad \tau _{{xy}}^{{hs}}\left( {0,y} \right) = - \tau _{{xy}}^{{}}(0,y)$

Отсюда получим

(3.4)

$\begin{gathered} C + \sum\limits_{k = 1}^\infty {2\operatorname{Re} \left\{ {{{\sigma }_{k}}\frac{{{{s}_{x}}\left( {{{\lambda }_{k}},y} \right)}}{{{{M}_{k}}}}} \right\}} = {{C}_{0}} + \sum\limits_{k = 1}^\infty {2\operatorname{Re} \text{[}{{A}_{k}}{{s}_{x}}({{\lambda }_{k}},y){{e}^{{{{\lambda }_{k}}|\beta |}}}]} \\ \sum\limits_{k = 1}^\infty {2\operatorname{Re} \left\{ {{{\tau }_{k}}\frac{{{{t}_{{xy}}}\left( {{{\lambda }_{k}},y} \right)}}{{{{\lambda }_{k}}{{M}_{k}}}}} \right\}} = - \sum\limits_{k = 1}^\infty {2\operatorname{Re} [{{A}_{k}}{{t}_{{xy}}}({{\lambda }_{k}},y){{e}^{{{{\lambda }_{{_{k}}}}|\beta |}}}]} \\ \end{gathered} $

Умножим равенства (3.4) на функции, биортогональные к собственным функциям Папковича–Фадля, и проинтегрируем. Следуя [2], на основании соотношений биортогональности найдем

(3.5)

${{C}_{0}} = C,\quad {{\sigma }_{k}} = {{A}_{k}}{{M}_{k}}{{e}^{{{{\lambda }_{k}}|\beta |}}},\quad {{\tau }_{k}} = - {{A}_{k}}{{M}_{k}}{{\lambda }_{k}}{{e}^{{{{\lambda }_{k}}|\beta |}}}$

Подставив эти выражения в формулы (3.1), (3.2) и складывая их с соответствующими формулами (2.10), получим полное решение неоднородной задачи для полуполосы со свободными длинными сторонами и торцом, у которой в сечении x = β действует направленная вдоль оси $x$ четно-симметричная нагрузка 2X(y).

Элементарные решения удобно выделить из полного решения. Сумма элементарных решений (2.10) и (3.1) равна:

(3.6)

$\begin{gathered} \sigma _{x}^{0}(x,y) = C\operatorname{sign} (x - \beta ) + C \\ {{U}^{0}}(x,y) = \frac{{C{\text{|}}x - \beta {\text{|}}}}{{2(1 + \nu )}} + \frac{{Cx}}{{2(1 + \nu )}} + {{B}_{0}} \\ {{V}^{0}}(x,y) = - \frac{{C\nu y}}{{2(1 + \nu )}}\operatorname{sign} (x - \beta ) - \frac{{C\nu y}}{{2(1 + \nu )}} \\ \sigma _{y}^{0}(x,y) = \tau _{{xy}}^{0}(x,y) = 0,\quad C = \frac{1}{2}\int\limits_{ - 1}^1 {X(y)dy} \\ \end{gathered} $

Если считать, что

(3.7)

${{B}_{0}} = - \frac{{C\beta }}{{2(1 + \nu )}}$

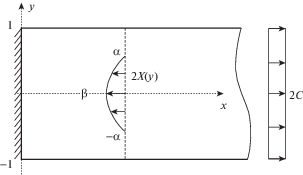
то тогда ${{U}^{0}}(0,y) = 0$.

3.2. Решение неоднородной задачи для полуполосы с жестко защемленным торцом. Рассмотрим неоднородную задачу для полуполосы Π с жестко защемленным торцом (рис. 2).

Рис. 2

Вновь воспользуемся формулами (2.10), (3.1), (3.2) и будем считать, что при x = 0

(3.8)

${{U}^{{hs}}}(0,y) = - U(0,y),\quad {{V}^{{hs}}}(0,y) = - V(0,y)$

При ${{C}_{0}} = C$ и B₀, равной (3.7), элементарное решение (3.6) удовлетворяет условию отсутствия перемещений на торце полуполосы. Поэтому из (3.8) получим следующие два уравнения относительно коэффициентов Лагранжа σ_k и τ_k:

(3.9)

$\begin{gathered} \sum\limits_{k = 1}^\infty {2\operatorname{Re} \left\{ {{{\lambda }_{k}}{{\sigma }_{k}}\frac{{\xi \left( {{{\lambda }_{k}},y} \right)}}{{{{\lambda }_{k}}{{M}_{k}}}}} \right\} - \sum\limits_{k = 1}^\infty {2\operatorname{Re} } \left\{ {{{\tau }_{k}}\frac{{\xi \left( {{{\lambda }_{k}},y} \right)}}{{{{\lambda }_{k}}{{M}_{k}}}}} \right\}} = - \sum\limits_{k = 1}^\infty {2\operatorname{Re} \text{[}{{A}_{k}}\xi ({{\lambda }_{k}},y){{e}^{{{{\lambda }_{k}}|\beta |}}}]} \\ \, - \sum\limits_{k = 1}^\infty {2\operatorname{Re} \left\{ {{{\sigma }_{k}}\frac{{\chi \left( {{{\lambda }_{k}},y} \right)}}{{{{M}_{k}}}}} \right\} + \sum\limits_{k = 1}^\infty {2\operatorname{Re} } \left\{ {\frac{{{{\tau }_{k}}}}{{{{\lambda }_{k}}}}\frac{{\chi \left( {{{\lambda }_{k}},y} \right)}}{{{{M}_{k}}}}} \right\}} = \sum\limits_{k = 1}^\infty {2\operatorname{Re} [{{A}_{k}}\chi ({{\lambda }_{k}},y){{e}^{{{{\lambda }_{k}}|\beta |}}}]} \\ \end{gathered} $

Отсюда, как и выше, придем к системе из двух алгебраических уравнений:

(3.10)

${{\lambda }_{k}}{{\sigma }_{k}} - {{\tau }_{k}} = - {{\lambda }_{k}}{{A}_{k}}{{M}_{k}}{{e}^{{{{\lambda }_{k}}|\beta |}}},\quad - {{\sigma }_{k}} + \frac{{{{\tau }_{k}}}}{{{{\lambda }_{k}}}} = {{A}_{k}}{{M}_{k}}{{e}^{{{{\lambda }_{k}}|\beta |}}}$

Уравнения (3.10) линейно зависимы, поэтому система (3.10) имеет бесконечное множество решений. Физически это означает, что решение из правой полуполосы $\Pi $ может быть продолжено в левую бесконечным числом комбинаций четно-симметричных и нечетно-симметричных продолжений. В частности, если оно продолжено как четно-симметричное, то

(3.11)

${{\tau }_{k}} = 0,\quad {{\sigma }_{k}} = - {{A}_{k}}{{M}_{k}}{{e}^{{{{\lambda }_{k}}|\beta |}}}$

Если же оно продолжено как нечетно-симметричное, то

(3.12)

${{\sigma }_{k}} = 0,\quad {{\tau }_{k}} = {{\lambda }_{k}}{{A}_{k}}{{M}_{k}}{{e}^{{{{\lambda }_{k}}|\beta |}}}$

4. Заключение. 1. В статье предложен основанный на соотношении ортогональности Папковича метод решения неоднородных краевых задач теории упругости в свободной полосе. Показана эквивалентность решения неоднородной задачи и задачи с разрывами продольных нормальных напряжений. С помощью этого же соотношения ортогональности или соотношений ортогональности Папковича, записанных в иной форме, можно получить другие простые решения различных задач с разрывами напряжений или перемещений и эквивалентных им неоднородных задач. Все решения будут представляться рядами по собственным функциям Папковича–Фадля.

2. В случае защемленного торца напряжения не имеют особенности в угловых точках полуполосы, в отличие от соответствующих решений для бесконечного клина. Причина этого заключается в том, что, в отличие от решения, полученного в статье, в решении для клина тип граничных условий меняется в точке (вершине клина), лежащей на одной координатной линии, а именно вдоль границы клина. В статье [9] было показано, что в задачах для полуполосы или прямоугольника в этом случае соответствующей особенностью должны обладать функции, биортогональные к функциям Папковича–Фадля. Поэтому решение для клина не может рассматриваться как асимптотическое в соответствующих задачах для полуполосы, т.к. это и физически и математически разные задачи.

3. Функция X(y) должна обращаться в нуль в окрестности точек ($x = \beta ,$ $y = \pm 1$). Если это условие не выполняется, то решение задачи может оказаться нерегулярным в этих точках в смысле Н.И. Мусхелишвили [10].

4. Известно, что соотношение ортогональности Папковича остается справедливым и для других типов однородных граничных условий на сторонах полосы, в частности, когда ее стороны жестко защемлены. Поэтому рассмотренным в этой статье методом можно построить простые точные решения для широкого круга (с различными граничными условиями) неоднородных краевых задач в полуполосе (в прямоугольнике).

Благодарности. Исследование М.Д. Коваленко и И.В. Меньшовой (разделы 3 и 4) выполнено при финансовой поддержке РФФИ и Государственного фонда естественных наук Китая в рамках научного проекта № 20-51-53021. Исследование А.П. Кержаева (разделы 1 и 2) выполнено за счет гранта Российского научного фонда (проект № 19-71-00094). The research of G. Yu was funded by the National Natural Science Foundation of China (No. 51674150) and NSFC-RFBR (No. 5191101589).

Список литературы

Коваленко М.Д., Шуляковская Т.Д. Разложения по функциям Фадля–Папковича в полосе. Основы теории // Изв. РАН. МТТ. 2011. № 5. С. 78–98.
Коваленко М.Д., Меньшова И.В., Шуляковская Т.Д. Разложения по функциям Фадля–Папковича. Примеры решений в полуполосе // Изв. РАН. МТТ. 2013. № 5. С. 121–144.
Папкович П.Ф. Об одной форме решения плоской задачи теории упругости для прямоугольной полосы // Докл. АН СССР. 1940. Т. 27. № 4. С. 335–339.
Kasahara K. Earthquake Mechanics. Cambridge: Cambridge Univ. Press, 1981.
Ketch V., Teodorescu P. Introduction to the Theory of Generalized Functions with Applications in Engineering. New York: Wiley, 1978.
Timoshenko S.P., Goodier J.N. Theory of Elasticity. New-York: McGraw-Hill, 1951.
Yu G., Kovalenko M.D., Menshova I.V., Kerzhaev A.P. Two problems for a strip with a transverse crack: Exact solutions // J. Phys.: Conf. Ser. 2019. V. 1215. 012037.
Kovalenko M.D., Menshova I.V., Kerzhaev A.P. On the exact solutions of the biharmonic problem of the theory of elasticity in a half-strip // Z. Angew. Math. Phys. 2018. V. 69. 121.
Kovalenko M.D., Menshova I.V., Kerzhaev A.P., Yu G. Mixed boundary value problems in the theory of elasticity in an infinite strip // Acta Mech. 2018. V. 229. № 11. P. 4339–4356.
Мусхелишвили Н.И. Некоторые основные задачи математической теории упругости. М.; Л.: Изд-во АН СССР, 1949. 635 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика твердого тела

Архивы выпусков Информация о журнале Отправить рукопись в журнал