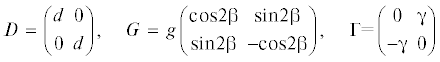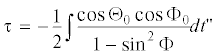Известия РАН. Механика твердого тела, 2021, № 2, стр. 42-50

АНАЛИЗ ДЕЙСТВИЯ ВОЗМУЩЕНИЙ ЛИНЕЙНЫХ РЕЗОНАНСНЫХ СИСТЕМ С ДВУМЯ СТЕПЕНЯМИ СВОБОДЫ

В. Ф. Журавлев^a, *, А. Г. Петров^a, **

^a Институт проблем механики, РАН им. А.Ю. Ишлинского
Москва, Россия

^* E-mail: zhurav@ipmnet.ru
^** E-mail: petrovipmech@gmail.com

Поступила в редакцию 12.03.2020
После доработки 14.03.2020
Принята к публикации 16.03.2020

DOI: 10.31857/S0572329921020185

Аннотация

Рассматривается система с двумя степенями свободы в случае двухкратной собственной частоты. Невозмущенная система состоит из двух независимых осцилляторов. Координаты системы описывают эллиптическую траекторию с четырьмя элементами орбиты. Проводится анализ действия линейных возмущений (сил) на элементы орбиты. Возмущения подразделяются на шесть типов сил и для каждого типа сил получена система дифференциальных уравнений для элементов орбиты. Для всех шести типов сил найдено общее решение системы дифференциальных уравнений в элементарных функциях.

Ключевые слова: резонансные системы, две степени свободы, линейные возмущения, эволюции эллиптической траектории

Координаты системы с двумя степенями свободы в случае двухкратной собственной частоты изменяются по эллиптической траектории [1]. Под действием малых возмущающих сил эллиптическая траектория изменяется. Для описания изменений элементов эллиптической орбиты применяется система дифференциальных уравнений, полученная методом осреднения [2]. Прикладываемые к системе линейные по координатам и скоростям силы подразделяются на шесть типов. Три типа сил, зависящие от координат, называются позиционными силами, остальные три типа сил зависят от скоростей и называются скоростными силами [3, 4]. В [1, 3] показано, что к чистым эволюциям формы колебаний приводят четыре типа сил: силы первого типа приводят только к изменению частоты, второго и третьего типа – только к изменению полуосей эллипса и силы четвертого типа приводят к прецессии эллипса. Эти четыре типа сил удобны для решения задачи управления формой колебаний. Остальные два типа сил приводят сразу ко всем типам эволюции формы и разрушают ее. Разрушение формы для этих типов сил описывается нелинейной системой дифференциальных уравнений четвертого порядка. Данная статья посвящена интегрированию этих систем уравнений. В результате получено описание эволюции форм в элементарных функциях для любых начальных условий.

1. Постановка задачи. Рассмотрим, следуя [1], систему

(1.1)

${{\ddot {q}}_{i}} + {{q}_{i}} = {\varepsilon }{{Q}_{i}}(t,q,\dot {q}),\quad i = 1,\;2$

Если ε = 0, то решение этой системы записывается в виде

(1.2)

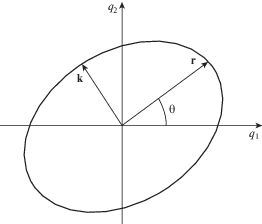
$\begin{gathered} {{q}_{1}} = r\cos (t + {\tau })\cos {\theta } - k\sin (t + {\tau })\sin {\theta } \\ {{q}_{2}} = r\cos (t + {\tau })\sin {\theta } + k\sin (t + {\tau })\cos {\theta } \\ {{p}_{1}} = {{{\dot {q}}}_{1}} = - r\sin (t + {\tau })\cos {\theta } - k\cos (t + {\tau })\sin {\theta } \\ {{p}_{2}} = {{{\dot {q}}}_{2}} = - r\sin (t + {\tau })\sin {\theta } + k\cos (t + {\tau })\cos {\theta } \\ \end{gathered} $

Постоянные интегрирования называются элементами орбиты. Их геометрический смысл ясен из рис. 1 (r и k – полуоси эллиптической траектории, параметр $\tau $ характеризует положение точки на эллипсе в начальный момент). Если правые части (1.1) ненулевые, то элbементы орбиты становятся функциями времени. Чтобы получить уравнения, описывающие их изменение, нужно сделать в (1.1) замену переменных по формулам (1.2). Это приводит к следующим уравнениям

$\begin{gathered} \dot {r} = - {\varepsilon }({{Q}_{1}}\cos {\theta } + {{Q}_{2}}\sin {\theta })\sin t,\quad \dot {k} = - {\varepsilon }({{Q}_{1}}\sin {\theta } - {{Q}_{2}}\cos {\theta })\cos t \\ {\dot {\theta }} = \frac{{\varepsilon }}{{{{r}^{2}} - {{k}^{2}}}}\left[ {k({{Q}_{1}}\cos {\theta } + {{Q}_{2}}\sin {\theta })\cos t + r({{Q}_{1}}\sin {\theta } - {{Q}_{2}}\cos {\theta })\sin t} \right] \\ \dot {\tau } = - \frac{{\varepsilon }}{{{{r}^{2}} - {{k}^{2}}}}\left[ {r({{Q}_{1}}\cos {\theta } + {{Q}_{2}}\sin {\theta })\cos t + k({{Q}_{1}}\sin {\theta } - {{Q}_{2}}\cos {\theta })\sin t} \right] \\ \end{gathered} $

Рис. 1

Осредненная по периоду автономная система уравнений для элементов орбиты имеет вид

(1.3)

$\begin{gathered} \dot {r} = - {\varepsilon }({{Q}_{{12}}}\cos {\theta } + {{Q}_{{22}}}\sin {\theta }),\quad \dot {k} = - {\varepsilon }({{Q}_{{11}}}\sin {\theta } - {{Q}_{{21}}}\cos {\theta }) \\ {\dot {\theta }} = \frac{{\varepsilon }}{{{{r}^{2}} - {{k}^{2}}}}\left[ {k({{Q}_{{11}}}\cos {\theta } + {{Q}_{{21}}}\sin {\theta }) + r({{Q}_{{12}}}\sin {\theta } - {{Q}_{{22}}}\cos {\theta })} \right] \\ \dot {\tau } = - \frac{{\varepsilon }}{{{{r}^{2}} - {{k}^{2}}}}\left[ {r({{Q}_{{11}}}\cos {\theta } + {{Q}_{{21}}}\sin {\theta }) + k({{Q}_{{12}}}\sin {\theta } - {{Q}_{{22}}}\cos {\theta })} \right] \\ {{Q}_{{11}}} = \overline {{{Q}_{1}}\cos t} ,\quad {{Q}_{{12}}} = \overline {{{Q}_{1}}\sin t} ,\quad {{Q}_{{21}}} = \overline {{{Q}_{2}}\cos t} ,\quad {{Q}_{{22}}} = \overline {{{Q}_{2}}\sin t} \\ \end{gathered} $

Здесь черта сверху означает знак осреднения по явному вреbмени

$\bar {f} = \frac{1}{{2{\pi }}}\int\limits_0^{2{\pi }} f (t)dt$

Аналогичная система уравнений была получена в [2].

2. Анализ действия возмущений в линейном случае. Естественно начать анализ с линейных по координатам ${{q}_{1}}$, ${{q}_{2}}$ и скоростям ${{\dot {q}}_{1}}$, ${{\dot {q}}_{2}}$ сил ${{Q}_{1}}$, ${{Q}_{2}}$

$\left( {\begin{array}{*{20}{c}} {{{Q}_{1}}} \\ {{{Q}_{2}}} \end{array}} \right) = P\left( {\begin{array}{*{20}{c}} {{{q}_{1}}} \\ {{{q}_{2}}} \end{array}} \right) + R\left( {\begin{array}{*{20}{c}} {{{{\dot {q}}}_{1}}} \\ {{{{\dot {q}}}_{2}}} \end{array}} \right)$

Произвольные матрицы позиционных сил P и скоростных сил $R$ единственным образом разлагаются на симметрическую и кососимметрическую части. В свою очередь, симметрические части этих матриц могут быть единственным образом разложены на скалярную матрицу и на матрицу с нулевым следом. В результате получаем для матриц P и $R$ следующие представления:

$\begin{array}{*{20}{c}} {P = C + H + N,\quad R = D + G + Г} \\ {C = \left( {\begin{array}{*{20}{c}} c&0 \\ 0&c \end{array}} \right),\quad H = h\left( {\begin{array}{*{20}{c}} {\cos 2{\alpha }}&{\sin 2{\alpha }} \\ {\sin 2{\alpha }}&{ - \cos 2{\alpha }} \end{array}} \right),\quad N = \left( {\begin{array}{*{20}{c}} 0&n \\ { - n}&0 \end{array}} \right)} \end{array}$

Полученные шесть типов сил $Q$ имеют следующие наименования: $Cq$ – потенциальные силы сферического типа; Hq – потенциальные силы гиперболического типа; $Nq$ – в литературе встречается несколько названий для этих сил: циркулярные силы, псевдогироскопические, собственно неконсервативные силы, силы радиальной коррекции; $D\dot {q}$ – диссипативные силы сферического типа, если d < 0; $G\dot {q}$ – скоростные силы гиперболического типа; $Г\dot {q}$ – гироскопические силы. Симметрические матрицы $H$ и G, имеющие нулевой след, называются девиаторами.

Коэффициенты $h$ и $g$ определяют нормы девиаторов гиперболических сил, а углы ${\alpha }$ и ${\beta }$ ориентацию главных осей жесткости и демпфирования относительно осей ${{q}_{1}}$ и ${{q}_{2}}$.

При подстановке соответствующих сил в уравнения (1.3) и последующего осреднения получим шесть систем уравнений для параметров орбиты.

Рассмотрим более подробно эту процедуру на примере потенциальной силы.

Для невозмущенной системы (1.1) имеем решение (1.2)

$\begin{array}{*{20}{c}} {{{q}_{1}} = r\cos t\cos {\theta } - k\sin t\sin {\theta },\quad {{q}_{2}} = r\cos t\sin {\theta } + k\sin t\cos {\theta }} \end{array}$

Находим компоненты потенциальных сил на невозмущенном решении ${{Q}_{1}} = c{{q}_{1}}$, Q₂ = cq₂ и осредненные по периоду выражения

$\begin{array}{*{20}{c}} {{{Q}_{{11}}} = \frac{1}{2}cr\cos {\theta },\quad {{Q}_{{12}}} = - \frac{1}{2}ck\sin {\theta }} \\ {{{Q}_{{21}}} = \frac{1}{2}cr\sin {\theta },\quad {{Q}_{{22}}} = \frac{1}{2}ck\cos {\theta }} \end{array}$

Подставляя эти выражения в уравнения (1.2), получим следующие осредненные уравнения для элементов орбиты $\dot {r} = 0$, $\dot {k} = 0$, ${\dot {\theta }} = 0$, ${\dot {\tau }} = - (1{\text{/}}2)c{\varepsilon }.$

С помощью найденных значений и (1.2) находим решение

${{q}_{1}} = r\cos (1 - (1{\text{/}}2)c{\varepsilon })t,\quad {{q}_{2}} = k\sin (1 - (1{\text{/}}2)c{\varepsilon })t$

Для всех остальных случаев скорости изменений параметров орбиты находятся аналогично. Результаты представлены в таблице.

Из приведенной таблицы следует, что к чистым эволюциям формы колебаний приводят четыре типа сил из шести.

1. Потенциальные силы сферического типа Cq приводят только к изменению частоты $1 \to 1 - (1{\text{/}}2)c{\varepsilon }$.

2. Циркулярные силы Nq приводят только к изменению осей эллипса

$r = {{r}_{0}}{\text{ch}}(n{\varepsilon }t{\text{/}}2) - {{k}_{0}}{\text{sh}}(n{\varepsilon }t{\text{/}}2),\quad k = {{k}_{0}}{\text{ch}}(n{\varepsilon }t{\text{/}}2) - {{r}_{0}}{\text{sh}}(n{\varepsilon }t{\text{/}}2)$

3. Диссипативные (или ускоряющие) силы $D\dot {q}$ также приводят только к изменению осей эллипса

$r = {{r}_{0}}{\mkern 1mu} {{e}^{{d{\varepsilon }t/2}}},\quad k = {{k}_{0}}{\mkern 1mu} {{e}^{{d{\varepsilon }t/2}}}$

4. Гироскопические силы приводят только к прецессии формы колебаний θ = θ₀ + + $\frac{1}{2}({{k}^{2}} - {{r}^{2}}){\gamma \varepsilon }t$

Если возникает задача управления формой колебаний, то именно эти силы и следует выбирать для управления соответствующими эволюциями формы. Все эти результаты приведены в [1].

Гиперболические силы Hq и $G\dot {q}$ в общем случае приводят сразу ко всем типам эволюции формы. Эти случаи описываются достаточно сложной системой дифференциальных уравнений, но их тоже можно точно проинтегрировать. В этом и состоит цель данного исследования.

3. Эволюция системы под действием сил Hq. Систему уравнений под действием $Hq$ можно записать в комплексной форме

(3.1)

$\begin{array}{*{20}{c}} {\dot {r} + i\dot {k} = - \frac{1}{2}i{\varepsilon }h\sin 2({\theta } - {\alpha })(r + ik)} \\ {{\dot {\theta }} = - \frac{1}{2}{ \varepsilon }h\frac{{kr}}{{{{k}^{2}} - {{r}^{2}}}}\cos 2({\theta } - {\alpha }),\quad {\dot {\tau }} = \frac{1}{2}{\varepsilon }h\frac{{{{r}^{2}} + {{k}^{2}}}}{{{{k}^{2}} - {{r}^{2}}}}\cos 2({\theta } - {\alpha })} \end{array}$

От переменных $r$, k, $\theta $ перейдем к новым переменных $\rho $, $\Phi $, $\Theta $ с помощью замен

$\begin{array}{*{20}{c}} {r + ik = {\rho }{{e}^{{i\Phi /2}}},\quad \Theta = 2({\theta } - {\alpha }),\quad t' = {\varepsilon }ht.} \end{array}$

Отсюда следуют соотношения

$\frac{{d{\rho }}}{{dt{\text{'}}}} + \frac{1}{2}i{\rho }\frac{{d\Phi }}{{dt{\text{'}}}} = - \frac{1}{2}{\rho }i\sin \Theta ,\quad {\text{tg}}\Phi = \frac{{2rk}}{{{{r}^{2}} - {{k}^{2}}}},\quad \frac{{{{r}^{2}} + {{k}^{2}}}}{{{{k}^{2}} - {{r}^{2}}}} = - \frac{1}{{\cos \Phi }}$

с помощью которых система уравнений (4) в новых переменных принимает вид

(3.2)

$\begin{array}{*{20}{c}} {{\text{\$ }}\frac{{d\rho }}{{dt{\text{'}}}} = 0,\quad \frac{{d\Phi }}{{dt{\text{'}}}} = - \sin \Theta ,\quad \frac{{d\Theta }}{{dt'}} = {\text{tg}}\Phi \cos \Theta ,\quad 2\frac{{d\tau }}{{dt{\text{'}}}} = - \frac{{\cos \Theta }}{{\cos \Phi }}} \end{array}$

Система уравнений имеет два интеграла

(3.3)

$\rho = \sqrt {r_{0}^{2} + k_{0}^{2}} ,\quad \cos \Phi \cos \Theta = \cos {{\Phi }_{0}}\cos {{\Theta }_{0}}$

где индексом “0” обозначены начальные значения соответствующих переменных. Из соотношений для переменных r, k

${{r}^{2}} + {{k}^{2}} = r_{0}^{2} + k_{0}^{2},\quad {{r}^{2}} - {{k}^{2}} = (r_{0}^{2} + k_{0}^{2})\cos \Phi ,\quad 2rk = (r_{0}^{2} + k_{0}^{2})\sin \Phi $

выражаем r и k через $\Phi $

(3.4)

$\begin{gathered} r = \frac{1}{2}\sqrt {r_{0}^{2} + k_{0}^{2}} \left( {\sqrt {1 + \sin \Phi } + \sqrt {1 - \sin \Phi } } \right) \\ k = \frac{1}{2}\sqrt {r_{0}^{2} + k_{0}^{2}} \left( {\sqrt {1 + \sin \Phi } - \sqrt {1 - \sin \Phi } } \right) \\ \end{gathered} $

Зависимость от времени $\Phi (t{\text{'}})$ можно найти из уравнения ${{d}^{2}}\sin \Phi {\text{/}}d{{t}^{{'2}}} + \sin \Phi = 0$, которое получается так. Преобразуем вторую производную $\sin \Phi $ с помощью уравнений (3.2) и интеграла (3.3).

$\begin{array}{*{20}{c}} {\frac{{{{d}^{2}}\sin \Phi }}{{d{{{t'}}^{2}}}} = \frac{d}{{dt}}(\cos \Phi ( - \sin \Theta )) = - \cos {{\Phi }_{0}}\cos {{\Theta }_{0}}\frac{d}{{dt}}{\text{tg}}\,\Theta = } \\ { - \;\frac{{\cos \Phi \cos \Theta }}{{{{{\cos }}^{2}}\Theta }}{\text{tg}}\,\Phi \cos \Theta = - \sin \Phi } \end{array}$

Решение этого уравнения имеет вид $\sin \Phi = a\cos t{\text{'}} + b\sin t{\text{'}}$. Выразив постоянные $a$ и $b$ через начальные данные, получим

(3.5)

$\begin{gathered} \sin \Phi = \sin {{\Phi }_{0}}\cos t{\text{'}} - \cos {{\Phi }_{0}}\sin {{\Theta }_{0}}\sin t{\text{'}} \\ \sin {{\Phi }_{0}} = \frac{{2{{r}_{0}}{{k}_{0}}}}{{r_{0}^{2} + k_{0}^{2}}},\quad \cos {{\Phi }_{0}} = \frac{{r_{0}^{2} - k_{0}^{2}}}{{r_{0}^{2} + k_{0}^{2}}} \\ \end{gathered} $

Из уравнения (3.2) для $\tau $ с помощью (3.3) найдем

После подстановки выражения (3.5) интеграл вычисляется

(3.6)

${\tau } = - \frac{1}{2}{\text{ arctg}}\left[ {\frac{{{{{\left( {\sin {{\Phi }_{0}}} \right)}}^{2}} + {{{\left( {\cos {{\Theta }_{0}}} \right)}}^{2}}{{{\left( {\cos {{\Phi }_{0}}} \right)}}^{2}}}}{{\cos {{\Theta }_{0}}\cos {{\Phi }_{0}}}}{\text{tg}}t{\text{'}} + \sin {{\Phi }_{0}}{\text{tg}}{{\Theta }_{0}}} \right]$

Таким образом, найдены все зависимости от времени $t{\text{'}} = {\varepsilon }ht$: зависимости $\Phi (t{\text{'}})$ и $\Phi (t{\text{'}})$ находятся по (3.5) и (3.3) соответственно, зависимости $r(t{\text{'}})$ и $k(t{\text{'}})$ находятся подстановкой (3.5) в (3.4) и зависимость $\tau (t{\text{'}})$ находится по формуле (3.6).

Функцию $\tau (t{\text{'}})$ удобно выразить через функцию $T(t{\text{'}})$ так: $\tau (t{\text{'}}) = \frac{1}{2}t{\text{'}}\sigma + T(t{\text{'}})$, где $\sigma = {\text{sign}}[{\text{cos}}{{\Theta }_{0}}{\text{cos}}{{\Phi }_{0}}]$, а функция $T(t{\text{'}})$ имеет период равный $\pi $.

Все параметры орбиты претерпевают весьма сложное изменение, но через каждый период повторяются. Для функций $r$ и $k$ период равен $2\pi {\text{/}}(\varepsilon h)$, а для $\Theta $ и $T$ период в два раза меньше.

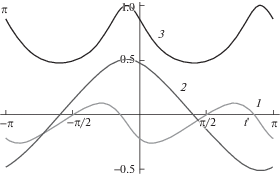
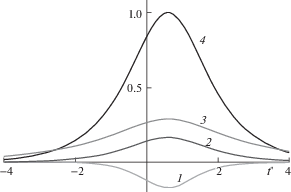
На рис. 2 изображены графики функций $T(t{\text{'}}) - 1$, $k(t{\text{'}}) - 2$, $\cos \Theta (t{\text{'}}) - 3$ при ${{\Phi }_{0}} = 1$, ${{\Theta }_{0}} = 0.5$. Они обозначены цифрами 1, 2 и 3 соответственно.

Рис. 2

Отдельно рассмотрим вырожденный случай $\Theta = {\pi /}2$, ${\tau } = {{{\tau }}_{0}}$, $\Phi = {{\Phi }_{0}} - t{\text{'}}$,

$\begin{gathered} r = \frac{1}{2}\sqrt {r_{0}^{2} + k_{0}^{2}} \left( {\sqrt {1 + \sin ({{\Phi }_{0}} - t{\text{'}})} + \sqrt {1 - \sin ({{\Phi }_{0}} - t{\text{'}})} } \right) \\ k = \frac{1}{2}\sqrt {r_{0}^{2} + k_{0}^{2}} \left( {\sqrt {1 + \sin ({{\Phi }_{0}} - t{\text{'}})} - \sqrt {1 - \sin ({{\Phi }_{0}} - t{\text{'}})} } \right) \\ \end{gathered} $

Начальное значение ${{\Phi }_{0}}$ находится из уравнений $\cos {{\Phi }_{0}} = \frac{{{{r}_{0}}}}{{\sqrt {r_{0}^{2} + k_{0}^{2}} }}$, sinΦ₀ = $\frac{{{{k}_{0}}}}{{\sqrt {r_{0}^{2} + k_{0}^{2}} }}.$

4. Эволюция системы под действием сил $G\dot {q}$. Систему уравнений можно записать в комплексной форме

(4.1)

$\begin{gathered} \dot {r} + i\dot {k} = \frac{1}{2}{\varepsilon }g\cos 2({\theta } - {\beta })(r - ik) \\ {\dot {\theta }} = \frac{1}{2}{\varepsilon }g\frac{{{{r}^{2}} + {{k}^{2}}}}{{{{k}^{2}} - {{r}^{2}}}}\sin 2({\theta } - {\beta }),\quad {\dot {\tau }} = - {\varepsilon }g\frac{{rk}}{{{{k}^{2}} - {{r}^{2}}}}\sin 2({\theta } - {\beta }) \\ \end{gathered} $

От переменных r, k, $\theta $ перейдем к новым переменным $\rho $, $\Phi $, $\Theta $ с помощью замен

(4.2)

$\begin{array}{*{20}{c}} {r + ik = {\rho }{{e}^{{i\Phi /2}}},\quad \Theta = 2({\theta } - {\beta }),\quad t{\text{'}} = {\varepsilon }gt} \end{array}$

Отсюда следуют соотношения

$\begin{array}{*{20}{c}} {\frac{{d{\rho }}}{{dt{\text{'}}}} + \frac{1}{2}i{\rho }\frac{{d\Phi }}{{dt{\text{'}}}} = \frac{1}{2}{\rho }\cos \Theta {{e}^{{ - i\Phi }}}} \\ {{\text{tg}}\,\Phi = \frac{{2rk}}{{{{r}^{2}} - {{k}^{2}}}},\quad \frac{{{{r}^{2}} + {{k}^{2}}}}{{{{r}^{2}} - {{k}^{2}}}} = \frac{1}{{\cos \Phi }}} \end{array}$

(4.3)

$r = {\rho }\cos (\Phi {\text{/}}2),\quad k = {\rho }\sin (\Phi {\text{/}}2)$

с помощью которых система уравнений (3.1) в новых переменных принимает вид

(4.4)

$\begin{gathered} \frac{{d{\rho }}}{{dt{\text{'}}}} = \frac{1}{2}{\rho }\cos \Theta \cos \Phi ,\quad \frac{{d\Phi }}{{dt'}} = - \cos \Theta \sin \Phi \\ \frac{{d\Theta }}{{dt{\text{'}}}} = - \frac{{\sin \Theta }}{{\cos \Phi }},\quad 2\frac{{d{\tau }}}{{dt'}} = \sin \Theta {\text{tg}}\Phi \\ \frac{{dr}}{{dt{\text{'}}}} = \frac{1}{2}r\cos \Theta ,\quad \frac{{dk}}{{dt{\text{'}}}} = - \frac{1}{2}k\cos \Theta \\ \end{gathered} $

Безразмерное время $t{\text{'}}$ меняется в пределах $(0,\infty )$ при g > 0 и $(0, - \infty )$ при g < 0.

Система уравнений (4.4) имеет интегралы

(4.5)

$rk = {{r}_{0}}{{k}_{0}} \Rightarrow {{{\rho }}^{2}}\sin \Phi = {\rho }_{0}^{2}\sin {{\Phi }_{0}},\quad \sin \Theta {\text{ctg}}\,\Phi = \sin {{\Theta }_{0}}{\text{ctg}}\,{{\Phi }_{0}}$

где индексом “0” обозначены начальные значения соответствующих функций.

C помощью последнего интеграла можно в уравнении для Φ исключить $\Theta $

$\frac{{d\sin \Phi }}{{dt{\text{'}}}} = - \sin \Phi \cos \Phi \cos \Theta = - \sigma \sin \Phi \sqrt {1 - {{s}^{2}}{{{\sin }}^{2}}\Phi } $

$s = \sqrt {1 + {{{\left( {\sin {{\Theta }_{0}}{\text{ctg}}\,{{\Phi }_{0}}} \right)}}^{2}}} ,\quad \sigma = {\text{sign}}(\cos {{\Phi }_{0}}\cos {{\Theta }_{0}})$

Общее решение этого уравнения

(4.6)

$\sin \Phi = \pm {{(s{\text{ch}}\,(t{\text{'}} \pm {{t}_{0}}))}^{{ - 1}}}$

Из начального условия получаем уравнение $\sin {{\Phi }_{0}} = {{(s\,{\text{ch}}\,(\sigma {{t}_{0}}))}^{{ - 1}}}$. Из него находится положительное значение постоянной t₀. Знаки в решении (4.6) выбираются так. Первый знак должен совпадать со знаком $\sin {{\Phi }_{0}}$. Знак при t₀ положителен, если производная функции ${{{\text{(sin}}\Phi (t{\text{'}}))}^{2}}$ при $t{\text{'}} = 0$ отрицательна, в противном случае знак отрицательный. Знак производной функции ${{(\sin \Phi (t{\text{'}}))}^{2}}$ совпадает со знаком числа $ - {\text{cos}}{{\Phi }_{0}}{\text{cos}}{{\Theta }_{0}}$. С учетом выбора знаков решение (4.6) можно представить в виде

(4.7)

$\sin \Phi = {\text{sign}}(\sin {{\Phi }_{0}}){{\left[ {s\,{\text{ch}}(t{\text{'}} + {\text{sign}}(\cos {{\Phi }_{0}}\cos {{\Theta }_{0}}){{t}_{0}})} \right]}^{{ - 1}}}$

Если знак ${\text{sign}}(\cos {{\Phi }_{0}}\cos {{\Theta }_{0}}) = - 1$ отрицателен и g > 0, то все функции меняются не монотонно, достигая следующих максимальных значений в точке $t = {{t}_{0}}$

(4.8)

$\begin{gathered} \sin \Phi ({{t}_{0}}) = 1{\text{/}}s,\quad \sin {{\Theta }_{0}} = 1, \\ r({{t}_{0}}) = \sqrt {\frac{{{{r}_{0}}{{k}_{0}}}}{{s + \sqrt {{{s}^{2}} - 1} }}} ,\quad 2\tau {\text{'}}({{t}_{0}}) = \frac{{{\text{sign}}(\sin {{\Theta }_{0}}{\text{ctg}}\,{{\Phi }_{0}})}}{{\sqrt {{{s}^{2}} - 1} }} \\ \end{gathered} $

Через функцию sinΦ выражаются все элементы орбиты. Из интегралов (4.5) находим

${\rho } = {{{\rho }}_{0}}\sqrt {\sin {{\Phi }_{0}}{\text{/sin}}\Phi } ,\quad \sin \Theta = \sin {{\Theta }_{0}}{\text{ctg }}{{\Phi }_{0}}{\text{tg }}\Phi $

Переменные r и k находим из (4.3)

$k = \sqrt {{{r}_{0}}{{k}_{0}}\left| {{\text{tg}}(\Phi {\text{/}}2)} \right|} ,\quad r = \sqrt {{{r}_{0}}{{k}_{0}}\left| {{\text{ctg}}(\Phi {\text{/}}2)} \right|} $

которые можно выразить через функцию времени sinΦ, определяемой по (4.7)

$\begin{gathered} k = \sqrt {\frac{{{{r}_{0}}{{k}_{0}}\left| {\sin \Phi } \right|}}{{1 + \cos \Phi }}} = \sqrt {\frac{{{{r}_{0}}{{k}_{0}}\left| {\sin \Phi } \right|}}{{1 - \cos \Phi }}} \\ r = \sqrt {\frac{{{{r}_{0}}{{k}_{0}}(1 - \cos \Phi )}}{{\left| {\sin \Phi } \right|}}} = \sqrt {\frac{{{{r}_{0}}{{k}_{0}}(1 + \cos \Phi )}}{{\left| {\sin \Phi } \right|}}} \\ \end{gathered} $

Из этого решения следует, что площадь эллиптической орбиты сохраняется, эллипс вытягивается в бесконечную прямую, а угол наклона к оси x большей полуоси эллиптической орбиты r стремится к нулю.

Уравнение для τ также интегрируется, откуда находится

$2{\tau } = \frac{{{\text{tg}}{{\Phi }_{0}}}}{{{\text{sin}}{{\Theta }_{0}}}}{\text{arctg}}\left( {\frac{{{\text{tg}}{{\Phi }_{0}}}}{{{\text{sin}}{{\Theta }_{0}}}}{\text{th}}(t{\text{'}} \pm {{t}_{0}})} \right)$

На рис. 3 представлены графики зависимостей

$2{\tau '}(t{\text{'}}) = \sin \Theta (t{\text{'}}){\text{tg}}\Phi (t{\text{'}}),\quad k(t{\text{'}}),\quad \sin \Theta (t{\text{'}}),\quad \sin \Phi (t{\text{'}})$

при значениях параметров ${{\Theta }_{0}} = 1$, ${{\Phi }_{0}} = 3$. Они помечены цифрами 1, 2, 3, 4 соответственно.

Рис. 3

При $g > 0$ функции меняются на отрезке $(0,\infty )$, а при $g < 0$ – на отрезке $(0, - \infty )$.

При $t = {{t}_{0}} = 0.597$ они достигают экcтремума.

Экстремальные значения, вычисленные по формулам (18) таковы

$\sin \Phi ({{t}_{0}}) = 0.167,\quad \sin {{\Theta }_{0}} = 1,\quad r({{t}_{0}}) = 0.29,\quad 2\tau {\text{'}}({{t}_{0}}) = - 0.169$

Как при положительном так и при отрицательном значениях g при $t \to \infty $ полуоси эллипса стремятся принять направления декартовых осей ${{q}_{1}}$ и ${{q}_{2}}$, одна из осей стремится к нулю, а вторая растет до бесконечности. Площадь эллипса при этом сохраняется.

5. Заключение. К чистым эволюциям формы колебаний приводят четыре типа сил.

1. Потенциальные силы сферического типа Cq приводят только к изменению частоты $1 \to 1 - (1{\text{/}}2)c{\varepsilon }$.

2. Циркулярные силы Nq приводят только к изменению осей эллипса

$r = {{r}_{0}}{\text{сh}}(n{\varepsilon }t{\text{/}}2) - {{k}_{0}}{\text{sh}}(n{\varepsilon }t{\text{/}}2),\quad k = {{k}_{0}}{\text{сh}}(n{\varepsilon }t{\text{/}}2) - {{r}_{0}}{\text{sh}}(n{\varepsilon }t{\text{/}}2)$

3. Диссипативные (или ускоряющие) силы $D\dot {q}$ также приводят только к изменению осей эллипса

$r = {{r}_{0}}{\mkern 1mu} {{e}^{{d{\varepsilon }t/2}}},\quad k = {{k}_{0}}{\mkern 1mu} {{e}^{{d{\varepsilon }t/2}}}$

4. Гироскопические силы приводят только к прецессии формы колебаний θ = θ₀ + + $\frac{1}{2}({{k}^{2}} - {{r}^{2}}){\gamma \varepsilon }t$.

Если возникает задача управления формой колебаний, то именно эти силы и следует выбирать для управления соответствующими эволюциями формы. Все эти результаты приведены в [1, 3, 4].

Гиперболические силы $Hq$ и $G\dot {q}$ в общем случае описываются достаточно сложной нелинейной системой дифференциальных уравнений. Решение их в общем случае представлено в элементарных функциях. Для сил $Hq$ функция sinΦ меняется по гармоническому закону и через нее выражены все элементы орбиты: полуоси эллипса по формулам (3.4), его площадь меняется по гармоническому закону $2rk = (r_{0}^{2} + k_{0}^{2})$sinΦ, угол прецессии ${\theta }$ выражается через функцию Φ по формулам $\Theta = 2({\theta } - {\alpha })$, cosΦcosΘ = = $cos{{\Phi }_{0}}cos{{\Theta }_{0}}$. Все элементы орбиты меняются по периодическому закону с периодом $2{\pi /}({\varepsilon }h)$.

Из решения задачи о движении системы под действием силы Gq следует, что площадь эллиптической орбиты сохраняется, эллипс вытягивается в бесконечную прямую, а угол наклона к оси $q$ большей полуоси эллиптической орбиты $r$ стремится к нулю.

Работа выполнена в рамках госзадания (номер госрегистрации АААА-А20-120011690138-6).

Таблица 1

	$Cq$	$Hq$	$Nq$	$D\dot {q}$	$G\dot {q}$	$Г\dot {q}$
$\dot {r}$	0	$\frac{1}{2}hk{\varepsilon }\sin (2({\theta } - {\alpha }))$	$ - \frac{{kn{\varepsilon }}}{2}$	$\frac{{dr{\varepsilon }}}{2}$	$\frac{1}{2}gr{\varepsilon }\cos (2({\theta } - {\beta }))$	0
$\dot {k}$	0	$ - \frac{1}{2}hr{\varepsilon }\sin (2({\theta } - {\alpha }))$	$ - \frac{{rn{\varepsilon }}}{2}$	$\frac{{dk{\varepsilon }}}{2}$	$ - \frac{1}{2}gk{\varepsilon cos(2(\theta } - {\beta ))}$	0
$\dot {\theta }$	0	$ - hkr{\varepsilon }\frac{{\cos (2({\theta } - {\alpha }))}}{{{{k}^{2}} - {{r}^{2}}}}$	0	0	$\frac{1}{2}g{\varepsilon }\frac{{{{k}^{2}} + {{r}^{2}}}}{{{{k}^{2}} - {{r}^{2}}}}\sin (2({\theta } - {\beta }))$	$ - \frac{1}{2}{\gamma \varepsilon }$
$\dot {\tau }$	$ - \frac{1}{2}c{\varepsilon }$	$\frac{1}{2}h{\varepsilon }\frac{{{{r}^{2}} + {{k}^{2}}}}{{{{k}^{2}} - {{r}^{2}}}}\cos (2({\theta } - {\alpha }))$	0	0		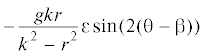0

Список литературы

Журавлев В.Ф. Управляемый маятник Фуко как модель одного класса свободных гироскопов// МТТ. 1997. Вып 6. С. 27–35.
Friedland B., Hulton M.F. Theory and error analysis of vibrating-member gyroscope // IEEE Trans. on Autom. Contr. 1978. V. 23. № 4. P. 545–556.
Климов Д.М., Журавлев В.Ф., Жбанов Ю.К. Кварцевый полусферический резонатор (Волновой твердотельный гироскоп). М.: Изд-во “Ким Л.А.” 2017. 194 с.
Журавлев В.Ф., Петров А.Г., Шундерюк М.М. Избранные задачи гамильтоновой механики. М.: ЛЕНАНД, 2015. 304 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика твердого тела

Архивы выпусков Информация о журнале Отправить рукопись в журнал