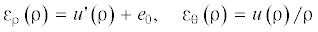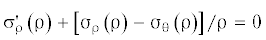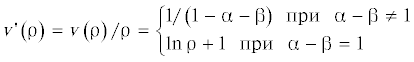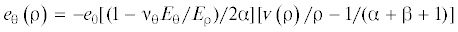Известия РАН. Механика твердого тела, 2021, № 2, стр. 31-41

Введение. Сильфон, как его определяет энциклопедия, это – тонкостенная (обычно металлическая) цилиндрическая оболочка с поперечной гофрированной боковой поверхностью. Сильфон расширяется или сжимается вдоль оси (подобно пружине) под действием разности давления внутри и снаружи или от внешнего силового воздействия. Применяется в пневмоавтоматике (как чувствительный орган), для гибкого соединения трубопроводов, для амортизации и др. Именно таким мы будем представлять себе сильфон. Но если предлагаемые заводами-изготовителями сильфоны являются, как правило, цельнометаллическими конструкциями из однородного и изотропного материала, то мы будем рассматривать сильфон как композиционную конструкцию, элементы которой изготовлены из композиционного материала. Причем такую пространственную конструкцию, которая может быть использована как гражданское или промышленное сооружение большой высоты и, вообще, большого объема. Забегая вперед скажем, что главным преимуществом предлагаемой конструкции является отсутствие изгибаемых, скручиваемых или сложно нагружаемых несущих элементов конструкции – все несущие элементы конструкции под действием внешней осевой нагрузки работают полным поперечным сечением только на растяжение или сжатие.

Мысль о потребности композиционного сильфона возникла у автора этих строк, когда в одной из телевизионных передач был показан американский научно-исследовательский аппарат, работающий на Марсе. Довольно заметную часть этого аппарата занимало нечто, имеющее вид сильфона. Все агрегаты и конструкции, связанные с космическими исследованиями, должны подчиняться жестким требованиям прочности, устойчивости к сохранению формы, заданной степени деформируемости и при этом быть минимизированы по весу. Такая оптимизационная задача для такой геометрически сложной конструкции, как сильфон, с таким большим количеством параметров оптимизации может быть решена только как композиционная конструкция из композиционных материалов. Теоретическое решение такой задачи с построением минимизирующей функции в общем случае не представляется возможным. Разве что, для какого-то частного случая с существенными упрощениями. Мы не ставим перед собой такой задачи. Целью предлагаемой работы являются расчеты на прочность и жесткость отдельных элементов конструкции композиционного сильфона. При оптимизации сильфона методом вариантного проектирования возможность рассчитывать элементы конструкции на прочность и жесткость многократно сокращают трудозатраты оптимизации и поэтому расчеты на прочность и жесткость могут быть признаны главными при проектировании оптимального композиционного сильфона.

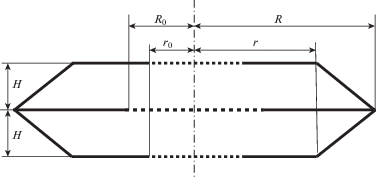
Конструкция сильфона. Мы будем рассматривать сильфон в виде конструкции, состоящей из некоторого числа одинаковых конструкционных фрагментов, которые условимся называть сильфониками. На рис. 1 изображена расчетная схема сильфоника. Каждый сильфоник имеет форму двояковыпуклой симметричной линзы. Поверхности такой линзы имеют вид круговых прямых усеченных конусов, полученных вращением вокруг оси конуса наклонного отрезка прямой линии. Мы будем называть боковые поверхности конусов оболочками сильфоника. Оболочки каждого сильфоника шарнирно соединены друг с другом краями своих больших оснований. Внутри сильфоника к соединению краев его оболочек шарнирно крепится кольцевая пластина, выполняющая роль диафрагмы. Эту пластину мы назовем большой диафрагмой, а отверстие в ней, край которого является окружностью, концентрической внешнему краю, назовем отверстием большой диафрагмы. Все сильфоники шарнирно соединены друг с другом краями меньших оснований своих оболочек. Внутри сильфона к соединению сильфоников шарнирно крепится еще одна кольцевая пластина, выполняющая роль диафрагмы, разделяющей два соседних сильфоника. Эту диафрагму мы назовем малой диафрагмой, а отверстие в ней, край которого является окружностью, концентрической внешнему контуру малой диафрагмы, – отверстием в малой диафрагме. Мы примем, что крайние сильфоники всего сильфона на концевых сторонах имеют малую диафрагму с отверстием такой же формы и размеров и сделаны из того же материала, что и внутренние малые диафрагмы, но имеют половинную толщину.

Геометрические характеристики сильфона: $r$ – радиус окружности малого основания оболочки, $R$ – радиус окружности большого основания оболочки, $H$ – высота оболочки – расстояние между большим и малым ее основаниями, ${{r}_{0}}$ – радиус отверстия в малой диафрагме, ${{R}_{0}}$ – радиус отверстия в большой диафрагме, $h$ – толщина оболочки, ${{h}_{r}}$ – толщина малой диафрагмы, ${{h}_{R}}$ – толщина большой диафрагмы.

Поместим одну оболочку сильфоника в цилиндрические координаты ${\rho ,\theta },z$ так, чтобы ось вращения оболочки совместилась с координатной осью z, а ее большое основание при этом совместилось с плоскостью полярных координат ρ, θ (ρ – полярный радиус, θ – угол направления полярного луча). Таким образом,

Условимся, что нижний индекс ρ обозначает радиальное направление, а нижний индекс ${\theta }$ обозначает тангенциальное направление.

Деформационные характеристики ортотропного сильфона:

${{E}_{{\rho }}},\;{{E}_{{\theta }}},\;{{{\nu }}_{{\rho }}}{\text{,}}\;{{{\nu }}_{{\theta }}}$ – модули нормальной упругости и коэффициенты поперечной деформации оболочки,

$E_{{\rho }}^{r},\;E_{{\rho }}^{r},\;{\nu }_{{\rho }}^{r},\;\nu _{{\theta }}^{r}$ – модули нормальной упругости и коэффициенты поперечной деформации малой диафрагмы,

$E_{{\rho }}^{R},\;E_{{\rho }}^{R},\;{\nu }_{{\rho }}^{R},\;{\nu }_{{\theta }}^{R}$ – модули нормальной упругости и коэффициенты поперечной деформации большой диафрагмы.

1. Постановка задачи. Задачу о напряженно-деформированном состоянии всего сильфона мы сведем к расчету напряженно-деформированного состояния отдельных элементов сильфоника – оболочки, малой и большой диафрагм. При этом задача будет решаться в три этапа.

1-й этап. Рассматривается такое продольно-осевое сжатие сильфона внешними силами, когда все сильфоники, составляющие сильфон, превратятся в пластины. Иначе говоря, когда все оболочки всех сильфоников сплющатся в пластины. Ясно, что все перечисленные элементы каждого сильфоника окажутся при этом в осесимметричном состоянии. Это состояние мы будем полагать плоским напряженным состоянием. Это соответствует предположению, что в процессе эксплуатации сильфона он не будет подвергаться сжатию, требующему рассмотрения пространственного напряженного состояния его элементов.

Подчеркнем, что все расчеты будут выполняться в предположении, что все элементы конструкции и физически и геометрически сохраняют линейно упругую деформируемость. В рамках принятых гипотез получаемое решение при этом является точным.

Обратим внимание также, что мы исключаем возможность эксплуатации сильфона на растяжение. Принятая постановка задачи имеет эксплуатационный смысл только при работе сильфона на сжатие.

Читатель не найдет в списке цитируемой литературы ссылки на работы авторов, которые являлись бы прямо или косвенно предтечей работ [1, 2], выполненных автором настоящей статьи в 2008 году. Мысли о трансформировании пологой оболочки вращения в круглую пластину впервые возникли в далеком 1971 году. Тогда казалось маловероятным, что эта задача еще не решена. Уверенность, что это именно так, в результате упорных поисков, была обретена лишь спустя 37 лет.

2-й этап. Вычисляется предельное значение силы, сжимающей сильфон, до которой нагружение сильфона происходит в режиме устойчивого равновесия. На этом этапе в рамках принятых упрощений решение также является точным [3].

3-й этап. Квадратичной аппроксимацией крайних в процессе нагружения сильфона значений напряженно-деформированного состояния получается закон текущих значений напряженно-деформированного состояния от начала нагружения до предельного значения сжимающей сильфон силы.

Радиальное перемещение, деформации и напряжения во всех элементах сильфона мы условимся обозначать одинаково: u(ρ) – перемещение; ${{{\varepsilon }}_{{\rho }}}\left( {\rho } \right),\;{{{\varepsilon }}_{{\theta }}}\left( {\rho } \right)$ – радиальные и тангенциальные деформации; ${{{\sigma }}_{{\rho }}}\left( {\rho } \right),\;{{{\sigma }}_{{\theta }}}\left( {\rho } \right)$ – радиальные и тангенциальные напряжения.

2. Мембранные усилия в оболочке, трансформированной в пластину. При трансформировании конической оболочки в пластину радиальная деформация ε_ρ складывается из двух деформаций: из деформации сжатия ${{e}_{0}}$ меридиана оболочки до ширины кольца $R - r$, представляющего собой проекцию оболочки на плоскость координат ρ, θ, и из радиальной деформации u(ρ) от осесимметричного смещения точек этого кольца, которая равна $u{\kern 1pt} '\left( {\rho } \right)$.

Дифференциал длины дуги меридиана оболочки

является начальной длиной деформируемого элемента dl меридиана оболочки, а дифференциал dρ является результатом его укорочения, т.е. является конечной длиной деформируемого элемента. Относительная деформация сжатия e₀ меридиана до длины $R - r$ определяется отношением приращения длины $d{\rho } - dl$ деформируемого элемента к его первоначальной длине dl:

Тангенциальная деформация ${{{\varepsilon }}_{{\theta }}}\left( {\rho } \right)$ является следствием только осесимметричного смещения точек кольца u(ρ) и, следовательно, равна 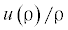. Таким образом, относительные радиальная и тангенциальная деформации кольца, представляющего собой проекцию усеченного конуса на плоскость его основания, определяются формулами:

По закону Гука при плоском напряженном состоянии для осесимметрично деформированной круглой пластины, когда оси изотропии совпадают с координатными линиями, мы имеем

Осесимметричное плоское напряженное состояние описывается одним уравнением равновесия

Исключив в уравнении (2.4) напряжения подстановкой (2.3), а потом деформации подстановкой (2.2), получим разрешающее дифференциальное уравнение в перемещениях

Уравнение (2.5) является неоднородным уравнением Эйлера [4]. Однородное уравнение с каноническими коэффициентами

является разрешающим уравнением осесимметричной задачи теории упругости, называемой задачей Ламе. Отсюда видно, что задача Ламе является частным случаем решаемой здесь задачи.

Общее решение уравнения Эйлера (2.5), полученное методом вариации произвольных постоянных, имеет вид

где ${{C}_{1}},\;{{C}_{2}}$ – произвольные постоянные и

Чтобы избежать громоздких формул, введем дополнительные функции

Используя эти функции и перемещения (2.6), по формулам (2.2) запишем деформации оболочки

Подставив эти деформации в формулы закона Гука (2.3), мы получим напряжения

где

3. Мембранные усилия в малой диафрагме. Внутрь малого основания оболочки вставлена упругая пластина толщиной, равной полутолщине малой диафрагмы ${{h}_{r}}{\text{/}}2$, и шарнирно соединена с краем основания оболочки. Перемещения и напряжения в малой пластине являются осесимметричными, как и у оболочки. Поэтому перемещения, деформации и напряжения описываются формулами (2.6), (2.7), (2.8), в которых ${{e}_{0}} \equiv 0$:

где $C_{1}^{r},\;C_{2}^{r}$ – произвольные постоянные, и

4. Мембранные усилия в большой диафрагме. Внутрь большого основания оболочки вставлена упругая пластина толщиной, равной полутолщине большой диафрагмы ${{h}_{R}}{\text{/}}2$, и шарнирно соединена с краем основания. Перемещения и напряжения в большой пластине являются осесимметричными, как и у оболочки. Поэтому перемещения, деформации и напряжения описываются формулами (2.6), (2.7), (2.8), в которых ${{e}_{0}} \equiv 0$:

где $C_{1}^{R},\;C_{2}^{R}$ – произвольные постоянные, и

5. Граничные условия сплющенного сильфоника. Внутренний контур малой диафрагмы свободен от внешних воздействий. Поэтому ${{{\sigma }}_{{\rho }}}\left( {{{r}_{0}}} \right) = 0.$ Это условие дает

С учетом этого можно записать:

При сплющивании в сильфоне всех сильфоников в пластину малые диафрагмы сильфона оказываются объятыми кольцевыми пластинами, в которые превращаются оболочки. Поэтому в расчетной схеме шарнирное соединение малой пластины с краем малого основания оболочки мы принимаем такое, что нормальные напряжения σ_ρ по контакту пластины и оболочки равны и имеют одинаковые знаки.

Внутренний контур большой диафрагмы свободен от внешних воздействий. Поэтому ${{{\sigma }}_{{\rho }}}\left( {{{R}_{0}}} \right) = 0.$ Это условие дает

С учетом этого можно записать:

При сплющивании сильфона его большие диафрагмы осесимметрично растягиваются краями больших оснований оболочек сильфоника. А так как оболочки проецируются на большие диафрагмы, то в расчетной схеме мы принимаем, что шарнирное соединение большой пластины с краем большого основания оболочки такое, что нормальные напряжения σ_ρ по контакту пластины и оболочки равны по абсолютной величине, но имеют разные знаки: край оболочки сжат, а край большой пластины растянут.

По контакту пластин со сплющенной оболочкой выполняются условия непрерывности радиальных смещений и условия непрерывности радиальных усилий. Отсутствие силовых факторов на внутренних контурах диафрагм мы уже учли. Поэтому перечисленные граничные условия выражаются четырьмя равенствами, которые образуют систему четырех линейных алгебраических уравнений с четырьмя неизвестными: ${{C}_{1}},{{C}_{2}},C_{1}^{r},C_{1}^{R}$. Запишем ее в матричной форме

Ненулевые элементы матриц этой системы уравнений:

Решение этой системы уравнений открывает возможность вычисления перемещений деформаций и напряжений всех элементов расчетной схемы от действия мембранных усилий в сильфонике, трансформированном в пластину.

Обратим внимание, что результаты этих расчетов могут существенно превосходить пределы упругости применяемых в конструкции материалов. Однако это не должно быть основанием, чтобы признать их ошибочными. Следует вспомнить, что мы гипотетически приняли неограниченную упругость, имея при этом в виду, что рабочая нагрузка на сильфон будет меньше нагрузки, при которой все сильфоники сплющиваются.

6. Предельное нагружение сильфона. Гипотетически мы примем, что в процессе трансформирования оболочки в кольцевую пластину прямолинейные образующие конуса остаются прямолинейными. Иными словами, мы будем считать, что потеря устойчивости формы оболочки прогибом ее стенки не наблюдается.

Пусть ${{F}_{*}}$ – такое значение силы F, под действием которой оболочка в форме кругового усеченного конуса с прямолинейными образующими может сохранять первоначальную форму, но при увеличении ${{F}_{*}}$ на как угодно малую величину выпуклость конуса может скачкообразно выгнуться в противоположную сторону. Произойдет прощелкивание оболочки. Мы назовем силу ${{F}_{*}}$ критической силой прощелкивания.

Пусть ${\xi }$ является тем текущим значением длины, на которое уменьшилось начальное расстояние между основаниями конуса под действием переменной силы F. Очевидно, что при трансформировании конуса в пластину значение ${\xi }$ изменяется от 0 до H.

Мы обозначим ${\xi }_{*}^{{}}$ – такое значение ${\xi } \in \left( {0,\;H} \right)$, при котором F равно ${{F}_{*}}$.

Трансформирование конической оболочки в круглую кольцевую пластину будем осуществлять путем увеличения ${\xi }$ не простым увеличением нагрузки на оболочку, а специальным методом нагружения, называемым нагружением перемещением.

Нагружение перемещением характеризуется следующими особенностями: 1) перемещение ${\xi }$ монотонно увеличивается в течение всего процесса нагружения перемещением; 2) сила F увеличивается от начала нагружения до значения ${{F}_{*}}$ и уменьшается от ${{F}_{*}}$ до нуля; 3) оболочка остается в статическом равновесии все время нагружения.

Такое нагружение можно осуществить, если оболочку сделать сжимаемым элементом какой-то статически неопределимой системы.

На первом этапе роста ${\xi }$ сила F увеличивается от F = 0 до $F = {{F}_{*}}$. Положительному приращению ${\xi }$ соответствует положительное приращение F: $\Delta {\xi } > 0,$ $\Delta F > 0$. Такое соотношение знаков приращений означает, что при $0 \leqslant {\xi } < {\xi }_{*}^{{}}$ оболочка находится в состоянии устойчивого равновесия.

На втором этапе роста ${\xi }$ сила F уменьшается от $F = F_{*}^{{}}$ при ${\xi } = {\xi }_{*}^{{}}$ до нуля при ${\xi } = H$. Такое изменение F будет очевидным, если заметить, что при ${\xi } = H$ оболочка становится пластиной, которая находится в состоянии безразличного равновесия. Но при безразличном равновесии пластины мы имеем F = 0. При ${\xi } > {\xi }_{*}^{{}}$ положительному приращению ${\xi }$ соответствует отрицательное приращение F: $\Delta {\xi } > 0,$ $\Delta F < 0$. Такое соотношение знаков приращений означает, что при ${\xi }_{*}^{{}} < {\xi } \leqslant H$ оболочка находится в состоянии неустойчивого равновесия. Неустойчивость является таким статическим равновесием оболочки под нагрузкой, при котором оболочка может сохранять начальную форму, но может также скачкообразно изменить направление выпуклости на противоположное.

Теперь рассмотрим поведение оболочки в двухсторонней окрестности точки ${\xi }_{*}^{{}}$. При ${\xi } < {\xi }_{*}^{{}}$ оболочка находится в состоянии устойчивого равновесия. При ${\xi } > {{{\xi }}_{*}}$ оболочка находится в состоянии неустойчивого равновесия. Следовательно, если ${\delta }F > 0$ суть как угодно малое приращение F, тогда при $F = F_{*}^{{}} + {\delta }F$ оболочка изменит направление выпуклости. Произойдет явление, которое называют прощелкиванием оболочки. Таким образом, сила ${{F}_{*}}$ является максимальным значением силы F, если начальная нагрузка удовлетворяет неравенству $F < F_{*}^{{}}$. Если начальное значение нагрузки удовлетворяет неравенству $F > F_{*}^{{}}$, то начальная нагрузка сразу вызовет прощелкивание оболочки. Поэтому ${{F}_{*}}$ является минимальной силой для любой силы $F \geqslant F_{*}^{{}}$, вызывающей прощелкивание оболочки. Таким образом, эксплуатационные нагрузки на оболочку сильфоника и, следовательно, на весь сильфон заключены в интервале от F = 0 до $F \leqslant F_{*}^{{}}$. Это дает основание называть ${{F}_{*}}$ критической силой сжатия сильфона.

7. Критическая сила сжатия сильфона. Исследование функциональной зависимости $F\left( {\xi } \right)$ является самостоятельной задачей. Природа зависимости $F\left( {\xi } \right)$ не вытекает из результатов, которые были получены в предыдущих разделах этой работы. В то же время зависимость $F\left( {\xi } \right)$ является необходимой для решения задачи о критической силе ${{F}_{*}}$. Поэтому мы вынуждены ограничиться приближенной зависимостью $F\left( {\xi } \right)$. Возьмем квадратичную аппроксимацию $F\left( {\xi } \right) = {{A}_{0}} + {{A}_{1}}{\xi } + {{A}_{2}}{{{\xi }}^{2}}$.

Как установлено выше,

Подчиняя квадратный трехчлен этим условиям, получаем

При трансформировании круглой конической оболочки сильфоника с прямолинейными образующими в круглую пластину равнодействующая сжимающих сил F(ξ) совершает работу

По формулам напряжений и деформаций элементов расчетной схемы, полученным выше, можно вычислить потенциальную энергию U упругой деформации всех элементов расчетной схемы: P – потенциальная энергия оболочки, трансформированной в кольцевую пластину; ${{P}^{r}}$ – потенциальная энергия малой пластины, которая равна малой диафрагме половинной толщины, и ${{P}^{R}}$ – потенциальная энергия большой пластины, которая равна большой диафрагме половинной толщины. Таким образом,

Работа $W$ силы $F$ в процессе трансформирования расчетной схемы в виде полусильфоника в плоское тело расходуется на создание вычисленной выше потенциальной энергии $U$. Поэтому $W = U$. Отсюда следует

8. Текущее напряженно-деформированное состояние сильфона. Мы будем рассматривать текущее состояние сильфона (будем считать сильфон практически применимым) в пределах ${\xi } \in (0,{\xi }_{*}^{{}})$, т.е. при сжатии сильфона докритической силой $F < F_{*}^{{}}$.

Значение критической силы мы вычисляем по формуле (7.2).

Пусть ${\Omega } = {\Omega }\left( {{\xi },{\rho }} \right)$ – матрица-столбец, элементами которой являются компоненты напряженно-деформированного состояния (перемещение, деформация, напряжение) любого из элементов сильфоника (оболочка, малая диафрагма, большая диафрагма).

Так как $F\left( 0 \right) = 0$, то ${\Omega }\left( {0,{\rho }} \right) = 0$.

В предыдущих параграфах мы вычислили все элементы матрицы ${\Omega }\left( {H,{\rho }} \right)$.

Если оболочка прощелкнет (сменит направление выгнутости), то она будет в напряженно-деформированном состоянии, описываемом матрицей ${\Omega }\left( {{\xi },{\rho }} \right)$ при ${\xi } < H$. Поэтому ${\xi } = H$ является точкой локального экстремума функций матицы ${\Omega }\left( {{\xi },{\rho }} \right)$. Следовательно, $\partial {\Omega }\left( {H,{\rho }} \right){\text{/}}\partial {\xi } = 0$.

Подчиняя квадратичную зависимость ${\Omega }\left( {{\xi },{\rho }} \right) = {{B}_{0}} + {{B}_{1}}{\xi } + {{B}_{2}}{{{\xi }}^{2}}$ выявленным условиям, получаем

При ${\xi } \to {\xi }_{*}^{{}} = H{\text{/}}2$ (7.1) напрbяженно-деформированное состояние сильфона стремится к своему практически предельному (но не допустимому) состоянию. Подставляя ${\xi } = H{\text{/}}2$ в формулу (8.1), мы получаем матрицу, элементы которой определяют это состояние

Формула (7.1) относительно ${\xi /}H$ представляет собой квадратное уравнение

Выше мы установили, что ${\xi } < H{\text{/}}2$. С учетом этого принимаем

Подставляя это выражение в (8.1), мы получаем формулу

которая определяет все компоненты напряженно-деформированного состояния любого элемента сильфоника как функции прямо пропорциональные функциям этих компонентов в сплющенном сильфонике. Коэффициент пропорциональности является функцией значений текущей нагрузки на сильфон $F \in (0,F_{*}^{{}})$. Ясно, что в записанной выше формуле оболочка сильфоника заменяется проекцией оболочки на координатную плоскость ρ, θ.

Заключение. Полученный метод расчета напряженно-деформированного состояния пространственной конструкции, имеющей вид сильфона, не дает основания предлагать варианты конкретного практического применения такой конструкции. Однако не требуется богатого воображения, чтобы утверждать, что рассматриваемый сильфон, как обоснованно рассчитанная на прочность и устойчивость вариантно минимизированная по массе упругая композиционная конструкция, может быть востребован в разнообразных средах от океанических глубин до безвоздушного пространства в космосе.