Известия РАН. Механика твердого тела, 2021, № 4, стр. 77-88
ИЗГИБ И УСТОЙЧИВОСТЬ КОНСОЛЬНОГО СТЕРЖНЯ ПОД ДЕЙСТВИЕМ ДАВЛЕНИЯ НА ЕГО ПОВЕРХНОСТИ И ПРОДОЛЬНОЙ СИЛЫ
a Институт машиноведения им. А.А. Благонравова РАН
Москва, Россия
b Институт механики УФИЦ РАН
Уфа, Россия
c Башкирский государственный университет
Уфа, Россия
* E-mail: ilgamov@anrb.ru
Поступила в редакцию 23.08.2020
После доработки 04.09.2020
Принята к публикации 29.10.2020
Аннотация
Линейный изгиб консольного стержня, находящегося под всесторонним давлением и продольной силой, рассматривается в статической и динамической постановках. Учитывается поперечная распределенная сила на стержень, возникающая при изгибе в результате образования разности площадей выпуклой и вогнутой частей поверхности. Сжимающая сила может быть неизменного направления и изменяющейся при изгибе. В частности следящая сила образуется в результате действия давления на концевое сечение стержня. Дается сравнение с классической задачей об устойчивости. Изучены особенности одновременного действия сил неизменного и изменяющегося направлений.
1. Введение. Как известно, устойчивость прямолинейной формы консольного стержня зависит от поведения продольной сжимающей силы. Имеется качественная разница в задаче его устойчивости при сжимающих силах неизменного направления и с поворотом направления в соответствии с ориентацией концевого поперечного сечения. “E.Л. Николаи был, по всей вероятности, первым, кто рассмотрел задачу об устойчивости упругой системы, нагруженной следящими силами …. В работе 1928 г. [1] исследуется устойчивость прямолинейной формы гибкого стержня, один конец которого защемлен, а другой – нагружен сжимающей силой …. Было установлено, что не существует никаких иных форм равновесия, кроме прямолинейной” – так начинается глава об устойчивости равновесия упругих систем при наличии следящих сил в книге [2]. В ней и в [3] излагается история этой задачи и ее особенности. К первым исследованиям в этом направлении относятся работы [4–6]. Динамический подход к задаче был предложен в [1–3] и далее развит в [7] и в последующих работах.
В уравнении изгибного движения стержня в одной из главных плоскостей инерции
(1.1)
$D\frac{{{{\partial }^{4}}w}}{{\partial {{x}^{4}}}} + P\frac{{{{\partial }^{2}}w}}{{\partial {{x}^{2}}}} + \rho F\frac{{{{\partial }^{2}}w}}{{\partial {{t}^{2}}}} = q$(1.2)
${{P}_{*}} \approx 2{{\pi }^{2}}{D \mathord{\left/ {\vphantom {D {{{L}^{2}}}}} \right. \kern-0em} {{{L}^{2}}}}$Начиная с обобщающих работ по теории тонких пластин и оболочек [8, 9] до недавней монографии [10] поперечная распределенная сила принимается равной q = p1 – р2, где p1 и р2– избыточные давления на поверхности, перпендикулярные плоскости изгиба. Эти давления p1 и p2 положительны, если общее давление превышает атмосферное давление p0, отрицательны при меньшем значении общего давления, чем p0. Учет разности площадей выпуклой и вогнутой поверхностей, появляющейся при изгибе стержня и цилиндрическом изгибе пластины, приводит к выражению [11, 12]
(1.3)
$q = {{p}_{1}} - {{p}_{2}} + {{p}_{m}}F\frac{{{{\partial }^{2}}w}}{{\partial {{x}^{2}}}},\quad {{p}_{m}} = \frac{{{{p}_{1}} + {{p}_{2}}}}{2}$Распределенная поперечная сила pmF(∂2w/∂x2) при pm > 0 направлена в сторону вогнутости, при рт < 0 (вакуумирование) – в сторону выпуклости. Из (1.1), (1.3) при p1 = = р2 (рт = р) и условиях свободного опирания обоих концов стержня следует статическое критическое значение [13, 14]
(1.4)
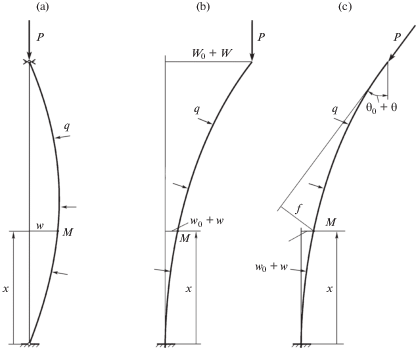
${{(P - pF)}_{*}} = {{{{\pi }^{2}}D} \mathord{\left/ {\vphantom {{{{\pi }^{2}}D} {{{L}^{2}}}}} \right. \kern-0em} {{{L}^{2}}}}$Таким образом, окружающее давление в этом примере приводит к увеличению критического значения сжимающей силы. При вакуумировании (р < 0) происходит его уменьшение. Это увеличение объясняется тем, что поперечная распределенная сила q (при р > 0) стремится уменьшить прогиб (рис. 1, а). Происходит увеличение эффективной изгибной жесткости. Если сила Р возникает в результате действия давления р на торцевое сечение площадью F (Р = pF), то стержень не теряет устойчивость прямолинейной формы. Этот результат, следующий из простейшей теории изгиба, согласуется с выводом об устойчивости упругой полосы под всесторонним давлением, полученным впервые в [15] исходя из соотношений теории упругости. Устойчивость стержня при гидростатическом давлении рассмотрена в [13]. Соответствующий обзор работ в этом направлении содержится в [14]. Поведение вращающегося консольного вала, находящегося под переменным по длине давлением, изучено в [16], а динамика трубчатого консольного стержня с истекающей жидкостью – в [17].
Насколько известно, влияние давления на боковую поверхность консольного стержня до сих пор изучено недостаточно. В данной статье рассматривается статическая и динамическая устойчивость консольного стержня в случае, когда кроме давления на его поверхность действует сжимающая сила неизменного направления или следящая сила.
2. Постановка задачи. Линейная задача о продольном изгибе консольного стержня под действием сжимающей силы рассматривается в случае всестороннего давления на его боковую поверхность. Сечение его имеет форму круга или прямоугольника. Собственный вес стержня не учитывается. За начальное принимается некоторое отклоненное от прямой состояние, определяемое прогибом w0(x). Предполагается, что в начальном состоянии под атмосферным давлением p0, действующим на боковую поверхность и концевое сечение стержня, отсутствуют напряжения. Избыточное давление р является равномерным по всей поверхности стержня и не зависит от его деформации, на концевое сечение стержня р не действует. Таким образом, в выражении (1.3) p1 = р2 = р. Тогда распределенная поперечная сила в соответствии с (1.3) и с учетом начального прогиба w0 равна
и при р > 0 направлена в сторону вогнутости, так как площадь вогнутой стороны меньше площади выпуклой стороны поверхности стержня.Рассматриваются случаи сжимающей силы неизменного направления (рис. 1, b) и следящей силы (рис. 1, с). В первом случае вертикально направленная сила Р создает изгибающий момент P(W0 + W – w0 – w) относительно точки М с направлением по часовой стрелке. Здесь W0, W – начальное и текущее перемещение конца х = L. Так же направлен изгибающий момент от распределенной силы q (2.1) на длине L – x относительно точки М. Поэтому вместо коэффициента Р во втором члене уравнения (1.1) принимаем Р + pF (при таком рассуждении правая часть (1.1) равна нулю). Кроме того, вертикально направленная сила Р дает на х = L перерезывающую силу Psin(θ0 + θ) ≈ ≈ Р(θ0 + θ) = P(∂(w0 + w)/∂х) (рис. 1, b). Она равна внутренней перерезывающей силе D∂3w/∂х3. Уравнение (1.1) с учетом сказанного запишем в виде
(2.2)
$\begin{gathered} \frac{{{{\partial }^{4}}w}}{{\partial {{\xi }^{4}}}} + {{\gamma }^{2}}\frac{{{{\partial }^{2}}({{w}_{0}} + w)}}{{\partial {{\xi }^{2}}}} + \frac{{{{\partial }^{2}}w}}{{{{\omega }^{2}}\partial {{t}^{2}}}} = 0 \\ \xi = \frac{x}{L},\quad {{\alpha }^{2}} = \frac{{pF{{L}^{2}}}}{D},\quad {{\beta }^{2}} = \frac{{P{{L}^{2}}}}{D},\quad {{\omega }^{2}} = \frac{D}{{\rho F{{L}^{4}}}},\quad {{\gamma }^{2}} = {{\beta }^{2}} - {{\alpha }^{2}} \\ \end{gathered} $Безразмерный параметр α характеризует влияние давления окружающей среды на изгиб стержня. Для прямоугольного и кругового поперечных сечений
(2.3)
${{\alpha }^{2}} = 12\frac{p}{E}{{\left( {\frac{L}{h}} \right)}^{2}},\quad {{\alpha }^{2}} = 16\frac{p}{E}{{\left( {\frac{L}{d}} \right)}^{2}}$Граничные условия имеют вид
(2.4)
$\begin{gathered} w = 0{\text{ (}}\xi {\text{ = 0),}}\quad \frac{{\partial w}}{{\partial \xi }} = 0\quad {\text{(}}\xi {\text{ = 0)}} \\ \frac{{{{\partial }^{2}}w}}{{{{\partial }^{2}}\xi }} = 0\quad {\text{(}}\xi = {\text{1),}}\quad \frac{{{{\partial }^{3}}w}}{{{{\partial }^{3}}\xi }} = - {{\beta }^{2}}\frac{{\partial ({{w}_{0}} + w)}}{{\partial \xi }}\quad {\text{(}}\xi = {\text{1)}} \\ \end{gathered} $Если как обычно не учитывать поперечную силу q (2.1) от всестороннего давления на боковую поверхность стержня, то в уравнении (2.2) будет γ = β.
В случае следящей силы (рис. 1, с) изгибающий момент равен – Pf, где расстояние f = w/cos(θ0 + θ) + [L – х – (w0 + w)tg(θ0 + θ)] ≈ w + L – x. Приравнивая – P(w + L – x) внутреннему изгибающему моменту D∂2w/∂x2 и продифференцировав по х это равенство два раза и с учетом инерционной силы, получаем уравнение (1.1). Так же как в предыдущем случае поведения силы Р выражение изгибающего момента имеет переменный по х член – P(w0 + w). Направление изгибающего момента от распределенной силы q не меняется. Поэтому в (1.1) вместо коэффициента Р имеем Р – pF. Следовательно, в уравнении (2.2) будет тот же коэффициент γ2 = β2 – α2. При этом на конце х = L изгибающий момент и перерезывающая сила равны нулю. Поэтому граничные условия (2.4) сохраняют свой вид за исключением последнего условия, где необходимо положить правую часть равной нулю.
В некоторых работах (например, в [2, 3]) вместо последних двух условий (2.4) ставятся кинематические уравнения: w(l) = W, (dw/dξ)ξ=1= Ф, где W, Ф – отклонение и угол поворота нагруженного конца стержня.
3. Сжимающая сила неизменного направления. Для простоты примем функцию начального отклонения в виде
Тогда в статической постановке уравнение (2.2) имеет решения
(3.2)
$\begin{gathered} w = {{C}_{0}} + {{C}_{1}}\xi + {{C}_{2}}\sin \gamma \xi + {{C}_{3}}\cos \gamma \xi \quad ({{\gamma }^{2}} = {{\beta }^{2}} - {{\alpha }^{2}} > 0) \\ w = {{C}_{0}} + {{C}_{1}}\xi + {{C}_{2}}{\text{sh}}\gamma \xi + {{C}_{3}}{\text{ch}}\gamma \xi \quad ({{\gamma }^{2}} = {{\alpha }^{2}} - {{\beta }^{2}} > 0) \\ \end{gathered} $Определив константы первого решения (3.2) по условиям (2.4), находим
(3.3)
$\frac{w}{{{{W}_{0}}}} = \frac{{{{\beta }^{2}}\left( {\sin \gamma - \gamma \xi \cos \gamma - \sin \gamma (1 - \xi )} \right)}}{{\gamma ({{\beta }^{2}}{\text{cos}}\gamma - {{\alpha }^{2}})}}$Дополнительный прогиб верхней точки (ξ = 1, w = W) равен
(3.4)
$\frac{W}{{{{W}_{0}}}} = \frac{{{{\beta }^{2}}\left( {\sin \gamma - \gamma \cos \gamma } \right)}}{{\gamma ({{\beta }^{2}}{\text{cos}}\gamma - {{\alpha }^{2}})}}$В отсутствии избыточного давления (α = 0, γ = β) из (3.4) следует
С возрастанием параметра нагрузки β прогиб увеличивается. При β = π/2 решение (3.5) неограниченно возрастает. Это дает известное критическое значение сжимающей силы [1–3]
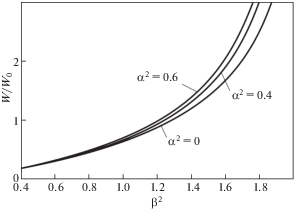
Изменение отношения W/W0 по β2 при заданных значениях α2 по формуле (3.4) показано на рис. 2. Как видно, чем больше α2 (давление р), тем быстрее возрастает прогиб при увеличении β2 (сжимающей силы). Критическое значение параметра β2 определяется из уравнения
(3.7)
$\cos \sqrt {{{\beta }^{2}} - {{\alpha }^{2}}} = {{{{\alpha }^{2}}} \mathord{\left/ {\vphantom {{{{\alpha }^{2}}} {{{\beta }^{2}}}}} \right. \kern-0em} {{{\beta }^{2}}}}$Рис. 2.
Зависимость относительного прогиба верхнего торца стержня W/W0 от безразмерного параметра сжимающей нагрузки неизменного направления β2
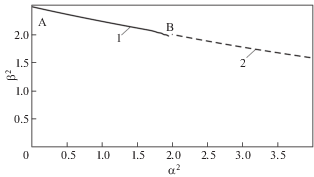
На рис. 3 сплошной линией приведена зависимость β2(α2) по (3.7).
При малых значениях α2 по сравнению с (π/2)2 приняв β2 = (π/2)2 – ε, ε $ \ll $ (π/2)2 и учитывая ${\text{cos}}\sqrt {{{(\pi } \mathord{\left/ {\vphantom {{(\pi } 2}} \right. \kern-0em} 2}{{)}^{2}} - \varepsilon - {{\alpha }^{2}}} \approx {\text{sin}}(({{\alpha }^{2}} + \varepsilon )/\pi ) \approx {{({{\alpha }^{2}} + \varepsilon )} \mathord{\left/ {\vphantom {{({{\alpha }^{2}} + \varepsilon )} \pi }} \right. \kern-0em} \pi }$, получаем уравнение ε2 – – ${{(\pi {\text{/}}2)}^{2}}\varepsilon $ + π(4 – π)(α/2)2 = 0, откуда определяются
(3.8)
$\varepsilon \approx \frac{{\pi (4 - \pi ){{\alpha }^{2}}}}{{{{\pi }^{2}} - 4{{\alpha }^{2}}}},\quad \beta _{*}^{2} = {{\left( {\frac{\pi }{2}} \right)}^{2}} - \frac{{\pi (4 - \pi ){{\alpha }^{2}}}}{{{{\pi }^{2}} - 4{{\alpha }^{2}}}}$В этом случае вместо (3.6) критическое значение сжимающей силы равно
(3.9)
${{P}_{*}} = {{\beta _{*}^{2}D} \mathord{\left/ {\vphantom {{\beta _{*}^{2}D} {{{L}^{2}}}}} \right. \kern-0em} {{{L}^{2}}}}$При α2 = β2уравнение (2.2) d4w/dξ4 = 0 рассматривается совместно с условиями (2.4), которые остаются без изменения. Константы решения
этого уравнения равны С0 = 0, С1 = 0, С2 = –3, С3 = W0β2/(2 – β2). Дополнительный прогиб(3.10)
$\frac{w}{{{{W}_{0}}}} = \frac{{{{\beta }^{2}}}}{{2 - {{\beta }^{2}}}}\left( {{{\xi }^{2}} - \frac{{{{\xi }^{3}}}}{3}} \right)$(3.11)
${{P}_{*}} = {{2D} \mathord{\left/ {\vphantom {{2D} {{{L}^{2}}}}} \right. \kern-0em} {{{L}^{2}}}}$Это предельное уменьшение силы ${{P}_{*}}$ из-за действия бокового избыточного давления при β > α. На рис. 3 значению (3.11) соответствует точка В. Таким образом, при повышении избыточного давления р и соответствующего параметра α2 от нуля до α2 = 2 параметр β2 снижается от (π/2)2 (точка А) до 2 (точка В). Соответствующие значения ${{P}_{*}}$ даются формулами (3.6) и (3.11).
Критическое значение избыточного давления ${{p}_{*}}$ для стального стержня круглого сечения (α2 = 2, Е = 2 × 105 МПа, L/d = 200) в соответствии с (2.3) равно ${{p}_{*}}$ = 2.5 МПа (25 атм).
Так как р представляет собой избыточное давление, то вакуумированию соответствуют отрицательные значения параметра α2 в уравнениях (3.7), (3.8). При этом абсолютное значение отрицательного давления р должно быть меньше атмосферного давления р0. Другое ограничение состоит в неравенстве Р > |р|F (β2 > |α2|, γ2 > 0). Тогда справедливыми остаются первое решение (3.1) и последующие выражения.
При α = 0, γ = β имеем те же результаты (3.5), (3.6). Как видно из рис. 3, при α2 < 0 критическое значение сжимающей силы ${{P}_{*}}$ возрастает. Этот эффект объясняется тем, что при р < 0 направление распределенной поперечной силы q (2.1) меняет знак. Теперь она направлена в сторону выпуклости.
Удовлетворение второго решения (3.2) при начальном прогибе (3.1) условиям (2.4) дает
(3.12)
$\frac{w}{{{{W}_{0}}}} = \frac{{{{\beta }^{2}}({\text{sh}}\gamma - \gamma \xi {\text{ch}}\gamma - {\text{sh}}\gamma (1 - \xi ))}}{{\gamma ({{\beta }^{2}}{\text{ch}}\gamma - {{\alpha }^{2}})}}$Следующее из (3.12) уравнение устойчивости представим в двух видах
(3.13)
${{\alpha }^{2}} - {{\beta }^{2}}ch\sqrt {{{\alpha }^{2}} - {{\beta }^{2}}} = 0,\quad {{\gamma }^{2}} - {{\beta }^{2}}(ch\gamma - 1) = 0$Первый из них является аналогом уравнения (3.7) и может быть анализирован, как (3.7). В частности, можно вывести приближенное соотношение β2(α2) при малом отличии β2 от 2 (точка В на рис. 3). В этом случае надо принять β2 = 2 – ε, ε $ \ll $ 2.
Второй вид (3.13) предпочтительнее в том отношении, что можно задаваться значением γ и находить β2. После этого определяется соответствующее значение α2 = γ2+ β2. Так построена часть кривой правее точки В на рис. 3. При значениях α2 и β2, не сильно отличающихся от 2 (точка В), и соответственно γ ≤ 2, используя разложение ${\text{ch}}\gamma = 1 + {{({{\gamma }^{2}}} \mathord{\left/ {\vphantom {{({{\gamma }^{2}}} 2}} \right. \kern-0em} 2}) + {{({{\gamma }^{4}}} \mathord{\left/ {\vphantom {{({{\gamma }^{4}}} 2}} \right. \kern-0em} 2}4)$, из второго уравнения (3.13) получаем явные связи
(3.14)
${{\beta }^{2}} = \frac{{24}}{{12 + {{\gamma }^{2}}}},\quad {{\alpha }^{2}} = 12\left( {\frac{2}{{{{\beta }^{2}}}} - 1} \right) + {{\beta }^{2}}$Пусть γ = 1, тогда по (3.14) β2 = 24/13, α2 = 37/13. Эти приближенные значения практически не отличаются от данных по точным уравнениям (3.13). Критические значения сжимающей силы и избыточного давления равны
На рис. 3 построена штриховая кривая по (3.14). Участок А – В соответствует преобладающей сжимающей силе, участок правее точки В – преобладающему давлению.
4. Сжимающая следящая сила. Решения уравнения (2.2) для этого случая имеют тот же вид (3.2). Примем также выражение (3.1). Рассмотрим первое решение (3.2). В последнем из условий (2.4) правая часть равняется нулю. Из этих условий находим
(4.1)
$\begin{gathered} {{C}_{0}} + {{C}_{3}} = 0,\quad {{C}_{1}} + \gamma {{C}_{2}} = 0 \\ {{C}_{2}}\sin \gamma + {{C}_{3}}\cos \gamma = 0 \\ {{C}_{2}}\cos \gamma - {{C}_{3}}\sin \gamma = 0 \\ \end{gathered} $Отсюда следует С0 = 0, С1 = 0, С2 = 0, С3 = 0. Поэтому согласно первому решению (3.2) w = 0. Этот результат не меняется и при отрицательном значении α2 (при вакуумировании). Второе решение (3.2) при удовлетворении граничным условиям также обращается в нуль.
Таким образом, учет влияния окружающего давления на стержень не приводит к изменению классического результата об отсутствии отклоненного равновесного состояния стержня при действии следящей силы [1–3].
Как известно [1–3, 5, 7], для суждения об устойчивости консольного стержня в случае следящей сжимающей силы требуется рассмотрение его динамики. Принимаем w = W(ξ)ехр(iΩt). Из (2.2) следует
(4.2)
$\frac{{{{d}^{4}}W}}{{d{{\xi }^{4}}}} + {{\gamma }^{2}}\frac{{{{d}^{2}}W}}{{d{{\xi }^{2}}}} - {{\mu }^{2}}W = 0,\quad {{\mu }^{2}} = \frac{{{{\Omega }^{2}}}}{{{{\omega }^{2}}}}$Решение уравнения (4.2) имеет вид
(4.3)
$\begin{gathered} W = {{C}_{0}}\sin {{\gamma }_{1}}\xi + {{C}_{1}}\cos {{\gamma }_{1}}\xi + {{C}_{2}}{\text{sh}}{{\gamma }_{2}}\xi + {{C}_{3}}{\text{ch}}{{\gamma }_{2}}\xi \\ {{\gamma }_{{1,2}}} = \frac{\gamma }{2}\left( { \pm 1 + \sqrt {1 + {{{\left( {\frac{{2\mu }}{\gamma }} \right)}}^{2}}} } \right) \\ \end{gathered} $Такое решение рассмотрено в [6, 7]. Удовлетворение (4.3) условиям (2.4) с нулевой правой частью в четвертом условии приводит к системе четырех уравнений относительно констант. Соответствующее трансцендентное уравнение позволяет установить значение нагрузки, когда параметр μ = Ω/ω становится комплексным. Если он имеет отрицательную мнимую часть, то exp(iΩt) неограниченно возрастает со временем. При этом критическое значение следящей силы в отсутствии давления определяется формулой (1.2). С учетом обозначений (2.2) имеем $\gamma _{*}^{2} = {{P}_{*}}{{{{L}^{2}}} \mathord{\left/ {\vphantom {{{{L}^{2}}} D}} \right. \kern-0em} D}$.
Так как при одновременном действии следящей силы и бокового давления γ2 = β2 – α2, то можно записать $\beta _{*}^{2} = \gamma _{*}^{2} + {{\alpha }^{2}}$ или
Таким образом, при действии на стержень избыточного бокового давления критическое значение следящей силы возрастает. Наоборот, при вакуумировании поверхности стержня это значение уменьшается.
До сих пор все результаты относились к постановке задачи, где на верхний срез стержня избыточное давление р не действует. Если это допущение снять и принять, что следящая сила возникает в результате действия давления р, то Р = рF или β2 = α2. Поэтому γ2 = 0. Пример такой постановки задачи рассматривается далее.
В случае постановки задачи согласно рис. 1, а имеем γ2 = β2 – α2. Так как при силе сжатия Р = рF и α2 = β2, γ2 = 0, то не происходит потери устойчивости стержня. Это известный результат, отмеченный во введении к статье.
5. Совместное действие давления, сил неизменного и изменяющегося направления. Если на верхний торец стержня действует одновременно вертикальная сила Р1 и следящая сила Р2, можно предположить, что при преобладающем действии первой из них поведение стержня будет ближе к случаю на рис. 1, b. В противном случае возможна реализация поведения в случае рис. 1, с.
Статический изгиб описывается уравнением (2.2) без последнего члена, в котором ${{\gamma }^{2}} = \beta _{1}^{2} + \beta _{2}^{2} - {{\alpha }^{2}}$, где $\beta _{1}^{2} = {{{{P}_{1}}{{L}^{2}}} \mathord{\left/ {\vphantom {{{{P}_{1}}{{L}^{2}}} D}} \right. \kern-0em} D}$, $\beta _{2}^{2} = {{{{P}_{2}}{{L}^{2}}} \mathord{\left/ {\vphantom {{{{P}_{2}}{{L}^{2}}} D}} \right. \kern-0em} D}$, ${{\alpha }^{2}} = {{pF{{L}^{2}}} \mathord{\left/ {\vphantom {{pF{{L}^{2}}} D}} \right. \kern-0em} D}$. В последнем из граничных условий (2.4) вместо β2 будет $\beta _{1}^{2}$. Вместо (3.3) теперь решение имеет вид
(5.1)
$\frac{w}{{{{W}_{0}}}} = \frac{{\beta _{1}^{2}\left( {\sin \gamma - \gamma \xi \cos \gamma - \sin \gamma (1 - \xi )} \right)}}{{\gamma (\beta _{1}^{2}{\text{cos}}\gamma + \beta _{2}^{2} - {{\alpha }^{2}})}},\quad {{\gamma }^{2}} = \beta _{1}^{2} + \beta _{2}^{2} - {{\alpha }^{2}}$При β2 = 0 отсюда следует решение (3.3). Более подробно рассмотрим случай α = 0. Решение (5.1) неограниченно возрастает при
(5.2)
$\cos \sqrt {\beta _{1}^{2} + \beta _{2}^{2}} = - {{\beta _{2}^{2}} \mathord{\left/ {\vphantom {{\beta _{2}^{2}} {\beta _{1}^{2}}}} \right. \kern-0em} {\beta _{1}^{2}}}$Уравнение (5.2) справедливо в пределах $ - 1 < {{\beta _{2}^{2}} \mathord{\left/ {\vphantom {{\beta _{2}^{2}} {\beta _{1}^{2}}}} \right. \kern-0em} {\beta _{1}^{2}}} < 1$. Следовательно, следящая сила Р2 должна быть меньше силы Р1. Будем считать, что сила Р1 только сжимающая ($\beta _{1}^{2} > 0$), а Р2 может быть как сжимающей ($\beta _{2}^{2} > 0$), так и растягивающей $(\beta _{2}^{2} < 0)$. Интервал $ - 1 < {{\beta _{2}^{2}} \mathord{\left/ {\vphantom {{\beta _{2}^{2}} {\beta _{1}^{2}}}} \right. \kern-0em} {\beta _{1}^{2}}} < 0$ соответствует растягивающей силе Р2 ($\beta _{2}^{2} < 0$). Если, например, ${{\beta _{2}^{2}} \mathord{\left/ {\vphantom {{\beta _{2}^{2}} {\beta _{1}^{2}}}} \right. \kern-0em} {\beta _{1}^{2}}}$ = –1/2, то из уравнения (5.2) следует $\beta _{1}^{2} = {{2{{\pi }^{2}}} \mathord{\left/ {\vphantom {{2{{\pi }^{2}}} 9}} \right. \kern-0em} 9}$. Таким образом, критическое значение сжимающей силы неизменного направления равно
Оно меньше, чем значение (3.6) в отсутствие растягивающей следящей силы Р2. При ${{\beta _{2}^{2}} \mathord{\left/ {\vphantom {{\beta _{2}^{2}} {\beta _{1}^{2}}}} \right. \kern-0em} {\beta _{1}^{2}}} = - {1 \mathord{\left/ {\vphantom {1 {\sqrt 2 }}} \right. \kern-0em} {\sqrt 2 }}$ имеем $\beta _{1}^{2} = 0.213{{\pi }^{2}}$, т.е. с увеличением растягивающей силы Р2 критическое значение сжимающей силы ${{P}_{{1*}}}$ уменьшается.
Интервал ${{\beta _{2}^{2}} \mathord{\left/ {\vphantom {{\beta _{2}^{2}} {\beta _{1}^{2}}}} \right. \kern-0em} {\beta _{1}^{2}}} > 0$ соответствует сжимающей следящей силе Р2. Если ${{\beta _{2}^{2}} \mathord{\left/ {\vphantom {{\beta _{2}^{2}} {\beta _{1}^{2}}}} \right. \kern-0em} {\beta _{1}^{2}}} = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}$, то из уравнения (5.2) получаем $\beta _{1}^{2} = {{8{{\pi }^{2}}} \mathord{\left/ {\vphantom {{8{{\pi }^{2}}} {27}}} \right. \kern-0em} {27}}$ и
Это значение больше, чем критическое значение (3.6) при Р2 = 0 (числовой коэффициент в (5.4) равен 0.296 против 0.25 в (3.6)).
Предельное увеличение при ${{\beta _{2}^{2}} \mathord{\left/ {\vphantom {{\beta _{2}^{2}} {\beta _{1}^{2}}}} \right. \kern-0em} {\beta _{1}^{2}}} = 1$ достигает $\beta _{1}^{2} = {{{{\pi }^{2}}} \mathord{\left/ {\vphantom {{{{\pi }^{2}}} 2}} \right. \kern-0em} 2}$. Таким образом при равенстве сжимающих сил Р1 и Р2 критическое значение
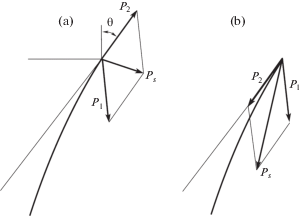
в два раза выше, чем в отсутствии следящей силы.Эти результаты, на первый взгляд парадоксальные, объясняются тем, что при Р1 > 0, Р2 < 0 их равнодействующая Рs создает больший изгибающий момент за счет увеличения соответствующего плеча (рис. 4, а). Наоборот, при Р1 > 0, Р2 > 0 их равнодействующая Рs создает меньший изгибающий момент за счет резкого уменьшения плеча (рис. 4, b).
Отметим, при α = 0 приходим к задаче, рассмотренной в книге [3]. В ней предполагается, что сжимающая сила прикладывается под углом θ, отличным от dw/dx при ξ = 1. Определяется то значение θ, когда стержень теряет устойчивость.
В общем случае из (5.1) следует уравнение устойчивости
(5.6)
$\cos \sqrt {\beta _{1}^{2} + \beta _{2}^{2} - {{\alpha }^{2}}} = - \frac{{\beta _{2}^{2} - {{\alpha }^{2}}}}{{\beta _{1}^{2}}}$В частном случае $\beta _{2}^{2} - {{\alpha }^{2}} = - {{\beta _{1}^{2}} \mathord{\left/ {\vphantom {{\beta _{1}^{2}} 2}} \right. \kern-0em} 2}$ из (5.6) следует $\beta _{1}^{2} = {{2{{\pi }^{2}}} \mathord{\left/ {\vphantom {{2{{\pi }^{2}}} 9}} \right. \kern-0em} 9}$. Критическое значение силы ${{P}_{{1*}}}$ дается формулой (5.3). Следовательно, для реализации этого варианта требуется меньшее значение растягивающей следящей силы ($\beta _{2}^{2} < 0$), чем в рассмотренном выше случае (при α = 0), если окружающее давление положительно (α2 > 0). Наоборот, при вакуумировании (α2 < 0) растягивающая сила Р2 должна быть выше для достижения значения (5.3).
В качестве примера одновременного действия положительных сил Р1 и Р2 можно привести схему, где сила Р1 создается весом шара радиуса R из материала с плотностью ρ. Она равна Р1 = (4π/3)R3gρ, где g – гравитационное ускорение. Следящая сила представляет собой равнодействующую давления на поверхность шара за вычетом площади поперечного сечения стержня. Она равна Р2 = рF, где F – площадь сечения стержня.
Так как в данном примере $\beta _{2}^{2} = {{\alpha }^{2}}$, то из (5.6) следует cosβ1 = 0, β1 = π/2. Поэтому критическое значение ${{P}_{{1*}}}$ определяется формулой (3.6). Таким образом, данная постановка задачи не приводит к какой-либо зависимости изгиба и устойчивости от избыточного давления р. С учетом изгибной жесткости стержня D = πEd4/64 выражение (3.6) дает
Для указанного выше шара связь между входными параметрами имеет вид
При L = 0.1 м, d = 0.001 м, R = 0.02 м, E = 2 × 1011 кг/м ⋅ с2, ρ = 7.8 кг/м3, g = 10 м/с2 условие (5.8) выполняется. Критическое значение силы веса равно ${{P}_{{1*}}}$ = 2.42 кг ⋅ м/с2.
Если $\beta _{2}^{2} - {{\alpha }^{2}} = - \beta _{1}^{2}$ (${{\gamma }^{2}} = 0$), то будет иметь место решение (3.10), где вместе β2 следует подставить $\beta _{1}^{2}$.
Уравнение (5.6) позволяет анализировать варианты упругой устойчивости консольного стержня в зависимости от внешних сил.
6. Заключение. 1. Известные особенности устойчивости прямолинейной формы консольного стержня еще более усложняются при действии на его боковую поверхность избыточного давления. Это давление может оказывать как стабилизирующее, так и дестабилизирующее влияние на прямолинейную форму стержня. Эти эффекты тесно связаны с направлением сил и граничными условиями.
2. В отличие от случая двухопорного стержня положительное избыточное давление на поверхность консольного стержня уменьшает критическое значение сжимающей силы неизменного направления, а вакуумирование – увеличивает.
3. Действие избыточного давления на поверхность консольного стержня не вносит изменения в известный результат об отсутствии равновесного отклоненного положения под действием сжимающей следящей силы. Происходит стабилизация динамического поведения при действии положительного избыточного давления и дестабилизация при вакуумировании.
4. При одновременном действии сжимающей силы неизменного направления и сжимающей следящей силы происходит уменьшение критического значения первой из них. В случае растягивающей следящей силы это значение увеличивается, что объясняется изменением направления их равнодействующей.
5. Действие окружающего избыточного давления приводит к большему разнообразию упругого поведения стержня. Например, при следящей силе, возникающей в результате действия давления не только на боковую поверхность, но и на торцевое сечение стержня исчезает влияние этого давления на изгиб и устойчивость.
Работа поддержана средствами государственного бюджета по госзаданию (№ 0246-2019-0088) и грантом РФФИ (№ 18-01-00150).
Список литературы
Николаи Е.Л. Труды по механике. М.: Гостехтеориздат, 1955. 582 с.
Болотин В.В. Неконсервативные задачи теории упругой устойчивости. М.: Физматлит, 1961. 339 с.
Пановко Я.Г., Губанова И.И. Устойчивость и колебания упругих систем. М.: Физматлит, 1967. 420 с.
Pfluger A. Stabilitats probleme der Elostostatik. Berlin: Springer-Verlag, 1950. 217 p.
Феодосьев В.И. Избранные задачи и вопросы по сопротивлению материалов. М.: Гостехиздат, 1973. 400 с.
Beck M. Die Knicklast des einseitig eingespanten tangential gedruckten Stabes // Zeitschr. Angew Math. Phys. 1952. V. 3. № 3. P. 225–228.
Дейнеко К.С., Леонов М.Л. Динамический метод исследования устойчивости сжатого стержня // ПММ. 1955. Т. 19. № 6. С. 738–744.
Rayleigh Strutt J.W. The Theory of Sound. Vol. 1. London: Macmillan, 1894. 500 p. = Стретт Дж.В. Теория звука. Т. 1. М.: Гостехиздат, 1955. 504 с.
Love A. A Treafise on the Mathematical Theory of Elasticity. Cambridge: Univ. Press, 1927. 643 p. = Ляв А. Математическая теория упругости. М.; Л.: ОНТИ, 1935. 674 с.
Shen H.Sh. Postbuckling Behavior of Plates and Shells. Shanghai Jiao Tong University, 2017. 675 p.
Ильгамов M.A. Влияние давления окружающей среды на изгиб тонкой пластины и плёнки // ДАН. 2017. Т. 476. № 4. С. 402–405.
Ильгамов М.А. Изгибные колебания пластины при изменении среднего давления на ее поверхностях // Акустический журнал. 2018. Т. 64. № 5. С. 598–604.
Handelman G.H. Buckling under locally hydrostatic pressure // J. Appl. Mech. 1946. V. 13. P. 198–200.
Ilgamov M.A. Static Problems of Hydroelasticity. M.: Nauka, 1998. 209 p.
Ишлинский А.Ю. Рассмотрение вопросов об устойчивости равновесия упругих тел с точки зрения математической теории упругости // Украинский математический журнал. 1954. Т. 6. № 2. С. 140–146.
Newland D.E. Whirling of a cantilever elastic shaft subjected to external pressure // J. Mech. Eng. Sci. 1972. V. 14. № 1. P. 11–18.
Ilgamov M.A., Tang D., Dowell E. Flutter and forced response of a cantilevered pipe: the influence of internal pressure and nozzle discharge // J. Fluids Struct. 1994. № 8. P. 139–156.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика твердого тела