1. На главную
  2. Электронные версии
  3. Известия РАН. Механика твердого тела
  4. № 4, 2021

Известия РАН. Механика твердого тела, 2021, № 4, стр. 64-76

ПРИНЦИПИАЛЬНЫЕ ВОПРОСЫ ТЕОРИИ КОМБИНИРОВАННЫХ СВОБОДНЫХ ГИРОСКОПОВ, ФУНКЦИОНИРУЮЩИХ НА ДВУХ РАБОЧИХ МОДАХ

С. Е. Переляев *

Институт проблем механики им. А.Ю. Ишлинского РАН
Москва, Россия

* E-mail: pers2030@yandex.ru

Поступила в редакцию 28.08.2020
После доработки 14.09.2020
Принята к публикации 28.09.2020

Полный текст (PDF)

Аннотация

Изложены принципиальные вопросы теории новых гироскопических датчиков на основе упругого осесимметричного резонатора – волнового твердотельного гироскопа (ВТГ), в полусферическом кварцевом резонаторе которого одновременно могут возбуждаться и существовать различные рабочие формы (моды) стоячих волн упругих колебаний. В предлагаемом исследовании рассматриваются принципиальные вопросы теории новых гироскопических инерциальных датчиков ориентации семейства “обобщенный” маятник Фуко. Описан принципиальный физический эффект, лежащий в основе функционирования таких приборов, входящих в рассматриваемый класс свободных гироскопов. Представлены прикладные аспекты реализации фундаментальной теории нового “обобщенного” неуправляемого маятника Фуко в высокоточных инерциальных датчиках ориентации, функционирующих одновременно на двух рабочих модах колебаний. Предложены основные способы реализации двухмодового “обобщенного” неуправляемого маятника Фуко в современных инженерно-конструкторских решениях точных волновых твердотельных гироскопах нового поколения.

Ключевые слова: классический маятник Фуко, идеальный двухмерный осциллятор, полусферический кварцевый резонатор (волновой твердотельный гироскоп), теория инерциальных датчиков ориентации, “обобщенный” неуправляемый маятник Фуко

1. Введение. Опыты, проведенные в 1851 году французским механиком и астрономом Леоном Фуко [1], а также опыты его многочисленных последователей дали только качественные результаты, подтверждающие с достаточной по тем временам точностью факт вращения Земли с угловой скоростью 11 град/ч относительно местной (Пантеон, г. Париж) вертикали (погрешность составляла по тем временам весьма небольшую величину порядка 1 град/ч). Математическое исследование основных источников погрешностей классического неуправляемого маятника Фуко и новое аналитическое доказательство вращения Земли дал в своей докторской диссертации в 1879 году нидерландский физик-экспериментатор Хайкес Каммерлинг-Оннес [2]. Известно, что математический осциллятор с двумя степенями свободы, выполняющий в современных гироскопах роль маятника Фуко, обычно реализован в виде одной из форм собственных колебаний упругой среды, обладающей осевой симметрией. При этом, в отличие от классического маятника Фуко, вращение упругой среды вокруг оси симметрии датчика вовлекает реализованную форму собственных колебаний во вращение относительно абсолютного (инерциального) пространства. В соответствующем выбранной форме колебаний собственном подпространстве принципиальные вопросы теории нового датчика инерциальной информации могут рассматриваться в рамках одних и тех же уравнений, аналогичных уравнениям классического неуправляемого маятника Фуко.

В данной работе впервые рассмотрены принципиальные вопросы теории функционирования многомодовых ВТГ, в которых одновременно производится возбуждение и поддержание сразу нескольких рабочих мод (форм) упругих колебаний кромки осесимметричного резонатора (например, второй и третьей).

2. Основные сведения из механики новых гироскопических систем. В современной практике мировой гироскопии появился целый класс новых приборов, в которых фактически реализована идея “обобщенного” маятника Фуко: струнный гироскоп [3], кольцевой гироскоп [4], полусферический кварцевый резонатор (волновой твердотельный гироскоп) [5–11, 15], ВТГ с металлическим цилиндрическим резонатором [12–14], “квапазон” [17], сферичеcкий кварцевый резонатор [18]. Все указанные выше новые инерциальные датчики ориентации весьма успешно конкурируют с классическими гироскопами, однако их теория существенно отличается от фундаментальной теории известных симметричных и несимметричных механических гироскопов [19]. Например, кинетический момент, который в механических гироскопах всегда стремились сделать как можно большим, в перечисленных выше новых датчиках должен быть равен нулю [16]. Математический маятник (осциллятор) с двумя степенями свободы, играющий в этих новых приборах роль “обобщенного” маятника Фуко, как правило, реализован в виде одной из форм собственных колебаний упругой среды, обладающей осевой симметрией. При этом, в отличие от классического маятника Фуко, вращение упругой среды вокруг оси симметрии инерциального датчика вовлекает реализованную форму собственных колебаний во вращение относительно неподвижного пространства. Исключение составляет струнный гироскоп, однако отношение угловой скорости (прецессии) формы колебаний относительно упругого тела к угловой скорости тела относительно пространства является строго постоянной величиной, зависящей от номера формы (моды) рабочих колебаний и почти независящей от свойств самого упругого материала.

Эта известная постоянная получила название масштабного коэффициента прецессии инерциального датчика, или коэффициента Брайана, по имени первого исследователя колебаний упругой оболочки [20]. Основой волнового твердотельного гироскопа (ВТГ) является прецессия механической стоячей волны на кромке полусферической кварцевой оболочки, скорость которой оказалась пропорциональной скорости вращения основания прибора. При этом эти скорости оказались связаны постоянным коэффициентом Брайана, не зависящим от измеряемой угловой скорости. В публикации [21] рассмотрен подробный вывод основных уравнений новых гироскопических датчиков на примере тонкого упругого кольца. Представлены дифференциальные уравнения колебаний такого кольца в своей плоскости и показано, что эти уравнения допускают точное аналитическое решение в виде гармонической волны. При произвольных начальных условиях эти общие аналитические решения определяют в горизонтальной плоскости (x, y) эллипс. В случае, когда эллипс вырождается в отрезок прямой, общее аналитическое решение определяет в тонком вибрирующем кольце механическую стоячую волну. В случае противоположного вырождения, когда эллипс превращается в окружность, общее решение определяет в тонком упругом кольце бегущую волну, которая не обладает необходимыми инерционными свойствами. Если угловая скорость основания кольца ω $ \ne 0,$ то прямолинейных колебаний в плоскости (x, y) идеальный двухмерный осциллятор в общем случае не имеет. Иными словами, во вращающемся упругом кольце стоячие механические волны невозможны. Однако в этом случае в кольце существуют такие колебания, которые в некоторой вращающейся системе координат имеют вид стоячих волн. Такие волны принято называть “прецессирующими” волнами. В публикации [11] подробно изложены принципиальные теоретические основы эксперимента Линча–Скотта и представлен вывод важной для целей современной прикладной гироскопии формулы:

(2.1)
$\varphi = - \frac{2}{{{{\kappa }^{2}} + 1}}\int {\omega (t)dt} $
здесь κ – номер моды (формы) колебаний, κ = 2, 3, 4 …; ω$\left( t \right)$ – угловая скорость вращения основания (произвольная функция). Следует отметить, что в современных датчиках ВТГ возбуждается одна из рабочих мод (форм) колебаний резонатора, например, вторая (κ = 2).

Формула (2.1) представляет обобщение результата Брайана для тонкого упругого кольцевого резонатора. Эффект Брайана [20], как эффект прецессии стоячей волны при вращении резонатора с постоянной угловой скоростью, является эффектом расщепления двукратных частот, поэтому этот эффект имеет малое отношение к тому, что экспериментально было открыто Линчем-Скоттом [15] в 1982 году и использовано в известном патенте Линча [9]. Хотя авторы патента ошибочно и сослались на формулу Брайана [20], на самом деле, в подтверждение своей идеи они привели результат эксперимента, в котором поворот первоначально неподвижного вибрирующего резонатора ВТГ на угол φ = 90 град., вызывал поворот стоячей волны на угол φb = 30 град., относительно кромки самого резонатора без каких-либо изменений самой формы стоячей волны. Тем самым была установлена важная для целей практического применения в принципиально новых гироскопах следующая экспериментальная формула:

(2.2)
${{\varphi }_{b}} = - 1{\text{/}}3(\varphi )$

Полученная в эксперименте формула (2.2) связывает уже не постоянные скорости поворота резонатора, а сами углы поворота при явно непостоянных угловых скоростях. Изложенное выше можно суммировать в виде теоремы.

Теорема 1. Какой бы ни была зависимость угловой скорости тонкого упругого кольца от времени (в классе дифференцируемых на бесконечном полуинтервале функций), существует и единственная вращающаяся относительно кольца система координат, в которой при определенных начальных условиях колебания кольца представляют собой механические стоячие волны [21].

Скорость такой системы координат выражается формулой (2.1). Частным случаем из нее вытекает известный результат Брайана [20], установленный им только для постоянной угловой скорости $(\dot {\omega } = 0)$ осесимметричного резонатора:

(2.3)
${{\omega }_{b}} = - \frac{2}{{1 + {{k}^{2}}}}\omega $

Заметим, что выражение, верное для стационарного случая, как правило, не бывает верным для нестационарного. Формула (2.1) описывает новый физический эффект, не замеченный Брайаном, и впервые установленный экспериментально, авторами известного патента “Vibratory rotational sensor” [9]. Следует заметить, что формулу (2.1) ввиду ее точного характера можно сколько угодно раз аналитически дифференцировать.

В частности, можно отметить, что ускорение механической стоячей волны пропорционально угловому ускорению самого упругого вибрирующего кольца:

(2.4)
$\left( {\frac{{{{d}^{2}}\varphi }}{{d{{t}^{2}}}}} \right) = \frac{2}{{{{\kappa }^{2}} + 1}}\left( {\frac{{d\omega }}{{dt}}} \right)$

Поскольку ускорение тонкого упругого кольца пропорционально приложенному к нему моменту внешних сил M $(I\ddot {\omega } = M)$, то можно объективно утверждать, что этот момент вызывает не только ускорение кольца, но и ускорение прецессирующей стоячей волны.

Все сказанное выше позволяет определить обсуждаемый здесь физический эффект в неравномерно вращающемся кольце как эффект инертности упругих волн в нем.

Эффект (2.1), который установлен [11] для общего вида уравнения колебаний без каких-либо приближений, с различной степенью точности верен и для произвольных упругих тел, обладающих осевой симметрией. Различие будет состоять только в величине масштабного коэффициента, равного для кольца 2/(${{\kappa }^{2}} + 1$). Можно показать, что для кварцевой полусферы имеем следующую известную формулу прецессии угла волны

(2.5)
${{\varphi }_{b}} = - 0.312\mathop \smallint \limits_0^t \omega (t)dt$
что соответствует повороту осей колебаний механической стоячей волны относительно кромки оболочки на угол 28.1 град. или относительно инерциального пространства на угол 61.9 град при повороте основания данной оболочки на фиксированный угол 90 град.

В соответствующем выбранной форме колебаний собственном подпространстве, все принципиальные вопросы теории подобного высокоточного датчика инерциальной информации, могут рассматриваться в рамках одних и тех же уравнений, аналогичных уравнениям классического маятника Фуко. По этой причине весь этот класс приборов может быть назван “обобщенным” маятником Фуко [21]. Многие исследователи предполагают, что Земля не вовлекает плоскость колебаний маятника во вращение вокруг местной вертикали. Между тем благодаря нелинейным эффектам неуправляемый маятник Фуко обладает собственной скоростью прецессии вокруг местной вертикали, поэтому необходимо контролировать его собственную прецессию, без чего невозможно осуществлять достоверные и точные измерения угловой скорости вращения Земли.

3. Теория функционирования двухмодового интегрирующего свободного гироскопа типа “обобщенный” маятник Фуко. Общая математическая модель осциллирующей системы, которая показывает пространственное движение, обнаруженное Фуко, излагается в соответствие с фундаментальной теорией, достаточно строго изложенной в известной публикации [22]. Данная теория касается большинства современных вибрирующих (осциллирующих) гироскопических механических систем (в частности ВТГ), которые функционируют, как правило, на одной основной (второй) иногда третьей рабочей моде колебаний. Предлагается рассмотреть основы теории принципиально новых комбинированных инерциальных датчиков ориентации, которые функционируют одновременно на двух (n = 2, 3) или даже трех рабочих модах колебаний кромки полусферы резонатора ВТГ. Применительно к идеальной осемметричной полусфере волнового твердотельного гироскопа рассмотрим по аналогии с [21, 22] дифференциальные уравнения пространственных движений в горизонтальной плоскости кромки резонатора, описывающие динамику двух идеальных двухмерных неуправляемых осцилляторов на двух (n = 2, 3) основных рабочих модах (формах) колебаний механических стоячих волн:

(3.1)
${{\ddot {x}}_{n}} + \Omega _{n}^{2}{{x}_{n}} - 2c\omega {{\dot {y}}_{n}} = 0\quad (n = 2,3)$
(3.2)
${{\ddot {y}}_{n}} + \Omega _{n}^{2}{{y}_{n}} + 2c\omega {{\dot {x}}_{n}} = 0\quad (n = 2,3)$

Здесь переменные ${{x}_{n}}$ и ${{y}_{n}}$ представляют собой текущие координаты двух осциллирующих точек в заданных декартовых системах координат (см. рис. 1. и рис. 2.), которые являются наглядными геометрическими интерпретациями двух орбит эллиптических вибраций.

Рис. 1.

Орбитальная траектория вибрирующей точки (x1, y1) второй моды (формы) колебаний стоячей волны и основные параметры двухмерного осциллятора

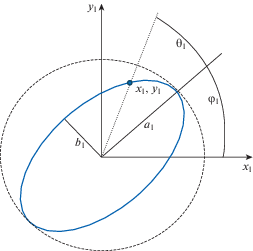
Рис. 2.

Орбитальная траектория вибрирующей точки (x2, y2) третьей моды (формы) колебаний стоячей волны и основные параметры двухмерного осциллятора

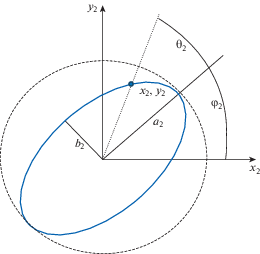
Рабочие моды (формы) колебаний этих двух осцилляторов условно обозначены n = 2, 3. Они соответствуют двум основным (n = 2, 3) рабочим модам или формам механических стоячих волн упругих колебаний кромки полусферического резонатора, как это показано ниже на рис. 3. На каждом рассматриваемом эллипсе имеем соответственно две точки ${{a}_{{\left( n \right)}}},$ которые имеют определенные амплитуды колебаний и расположены на продольных осях двух вибрирующих элементов одного комбинированного свободного двухмодового гироскопа; θ1, θ2 – углы, которые характеризуют направления (фазы) вибраций в системе координат осесимметричного резонатора; φ1, φ2 – углы наклона больших полуосей эллипсов к осям ${{x}_{1}}~$ и ${{x}_{2}}~$ (определяют текущие местоположения двух рассматриваемых форм (мод) механических стоячих волн колебаний на кромке осциллирующего полусферического резонатора, в которых наблюдаются его радиальные отклонения от окружности); Ωn – рабочие частоты колебаний (вибраций) двух идеальных осцилляторов; c – постоянный коэффициент, который зависит от заданной моды и соответствующего данной моде колебаний коэффициента Брайана комбинированного свободного гироскопа; ω – произвольная угловая скорость основания двухмодового гироскопа, которая измеряется в плоскости нормальной горизонтальной системе координат OXY.

Рис. 3.

Рабочие формы (моды) колебаний механической стоячей волны осесимметрического резонатора ВТГ: (а) 2-я мода (форма); (b) 3-я мода (форма).

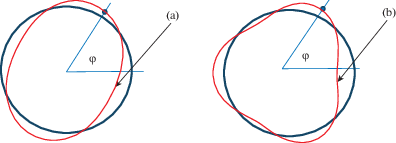
Существенная особенность дифференциальных уравнений (3.1)–(3.2) наличие известных гироскопических членов, представляющих собой составляющие $2c\omega {{\dot {x}}_{n}},2c\omega {{\dot {y}}_{n}}~$ ускорения Кориолиса на горизонтальные оси OXY указанных выше идеальных двухмерных осцилляторов. Заметим, что эти составляющие полностью соответствуют гироскопическим членам классического неуправляемого “обобщенного” маятника Фуко. Можно привести пример целого класса гироскопов, идеальное пространственное движение которых достаточно точно характеризуется системой дифференциальных уравнений вида (3.1)–(3.2). Все такие инерциальные датчики ориентации обладают гироскопическим эффектом, обнаруженным Фуко. Ниже представим обобщающий анализ одного нового типа комбинированных инерциальных датчиков – волновых твердотельных гироскопов (ВТГ), которые функционируют не на одной рабочей моде, а как минимум на двух модах (формах) (см. рис. 3) резонансных колебаний полусферы одновременно. Имея на входе такого идеального свободного ВТГ нулевую угловую скорость (ω = 0) движения основания прибора в пространстве, перемещения двух вибрирующих материальных точек $\left( {{{x}_{1}},{{у}_{1}}} \right)$ и $\left( {{{x}_{2}},{{у}_{2}}} \right)~$ такого комбинированного осциллятора, можно наглядно представить двумя эллипсами, которые могут быть определены на основании аналитических решений дифференциальных уравнений вида (3.1)–(3.2). Это легко проверить, подставив в них следующие обобщающие аналитические выражения:

(3.3)
$~{{x}_{{(n)}}} = {{a}_{{(n)}}}(t){\text{cos}}(n{{\theta }_{{(n)}}}){\text{cos}}(n{{\varphi }_{{(n)}}}) - {{b}_{{(n)}}}(t){\text{sin}}(n{{\theta }_{{(n)}}}){\text{sin}}(n{{\varphi }_{{(n)}}})$
(3.4)
${{y}_{{(n)}}} = {{a}_{{(n)}}}(t){\text{cos}}(n{{\theta }_{{(n)}}}){\text{sin}}(n{{\varphi }_{{(n)}}}) + {{b}_{{(n)}}}(t){\text{sin}}(n{{\theta }_{{(n)}}}){\text{cos}}(n{{\varphi }_{{(n)}}})$

Выражения (3.3)–(3.4) определяют мгновенное положение двух вибрирующих материальных точек $\left( {{{x}_{1}},{{у}_{1}}} \right)$ и $\left( {{{x}_{2}},{{у}_{2}}} \right)~$ на орбитальных траекториях двух вибрирующих эллипсов, при этом скорости перемещения каждой из двух точек по указанным траекториям будут равны

(3.5)
${{\dot {x}}_{{(n)}}} = {{\Omega }_{n}}( - {{a}_{{(n)}}}(t){\text{sin}}(n{{\theta }_{{(n)}}}){\text{cos}}(n{{\varphi }_{{(n)}}}) - {{b}_{{(n)}}}(t){\text{cos}}(n{{\theta }_{{(n)}}}){\text{sin}}(n{{\varphi }_{{(n)}}}))$
(3.6)
${{\dot {y}}_{{(n)}}} = {{\Omega }_{n}}( - {{a}_{{(n)}}}(t){\text{sin}}(n{{\theta }_{{(n)}}}){\text{sin}}(n{{\varphi }_{{(n)}}}) + {{b}_{{(n)}}}\left( t \right){\text{cos}}(n{{\theta }_{{(n)}}}){\text{cos}}(n{{\varphi }_{{(n)}}}))$

Здесь параметры $~{{a}_{{\left( n \right)}}},{{b}_{{\left( n \right)}}}$ – являются переменными, называемыми амплитудами и квадратурами рабочих колебаний двух гармонических осцилляторов, которые определяют основные динамические характеристики свободного движения неуправляемого “обобщенного” маятника Фуко. При этом $~{{a}_{{\left( n \right)}}},{{b}_{{\left( n \right)}}}$ – непосредственно определяют формы эллипсов колебаний, а углы ${{\theta }_{{(n)}}}$ – их ориентацию на горизонтальной плоскости OXY; углы ${{\theta }_{{(n)(0)}}}$ – являются начальными значениями (основные фазы) двух орбитальных углов θ(n), которые определяют положения двух материальных точек на двух вибрирующих эллипсах.

Все эти рассматриваемые параметры представлены на рис. 1 и рис. 2, на которых наглядно отображены основные орбитальные элементы комбинированного (двухмодового) свободного (неуправляемого) волнового твердотельного гироскопа. В приведенных выше обобщающих аналитических решениях (3.3)–(3.4) и (3.5)–(3.6) нижний индекс $\left( n \right) = 2,3$ задает соответственно вторую (n = 2) и третью (n = 3) рабочую моду колебаний стоячих волн двух идеальных двухмерных осцилляторов. В формулах (3.5)–(3.6) орбитальные углы θ(n) определяются следующим известным аналитическим выражением:

${{\theta }_{{(n)}}} = {{\Omega }_{n}}t + {{\theta }_{{(n)(0)}}}$

В частности, два орбитальных угла θ(n) измеряются на соответствующих окружностях радиуса ${{a}_{{\left( n \right)}}}$ каждой заданной рабочей моды стоячих волн колебаний. Основные параметры этих двух орбит $~{{a}_{{\left( n \right)}}}$ и $~{{b}_{{\left( n \right)}}}$ тесно связаны с нормированными энергиями колебаний ${{E}_{{(n)}}}$ и соответствующими кинетическими моментами ${{H}_{{(n)}}}$ [22] двух рассматриваемых идеальных двухмерных осцилляторов следующими соотношениями:

(3.7)
$~{{a}_{{(n)}}} = {{[{{E}_{{(n)}}} + \sqrt {(E_{{(n)}}^{2} - \Omega _{n}^{2}H_{{(n)}}^{2})} ]}^{{1/2}}}{\text{/}}{{\Omega }_{n}}\quad (n) = 2,3$
(3.8)
$~{{b}_{{(n)}}} = {{[{{E}_{{(n)}}} - \sqrt {(E_{{(n)}}^{2} - \Omega _{n}^{2}H_{{(n)}}^{2})} ]}^{{1/2}}}{\text{/}}{{\Omega }_{n}}\quad (n) = 2,3$

При этом постоянные энергии E(n) этих двух комбинированных осцилляторов их кинетические моменты H(n) могут быть выражены простыми аналитическими выражениями:

(3.9)
${{E}_{{(n)}}} = [\Omega _{n}^{2}(x_{{(n)}}^{2} + y_{{(n)}}^{2}) + (\dot {x}_{{(n)}}^{2} + \dot {y}_{{(n)}}^{2})]{\text{/}}2\quad \left( n \right) = 2,3$
(3.10)
${{H}_{n}} = ({{x}_{{(n)}}}{{\dot {y}}_{{(n)}}} - {{y}_{{(n)}}}{{\dot {x}}_{{(n)}}})~\quad \left( n \right) = 2,3$

Данные параметры E(n) и H(n), для рассматриваемых идеальных двухмерных осцилляторов колебаний вида (3.1)–(3.2), являются постоянными величинами и поэтому их можно довольно просто выразить через введенные выше параметры – амплитуд a(n) и квадратур b(n) второй и третьей рабочих мод колебаний комбинированного гироскопа:

(3.11)
${{E}_{{(n)}}} = \Omega _{n}^{2}(a_{{(n)}}^{2} + b_{{(n)}}^{2}){\text{/}}2\quad ~~\left( n \right) = 2,3~$
(3.12)
${{H}_{n}} = \Omega _{n}^{{}}({{a}_{{(n)}}}b_{{(n)}}^{{}})~\quad \left( n \right) = 2,3$

На основании выражений (3.11)–(3.12) можно сделать следующий важный вывод о том, что движения двух материальных точек $\left( {{{x}_{1}},{{у}_{1}}} \right)$ и $\left( {{{x}_{2}},{{у}_{2}}} \right)$ по траекториям двух вибрирующих эллипсов переходят в движения, которые описываются двумя прямыми линиями, тогда и только тогда, когда для заданных выше двух рабочих мод колебаний идеальных осцилляторов выполняются два безусловных требования: $b_{{(2)}}^{{}} = 0~$ и ${{b}_{{(3)}}} = 0.$ Последнее означает, что при выполнении этих двух основных требований кинетические моменты Hn двух идеальных осцилляторов также будут строго равны нулю (${{H}_{n}} \equiv 0).$

Искомые углы $2{{\varphi }_{{(n)}}}$ и $~3{{\varphi }_{{(n)}}}~$ наклона продольных осей двух указанных выше вибрирующих эллипсов определяются следующими аналитическими выражениями:

(3.13)
${\text{sin}}(n{{\varphi }_{{(n)}}}) = [\Omega _{n}^{2}x_{{(n)}}^{{}}y_{{(n)}}^{{}} + \dot {x}_{{(n)}}^{{}}\dot {y}_{{(n)}}^{{}}]{\text{/}}[\sqrt {(E_{{(n)}}^{2} - \Omega _{n}^{2}H_{{(n)}}^{2})} ]\quad (n) = 2,3~~$
(3.14)
${\text{cos}}(n{{\varphi }_{{\left( n \right)}}}) = [\Omega _{n}^{2}(x_{{\left( n \right)}}^{2} - y_{{\left( n \right)}}^{2}) + (\dot {x}_{{\left( n \right)}}^{2} - \dot {y}_{{\left( n \right)}}^{2})]{\text{/}}2[\sqrt {(E_{{\left( n \right)}}^{2} - \Omega _{n}^{2}H_{{\left( n \right)}}^{2})} ]\quad \left( n \right) = 2,3~$

Можно показать, что соответствующие углы $n{{\varphi }_{{(n)}}}$ наклона двух рассматриваемых эллипсов колебаний на второй (n = 2) и третьей (n = 3) рабочих модах функционирования идеальных двухмерных осцилляторов являются постоянными для движений, которые задаются дифференциальными уравнениями (3.1)–(3.2) только для частного случая, когда входная угловая скорость основания двухмодового гироскопа равна нулю (ω = 0).

Наконец орбитальные углы θ(n) двух эллиптических траекторий соответствующих двум рабочим модам (n = 2, 3) механических стоячих волн колебаний могут быть представлены следующими аналитическими выражениями:

(3.15)
${\text{sin}}(n{{\theta }_{{\left( n \right)}}}) = - {{\Omega }_{n}}(x_{{\left( n \right)}}^{{}}\dot {x}_{{\left( n \right)}}^{{}} + y_{{\left( n \right)}}^{{}}\dot {y}_{{\left( n \right)}}^{{}}){\text{/}}\sqrt {(E_{{\left( n \right)}}^{2} - \Omega _{n}^{2}H_{{\left( n \right)}}^{2})} \quad \left( n \right) = 2,3$
(3.16)
${\text{cos}}(n{{\theta }_{{\left( n \right)}}}) = [\Omega _{n}^{2}(x_{{\left( n \right)}}^{2} + y_{{\left( n \right)}}^{2}) - (\dot {x}_{{\left( n \right)}}^{2} + \dot {y}_{{\left( n \right)}}^{2})]{\text{/}}\sqrt {(E_{{\left( n \right)}}^{2} - \Omega _{n}^{2}H_{{\left( n \right)}}^{2})} \quad \left( n \right) = 2,3~~~$

Следует заметить, что эти два орбитальных угла не являются строго постоянными, однако можно отметить, что их значения увеличиваются со временем строго по линейному закону.

Здесь следует рассмотреть важные для практических реализаций конкретных комбинированных двухмодовых свободных гироскопов следующие прикладные аспекты.

Случай 1: Входная угловая скорость не равна нулю (ω ≠ 0). В данном случае решения уравнений (3.1)–(3.2) не являются периодическими с частотами Ωn и орбиты двух рассматриваемых материальных точек $\left( {{{x}_{1}},{{у}_{1}}} \right)$ и $\left( {{{x}_{2}},{{у}_{2}}} \right)$ больше не являются эллипсами.

Случай 2: Входная угловая скорость основания ω относительно абсолютно точных величин рабочих частот Ωn$\left( {\left( n \right) = 2,3} \right)~$ идеальных двухмерных осцилляторов является относительно малой величиной. В данном случае внешний вид двух таких орбит почти точно соответствует двум эллипсам, которые медленно прецессируют, а колебания самих материальных точек $\left( {{{x}_{1}},{{у}_{1}}} \right)$ и $\left( {{{x}_{2}},{{у}_{2}}} \right)$ на этих орбитах будут почти периодическими.

В данном случае целесообразно определить основные параметры $~{{a}_{{(n)}}},{{b}_{{(n)}}},{{\varphi }_{{(n)}}}$ и ${{\theta }_{{(n)(0)}}},$ как осциллирующие на двух основных рабочих модах орбитальные элементы, по аналогии с орбитальными элементами, используемыми в классической небесной механике. Важно отметить, что применительно к гармоническим двухмерным осцилляторам, предлагается определять не мгновенные положения материальных точек $\left( {{{x}_{1}},{{y}_{1}}} \right)$ и $\left( {{{x}_{2}},{{y}_{2}}} \right)~$ на соответствующих эллипсах, движение по орбитам которых происходит с частотами на много превышающими частоту измеряемой каждым таким осциллятором входной угловой скорости основания прибора, а непосредственно сами орбитальные элементы. Соответственно, вместо непосредственного решения исходных дифференциальных уравнений второго порядка (3.1)–(3.2), при действии на вход двух осцилляторов переменной угловой скорости ω ≠ 0, предлагается воспользоваться решением орбитальных уравнений первого порядка относительно переменных $~{{a}_{{(n)}}},{{b}_{{(n)}}},{{\varphi }_{{(n)}}}$ и ${{\theta }_{{(n)(0)}}}$.

Используя указанные орбитальные параметры, которые заданы выражениями (3.7)–(3.8), (3.13)–(3.14) и (3.15)–(3.16) можно показать, что новые дифференциальные уравнения для медленных переменных $~{{a}_{{(n)}}},{{b}_{{(n)}}},{{\varphi }_{{(n)}}}$ и ${{\theta }_{{(n)(0)}}}$ имеют следующие аналитические выражения:

(3.17)
${{\dot {a}}_{{(n)}}} = - 2{{{{\omega }}}_{{(n)}}}{{b}_{{(n)}}}~{\text{sin}}(n{{\theta }_{{(n)}}}){\text{/}}n\quad n = 2,3$
(3.18)
${{\dot {b}}_{{(n)}}} = 2{{{{\omega }}}_{{(n)}}}{{a}_{{(n)}}}{\text{sin}}(n{{\theta }_{{(n)}}}){\text{/}}n\quad (n) = 2,3~$
(3.19)
${{\dot {\varphi }}_{{(n)}}} = 2{{{{\omega }}}_{{(n)}}}(b_{{(n)}}^{2}{\text{co}}{{{\text{s}}}^{2}}({{\theta }_{{(n)}}}) - a_{{(n)}}^{2}{\text{si}}{{{\text{n}}}^{2}}({{\theta }_{{(n)}}}){\text{/}}(a_{{(n)}}^{2} - b_{{(n)}}^{2})\quad (n) = 2,3~$
(3.20)
${{\dot {\theta }}_{{(n)}}} = - 2{{{{\omega }}}_{{(n)}}}{{a}_{{(n)}}}{{b}_{{(n)}}}{\text{cos}}\left( {n{{\theta }_{{(n)}}}} \right){\text{/}}(~a_{{(n)}}^{2} - b_{{(n)}}^{2}) + {{\Omega }_{{(n)}}}~\quad (n) = 2,3$

Здесь во всех дифференциальных уравнениях (3.17)–(3.20) входная угловая скорость ${{\omega }}$ соответствует выражению

${{{{\omega }}}_{{(n)}}} = n{{k}_{b}}{{\omega }}$
где kb – коэффициент Брайана, n – номер (2,3) рассматриваемой моды (формы) колебаний.

Дифференциальные уравнения (3.17)–(3.20) являются точными и явно зависят от входной угловой скорости ω основания комбинированного двухмодового инерциального датчика. Следует отметить, что здесь величина входной угловой скорости ω не имеет каких-либо абсолютных ограничений. Обычно (во многих реальных практических ситуациях) входная угловая скорость ω намного меньше, чем рабочие частоты Ω(n) рассматриваемых идеальных двухмерных осцилляторов. Более того, как выше отмечалось в таких инерциальных датчиках величины квадратур второй (${{b}_{{\left( 2 \right)}}})$ и третьей $({{b}_{{\left( 3 \right)}}})$ рабочих мод колебаний этих двухмерных осцилляторов абсолютно точно поддерживаются нулевыми (${{b}_{{\left( n \right)}}} = 0).$ Поэтому на основании точного уравнения (3.20) имеем следующие выражения:

${{\dot {\theta }}_{{(n)}}} \approx {{\Omega }_{n}},\quad {{\theta }_{{(n)}}} \approx {{\Omega }_{n}}t + {{\theta }_{{(n)(0)}}}$

Можно также отметить, что правые части всех четырех дифференциальных уравнений (3.17)–(3.20) являются практически периодическими с периодами пропорциональными двум рабочим модам колебаний рассматриваемых идеальных двухмерных осцилляторов.

Более того, за полные периоды T2 и T3 колебаний на второй Ω2$({{Т}_{2}} = 2\pi {\text{/}}{{\Omega }_{2}})$ и третьей Ω3$({{Т}_{3}} = 2\pi {\text{/}}\Omega _{3}^{{}}$) резонансных частотах (соответствующих двум рабочим модам) все орбитальные параметры, за исключением двух орбитальных углов θ(2) и θ(3), остаются практически постоянными величинами. Поэтому приближенные решения уравнений (3.17)–(3.19) в течение указанных полных периодов определяются следующими выражениями:

(3.21)
${{a}_{{\left( n \right)}}}\left( {t + T} \right) \approx a_{n}^{{}}\left( t \right) - {{{{\omega }}}_{{\left( n \right)}}}{{b}_{{\left( n \right)}}}\left( t \right){\text{/}}\mathop \smallint \limits_t^{t + T} {\text{sin}}(n{{\theta }_{{\left( n \right)}}})dt$
(3.22)
${{b}_{{\left( n \right)}}}\left( {t + T} \right) \approx {{b}_{n}}\left( t \right) + {{{{\omega }}}_{{\left( n \right)}}}{{a}_{{\left( n \right)}}}(t){\text{/}}\mathop \smallint \limits_t^{t + T} {\text{sin}}(n{{\theta }_{{\left( n \right)}}})dt$
(3.23)
${{\varphi }_{{(n)}}}\left( {t + T} \right) \approx {{\varphi }_{n}}(t) + \frac{{2{{\omega }_{{\left( n \right)}}}}}{{(~a_{{\left( n \right)}}^{2}(t) - b_{{\left( n \right)}}^{2}(t))}}\mathop \smallint \limits_t^{t + T} (b_{{\left( n \right)}}^{2}{\text{co}}{{{\text{s}}}^{2}}({{\theta }_{{(n)}}}) - (b_{{\left( n \right)}}^{2}{\text{si}}{{{\text{n}}}^{2}}({{\theta }_{{(n)}}}))dt~~~~~$

Одновременно имеем

$\mathop \smallint \limits_t^{t + T} {\text{sin}}(n{{\theta }_{{\left( n \right)}}})dt = 0,\quad \mathop \smallint \limits_t^{t + T} {{\sin }^{2}}{{\theta }_{{\left( n \right)}}}dt = \mathop \smallint \limits_t^{t + T} {{\cos }^{2}}{{\theta }_{{\left( n \right)}}}dt = 1{\text{/}}2$

Поэтому очевидно, что уравнения (3.21)–(3.23) становятся равными следующим выражениям:

${{a}_{{\left( n \right)}}}(t + T) \approx {{a}_{n}}\left( t \right)$
${{b}_{{\left( n \right)}}}\left( {t + T} \right) \approx {{b}_{n}}\left( t \right)$
${{\varphi }_{{(n)}}}\left( {t + T} \right) \approx {{\varphi }_{n}}\left( t \right) + \frac{{{{{{\omega }}}_{{\left( n \right)}}}(~b_{{\left( n \right)}}^{2}(t) - a_{{\left( n \right)}}^{2}(t))}}{{(~a_{{\left( n \right)}}^{2}(t) - b_{{\left( n \right)}}^{2}(t))}}$

Аналогичные результаты могут быть получены при решении следующих более простых дифференциальных уравнений первого порядка:

(3.24)
${{\dot {a}}_{{\left( n \right)}}}\left( t \right) = 0,\quad {{\dot {b}}_{{\left( n \right)}}}\left( t \right) = 0,\quad {{\dot {\varphi }}_{{(n)}}}(t) = - {{\omega }_{{(n)}}},\quad {{\dot {\theta }}_{{(n)}}} = {{\Omega }_{n}}$

Таким образом, что касается долговременного функционирования рассматриваемого двухмодового (n = 2, 3) гироскопа – идеального осциллятора класса неуправляемого “обобщенного” маятника Фуко, то есть исследуя изменения основных орбитальных параметров ${{\dot {a}}_{{(n)}}},{{\dot {b}}_{{(n)}}},{{\dot {\varphi }}_{{(n)}}}$ и ${{\dot {\theta }}_{{(n)}}}$ на достаточно большом общем числе периодов наблюдения Tn, то можно заметить, что все указанные выше переменные достаточно точно соответствуют дифференциальным уравнениям вида (3.24). Данные уравнения описывают два вибрирующих эллипса, которые имеют постоянные формы $({{a}_{{(n)}}} = {{b}_{{(n)}}}$ = = const) и прецессируют с постоянной угловой скоростью. Поскольку системы координат, в которых прецессируют указанные эллипсы, обычно фиксируются относительно измерительных (приборных) осей комбинированного гироскопа, то в инерциальном пространстве (неподвижных звезд) оба представленных эллипса прецессируют с нулевой угловой скоростью и остаются неподвижными. Тем самым подтверждается наличие известных гироскопических членов Кориолиса в исходных дифференциальных уравнениях вида (3.1)–(3.2), описывающих поведение “обобщенного” неуправляемого маятника Фуко.

4. Способ определения углов поворота двухмодового гироскопа. Для реализации нового способа функционирования двухмодового “обобщенного” неуправляемого маятника Фуко необходимо в каждой конкретной конструкции нового волнового твердотельного гироскопа организовать достаточно точный съем первичной информации перемещений двух материальных точек, которые показаны на рис. 1. и рис. 2.

В предлагаемом новом способе необходимо вычислять нормированные энергии E(n) (n = 2, 3) и/или амплитуды a(n) колебаний двух осцилляторов и их кинетические моменты Hn (n = 2, 3) и/или квадратуры b(n) колебаний в соответствии с формулами (3.9) и (3.10). Определив полные энергии колебаний и их кинетические моменты можно достаточно точно контролировать по формулам (3.7) и (3.8) соответствующие амплитуды и квадратуры двух рабочих мод (форм) колебаний механических стоячих волн.

Отметим, что все вычисления по указанным выше формулам основываются только на точных измерениях переменных ${{x}_{{\left( n \right)}}}\left( t \right)$ и ${{y}_{{\left( n \right)}}}\left( t \right),$ а также, соответственно, их первых производных ${{\dot {x}}_{{\left( n \right)}}}\left( t \right)$ и ${{\dot {y}}_{{\left( n \right)}}}\left( t \right),~$которые задают положение волны на кромке резонатора. Этих первичных данных полностью достаточно для определения двух искомых углов 2φ2 и 3φ3 наклона рассматриваемых эллипсов колебаний (см. рис. 1 и рис. 2) в соответствие с исходными формулами (3.13) и (3.14), что и представляет собой конечную цель нового способа реализации “обобщенного” неуправляемого маятника Фуко – комбинированного (двухмодового) свободного (интегрирующего) ВТГ. При произвольных начальных условиях аналитические выражения (3.3)–(3.4) определяют в горизонтальной плоскости $\left( {x,y} \right)$ два вибрирующих эллипса, которые соответствуют двум рабочим модам (формам) колебаний.

В случае, когда эллипсы вырождаются в отрезки прямых, решения (3.3)–(3.4) определяют в рассматриваемых идеальных двухмерных осцилляторах механические стоячие волны, которые обладают важными инерционными свойствами. В случае противоположного вырождения, когда соответствующие эллипсы превращаются в окружности, формулы (3.3)–(3.4) определяют в этих же осцилляторах бегущие волны, которые не обладают необходимыми инерционными свойствами. Исходя из этого, для самых простых прикладных способов реализации двухмодовых свободных ВТГ, достаточно поддерживать заданные амплитуды ${{a}_{{(n)}}} = {\text{const}}$ и нулевые квадратуры ${{b}_{{(n)}}}$ = 0 в узлах двух форм колебаний кромки полусферического резонатора ВТГ.

Можно показать, что для режима свободной волны и применительно к третьей моде (форме стоячей волны) колебаний для высокодобротной кварцевой полусферы, имеем следующую формулу прецессию угла волны:

${{\varphi }_{b}} = - 0.248\mathop \smallint \limits_0^t \omega \left( t \right)dt$
что соответствует повороту осей колебаний стоячей волны относительно кромки оболочки на угол 22.32 град. или относительно инерциального пространства на угол 67.68 град. при повороте основания данной оболочки на фиксированный угол 90 град.

В данном способе реализации режима измерения углов поворота основания двухмодового инерциального датчика относительно исходного (начального) положения необходимы два независимых канала съема первичной информации измерения положения механической стоячей волны колебаний и определения произвольных поворотов основания в соответствии с формулами преобразований (3.13)–(3.14), поэтому точность предлагаемого способа реализации нового двумодового интегрирующего гироскопа приблизительно в 1.4 раза превышает точность классического одномодового ВТГ.

Что касается прикладных аспектов реализации теории интегрирующих гироскопов на базе новых конструкций [23, 24] двухмодовых волновых твердотельных гироскопов, то следует отметить, что в уравнениях (3.1)–(3.2) следует, вместо входной угловой скорости ω, ввести общий параметр $n{{k}_{b}}$ω, где n – номер рассматриваемой моды (формы) колебаний, kb – коэффициент Брайана конкретной реализации обобщенного маятника Фуко.

5. Заключение. Выполненные в данной работе теоретические исследования функционирования новых двухмодовых инерциальных датчиков ориентации позволяют сформулировать следующие основные результаты:

1. Теория двумодовых инерциальных датчиков ориентации позволяет синтезировать точную математическую модель функционирования новых свободных гироскопов семейства “обобщенный” неуправляемый маятник Фуко.

2. Математическая модель двумодового ВТГ обычно используется для изучения перемещений кромки высокодобротного полусферического резонатора одновременно на второй и третьей рабочих модах (формах) упругих колебаний и создания методов точного съема первичной информации о положении механической стоячей волны.

3. Два одновременно функционирующих канала инерциальной информации повышают точность предлагаемого способа реализации двухмодового интегрирующего гироскопа приблизительно в 1.4 раза по сравнению с точностью классического одномодового ВТГ.

Список литературы

  1. Foucault L. Demonstration physique du mouvement de la Terre au moyen du pendule // C.r. Acad. sci. Paris, 1851. V. 32. P. 135–138.

  2. Kamerlingh Onnes H. Nieuwe bewijzen voor de aswenteling der aarde. Ph. D. Disertation. Groningen, Netherlands, 1879.

  3. Quick W.H. Theory of vibrating string as an angular motion sensor // Trans. ASME. Ser. E. J. Appl. Mech. 1964. V. 31. № 3. P. 523–534.

  4. Stiles J.C. Vibrating ring gyro // U.S. Patent. No. 3, 924, 475. 1975.

  5. Loper E.J., Lynch D.D. Sonic Gyro Fabrication and Testing, Delco Electronics Division, report R77-64, August 1977.

  6. Loper E.J., Lynch D.D. Sonic Vibration Bell Gyro // US Patent. No. 4, 157, 041. 1979.

  7. Loper E.J., Lynch D.D. The HRG: a new low-noise inertial rotation sensor // Proc. 16th Joint Services Data Exchange for Inertial Systems. Los Angeles. 1982. P. 432–433.

  8. Loper E.J., Lynch D.D. Projected system performance based on recent HRG test results // IEEE/AIAA 5th Digital Avionics Systems Conference, 31 Oct. 3 Nov. 1983. P. S83–105.

  9. Loper E.J., Lynch D.D. Vibratory rotational sensor. EU Patent, No. 0141621 A2. 1984.

  10. Lynch D.D. Vibrating gyro analysis by method of averaging // 2nd Saint-Petersburg Interv. Conf. On Gyroscopic Technology and Navigation. St.-Petersburg, 1995. P. 26–34.

  11. Журавлев В.Ф., Климов Д.М. Волновой твердотельный гироскоп. М.: Наука, 1985. 125 с.

  12. Burdess J.S. The dynamics of a thin piezoelectric cylinder gyroscope // Proc. Inst. Mech. Engrs. (London). 1986. V. 200. № C4. P. 271–280.

  13. Koning M.G. Vibrating Cylinder Gyroscope and Method // US Patent. No. 4, 793, 195. 1988.

  14. Fox C.H.J. Vibrating cylinder rate gyro, theory of operation and error analysis // DGON Symposium Gyro Technology. Stuttgart, 1988. P. 5.0–5.23.

  15. Scott W.B. Delco makes low-cost gyro prototype // Aviation Week and Space Technology. 25 October 1982. P. 64–72.

  16. Журавлев В.Ф. Теоретические основы волнового твердотельного гироскопа (ВТГ) // Изв. РАН. МТТ. 1993. № 3. С. 6–19.

  17. Leger P. Quapason – a new low-cost vibrating gyroscope // 3nd Saint-Petersburg Intern. Conf. On Integrated Navigation Systems. St.-Petersburg, 1996. Pt. 1. P. 143–149.

  18. Zhuravlev V., Perelyaev S., Borodulin D. The Generalized Foucault Pendulum is a 3D Integrating Gyroscopes Using the Three-Dimensional Precession of Standing Waves in a Rotating Spherically Symmetric Elastic Solid // 2019 DGON Inertial Sensors and Systems (ISS 2019). IEEE, 2019. P. 59–70.

  19. Ишлинский А.Ю. Ориентация, гироскопы и инерциальная навигация. М.: Наука, 1976. 670 с.

  20. Bryan G.H. On the beats in the vibrations of a revolving cylinder or bell // Proc. Camb. Phil. Soc. Vol VII. Nov. 24. 1890. P. 101–111.

  21. Журавлев В.Ф. Принципиальные вопросы теории новых гироскопических датчиков семейства “обобщенный маятник Фуко” // Проблемы механики. Сб. статей. К 90-летию со дня рождения А.Ю.Ишлинского / Под ред. Д.М. Климова. М.: Физмазлит, 2003. С. 369–386.

  22. Friedland B., Hutton M.F. Theory and Error Analysis of Vibrating-Member Gyroscope // IEEE Transactions on Automatic Control. 1978. V. AC-23. № 4. P. 545–556.

  23. Переляев С.Е., Бодунов Б.П., Бодунов С.Б. Волновой твердотельный гироскоп – инерциальный датчик нового поколения // Материалы ХXIV Санкт-Петербургской межд. конф. по интегрированным навигационным системам. СПб.: ОАО Концерн “ЦНИИ Электроприбор”, 2017. С. 287–290.

  24. Журавлев В.Ф., Переляев С.Е., Бодунов Б.П., Бодунов С.Б. Миниатюрный волновой твердотельный гироскоп нового поколения для бескарданных инерциальных навигационных систем беспилотных летательных аппаратов // XXVI Санкт-Петербургская международная конференция по интегрированным навигационным системам. СПб.: Концерн “ЦНИИ Электроприбор”, 2019. С. 250–254.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика твердого тела

Архивы выпусков Информация о журнале Отправить рукопись в журнал