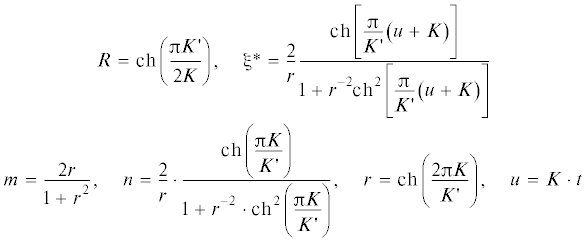Известия РАН. Механика твердого тела, 2021, № 5, стр. 92-98
К РАСЧЕТУ НЕЛИНЕЙНОГО ПРОДОЛЬНОГО ИЗГИБА СТЕРЖНЯ
К. Н. Анахаев *
Институт прикладной математики и автоматизации Кабардино-Балкарского научного центра Российской академии наук
Нальчик, Россия
* E-mail: anaha13@mail.ru
Поступила в редакцию 09.05.2020
После доработки 11.08.2020
Принята к публикации 07.09.2020
Аннотация
Рассматривается классическая задача нелинейного продольного изгиба стержня от действия сжимающей продольной силы. Получены расчетные зависимости в элементарных функциях для прямого аналитического определения основных параметров изогнутого стержня, таких как координаты очертания стержня, изгибаемые углы по длине стержня, эпюры моментов силы и внутренней энергии изгиба. Сравнение полученных расчетных значений с результатами известных (базовых) решений (Сикорского Ю.С., Попова Е.П., Захарова Ю.В. – Охоткина К.Г.) дало, в целом, достаточно близкую сходимость результатов (~1–2%), приведены примеры расчета, в том числе со сравнением с данными линейного расчета. Полученные результаты могут быть использованы как для теоретических исследований, так и для инженерных расчетов на практике, в частности при определении (обратным методом) жесткости стержней произвольного поперечного сечения, либо модуля упругости различных материалов (композитных) при известных сечениях стержня, в том числе при конструировании защитных сооружений от опасных склоновых геофизических процессов и др.
Введение. В статье рассматривается классическая задача нелинейного продольного изгиба тонкого упругого стержня от действия сжимающей продольной силы. Результаты имеющихся аналитических решений указанной задачи представлены в сложных эллиптических функциях Якоби (не выражающихся через элементарные функции) и определение по ним основных параметров изогнутого стержня, таких как координаты очертания стержня, изгибаемые углы по длине стержня, эпюры моментов силы и внутренней энергии изгиба, предполагает использование при проведении прикладных исследований численных методов.
Материалы и методы исследований. Строгое решение классической задачи нелинейного продольного изгиба тонкого упругого стержня длиной $L$ с жестко защемленным одним концом в центре координат $xOy$, на другой свободный конец которого действует продольная сжимающая сила P (рис. 1), рассматривалась в работах [1–4]. В частности, для данного случая на основе уравнения равновесия стержня, приведенного к виду уравнения нелинейного маятника [3–6]
(1)
$\frac{{{{d}^{2}}{{\theta }}}}{{d{{l}^{2}}}} + \frac{P}{{EJ}}\sin {{\theta }} = \frac{{{{d}^{2}}{{\theta }}}}{{d{{t}^{2}}}} + {{{{\beta }}}^{2}}\sin {{\theta }} = 0$(2)
${{\theta }} = 2\arcsin \left[ {{{\lambda }} \cdot {\text{sn}}\left( {u,{{\lambda }}} \right)} \right]$В формулах (1) и (2) даны следующие обозначения: E – модуль упругости материала стержня J; – момент инерции сечения стержня; $EJ$ – изгибная жесткость стержня; $l$ – текущее значение длины дуги стержня; $t = l{\text{/}}L$ – приведенная длина стержня; β = = $\sqrt {\frac{{P{{L}^{2}}}}{{EJ}}} $ – силовой коэффициент подобия [3]; ${\text{sn}}\left( {u,{{\lambda }}} \right)$ – эллиптический синус Якоби при модуле ${{\lambda }} = \sin {{\alpha }}$ (α – модулярный угол) и аргументе $u = K\left( {{\lambda }} \right) \cdot t$, где $K\left( {{\lambda }} \right)$ – полный эллиптический интеграл 1 рода при модуле λ.
При этом собственное (относительное) значение силы $\bar {P}$ [2, 4, 5] для рассматриваемой схемы будет равно
где ${{P}_{E}} = {{\left( {\frac{{{\pi }}}{2}} \right)}^{2}}\frac{{EJ}}{{{{L}^{2}}}}$ – эйлерова критическая сила.В формуле (3) и далее обозначение модуля λ в эллиптических интегралах и функциях опущено для упрощения записей, то есть $K\left( {{\lambda }} \right) \equiv K$, $K{\kern 1pt} '\left( {{\lambda }} \right) \equiv K{\kern 1pt} '$, $E\left( {{\lambda }} \right) \equiv E$, $E({{\varphi }},{{\lambda }}) \equiv E{\text{(}}\varphi {\text{)}}$, ${\text{sn}}\left( {u,{{\lambda }}} \right) \equiv {\text{sn}}\left( u \right)$, ${\text{cn}}\left( {u,{{\lambda }}} \right) \equiv {\text{cn}}\left( u \right)$, ${\text{dn}}\left( {u,{{\lambda }}} \right) \equiv {\text{dn}}\left( u \right)$.
В результате интегрирования соотношений $dx{\text{/}}dl = {\text{cos}}\theta = 1 - 2{{{{\lambda }}}^{2}}{\text{s}}{{{\text{n}}}^{2}}(u)$ и $dy{\text{/}}dl$ = sinθ = 2λ · sn(u)dn(u), где dn(u) – эллиптическая дельта-функция Якоби, вдоль длины стержня и преобразований в [4] получены расчетные зависимости для определения координат x и y изогнутой оси стержня в зависимости от значений эллиптических интегралов и функций Якоби в виде (при L = 1):
(4)
$x = - t + \frac{2}{K}E\left[ {{\text{am}}\left( u \right)} \right],\quad y = \frac{{2{{\lambda }}}}{K}\left[ {1 - {\text{cn}}\left( u \right)} \right]$Следует отметить, что выполнение прикладных аналитических расчетов для инженерных задач по полученным зависимостям (4) с эллиптическими функциями и интегралами (не выражающимися через элементарные функции) представляет собой значительные математические трудности, связанные с использованием специальных графиков и таблиц, необходимостью нелинейно-перекрестного (и обратного) интерполирования их данных и т.д. Результаты же численных решений, определяя дискретные значения специальных функций (интегралов) в отдельных точках, ограничены в возможностях выявления обобщенных причинно-следственных связей исходных факторов и оценке их влияния на итоговые результаты [11–14].
В связи с этим, ниже приводятся расчетные зависимости, позволяющие выразить вышеизложенные результаты в элементарных функциях, полученных на основе гидромеханических решений (с погрешностью ≪1–2%), с расширением области определяемых характеристик стержня.
При этом для прямого расчета эллиптического синуса Якоби sn(u) получена новая формула, основанная на работах [11, 12, 15], в виде:
(5)
${\text{sn}}\left( u \right) = \frac{{(1 + {{R}^{{ - 2}}})\sin \left( {\frac{{{{\pi }}u}}{{2K}}} \right)}}{{1 + {{R}^{{ - 2}}} \cdot {{{\sin }}^{2}}\left( {\frac{{{{\pi }}u}}{{2K}}} \right)}}\quad \left( {{\text{при}}\,\frac{{K{\kern 1pt} '}}{{2K}} \geqslant 1\,\,{\text{или}}\,\,{{\lambda }} \leqslant 0.171259} \right)$(6)
${\text{sn}}\left( u \right) = \frac{{\left( {{{\xi }}{\kern 1pt} *\; - n} \right)\left( {1 - m} \right)}}{{{{\xi }}{\kern 1pt} *\left( {1 + m - 2n} \right) + n\left( {1 + m} \right) - 2m}}\quad \left( {{\text{при}}\,\,\frac{{K{\kern 1pt} '}}{{2K}} < 1\,\,{\text{или}}\,\,{{\lambda }} > 0.171259} \right)$При этом эллиптический косинус Якоби cn(u) равен [1, 7, 8] ${\text{cn}}(u) = \sqrt {1 - {\text{s}}{{{\text{n}}}^{2}}\left( u \right)} $.
Значения K и $K{\kern 1pt} '$ (полного эллиптического интеграла 1 рода при дополнительном модуле ${{\lambda }}{\kern 1pt} ' = \sqrt {1 - {{{{\lambda }}}^{2}}} $) могут быть определены по зависимостям [10–14]:
(8)
$K = \frac{{{\pi }}}{2} + \frac{{\ln \sqrt {1 - {{{{\lambda }}}^{2}}} }}{{\ln [0.35(1 - 0.2\sqrt {1 - {{{{\lambda }}}^{2}}} )]}}$(9)
$\begin{gathered} K{\kern 1pt} ' = \frac{{2K}}{{{\pi }}}{\text{Arch}}\frac{{1 + \sqrt {1 - {{{{\lambda }}}^{2}}} }}{{{\lambda }}}\quad (при\;\;{{\lambda }} \leqslant 0.45) \\ K{\kern 1pt} ' = \frac{{{\pi }}}{2} + \frac{{\ln {{\lambda }}}}{{\ln \left[ {0.35\left( {1 - 0.2{{\lambda }}} \right)} \right]}}\quad (при\;\;{{\lambda }} > 0.45) \\ \end{gathered} $В зависимости (4) величина неполного эллиптического интеграла 2 рода $E\left[ {{\text{am}}\left( u \right)} \right]$ находится по нижеследующим усовершенствованным формулам (10) [14], подставляя в них вместо φ величину эллиптической амплитуды Якоби ${\text{am}}(u) = \arcsin \left[ {{\text{sn}}\left( u \right)} \right]$, в котором значение эллиптического синуса Якоби sn(u) рассчитывается по (5)–(9):
(10)
$\begin{array}{*{20}{c}} {} \\ {E\left( {{\varphi }} \right) = } \\ {} \end{array}\left\{ \begin{gathered} {{\varphi }} - \left( {{{\varphi }} - \sin {{\varphi }}} \right)\frac{{{{{{\alpha }}}_{0}}}}{{90^\circ }},\,\,\,0 \leqslant {{\varphi }} \leqslant 1 \hfill \\ \left[ {2E + \left( {1 - 0.1{{\pi }}\frac{{{{{{\alpha }}}_{0}}}}{{180^\circ }}} \right)\frac{{{{\pi }} - 2{{\varphi }}}}{{{{\varphi }} - 1}}} \right]\frac{{{{\varphi }} - 1}}{{{{\pi }} - 2}},\,\,\,1 < {{\varphi }} \leqslant \frac{{{\pi }}}{2} \hfill \\ \end{gathered} \right.$Результаты исследования и их обсуждение. Значения E(φ), полученные по зависимостям (10), достаточно близко (~1%) согласуются с графиками точного решения [7, 9], а для граничных участков полностью совпадают с точными формулами. В частности, при ${{{{\alpha }}}_{0}} = 0;$ π/2 и ${{\varphi }} = 0;$ π/2, соответственно, $E\left( {{{\varphi }},0} \right) = {{\varphi }}$; $E\left( {{{\varphi }},1} \right) = \sin {{\varphi }}$ и $E\left( {0,{{\lambda }}} \right) = 0$; $E\left( {{{\pi /}}2,{{\lambda }}} \right) = E$.
Таким образом, подставляя значения рекомендуемых расчетных зависимостей в элементарных функциях (5)–(11) в формулы (4), полностью рассчитываются координаты изогнутой оси стержня для заданных значений модуля λ. При этом, для свободного конца стержня (точки A: $t = 1$, $u = K$) формулы (4) получат вид:
Значения изгибающих моментов в любой точке стержня определяются по формуле [1] $M = \bar {P}\left( {{{y}_{A}} - y} \right)$, подставляя в которую величины yA, y из (12), (4) и преобразовывая, окончательно получим
Изгибающий момент M для концевой свободной точки стержня (t = 1) и точки заделки (t = 0) имеет, соответственно, минимальное (нулевое) и максимальное значения, ${{M}_{{\min }}} = 0$ и ${{M}_{{\max }}} = 2\bar {P}{{\lambda /}}K$.
Аналогично, угол ${{\theta }}$ между касательной к текущей точке изогнутого стержня и осью $0x$ (см. рис. 1), определяемый по формуле (2), для точек t = 1 и t = 0 принимает значения, соответственно, ${{{{\theta }}}_{{\max }}} = 2\arcsin \left( {{\lambda }} \right)$ и ${{{{\theta }}}_{{\min }}} = 0$.
Приращение угла изгиба θ вдоль длины стержня определится производной
(14)
${{\theta }}{\kern 1pt} ' = \frac{{d{{\theta }}}}{{dt}} = - 2{{\lambda }}K \cdot {\text{cn}}\left( {K \cdot t} \right)$Внутренняя энергия изгиба стержня V определится (при ${{\varphi }} = 0$) по зависимости [3]
(15)
$V = \bar {P}L\left\{ {\frac{2}{{{\beta }}}\left[ {E - E\left( {{\varphi }} \right)} \right] - 2(1 - {{{{\lambda }}}^{2}})} \right\} = 2\bar {P}L\left( {\frac{E}{{{\beta }}} + {{{{\lambda }}}^{2}} - 1} \right)$Вышеприведенные расчетные зависимости в элементарных функциях при заданных значениях модуля λ позволяют напрямую рассчитать все необходимые характеристики продольно изогнутого стержня. Для исходной же заданной величины силовой нагрузки $\bar {P}$ значение модуля λ находится методом подбора из зависимости (3), подставляя в нее вместо K его значение из формулы (8).
В нижеследующих таблицах 1 и 2 дается сравнение значений координат изогнутого стержня, подсчитанных по рекомендуемым зависимостям (4)–(12) с результатами базового решения Сикорского Ю.С. [1, с. 74, таблицы a , b], основанного на нелинейно-перекрестном (и обратном) интерполировании табличных данных, соответственно, при силовой нагрузке $\bar {P} = 1.293$ для заданных значений амплитуды ${{\varphi }} = {\text{am}}(u)$ = = arcsin[sn(K · t)], равных 0; 30°; 60°; 90°, и для концевой точки (t = 1) стержня при различных (девяти) значениях силовой нагрузки $\bar {P}$. При этом значения t получены обратным расчетом из заданных величин амплитуды ${{\varphi }}$.
Таблица 1.
Координаты изогнутого стержня при $\bar {P} = 1.293$ и заданных амплитудах $\varphi $
| Амплитуда φ (в град.) | Приведенная длина стержня $t$ | Координата $x$ | Координата $y$ | ||||
|---|---|---|---|---|---|---|---|
| базовое решение [1] | по автору (4)–(12) | % | базовое решение [1] | по автору (4)–(12) | % | ||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 30 | 0.299 | 0.277 | 0.275 | –0.6 | 0.096 | 0.096 | 0 |
| 60 | 0.629 | 0.469 | 0.457 | –2.5 | 0.360 | 0.358 | –0.7 |
| 90 | 1 | 0.560 | 0.577 | +3.0 | 0.720 | 0.715 | –0.7 |
Таблица 2.
Координаты концевой точки изогнутого стержня при силовых нагрузках $\bar {P}$
| Номера | Силовая нагрузка $\bar {P}$ | Координата $x$ | Координата $y$ | ||||
|---|---|---|---|---|---|---|---|
| базовое решение [1] | по автору (4)–(12) | % | базовое решение [1] | по автору (4)–(12) | % | ||
| I | 1.015 | 0.970 | 0.972 | +0.2 | 0.220 | 0.219 | –0.3 |
| II | 1.064 | 0.881 | 0.887 | +0.8 | 0.422 | 0.422 | 0 |
| III | 1.152 | 0.741 | 0.752 | +1.5 | 0.593 | 0.593 | 0 |
| IV | 11.293 | 0.560 | 0.577 | +3.0 | 0.720 | 0.718 | –0.2 |
| V | 1.518 | 0.349 | 0.363 | +4.2 | 0.792 | 0.787 | –0.6 |
| VI | 1.884 | 0.123 | 0.131 | +6.5 | 0.803 | 0.799 | –0.5 |
| VII | 2.541 | –0.107 | –0.108 | +1.2 | 0.750 | 0.748 | –0.3 |
| VIII | 4.029 | –0.340 | –0.345 | +1.4 | 0.625 | 0.624 | –0.1 |
| IX | 9.116 | –0.577 | –0.578 | +0.1 | 0.421 | 0.421 | 0 |
Как следует из таблиц 1 и 2, результаты подсчетов координат изогнутого стержня, в том числе и концевой точки стержня, при различных значениях силовой нагрузки $\bar {P}$ и амплитуд ${{\varphi }}$, подсчитанные по предлагаемым зависимостям на основе элементарных функций (4)–(12), достаточно близко (в целом ~ до 2–3%) согласуются с результатами базового решения Сикорского Ю.С. [1], основанным на нелинейно-перекрестном (и обратном) интерполировании табличных данных (Примечание: Отдельные отклонения в таблицах по координате x могут быть обусловлены, в частности, погрешностями интерполяции в базовом решении [1]).
Кроме этого, расчет по формулам (4)–(12) абсциссы концевой точки изогнутого стержня для заданной силовой нагрузки $\bar {P} = 2.160$ показал близкое совпадение (x = 0.011) с нулевым значением точного решения Попова Ю.С. [3, рис. 5.4 , с. 114].
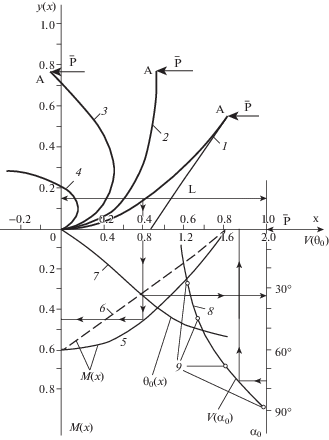
На рисунке приведена схема изогнутого стержня от действия продольной силовой нагрузки $\bar {P}$ с рассчитанными по рекомендуемым формулам (4)–(12) значениями:
– для заданных величин λ2, равных $\sqrt {0.2} $ (${{\alpha }} = 0.1476{{\pi }}$), $\sqrt {0.5} $ (${{\alpha }} = 0.25{{\pi }}$), $\sqrt {0.85} $ (α = $0.3734{{\pi }}$), $\sqrt {0.99999} $ (${{\alpha }} = 0.4990{{\pi }}$) (кривые 1–4), близко совпадающих с очертаниями указанных кривых по численному расчету [4, рис. 3 , с. 129];
– для эпюр изгибающих моментов силы $M\left( x \right)$ по длине стержня при значении λ2 = $\sqrt {0.2} $ с учетом нелинейности (кривая 5) и линейной задачи (прямая 6);
– для графиков углов изгиба ${{{{\theta }}}_{0}}\left( x \right) = \frac{{{\theta }}}{{{\pi }}} \cdot {{180}^{{^{ \circ }}}}$ (между касательной к текущей точке и осью 0x – в градусах) при ${{{{\lambda }}}^{2}} = \sqrt {0.2} $ (кривая 7) и внутренней энергии изгиба стержня $V({{{{\alpha }}}_{0}})$ в зависимости от значений модулярного угла ${{{{\alpha }}}_{0}}$ (кривая 8);
– для точек на кривой внутренней энергии изгиба $V\left( {{{{{\alpha }}}_{0}}} \right)$, соответствующих стержням с значениями λ2, равными $\sqrt {0.2} $; $\sqrt {0.5} $; $\sqrt {0.85} $; $\sqrt {0.99999} $ (точки 9).
Как следует из рисунка, максимальные значения изгибающих моментов $M\left( x \right)$ и внутренней энергии изгиба $V\left( {{{{{\alpha }}}_{0}}} \right)$ сосредоточены в начальной точке задела стержня О, в которой угол ${{{{\theta }}}_{0}}\left( x \right)$ сопряжения с осью $0x$ имеет нулевое значение. При этом сравнительная оценка эпюр изгибающих моментов по длине стержня для нелинейной (кривая 5) и линейной (прямая 6) задач показывает значительное занижение значений последней. В частности, занижение значений для рассмотренного случая изгибаемого стержня при ${{{{\lambda }}}^{2}} = \sqrt {0.2} $ достигает до 30% и более, что указывает на неприемлемость применения “чисто линейного” метода при решении прикладных задач на практике.
Заключение. В работе рассматривается классическая задача нелинейного продольного изгиба стержня от действия сжимающей продольной силы. При этом получены расчетные зависимости в элементарных функциях для прямого аналитического определения основных параметров изогнутого стержня, таких как координаты очертания стержня, изгибаемые углы по длине стержня, эпюры моментов силы и внутренней энергии изгиба. Сравнение полученных расчетных значений с результатами известных (базовых) решений (Сикорского Ю.С., Попова Е.П., Захарова Ю.В. – Охоткина К.Г.) дало в целом достаточно близкую сходимость результатов (~1–2%), приведены примеры расчета, в том числе сj сравнением с данными линейного расчета. Полученные результаты могут быть использованы как для теоретических исследований, так и для инженерных расчетов на практике, в том числе и при определении (обратным методом) жесткости стержней произвольного поперечного сечения, либо модуля упругости различных материалов (композитных) при известных сечениях стержня, в том числе при конструировании защитных сооружений от опасных склоновых геофизических процессов и др.
Рис. 1.
Расчетная схема продольного изгиба стержня: 1–4 – очертания изогнутых стержней для заданных значений λ2, равных $\sqrt {0.2} $, $\sqrt {0.5} $, $\sqrt {0.85} $, $\sqrt {0.99999} $; 5, 6 – эпюры моментов силы M(x) по длине стержня при ${{\lambda }^{2}} = \sqrt {0.2} $ для нелинейной и линейной задач; 7, 8 – графики углов изгиба ${{\theta }_{0}}\left( x \right)$ по длине стержня при ${{\lambda }^{2}} = \sqrt {0.2} $ и внутренней энергии изгиба стержня $V({{\alpha }_{0}})$ в зависимости от модулярного угла ${{\alpha }_{0}}$; 9 – точки энергии изгиба $V({{\alpha }_{0}})$, соответствующие стержням с значениями λ2, равными $\sqrt {0.2} $, $\sqrt {0.5} $, $\sqrt {0.85} $, $\sqrt {0.99999} $.
Список литературы
Сикорский Ю.С. Элементы теории эллиптических функций с приложениями к механике. М.–Л.: НКТП СССР, 1936. 365 с.
Коллатц Л. Задачи на собственные значения с техническими приложениями. М.: Наука, 1968. 503 с.
Попов Е.П. Теория и расчет гибких упругих стержней. М.: Наука, 1986. 294 с.
Захаров Ю.В., Охоткин К.Г. Нелинейный изгиб тонких упругих стержней // Прикладная механика и техническая физика. 2002. Т. 43. № 5. С. 124–131.
Захаров Ю.В., Захаренко А.А. Динамическая потеря устойчивости в нелинейной задаче о консоли // Вычислительные технологии. 1999. Т. 4. № 1. С. 48–54.
Анахаев К.Н. К расчету математического маятника // Доклады Академии наук. 2014. Т. 459. № 3. С. 288–293.
Янке Е., Эмде Ф., Леш Ф. Специальные функции. М.: Наука, 1977. 342 с.
Милн-Томсон Л. Эллиптические функции Якоби и тэта-функции / Справочник по специальным функциям. Под ред. Абрамовица М., Стиган И. М.: Наука, 1979. С. 380–400.
Милн-Томсон Л. Эллиптические интегралы / Справочник по специальным функциям. Под ред. Абрамовица М., Стиган И. М.: Наука, 1979. С. 401–441.
Анахаев К.Н. О методах расчёта потенциальных (фильтрационных) потоков на основе эллиптических интегралов Якоби // Гидротехническое строительство. 2008. № 8. С. 7–9.
Анахаев К.Н. О совершенствовании гидромеханических методов расчета потенциальных (фильтрационных) потоков // “Инженерные системы – 2009”. Труды междунар. науч.-практ. конф. Т. 2. М.: РУДН, 2009. С. 588–595.
Анахаев К.Н. Об определении эллиптических функций Якоби // Вестник РУДН. Серия: Математика. Информатика. Физика. 2009. № 2. С. 90–95.
Анахаев К.Н. О полных эллиптических интегралах 3-го рода в задачах механики // Доклады Академии наук. 2017. Т. 473. № 2. С. 151–153.
Анахаев К.Н. Эллиптические интегралы в нелинейных задачах механики // Доклады Российской Академии наук. Физика. Технические науки. 2020. Т. 491. № 2. С. 24–29.
Анахаев К.Н. О расчете потенциальных потоков // Доклады Академии наук. 2005. Т. 401. № 3. С. 337–341.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика твердого тела