Известия РАН. Механика твердого тела, 2021, № 5, стр. 99-112
РАСЧЕТ ФОРМООБРАЗОВАНИЯ КОСМИЧЕСКОЙ ЗОНТИЧНОЙ АНТЕННЫ ПРИ СИЛЬНОМ ИЗГИБЕ РАДИАЛЬНЫХ СТЕРЖНЕЙ, СВЯЗАННЫХ ПО ПАРАЛЛЕЛЯМ РАСТЯЖИМЫМИ ТРОСАМИ
С. В. Русских a, b, *, Ф. Н. Шклярчук b, a, **
a Московский авиационный институт (национальный исследовательский университет)
Москва, Россия
b Институт прикладной механики Российской академии наук
Москва, Россия
* E-mail: sergey.russkih@rambler.ru
** E-mail: shklyarchuk@list.ru
Поступила в редакцию 20.06.2020
После доработки 28.07.2020
Принята к публикации 31.08.2020
Аннотация
Рассматривается циклически симметричная зонтичная антенна, каркас которой состоит из гибких нерастяжимых радиальных стержней, связанных в узлах по параллелям растяжимыми тросами. В начальном транспортировочном положении многозвенные стержни уложены в упаковки, ориентированные в направлении оси системы. После устранения связей упаковок стержни развертываются в радиальных плоскостях под действием упругих пружин, соединяющих звенья, и фиксируются в прямолинейных положениях под заданным углом по отношению к оси, при котором все тросы, связывающие однотипные узлы стержней, принимают форму правильных многоугольников, оставаясь при этом ненатянутыми. Далее под действием силы демпфирующего гидроцилиндра с предварительно сжатыми пружинами корневые части всех стержней медленно поворачиваются до упоров. В конечном положении радиальные стержни, соединенные в узлах натянутыми тросами, принимают изогнутую форму. Жесткости тросов на растяжение определяются так, чтобы радиальные и осевые координаты узлов изогнутых стержней совпадали с координатами точек заданной поверхности вращения.
Построена модель сильного изгиба гибкого нерастяжимого стержня с учетом действующих на него в узлах неизвестных радиальных реакций натянутых тросов. Звенья стержня рассматриваются как последовательно соединенные между собой в узлах “консольные” элементы в местных системах координат, которые могут совершать большие перемещения и повороты. Изгиб каждого элемента описывается двумя заданными функциями, усадка элемента за счет изгиба учитывается в квадратичном приближении. Полученные нелинейные уравнения деформирования системы с учетом геометрических связей в узлах решаются по методу последовательных приближений относительно неизвестных реакций тросов. По полученным значениям реакций затем при заданных координатах узлов определяются требуемые жесткости тросов на растяжение.
В качестве примера расчета рассмотрена параболическая антенна при различных числах радиальных стержней и составляющих из звеньев. Выполнены оценки точности предложенной расчетной модели формообразования антенны.
1. Введение. Составные космические антенны больших размеров выводятся в космос в сложенном состоянии и развертываются в условиях вакуума и невесомости.
Вопросы проектирования и расчета складных антенн зонтичного типа рассмотрены в книге [1]. Обзор современных трансформируемых конструкций антенн представлен в [2, 3]. Применение метода конечных элементов и коммерческих программных комплексов для численного моделирования статики и динамики крупногабаритных космических антенн рассмотрено в [4–8]. Нелинейные уравнения динамики развертывания плоской системы последовательно соединенных упругими шарнирами с упорами гибких нерастяжимых стержней, сложенных в начальном состоянии в упаковку, получены в [9, 10], где приведены аналитические выражения в виде формул для всех коэффициентов уравнений в обобщенных координатах.
Заданная деформированная форма антенны после развертывания и успокоения колебаний получается при проектировании конструкции как статически неопределимой системы путем определения требуемых для устойчивого равновесия этой формы внутренних усилий силовых элементов. Для этого требуется решить обратную геометрически нелинейную задачу деформирования системы с ограничениями и определить необходимые геометрические и жесткостные параметры ее некоторых регулируемых элементов. В [11] разработан алгоритм численного решения геометрически нелинейной задачи формообразования космической зонтичной антенны в виде пологой параболической поверхности вращения с циклически симметрично расположенными гибкими радиальными стержнями, соединенными по параллелям растяжимыми тросовыми элементами. В настоящей работе этот подход обобщается для антенны с непологой поверхностью вращения. В этом случае при решении задачи формообразования за счет деформирования гибких радиальных стержней рассматривается их сильный изгиб с большими перемещениями и углами поворота элементов.
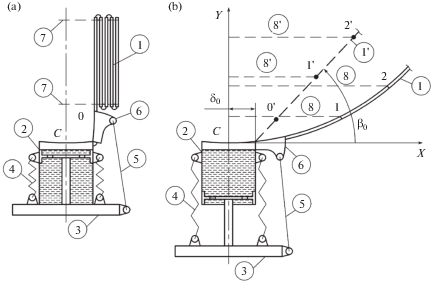
2. Постановка задачи. Схема предлагаемой циклически симметричной космической антенны зонтичного типа с n радиальными стержнями 1, каждый из которых состоит из m звеньев, показана на рис. 1 в сложенном состоянии (a) и в конечном деформированном состоянии (b). Раскрытие и формообразование антенны происходит следующим образом. По сигналу устраняется удерживающая связь между корпусом демпфирующего гидроцилиндра 2 и штоком 3 и начинается медленное движение штока под действием предварительно сжатых пружин 4, за счет чего с помощью тросов 5 и рычагов 6 упаковки стержней 1 поворачиваются в радиальных плоскостях. При некотором отклонении упаковок разрываются связи 7 и многозвенные стержни с упругими шарнирными соединениями развертываются с фиксацией на упорах в прямолинейном положении. Считается, что в некотором заданном отклоненном положении (1', рис. 1, b) выпрямившихся стержней (при угле ${{\beta }_{0}}$ между осью X и осью стержня) в силу выбора начальных длин участков тросов 8, соединяющих в плоскостях параллелей соответствующие узлы k = 1, 2, …, m стержней, эти участки становятся прямолинейными (без провисаний), но еще ненатянутыми. При этом все тросы k = 1, 2, …, m будут иметь форму правильных n-угольников. Следует заметить, что после быстрого (динамического) раскрытия упаковок упруго соединенных звеньев, каждый из n стержней станет прямолинейным в отклоненном на угол ${{\tilde {\beta }}_{n}} > {{\beta }_{0}}$ положении с некоторым разбросом по времени и по углам ${{\tilde {\beta }}_{n}}$. Отклонения стержней при медленном (квазистатическом) ходе штока 3 демпфирующего гидроцилиндра будут выравниваться под действием соединяющих их тросов k = 1, 2, …, m поскольку во всех n элементах каждого из этих тросов усилия при циклической симметрии системы должны быть одинаковы.
При повороте рычагов 6 до упора тросы будут растягиваться, а стержни изгибаться в радиальных плоскостях под действием реакций тросов в узлах k = 1, 2, …, m. Конечная изогнутая форма 1 стержня с растянутыми тросами 8 показана на рис. 1, b. Полотно антенны соединяется со стержнями в отдельных точках, включая узлы; в сложенном состоянии оно находится в пространстве между упаковками стержней. При раскрытии и формообразовании составной конструкции антенны реакции полотна не учитываются.
Осесимметричная поверхность антенны имеет заданную форму $Y = F(X)$, рис. 1, b. При проектировании и расчете составной циклический симметричной конструкции антенны требуется, чтобы координаты узловых точек k = 1, 2, …, m изогнутых радиальных стрежней совпадали с соответствующими координатами поверхности антенны ${{X}_{k}}$, ${{Y}_{k}} = F({{X}_{k}})$, k = 0, 1, …, m. Центральный участок C–0 после поворота рычага 6 до упора считается абсолютно жестким и профилированным по форме $Y = F(X)$; $X = Y$ = 0 в точке C и ${{X}_{0}} = {{a}_{0}}$, ${{Y}_{0}} = F({{a}_{0}})$, ${{\theta }_{0}} = {\text{arctg}}(F{\kern 1pt} '({{a}_{0}}))$ в точке 0. Упругая часть стержня состоит из $m$ звеньев примерно одинаковой длины ${{a}_{k}}$, k = 1, 2, …, m (для удобства складывания их в упаковки). При заданных значениях ak координаты узлов изогнутого нерастяжимого стержня Xk, $k = 1,2, \ldots ,m$ вычисляются последовательно из соотношений
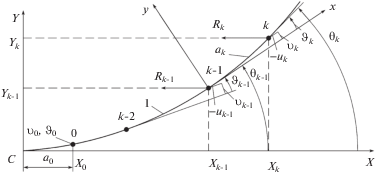
Для описания сильного изгиба стержня каждое его звено k = 1, 2, …, m будем рассматривать как конечный элемент (КЭ) в местной системе координат xy, который в узле k – 1 жестко связан с $(k - 1)$-м КЭ, рис. 2. Координаты и угол наклона оси стержня в узле k – 1 равны ${{X}_{{k - 1}}}$, ${{Y}_{{k - 1}}}$, ${{\theta }_{{k - 1}}}$. Относительное поперечное перемещение $\upsilon (x)$ и угол поворота $\vartheta (x)$ k-го КЭ как консольного стержня длины ak записываются в виде [11]
(2.1)
$\begin{gathered} \upsilon (x) = {{\upsilon }_{k}}{{\varphi }_{k}}(x) + {{\vartheta }_{k}}{{\psi }_{k}}(x),\quad \vartheta (x) = \upsilon {\kern 1pt} '(x) \\ {{\varphi }_{k}}(x) = 3\frac{{{{x}^{2}}}}{{a_{k}^{2}}} - 2\frac{{{{x}^{3}}}}{{a_{k}^{3}}},\quad {{\psi }_{k}}(x) = \frac{{{{x}^{3}}}}{{a_{k}^{2}}} - \frac{{{{x}^{2}}}}{{{{a}_{k}}}} \\ \end{gathered} $(2.2)
${{u}_{k}} = - \frac{1}{2}\int\limits_0^{{{a}_{k}}} {{{{(\upsilon {\kern 1pt} ')}}^{2}}dx} = - \frac{1}{2}\left( {\frac{6}{{5{{a}_{k}}}}\upsilon _{k}^{2} - \frac{1}{{10}}{{\upsilon }_{k}}{{\vartheta }_{k}} + \frac{{{{a}_{k}}}}{{15}}\vartheta _{k}^{2}} \right)$Потенциальная энергия изгиба стержня
(2.3)
$П = \sum\limits_{k = 1}^m {{{П}_{k}}} ,\quad {{П}_{k}} = \frac{1}{2}\frac{{12E{{I}_{k}}}}{{a_{k}^{3}}}\left( {\upsilon _{k}^{2} - {{a}_{k}}{{\upsilon }_{k}}{{\vartheta }_{k}} + \frac{{a_{k}^{2}}}{3}\vartheta _{k}^{2}} \right)$Перемещения и углы поворота в узлах стержня k = 1, 2, …, m определяются следующим образом
(2.4)
$\begin{gathered} {{X}_{k}} = {{a}_{0}} + \sum\limits_{i = 1}^k {[({{a}_{i}} + {{u}_{i}})\cos {{\theta }_{{i - 1}}} - {{\upsilon }_{i}}\sin {{\theta }_{{i - 1}}}]} \\ {{Y}_{k}} = {{\upsilon }_{0}} + \sum\limits_{i = 1}^k {[({{a}_{i}} + {{u}_{i}})\sin {{\theta }_{{i - 1}}} + {{\upsilon }_{i}}\cos {{\theta }_{{i - 1}}}]} \\ {{\theta }_{k}} = {{\vartheta }_{0}} + \sum\limits_{i = 1}^k {{{\vartheta }_{i}}} \\ \end{gathered} $Вариация работы сил Rk на перемещениях $\delta {{X}_{k}}$ (рис. 2) записывается в виде
(2.5)
$ - \delta А = \sum\limits_{k = 1}^m {{{R}_{k}}\delta {{X}_{k}}} = \sum\limits_{k = 1}^m {{{R}_{k}}} \sum\limits_{i = 1}^k {\left( {{{\xi }_{i}} + {{y}_{i}}\sum\limits_{j = 1}^{i - 1} {\delta {{\vartheta }_{j}}} } \right)} $Двойная и тройная суммы в (2.5) преобразуются как
Тогда получим
(2.6)
$ - \delta А = \sum\limits_{k = 1}^m {\left[ {\delta {{\upsilon }_{k}}({{c}_{{k - 1}}}{{p}_{k}} - {{s}_{{k - 1}}})\sum\limits_{i = k}^m {{{R}_{i}}} + \delta {{\vartheta }_{k}}\left( {{{q}_{k}}{{c}_{{k - 1}}}\sum\limits_{i = k}^m {{{R}_{i}}} + (1 - {{\delta }_{{km}}})\sum\limits_{i = k + 1}^m {{{y}_{i}}\sum\limits_{j = i}^m {{{R}_{j}}} } } \right)} \right]} $Уравнения равновесия изогнутого стержня в обобщенных координатах ${{\upsilon }_{k}}$ и ${{\vartheta }_{k}}$, k = = 1, 2, …, m, получаются на основании принципа возможных перемещений $\delta П - \delta А$ = 0 и с учетом (2.3), (2.6) записываются в виде
(2.7)
$\begin{gathered} \frac{{12E{{I}_{k}}}}{{a_{k}^{3}}}\left( {{{\upsilon }_{k}} - \frac{{{{a}_{k}}}}{2}{{\vartheta }_{k}}} \right) + ({{c}_{{k - 1}}}{{p}_{k}} - {{s}_{{k - 1}}})\sum\limits_{i = k}^m {{{R}_{i}}} = 0 \\ \frac{{12E{{I}_{k}}}}{{a_{k}^{3}}}\left( { - \frac{{{{a}_{k}}}}{2}{{\upsilon }_{k}} + \frac{{a_{k}^{2}}}{3}{{\vartheta }_{k}}} \right) + {{q}_{k}}{{c}_{{k - 1}}}\sum\limits_{i = k}^m {{{R}_{i}}} + (1 - {{\delta }_{{km}}})\sum\limits_{i = k + 1}^m {{{y}_{i}}\sum\limits_{j = i}^m {{{R}_{j}}} } = 0 \\ k = 1,2, \ldots ,m \\ \end{gathered} $Приведем уравнения (2.7) к безразмерному виду. Для этого введем следующие обозначения:
(2.8)
$\begin{gathered} {{{\bar {\upsilon }}}_{k}} = \frac{{{{\upsilon }_{k}}}}{{{{a}_{k}}}},\quad {{{\bar {u}}}_{k}} = \frac{{{{u}_{k}}}}{{{{a}_{k}}}} = \frac{1}{2}({{p}_{k}}{{{\bar {\upsilon }}}_{k}} + {{{\bar {q}}}_{k}}{{\vartheta }_{k}}) \\ {{p}_{k}} = - \frac{1}{5}\left( {6{{{\bar {\upsilon }}}_{k}} - \frac{1}{4}{{\vartheta }_{k}}} \right),\quad {{{\bar {q}}}_{k}} = - \frac{1}{5}\left( {\frac{1}{3}{{\vartheta }_{k}} - \frac{1}{4}{{{\bar {\upsilon }}}_{k}}} \right) \\ \xi _{k}^{\upsilon } = {{c}_{{k - 1}}}{{p}_{k}} - {{s}_{{k - 1}}},\quad \xi _{k}^{\vartheta } = {{c}_{{k - 1}}}{{{\bar {q}}}_{k}},\quad {{\eta }_{i}} = \frac{{{{y}_{i}}}}{{{{a}_{i}}}} = - [(1 + {{{\bar {u}}}_{i}}){{s}_{{i - 1}}} + {{{\bar {\upsilon }}}_{i}}{{c}_{{i - 1}}}] \\ \end{gathered} $С учетом (2.8) уравнения (2.7) записываются в виде
Преобразуем двойную сумму во втором уравнении:
В результате уравнения (2.7) для обобщенных координат ${{\bar {\upsilon }}_{k}}$ и ${{\vartheta }_{k}}$, k = 1, 2, …, m будут иметь вид
(2.9)
$\begin{gathered} \frac{{12E{{I}_{k}}}}{{a_{k}^{2}}}\left( {{{{\bar {\upsilon }}}_{k}} - \frac{1}{2}{{\vartheta }_{k}}} \right) + \xi _{k}^{\upsilon }\sum\limits_{i = k}^m {{{R}_{i}}} = 0 \\ \frac{{12E{{I}_{k}}}}{{a_{k}^{2}}}\left( { - \frac{1}{2}{{{\bar {\upsilon }}}_{k}} + \frac{1}{3}{{\vartheta }_{k}}} \right) + \xi _{k}^{\vartheta }\sum\limits_{i = k}^m {{{R}_{i}}} + (1 - {{\delta }_{{km}}})\sum\limits_{i = k + 1}^m {{{R}_{i}}{{\zeta }_{{ki}}}} = 0 \\ k = 1,2, \ldots ,m \\ \end{gathered} $Уравнения (2.9) для их численного решения запишем в матричном виде в зависимости от векторов перемещений ${\mathbf{V}} = \{ {{\bar {\upsilon }}_{k}}\} $, углов поворота ${\mathbf{\Omega }} = \{ {{\vartheta }_{k}}\} $ и реакций тросов ${\mathbf{R}} = \{ {{R}_{k}}\} $:
(2.10)
$\begin{gathered} 12{\mathbf{G}}\left( {{\mathbf{V}} - \frac{1}{2}{\mathbf{\Omega }}} \right) + {\mathbf{AR}} = 0 \\ 12{\mathbf{G}}\left( { - \frac{1}{2}{\mathbf{V}} + \frac{1}{3}{\mathbf{\Omega }}} \right) + {\mathbf{BR}} = 0 \\ \end{gathered} $(2.11)
${\mathbf{B}} = \left[ {\begin{array}{*{20}{c}} {\xi _{1}^{\vartheta }}&{\xi _{1}^{\vartheta }}& \ldots &{\xi _{1}^{\vartheta }}&{\xi _{1}^{\vartheta }} \\ 0&{\xi _{2}^{\vartheta }}& \ldots &{\xi _{2}^{\vartheta }}&{\xi _{2}^{\vartheta }} \\ \ldots & \ldots & \ldots & \ldots & \ldots \\ 0&0& \ldots &{\xi _{{m - 1}}^{\vartheta }}&{\xi _{{m - 1}}^{\vartheta }} \\ 0&0& \ldots &0&{\xi _{m}^{\vartheta }} \end{array}} \right] + $3. Алгоритм решения задачи. Формообразование поверхности вращения (или в данном случае – изогнутого радиального стержня каркаса, на который накладывается с некоторым натяжением мягкая оболочка) согласно уравнению $Y = F(X)$ может осуществляться в пределах рассматриваемых элементов за счет выбора реакций ${{R}_{k}}$ натянутых тросов, расположенных в плоскостях параллелей, или за счет изгибных жесткостей $E{{I}_{k}}$ элементов радиальных стержней, или за счет изменения тех и других одновременно. Решение такой нелинейной задачи является неединственным и в некоторых областях изменения указанных параметров оно может не существовать.
Здесь рассматривается случай, когда уравнение заданной формы $Y = F(X)$ удовлетворяется в точках k = 1, 2, …, m за счет регулируемых реакций тросов ${{R}_{k}}$ только по координатам ${{X}_{k}}$ и ${{Y}_{k}} = F({{X}_{k}})$, а углы наклона ${{\theta }_{k}}$ в этих точках остаются свободными, т.е. не требуется выполнение условия ${{\theta }_{k}} = {\text{arctg}}(F'({{X}_{k}}))$. Жесткости $E{{I}_{k}}$ элементов изгибаемого стержня считаются заданными.
Эквивалентное перемещение ${{\upsilon }_{k}}$ изогнутого стержня, точно соответствующее заданной форме по координатам Xk, ${{Y}_{k}} = F({{X}_{k}})$ определяется из кинематических соотношений:
(3.1)
$\upsilon {}_{k} = - ({{X}_{k}} - {{X}_{{k - 1}}})\cos {{\theta }_{{k - 1}}} + ({{Y}_{k}} - {{Y}_{{k - 1}}})\cos {{\theta }_{{k - 1}}},\quad k = 1,2, \ldots ,m$В результате безразмерные перемещения ${{\bar {u}}_{k}}$, ${{\bar {\upsilon }}_{k}}$ и параметры (2.8), входящие в уравнения (2.9) и, соответственно, в нелинейные матрицы A, B (2.11), зависят от неизвестных углов ${{\vartheta }_{i}}$, i = 1, 2, …, m. Таким образом, при выполнении кинематических соотношений (3.1) основными неизвестными будут ${{\vartheta }_{k}}$ и ${{R}_{k}}$, k = 1, 2, …, m, т.е. – векторы ${\mathbf{\Omega }} = \{ {{\vartheta }_{k}}\} $ и ${\mathbf{R}} = \{ {{R}_{k}}\} $, для определения которых имеем уравнения (2.10). Для удобства решения систему двух матричных уравнений (2.10) путем исключения вектора R приведем к одному уравнению, содержащему только неизвестные параметры ${{\vartheta }_{1}}$, ${{\vartheta }_{2}}$, …, ${{\vartheta }_{m}}$:
(3.2)
${\mathbf{G\Omega }} = \left( {\frac{1}{2}{\mathbf{A}} + {\mathbf{B}}} \right){{\left( {\frac{1}{3}{\mathbf{A}} + \frac{1}{2}{\mathbf{B}}} \right)}^{{ - 1}}}{\mathbf{GV}} = {\mathbf{P}}$Это уравнение с учетом системы соотношений (3.1) решается методом последовательных приближений по схеме ${\mathbf{G}}{{{\mathbf{\Omega }}}^{{(r + 1)}}} = {{{\mathbf{P}}}^{{(r)}}}$, где r = 0, 1, … – номер приближения по набору неизвестных параметров ${{\vartheta }_{1}}$, ${{\vartheta }_{2}}$, …, ${{\vartheta }_{m}}$; ${{{\mathbf{P}}}^{{(r)}}}$ – вектор (правая часть уравнения (3.2)), зависящий от $\vartheta _{1}^{{(r)}}$, $\vartheta _{2}^{{(r)}}$, …, $\vartheta _{m}^{{(r)}}$. В начальном (нулевом) приближении при r = 0 для углов ${{\vartheta }_{k}}$ будем использовать точные значения $\vartheta _{k}^{{(0)}} = \vartheta _{k}^{0}$, соответствующие заданной форме изогнутого стержня $Y = F(X)$ в точках k, которые определяются как $\vartheta _{k}^{0} = \theta _{k}^{0} - {{\vartheta }_{0}} - \sum\limits_{i = 1}^{k - 1} {\vartheta _{i}^{0}} $ при $\theta _{k}^{0} = {\text{arctg}}(F'({{X}_{k}}))$, $k = 1,2, \ldots ,m$.
После получения сходящегося с заданной точностью решения для вектора ${\mathbf{\Omega }} = \{ {{\vartheta }_{k}}\} $ вычисляется вектор реакций тросов ${\mathbf{R}}$ из уравнения, которое получается из системы (2.10) путем исключения вектора ${\mathbf{G\Omega }}$:
(3.3)
${\mathbf{R}} = - {{\left( {\frac{1}{3}{\mathbf{A}} + \frac{1}{2}{\mathbf{B}}} \right)}^{{ - 1}}}{\mathbf{GV}}$В исходном состоянии после раскрытия системы радиальный стержень 1' является прямолинейным и отклоненным по отношению к оси X на некоторый угол β0, рис. 1, b. Координаты точки $k{\kern 1pt} ' = 1{\kern 1pt} ',2{\kern 1pt} ', \ldots ,m{\kern 1pt} '$ стержня в исходном состоянии равны ${{X}_{{k{\kern 1pt} '}}}\, = \,{{L}_{{k{\kern 1pt} '}}}{\text{cos}}{{\beta }_{0}}$, где ${{L}_{{k'}}} = ({{a}_{0}} - {{\delta }_{0}}) + \sum\limits_{i = 1}^k {{{a}_{i}}} $ – расстояние между шарниром, соединяющим гидроцилиндр 2 с поворотным кронштейном 6 (рис. 1, a), и точкой $k{\kern 1pt} '$. Длина k-го троса в виде правильного n-угольника, соединяющего по параллели k-е точки всех n радиальных стержней, выбирается так, что в исходном состоянии он является нерастянутым и не имеет провисаний. После поворота кронштейна 6 до упора (угол наклона стержня в корневой точке 0 станет равным ${{\vartheta }_{0}}$) k-й трос натянется с усилием ${{T}_{k}} = {{F}_{k}}\sigma ({{\varepsilon }_{k}})$, где ${{F}_{k}}$ – площадь поперечного сечения, $\sigma ({{\varepsilon }_{k}})$ – растягивающее напряжение в $k$-м тросе. Относительное удлинение k-го троса в конечном натянутом состоянии будет
где ${{X}_{k}}$ – известная координата узла k в конечном деформированном состоянии (т.е. координата заданной формы), а ${{X}_{{k'}}} = {{L}_{{k'}}}\cos {{\beta }_{0}}$ – координата узла $k'$ в исходном недеформированном положении стержня.Реакция k-го троса в k-м узле стержня определяется из уравнения равновесия узла
(3.5)
${{R}_{k}} = 2{{T}_{k}}\sin \frac{\pi }{n} = 2{{F}_{k}}\sigma ({{\varepsilon }_{k}})\sin \frac{\pi }{n}$При линейно-упругом деформировании тросов $\sigma ({{\varepsilon }_{k}}) = {{E}_{T}}{{\varepsilon }_{k}}$ при ${{\varepsilon }_{k}} > 0$ и $\sigma ({{\varepsilon }_{k}}) = 0$ при ${{\varepsilon }_{k}} \leqslant 0$, где ${{E}_{T}}$ – модуль упругости материала троса. По найденным значениям ${{R}_{k}}$ можно определить необходимые площади ${{F}_{k}}$ или жесткости на растяжение ${{E}_{T}}{{F}_{k}}$ тросов для получения формы ${{Y}_{k}} = F({{X}_{k}})$ изогнутых радиальных стержней.
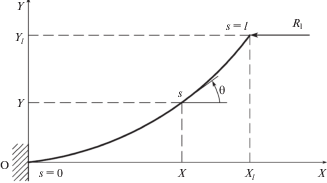
4. Сильный изгиб консольного стержня. Для верификации разработанной КЭ-модели сильного изгиба стержня, описываемой уравнениями (2.9), рассмотрим стержень длиной l с постоянной изгибной жесткостью EI, который неподвижно закреплен на конце s = 0 и нагружен на конце s = l продольной сжимающей силой ${{R}_{l}}$, превышающей критическую силу потери устойчивости (эластика Эйлера). Дифференциальные уравнения изгиба нерастяжимого стержня (рис. 3) записываются в виде
(4.1)
$\frac{{dX}}{{ds}} = \cos \theta ,\quad \frac{{dY}}{{ds}} = \sin \theta ,\quad \frac{{d\theta }}{{ds}} = \frac{{{{R}_{l}}}}{{EI}}({{Y}_{l}} - Y)$Начальные условия при s = 0: $X = 0$, $Y = 0$, $\theta = 0$.
Выполнены сравнения решений дифференциальных уравнений (4.1) с решениями системы алгебраических уравнений (2.9) для КЭ-модели при трех различных значениях параметра $\nu = {{R}_{l}}{{l}^{2}}{\text{/}}EI$: 2.5, 3.0, 3.5. Использовались следующие значения начальных (нулевых) приближений ${{\bar {Y}}_{l}} = {{Y}_{l}}{\text{/}}l < 1$ для “пристрелки” при численных решениях уравнений (4.1) методом последовательных приближений в комбинации с методом Адамса: ${{\bar {Y}}_{l}} = 0.25$ и ${{\bar {Y}}_{l}} = 0.40$ при $\nu = 2.5$; ${{\bar {Y}}_{l}} = 0.50$ и ${{\bar {Y}}_{l}} = 0.75$ при $\nu = 3.0$; ${{\bar {Y}}_{l}} = 0.65$ и ${{\bar {Y}}_{l}} = 0.90$ при $\nu = 3.5$ (два начальных значения ${{\bar {Y}}_{l}}$ для одного $\nu $ приводят к одному и тому же результату). Результаты сходящихся с точностью до 10–9 решений для углов поворота $\theta ({s \mathord{\left/ {\vphantom {s l}} \right. \kern-0em} l})$ в точках ${s \mathord{\left/ {\vphantom {s l}} \right. \kern-0em} l} = {1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4},\;{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2},\;{3 \mathord{\left/ {\vphantom {3 4}} \right. \kern-0em} 4},\;1.0$ приведены в табл. 1 в строках I.
Таблица 1.
Верификация полученной КЭ-модели сильного изгиба стержня
| $\nu $ | Вар. | ${{\bar {Y}}_{l}}$ | $\theta ({1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4})$ | $\theta ({1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2})$ | $\theta ({3 \mathord{\left/ {\vphantom {3 4}} \right. \kern-0em} 4})$ | $\theta (1)$ |
|---|---|---|---|---|---|---|
| 2.5 | I | 0.2037 | 0.1241 | 0.2290 | 0.2990 | 0.3236 |
| II | 0.1879 | 0.1141 | 0.2107 | 0.2752 | 0.2978 | |
| III | 0.1995 | 0.1214 | 0.2241 | 0.2926 | 0.3166 | |
| 3.0 | I | 0.6636 | 0.4825 | 0.8806 | 1.1368 | 1.2245 |
| II | 0.6678 | 0.4839 | 0.8844 | 1.1423 | 1.2304 | |
| III | 0.6640 | 0.4824 | 0.8806 | 1.1369 | 1.2246 | |
| 3.5 | I | 0.7704 | 0.6503 | 1.1739 | 1.5002 | 1.6095 |
| II | 0.7772 | 0.6532 | 1.1823 | 1.5116 | 1.6213 | |
| III | 0.7713 | 0.6506 | 1.1747 | 1.5014 | 1.6107 |
При использовании КЭ-модели стержень делился на m = 4 и m = 8 одинаковых “консольных” КЭ (${{a}_{k}} = {l \mathord{\left/ {\vphantom {l m}} \right. \kern-0em} m}$, $E{{I}_{k}} = EI$, ${{R}_{k}} = 0$ при $k = 1,2, \ldots ,m - 1$). В качестве нулевого приближения при решении уравнений (2.9) методом последовательных приближений в этом случае использовались результаты решения уравнений (4.1) для $\theta ({s \mathord{\left/ {\vphantom {s l}} \right. \kern-0em} l})$. Полученные решения для рассмотренных случаев (ν, m) приведены в табл. 1 (строки II и III для m = 4 и m = 8, соответственно).
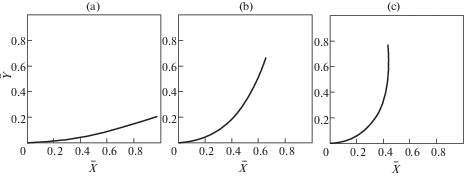
На рис. 4, a, b, c показаны формы изгиба стержня в безразмерных координатах $\bar {X} = {X \mathord{\left/ {\vphantom {X l}} \right. \kern-0em} l}$, $\bar {Y} = {Y \mathord{\left/ {\vphantom {Y l}} \right. \kern-0em} l}$ для значений $\nu = {{R}_{l}}{{l}^{2}}{\text{/}}EI$, равных 2.5, 3.0, 3.5, соответственно.
Сравнения результатов решения уравнений (4.1) и (2.9) показывают, что КЭ-модель сильного изгиба стержня имеет достаточно высокую точность.
5. Примеры расчета. Рассмотрим параболическую антенну с формой $Y = \lambda {{X}^{2}}$ при трех значениях параметра $\lambda $: 1/15, 1/10, 1/5; число радиальных стержней n = 24. Углы наклона стержней в начальном прямолинейном положении (рис. 1, b), в котором участки тросов, соединяющих k-е узлы стержней, также являются прямолинейными и ненатянутыми, приняты равными ${{\beta }_{0}} = {{60}^{0}}$ при $\lambda = {1 \mathord{\left/ {\vphantom {1 {15}}} \right. \kern-0em} {15}}$ и $\lambda = {1 \mathord{\left/ {\vphantom {1 {10}}} \right. \kern-0em} {10}}$, ${{\beta }_{0}}$ = 70° при λ = 1/5. Длина центрального недеформируемого участка равна ${{a}_{0}} = 0.25$ м (${{\delta }_{0}} = 0$). Максимальный диаметр антенны составляет около 20 м.
Выполнены расчеты сильного изгиба радиальных стержней антенны под действием реакций растянутых тросов в конечном деформированном состоянии циклически симметричной системы. Результаты получены путем решения нелинейных алгебраических уравнений (3.2), (3.3) по методу последовательных приближений с точностью до 10–9 относительно неизвестных ${{\theta }_{k}}$, ${{R}_{k}}$ с учетом условий связи (3.1), обеспечивающих точное выполнение заданной формы антенны в узлах по координатам ${{X}_{k}}$, ${{Y}_{k}}$, k = = 1, 2, …, m. При этом в качестве начальных приближений для ${{\theta }_{k}}$ использовались значения $\theta _{k}^{0}$ заданной формы, т.е. $\theta _{k}^{{(0)}} = \theta _{k}^{0}$.
Рассмотрены два расчетных случая для каждой из 3-х антенн, отличающихся значением $\lambda $:
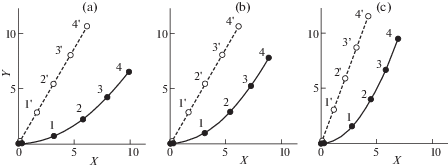
1) Радиальный стержень антенны делится на 4 упругих звена ($m = 4$, k = 1, 2, 3, 4) длиной ${{a}_{k}} = 3$ м; заданные изгибные жесткости этих звеньев $E{{I}_{k}}$, Па · м4 и проектные углы наклона в узлах заданной формы $\theta _{k}^{0} = {\text{arctg(2}}\lambda {{X}_{k}}{\text{)}}$ представлены в табл. 2. Формы радиального стержня в начальном недеформированном состоянии (пунктирная линия) и в требуемом конечном деформируемом состоянии (сплошная линия) для $m = 4$ при $\lambda = {1 \mathord{\left/ {\vphantom {1 {15}}} \right. \kern-0em} {15}},\;{1 \mathord{\left/ {\vphantom {1 {10}}} \right. \kern-0em} {10}},\;{1 \mathord{\left/ {\vphantom {1 5}} \right. \kern-0em} 5}$ представлены на рис. 5, a, b, c, соответственно, в координатах $X$, $Y$, м.
Таблица 2.
Исходные данные и результаты расчета параметров антенны при m = 4
| $\lambda $ | $k$ | $E{{I}_{k}}$ | $\theta _{k}^{0}$ | ${{\theta }_{k}}$ | ${{R}_{k}}$ | ${{\varepsilon }_{k}}$ | ${{E}_{T}}{{F}_{k}}$ |
|---|---|---|---|---|---|---|---|
| $\frac{1}{{15}}$ | 1 | 1978.3237 | 0.3986 | 0.3885 | 47.8979 | 0.9467 | 193.8079 |
| 2 | 1643.2336 | 0.6526 | 0.6483 | 41.6127 | 0.8361 | 190.6416 | |
| 3 | 1213.0318 | 0.8143 | 0.8099 | 6.1016 | 0.7195 | 32.4871 | |
| 4 | 671.2248 | 0.9214 | 0.9019 | 17.6858 | 0.6136 | 110.4073 | |
| $\frac{1}{{10}}$ | 1 | 1978.3237 | 0.5503 | 0.5342 | 96.4922 | 0.8935 | 413.6997 |
| 2 | 1643.2336 | 0.8197 | 0.8182 | 54.8316 | 0.7167 | 293.0548 | |
| 3 | 1213.0318 | 0.9651 | 0.9608 | 5.4540 | 0.5634 | 37.0847 | |
| 4 | 671.2248 | 1.0545 | 1.0391 | 13.6527 | 0.4397 | 118.9434 | |
| $\frac{1}{5}$ | 1 | 1978.3237 | 0.8352 | 0.8165 | 217.5199 | 1.5098 | 551.8955 |
| 2 | 1643.2336 | 1.0604 | 1.0634 | 54.1653 | 1.1016 | 188.3499 | |
| 3 | 1213.0318 | 1.1626 | 1.1585 | 1.7656 | 0.8357 | 8.0929 | |
| 4 | 671.2248 | 1.2224 | 1.2129 | 8.6875 | 0.6491 | 51.2688 |
Рис. 5.
Формы радиального стержня в начальном и конечном положениях для $n = 24$, m = 4 и $\lambda = {1 \mathord{\left/ {\vphantom {1 {15}}} \right. \kern-0em} {15}}$ (a), $\lambda = {1 \mathord{\left/ {\vphantom {1 {10}}} \right. \kern-0em} {10}}$ (b), $\lambda = {1 \mathord{\left/ {\vphantom {1 5}} \right. \kern-0em} 5}$ (c)
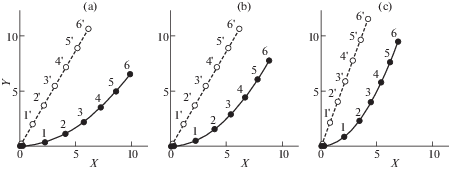
2) Радиальный стержень делится на 6 упругих звеньев ($m = 6$, k = 1, 2, …, 6) длиной ${{a}_{k}} = 2$ м; для этого случая значения $E{{I}_{k}}$, Па · м4 и углы $\theta _{k}^{0}$ представлены в табл. 3. Формы радиального стержня в начальном и требуемом конечном состояниях при $\lambda = {1 \mathord{\left/ {\vphantom {1 {15}}} \right. \kern-0em} {15}}$, 1/10, 1/5 представлены в координатах $X$, $Y$, м на рис. 6, a, b, c, соответственно.
Таблица 3.
Исходные данные и результаты расчета параметров антенны при m = 6
| $\lambda $ | $k$ | $E{{I}_{k}}$ | $\theta _{k}^{0}$ | ${{\theta }_{k}}$ | ${{R}_{k}}$ | ${{\varepsilon }_{k}}$ | ${{E}_{T}}{{F}_{k}}$ |
|---|---|---|---|---|---|---|---|
| $\frac{1}{{15}}$ | 1 | 7656.4383 | 0.2876 | 0.2822 | 260.5498 | 0.9728 | 1025.9801 |
| 2 | 6684.4295 | 0.4961 | 0.4961 | 105.2135 | 0.9113 | 442.2760 | |
| 3 | 6013.2047 | 0.6526 | 0.6458 | 151.509 | 0.8352 | 694.9330 | |
| 4 | 4204.6526 | 0.7681 | 0.7717 | 10.4413 | 0.7567 | 52.8544 | |
| 5 | 4204.6526 | 0.8547 | 0.8465 | 5.4236 | 0.6820 | 30.4614 | |
| 6 | 1631.6882 | 0.9214 | 0.9109 | 66.9765 | 0.6131 | 418.4988 | |
| $\frac{1}{{10}}$ | 1 | 7656.4383 | 0.4116 | 0.3987 | 592.7990 | 0.9427 | 2408.7411 |
| 2 | 6013.2047 | 0.6609 | 0.6611 | 326.3337 | 0.8311 | 1504.1060 | |
| 3 | 5193.4296 | 0.8197 | 0.8157 | 105.8771 | 0.7147 | 567.4419 | |
| 4 | 4204.6526 | 0.9250 | 0.9277 | 2.8618 | 0.6095 | 17.9877 | |
| 5 | 4204.6526 | 0.9993 | 0.9927 | 10.1289 | 0.5179 | 74.9241 | |
| 6 | 1631.6882 | 1.0545 | 1.0459 | 50.4612 | 0.4386 | 440.6749 | |
| $\frac{1}{5}$ | 1 | 7656.4383 | 0.6849 | 0.6686 | 1225.6470 | 1.6655 | 2819.0376 |
| 2 | 6684.4295 | 0.9357 | 0.9416 | 428.9441 | 1.3402 | 1226.0534 | |
| 3 | 6684.4295 | 1.0604 | 1.0561 | 43.6339 | 1.0934 | 152.8741 | |
| 4 | 5193.4296 | 1.1352 | 1.1358 | 36.4977 | 0.9070 | 154.1510 | |
| 5 | 4204.6526 | 1.1856 | 1.1817 | 12.6620 | 0.7617 | 63.6785 | |
| 6 | 1631.6882 | 1.2224 | 1.2165 | 30.3713 | 0.6449 | 180.4132 |
Рис. 6.
Формы радиального стержня в начальном и конечном положениях для $n = 24$, m = 6 и $\lambda = {1 \mathord{\left/ {\vphantom {1 {15}}} \right. \kern-0em} {15}}$ (a), $\lambda = {1 \mathord{\left/ {\vphantom {1 {10}}} \right. \kern-0em} {10}}$ (b), $\lambda = {1 \mathord{\left/ {\vphantom {1 5}} \right. \kern-0em} 5}$ (c)
Полученные значения ${{\theta }_{k}}$, ${{R}_{k}}$, Н, а также относительные деформации растяжения тросов ${{\varepsilon }_{k}}$ и требуемые для получения заданной формы антенны жесткости тросов на растяжение ${{E}_{T}}{{F}_{k}}$ (Па · м2), которые определяются по формуле ${{R}_{k}} = 2{{E}_{T}}{{F}_{k}}{{\varepsilon }_{k}}\sin ({\pi \mathord{\left/ {\vphantom {\pi n}} \right. \kern-0em} n})$, приведены в табл. 2 и табл. 3 соответственно для случаев m = 4 и $m = 6$, $k = 1,2, \ldots ,m$.
В табл. 4 и табл. 5 для случаев m = 4 и $m = 6$, соответственно, приведено сравнение точности решения путем сравнения изгибающих моментов ${{M}_{k}}$, Н · м, $k = 1,2$, ..., m – 1, в узлах стержня в конечном деформированном состоянии: I – вычисленные из уравнения равновесия отсеченной части при найденных реакциях ${{R}_{k}}$: Mk = $\sum\limits_{i = k + 1}^m {{{R}_{k}}({{Y}_{i}} - {{Y}_{k}})} $; II – найденные при решении нелинейной задачи в перемещениях по методу конечных элементов средние значения в узле: ${{M}_{k}} = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}({{M}_{k}}({{a}_{k}}) + {{M}_{{k + 1}}}(0))$, где Mk(ak) = ${{2E{{I}_{k}}} \mathord{\left/ {\vphantom {{2E{{I}_{k}}} {{{a}_{k}}}}} \right. \kern-0em} {{{a}_{k}}}}( - 3{{\bar {\upsilon }}_{k}}$ + + 2ϑk), ${{M}_{{k + 1}}}(0) = {{2E{{I}_{{k + 1}}}} \mathord{\left/ {\vphantom {{2E{{I}_{{k + 1}}}} {{{a}_{{k + 1}}}}}} \right. \kern-0em} {{{a}_{{k + 1}}}}}(3{{\bar {\upsilon }}_{{k + 1}}} - 2{{\vartheta }_{{k + 1}}})$. Результаты сравнения показывают высокую точность, полученную при решении нелинейных алгебраических уравнений КЭ-модели методом последовательных приближений.
Таблица 4.
Результаты расчета изгибающих моментов в узлах стержня при m = 4
| $\lambda $ | Вар. | k = 1 | k = 2 | k = 3 |
|---|---|---|---|---|
| $\frac{1}{{15}}$ | I | 188.3897 | 88.6112 | 40.5765 |
| II | 193.7100 | 90.1060 | 40.9970 | |
| $\frac{1}{{10}}$ | I | 222.0288 | 79.5639 | 34.7384 |
| II | 230.6572 | 80.9606 | 34.9822 | |
| $\frac{1}{5}$ | I | 211.5091 | 52.4085 | 24.2377 |
| II | 225.4776 | 53.1092 | 24.3086 |
Таблица 5.
Результаты расчета изгибающих моментов в узлах стержня при m = 6
| $\lambda $ | Вар. | k = 1 | k = 2 | k = 3 | k = 4 | k = 5 |
|---|---|---|---|---|---|---|
| $\frac{1}{{15}}$ | I | 835.2111 | 573.4939 | 317.5385 | 209.1970 | 104.0202 |
| II | 848.8874 | 579.8688 | 319.7085 | 209.9830 | 104.5593 | |
| $\frac{1}{{10}}$ | I | 1026.0813 | 512.9911 | 283.3631 | 185.9495 | 86.4142 |
| II | 1055.8608 | 520.2044 | 284.7586 | 186.4288 | 86.7087 | |
| $\frac{1}{5}$ | I | 1295.6631 | 485.1380 | 277.4441 | 135.6802 | 56.7180 |
| II | 1351.8396 | 490.7088 | 278.1707 | 135.9047 | 56.8058 |
6. Заключение. Предложена конструктивная схема и разработана математическая модель для расчета формообразования циклически симметричной космической зонтичной антенны, образованной системой гибких многозвенных радиальных стержней, связанных по параллелям в определенных узловых точках растяжимыми тросами. Изгиб стержней в радиальной плоскости с учетом реакций тросов создается путем поворота корневых частей стержней силой медленно перемещающегося штока демпфирующего гидроцилиндра под действием предварительно сжатых пружин. Модель сильного изгиба нерастяжимого стержня антенны построена с использованием “консольных” конечных элементов (звеньев), допускающих большие перемещения и повороты как твердых тел и относительные упругие перемещения с двухчленной аппроксимацией по длине элемента с учетом его усадки за счет изгиба в квадратичном приближении. Полученные нелинейные уравнения решаются методом последовательных приближений относительно неизвестных реакций тросов при заданных значениях изгибных жесткостей элементов стержня и заданных радиальных и осевых координат узлов, точно соответствующих форме моделируемой антенны. По найденным значениям реакций тросов с учетом известных их перемещений в узлах определяются необходимые для обеспечения заданной формы антенны жесткости тросов на растяжение.
Выполнена оценка точности разработанной модели путем сравнения с численным решением задачи сильного изгиба консольного стержня под действием продольной сжимающей силы, превышающей критическую силу потери устойчивости стержня.
В качестве примера выполнены расчеты для параболической антенны с n = 24 радиальными стержнями и с m = 4 и m = 8 составляющих их звеньями (соответственно – тросов).
Работа выполнена в рамках государственного задания ИПРИМ РАН (номер госрегистрации темы АААА-А19-119012290118-3).
Список литературы
Гряник М.В., Ломан В.И. Развертываемые зеркальные антенны зонтичного типа. М.: Радио и связь, 1987. 72 с.
Лопатин А.В., Рутковская М.А. Обзор конструкций современных трансформируемых космических антенн // Вестник Сибирского государственного университета науки и технологи имени Академика М.Ф. Решетнева. 2007. № 2. С. 51–57.
Лопатин А.В., Рутковская М.А. Обзор Конструкций современных трансформируемых космических антенн // Вестник Сибирского государственного университета науки и технологи имени Академика М.Ф. Решетнева. 2007. № 3. С. 78–81.
Пономарев С.В. Трансформируемые рефлекторы антенн космических аппаратов // Вестник Томского государственного университета. Математика и механика. 2011. № 4. С. 110–119.
Бельков А.В., Евдокимов А.С. и др. Компьютерное моделирование перспективных космических рефлекторов // Вестник Самарского государственного технического университета. Физико-математические науки. 2008. № 2. С. 161–170.
Крылов А.В. Исследование процесса раскрытия антенного контура // Известия высших учебных заведений. Машиностроение. 2013. № 12. С. 45–50.
Усюкин В.И., Архипов М.Ю. Моделирование статики и динамики крупногабаритных рефлекторов космических антенн. М.: Изд-во МГТУ им. Н.Э. Баумана, 2012. 60 с.
Бужинский В.А., Клишев О.П., Мытарев А.И. Исследование влияния упругих колебаний крупногабаритных элементов конструкции космического аппарата на искажение геометрических характеристик рефлектора // Космонавтика и ракетостроение. 2007. № 2. С. 102–108.
Гришанина Т.В., Шклярчук Ф.Н. Динамика плоского движения тела с системой последовательно соединенных упруговязкими шарнирами гибких нерастяжимых стержней при больших углах поворота // Изв. РАН. МТТ. 2011. № 2. С. 109–117.
Русских С.В., Шклярчук Ф.Н. Динамика раскрытия космической зонтичной антенны, состоящей из многозвенных гибких радиальных стержней // Космонавтика и ракетостроение. 2020. № 2. С. 86–98.
Русских С.В., Шклярчук Ф.Н. Расчет формообразования космической зонтичной антенны, состоящей из гибких радиальных стержней, соединенных по параллелям растяжимыми тросовыми элементами // Космонавтика и ракетостроение. 2019. № 2. С. 95–103.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика твердого тела