Известия РАН. Механика твердого тела, 2021, № 5, стр. 27-44

1. Введение. Конструкции из композиционных материалов (КМ) широко внедряются в инженерную практику [1–6]. Современные КМ-изделия часто подвергаются высокоинтенсивному нагружению [5, 7], при котором компоненты композиции деформируются неупруго. Следовательно, моделирование неупругого поведения армированных конструкций является актуальной проблемой, которая на сегодняшний день находится на стадии становления [8, 9].

Упругопластическое поведение тонкостенных конструкций слоистой структуры (с изотропными слоями) исследовалось в [10]; вязкоупругопластическое деформирование армированных пластин моделировалось в [11], где впервые удалось рассчитать остаточные перемещения КМ-конструкции и остаточное напряженно-деформированное состояние (НДС) компонентов композиции после ее пластического динамического деформирования. Неупругое поведение многих материалов зависит от скорости их деформирования [12, 13], поэтому в [14] моделировалось упруговязкопластическое поведение КМ-пластин. Структурная же теория неупругого деформирования армированных сред, использующая определяющие соотношения теории пластического течения с учетом чувствительности материалов компонентов композиции к скорости их деформирования, а также с учетом их вязкоупругих свойств до настоящего времени не разработана. Используя терминологию, принятую в [15], такую модель неупругого поведения материалов компонентов композиции будем называть теорией вязкоупруго-вязкопластического деформирования.

Для описания слабого сопротивления тонкостенных армированных конструкций поперечному сдвигу (которое может проявляться даже при некоторых пространственных структурах армирования [16–18]) традиционно используют неклассические теории Тимошенко–Рейсснера [4, 5, 10, 19, 20], Амбарцумяна [11, 14, 21] или Редди [3, 22]; реже используется теория, базирующаяся на кинематической гипотезе ломаной линии [4].

Для численного интегрирования физически и геометрически нелинейных динамических задач механики тонкостенных конструкций, как правило, применяют явные методы [10, 11, 14, 23], чаще всего схему “крест”.

В связи со всем вышеизложенным данное исследование посвящено моделированию вязкоупруго-вязкопластического поведения гибких армированных пластин с учетом их возможного слабого сопротивления поперечным сдвигам. Численное решение соответствующих начально-краевых задач, возникающих при этом, предполагается строить по явной схеме типа “крест”.

2. Численно-аналитическое моделирование вязкоупруго-вязкопластического поведения КМ. Как и в [11, 14], считаем, что малые деформации ${{\varepsilon }_{{ij}}}$ можно разложить на сумму сжимаемых вязкоупругих ${{e}_{{ij}}}$ и несжимаемых пластических ${{p}_{{ij}}}$ составляющих

При этом вязкопластическое течение материала ассоциировано с мгновенной поверхностью нагружения f = 0, которая для конкретности задается в форме, соответствующей обобщению условия текучести Мизеса [14]:

где ${{\bar {e}}_{{ij}}}$ – компоненты девиатора вязкоупругих деформаций; ${{\xi }_{{ij}}}$ – компоненты девиатора скорости деформаций; ${{\sigma }_{{ij}}}$, ${{s}_{{ij}}}$ – компоненты тензора и девиатора напряжений; ${{\sigma }_{0}}$, ${{\varepsilon }_{0}}$ – средние напряжение и деформация; T – интенсивность касательных напряжений; $\chi $ – параметр Одквиста; H – интенсивность скоростей деформаций сдвига; ${{\tau }_{s}}$ – мгновенный предел текучести при чистом сдвиге, который равен T при определенных значениях H и $\chi $ в данный момент времени t; ${{\delta }_{{ij}}}$ – символ Кронекера; точка – производная по времени. Начальная поверхность нагружения $T = {{\tau }_{s}}\left( H \right) \equiv {{\tau }_{s}}\left( {0,H} \right)$ – обычный предел текучести, зависящий от скорости деформирования H [12, 13]. (В настоящем разделе, если не оговорено, по повторяющимся индексам проводится суммирование от 1 до 3.)

В работе [24] вязкоупругое поведение материала описывалось интегральными определяющими соотношениями. Однако в [25] показано, что для адекватного моделирования затухающих колебаний образцов целесообразно использовать не интегральную, а дифференциальную форму определяющих уравнений вязкоупругости [26]. В связи с этим, как и в [11, 27], считаем, что вязкоупругое деформирование материала описывается соотношениями модели Максвелла–Больцмана

где G – модуль сдвига; K – объемный модуль упругости; $\eta $ – коэффициент линейной вязкости при сдвиге; $\mu $ – коэффициент объемной вязкости.

Используя ассоциированный закон пластического течения [15, 24, 26, 27] при учете (2.2) и (2.3), получаем (см. равенство (1.12) в [14])

В случае пластического деформирования материала при чистом сдвиге (τ = = ${{\tau }_{s}}(\chi ,H)$) выполняется соотношение (см. равенства (1.15)–(1.18) в [14])

где $\tau $ – касательное напряжение при чистом сдвиге; γ_p – пластическая составляющая полной угловой деформации $\gamma $; $\xi $ – скорость деформации γ; ${{\tau }_{\chi }} \equiv \bar {G} = {{\tau }_{\chi }}\left( {\chi ,H} \right) = {{\tau }_{\chi }}\left( {{{\gamma }_{p}},\xi } \right)$ и ${{\tau }_{H}} = {{\tau }_{H}}\left( {\chi ,H} \right) = {{\tau }_{H}}\left( {{{\gamma }_{p}},\xi } \right)$ – известные из эксперимента функции, причем ${{\tau }_{\chi }} \equiv \bar {G}$ – касательный модуль при постоянстве скорости деформирования ($\xi = {\text{const}}$) на диаграмме $\tau \sim {{\gamma }_{p}}$ (для простоты предполагаем, что угловые деформации γ_p, γ и напряжение $\tau $ положительны).

Изменение касательного напряжения $\tau $ сопровождается приращением вязкоупругой части угловой деформации ${{\gamma }_{e}}$ (${{\gamma }_{e}} = \gamma - {{\gamma }_{p}}$). Согласно этому в случае чистого сдвига из первого равенства (2.4) с учетом (2.3) получаем

Выразим отсюда $\dot {\tau }$ и подставим в левую часть равенства (2.6), после чего при учете ${{\gamma }_{e}} = \gamma - {{\gamma }_{p}}$ получим соотношение

где (см. (2.7))

Умножим (2.8) на $\tau $, тогда получим энергетическое соотношение

Как и в рамках теории Прандтля–Рейсса–Хилла (${{\tau }_{H}} = 0$, $\eta \to \infty $) [23], теории вязкоупругопластического (${{\tau }_{H}} = 0$) [11] и теории упруговязкопластического ($\eta \to \infty $) [14] деформирования материала, предполагаем, что энергетическое равенство, аналогичное (2.10), справедливо при любых видах НДС. На основании этого, учитывая (2.3), будем иметь равенство

которое обобщает энергетические уравнения (20) в [11] и (1.24) в [14].

Подставим выражение (2.11) в правую часть равенства (2.5) и учтем разложение, аналогичное (2.1), для девиатора деформаций, тогда получим

В правой части этого равенства учтем первое соотношение (2.4), после чего будем иметь

откуда следует где c – параметр переключения: $c = 0$ при чисто вязкоупругом деформировании, разгрузке и нейтральном нагружении, $c = 1$ при активном вязкоупруго-вязкопластическом деформировании. Повторяя рассуждения из работы [14] (см. там соотношения (1.28)–(1.36)), получим

Подставим в (2.13) соотношение (2.12) и учтем постулат Друккера [15], тогда будем иметь выражение

Используя второе равенство (2.4) и учитывая соотношения (2.1) и (2.3), равенства (2.12) можно преобразовать к окончательному виду

где E, $\nu $ – модуль Юнга и коэффициент Пуассона при мгновенном деформировании материала; $\lambda $ – параметр Ламе; параметр переключения c определяется по формуле (2.14) или (2.13).

Если вязкость при упругом деформировании не учитывается ($\eta \to \infty $) и пластическое поведение материала не зависит от скорости его деформирования (${{\tau }_{H}} \equiv 0$), то из (2.15) при учете (2.14) и (2.16) получаются определяющие соотношения теории Прандтля–Рейсса–Хилла [23]. Если материал не чувствителен к скорости деформирования (${{\tau }_{H}} \equiv 0$), то из (2.14)–(2.16) вытекают определяющие уравнения вязкоупругопластической теории [11, 27]. Если же пренебречь вязкостью при упругом деформировании материала ($\eta \to \infty $), то равенства (2.15) с учетом (2.14), (2.16) редуцируются в определяющие соотношения упруговязкопластической теории [14].

Как и в работах [11, 14], для удобства последующего изложения определяющие уравнения для k-го компонента композиции целесообразно записать в матричной форме (см. (2.14)–(2.16))

Здесь и далее:

${{{\mathbf{V}}}_{k}} = ({v}_{{ij}}^{{(k)}})$, ${{{\mathbf{Z}}}_{k}} = (z_{{ij}}^{{(k)}})$, ${{{\mathbf{Y}}}_{k}} = (y_{{ij}}^{{(k)}})$ – симметричные 6 × 6-матрицы, характеризующие механическое состояние материала (${{{\mathbf{Z}}}_{k}}$ условно можно трактовать как матрицу “жесткости”, а ${{{\mathbf{V}}}_{k}}$ – как матрицу “вязкости” материала), причем ${{{\mathbf{Z}}}_{k}}$ и ${{{\mathbf{Y}}}_{k}}$ можно представить в виде ${{{\mathbf{\bar {Z}}}}_{k}} = (\bar {z}_{{ij}}^{{(k)}})$, ${{{\mathbf{\bar {\bar {Z}}}}}_{k}} = (\bar {\bar {z}}_{{ij}}^{{(k)}})$ – симметричные 6 × 6-матрицы. Ненулевые элементы матриц V_k, ${{{\mathbf{\bar {Z}}}}_{k}}$ и ${{{\mathbf{\bar {\bar {Z}}}}}_{k}}$ определяются так: т – операция транспонирования.

В соотношениях (2.18)–(2.20) все величины имеют прежний смысл, индекс k – номер компонента композиции: $k = 0$ – связующий материал, $k = 1,\;2,\; \ldots ,\;N$ – арматура k-го семейства; N – количество семейств армирующих волокон. (В выражениях (2.20) по повторяющемуся индексу m суммирования нет.) Равенства (2.18) задают соответствия между шестью элементами $f_{i}^{{(k)}}$ ($i = \overline {1,6} $) некоторого вектора-столбца ${{{\mathbf{f}}}_{k}}$ и компонентами симметричного тензора второго ранга $f_{{jl}}^{{(k)}}$, $j,l = \overline {1,3} $. (Согласно введенным обозначениям (2.18), ${{\xi }_{k}} \ne {{\dot {\varepsilon }}_{k}}$, $0 \leqslant k \leqslant N$.)

Как уже отмечалось во Введении, численное решение рассматриваемой задачи будем строить с использованием метода шагов по времени [10, 11, 14, 23], т.е. будем определять значения искомых функций в дискретные моменты времени ${{t}_{{n + 1}}} = {{t}_{n}} + \Delta $ ($n = 0,\;1,\;2,\; \ldots $), где $\Delta = {\text{const}} > 0$ – шаг по времени. При этом предполагаем, что в предыдущий момент времени ${{t}_{m}}$ уже известны значения следующих векторных функций:

где ${{x}_{i}}$ – координаты точек тела.

Так как в дальнейшем предполагается разработка явной схемы типа «крест» на трехточечном шаблоне по времени (${{t}_{{n - 1}}}$, ${{t}_{n}}$, ${{t}_{{n + 1}}}$), имеющей второй порядок точности по $\Delta $ [10], согласно результатам работ [11, 14], преобразуем первое и последнее слагаемые в правой части соотношения (2.17), используя формулу трапеций, также имеющую второй порядок точности по $\Delta $ [28]. В текущий момент времени ${{t}_{n}}$ на основании формулы трапеций имеем выражения

откуда где

Из равенств (2.23) с учетом предположений (2.21) вытекает, что шестикомпонентные векторы-столбцы $\mathop {{{\sigma }_{k}}}\limits^{n - 1/2} $ и $\mathop {{{{\dot {\varepsilon }}}_{k}}}\limits^{n - 1/2} $ в выражении (2.22) при $t = {{t}_{n}}$ уже известны.

Подстановка соотношений (2.22) в уравнение (2.17) приводит к матричному равенству

где I – единичная 6 × 6-матрица; $\mathop {{\mathbf{\bar {V}}}_{k}^{{ - 1}}}\limits^n $ – матрица, обратная 6 × 6-матрице $\mathop {{{{{\mathbf{\bar {V}}}}}_{k}}}\limits^n $. В данный момент времени ${{t}_{n}}$ соотношение (2.24) – определяющее уравнение для вязкоупруго-вязкопластического материала k-го компонента композиции.

Так как элементы матриц ${{{\mathbf{V}}}_{k}}$ и ${{{\mathbf{Z}}}_{k}}$ зависят от решения задачи (см. выражения (2.19) и (2.20)), равенство (2.24) при учете (2.23) и (2.25) является нелинейным. Для линеаризации этого соотношения, как и в [11, 14], целесообразно использовать метод, аналогичный методу переменных параметров упругости [29]. Тогда в текущий момент времени t_n на каждой итерации этого метода 6 × 6-матрица $\mathop {{{{\mathbf{{\rm B}}}}_{k}}}\limits^n = (\mathop {b_{{ij}}^{{(k)}}}\limits^n )$ и шестикомпонентный вектор-столбец $\mathop {{{{\mathbf{p}}}_{k}}}\limits^n = \{ \mathop {p_{i}^{{(k)}}}\limits^n \} $ ($i,j = \overline {1,6} $) в соотношении (2.24) будут известны.

Линеаризованное матричное уравнение (2.24) формально совпадает с аналогичными равенствами (51) в [11] и (2.10) в [14]. Следовательно, используя результаты работ [11, 14], на базе определяющего соотношения (2.24) можем построить структурную модель вязкоупруго-вязкопластического деформирования армированной среды. При этом в момент времени ${{t}_{n}}$ на данной итерации для КМ получаем следующее линейное определяющее соотношение, записанное в матричной форме:

где $\dot {\sigma }$, $\dot {\varepsilon }$ – шестикомпонентные векторы-столбцы скоростей осредненных напряжений ${{\dot {\sigma }}_{{ij}}}$ и деформаций ${{\dot {\varepsilon }}_{{ij}}}$ в композиции, по структуре аналогичные (2.18); ${\mathbf{B}} = \left( {{{b}_{{ij}}}} \right)$ – известная 6 × 6-матрица, ${\mathbf{p}} = \left\{ {{{p}_{i}}} \right\}$ – известный шестикомпонентный вектор-столбец, которые вычисляются по формулам (2.17) из [14] и зависят от текущего механического состояния (определенного на предыдущей итерации) компонентов композиции (от ${{{\mathbf{{\rm B}}}}_{k}}$ и ${{{\mathbf{p}}}_{k}}$; см. (2.24)) и структуры армирования, т.е. от плотностей ${{\omega }_{k}}$ и направлений армирования. Направление траектории волокна k-го семейства однозначно задается двумя углами сферической системы координат ${{\theta }_{k}}$ и ${{\varphi }_{k}}$, $0 \leqslant k \leqslant N$ (рис. 1).

Связь между скоростями деформаций k-го компонента ${{\dot {\varepsilon }}_{k}}$ (см. (2.24)) и скоростями осредненных деформаций композиции $\dot {\varepsilon }$ (см. (2.26)) определяется соотношениями (2.19) из [14].

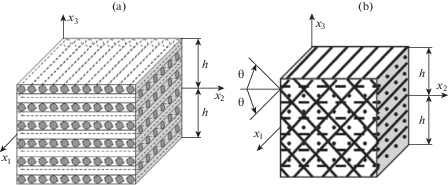
3. Моделирование динамического поведения гибкой КМ-пластины. Рассматриваем армированную пластину толщиной 2h, с которой свяжем декартову прямоугольную систему координат ${{x}_{i}}$ так, что плоскость ${{x}_{1}}{{x}_{2}}$ (${{x}_{3}} = 0$) − срединная плоскость конструкции ($\left| {{{x}_{3}}} \right| \leqslant h$). Пластина усилена N семействами волокон с плотностями армирования ${{\omega }_{k}}$ ($0 \leqslant k \leqslant N$); структура армирования в поперечном направлении ${{x}_{3}}$ однородна (рис. 2).

Предполагаем, что на лицевых поверхностях конструкции ($\left| {{{x}_{3}}} \right| = h$) можно пренебречь действием касательных распределенных внешних нагрузок. Для учета слабого сопротивления КМ-пластины поперечным сдвигам используем кинематические соотношения теорий Амбарцумяна или Редди [3, 21], согласно которым осредненные деформации композиции ${{\varepsilon }_{{ij}}}$ и перемещения точек ${{U}_{i}}$ гибкой КМ-пластины аппроксимируем так:

где ${{u}_{i}}$ – перемещения точек отсчетной плоскости (${{x}_{3}} = 0$) в тангенциальных направлениях ${{x}_{i}}$; w – прогиб; $\varepsilon _{{i3}}^{0}$ – деформации поперечных сдвигов в точках отсчетной плоскости; ${{t}_{0}}$ − начальный момент времени; ${{\partial }_{i}}$ – оператор частного дифференцирования по переменной ${{x}_{i}}$; $\Omega $ – область, занимаемая конструкцией в плане. В равенствах (3.1), (3.2) неизвестными являются функции ${{u}_{i}}$, w и $\varepsilon _{{i3}}^{0}$, которые зависят от времени t и двух пространственных координат ${{x}_{i}}$ ($i = 1,\;2$).

Моделируется механическое поведение КМ-конструкции как гибкой тонкостенной системы, поэтому напряжение ${{\sigma }_{{33}}}\left( {t,{\mathbf{r}}} \right)$ с приемлемой для практических приложений точностью можно линейно аппроксимировать по поперечной координате ${{x}_{3}}$ [20]:

где $\sigma _{{33}}^{{( \pm )}}\left( {t,{\mathbf{x}}} \right) \equiv {{\sigma }_{{33}}}\left( {t,{\mathbf{x}}, \pm h} \right)$ – нормальные напряжения на верхней (+) и нижней (–) лицевых плоскостях, известные из соответствующих силовых граничных условий.

Матричное соотношение (2.26) – система шести линейных алгебраических уравнений. Из третьего равенства этой системы, согласно соотношениям соответствия (2.18), можно определить скорость линейной поперечной деформации:

где скорость нормального напряжения ${{\dot {\sigma }}_{3}}$ в момент времени ${{t}_{n}}$ известна из (3.3) после его дифференцирования по времени t. Скорости деформаций ${{\dot {\varepsilon }}_{i}}$ в правой части (3.4) вычисляются путем дифференцирования по времени соотношений (3.1), т.е. зависят от функций w, $\dot {w}$, ${{\dot {u}}_{l}}$ и $\dot {\varepsilon }_{{l3}}^{0}$ ($l = 1,\;2$).

Уравнения движения гибкой КМ-пластины при учете равенств (3.2) и (3.3) имеют вид (массовые нагрузки не учитываются) [21]:

где ${{\rho }_{0}}$, ${{\rho }_{k}}$ – объемная плотность материалов связующего и волокон k-го семейства; ${{\gamma }_{i}}$ – введенные для удобства функции; ${{F}_{{ij}}}$, ${{F}_{{i3}}}$, ${{M}_{{ij}}}$ – внутренние силовые факторы.

Для однозначного интегрирования исследуемой задачи необходимо использовать начальные и граничные условия. Силовые граничные условия, заданные на кромке ${{\Gamma }_{p}}$, определяются равенствами [21]:

Кинематические граничные условия, заданные на кромке ${{\Gamma }_{u}}$, имеют вид (см. (3.2) и (3.7)):

Начальные условия при $t = {{t}_{0}}$ определяются так [21]:

Здесь:

${{P}_{i}}$ – заданные на кромке ${{\Gamma }_{p}}$ мембранные силы по направлениям ${{x}_{i}}$ ($i = 1,\;2$); ${{P}_{{n3}}}$ – заданная на ${{\Gamma }_{p}}$ поперечная сила; ${{M}_{{nn}}}$, ${{M}_{{n\tau }}}$ – заданные на кромке ${{\Gamma }_{p}}$ изгибающий и крутящий моменты; ${{w}_{ * }}$ – заданный на кромке ${{\Gamma }_{u}}$ прогиб; ${{U}_{{i * }}}$ – заданные на торцевой поверхности пластины перемещения в тангенциальных направлениях ${{x}_{i}}$; ${{w}_{0}}$, ${{\dot {w}}_{0}}$, ${{U}_{{0i}}}$, ${{V}_{{0i}}}$ ($i = 1,\;2$) – заданные в начальный момент времени ${{t}_{0}}$ перемещения и скорости точек конструкции; $\Gamma = {{\Gamma }_{p}} \cup {{\Gamma }_{u}}$ – контур, ограничивающий область $\Omega $, занимаемую пластиной в плане; $\beta $ – угол, задающий направление внешней нормали к Г. Возможно задание и пяти смешанных из (3.8) и (3.9) граничных условий, например при моделировании шарнирного опирания кромки [21].

4. Численный метод расчета. Как отмечалось в разделе 2, численное интегрирование рассматриваемой задачи будем строить на основе алгоритма шагов по времени [7, 10, 11, 14, 23, 30]. Поэтому считаем, что в дискретные моменты времени ${{t}_{m}}$ помимо величин, указанных в (2.21), известны значения следующих функций:

следовательно, используя (3.6), при $t = {{t}_{n}}$ можем определить все силовые факторы и внешние нагрузки, входящие в (3.3) и (3.5).

Производные по времени (за исключением второго равенства (2.22)) будем аппроксимировать центральными конечными разностями [11, 14], что позволяет построить явную численную схему интегрирования исходной задачи. После замены вторых производных по t в левых частях равенств (3.5) их конечно-разностными аналогами, учитывая обозначения, аналогичные (4.1), получим

Правые части здесь известны, поэтому при учете (4.1) и необходимых граничных условий (3.8) и (3.9) из уравнений (4.2) можем вычислить по явной схеме значения неизвестных функций $\mathop w\limits^{n + 1} $, $\mathop {{{u}_{i}}}\limits^{n + 1} $ и $\mathop {{{\gamma }_{i}}}\limits^{n + 1} $ в следующий момент времени ${{t}_{{n + 1}}}$. При известных $\mathop w\limits^{n + 1} $, $\mathop {{{u}_{i}}}\limits^{n + 1} $, $\mathop {{{\gamma }_{i}}}\limits^{n + 1} $ по формулам (3.1) с учетом (3.7) определяем осредненные деформации композиции $\mathop {{{\varepsilon }_{{ij}}}}\limits^{n + 1} $. Согласно (3.1) и (3.7) при учете предположений (4.1), деформации $\mathop {{{\varepsilon }_{{ij}}}}\limits^{n - 1} $ уже известны, поэтому на основании формул численного дифференцирования по t с использованием (3.4) можно вычислить и скорости осредненных деформаций $\mathop {{{{\dot {\varepsilon }}}_{{ij}}}}\limits^n $ при $t = {{t}_{n}}$. Затем по формулам (2.19) из [14] вычисляем скорости деформаций материалов композиции $\mathop {{{{\dot {\varepsilon }}}_{k}}}\limits^n $ (см. (2.18)), а из соотношений (2.24) и (2.22) – скорости напряжений $\mathop {{{{\dot {\sigma }}}_{k}}}\limits^n $ и ускорения деформаций $\mathop {{{{\ddot {\varepsilon }}}_{k}}}\limits^n $ ($0 \leqslant k \leqslant N$) в тех же компонентах. Используя третье соотношение (2.3) и формулу трапеций, параметр Одквиста ${{\chi }^{{(k)}}}$ в момент времени ${{t}_{n}}$ с точностью порядка ${{\Delta }^{2}}$ можно вычислить так:

где согласно (4.1) функции $\mathop {{{\chi }^{{(k)}}}}\limits^{n - 1} $ и $\mathop {\dot {p}_{{ij}}^{{(k)}}}\limits^{n - 1} $ уже известны. Скорости пластических деформаций компонентов композиции $\mathop {\dot {p}_{{ij}}^{{(k)}}}\limits^n $ в (4.3) при $t = {{t}_{n}}$ можно определить по формуле (2.5) при учете (2.11). Так как при этом $\mathop {\dot {p}_{{ij}}^{{(k)}}}\limits^n $ уточняются в процессе реализации метода переменных параметров упругости, то по формуле (4.3) итерационно уточняется значение $\mathop {{{\chi }^{{(k)}}}}\limits^n \left( {\mathbf{r}} \right)$. В качестве начального приближения можно принять $\mathop {{{\chi }^{{(k)}}}}\limits^n = \mathop {{{\chi }^{{(k)}}}}\limits^{n - 1} $. Дальнейшее решение рассматриваемой задачи строится так же, как и в [11, 14].

Согласно структуре левых частей уравнений (4.2), для начала расчетов по разработанной численной схеме необходимо знать значения функций $\mathop w\limits^m $, $\mathop {{{u}_{i}}}\limits^m $ и $\mathop {{{\gamma }_{i}}}\limits^m $ ($m = 0,\;1$). Функции $\mathop w\limits^0 $, $\mathop {{{u}_{i}}}\limits^0 $ и $\mathop {{{\gamma }_{i}}}\limits^0 $ известны из начальных условий, а значения функций $\mathop w\limits^1 $, $\mathop {{{u}_{i}}}\limits^1 $ и $\mathop {{{\gamma }_{i}}}\limits^1 $ определяются по формуле Тейлора при использовании начальных условий (3.10) и уравнений движения (3.5) в начальный момент времени $t = {{t}_{0}}$ (см. выражения (69) в [11]).

Если область $\Omega $, занимаемая конструкцией в плане, прямоугольна, то после замены в уравнениях (4.2) и граничных условиях (3.8) производных ${{\partial }_{i}}\left( \centerdot \right)$ их конечно-разностными аналогами получим окончательно явную численную схему типа “крест”. Если область $\Omega $ имеет неканоническую форму, то дискретизацию соотношений (4.2) и (3.8) можно провести на основе вариационно-разностного подхода, использованного в [10]. Необходимые условия устойчивости схемы типа “крест” вытекают из критерия устойчивости Куранта и для тонкостенных однородных конструкций приведены в [10]. Если эти условия выполняются для каждого компонента композиции, то они с запасом выполняются и для КМ-пластины.

5. Обсуждение результатов расчетов. Исследуем неупругое динамическое деформирование относительно тонкой прямоугольной пластины ($\Omega $: $\left| {{{x}_{1}}} \right| \leqslant a$, $\left| {{{x}_{2}}} \right| \leqslant b$; $a = 3b$, $b = 50$ см, $2h = 2$ см; $2h{\text{/}}2b = 1{\text{/}}50$). По всем кромкам ($\Gamma = {{\Gamma }_{u}}$) конструкция жестко закреплена (см. (3.9) и (3.11) при ${{w}_{ * }} = {{U}_{{i * }}} = 0$) и при $t = {{t}_{0}} = 0$ покоится (см. (3.10) и (3.11) при ${{w}_{0}} = {{U}_{{0i}}} = 0$ и ${{\dot {w}}_{0}} = {{V}_{{0i}}} = 0$, $i = 1,2$). Пластина нагружена избыточным давлением со стороны нижней лицевой плоскости, вызванным приходом воздушной взрывной волны [30]:

где t_max – время, при котором давление $p\left( t \right)$ достигает наибольшего значения ${{p}_{{\max }}} > 0$; ${{t}_{{{\text{min}}}}}$ – время, при превышении которого можно пренебречь p(t) по сравнению с p_max (соотношение (5.2) получено при условии $p\left( {{{t}_{{{\text{min}}}}}} \right) = 0.01{{p}_{{\max }}}$). Согласно экспериментальным данным [30], в расчетах примем ${{t}_{{{\text{max}}}}} = 0.1$ мс, ${{t}_{{{\text{min}}}}} = 2$ мс и ${{p}_{{\max }}} = 3$ МПа.

Конструкция изготовлена из эпоксидной смолы [31] и армирована стеклянными волокнами [32]. Диаграмма неупругого деформирования материала композиции при активном нагружении и постоянстве скорости деформации определяется следующей зависимостью при растяжении–сжатии:

где $\sigma $, ${{\varepsilon }_{p}}$ – осевое напряжение и соответствующая пластическая составляющая линейной деформации $\varepsilon $; $E_{{\text{s}}}^{{(k)}} = E_{{\text{s}}}^{{(k)}}\left( {\dot {\varepsilon }} \right)$ – модуль линейного упрочнения k-го материала композиции; $\sigma _{{\text{s}}}^{{(k)}} = \sigma _{{\text{s}}}^{{(k)}}\left( {\dot {\varepsilon }} \right)$ – условный предел текучести при значении скорости деформировании $\dot {\varepsilon } = {\text{const}}$. Физико-механические характеристики компонентов композиции представлены в таблице 1, где $a = \sqrt {E{\text{/}}\rho } $ – скорость звука в соответствующем материале. Объемная вязкость материалов в расчетах не учитывается: ${{\mu }^{{(k)}}} \to \infty $, $0 \leqslant k \leqslant N$ (см. (2.4) и (2.20)). Диаграмму неупругого деформирования при чистом сдвиге $\tau \sim {{\gamma }_{p}}$ можно рассчитать, используя зависимость (5.3), по формулам, приведенным в [23].

Рассматриваются две однородных (${{\theta }_{k}} = {\text{const}}$, ${{\varphi }_{k}} = {\text{const}}$ и ${{\omega }_{k}} = {\text{const}}$, $1 \leqslant k \leqslant N$) структуры армирования: 1) плоско-ортогональное 2D-армирование (рис. 2,a), когда волокна двух ($N = 2$) семейств уложены в направлениях $O{{x}_{1}}$ и $O{{x}_{2}}$ с плотностями армирования ${{\omega }_{1}} = 0.1$ и ${{\omega }_{2}} = {\text{0}}{\text{.3}}$ соответственно; 2) пространственное 4D-армирование (рис. 2,b), когда два первых семейства волокон по-прежнему уложены по направлениям $O{{x}_{1}}$ и $O{{x}_{2}}$, а третье и четвертое семейства – по направлениям, которые задаются углами (см. рис. 1): ${{\theta }_{3}} = \pi {\text{/}}4$, ${{\theta }_{4}} = 3\pi {\text{/}}4$, ${{\varphi }_{3}} = {{\varphi }_{4}} = \pi {\text{/}}2$ (т.е. на рис. 2,b угол $\theta = \pi {\text{/}}4$). Плотности армирования во второй структуре имеют значения: ${{\omega }_{1}} = {\text{0}}{\text{.05}}$, ${{\omega }_{2}} = {\text{0}}{\text{.3}}$ и ${{\omega }_{3}} = {{\omega }_{4}} = {\text{0}}{\text{.025}}$. В обеих структурах общий расход волокон одинаков.

Так как пластина в плане имеет каноническую прямоугольную форму, то по направлениям ${{x}_{1}}$, ${{x}_{2}}$ вводится равномерная сетка $\Delta {{x}_{1}} = \Delta {{x}_{2}} = 2b{\text{/}}100 = 1$ см, шаг по времени $\Delta = 1$ мкс, а правые части в уравнениях (4.2) аппроксимируются их конечно-разностными аналогами. При указанной дискретизации области интегрирования отношения $\Delta {{x}_{1}}{\text{/}}\Delta = 10$ км/с и $2h{\text{/}}\Delta = 20$ км/с существенно превышают значения a, указанные в таблице. Следовательно, необходимые условия устойчивости схемы «крест» выполняются для каждого материала композиции [10], а значит, и для рассматриваемой композиции в целом, причем со значительным запасом.

На рис. 3 изображены зависимости прогиба (в мм) центральных точек (${{w}_{0}}(t) \equiv w$(t, 0, 0)) рассматриваемых КМ-пластин от времени (в мс) в окрестности начального момента (рис. 3,a) и в окрестности $t = 500$ мс (рис. 3,b). Номера кривых соответствуют номерам структур армирования. Кривые, номера которых помечены штрихом, получены без учета чувствительности материалов композиции к изменению скорости деформирования. (Для этих кривых расчеты проводились по табличным данным, соответствующим скорости деформации $\dot {\varepsilon } = 5 \times {{10}^{{ - 4}}}$ с^–1.) Кривые 1′ и 2′ на рис. 3,a не изображены, так как они визуально почти не отличаются от кривых 1 и 2 соответственно.

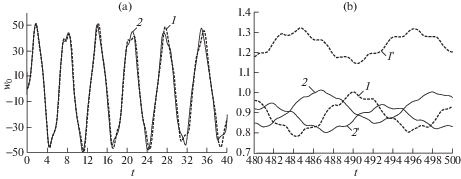
Из сравнения ординат точек кривых 1 и 2 на рис. 3,a и 3,b видно, что к моменту времени $t = 500$ мс стеклопластиковые пластины с обеими структурами армирования почти полностью перестают колебаться. Сопоставление кривых на рис. 3,a свидетельствует о том, что для относительно тонкой КМ-пластины замена традиционной 2D-структуры армирования (см. рис. 2,a) на пространственную 4D-структуру (см. рис. 2,b) не приводит к уменьшению максимального значения прогиба. Аналогично, согласно поведению этих же кривых на рис. 3,b, такая замена структуры армирования в тонкой пластине не приводит к значительному уменьшению величины остаточного прогиба в центральной точке конструкции. Сравнение же кривых 1′ и 2′ на рис. 3,b показывает, что при расчете тонких КМ-пластин по вязкоупругопластической модели деформирования замена 2D-структуры армирования на 4D-структуру приводит к существенному уменьшению величины остаточного прогиба в центральной точке.

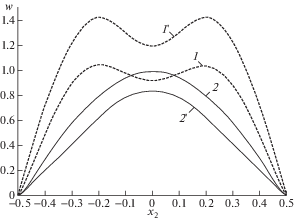
На рис. 4 изображены зависимости прогибов (в мм) исследуемых пластин от координаты ${{x}_{2}}$ (в м), определенные в центральных поперечных сечениях (${{x}_{1}} = 0$) при t = = 500 мс, когда конструкции практически уже перестали осциллировать. Обозначение кривых на рис. 4 такое же, к ак и на рис. 3. Поведение кривых 2 и 2′ на рис. 4 свидетельствует о том, что остаточный прогиб КМ-пластины с пространственным армированием имеет традиционный $ \cap $-образный вид, а поведение кривых 1 и 1′ показывает, что остаточный прогиб пластин с 2D-армированием имеет необычный M-образный вид. А значит, конструкции с 2D-структурой армирования после динамического неупругого деформирования приобретают остаточную форму гофрированного вида со складками, ориентированными в продольном направлении $O{{x}_{1}}$.

На рис. 5 изображены зависимости наибольших значений интенсивности деформаций $\varepsilon _{ * }^{{(k)}}$ ($\varepsilon _{{\text{m}}}^{{(k)}}\left( t \right) = \mathop {\max }\limits_{\mathbf{r}} \varepsilon _{ * }^{{(k)}}\left( {t,{\mathbf{r}}} \right)$, $\left| {{{x}_{1}}} \right| \leqslant a$, $\left| {{{x}_{2}}} \right| \leqslant b$ и $\left| {{{x}_{3}}} \right| \leqslant h$) компонентов композиции рассматриваемых пластин от времени (в мс) в окрестности начального момента (рис. 5,a) и в окрестности $t = 500$ мс (рис. 5,b). Кривые на рис. 5 имеют двойное обозначение: первая цифра обозначает номер структуры армирования, вторая цифра (после дефиса) – номер k-го компонента композиции ($k = 0$ – связующее, $k = 2$ – арматура второго семейства, уложенная в направлении $O{{x}_{2}}$ и испытывающая наиболее интенсивное деформирование). Штрих у номера кривой имеет прежний смысл. На рис. 5,a (чтобы его не загромождать) приведены зависимости $\varepsilon _{{\text{m}}}^{{(0)}}\left( t \right)$ только для связующего материала.

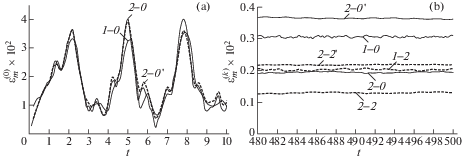
Сравнение кривых 1-0 и 2-0 на рис. 5,a демонстрирует, что замена в относительно тонкой пластине 2D-структуры армирования на 4D-структуру приводит к увеличению наибольшего значения $\varepsilon _{{{\text{max}}}}^{{(0)}} = \mathop {\max }\limits_{t \geqslant 0} \varepsilon _{{\text{m}}}^{{(0)}}\left( t \right)$ в связующей матрице примерно на 14%. Поведение же кривых 2-0 и 2-0′ на рис. 5,a свидетельствует о том, что учет и неучет чувствительности материалов композиции к скорости их деформирования для тонкой стеклопластиковой пластины с 4D-структурой армирования практически не влияет на величину $\varepsilon _{{{\text{max}}}}^{{(0)}}$ в связующем. Напротив, сопоставление кривых 1-0, 1-2 и 2-0, 2-2 на рис. 5,b показывает, что такая замена структуры армирования позволяет существенно уменьшить интенсивность остаточных деформаций рассматриваемых компонентов композиции. Сравнение же кривых 2-0, 2-2 и 2-0′, 2-2′ указывает на то, что расчет, выполненный для тонкой пластины с 4D-структурой армирования без учета чувствительности материалов композиции к изменению скорости их деформирования (кривые 2-0′ и 2-2′), существенно (почти вдвое для связующего) завышает величину интенсивности остаточных деформаций компонентов композиции по сравнению с расчетом, учитывающим эту чувствительность (кривые 2-0 и 2-2).

Результаты, которые обсуждались выше, касаются относительно тонких КМ-пластин (относительная толщина равна 1/50). Проведенные дополнительные расчеты показывают, что при увеличении относительной толщины пластин положительный эффект от замены плоско-перекрестных структур армирования (см. рис. 2,a) на пространственные структуры (см. рис. 2,b) существенно возрастает как при учете, так и неучете чувствительности компонентов композиции к скорости их деформирования. Так, в работе [14] показано, что для стеклопластиковой пластины с относительной толщиной 1/10 замена 2D-структурой армирования на 4D-структуру приводит к уменьшению максимального значения прогиба почти на 20%, а величины $\varepsilon _{{{\text{max}}}}^{{(0)}}$ – на 30% (при учете указанной чувствительности).

6. Заключение. Разработанная модель вязкоупруго-вязкопластического деформирования армированных пластин позволяет определять остаточные перемещения и остаточное деформированное состояние компонентов композиции при учете их чувствительности к изменению скорости деформирования.

Анализ динамического вязкоупругопластического и вязкоупруго-вязкопластического поведения стеклопластиковых пластин, материалы композиции которых слабо чувствительны к скорости деформирования, показал, что даже для относительно тонких КМ-конструкций неучет этой чувствительности может существенно (даже в разы) завышать величину интенсивности остаточных деформаций компонентов композиции. Это различие возрастает с увеличением относительной толщины пластин и с увеличением чувствительности материалов композиции к изменению скорости их деформирования.

Даже в случае относительно тонких стеклопластиковых пластин (с относительной толщиной 1/50) замена традиционной ортогональной 2D-структуры армирования (рис. 2,a) на пространственную 4D-структуру (рис. 2,b) позволяет существенно уменьшить интенсивность остаточных деформаций компонентов композиции (особенно связующей матрицы). Положительный эффект от такой замены структур армирования резко возрастает с увеличением относительной толщины конструкции. Так, для стеклопластиковых пластин с относительной толщиной порядка 1/10 указанная замена структур армирования позволяет значительно уменьшить не только остаточные прогибы конструкции и остаточные деформации компонентов композиции, но и максимальный (достигаемый в процессе осцилляций) прогиб и максимальные значения интенсивности деформаций компонентов композиции.

Обнаружено, что после неупругого динамического деформирования стеклопластиковой удлиненной пластины она может приобретать гофрированную остаточную форму с ориентацией складок в продольном направлении.

Высокопрочные стеклянные волокна при их интенсивном деформировании запасают упругую энергию в большом количестве, поэтому после прекращения действия внешней динамической нагрузки арматура стремится вернуть КМ-пластину в исходное положение даже несмотря на то, что низкопрочное эпоксисвязующее подвергается при этом значительному циклическому пластическому деформированию. Вследствие чего амплитуда поперечныхколебаний тонкостенной КМ-конструкции при нагрузке взрывного типа в окрестности начального момента времени на порядок и более превышает величину остаточного прогиба. Подобное поведение не характерно для неупруго деформируемых однородных пластин при интенсивном динамическом нагружении.

Работа выполнена в рамках государственного задания (№ госрегистрации 121030900260-6).