Известия РАН. Механика твердого тела, 2021, № 5, стр. 45-63
УПРАВЛЕНИЕ ФОРМОЙ СЛОИСТЫХ КОМПОЗИТНЫХ ПЛАСТИН С ПЬЕЗОЭЛЕКТРИЧЕСКИМИ НАКЛАДКАМИ ПРИ ТЕПЛОВОМ НАГРУЖЕНИИ НА ОСНОВЕ МЕТОДА ОТСЧЕТНЫХ ПОВЕРХНОCТЕЙ
Г. М. Куликов a, *, С. В. Плотникова a
a Тамбовский государственный технический университет
Тамбов, Россия
* E-mail: gmkulikov@mail.ru
Поступила в редакцию 17.01.2021
После доработки 20.01.2021
Принята к публикации 25.01.2021
Аннотация
В данной работе предложен гибридный конечный элемент для моделирования в пространственной постановке связанных термоэлектромеханических полей в композитных пластинах с пьезоэлектрическими накладками, основанный на методе отсчетных поверхностей. Согласно методу отсчетных поверхностей в слоях пластины и пьезоэлектрических накладках выбираются отсчетные поверхности параллельные срединной поверхности для введения в качестве искомых функций температуры, перемещений и электрических потенциалов этих поверхностей. Вначале вычисляется распределение температуры в слоистой пластине путем решения методом конечных элементов задачи теплопроводности. Полученные результаты используется в качестве входных данных для решения задачи термоэлектроупругости. На основе разработанной конечно-элементной модели предложен метод определения оптимальных электрических потенциалов, подаваемых на электроды актуаторов, с целью приведения пластины к заданной форме за счет использования обратного пьезоэлектрического эффекта.
Введение. В настоящее время устройства и технические системы на основе пьезоактивных материалов проникли в авиационную и космическую технику и широко используются в адаптивных композитных конструкциях. Подобные конструкции с встроенными в них пьезокерамическими материалами способны в значительных пределах менять свои технические характеристики в соответствии с условиями эксплуатации и позволяют эффективно управлять их деформациями. Преимуществом пьезокерамики является то, что в силу прямого и обратного пьезоэлектрических эффектов она может одновременно выполнять функции как сенсора, так и актуатора. Проектирование адаптивных конструкций представляет собой многогранную деятельность, включающую исследования по теплопередаче, механике композитных материалов и конструкций, сенсорам и актуаторам, методам оптимизации. Таким образом, расчет и моделирование тонкостенных композитных конструкций с пьезоэлектрическими сенсорами и актуаторами при тепловых и механических воздействиях на основе пространственной теории термопьезоэлектричества является актуальной задачей.
Расчет термоэлектроупругих слоистых конструкций на основе теории оболочек первого порядка (теория Тимошенко–Миндлина) с использованием четырехузловых конечных элементов выполнен в работах [1, 2]. При этом для описания температуры и электрического потенциала применена дискретная модель слоистых оболочек первого порядка. Конечные элементы для расчета слоистых композитных пластин при тепловых воздействиях на основе теории пластин третьего порядка предложены в работах [3, 4]. В девяностых годах для анализа связанных температурных, механических и электрических полей в слоистых пьезоэлектрических конструкциях стали использоваться трехмерные изопараметрические элементы [5–8]. Однако для расчета адаптивных тонкостенных конструкций такие конечные элементы являются вычислительно неэффективными. В связи с этим получили развитие конечные элементы для расчета в пространственной постановке слоистых пьезоэлектрических конструкций на основе дискретных теорий первого и третьего порядков [9–11] путем использования степенных полиномов для аппроксимации температуры, перемещений и электрического потенциала в пределах слоя. Более общие геометрически точные конечные элементы оболочки для расчета слоистых пьезоэлектрических конструкций на основе метода отсчетных поверхностей [12] с использованием полиномов Лагранжа произвольной степени построены в работе [13]. Согласно методу отсчетных поверхностей в слоях оболочки выбираются отсчетные поверхности параллельные срединной поверхности с целью введения в качестве искомых функций температуры, перемещений и электрических потенциалов этих поверхностей. Отметим, что геометрически точные конечные элементы оболочки [13] не предназначены для расчета композитных конструкций с распределенными на лицевых поверхностях пьезоэлектрическими актуаторами, что представляет интерес для решения задачи управления формой адаптивных композитных конструкций.
В данной работе на основе метода отсчетных поверхностей, расположенных в слоях пластины и пьезоэлектрических накладках в узловых точках полинома Чебышева, построен пространственный четырехузловой конечный элемент слоистой композитной пластины с учетом условия эквипотенциальности на электродах, обобщающий конечный элемент [14] на случай теплового нагружения и позволяющий эффективно решать задачи о приведении пластины к заданной форме и о возврате деформированной пластины к ее первоначальной форме. На возможность компенсации температурных деформаций за счет обратного пьезоэлектрического эффекта указано в работе [15]. Анализ численных алгоритмов и методов управления формой адаптивной конструкции представлен в обзоре [16].
1. Конечный элемент для решения задачи теплопроводности для слоистой пластины на основе метода отсчетных поверхностей. Рассмотрим пластину толщиной h, состоящую из N слоев. Срединная поверхность пластины $\Omega $ описывается декартовыми координатами ${{x}_{1}}$, ${{x}_{2}}$, а координата ${{x}_{3}}$ отсчитывается вдоль нормали к этой поверхности. В n-м слое пластины выбираем Inотсчетных поверхностей параллельных срединной поверхности, где ${{I}_{n}} \geqslant 3$. При этом ${{I}_{n}} - 2$ поверхности расположены внутри слоя в узловых точках полинома Чебышева, что обеспечивает равномерную сходимость метода, другие две совпадают с поверхностями раздела слоев. Таким образом, общее число отсчетных поверхностей в пакете равно ${{N}_{{\text{S}}}} = \sum\nolimits_n {{{I}_{n}}} - N + 1$. Координаты отсчетных поверхностей определяем по формулам [17]:
Согласно методу отсчетных поверхностей [17] полагаем, что температура ${{T}^{{(n)}}}$, компоненты градиента температуры $\Gamma _{i}^{{(n)}} = T_{{,i}}^{{(n)}}$ и теплового потока $q_{i}^{{\left( n \right)}} = - k_{{ij}}^{{(n)}}{{\Gamma }}_{j}^{{(n)}}$, где $k_{{ij}}^{{(n)}}$ – коэффициенты теплопроводности, распределены по толщине n-го слоя по следующему закону:
(1.2)
$\left[ {{{T}^{{(n)}}}\Gamma _{i}^{{(n)}}q_{i}^{{(n)}}} \right] = \sum\limits_{{{i}_{n}}} {{{L}^{{(n){{i}_{n}}}}}{{{\left[ {{{T}^{{(n){{i}_{n}}}}}\Gamma _{i}^{{(n){{i}_{n}}}}q_{i}^{{(n){{i}_{n}}}}} \right]}}^{{}}}} ,\quad x_{3}^{{[n - 1]}} \leqslant {{x}_{3}} \leqslant x_{3}^{{[n]}}$Здесь ${{T}^{{(n){{i}_{n}}}}}$, $\Gamma _{i}^{{(n){{i}_{n}}}}$, $q_{i}^{{(n){{i}_{n}}}}$ – температура, компоненты градиента температуры и теплового потока на отсчетных поверхностях; ${{L}^{{(n){{i}_{n}}}}}({{x}_{3}})$ – базисные полиномы Лагранжа степени ${{I}_{n}} - 1$:
(1.3)
${{L}^{{(n){{i}_{n}}}}} = \prod\limits_{{{j}_{n}} \ne {{i}_{n}}} {\frac{{{{x}_{3}} - x_{3}^{{(n){{j}_{n}}}}}}{{x_{3}^{{(n){{i}_{n}}}} - x_{3}^{{(n){{j}_{n}}}}}}} $В силу формул (1.2), (1.3) соотношения между градиентом температуры и температурой отсчетных поверхностях n-го слоя имеют вид
(1.4)
${{\Gamma }}_{\alpha }^{{(n){{i}_{n}}}} = T_{{,\alpha }}^{{(n){{i}_{n}}}}\quad (\alpha = 1,\;2),\quad {{\Gamma }}_{3}^{{(n){{i}_{n}}}} = \sum\limits_{{{j}_{n}}} {{{M}^{{(n){{j}_{n}}}}}(x_{3}^{{(n){{i}_{n}}}}){{T}^{{(n){{j}_{n}}}}}} $(1.5)
${{M}^{{(n){{j}_{n}}}}}(x_{3}^{{(n){{i}_{n}}}}) = \frac{1}{{x_{3}^{{(n){{j}_{n}}}} - x_{3}^{{(n){{i}_{n}}}}}}\prod\limits_{{{k}_{n}} \ne {{i}_{n}},\,{{j}_{n}}} {\frac{{x_{3}^{{(n){{i}_{n}}}} - x_{3}^{{(n){{k}_{n}}}}}}{{x_{3}^{{(n){{j}_{n}}}} - x_{3}^{{(n){{k}_{n}}}}}}} \quad {\text{при}}\quad {{j}_{n}} \ne {{i}_{n}}$Вариационное уравнение теплопроводности для слоистой пластины относительно градиента температуры и температуры отсчетных поверхностей [13] запишем в виде
(1.6)
$\delta \iint\limits_\Omega {\sum\limits_n {\sum\limits_{{{i}_{n}}} {\sum\limits_{{{j}_{n}}} {\frac{1}{2}{{\Lambda }^{{(n){{i}_{n}}{{j}_{n}}}}}{{{({\mathbf{\Gamma }}_{{}}^{{(n){{i}_{n}}}})}}^{{\text{т}}}}{{{\mathbf{k}}}^{{(n)}}}{\mathbf{\Gamma }}_{{}}^{{(n){{j}_{n}}}}} } } }d{{x}_{1}}d{{x}_{2}} = \iint\limits_\Omega {(\hat {q}_{3}^{ - }\delta {{T}^{{[0]}}} - \hat {q}_{3}^{ + }\delta {{T}^{{[N]}}})d{{x}_{1}}d{{x}_{2}}}$(1.7)
${{{{\Lambda }}}^{{(n){{i}_{n}}{{j}_{n}}}}} = \int\limits_{x_{3}^{{[n - 1]}}}^{x_{3}^{{[n]}}} {{{L}^{{(n){{i}_{n}}}}}{{L}^{{(n){{j}_{n}}}}}d{{x}_{3}}} $Здесь ${{T}^{{[0]}}}$, ${{T}^{{[N]}}}$ – температура нижней и верхней лицевых поверхностей ${{\Omega }^{ - }}$ и ${{\Omega }^{ + }}$; $\hat {q}_{3}^{ - }$, $\hat {q}_{3}^{ + }$ – заданные тепловые потоки на лицевых поверхностях.
Для построения конечно-элементной модели разобьем пластину на прямоугольные элементы, причем число слоев в конечных элементах с пьезоэлектрическими накладками и без них будет отличаться. Предположим для определенности, что накладки расположены на верхней поверхности, тогда число слоев определяется как $N = {{N}_{0}}$ для конечных элементов, не содержащих накладок, и $N = {{N}_{0}} + 1$ для элементов с накладками, где N0 – число слоев в слоистой пластине.
Температура и градиент температуры отсчетных поверхностей n-го слоя в пределах четырехузлового конечного элемента аппроксимируются согласно билинейному закону:
(1.9)
${{{\mathbf{\Gamma }}}^{{(n){{i}_{n}}}}} = \sum\limits_r {{{N}_{r}}{\mathbf{\Gamma }}_{r}^{{(n){{i}_{n}}}},} \quad {\mathbf{\Gamma }}_{r}^{{(n){{i}_{n}}}} = {{[\Gamma _{{1r}}^{{(n){{i}_{n}}}}\;\Gamma _{{2r}}^{{(n){{i}_{n}}}}\;\Gamma _{{3r}}^{{(n){{i}_{n}}}}]}^{{\text{т}}}}$Введем дополнительные матричные обозначения:
(1.10)
${\mathbf{T}} = {{[{\mathbf{T}}_{1}^{{\text{т}}}\;{\mathbf{T}}_{2}^{{\text{т}}}\;{\mathbf{T}}_{3}^{{\text{т}}}\;{\mathbf{T}}_{4}^{{\text{т}}}]}^{{\text{т}}}}$Учитывая соотношения (1.4), (1.9), (1.10), градиент температурного поля в узлах конечного элемента представим в форме
(1.11)
${\mathbf{\Gamma }}_{r}^{{(n){{i}_{n}}}} = {\mathbf{B}}_{{\theta r}}^{{(n){{i}_{n}}}}{\mathbf{T}}$Здесь ${\mathbf{B}}_{{\theta r}}^{{(n){{i}_{n}}}}$ – постоянные матрицы порядка $3 \times 4{{N}_{{\text{S}}}}$ [13]. Чтобы применить аналитическое интегрирование в пределах конечного элемента, билинейную аппроксимацию для градиента температуры (1.9) запишем в виде
(1.12)
${{{\mathbf{\Gamma }}}^{{(n){{i}_{n}}}}} = \sum\limits_{{{r}_{1}},{{r}_{2}}} {{{{\left( {\xi {}_{1}} \right)}}^{{{{r}_{1}}}}}{{{\left( {{{\xi }_{2}}} \right)}}^{{{{r}_{2}}}}}{\mathbf{\Gamma }}_{{{{r}_{1}}{{r}_{2}}}}^{{(n){{i}_{n}}}}} ,\quad {\mathbf{\Gamma }}_{{{{r}_{1}}{{r}_{2}}}}^{{(n){{i}_{n}}}} = [\Gamma _{{1{{r}_{1}}{{r}_{2}}}}^{{(n){{i}_{n}}}}\;\Gamma _{{2{{r}_{1}}{{r}_{2}}}}^{{(n){{i}_{n}}}}\;\Gamma _{{3{{r}_{1}}{{r}_{2}}}}^{{(n){{i}_{n}}}}]$(1.13)
${\mathbf{\Gamma }}_{{{{r}_{1}}{{r}_{2}}}}^{{(n){{i}_{n}}}} = {\mathbf{B}}_{{\theta {{r}_{1}}{{r}_{2}}}}^{{(n){{i}_{n}}}}{\mathbf{T}}$Здесь и далее, индексы ${{r}_{1}}$, ${{r}_{2}}$ принимают значения 0 или 1.
Подставляя (1.8), (1.12) в вариационное уравнение (1.6) и выполняя аналитическое интегрирование в пределах конечного элемента, приходим к системе линейных уравнений
Здесь ${{{\mathbf{F}}}_{\theta }}$ – вектор теплового нагружения. При сборке элементов в ансамбль следует учитывать, что число слоев в конечных элементах с накладками превышает число слоев в элементах без накладок и, следовательно, размерность матрицы ${{{\mathbf{K}}}_{{\theta \theta }}}$ зависит от типа конечного элемента.
2. Конечный элемент для решения задачи термоэлектроупругости для слоистой пьезоэлектрической пластины на основе метода отсчетных поверхностей. Согласно методу отсчетных поверхностей, примененному для решения связанной задачи термоэлектроупругости [12], полагаем, что перемещения $u_{i}^{{(n)}}$, деформации $\varepsilon _{{ij}}^{{(n)}}$, напряжения $\sigma _{{ij}}^{{(n)}}$, электрический потенциал ${{\varphi }^{{(n)}}}$, компоненты векторов напряженности электрического поля $E_{i}^{{(n)}}$ и электрического смещения $D_{i}^{{\left( n \right)}}$ распределены по толщине n-го слоя пластины по закону аналогичному (1.2), (1.3):
(2.1)
$[u_{i}^{{(n)}}\varepsilon _{{ij}}^{{(n)}}\sigma _{{ij}}^{{(n)}}{{\varphi }^{{(n)}}}E_{i}^{{(n)}}D_{i}^{{(n)}}] = \sum\limits_{{{i}_{n}}} {{{L}^{{(n){{i}_{n}}}}}[u_{i}^{{(n){{i}_{n}}}}\varepsilon _{{ij}}^{{(n){{i}_{n}}}}\sigma _{{ij}}^{{(n){{i}_{n}}}}{{\varphi }^{{(n){{i}_{n}}}}}E_{i}^{{(n){{i}_{n}}}}D_{i}^{{(n){{i}_{n}}}}]} $Соотношения между деформациями и перемещениями отсчетных поверхностей, а также между напряженностью и потенциалом электрического поля отсчетных поверхностей имеют вид
(2.2)
$2\varepsilon _{{\alpha \beta }}^{{(n){{i}_{n}}}} = u_{{\alpha ,\beta }}^{{(n){{i}_{n}}}} + u_{{\beta ,\alpha }}^{{(n){{i}_{n}}}},\quad 2\varepsilon _{{\alpha 3}}^{{(n){{i}_{n}}}} = u_{{3,\alpha }}^{{(n){{i}_{n}}}} + \beta _{\alpha }^{{(n){{i}_{n}}}}\quad (\alpha ,\beta = 1,\;2)$(2.3)
$E_{\alpha }^{{(n){{i}_{n}}}} = - \varphi _{{,\alpha }}^{{(n){{i}_{n}}}},\quad E_{3}^{{(n){{i}_{n}}}} = - \sum\limits_{{{j}_{n}}} {{{M}^{{(n){{j}_{n}}}}}(x_{3}^{{(n){{i}_{n}}}}){{\varphi }^{{(n){{j}_{n}}}}}} $Уравнения состояния линейной теории термопьезоэлектричества представим в форме
(2.4)
$\sigma _{{ij}}^{{(n){{i}_{n}}}} = C_{{ijkl}}^{{(n)}}\varepsilon _{{kl}}^{{(n){{i}_{n}}}} - e_{{kij}}^{{(n)}}E_{k}^{{(n){{i}_{n}}}} - \gamma _{{ij}}^{{(n)}}{{\Theta }^{{(n){{i}_{n}}}}}$Подставляя аппроксимации (1.2), (2.1) в смешанный вариационный принцип термоэлектроупругости для слоистого тела [18], в котором независимыми варьируемыми переменными являются перемещения $u_{i}^{{(n)}}$, электрический потенциал ${{\varphi }^{{(n)}}}$, независимые от поля перемещений деформации $\eta _{{ij}}^{{(n)}}$ и напряжения $\sigma _{{ij}}^{{(n)}}$, и интегрируя по поперечной координате с учетом (1.7), получим вариационное уравнение для построения гибридного конечного элемента слоистой пьезоэлектрической пластины при тепловом нагружении
(2.5)
$\begin{gathered} \iint\limits_{{\Omega }} {\sum\limits_n {\sum\limits_{{{i}_{n}}} {\sum\limits_{{{j}_{n}}} {{{\Lambda }^{{(n){{i}_{n}}{{j}_{n}}}}}[ - \delta {{{({{{\mathbf{\eta }}}^{{(n){{i}_{n}}}}})}}^{{\text{т}}}}({{{\mathbf{\sigma }}}^{{(n){{j}_{n}}}}} - {{{\mathbf{C}}}^{{(n)}}}{{{\mathbf{\eta }}}^{{(n){{j}_{n}}}}} + {{{({{{\mathbf{e}}}^{{(n)}}})}}^{{\text{т}}}}{{{\mathbf{E}}}^{{(n){{j}_{n}}}}} + {{{\mathbf{\gamma }}}^{{(n)}}}{{\Theta }^{{(n){{j}_{n}}}}})} } } } - \\ - \;\delta {{({{{\mathbf{E}}}^{{(n){{i}_{n}}}}})}^{{\text{т}}}}({{{\mathbf{e}}}^{{(n)}}}{{{\mathbf{\eta }}}^{{(n){{j}_{n}}}}} + {{ \in }^{{(n)}}}{{{\mathbf{E}}}^{{(n){{j}_{n}}}}} + {{{\mathbf{r}}}^{{(n)}}}{{\Theta }^{{(n){{j}_{n}}}}}) - \\ - \;\delta {{({{{\mathbf{\sigma }}}^{{(n){{i}_{n}}}}})}^{{\text{т}}}}({{{\mathbf{\eta }}}^{{(n){{j}_{n}}}}} - {{{\mathbf{\varepsilon }}}^{{(n){{j}_{n}}}}}) + \delta {{({{{\mathbf{\varepsilon }}}^{{(n){{i}_{n}}}}})}^{{\text{T}}}}{{{\mathbf{\sigma }}}^{{(n){{j}_{n}}}}}]d{{x}_{1}}d{{x}_{2}} = \\ = \;\iint\limits_\Omega {(\delta {{{({{{\mathbf{u}}}^{{[N]}}})}}^{{\text{т}}}}{{{{\mathbf{\hat {\sigma }}}}}^{ + }} - \delta {{{({{{\mathbf{u}}}^{{[0]}}})}}^{{\text{т}}}}{{{{\mathbf{\hat {\sigma }}}}}^{ - }} + \delta {{\varphi }^{{[N]}}}\hat {D}_{3}^{ + } - \delta {{\varphi }^{{[0]}}}\hat {D}_{3}^{ - })d{{x}_{1}}d{{x}_{2}}} \\ \end{gathered} $(2.6)
${{\varepsilon }^{{(n){{i}_{n}}}}} = {{[\varepsilon _{{11}}^{{(n){{i}_{n}}}}\;\varepsilon _{{22}}^{{(n){{i}_{n}}}}\;\varepsilon _{{33}}^{{(n){{i}_{n}}}}\;2\varepsilon _{{12}}^{{(n){{i}_{n}}}}\;2\varepsilon _{{13}}^{{(n){{i}_{n}}}}\;2\varepsilon _{{23}}^{{(n){{i}_{n}}}}]}^{{\text{т}}}}$Для интерполяции перемещений, деформаций, потенциала и напряженности электрического поля отсчетных поверхностей n-го слоя в пределах четырехузлового конечного элемента пластины воспользуемся стандартными билинейными аппроксимациями
(2.7)
$u_{i}^{{(n){{i}_{n}}}} = \sum\limits_r {{{N}_{r}}u_{{ir}}^{{(n){{i}_{n}}}}} ,\quad \varepsilon _{{ij}}^{{(n){{i}_{n}}}} = \sum\limits_r {{{N}_{r}}\varepsilon _{{ijr}}^{{(n){{i}_{n}}}}} $(2.8)
${{\varphi }^{{(n){{i}_{n}}}}} = \sum\limits_r {{{N}_{r}}\varphi _{r}^{{(n){{i}_{n}}}}} ,\quad E_{i}^{{(n){{i}_{n}}}} = \sum\limits_r {{{N}_{r}}E_{{ir}}^{{(n){{i}_{n}}}}} $(2.9)
${{{\mathbf{\varepsilon }}}^{{(n){{i}_{n}}}}} = \sum\limits_{{{r}_{1}},\,{{r}_{2}}} {{{{\left( {\xi {}_{1}} \right)}}^{{{{r}_{1}}}}}{{{\left( {{{\xi }_{2}}} \right)}}^{{{{r}_{2}}}}}{\mathbf{\varepsilon }}_{{{{r}_{1}}{{r}_{2}}}}^{{(n){{i}_{n}}}},\quad } {\mathbf{\varepsilon }}_{{{{r}_{1}}{{r}_{2}}}}^{{(n){{i}_{n}}}} = {{[\varepsilon _{{11{{r}_{1}}{{r}_{2}}}}^{{(n){{i}_{n}}}}\;\varepsilon _{{22{{r}_{1}}{{r}_{2}}}}^{{(n){{i}_{n}}}}\;\varepsilon _{{33{{r}_{1}}{{r}_{2}}}}^{{(n){{i}_{n}}}}\;2\varepsilon _{{12{{r}_{1}}{{r}_{2}}}}^{{(n){{i}_{n}}}}\;2\varepsilon _{{13{{r}_{1}}{{r}_{2}}}}^{{(n){{i}_{n}}}}\;2\varepsilon _{{23{{r}_{1}}{{r}_{2}}}}^{{(n){{i}_{n}}}}]}^{{\text{т}}}}$(2.10)
${{{\mathbf{E}}}^{{(n){{i}_{n}}}}} = \sum\limits_{{{r}_{1}},\,{{r}_{2}}} {{{{\left( {\xi {}_{1}} \right)}}^{{{{r}_{1}}}}}{{{\left( {{{\xi }_{2}}} \right)}}^{{{{r}_{2}}}}}{\mathbf{E}}_{{{{r}_{1}}{{r}_{2}}}}^{{(n){{i}_{n}}}}} ,\quad {\mathbf{E}}_{{{{r}_{1}}{{r}_{2}}}}^{{(n){{i}_{n}}}} = {{[E_{{1{{r}_{1}}{{r}_{2}}}}^{{(n){{i}_{n}}}}\;E_{{2{{r}_{1}}{{r}_{2}}}}^{{(n){{i}_{n}}}}\;E_{{3{{r}_{1}}{{r}_{2}}}}^{{(n){{i}_{n}}}}]}^{{\text{т}}}}$Соотношения (2.2), (2.3) с учетом аппроксимаций (2.9), (2.10) запишем в матричной форме
(2.11)
${\mathbf{\varepsilon }}_{{{{r}_{1}}{{r}_{2}}}}^{{(n){{i}_{n}}}} = {\mathbf{B}}_{{u{{r}_{1}}{{r}_{2}}}}^{{(n){{i}_{n}}}}{\mathbf{q}},\quad {\mathbf{E}}_{{{{r}_{1}}{{r}_{2}}}}^{{(n){{i}_{n}}}} = - {\mathbf{B}}_{{\varphi {{r}_{1}}{{r}_{2}}}}^{{(n){{i}_{n}}}}{\mathbf{\Phi }}$(2.12)
${\mathbf{q}} = {{[{\mathbf{q}}_{1}^{{\text{т}}}\;{\mathbf{q}}_{2}^{{\text{т}}}\;{\mathbf{q}}_{3}^{{\text{т}}}\;{\mathbf{q}}_{4}^{{\text{т}}}]}^{{\text{т}}}},\quad {\mathbf{\Phi }} = {{[{\mathbf{\Phi }}_{1}^{{\text{т}}}\;{\mathbf{\Phi }}_{2}^{{\text{т}}}\;{\mathbf{\Phi }}_{3}^{{\text{т}}}\;{\mathbf{\Phi }}_{4}^{{\text{т}}}]}^{{\text{т}}}}$Также при построении гибридного конечного элемента вводятся независимые аппроксимации напряжений ${\mathbf{\sigma }}_{{}}^{{(n){{i}_{n}}}}$ и деформаций ${\mathbf{\eta }}_{{}}^{{(n){{i}_{n}}}}$, позволяющие обеспечить корректный ранг матрицы жесткости [19]:
(2.13)
${{{\mathbf{\sigma }}}^{{(n){{i}_{n}}}}} = \sum\limits_{{{r}_{1}} + {{r}_{2}} < 2} {{{{\left( {{{\xi }_{1}}} \right)}}^{{{{r}_{1}}}}}{{{\left( {{{\xi }_{2}}} \right)}}^{{{{r}_{2}}}}}{{Q}_{{{{r}_{1}}{{r}_{2}}}}}{\mathbf{\sigma }}_{{{{r}_{1}}{{r}_{2}}}}^{{(n){{i}_{n}}}}} $(2.14)
${{{\mathbf{\eta }}}^{{(n){{i}_{n}}}}} = \sum\limits_{{{r}_{1}} + {{r}_{2}} < 2} {{{{\left( {{{\xi }_{1}}} \right)}}^{{{{r}_{1}}}}}{{{\left( {{{\xi }_{2}}} \right)}}^{{{{r}_{2}}}}}{{Q}_{{{{r}_{1}}{{r}_{2}}}}}{\mathbf{\eta }}_{{{{r}_{1}}{{r}_{2}}}}^{{(n){{i}_{n}}}}} $(2.15)
${{Q}_{{00}}} = \left[ {\begin{array}{*{20}{c}} 1&0&0&0&0&0 \\ 0&1&0&0&0&0 \\ 0&0&1&0&0&0 \\ 0&0&0&1&0&0 \\ 0&0&0&0&1&0 \\ 0&0&0&0&0&1 \end{array}} \right],\quad {{Q}_{{01}}} = \left[ {\begin{array}{*{20}{c}} 1&0&0 \\ 0&0&0 \\ 0&1&0 \\ 0&0&0 \\ 0&0&1 \\ 0&0&0 \end{array}} \right],\quad {{Q}_{{10}}} = \left[ {\begin{array}{*{20}{c}} 0&0&0 \\ 1&0&0 \\ 0&1&0 \\ 0&0&0 \\ 0&0&0 \\ 0&0&1 \end{array}} \right]$Подставляя конечно-элементные аппроксимации (2.7)–(2.10), (2.13), (2.14) в смешанное вариационное уравнение (2.5), интегрируя аналитически в пределах конечного элемента и исключая напряжения ${\mathbf{\sigma }}_{{{{r}_{1}}{{r}_{2}}}}^{{(n){{i}_{n}}}}$ и независимые от поля перемещений деформации ${\mathbf{\eta }}_{{{{r}_{1}}{{r}_{2}}}}^{{(n){{i}_{n}}}}$, приходим к разрешающей системе линейных уравнений
(2.16)
$\left[ {\begin{array}{*{20}{l}} {{{{\mathbf{K}}}_{{uu}}}}&{{{{\mathbf{K}}}_{{u\varphi }}}} \\ {{{{\mathbf{K}}}_{{\varphi u}}}}&{{{{\mathbf{K}}}_{{\varphi \varphi }}}} \end{array}} \right]\left[ {\begin{array}{*{20}{l}} q \\ {\mathbf{\Phi }} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{{{\mathbf{F}}}_{u}}} \\ {{{{\mathbf{F}}}_{\varphi }}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{{{\mathbf{F}}}_{{u\theta }}}} \\ {{{{\mathbf{F}}}_{{\varphi \theta }}}} \end{array}} \right]$Здесь ${{{\mathbf{K}}}_{{uu}}}$, ${{{\mathbf{K}}}_{{u\varphi }}}$, ${{{\mathbf{K}}}_{{\varphi u}}} = {\mathbf{K}}_{{u\varphi }}^{{\text{т}}}$, ${{{\mathbf{K}}}_{{\varphi \varphi }}}$ – механическая, пьезоэлектрическая и диэлектрическая матрицы жесткости конечного элемента, ${{{\mathbf{F}}}_{u}}$, ${{{\mathbf{F}}}_{\varphi }}$ – векторы механических и электрических нагрузок, ${{{\mathbf{F}}}_{{u\theta }}}$ и ${{{\mathbf{F}}}_{{\varphi \theta }}}$ – векторы температурных нагрузок:
(2.17)
${{{\mathbf{K}}}_{{uu}}} = \sum\limits_n {\sum\limits_{{{i}_{n}}} {\sum\limits_{{{j}_{n}}} {{{{{\Lambda }}}^{{(n){{i}_{n}}{{j}_{n}}}}}\sum\limits_{{{r}_{1}} + {{r}_{2}} < 2} {\frac{1}{{{{3}^{{{{r}_{1}} + {{r}_{2}}}}}}}{{{({\mathbf{B}}_{{u{{r}_{1}}{{r}_{2}}}}^{{(n){{i}_{n}}}})}}^{{\text{т}}}}{{Q}_{{{{r}_{1}}{{r}_{2}}}}}Q_{{{{r}_{1}}{{r}_{2}}}}^{{\text{т}}}{{{\mathbf{C}}}^{{(n)}}}{{Q}_{{{{r}_{1}}{{r}_{2}}}}}Q_{{{{r}_{1}}{{r}_{2}}}}^{{\text{т}}}{\mathbf{B}}_{{u{{r}_{1}}{{r}_{2}}}}^{{(n){{j}_{n}}}}} } } } $(2.18)
${{{\mathbf{F}}}_{{u\theta }}} = \sum\limits_n {\sum\limits_{{{i}_{n}}} {\sum\limits_{{{j}_{n}}} {{{{{\Lambda }}}^{{(n){{i}_{n}}{{j}_{n}}}}}\sum\limits_{{{r}_{1}} + {{r}_{2}} < 2} {\frac{1}{{{{3}^{{{{r}_{1}} + {{r}_{2}}}}}}}{{{({\mathbf{B}}_{{u{{r}_{1}}{{r}_{2}}}}^{{(n){{i}_{n}}}})}}^{{\text{т}}}}{{Q}_{{{{r}_{1}}{{r}_{2}}}}}{{{\mathbf{\gamma }}}^{{(n)}}}\Theta _{{{{r}_{1}}{{r}_{2}}}}^{{(n){{j}_{n}}}}} } } } $Величины $\Theta _{{{{r}_{1}}{{r}_{2}}}}^{{(n){{i}_{n}}}}$ находятся в результате решения задачи теплопроводности как линейная комбинация приращения температуры $\Theta _{r}^{{(n){{i}_{n}}}} = T_{r}^{{(n){{i}_{n}}}} - {{T}_{0}}$ в узлах конечного элемента [13]:
(2.19)
$\Theta _{{{{r}_{1}}{{r}_{2}}}}^{{(n){{i}_{n}}}} = \frac{1}{4}[\Theta _{1}^{{(n){{i}_{n}}}} + (1 - 2{{r}_{1}})\Theta _{2}^{{(n){{i}_{n}}}} + (1 - 2{{r}_{1}})(1 - 2{{r}_{2}})\Theta _{3}^{{(n){{i}_{n}}}} + (1 - 2{{r}_{2}})\Theta _{4}^{{(n){{i}_{n}}}}]$При решении сенсорной задачи выполнялось условие эквипотенциальности на электродах верхних поверхностей пьезоэлектрических накладок, то есть предполагалось, что
(2.20)
$\varphi _{1}^{{\left[ N \right]}} = \varphi _{2}^{{\left[ N \right]}} = \varphi _{3}^{{\left[ N \right]}} = \varphi _{4}^{{\left[ N \right]}}$Для учета условия (2.20) применяется метод штрафных функций, в соответствии с которым к диэлектрической матрице жесткости добавляется штрафная матрица с достаточно большим положительным множителем $\lambda $:
(2.21)
${\mathbf{K}}_{{\varphi \varphi }}^{*} = {\mathbf{K}}_{{\varphi \varphi }}^{{}} + \lambda {\mathbf{\hat {K}}}$Чтобы сохранить симметрию диэлектрической матрицы жесткости (2.21), ненулевые компоненты штрафной матрицы выбираются следующим образом:
(2.22)
${{{\mathbf{\hat {K}}}}_{{{{N}_{{\text{S}}}},{{N}_{{\text{S}}}}}}} = 2,\quad {{{\mathbf{\hat {K}}}}_{{{{N}_{{\text{S}}}},2{{N}_{{\text{S}}}}}}} = - 1,\quad {{{\mathbf{\hat {K}}}}_{{{{N}_{{\text{S}}}},4{{N}_{{\text{S}}}}}}} = - 1$При получении глобальной матрицы жесткости учитываем, что, как уже отмечалось, число слоев в конечных элементах с накладками превышает число слоев в элементах без накладок и, следовательно, размерность матриц ${{{\mathbf{K}}}_{{uu}}}$, ${{{\mathbf{K}}}_{{u\varphi }}}$, ${{{\mathbf{K}}}_{{\varphi \varphi }}}$ зависит от типа конечного элемента. После сборки элементов в ансамбль приходим к глобальной системе линейных алгебраических уравнений, которую для решения задачи управления формой удобно записать в виде
где K – глобальная матрица жесткости; ${\mathbf{X}}$ – глобальный вектор узловых перемещений и электрических потенциалов; F – глобальный вектор, механических, электрических и температурных нагрузок:(2.24)
${\mathbf{K}} = \left[ {\begin{array}{*{20}{l}} {{\mathbf{K}}_{{uu}}^{{\text{G}}}}&{{\mathbf{K}}_{{u\varphi }}^{{\text{G}}}} \\ {{\mathbf{K}}_{{\varphi u}}^{{\text{G}}}}&{{\mathbf{K}}_{{\varphi \varphi }}^{{\text{G}}}} \end{array}} \right],\quad {\mathbf{X}} = \left[ {\begin{array}{*{20}{l}} {{{q}^{{\text{G}}}}} \\ {{{{\mathbf{\Phi }}}^{{\text{G}}}}} \end{array}} \right],\quad {\mathbf{F}} = \left[ {\begin{array}{*{20}{c}} {{\mathbf{F}}_{u}^{{\text{G}}} + {\mathbf{F}}_{{u\theta }}^{{\text{G}}}} \\ {{\mathbf{F}}_{\varphi }^{{\text{G}}} + {\mathbf{F}}_{{\varphi \theta }}^{{\text{G}}}} \end{array}} \right]$3. Решение задачи управления формой слоистой пластины. Обозначим через L число пьезоэлектрических накладок на верхней лицевой поверхности пластины. Пусть ${\mathbf{V}} = {{\left[ {{{V}_{1}}\,{{V}_{2}}\; \ldots \;{{V}_{L}}} \right]}^{{\text{т}}}}$ – вектор электрических потенциалов, подаваемых на электроды накладок, тогда вектор внешних нагрузок можно записать в виде
где P – матрица порядка $4{{N}_{{\text{S}}}}M \times L$, где M – число узлов конечно-элементной сетки. Элементы матрицы ${{p}_{{kl}}}$ равны 1, если k-я компонента вектора правых частей отвечает наличию потенциала на электроде l-й накладки, и нулю в противном случае; F0 – вектор правых частей, зависящий от поверхностных нагрузок.Поставим задачу о приведении деформированной в результате теплового нагружения срединной поверхности пластины к ее недеформированному состоянию. В этом случае целевая функция задачи оптимизации имеет вид
(3.2)
$J({\mathbf{V}}) = \frac{1}{2}{{\left( {{\mathbf{RX}}} \right)}^{{\text{т}}}}\left( {{\mathbf{RX}}} \right) \to \min $Для решения задачи оптимизации (3.2) применим прямой метод. Из соотношений (2.23), (3.1) следует, что ${\mathbf{X}} = {{{\mathbf{K}}}^{{ - 1}}}\left( {{{{\mathbf{F}}}_{0}} + {\mathbf{PV}}} \right)$, поэтому
(3.3)
$\frac{{\partial {\mathbf{X}}}}{{\partial {\mathbf{V}}}} = {{{\mathbf{K}}}^{{ - 1}}}{\mathbf{P}}$Необходимое условие минимума функции (3.2) с учетом (3.3) и симметрии матрицы ${\mathbf{K}}$ можно записать в виде
где ${\mathbf{A}}$– симметричная матрица порядка L × L; ${\mathbf{B}}$ – вектор правых частей, определяемые по формулам(3.5)
${\mathbf{A}} = {{{\mathbf{P}}}^{{\text{т}}}}{{{\mathbf{K}}}^{{ - 1}}}{{{\mathbf{R}}}^{{\text{т}}}}{\mathbf{R}}{{{\mathbf{K}}}^{{ - 1}}}{\mathbf{P}},\quad {\mathbf{B}} = - {{({\mathbf{R}}{{{\mathbf{K}}}^{{ - 1}}}{\mathbf{P}})}^{{\text{т}}}}{\mathbf{R}}{{{\mathbf{K}}}^{{ - 1}}}{{{\mathbf{F}}}_{0}}$Система линейных уравнений (3.4), (3.5) решается методом исключения Гаусса. В результате находим электрические потенциалы, которые необходимо подать на электроды накладок, чтобы привести пластину к недеформируемому состоянию.
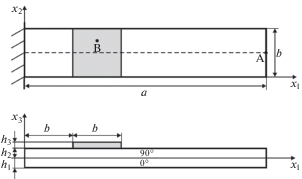
4. Численные результаты. 4.1. Консольная пластина с пьезоэлектрической накладкой. Для оценки эффективности разработанного конечного элемента GeXSaS4 рассмотрим задачу о нагреве двухслойной пластины длиной a = 100 мм и шириной b = 20 мм, изображенной на рис. 1. Пластина состоит из двух слоев углепластика толщиной ${{h}_{1}} = {{h}_{2}} = 1$ мм с направлением волокон [0/90]. На расстоянии 20 мм от заделки на верхней поверхности пластины расположена квадратная накладка из пьезокерамики PZT-5A толщиной ${{h}_{3}} = 0.5$ мм. Материальные константы пьезокерамики PZT-5A соответствуют работе [20]:
Материальные константы углепластика [21] следующие:
Нижняя лицевая поверхность пластины ${{\Omega }^{ - }}$ подвергается действию теплового потока $\hat {q}_{3}^{ - } = {{10}^{3}}$ Вт/м2. Верхняя поверхность пластины ${{\Omega }^{ + }}$, а также наружная поверхность и торцы накладки поддерживаются при заданной температуре ${{\Theta }^{{[N]}}} = {{T}^{{[N]}}} - {{T}_{0}} = 0$ K, где N = 2 или 3. Предполагается, что электрод на поверхности раздела накладки и пластины заземлен, а на электроде наружной поверхности накладки выполняется условие эквипотенциальности.
Учитывая условия симметрии, моделировалась половина пластины ($b{\text{/}}2 \leqslant {{x}_{2}} \leqslant b$) с использованием регулярных конечно-элементных сеток. В табл. 1 приведено исследование сходимости разработанного конечного элемента GeXSaS4 в зависимости от выбранных сеток и от числа отсчетных поверхностей In в слоях пластины и накладке. Как видим, редкая сетка 20 × 2 обеспечивает достаточно надежные результаты по сравнению с эталонными, полученными с использованием сетки 240 × 24.
Таблица 1.
Исследование сходимости в пластине с пьезоэлектрической накладкой
| Сетка | 20 × 2 | 60 × 6 | 120 × 12 | 240 × 24 | 240 × 24 | 240 × 24 |
|---|---|---|---|---|---|---|
| In | 7 | 7 | 7 | 3 | 5 | 7 |
| ${{u}_{3}}({\text{A}},0)$, мкм | –17.40 | –17.47 | –17.52 | –17.45 | –17.55 | –17.56 |
| $\Theta \,({\text{B}}, - {{h}_{1}})$, K | 2.771 | 2.884 | 2.893 | 2.855 | 2.893 | 2.895 |
| $\varphi ({\text{B}},{{h}_{2}} + {{h}_{3}}),$ В | 2.257 | 2.265 | 2.267 | 2.267 | 2.267 | 2.267 |
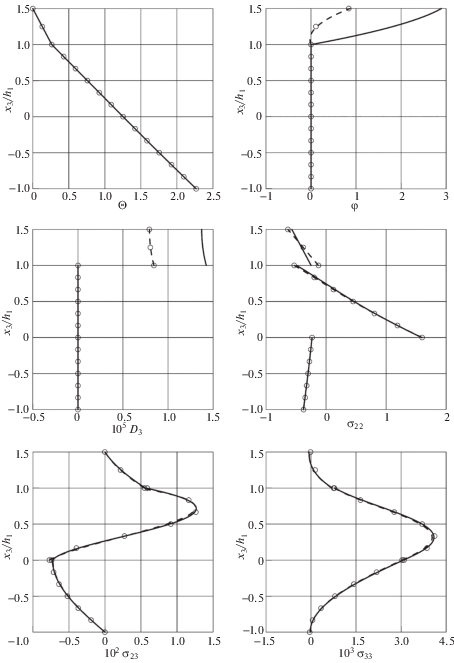
Проведено также сравнение с результатами расчета на основе 20-узлового конечного элемента SOLID226 [22]. Как известно, трехмерные пьезоэлектрические элементы программного комплекса ANSYS [22], в частности SOLID226, не предоставляют пользователям возможности учета пироэлектрического эффекта, поэтому сравнение возможно, только при условии ${{r}_{3}} = 0.$ На рис. 2 показано распределение температуры, электрического потенциала, электрического смещения и напряжений по толщине пакета в точке ${\text{B(3}}b{\text{/2,}}\,{\text{3}}b{\text{/4)}}$ для двух значений пироэлектрической константы, вычисленные с помощью элемента GeXSaS4 на сетке 240 × 24 при выборе семи отсчетных поверхностей в слоях пластины и накладке (${{I}_{1}} = {{I}_{2}} = {{I}_{3}} = 7$) и конечного элемента SOLID226 путем использования трехмерных сеток 240 × 24 × 6 в слоях пластины и накладке. Как видим, учет пироэлектрической константы практически не влияет на результаты расчета напряжений, однако ее влияние на потенциал и смещение электрического поля в пьезоэлектрической накладке существенно.
Рис. 2.
Зависимости температуры $\Theta $ (K), электрического потенциала φ (В), электрического смещения ${{D}_{3}}$ (Кл/м2) и напряжений ${{\sigma }_{{22}}},\,{{\sigma }_{{23}}},\,{{\sigma }_{{33}}}\,$ (МПа) в точке B от поперечной координаты в пластине с пьезоэлектрической накладкой: конечный элемент GeXSaS4 при ${{r}_{3}} = 7.0 \times {\text{1}}{{{\text{0}}}^{{ - {\text{4}}}}}$ Кл/м2K (──) и ${{r}_{3}} = 0\,$ (─ ─); элемент SOLID226 [22] (○)
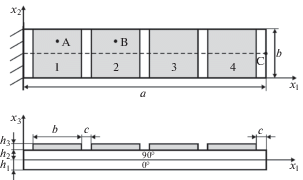
4.2. Консольная пластина с четырьмя пьезоэлектрическими накладками. Далее рассмотрим двухслойную пластину, изображенную на рис. 3. Длина и ширина прямоугольной пластины, толщины слоев ${{h}_{1}}$, ${{h}_{2}}$ и накладок ${{h}_{3}}$, направления армирования в композитных слоях и использованные в пластине и накладках материалы описаны в разделе 4.1. Расстояния между квадратными накладками и расстояния от накладок до краев пластины приняты равными c = 4 мм. Параметры теплового нагружения пластины соответствуют разделу 4.1. Электроды на поверхностях раздела пьезоэлектрических накладок и пластины заземлены. С учетом симметрии моделировалась половина пластины ($b{\text{/}}2 \leqslant {{x}_{2}} \leqslant b$) с использованием регулярных конечно-элементных сеток.
Рассматриваются две задачи: тепловое нагружение пластины, при котором на электродах верхних накладок выполняется условие эквипотенциальности (задача Т) и управление деформированной формой пластины путем решения задачи оптимизации (3.2) при наличии температурных воздействий (задача О). В табл. 2, 3 представлено исследование сходимости конечного элемента GeXSaS4 в температурной задаче (Т) и задаче оптимизации (О) в зависимости от конечно-элементных сеток и от числа отсчетных поверхностей ${{I}_{n}}$. Здесь ${{\phi }_{l}}$ – электрический потенциал на верхнем электроде l‑й накладки, полученный в результате решения системы уравнений (2.23), (2.24); ${{V}_{l}}$ – электрический потенциал на электроде l-й накладки, найденный в результате решения системы уравнений (3.4), (3.5), где $l = 1,2,3,4$. Полученные результаты свидетельствуют об эффективности разработанного конечного элемента GeXSaS4 с точки зрения использования редких сеток.
Таблица 2.
Исследование сходимости в пластине с четырьмя накладками (задача Т)
| Сетка | 25 × 2 | 75 × 6 | 150 × 12 | 300 × 24 | 300 × 24 | 300 × 24 |
|---|---|---|---|---|---|---|
| In | 7 | 7 | 7 | 3 | 5 | 7 |
| ${{u}_{3}}({\text{C}},\,0)$, мкм | –12.58 | –12.82 | –12.93 | –12.67 | –12.97 | –13.00 |
| $\Theta ({\text{В}}, - {{h}_{1}})$, K | 2.293 | 2.308 | 2.311 | 2.312 | 2.312 | 2.312 |
| ${{\phi }_{1}}$, В | 2.522 | 2.662 | 2.674 | 2.632 | 2.673 | 2.675 |
| ${{\phi }_{2}}$, В | 2.821 | 2.917 | 2.921 | 2.881 | 2.920 | 2.921 |
| ${{\phi }_{3}}$, В | 2.824 | 2.918 | 2.922 | 2.882 | 2.921 | 2.922 |
| ${{\phi }_{4}}$, В | 2.827 | 2.919 | 2.922 | 2.882 | 2.920 | 2.921 |
Таблица 3.
Исследование сходимости в пластине с четырьмя накладками (задача О)
| Сетка | 25 × 2 | 75 × 6 | 150 × 12 | 300 × 24 | 300 × 24 | 300 × 24 |
|---|---|---|---|---|---|---|
| In | 7 | 7 | 7 | 3 | 5 | 7 |
| ${{u}_{3}}({\text{C}},\,0)$, мкм | –0.3185 | –0.2456 | –0.2266 | –0.2095 | –0.2167 | –0.2171 |
| ${{V}_{1}},$ В | –19.55 | –20.59 | –21.17 | –20.35 | –21.29 | –21.41 |
| ${{V}_{2}},$ В | –13.94 | –13.38 | –13.11 | –12.44 | –13.06 | –13.15 |
| ${{V}_{3}},$ В | –21.87 | –21.10 | –21.02 | –20.05 | –20.95 | –21.07 |
| ${{V}_{4}},$ В | –5.468 | –7.201 | –7.820 | –7.784 | –8.186 | –8.242 |
На рис. 4 приведены зависимости поперечного перемещения и нормального напряжения от продольной координаты. Отметим, что в результате решения задачи оптимизации срединную поверхность удается привести к форме близкой к исходной недеформированной, но при этом величина напряжений в пластине возрастает. На рис. 5 показаны распределения напряжений в точках ${\text{A}}(c + b{\text{/}}2,\;3b{\text{/}}4)$, ${\text{B}}(2c + 3b{\text{/}}2,\;3b{\text{/}}4)$ по толщине пакета путем решения обеих поставленных задач. Как видим, конечный элемент GeXSaS4 с высокой точностью воспроизводит поперечные компоненты тензора напряжений вблизи раздела слоев и на лицевых поверхностях пластины с учетом нулевых граничных условий. Результаты, показанные на рис. 4, 5, получены с помощью сетки 300 × 24 при выборе семи отсчетных поверхностей в слоях пластины и накладках, то есть ${{I}_{1}} = {{I}_{2}} = {{I}_{3}} = 7$.
Рис. 4.
Зависимости поперечного перемещения ${{u}_{3}}({{x}_{1}},\;3b{\text{/}}4,\;0)$ (мм) и нормального напряжения ${{\sigma }_{{11}}}({{x}_{1}}$, 3b/4, h2/2) (МПа) от продольной координаты в консольной пластине с четырьмя накладками: задача Т (──) и задача О (─ ─)
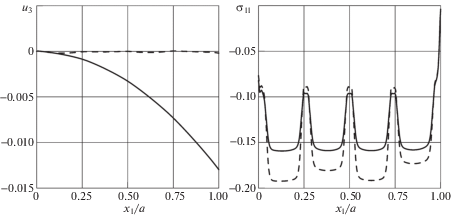
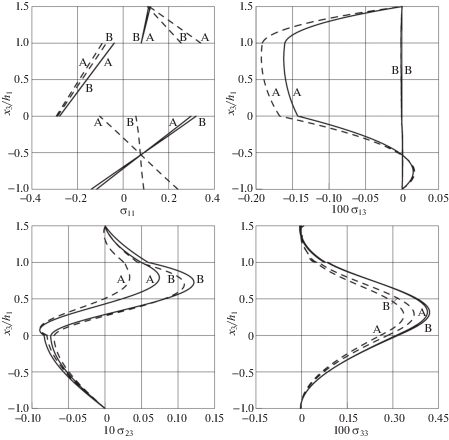
Рис. 5.
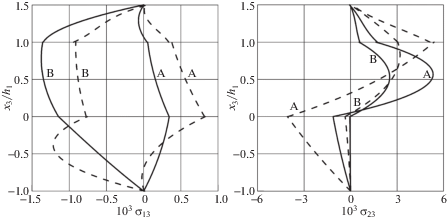
Зависимости напряжений ${{\sigma }_{{11}}}$, ${{\sigma }_{{13}}}$, ${{\sigma }_{{23}}}$, ${{\sigma }_{{33}}}$ (МПа) в точках A, B от поперечной координаты в консольной пластине с четырьмя накладками: задача Т (──) и задача О (─ ─)
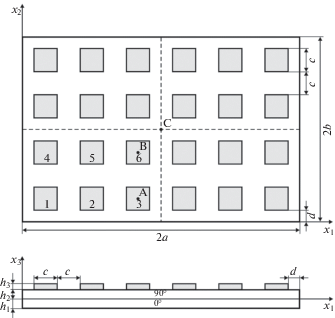
4.3. Защемленная прямоугольная пластина с пьезоэлектрическими накладками на верхней лицевой поверхности. В заключение рассмотрим защемленную по контуру прямоугольную пластину длиной $2a = 240$ мм и шириной $2b = 160$ мм (см. рис. 6). На верхней поверхности пластины расположены 24 пьезоэлектрические накладки, имеющие форму квадрата со стороной $с = 20$ мм. Расстояния от краев пластины до накладок d = 10 мм. Толщины слоев, направления армирования и свойства материалов совпадают с приведенными в разделе 4.1.
Пусть нижняя поверхность пластины подвергается действию температуры ${{\Theta }^{ - }} = 5$ K. Верхняя лицевая поверхность пластины, а также наружные поверхности и торцы накладок поддерживаются при заданной температуре ${{\Theta }^{ + }} = 0$ K. Электроды на границах раздела углепластика и накладок заземлены, а на верхних электродах накладок выполняется условие эквипотенциальности. Аналогично разделу 4.2 рассматриваем две задачи: температурное нагружение пластины (задача Т) и управление формой пластины в случае температурных воздействий (задача О). В силу симметрии рассматривается 1/4 часть пластины, в которой накладки пронумерованы. Приведенные ниже результаты получены с использованием сетки 120 × 80 при выборе пяти отсчетных поверхностей в слоях и накладках (${{I}_{1}} = {{I}_{2}} = {{I}_{3}} = 5$).
В табл. 4 приведены электрические потенциалы на верхних электродах m-й накладки ${{\phi }_{m}}$ и ${{V}_{m}}$, где $m = 1,\;2, \ldots ,\;6$, полученные в результате решения задач T и O, соответственно, а также поперечное перемещение в центре пластины. На рис. 7 изображены деформированные срединные поверхности пластины, полученные после решения задач Т и О. Как видим, в результате решения задачи оптимизации срединную поверхность удается привести к форме достаточно близкой к исходной. Однако величины напряжений существенно возрастают, на что указывают приведенные на рис. 8 зависимости нормальных напряжений от продольной координаты, выведенные для верхнего слоя пластины. На рис. 9 показаны распределения поперечных касательных напряжений в точках ${\text{А}}(5a{\text{/}}6,\;b{\text{/}}4)$, ${\text{В}}(5a{\text{/}}6,\;3b{\text{/}}4)$ по толщине пакета. Отметим, что граничные условия на лицевых поверхностях пластины и накладок и условия непрерывности на поверхностях раздела слоев и накладок выполняются с высокой точностью, что свидетельствует об эффективности конечного элемента GeXSaS4.
Таблица 4.
Результаты расчета поперечного перемещения в точке C и электрических потенциалов на электродах шести накладок в защемленной прямоугольной пластине
| Задача Т | ${{u}_{3}}({\text{C}},0)$, мкм | ${{\phi }_{1}}$, В | ${{\phi }_{2}}$, В | ${{\phi }_{3}}$, В | ${{\phi }_{4}}$, В | ${{\phi }_{5}}$, В | ${{\phi }_{6}}$, В |
|---|---|---|---|---|---|---|---|
| –63.56 | 5.271 | 7.240 | 7.699 | 7.520 | 6.452 | 7.849 | |
| Задача О | ${{u}_{3}}({\text{C}},0)$, мкм | ${{V}_{1}},$ В | ${{V}_{2}},$ В | ${{V}_{3}},$ В | ${{V}_{4}},$ В | ${{V}_{5}},$ В | ${{V}_{6}},$ В |
| –2.741 | 231.1 | 477.0 | 535.8 | 118.7 | 398.3 | 528.7 |
Рис. 7.
Деформированная срединная поверхность защемленной прямоугольной пластины: задача Т (слева) и задача О (справа)
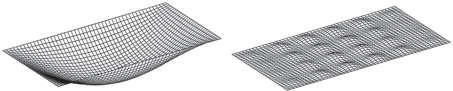
Рис. 8.
Зависимости напряжений ${{\sigma }_{{11}}}({{x}_{1}},\;b{\text{/}}4,\;{{h}_{2}}{\text{/}}2)$, ${{\sigma }_{{22}}}({{x}_{1}},\;b{\text{/}}4,\;{{h}_{2}}{\text{/}}2)$ (□) и ${{\sigma }_{{11}}}({{x}_{1}},\;3b{\text{/}}4,\;{{h}_{2}}{\text{/}}2)$, ${{\sigma }_{{22}}}({{x}_{1}}$, 3b/4, h2/2) (○) от продольной координаты в защемленной прямоугольной пластине: задача Т (──) и задача О (─ ─)
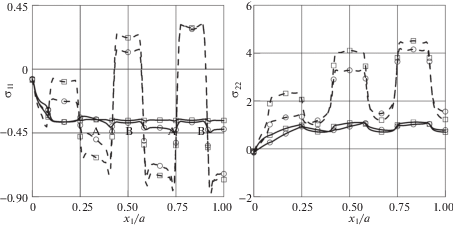
Рис. 9.
Зависимости напряжений ${{\sigma }_{{13}}}$, ${{\sigma }_{{23}}}$ (МПа) в точках A, B от поперечной координаты в защемленной прямоугольной пластине: задача Т (──) и задача О (─ ─)
Заключение. В работе построен четырехузловой гибридный конечный элемент на основе метода отсчетных поверхностей, расположенных в узловых точках полиномов Чебышева, который позволяет с высокой точностью рассчитывать в трехмерной постановке связанные температурные, электрические и механические поля в слоистых композитных пластинах с распределенными на лицевых поверхностях пьезоэлектрическими накладками как в сенсорных, так и актуаторных задачах. На основе разработанного конечного элемента предложен простой и эффективный алгоритм нахождения оптимальных электрических потенциалов на электродах пьезокерамических накладок, который позволяет привести деформированную пластину к исходной недеформированной форме за счет использования обратного пьезоэлектрического эффекта.
Благодарность. Работа выполнена при поддержке Российского научного фонда (проект 18-19-00092). Авторы благодарят А.О. Глебова за помощь с расчетами в ANSYS.
Список литературы
Lee H.J., Saravanos D.A. A mixed multi-field finite element formulation for thermopiezoelectric composite shells // Int. J. Solids Struct. 2000. V. 37. P. 4949–4967.
Varelis D., Saravanos D.A. Non-linear coupled multi-field mechanics and finite element for active multi-stable thermal piezoelectric shells // Int. J. Numer. Methods Eng. 2008. V. 76. P. 84–107.
Gu H., Chattopadhyay A., Li J., Zhou X. A higher order temperature theory for coupled thermo-piezoelectric-mechanical modeling of smart composites // Int. J. Solids Struct. 2000. V. 37. P. 6479–6497.
Jian J.P., Li D.X. Finite element formulations for thermopiezoelastic laminated composite plates // Smart Mater. Struct. 2008. V. 17. 13 p.
Rao S.S., Sunar M. Analysis of distributed thermopiezoelectric sensors and actuators in advanced intelligent structures // AIAA J. 1993. V. 31. P. 1280–1286.
Tzou H.S., Ye R. Piezothermoelasticity and precision control of piezoelectric systems: Theory and finite element analysis // J. Vibr. Acoust. 1994. V. 116. P. 489–495.
Görnandt A., Gabbert U. Finite element analysis of thermopiezoelectric smart structures // Acta Mechanica. 2002. V. 154. P. 129–140.
Shang F., Kuna M., Schrrzer M. A finite element procedure for three-dimensional analyses of thermopiezoelectric structures in static applications // Tech. Mech. 2002. V. 22. P. 235–243.
Lee H.J., Saravanos D.A. Coupled layerwise analysis of thermopiezoelectric composite beams // AIAA J. 1996. V. 34. P. 1231–1237.
Oh I.K., Han J.H., Lee I. Thermopiezoelastic snapping of piezolaminated plates using layerwise nonlinear finite elements // AIAA J. 2001. V. 39. P. 1188–1197.
Brischetto S., Carrera E. Coupled thermo-electro-mechanical analysis of smart plates embedding composite and piezoelectric layers // J. Therm. Stresses. 2012. V. 35. P. 766–804.
Kulikov G.M., Mamontov A.A., Plotnikova S.V. Coupled thermoelectroelastic stress analysis of piezoelectric shells // Compos. Struct. 2015. V. 124. P. 65–76.
Kulikov G.M., Plotnikova S.V. Coupled thermoelectroelastic analysis of thick and thin laminated piezoelectric structures by exact geometry solid-shell elements based on the sampling surfaces method // Int. J. Numer. Methods Eng. 2021. V. 122. P. 2446-2477.
Плотникова С.В., Куликов Г.М. Управление формой композитных пластин с распределенными пьезоэлектрическими актуаторами в трехмерной постановке // Механика композ. матер. 2020. Т. 56. № 5. С. 821–840.
Ha S.K., Keilers C., Chang F.K. Finite element analysis of composite structures containing distributed piezoceramic sensors and actuators // AIAA J. 1992. V. 30. № 3. P. 772–780.
Irschik H. A review on static and dynamic shape control of structures by piezoelectric actuation // Eng. Struct. 2002. V. 24. P. 5–11.
Kulikov G.M., Plotnikova S.V. Heat conduction analysis of laminated shells by a sampling surfaces method // Mech. Res. Commun. 2014. V. 55. P. 59–65.
Куликов Г.М., Плотникова С.В. Решение связанной задачи термопьезоэлектричества на основе геометрически точного элемента оболочки // Механика композ. матер. 2010. Т. 46. № 4. С. 513–534.
Kulikov G.M., Plotnikova S.V., Carrera E. Hybrid-mixed solid-shell element for stress analysis of laminated piezoelectric shells through higher-order theories // Adv. Struct. Mater. 2018. V. 81. P. 45–68.
Vel S.S., Batra R.C. Generalized plane strain thermopiezoelectric analysis of multilayered plates // J. Therm. Stresses. 2003. V. 26. P. 353–377.
Kapuria S., Sengupta S., Dumir P.C. Three-dimensional solution for a hybrid cylindrical shell under axisymmetric thermoelectric load // Arc. Appl. Mech. 1997. V. 67. P. 320–330.
ANSYS 2019 R2 Release / Canonsburg, USA: ANSYS Inc, 2019.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика твердого тела