Известия РАН. Механика твердого тела, 2021, № 5, стр. 127-140
ТРАЕКТОРИИ ПЛОСКОГО ДВИЖЕНИЯ ТЕЛА ВРАЩЕНИЯ В СРЕДЕ
К. Ю. Осипенко *
Институт проблем механики им. А.Ю. Ишлинского РАН
Москва, Россия
* E-mail: kirill-o@mail.ru
Поступила в редакцию 29.12.2020
После доработки 06.01.2021
Принята к публикации 14.01.2021
Аннотация
Получено аналитическое решение нелинейной системы уравнений, описывающей плоское движение тела вращения в безграничной среде. Считалось, что на боковой поверхности тела трение отсутствует, а нормальные напряжения определяются по методу локального взаимодействия и задаются по закону сопротивления Ньютона в виде инерционного давления, пропорционального квадрату нормальной составляющей скорости. Исследованы возможные траектории движения тела и получены условия устойчивости прямолинейного движения.
1. Введение. Решение задач о проникании тела и устойчивости его движения в точной постановке из-за сложной природы сил взаимодействия, как правило, возможно только разностными методами. Однако из-за большого числа параметров и определяющих функций такие расчеты часто оказываются мало пригодными для выявления общих закономерностей процесса проникания. Поэтому для изучения влияния параметров среды и тела на траекторию движения нередко используются приближенные подходы. Один из таких подходов – метод локального взаимодействия, впервые предложенный еще Ньютоном для определения сопротивления движению тел в газах и жидкостях. В настоящее время этот метод используется для решения задач гиперзвукового обтекания, движения в разреженном газе, проникания тела в грунты и металлы [1–4].
Ранее по методу локального взаимодействия изучались устойчивость при малых возмущениях прямолинейного движения тел вращения и неосесимметричных тел, на боковой поверхности которых действуют нормальные напряжения и трение [5–8]. Получены критерии устойчивости для тела вращения с учетом отрыва потока с его боковой поверхности при плоском и пространственном движениях [5–7] и для плоского движения неосесимметричного тела при безотрывном обтекании [8]. Исследовались траектории плоского движения осесимметричных тел [9]. Однако эти результаты были получены для линеаризованной системы уравнений при малых возмущениях относительно прямолинейного движения.
Ниже для случая контактного давления, задаваемого по формуле Ньютона, получено аналитическое решение, описывающее плоское движение осесимметричного тела при произвольных возмущениях и проанализированы возможные траектории движения тела. Напряжения, определяемые по формуле Ньютона, не зависят от знака нормальной составляющей скорости, поэтому решение имеет физический смысл только при безотрывном обтекании боковой поверхности тела.
Закон сопротивления Ньютона не учитывает прочность среды, поэтому для определения нормальных контактных напряжений при проникании тел в малопрочные среды чаще используется формула, в которой к инерционному слагаемому, совпадающему с законом Ньютона, добавляется постоянное прочностное слагаемое. Однако прочностное слагаемое при безотрывном обтекании влияет только на торможение тела, а результирующий момент и поперечная составляющая результирующей силы от него не зависят. Поэтому формула Ньютона может использоваться в случае движения тела в малопрочной среде с большой скоростью, когда инерционное слагаемое существенно превышает прочностное, а трением можно пренебречь.
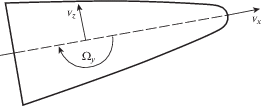
2. Постановка задачи. Твердое тело вращения массой $m$, длиной ${{L}_{m}}$ и моментом инерции при поперечном вращении I движется по инерции в безграничной среде. Цилиндрическая система координат $R,\varphi ,L$ $\left( {0 \leqslant \varphi \leqslant 2\pi } \right)$ и связанная с центром масс местная прямоугольная система координат $x = {{\left( {{{L}_{c}} - L} \right)} \mathord{\left/ {\vphantom {{\left( {{{L}_{c}} - L} \right)} {{{L}_{m}}}}} \right. \kern-0em} {{{L}_{m}}}},$ $y = {{R{\text{cos}}\varphi } \mathord{\left/ {\vphantom {{R{\text{cos}}\varphi } {{{L}_{m}}}}} \right. \kern-0em} {{{L}_{m}}}}$, $z = {{R{\text{sin}}\varphi } \mathord{\left/ {\vphantom {{R{\text{sin}}\varphi } {{{L}_{m}}}}} \right. \kern-0em} {{{L}_{m}}}}$ жестко связаны с телом. Предполагается, что движение тела плоское и определяется вектором скорости ${\mathbf{v}} = \left\{ {{{v}_{x}},0,{{v}_{z}}} \right\}$ центра масс, расположенного при L = Lc, и угловой скоростью вращения относительно центра масс $\Omega = \left\{ {0,{{\Omega }_{y}},0} \right\}$, зависящих от времени t (рис. 1 ). Тело имеет гладкий меридиан ${{R}_{b}} = {{R}_{b}}\left( L \right)$, $0 < L < {{L}_{m}}$ и, быть может, кромку L = Lm, где ${{R}_{b}}$ – радиус, L – расстояние от носика вдоль оси тела. Считается, что боковая поверхность тела обтекается безотрывно, но возможен отрыв потока с задней кромки тела (при L = Lm).
Контактное давление ${{\sigma }_{n}}$ на поверхности тела зададим по формуле сопротивления Ньютона в виде квадратичной зависимости давления на поверхности тела от нормальной составляющей скорости ${{V}_{n}}$:
Здесь Cf – коэффициент сопротивления, ${{\rho }_{0}}$ – средняя плотность среды.Введем новые безразмерные величины
Выражения для внешней нормали и проекции вектора скорости V произвольной точки на поверхности тела на нормаль в системе координат xyz определяются формулами
(2.2)
$\begin{gathered} V = \left| {\mathbf{V}} \right| = \Theta {{v}_{x}},\quad {{V}_{n}} = \left( {{\mathbf{n}} \cdot {\mathbf{V}}} \right) = \Theta {{v}_{x}}\sin \delta ,\quad {{a}_{3}} = \omega x - \eta \\ \Theta = \sqrt {{{{\left( {1 + \omega z} \right)}}^{2}} + {{a}^{2}}} ,\quad {\mathbf{n}} = \frac{{\left\{ {\gamma ,\cos \varphi ,\sin \varphi } \right\}}}{{\sqrt {1 + {{\gamma }^{2}}} }} \\ \end{gathered} $Здесь δ – локальный угол атаки (угол между касательной плоскостью в некоторой точке на поверхности тела и вектором скорости этой точки). В области “аэродинамической тени” $\left( {{{V}_{n}} < 0} \right)$ угол $\delta $ отрицательный.
Запишем общие выражения для результирующей силы и момента
(2.3)
${\mathbf{F}} = - L_{m}^{2}\int\limits_S {{{\sigma }_{n}}{\mathbf{n}}dS} ,\quad {\mathbf{M}} = - L_{m}^{2}\int\limits_S {{{\sigma }_{n}}\left[ {{\mathbf{R}} \times {\mathbf{n}}} \right]dS} ,\quad dS = r{{\gamma }_{0}}d\varphi dl$В кинематические соотношения (2.1) и (2.2) и выражения для результирующих (2.3) входят неизвестные функции $\kappa ,\eta ,\omega $, для которых ниже будет сформулирована задача.
3. Математическая постановка задачи. Система дифференциальных уравнений плоского движения жесткого тела в системе координат, связанной с центром масс тела, записывается в следующем виде (точкой обозначена производная по $t$):
После соответствующих подстановок и очевидных преобразований запишем задачу Коши [7, 8]:
(3.1)
$\begin{gathered} \kappa {\kern 1pt} ' = 2\kappa \left( { - {{f}_{\kappa }} + \omega \eta } \right),\quad \eta {\kern 1pt} ' = {{f}_{\eta }} - \eta {{f}_{\kappa }} + (1 + {{\eta }^{2}})\omega ,\quad \omega {\kern 1pt} ' = j{{f}_{\omega }} - {{f}_{\kappa }}\omega + \eta {{\omega }^{2}} \\ j = {{mL_{m}^{2}} \mathord{\left/ {\vphantom {{mL_{m}^{2}} I}} \right. \kern-0em} I},\quad \kappa = {{v_{{x0}}^{2}} \mathord{\left/ {\vphantom {{v_{{x0}}^{2}} {v_{x}^{2}}}} \right. \kern-0em} {v_{x}^{2}}};\quad s = 0:\quad \kappa = 1,\quad \eta = {{\eta }_{0}},\quad \omega = {{\omega }_{0}} \\ \end{gathered} $Здесь
(3.2)
$\begin{gathered} {{f}_{\kappa }} = \frac{{{{L}_{m}}{{F}_{x}}}}{{mv_{x}^{2}}} = \int\limits_0^1 {r\gamma \int\limits_0^{2\pi } {\sigma d\varphi dl} } ,\quad {{f}_{\eta }} = \frac{{{{L}_{m}}{{F}_{z}}}}{{mv_{x}^{2}}} = - \int\limits_0^1 {r\int\limits_0^{2\pi } {\sigma \sin \varphi d\varphi dl} } \\ {{f}_{\omega }} = \frac{{{{M}_{y}}}}{{mv_{x}^{2}}} = \int\limits_0^1 {r\left( {x - \gamma r} \right)\int\limits_0^{2\pi } {\sigma \sin \varphi d\varphi dl} } \\ \sigma = \frac{{L_{m}^{3}}}{{mv_{x}^{2}}}{{\sigma }_{n}} = K{{\Theta }^{2}}{{\sin }^{2}}\delta ,\quad K = \frac{{L_{m}^{3}{{\rho }_{0}}{{C}_{f}}}}{{2m}} \\ \end{gathered} $Проинтегрировав в выражениях для равнодействующих сил и моментов (3.2) по углу $\varphi $, получим
(3.3)
$\begin{gathered} {{f}_{{\eta \eta }}} = - 2\pi K{{J}_{1}},\quad {{f}_{{\eta \omega }}} = 2\pi K{{J}_{3}},\quad {{f}_{{\omega \eta }}} = 2\pi K{{J}_{3}},\quad {{f}_{{\omega \omega }}} = - 2\pi K{{J}_{4}} \\ {{J}_{1}} = \int\limits_0^1 {\frac{{r\gamma }}{{1 + {{\gamma }^{2}}}}dl} ,\quad {{J}_{2}} = \int\limits_0^1 {\frac{{r{{\gamma }^{3}}}}{{1 + {{\gamma }^{2}}}}dl} ,\quad {{J}_{3}} = \int\limits_0^1 {\frac{{r\gamma }}{{1 + {{\gamma }^{2}}}}\left( {x - \gamma r} \right)dl} \\ \end{gathered} $Автономная система (3.1), (3.3) имеет непрерывно дифференцируемые правые части, поэтому в любой конечной области фазового пространства $\kappa ,\eta ,\omega $ правые части системы (3.1) удовлетворяют условию Липшица и задача Коши корректна.
4. Аналитическое решение. Второе и третье уравнения системы (3.1) не зависят от κ, поэтому они могут решаться независимо от первого уравнения
(4.1)
$\eta {\kern 1pt} ' = {{f}_{\eta }} - \eta {{f}_{\kappa }} + (1 + {{\eta }^{2}})\omega ,\quad \omega {\kern 1pt} ' = j{{f}_{\omega }} - {{f}_{\kappa }}\omega + \eta {{\omega }^{2}}$Вычтем из первого уравнения системы (4.1), умноженного на $\omega $, второе уравнение, умноженное на η:
(4.2)
$\omega \eta {\kern 1pt} '\; - \eta \omega {\kern 1pt} ' = \omega {{f}_{\eta }} + {{\omega }^{2}} - j\eta {{f}_{\omega }}$Сделав замену переменных $\eta = \Psi \sin \theta $, $\omega = \Psi \cos \theta $ в уравнении (4.2), получим
(4.3)
$\begin{gathered} \theta {\kern 1pt} ' = \Gamma \left( \theta \right),\quad \Gamma \left( \theta \right) = D{{\cos }^{2}}\theta + E\sin \theta \cos \theta + F{{\sin }^{2}}\theta , \\ D = 1 + {{f}_{{\eta \omega }}},\quad E = {{f}_{{\eta \eta }}} - j{{f}_{{\omega \omega }}},\quad F = - j{{f}_{{\omega \eta }}}, \\ {{\Psi }_{0}} = \sqrt {\eta _{0}^{2} + \omega _{0}^{2}} ,\quad {{\theta }_{0}} = \arctan \left( {{{{{\eta }_{0}}} \mathord{\left/ {\vphantom {{{{\eta }_{0}}} {{{\omega }_{0}}}}} \right. \kern-0em} {{{\omega }_{0}}}}} \right),\quad {{\theta }_{0}} \in \left( { - {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2},{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}} \right) \\ \end{gathered} $Уравнение (4.3) не зависит от Ψ, поэтому оно является дифференциальным уравнение первого порядка с разделяющимися переменными. Запишем решение этого уравнения [10]:
(4.4)
$s = \left\{ {\begin{array}{*{20}{l}} \begin{gathered} \frac{1}{{\sqrt {{{E}^{2}}\, - \,4DF} }}\left( {{\text{ln}}\left| {\frac{{2F{\text{tg}}\theta \, + \,E\, - \,\sqrt {{{E}^{2}} - 4DF} }}{{2F{\text{tg}}\theta \, + \,E\, + \,\sqrt {{{E}^{2}} - 4DF} }}} \right| - } \right.\left. {\ln \left| {\frac{{2F{\text{tg}}{{\theta }_{0}}\, + \,E\, - \sqrt {{{E}^{2}} - 4DF} }}{{2F{\text{tg}}{{\theta }_{0}}\, + \,E\, + \,\sqrt {{{E}^{2}} - 4DF} }}} \right|} \right) \hfill \\ [{{E}^{2}}\, > \,4DF] \hfill \\ \end{gathered} \\ {\frac{2}{{\sqrt {4DF - {{E}^{2}}} }}\left( {{\text{arctg}}\frac{{2F\operatorname{t} g\theta + E}}{{\sqrt {4DF - {{E}^{2}}} }} - {\text{arctg}}\frac{{2F\operatorname{t} g{{\theta }_{0}} + E}}{{\sqrt {4DF - {{E}^{2}}} }}} \right),\quad [{{E}^{2}} < 4DF]} \\ {\frac{{ - 2}}{{2F{\text{tg}}\theta + E}} + \frac{2}{{2F{\text{tg}}{{\theta }_{0}} + E}},\quad [{{E}^{2}} = 4DF]} \end{array}} \right.$Теперь сложим первое уравнение системы (4.1), умноженное на $\eta $, со вторым уравнением, умноженным на ω:
(4.5)
$\begin{gathered} {{\Gamma }_{2}}\left( \theta \right) = {{D}_{2}}{{\cos }^{2}}\theta + {{E}_{2}}\sin \theta \cos \theta + {{F}_{2}}{{\sin }^{2}}\theta ,\quad {{D}_{1}} = j{{f}_{{\omega \omega }}} - {{f}_{{\kappa 0}}} \\ {{E}_{1}} = 1 + {{f}_{{\eta \omega }}} + j{{f}_{{\omega y\eta }}},\quad {{F}_{1}} = {{f}_{{\eta \eta }}} - {{f}_{{\kappa 0}}},\quad {{D}_{2}} = - {{f}_{{\kappa \omega \omega }}} \\ \end{gathered} $Уравнение (4.5) является дифференциальным уравнением Бернулли. Оно сводится к линейному дифференциальному уравнению подстановкой $\psi = {{\Psi }^{{ - 2}}}$. Запишем его общее решение [11]:
(4.6)
${{\Psi }^{{ - 2}}} = {{e}^{{\Phi \left( s \right)}}}(\Psi _{0}^{{ - 2}} - 2\Upsilon ),\quad \Upsilon = \int\limits_0^s {{{e}^{{ - \Phi \left( s \right)}}}{{\Gamma }_{2}}\left( \theta \right)ds} ,\quad \Phi \left( s \right) = - 2\int\limits_0^s {{{\Gamma }_{1}}\left( \theta \right)ds} $Формулы (4.4), (4.6) являются общим аналитическим решением системы уравнений (4.1). Выразив из этих формул $\eta $ и $\omega $ в зависимости от s и подставив их в первое уравнение системы (3.1), получим обыкновенное дифференциальное уравнение первого порядка с разделяющимися переменными. Его интегрирование дает функцию $\kappa \left( s \right)$. Функции $\kappa \left( s \right)$, $\eta \left( s \right)$, $\omega \left( s \right)$ являются решением системы (3.1) и полностью определяют траекторию движения тела.
5. Изучение возможных траекторий и устойчивости при ${{E}^{2}} > 4DF$. В этом случае возможны два основных варианта
1. При некотором s > 0 функция $\Psi _{0}^{{ - 2}} - 2\Upsilon $обращается в ноль. В этом случае движение тела будет неустойчивым, а возмущения ${{\eta }_{z}}$, ${{\omega }_{y}}$ будут становиться бесконечными на конечном отрезке траектории.
2. Функция $\Psi _{0}^{{ - 2}} - 2\Upsilon $ является положительной при любом s > 0.
Приравнивая правую часть дифференциального уравнения (4.3) к нулю можно найти точки покоя (положения равновесия). Линеаризуем дифференциальное уравнение (4.3) в малых окрестностях точек покоя
(5.1)
$\begin{gathered} \theta _{*}^{{}} = \arctan \left( {\frac{{ - E - \sqrt {{{E}^{2}} - 4DF} }}{{2F}}} \right)\quad {\text{при}}\quad \left| {\theta - \theta _{*}^{{}}} \right| \ll 1 \\ \theta {\kern 1pt} ' = \theta _{{**}}^{{}} + (\theta - \theta _{{**}}^{{}})\sqrt {{{E}^{2}} - 4DF} \\ \end{gathered} $Из (5.1) следует, что $\theta = {{\theta }_{ * }}$ является устойчивой точкой покоя, а $\theta = {{\theta }_{{ * * }}}$ неустойчивой.
При $F > 0$, $2F\tan {{\theta }_{0}} + E - \sqrt {{{E}^{2}} - 4DF} > 0$ функция $\theta \left( {s,{{\theta }_{0}}} \right)$, являющаяся решением уравнения (4.3), будет монотонно возрастать с ростом s, а если кроме того $\Psi _{0}^{{ - 2}} - 2\Upsilon $ является положительной при любом s > 0, то $\theta \to \theta _{*}^{{}} + \pi $ при $s \to \infty $. При $F < 0$ и $2F{\text{tg}}{{\theta }_{0}} + E - \sqrt {{{E}^{2}} - 4DF} > 0$ функция $\theta \left( {s,{{\theta }_{0}}} \right)$ будет монотонно убывать, а если кроме того $\Psi _{0}^{{ - 2}} - 2\Upsilon > 0$ при любом s > 0, то $\theta \to \theta _{*}^{{}} - \pi $ при $s \to \infty $. В остальных случаях решение монотонно изменяется в сторону $\theta _{*}^{{}}$, а если $\Psi _{0}^{{ - 2}} - 2\Upsilon > 0$ при любом s > 0, то $\theta \to \theta _{*}^{{}}$ при $s \to \infty $.
Если $Det\,2 > 0$, где $Det\,2 = E_{2}^{2} - 4{{D}_{2}}{{F}_{2}}$ то функция ${{\Gamma }_{2}}\left( \theta \right)$ обращается в ноль в точках ${{\theta }_{1}} \pm \pi n$, ${{\theta }_{2}} \pm \pi n$, где $n = 1,2 \ldots $, а ${{\theta }_{1}},\;{{\theta }_{2}}$ задаются выражениями
Из (4.5), (3.3) следует, что ${{F}_{2}} < 0$, поэтому ${{\theta }_{1}} < {{\theta }_{2}}$. Если $ - {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2} < {{\theta }_{1}} < \theta < {{\theta }_{2}} < {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}$, то ${{\Gamma }_{2}}\left( \theta \right) > 0$, а неравенство ${{\Gamma }_{2}}\left( \theta \right) < 0$ выполняется при $ - {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2} < \theta < {{\theta }_{1}}$ или ${{\theta }_{2}} < \theta < {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}$. Корни ${{\theta }_{1}} \pm \pi n$ и ${{\theta }_{2}} \pm \pi n$, соответствуют экстремумам функции $\Psi _{0}^{{ - 2}} - 2\Upsilon $, т.к. ее производная по s равна $ - 2{{e}^{{ - \Phi \left( s \right)}}}{{\Gamma }_{2}}\left( \theta \right)$. Линеаризовав функцию ${{\Gamma }_{2}}\left( \theta \right)$ в окрестности ее корней можно показать, что корень ${{\theta }_{1}}$ соответствует локальному максимуму функции $\Psi _{0}^{{ - 2}} - 2\Upsilon $, а ${{\theta }_{2}}$ минимуму.
Функция $\theta \left( {s,{{\theta }_{0}}} \right)$ является монотонной по s, поэтому в выражении (4.6) для $\Phi \left( s \right)$ можно перейти от интегрирования по ds к интегрированию по $d\theta $ и вычислить интеграл аналитически [10]:
(5.2)
$\begin{gathered} \Phi \left( \theta \right) = - 2\int\limits_{{{\theta }_{0}}}^\theta {{{\Gamma }_{1}}\left( \theta \right)\frac{{ds}}{{d\theta }}d\theta } = \frac{{ - 2}}{{{{E}^{2}} + {{{\left( {D - F} \right)}}^{2}}}}\left\{ {\mathop {\left[ {{{E}_{1}}E + \left( {{{D}_{1}} - {{F}_{1}}} \right)\left( {D - F} \right)} \right]\theta + }\limits_{} } \right. \\ \, + \frac{1}{2}\left[ {\left( {{{D}_{1}} - {{F}_{1}}} \right)E - {{E}_{1}}\left( {D - F} \right)} \right]{\text{ln|}}D{\text{co}}{{{\text{s}}}^{2}}\theta + E{\text{sin}}\theta {\text{cos}}\theta + F{\text{si}}{{{\text{n}}}^{2}}\theta {\text{|}} + \\ \,\left. { + \left[ {\frac{1}{2}\left( {{{D}_{1}} + {{F}_{1}}} \right){{E}^{2}} - \frac{1}{2}E{{E}_{1}}\left( {D + F} \right) + \left( {{{F}_{1}}D - {{D}_{1}}F} \right)\left( {D - F} \right)} \right]s\left( {\theta ,{{\theta }_{0}}} \right)} \right\}\left| {\begin{array}{*{20}{c}} {^{\theta }} \\ {_{{{{\theta }_{0}}}}} \end{array}} \right. \\ \end{gathered} $Выражение для $s\left( {\theta ,{{\theta }_{0}}} \right)$ приведено в (3.4). Преобразуем ${\text{exp}}[ - \Phi (\theta )]$ и ${{{\text{exp}}[ - \Phi (\theta )]} \mathord{\left/ {\vphantom {{{\text{exp}}[ - \Phi (\theta )]} {\Gamma (\theta )}}} \right. \kern-0em} {\Gamma (\theta )}}$, подставив в них $\Gamma \left( \theta \right)$ из (4.3) и $\exp \left[ { - \Phi \left( s \right)} \right]$ из (5.2):
(5.3)
$\frac{{\exp \left[ { - \Phi \left( \theta \right)} \right]}}{{\Gamma \left( \theta \right)}} = \frac{{\cos {{\theta }_{*}}\cos {{\theta }_{{**}}}\exp \left[ { - \Phi \left( \theta \right)} \right]}}{{F\sin \left( {\theta - {{\theta }_{*}}} \right)\sin \left( {\theta - {{\theta }_{{**}}}} \right)}}$Из (5.3) следует, что условие $\lim \left[ {{{\exp \left[ { - \Phi \left( \theta \right)} \right]} \mathord{\left/ {\vphantom {{\exp \left[ { - \Phi \left( \theta \right)} \right]} {\Gamma \left( \theta \right)}}} \right. \kern-0em} {\Gamma \left( \theta \right)}}} \right] \to \infty $ при $\theta \to {{\theta }_{k}}$, где ${{\theta }_{k}}$ может принимать значения ${{\theta }_{*}}$ или ${{\theta }_{*}} \pm \pi $, эквивалентно условию $\Lambda - \Pi < 1$, а условие $\lim \left\{ {\exp \left[ { - \Phi \left( \theta \right)} \right]} \right\} \to \infty $ при $\theta \to {{\theta }_{k}}$ эквивалентно условию $\Lambda - \Pi < 0$. Если функция $\Psi _{0}^{{ - 2}} - 2\Upsilon $ является положительной при любом $s > 0$, то $\theta \to {{\theta }_{k}}$ при $s \to \infty $. Из (5.3) видно, что при $\Lambda - \Pi < 0$ и $\Psi _{0}^{{ - 2}} - 2\Upsilon > 0$ интеграл от ${{\theta }_{0}}$ до ${{\theta }_{*}}$ функции ${{{\text{exp}}[ - \Phi (s)]} \mathord{\left/ {\vphantom {{{\text{exp}}[ - \Phi (s)]} {\Gamma (\theta )}}} \right. \kern-0em} {\Gamma (\theta )}}$ стремится к бесконечности при $\theta \to {{\theta }_{*}}$.
Рассмотрим в подпунктах 5.1–5.4 поведение функции $\Psi $ при движении тела по траектории в зависимости от начальных условий и параметров среды и тела.
5.1. Если $\Lambda - \Pi < 0$ и ${{\Gamma }_{2}}\left( {{{\theta }_{*}}} \right) > 0$, то движение тела будет неустойчивым, т.к. в этом случае $\Upsilon \left( {s = 0} \right) = 0$ и $\Upsilon \to + \infty $ при $\theta \to {{\theta }_{*}}$, а следовательно уравнение $\Psi _{0}^{{ - 2}} - 2\Upsilon = 0$ будет иметь корень на интервале $\left( {{{\theta }_{0}},{{\theta }_{*}} + \pi } \right)$ при F > 0 и $2F{\text{tan}}{{\theta }_{0}} + E - \sqrt {{{E}^{2}} - 4DF} > 0$, на интервале $({{\theta }_{0}},{{\theta }_{*}} - \pi )$ при F < 0 и $2F{\text{tg}}{{\theta }_{0}} + E - \sqrt {{{E}^{2}} - 4DF} > 0$ и на интервале $\left( {{{\theta }_{0}},{{\theta }_{ * }}} \right)$ в остальных случаях. Из (4.6) следует, что ${{\Psi }^{{ - 2}}} = 0$ при $\Psi _{0}^{{ - 2}} - 2\Upsilon = 0$, а следовательно ${{\eta }^{2}} + {{\omega }^{2}} \to \infty $ при $\Psi _{0}^{{ - 2}} - 2\Upsilon \to 0$.
5.2. Если $\Lambda - \Pi < 0$ и ${{\Gamma }_{2}}\left( {{{\theta }_{*}}} \right) < 0$, то движение будет неустойчивым, если ${{\Psi }_{0}} > {{\Psi }_{c}}$. Здесь ${{\Psi }_{c}}$ – это максимум функции $2\Upsilon $ на интервале $\left( {{{\theta }_{0}},{{\theta }_{*}} + \pi } \right)$ при $F > 0$ и 2Ftgθ0 + + E – $\sqrt {{{E}^{2}} - 4DF} $ > 0, максимум на интервале $\left( {{{\theta }_{0}},{{\theta }_{*}} - \pi } \right)$ при $F < 0$ и 2Ftgθ0 + + $E - \sqrt {{{E}^{2}} - 4DF} $ > 0 и максимум на интервале $\left( {{{\theta }_{0}},{{\theta }_{*}}} \right)$ в остальных случаях. Введем новые функции
(5.4)
${{\Xi }_{2}}\left( \theta \right) = \mathop {\lim }\limits_{\varepsilon \to 0,\varepsilon > 0} {{\left[ { - 2\exp \left[ {\Phi \left( {\theta - \varepsilon } \right)} \right]\int\limits_{{{\theta }_{0}}}^{\theta - \varepsilon } {\exp \left[ { - \Phi \left( \theta \right)} \right]\frac{{{{\Gamma }_{2}}\left( \theta \right)}}{{\Gamma \left( \theta \right)}}d\theta } } \right]}^{{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$Если ${{\Psi }_{0}} < {{\Psi }_{c}}$, то $\mathop {\lim }\limits_{s \to \infty } {{\Psi }^{{ - 2}}} = - 2\mathop {\lim }\limits_{s \to \infty } \left( {\exp \left[ {\Upsilon \Phi \left( s \right)} \right]} \right)$. В зависимости от ${{\theta }_{0}}$ и знака $\Gamma \left( {{{\theta }_{0}}} \right)$ этот предел может быть равен ${{\Xi }_{2}}\left( {{{\theta }_{*}}} \right)$, ${{\Xi }_{2}}\left( {{{\theta }_{*}} + \pi } \right)$, ${{\Xi }_{3}}\left( {{{\theta }_{*}}} \right)$ или ${{\Xi }_{3}}\left( {{{\theta }_{*}} - \pi } \right)$. В табл. 1 приведены выражения для ${{\Psi }_{c}}$ и ${{\Psi }_{k}} = - 2\mathop {\lim }\limits_{s \to \infty } \left\{ {\Upsilon \left( s \right)\exp \left[ {\Phi \left( s \right)} \right]} \right\}$ при различных начальных условиях и параметрах среды и тела.
Таблица 1
| № | ${{\Gamma }_{1}}\left( {{{\theta }_{0}}} \right)$ | $Det2$ | ${{\theta }_{0}}$ | ${{\Psi }_{с}}$ | ${{\Psi }_{k}}$ |
|---|---|---|---|---|---|
| 1 | $\Gamma \left( {{{\theta }_{0}}} \right) > 0$ | $Det2 > 0$ | ${{\theta }_{0}} < {{\theta }_{2}} < {{\theta }_{ * }}$ | ${{\Psi }_{с}} = {{\Xi }_{1}}\left( {{{\theta }_{2}}} \right)$ | ${{\Psi }_{k}} = {{\Xi }_{2}}\left( {{{\theta }_{ * }}} \right)$ |
| 2 | $\Gamma \left( {{{\theta }_{0}}} \right) > 0$ | $Det2 > 0$ | ${{\theta }_{ * }} < {{\theta }_{0}} < {{\theta }_{2}} < {{\theta }_{ * }} + \pi $ | ${{\Psi }_{с}} = {{\Xi }_{1}}\left( {{{\theta }_{2}}} \right)$ | ${{\Psi }_{k}} = {{\Xi }_{2}}\left( {{{\theta }_{ * }} + \pi } \right)$ |
| 3 | $\Gamma \left( {{{\theta }_{0}}} \right) > 0$ | $Det2 > 0$ | ${{\theta }_{ * }} < {{\theta }_{0}} < {{\theta }_{2}} + \pi < {{\theta }_{ * }} + \pi $ | ${{\Psi }_{с}}\, = \,{{\Xi }_{1}}({{\theta }_{2}}\, + \,\pi )$ | ${{\Psi }_{k}} = {{\Xi }_{2}}\left( {{{\theta }_{ * }} + \pi } \right)$ |
| 4 | $\Gamma \left( {{{\theta }_{0}}} \right) > 0$ | $Det2 > 0$ | ${{\theta }_{2}} < {{\theta }_{0}} < {{\theta }_{ * }}$ | ${{\Psi }_{c}} = + \infty $ | ${{\Psi }_{k}} = {{\Xi }_{2}}\left( {{{\theta }_{ * }}} \right)$ |
| 5 | $\Gamma \left( {{{\theta }_{0}}} \right) > 0$ | $Det2 > 0$ | ${{\theta }_{0}} < {{\theta }_{ * }} < {{\theta }_{1}} < {{\theta }_{2}}$ | ${{\Psi }_{c}} = + \infty $ | ${{\Psi }_{k}} = {{\Xi }_{2}}\left( {{{\theta }_{ * }}} \right)$ |
| 6 | $\Gamma \left( {{{\theta }_{0}}} \right) > 0$ | $Det2 > 0$ | ${{\theta }_{ * }} < {{\theta }_{1}} < {{\theta }_{2}} < {{\theta }_{0}} < {{\theta }_{ * }} + \pi $ | ${{\Psi }_{c}} = + \infty $ | ${{\Psi }_{k}} = {{\Xi }_{2}}\left( {{{\theta }_{ * }} + \pi } \right)$ |
| 7 | $\Gamma \left( {{{\theta }_{0}}} \right) > 0$ | $Det2 < 0$ | ${{\theta }_{0}} < {{\theta }_{ * }}$ | ${{\Psi }_{c}} = + \infty $ | ${{\Psi }_{k}} = {{\Xi }_{2}}\left( {{{\theta }_{ * }}} \right)$ |
| 8 | $\Gamma \left( {{{\theta }_{0}}} \right) > 0$ | $Det2 < 0$ | ${{\theta }_{ * }} < {{\theta }_{0}} < {{\theta }_{ * }} + \pi $ | ${{\Psi }_{c}} = + \infty $ | ${{\Psi }_{k}} = {{\Xi }_{2}}\left( {{{\theta }_{ * }} + \pi } \right)$ |
| 9 | $\Gamma \left( {{{\theta }_{0}}} \right) < 0$ | $Det2 > 0$ | ${{\theta }_{ * }} < {{\theta }_{1}} < {{\theta }_{0}}$ | ${{\Psi }_{с}} = {{\Xi }_{1}}\left( {{{\theta }_{1}}} \right)$ | ${{\Psi }_{k}} = {{\Xi }_{3}}\left( {{{\theta }_{ * }}} \right)$ |
| 10 | $\Gamma \left( {{{\theta }_{0}}} \right) < 0$ | $Det2 > 0$ | ${{\theta }_{ * }} - \pi < {{\theta }_{1}} < {{\theta }_{0}} < {{\theta }_{ * }}$ | ${{\Psi }_{с}} = {{\Xi }_{1}}\left( {{{\theta }_{1}}} \right)$ | ${{\Psi }_{k}} = {{\Xi }_{3}}\left( {{{\theta }_{ * }} - \pi } \right)$ |
| 11 | $\Gamma \left( {{{\theta }_{0}}} \right) < 0$ | $Det2 > 0$ | ${{\theta }_{ * }} - \pi < {{\theta }_{1}} - \pi < {{\theta }_{0}} < {{\theta }_{ * }}$ | ${{\Psi }_{с}}\, = \,{{\Xi }_{1}}({{\theta }_{1}} - \pi )$ | ${{\Psi }_{k}}\, = \,{{\Xi }_{3}}({{\theta }_{ * }} - \pi )$ |
| 12 | $\Gamma \left( {{{\theta }_{0}}} \right) < 0$ | $Det2 > 0$ | ${{\theta }_{1}} < {{\theta }_{2}} < {{\theta }_{ * }} < {{\theta }_{0}}$ | ${{\Psi }_{c}} = + \infty $ | ${{\Psi }_{k}} = {{\Xi }_{3}}\left( {{{\theta }_{ * }}} \right)$ |
| 13 | $\Gamma \left( {{{\theta }_{0}}} \right) < 0$ | $Det2 > 0$ | ${{\theta }_{ * }} < {{\theta }_{0}} < {{\theta }_{1}}$ | ${{\Psi }_{c}} = + \infty $ | ${{\Psi }_{k}} = {{\Xi }_{3}}\left( {{{\theta }_{ * }}} \right)$ |
| 14 | $\Gamma \left( {{{\theta }_{0}}} \right) < 0$ | $Det2 > 0$ | ${{\theta }_{ * }} - \pi < {{\theta }_{0}} < {{\theta }_{1}} < {{\theta }_{2}} < {{\theta }_{ * }}$ | ${{\Psi }_{c}} = + \infty $ | ${{\Psi }_{k}} = {{\Xi }_{3}}\left( {{{\theta }_{ * }} - \pi } \right)$ |
| 15 | $\Gamma \left( {{{\theta }_{0}}} \right) < 0$ | $Det2 < 0$ | ${{\theta }_{ * }} < {{\theta }_{0}}$ | ${{\Psi }_{c}} = + \infty $ | ${{\Psi }_{k}} = {{\Xi }_{3}}\left( {{{\theta }_{ * }}} \right)$ |
| 16 | $\Gamma \left( {{{\theta }_{0}}} \right) < 0$ | $Det2 < 0$ | ${{\theta }_{ * }} - \pi < {{\theta }_{0}} < {{\theta }_{ * }}$ | ${{\Psi }_{c}} = + \infty $ | ${{\Psi }_{k}} = {{\Xi }_{3}}\left( {{{\theta }_{ * }} - \pi } \right)$ |
Докажем, что предел ${{\Xi }_{2}}\left( {{{\theta }_{*}}} \right)$при $\Lambda - \Pi < 0$ и ${{\Gamma }_{2}}\left( {{{\theta }_{*}}} \right) < 0$ является конечным, т.е. в этом случае тело при $s \to \infty $ будет двигаться по круговой траектории. Подставим (5.3) в (5.4):
(5.5)
$\begin{gathered} \, \times {{\left| {\sin \left( {{{\theta }_{*}} - {{\theta }_{{**}}}} \right)} \right|}^{{ - \Lambda - \Pi }}}\operatorname{sgn} \left[ {\sin \left( {{{\theta }_{0}} - {{\theta }_{*}}} \right)\sin \left( {{{\theta }_{0}} - {{\theta }_{{**}}}} \right)} \right] \times \hfill \\ \, \times \mathop {\lim }\limits_{\varepsilon \to 0,\varepsilon > 0} \left[ {{{{\left| {\sin \left( { - \varepsilon } \right)} \right|}}^{{ - \Lambda + \Pi }}}\int\limits_{{{\theta }_{0}}}^{{{\theta }_{ * }} - \varepsilon } {\exp \left( {\frac{{2\left[ {{{E}_{1}}E + \left( {{{D}_{1}} - {{F}_{1}}} \right)\left( {D - F} \right)} \right]}}{{{{E}^{2}} + {{{\left( {D - F} \right)}}^{2}}}}\theta } \right) \times } } \right. \hfill \\ \end{gathered} $Функция ${{\left| {\sin \left( {\theta - {{\theta }_{*}}} \right)} \right|}^{{\Lambda - \Pi - 1}}}$ стремится к бесконечности при $\theta \to {{\theta }_{*}}$. Остальные функции являются конечными, поэтому для доказательства конечности ${{\Xi }_{2}}\left( {{{\theta }_{*}}} \right)$ достаточно доказать конечность ${\rm T}$:
(5.6)
${\rm T} = \mathop {\lim }\limits_{\varepsilon \to 0,\varepsilon > 0} \left\{ {{{{\left[ {\sin \left( { - \varepsilon } \right)} \right]}}^{{\Pi - \Lambda }}}\int\limits_{{{\theta }_{0}} - {{\theta }_{ * }}}^{ - \varepsilon } {{{{\left( {\sin \varphi } \right)}}^{{\Lambda - \Pi - 1}}}d\varphi } } \right\}$Под интегралом в (5.6) находится $\sin \varphi $ в отрицательной степени. Используем формулу, позволяющую увеличить степень $\sin \varphi $ [10]:
(5.7)
$\int {\frac{{dx}}{{{{{\sin }}^{p}}x}} = \frac{{\cos x}}{{(1 - p){{{\sin }}^{{p - 1}}}x}} + \frac{{p - 2}}{{p - 1}}\int {\frac{{dx}}{{{{{\sin }}^{{p - 2}}}x}}} } $После подстановки (5.7) в (5.6), получим
(5.8)
${\rm T} = \frac{1}{{\Lambda - \Pi }} + \frac{{\Pi - \Lambda - 1}}{{\Pi - \Lambda }}\mathop {\lim }\limits_{\varepsilon \to 0} \left[ {{{{\left[ {\sin \left( { - \varepsilon } \right)} \right]}}^{{\Pi - \Lambda }}}\int\limits_{{{\theta }_{0}} - {{\theta }_{ * }}}^{ - \varepsilon } {{{{\left( {\sin \varphi } \right)}}^{{\Lambda - \Pi + 1}}}d\theta } } \right]$Второе слагаемое в (5.8) равно нулю. Это можно доказать последовательным применением (5.7) к интегралу, входящему в (5.8), до тех пор, пока степень подынтегральной функции $\sin \varphi $ не станет больше нуля, и вычислением получающихся пределов. Таким образом, предел ${{\Xi }_{2}}\left( {{{\theta }_{*}}} \right)$ является конечным. Аналогичным образом доказывается конечность ${{\Xi }_{2}}\left( {{{\theta }_{*}} + \pi } \right)$, ${{\Xi }_{3}}\left( {{{\theta }_{*}}} \right)$ и ${{\Xi }_{3}}\left( {{{\theta }_{*}} - \pi } \right)$.
5.3. При $\Lambda - \Pi > 0$ и ${{\Gamma }_{2}}\left( {{{\theta }_{*}}} \right) < 0$ движение будет неустойчивым, если ${{\Psi }_{0}} > {{\Psi }_{c}}$, где ${{\Psi }_{c}}$ приведены в табл. 1.
5.4. При $\Lambda - \Pi > 0$ и ${{\Gamma }_{2}}\left( {{{\theta }_{*}}} \right) > 0$ движение будет асимптотически устойчивым, если ${{\Psi }_{0}} < \min \left( {{{\Psi }_{{c1}}},{{\Psi }_{{c2}}}} \right)$. Формулы для вычисления ${{\Psi }_{{c1}}}$ и ${{\Psi }_{{c2}}}$ приведены в табл. 2.
Таблица 2
| № | ${{\Gamma }_{1}}\left( {{{\theta }_{0}}} \right)$ | $Det2$ | ${{\theta }_{0}}$ | ${{\Psi }_{{с1}}}$ | ${{\Psi }_{{c2}}}$ |
|---|---|---|---|---|---|
| 1 | $\Gamma \left( {{{\theta }_{0}}} \right) > 0$ | $Det2 > 0$ | ${{\theta }_{0}} < {{\theta }_{1}} < {{\theta }_{ * }}$ | ${{\Psi }_{{с1}}} = {{\Xi }_{1}}\left( {{{\theta }_{1}}} \right)$ | ${{\Psi }_{{c2}}} = {{\Xi }_{1}}\left( {{{\theta }_{ * }}} \right)$ |
| 2 | $\Gamma \left( {{{\theta }_{0}}} \right) > 0$ | $Det2 > 0$ | ${{\theta }_{ * }} < {{\theta }_{0}} < {{\theta }_{1}} < {{\theta }_{ * }} + \pi $ | ${{\Psi }_{{с1}}} = {{\Xi }_{1}}\left( {{{\theta }_{1}}} \right)$ | ${{\Psi }_{{c2}}} = {{\Xi }_{1}}\left( {{{\theta }_{ * }} + \pi } \right)$ |
| 3 | $\Gamma \left( {{{\theta }_{0}}} \right) > 0$ | $Det2 > 0$ | ${{\theta }_{ * }} < {{\theta }_{0}} < {{\theta }_{1}} + \pi < {{\theta }_{ * }} + \pi $ | ${{\Psi }_{{с1}}} = {{\Xi }_{1}}\left( {{{\theta }_{1}} + \pi } \right)$ | ${{\Psi }_{{c2}}} = {{\Xi }_{1}}\left( {{{\theta }_{ * }} + \pi } \right)$ |
| 4 | $\Gamma \left( {{{\theta }_{0}}} \right) > 0$ | $Det2 > 0$ | ${{\theta }_{1}} < {{\theta }_{0}} < {{\theta }_{ * }}$ | ${{\Psi }_{{c1}}} = + \infty $ | ${{\Psi }_{{c2}}} = {{\Xi }_{1}}\left( {{{\theta }_{ * }}} \right)$ |
| 5 | $\Gamma \left( {{{\theta }_{0}}} \right) > 0$ | $Det2 > 0$ | ${{\theta }_{0}} < {{\theta }_{ * }} < {{\theta }_{1}} < {{\theta }_{2}}$ | ${{\Psi }_{{c1}}} = + \infty $ | ${{\Psi }_{{c2}}} = {{\Xi }_{1}}\left( {{{\theta }_{ * }}} \right)$ |
| 6 | $\Gamma \left( {{{\theta }_{0}}} \right) > 0$ | $Det2 > 0$ | ${{\theta }_{ * }} < {{\theta }_{1}} < {{\theta }_{2}} < {{\theta }_{0}} < {{\theta }_{ * }} + \pi $ | ${{\Psi }_{{c1}}} = + \infty $ | ${{\Psi }_{{c2}}} = {{\Xi }_{1}}\left( {{{\theta }_{ * }} + \pi } \right)$ |
| 7 | $\Gamma \left( {{{\theta }_{0}}} \right) > 0$ | $Det2 < 0$ | ${{\theta }_{0}} < {{\theta }_{ * }}$ | ${{\Psi }_{{c1}}} = + \infty $ | ${{\Psi }_{{c2}}} = {{\Xi }_{1}}\left( {{{\theta }_{ * }}} \right)$ |
| 8 | $\Gamma \left( {{{\theta }_{0}}} \right) > 0$ | $Det2 < 0$ | ${{\theta }_{ * }} < {{\theta }_{0}} < {{\theta }_{ * }} + \pi $ | ${{\Psi }_{{c1}}} = + \infty $ | ${{\Psi }_{{c2}}} = {{\Xi }_{1}}\left( {{{\theta }_{ * }} + \pi } \right)$ |
| 9 | $\Gamma \left( {{{\theta }_{0}}} \right) < 0$ | $Det2 > 0$ | ${{\theta }_{ * }} < {{\theta }_{2}} < {{\theta }_{0}}$ | ${{\Psi }_{{с1}}} = {{\Xi }_{1}}\left( {{{\theta }_{2}}} \right)$ | ${{\Psi }_{{c2}}} = {{\Xi }_{1}}\left( {{{\theta }_{ * }}} \right)$ |
| 10 | $\Gamma \left( {{{\theta }_{0}}} \right) < 0$ | $Det2 > 0$ | ${{\theta }_{ * }} - \pi < {{\theta }_{2}} < {{\theta }_{0}} < {{\theta }_{ * }}$ | ${{\Psi }_{{с1}}} = {{\Xi }_{1}}\left( {{{\theta }_{2}}} \right)$ | ${{\Psi }_{{c2}}} = {{\Xi }_{1}}\left( {{{\theta }_{ * }} - \pi } \right)$ |
| 11 | $\Gamma \left( {{{\theta }_{0}}} \right) < 0$ | $Det2 > 0$ | ${{\theta }_{ * }} - \pi < {{\theta }_{2}} - \pi < {{\theta }_{0}} < {{\theta }_{ * }}$ | ${{\Psi }_{{с1}}} = {{\Xi }_{1}}\left( {{{\theta }_{2}} - \pi } \right)$ | ${{\Psi }_{{c2}}} = {{\Xi }_{1}}\left( {{{\theta }_{ * }} - \pi } \right)$ |
| 12 | $\Gamma \left( {{{\theta }_{0}}} \right) < 0$ | $Det2 > 0$ | ${{\theta }_{1}} < {{\theta }_{2}} < {{\theta }_{ * }} < {{\theta }_{0}}$ | ${{\Psi }_{{c1}}} = + \infty $ | ${{\Psi }_{{c2}}} = {{\Xi }_{1}}\left( {{{\theta }_{ * }}} \right)$ |
| 13 | $\Gamma \left( {{{\theta }_{0}}} \right) < 0$ | $Det2 > 0$ | ${{\theta }_{ * }} < {{\theta }_{0}} < {{\theta }_{2}}$ | ${{\Psi }_{{c1}}} = + \infty $ | ${{\Psi }_{{c2}}} = {{\Xi }_{1}}\left( {{{\theta }_{ * }}} \right)$ |
| 14 | $\Gamma \left( {{{\theta }_{0}}} \right) < 0$ | $Det2 > 0$ | ${{\theta }_{ * }} - \pi < {{\theta }_{0}} < {{\theta }_{1}} < {{\theta }_{2}} < {{\theta }_{ * }}$ | ${{\Psi }_{{c1}}} = + \infty $ | ${{\Psi }_{{c2}}} = {{\Xi }_{1}}\left( {{{\theta }_{ * }} - \pi } \right)$ |
| 15 | $\Gamma \left( {{{\theta }_{0}}} \right) < 0$ | $Det2 < 0$ | ${{\theta }_{ * }} < {{\theta }_{0}}$ | ${{\Psi }_{{c1}}} = + \infty $ | ${{\Psi }_{{c2}}} = {{\Xi }_{1}}\left( {{{\theta }_{ * }}} \right)$ |
| 16 | $\Gamma \left( {{{\theta }_{0}}} \right) < 0$ | $Det2 < 0$ | ${{\theta }_{ * }} - \pi < {{\theta }_{0}} < {{\theta }_{ * }}$ | ${{\Psi }_{{c1}}} = + \infty $ | ${{\Psi }_{{c2}}} = {{\Xi }_{1}}\left( {{{\theta }_{ * }} - \pi } \right)$ |
6. Изучение возможных траекторий и устойчивости при ${{E}^{2}} < 4DF$. Из (4.4) и (4.6) следует, что функции $\Phi \left( \theta \right)$ и $\Upsilon \left( \theta \right)$ при ${{E}^{2}} < 4DF$ являются периодическими с периодом π. В случае $\Gamma \left( {{{\theta }_{0}}} \right) > 0$, ${{\theta }_{0}} < {{\theta }_{2}}$ и $Det2 > 0$ функция $\theta \left( s \right)$ монотонно возрастает с ростом s, а локальными максимумами функции $\Upsilon $ являются точки ${{\theta }_{2}} + \left( {n - 1} \right)\pi $, где $n = 1,2,3$, .... Для удобства анализа траектории и устойчивости движения перепишем $\Upsilon \left( s \right)$ в следующем виде
(6.1)
$\begin{gathered} {{{\rm X}}_{{11}}} = - 2\int\limits_{{{\theta }_{0}}}^{{{\theta }_{2}}} {\frac{{{{\Gamma }_{1}}\left( \theta \right)}}{{\Gamma \left( \theta \right)}}d\theta } ,\quad {{{\rm X}}_{{12}}} = - 2\int\limits_{{{\theta }_{2}}}^{{{\theta }_{2}} + \pi } {\frac{{{{\Gamma }_{1}}\left( \theta \right)}}{{\Gamma \left( \theta \right)}}d\theta } \\ {{{\rm X}}_{{13}}}\left( \theta \right) = - 2\int\limits_{{{\theta }_{2}} + N\pi }^\theta {\frac{{{{\Gamma }_{1}}\left( \theta \right)}}{{\Gamma \left( \theta \right)}}d\theta } = \Phi \left( {\theta - N\pi } \right) \\ \end{gathered} $Сумма в квадратных скобках (6.1) является геометрической прогрессией, поэтому выражение для $\Upsilon $ при $\theta > {{\theta }_{2}} + \pi $ можно упростить
(6.2)
$\Upsilon = {{{\rm X}}_{4}}\left( {{{\theta }_{0}},{{\theta }_{2}}} \right) + \frac{{\exp \left( { - {{{\rm X}}_{{11}}}} \right)\left[ {\exp \left( { - N{{{\rm X}}_{{12}}}} \right) - 1} \right]}}{{\exp \left( { - {{{\rm X}}_{{12}}}} \right) - 1}}{{{\rm X}}_{{15}}}\left( {{{\theta }_{2}},{{\theta }_{2}} + \pi } \right) + {{{\rm X}}_{4}}\left( {{{\theta }_{2}} + N\pi ,\theta } \right)$Представим $\Upsilon $ в виде суммы слагаемого, не зависящего от $N$, и слагаемого пропорционального $\exp \left( { - {{{\rm X}}_{{11}}} - N{{{\rm X}}_{{12}}}} \right)$:
(6.3)
$\begin{gathered} \Upsilon = {{{\rm X}}_{4}}\left( {{{\theta }_{0}},{{\theta }_{2}}} \right) + \frac{{\exp \left( { - {{{\rm X}}_{{11}}}} \right)}}{{1 - \exp \left( { - {{{\rm X}}_{{12}}}} \right)}}{{{\rm X}}_{{15}}}\left( {{{\theta }_{2}},{{\theta }_{2}} + \pi } \right) + \exp \left( { - {{{\rm X}}_{{11}}} - N{{{\rm X}}_{{12}}}} \right) \times \\ \, \times \left[ {\frac{{{{{\rm X}}_{{15}}}\left( {{{\theta }_{2}},{{\theta }_{2}} + \pi } \right)}}{{\exp \left( { - {{{\rm X}}_{{12}}}} \right) - 1}} + \int\limits_{{{\theta }_{2}} + N\pi }^\theta {\exp \left[ { - \Phi \left( \theta \right) + {{{\rm X}}_{{11}}} + N{{{\rm X}}_{{12}}}} \right]\frac{{{{\Gamma }_{2}}\left( \theta \right)}}{{\Gamma \left( \theta \right)}}d\theta } } \right] \\ \end{gathered} $Функция ${{{{\Gamma }_{2}}\left( \theta \right)} \mathord{\left/ {\vphantom {{{{\Gamma }_{2}}\left( \theta \right)} {\Gamma \left( \theta \right)}}} \right. \kern-0em} {\Gamma \left( \theta \right)}}$ является периодической с периодом π, поэтому заменив в (6.3) переменную интегрирования θ на $\theta - N\pi $ и подставив ${{{\rm X}}_{{13}}}\left( \theta \right)$ из (6.1) , выражение для $\Upsilon $ можно упростить
(6.4)
$\begin{gathered} \Upsilon = {{{\rm X}}_{4}}\left( {{{\theta }_{0}},{{\theta }_{2}}} \right) + \frac{{\exp \left( { - {{{\rm X}}_{{11}}}} \right)}}{{1 - \exp \left( { - {{{\rm X}}_{{12}}}} \right)}}{{{\rm X}}_{{15}}}\left( {{{\theta }_{2}},{{\theta }_{2}} + \pi } \right) + \\ \, + \exp \left( { - {{{\rm X}}_{{11}}} - N{{{\rm X}}_{{12}}}} \right)\left[ {\frac{{{{{\rm X}}_{{15}}}\left( {{{\theta }_{2}},{{\theta }_{2}} + \pi } \right)}}{{\exp \left( { - {{{\rm X}}_{{12}}}} \right) - 1}} + {{{\rm X}}_{{15}}}\left( {{{\theta }_{2}},\theta - N\pi } \right)} \right] \\ \end{gathered} $Из (6.4) следует, что если $\Phi \left( \theta \right) \to + \infty $ при $s \to + \infty $, то предел функции $\Upsilon \exp \left[ {\Phi \left( \theta \right)} \right]$ при $s \to + \infty $ является бесконечным. Если $\Phi \left( \theta \right) \to - \infty $ при $s \to + \infty $, то предел $\Upsilon {\text{exp}}[\Phi (\theta )]$ выражается формулой
(6.5)
$\mathop {\lim }\limits_{s \to \infty } \left\{ {\Upsilon \exp \left[ {\Phi \left( \theta \right)} \right]} \right\} = \left[ {\frac{{{{{\rm X}}_{{15}}}\left( {{{\theta }_{2}},{{\theta }_{2}} + \pi } \right)}}{{\exp \left( { - {{{\rm X}}_{{12}}}} \right) - 1}} + {{{\rm X}}_{{15}}}\left( {{{\theta }_{2}},\theta - N\pi } \right)} \right]\exp \left[ {\Phi \left( {\theta - N\pi } \right)} \right]$Случай $\Gamma \left( {{{\theta }_{0}}} \right) < 0$, $Det2 > 0$, ${{\theta }_{1}} < {{\theta }_{0}}$ отличается от (6.1) тем, что угол $\theta $ будет убывать при движении тела по траектории, локальными максимумами функции $\Upsilon $ будут точки ${{\theta }_{1}} - \left( {n - 1} \right)\pi $, а функция $\Upsilon $ в этом случае записывается в следующем виде
(6.6)
${{{\rm X}}_{{31}}} = - 2\int\limits_{{{\theta }_{0}}}^{{{\theta }_{1}}} {\frac{{{{\Gamma }_{1}}\left( \theta \right)}}{{\Gamma \left( \theta \right)}}d\theta } ,\quad {{{\rm X}}_{{32}}} = - 2\int\limits_{{{\theta }_{1}}}^{{{\theta }_{1}} - \pi } {\frac{{{{\Gamma }_{1}}\left( \theta \right)}}{{\Gamma \left( \theta \right)}}d\theta } $Рассмотрим ниже в подпунктах 6.1–6.5 траектории и устойчивость движения тела при различных начальных условиях и параметрах среды и тела.
6.1. Если $\Gamma \left( {{{\theta }_{0}}} \right) > 0$, $Det\,2 > 0$, ${{\theta }_{0}} < {{\theta }_{2}}$ и ${{{\rm X}}_{{12}}} > 0$, то угол $\theta $ будет возрастать при движении тела по траектории, а из формул (4.6), (6.1), (6.2) следует, что при ${{\theta }_{0}} < {{\theta }_{2}} + \pi $ функция $\Upsilon \left( s \right)$ принимает максимальные значения ${{{\rm X}}_{4}}\left( {{{\theta }_{0}},{{\theta }_{2}}} \right)$ и ${{{\rm X}}_{4}}\left( {{{\theta }_{0}},{{\theta }_{2}} + \pi } \right)$. Если ${{\theta }_{0}} > {{\theta }_{2}} + \pi $, то максимум функции может быть равен ${{\Upsilon }_{{m1}}}$ или ${{\Upsilon }_{{m2}}}$ при N = 1, $\theta = {{\theta }_{2}} + \pi $ и при $N = + \infty ,$ $\theta = {{\theta }_{2}} + N\pi $ соответственно
(6.7)
$\begin{gathered} {{\Upsilon }_{{m1}}} = {{{\rm X}}_{4}}\left( {{{\theta }_{0}},{{\theta }_{2}}} \right) + {{{\rm X}}_{{15}}}\left( {{{\theta }_{2}},{{\theta }_{2}} + \pi } \right)\exp \left( { - {{{\rm X}}_{1}}} \right) = {{{\rm X}}_{4}}\left( {{{\theta }_{0}},{{\theta }_{2}} + \pi } \right) \\ {{\Upsilon }_{{m2}}} = {{{\rm X}}_{4}}\left( {{{\theta }_{0}},{{\theta }_{2}}} \right) + \frac{{\exp \left( { - {{{\rm X}}_{{11}}}} \right)}}{{1 - \exp \left( { - {{{\rm X}}_{{12}}}} \right)}}{{{\rm X}}_{{15}}}\left( {{{\theta }_{2}},{{\theta }_{2}} + \pi } \right) \\ \end{gathered} $При ${{{\rm X}}_{{15}}}\left( {{{\theta }_{2}},{{\theta }_{2}} + \pi } \right) > 0$ выполняется неравенство ${{\Upsilon }_{{m2}}} > {{\Upsilon }_{{m1}}} > {{{\rm X}}_{4}}\left( {{{\theta }_{0}},{{\theta }_{2}}} \right)$, а при ${{{\rm X}}_{{15}}}\left( {{{\theta }_{2}},{{\theta }_{2}} + \pi } \right)$ < 0 выполняется неравенство ${{{\rm X}}_{4}}\left( {{{\theta }_{0}},{{\theta }_{2}}} \right) > {{\Upsilon }_{{m1}}} > {{\Upsilon }_{{m2}}}$. Если при движении тела по траектории выполняется неравенство $\Psi _{0}^{{ - 2}} - 2\Upsilon > 0$, то $\Phi \to + \infty $ и $\Psi \to 0$ при $s \to + \infty $, то есть возмущения будут затухать. Следовательно, необходимые и достаточные условия асимптотической устойчивости прямолинейного движения тела записываются в виде неравенства
(6.8)
$\Psi _{0}^{{ - 2}} > \left\{ {\begin{array}{*{20}{l}} {2{{{\rm X}}_{4}}\left( {{{\theta }_{0}},{{\theta }_{2}}} \right)\quad {\text{при}}\quad {{{\rm X}}_{{15}}}\left( {{{\theta }_{2}},{{\theta }_{2}} + \pi } \right) < 0} \\ {2{{\Upsilon }_{{m2}}}\quad {\text{при}}\quad {{{\rm X}}_{{15}}}\left( {{{\theta }_{2}},{{\theta }_{2}} + \pi } \right) > 0} \end{array}} \right.$При невыполнении условий (6.8) функция $\Psi _{0}^{{ - 2}} - 2\Upsilon $ обратится в нуль на конечном отрезке траектории, а $\Psi $ станет бесконечной. Движение тела в этом случае будет неустойчивым.
6.2. Если $\Gamma \left( {{{\theta }_{0}}} \right) > 0$, $Det\,2 > 0$, ${{\theta }_{2}} < {{\theta }_{0}}$ и ${{X}_{{12}}} > 0$, то в формулах (6.1)–(6.5) следует заменить ${{\theta }_{2}}$ на ${{\theta }_{2}} + \pi $, а условия асимптотической устойчивости примут вид
(6.9)
$\Psi _{0}^{{ - 2}} > \left\{ {\begin{array}{*{20}{l}} {2{{{\rm X}}_{4}}\left( {{{\theta }_{0}},{{\theta }_{2}} + \pi } \right)\quad {\text{при}}\quad {{{\rm X}}_{{15}}}\left( {{{\theta }_{2}},{{\theta }_{2}} + \pi } \right) < 0} \\ {2{{{\rm X}}_{4}}\left( {{{\theta }_{0}},{{\theta }_{2}} + \pi } \right) + \frac{{2\exp \left( { - {{{\rm X}}_{{11}}}} \right){{{\rm X}}_{{15}}}\left( {{{\theta }_{2}},{{\theta }_{2}} + \pi } \right)}}{{1 - \exp \left( { - {{{\rm X}}_{{12}}}} \right)}}\quad {\text{при}}\quad {{{\rm X}}_{{15}}}\left( {{{\theta }_{2}},{{\theta }_{2}} + \pi } \right) > 0} \end{array}} \right.$В функции X15 замена θ2 на ${{\theta }_{2}} + \pi $ не проводилась, так как ${{{\rm X}}_{{15}}}\left( {{{\theta }_{2}} + \pi ,{{\theta }_{2}} + 2\pi } \right)$ = ${{{\rm X}}_{{15}}}\left( {{{\theta }_{2}},{{\theta }_{2}} + \pi } \right)$.
6.3. Если $\Gamma \left( {{{\theta }_{0}}} \right) > 0$, $Det2 < 0$ и ${{{\rm X}}_{{22}}} > 0$, где выражение для ${{{\rm X}}_{{22}}}$ дано ниже в (6.10), то функция ${{\Gamma }_{2}}\left( \theta \right)$ не имеет корней и ее знак совпадает со знаком ${{\Gamma }_{2}}\left( {{{\theta }_{0}}} \right)$, поэтому $\Upsilon \left( s \right)$ будет больше нуля при ${{\Gamma }_{2}}\left( {{{\theta }_{0}}} \right) > 0$ и меньше нуля при ${{\Gamma }_{2}}\left( {{{\theta }_{0}}} \right) < 0$. При ${{\Gamma }_{2}}\left( {{{\theta }_{0}}} \right) < 0$ функция $\Psi _{0}^{{ - 2}} - 2\Upsilon $ является положительной, а движение тела будет асимптотически устойчивым. В случае ${{\Gamma }_{2}}\left( {{{\theta }_{0}}} \right) > 0$ условие асимптотической устойчивости записывается в виде
(6.10)
$\begin{gathered} \Psi _{0}^{{ - 2}} > 2{{{\rm X}}_{4}}\left( {{{\theta }_{0}},{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}} \right) + \frac{{2\exp \left( { - {{{\rm X}}_{{21}}}} \right)}}{{1 - \exp \left( { - {{{\rm X}}_{{22}}}} \right)}}{{{\rm X}}_{{25}}}\left( {{{ - \pi } \mathord{\left/ {\vphantom {{ - \pi } 2}} \right. \kern-0em} 2},{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}} \right) \\ {{{\rm X}}_{{21}}} = - 2\int\limits_{{{\theta }_{0}}}^{{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}} {\frac{{{{\Gamma }_{1}}\left( \theta \right)}}{{\Gamma \left( \theta \right)}}d\theta } ,\quad {{{\rm X}}_{{22}}} = - 2\int\limits_{{{ - \pi } \mathord{\left/ {\vphantom {{ - \pi } 2}} \right. \kern-0em} 2}}^{{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}} {\frac{{{{\Gamma }_{1}}\left( \theta \right)}}{{\Gamma \left( \theta \right)}}d\theta } , \\ {{{\rm X}}_{{23}}}\left( \theta \right) = - 2\int\limits_{{{ - \pi } \mathord{\left/ {\vphantom {{ - \pi } 2}} \right. \kern-0em} 2}}^{\theta - \left( {N + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}} \right)\pi } {\frac{{{{\Gamma }_{1}}\left( \theta \right)}}{{\Gamma \left( \theta \right)}}d\theta } ,\quad {{{\rm X}}_{{25}}}\left( {\xi ,\upsilon } \right) = \int\limits_\xi ^\upsilon {\exp \left[ { - {{{\rm X}}_{{23}}}\left( \theta \right)} \right]\frac{{{{\Gamma }_{2}}\left( \theta \right)}}{{\Gamma \left( \theta \right)}}d\theta } \\ \end{gathered} $6.4. Если $\Gamma \left( {{{\theta }_{0}}} \right) > 0$, $Det2 > 0$, ${{\theta }_{0}} < {{\theta }_{2}}$ и ${{{\rm X}}_{{12}}} < 0$ и выполняются условия
(6.11)
$\Psi _{0}^{{ - 2}} > 2{{{\rm X}}_{4}}\left( {{{\theta }_{0}},{{\theta }_{2}}} \right),\quad {{{\rm X}}_{{15}}}\left( {{{\theta }_{2}},{{\theta }_{2}} + \pi } \right) < 0,$6.5. При $\Gamma \left( {{{\theta }_{0}}} \right) < 0$, $Det2 > 0$, ${{\theta }_{2}} < {{\theta }_{0}}$ и ${{{\rm X}}_{{12}}} < 0$ рассуждения строятся аналогично подпункту 6.4, а критерии асимптотической устойчивости будут иметь следующий вид
6.6. В случае $\Gamma \left( {{{\theta }_{0}}} \right) < 0$, $Det2 > 0$, ${{\theta }_{1}} < {{\theta }_{0}}$ и ${{{\rm X}}_{{32}}} > 0$ угол $\theta $ будет убывать при движении тела по траектории, локальные максимумы функция $\Upsilon $ будут в точках ${{\theta }_{1}} - \left( {n - 1} \right)\pi $, а сама функция $\Upsilon $ имеет вид (6.6). Приводя рассуждения аналогичные подпункту 6.1, можно показать, что в этом случае условия асимптотической устойчивости записываются в следующем виде
(6.12)
$\Psi _{0}^{{ - 2}} > \left\{ {\begin{array}{*{20}{l}} {2{{{\rm X}}_{4}}\left( {{{\theta }_{0}},{{\theta }_{1}}} \right)\quad {\text{при}}\quad {{{\rm X}}_{{35}}}\left( {{{\theta }_{1}},{{\theta }_{1}} - \pi } \right) < 0} \\ {2{{{\rm X}}_{4}}\left( {{{\theta }_{0}},{{\theta }_{1}}} \right) + \frac{{2\exp \left( { - {{{\rm X}}_{{31}}}} \right)}}{{1 - \exp \left( { - {{{\rm X}}_{{32}}}} \right)}}{{{\rm X}}_{{35}}}\left( {{{\theta }_{1}},{{\theta }_{1}} - \pi } \right)\quad {\text{при}}\quad {{{\rm X}}_{{35}}}\left( {{{\theta }_{1}},{{\theta }_{1}} - \pi } \right) > 0} \end{array}} \right.$6.7. Если $\Gamma \left( {{{\theta }_{0}}} \right) < 0$, $Det\,2 < 0$, ${{\theta }_{0}} < {{\theta }_{1}}$ и ${{{\rm X}}_{{32}}} > 0$, то в условиях асимптотической устойчивости (6.12) следует заменить ${{\theta }_{1}}$ на ${{\theta }_{1}} - \pi $:
(6.13)
$\Psi _{0}^{{ - 2}} > \left\{ {\begin{array}{*{20}{l}} {2{{{\rm X}}_{4}}\left( {{{\theta }_{0}},{{\theta }_{1}} - \pi } \right)\quad {\text{при}}\quad {{{\rm X}}_{{35}}}\left( {{{\theta }_{1}},{{\theta }_{1}} - \pi } \right) < 0} \\ {2{{{\rm X}}_{4}}\left( {{{\theta }_{0}},{{\theta }_{1}} - \pi } \right) + \frac{{2\exp \left( { - {{{\rm X}}_{{31}}}} \right)}}{{1 - \exp \left( { - {{{\rm X}}_{{32}}}} \right)}}{{{\rm X}}_{{35}}}\left( {{{\theta }_{1}},{{\theta }_{1}} - \pi } \right)\quad {\text{при}}\quad {{{\rm X}}_{{35}}}\left( {{{\theta }_{1}},{{\theta }_{1}} - \pi } \right) > 0} \end{array}} \right.$6.8. Если $\Gamma \left( {{{\theta }_{0}}} \right) < 0$, $Det\,2 < 0$ и ${{{\rm X}}_{{42}}} > 0$, где ${{{\rm X}}_{{42}}}$ определено ниже в (6.14), то функция ${{\Gamma }_{2}}\left( \theta \right)$ не имеет корней и ее знак совпадает со знаком ${{\Gamma }_{2}}\left( {{{\theta }_{0}}} \right)$, поэтому $\Upsilon \left( s \right)$ будет больше нуля при ${{\Gamma }_{2}}\left( {{{\theta }_{0}}} \right) > 0$ и меньше нуля при ${{\Gamma }_{2}}\left( {{{\theta }_{0}}} \right) < 0$. При ${{\Gamma }_{2}}\left( {{{\theta }_{0}}} \right) < 0$ функция $\Psi _{0}^{{ - 2}} - 2\Upsilon $ является положительной, а движение тела будет асимптотически устойчивым. В случае ${{\Gamma }_{2}}\left( {{{\theta }_{0}}} \right) > 0$ условие асимптотической устойчивости записывается в следующем виде
(6.14)
$\begin{gathered} \Psi _{0}^{{ - 2}} > 2{{{\rm X}}_{4}}\left( {{{\theta }_{0}},{{ - \pi } \mathord{\left/ {\vphantom {{ - \pi } 2}} \right. \kern-0em} 2}} \right) + \frac{{2\exp \left( { - {{{\rm X}}_{{41}}}} \right){{{\rm X}}_{{45}}}\left( {{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2},{{ - \pi } \mathord{\left/ {\vphantom {{ - \pi } 2}} \right. \kern-0em} 2}} \right)}}{{1 - \exp \left( { - {{{\rm X}}_{{42}}}} \right)}} \\ {{{\rm X}}_{{41}}} = - 2\int\limits_{{{\theta }_{0}}}^{{{ - \pi } \mathord{\left/ {\vphantom {{ - \pi } 2}} \right. \kern-0em} 2}} {\frac{{{{\Gamma }_{1}}\left( \theta \right)}}{{\Gamma \left( \theta \right)}}d\theta } ,\quad {{{\rm X}}_{{42}}} = - 2\int\limits_{{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}}^{{{ - \pi } \mathord{\left/ {\vphantom {{ - \pi } 2}} \right. \kern-0em} 2}} {\frac{{{{\Gamma }_{1}}\left( \theta \right)}}{{\Gamma \left( \theta \right)}}d\theta } \\ {{{\rm X}}_{{43}}}\left( \theta \right) = - 2\int\limits_{{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}}^{\theta + \left( {N + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}} \right)\pi } {\frac{{{{\Gamma }_{1}}\left( \theta \right)}}{{\Gamma \left( \theta \right)}}d\theta } ,\quad {{{\rm X}}_{{45}}}\left( {\xi ,\upsilon } \right) = \int\limits_\xi ^\upsilon {\exp \left[ { - {{{\rm X}}_{{43}}}\left( \theta \right)} \right]\frac{{{{\Gamma }_{2}}\left( \theta \right)}}{{\Gamma \left( \theta \right)}}d\theta } \\ \end{gathered} $6.9. Случай $\Gamma \left( {{{\theta }_{0}}} \right) < 0$, $Det2 > 0$, ${{\theta }_{1}} < {{\theta }_{0}}$ и ${{{\rm X}}_{{32}}} < 0$ похож на 6.4 но угол θ будет убывать при движении тела по траектории. Запишем необходимые и достаточные условия асимптотической устойчивости
(6.15)
$\Psi _{0}^{{ - 2}} > 2{{{\rm X}}_{4}}\left( {{{\theta }_{0}},{{\theta }_{1}}} \right) > 0,\quad {{{\rm X}}_{{35}}}\left( {{{\theta }_{1}},{{\theta }_{1}} - \pi } \right) < 0$6.10. При $\Gamma \left( {{{\theta }_{0}}} \right) < 0$, $Det2 > 0$, ${{\theta }_{0}} < {{\theta }_{1}}$ и ${{X}_{{32}}} < 0$ рассуждения строятся аналогично подпункту 6.9, а критерии асимптотической устойчивости будут иметь вид
6.11. Если $\Gamma ({{\theta }_{0}})\, > \,0$, ${\text{Det}}2\, < \,0$, ${{\Gamma }_{2}}\left( {{{\theta }_{0}}} \right) > 0$ и ${{{\rm X}}_{{12}}} < 0$ или $\Gamma \left( {{{\theta }_{0}}} \right) < 0$, ${\text{Det}}\,2 < 0$, ${{\Gamma }_{2}}({{\theta }_{0}})$ > 0 и ${{{\rm X}}_{{32}}} < 0$, то возмущения станут бесконечными на конечном отрезке траектории, а движение тела будет неустойчивым.
6.12. Если $\Gamma \left( {{{\theta }_{0}}} \right) > 0$, ${\text{Det}}\,2 < 0$, ${{{\rm X}}_{{12}}} < 0$ и ${{\Gamma }_{2}}\left( {{{\theta }_{0}}} \right) < 0$, то из (6.5) следует, что предел $\Upsilon \exp \left[ {\Phi \left( \theta \right)} \right]$ при $s \to + \infty $ является ограниченной отрицательной периодической функцией с периодом $s\left( {{{3\pi } \mathord{\left/ {\vphantom {{3\pi } 2}} \right. \kern-0em} 2}} \right) - s\left( {{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}} \right)$. Отсюда следует, что $\Psi $ при $s \to + \infty $ будет положительной ограниченной периодической функцией
Из периодичности $\Psi $ и $\theta $ и ограниченности $\Psi $ следует периодичность и ограниченность возмущений $\eta $ и $\omega $.
6.13. Если $\Gamma \left( {{{\theta }_{0}}} \right) < 0$, ${\text{Det}}\,2 < 0$, ${{{\rm X}}_{{12}}} < 0$ и ${{\Gamma }_{2}}\left( {{{\theta }_{0}}} \right) < 0$, то аналогично подпункту 6.12 возмущения η и ω будут периодическими и ограниченными, а предел функции $\Psi $ при $s \to + \infty $ будет иметь следующий вид
7. Заключение. Возможны четыре варианта движения тела:
1. Тело движется асимптотически устойчиво, а возмущения $\eta $ и $\omega $ стремятся к нулю при длине траектории $s$ стремящейся к бесконечности.
2. Тело движется неустойчиво. В этом случае сумма ${{\eta }^{2}} + {{\omega }^{2}}$ становится равной бесконечности на конечном отрезке траектории.
3. При $s \to + \infty $ возмущения $\eta ,\omega $ стремятся к некоторым константам, а траектория тела становится круговой.
4. Возмущения $\eta $ и $\omega $ при $s \to + \infty $ являются периодическими функциями от длины траектории s.
Работа выполнена по теме госзадания (номер госрегистрации АААА-А20-120011690132-4) и при частичной финансовой поддержке Российским фондом фундаментальных исследований (проект № 20-08-00082а).
Список литературы
Бунимович А.И., Дубинский А.В. Развитие, современное состояние и приложения теории локального взаимодействия (обзор) // Изв. РАН. МЖГ. 1996. № 3. С. 3–18.
Мирошин Р.Н., Халидов И.А. Локальные методы в механике сплошных сред. СПб.: Изд-во СПб. ун-та, 2002. 303 с.
Котов В.Л., Константинов А.Ю. Численное моделирование плоскопараллельного движения конических ударников в грунтовой среде на основе модели локального взаимодействия // Вычислительная механика сплошных сред. 2014. № 3. С. 225–233.
Баничук Н.В., Иванова С.Ю. Игровой подход к решению задачи оптимизации формы ударника и структуры слоистой среды при высокоскоростном пробивании // Проблемы прочности и пластичности. 2016. Вып. 78. № 4. С. 426–435.
Симонов И.В. Об устойчивости движения удлиненного тела вращения в упругопластической среде при отрыве потока // ПММ. 2000. Т. 64. Вып. 2. С. 313–322.
Якунина Г.Е. Особенности высокоскоростного движения тел в плотных средах // ПММ. 2012. Т. 76. Вып. 3. С. 429–449.
Осипенко К.Ю. Устойчивость пространственного движения тела при учете отрыва потока и вращения вокруг оси симметрии // Изв. РАН. МТТ. 2016. № 4. С. 153–165.
Осипенко К.Ю. Устойчивость движения неосесимметричного тела в сопротивляющейся // ПММ. 2017. Т. 81. Вып. 6. С. 661–671.
Симонов И.В. О классификации траекторий плоскопараллельного движения тела вращения в прочной среде при отрыве потока // Докл. РАН. 2002. Т. 386. № 2. С. 198–202.
Брычков Ю.А., Маричев О.И., Прудников А.П. Таблицы неопределенных интегралов. М.: Физматлит, 2003. 200 с.
Зайцев В.Ф., Полянин А.Д. Справочник по обыкновенным дифференциальным уравнениям. М.: Физматлит, 2001. 576 с.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика твердого тела