Известия РАН. Механика твердого тела, 2021, № 5, стр. 141-151

1. Введение. Ранее, до 1970 года, точность измерений не позволяла наблюдать приливные деформации, возникающие из-за переменности центробежного потенциала. Это стало возможным с 1970 г. после создания сверхпроводящего гравиметра, позволяющего регистрировать малые вариации ускорения силы тяжести.

Следствием переменности центробежного потенциала, который определяется не только скоростью осевого вращения, но и положением мгновенной оси вращения в теле Земли, является зависимость геопотенциала от движения земного полюса [1, 2]. Из-за смещения главных осей инерции деформируемой Земли происходит изменение ее центробежных моментов инерции [3]. При этом деформации вязкоупругой мантии сопровождаются диссипацией энергии, что должно приводить к изменению структурных свойств модели полюсного прилива, введением слагаемых, определяемых вариациями центробежных моментов инерции или вариациями коэффициентов тессеральной гармоники геопотенциала [4, 5].

Следствием вязкости мантии Земли является малое смещение полюсного прилива и сдвиг фазы колебаний центробежных моментов инерции относительно колебаний земного полюса. Это смещение достаточно мало. Однако, для исследования движения земного полюса оно представляет значительный интерес и определяет амплитуду необходимого возмущения для поддержания установившегося чандлеровского колебания.

В данной статье для модели вязкоупругой Земли найдены вариации центробежных моментов инерции, вызванные квазипериодическим смещением оси вращения в теле Земли. Рассмотрено их сравнение с моделью, рекомендованной к учету Международной службой вращения Земли (МСВЗ) [1]. Сопоставляются основные свойства теоретического полюсного прилива согласно представленной модели и модели, рекомендованной МСВЗ. Движение земного полюса изучается на основе динамических уравнений Эйлера–Лиувилля с учетом вариаций коэффициентов геопотенциала, обусловленных приливными деформациями мантии Земли. Дан сравнительный анализ динамики движения земного полюса на чандлеровской частоте с учетом предложенной модели полюсного прилива и модели, рекомендованной МСВЗ.

2. Вариации центробежных моментов инерции деформируемой Земли. В работах [7, 8] был рассмотрен один из способов определения вариаций центробежных моментов инерции, вызванных полюсным приливом. Наряду с рассмотренным ранее подходом воспользуемся и другим способом. При тех же предположениях определим деформации вязкоупругого слоя осесимметричной Земли, возникающие при ее движении по инерции вокруг центра масс с помощью модального подхода [9, 10]. Модель Земли в грубом приближении представляет собой вязкоупругое твердое тело, состоящее из центральной части (ядра) и вязкоупругой мантии. При этом считается, что относительные перемещения точек подвижной среды на границе между ядром и мантией отсутствуют, а внешняя граница свободна. Вследствие предположения о малости деформаций мантии Земли будем рассматривать процесс деформирования в квазистатическом приближении.

Вектор упругого смещения задается в цилиндрических координатах, к которым делается переход от декартовых координат, связанных с твердой частью модели Земли (начало координат – центр масс Земли, ось x₃ направлена по ее оси симметрии, оси x₂ и x₁ в экваториальной плоскости, перпендикулярной оси x₃).

Вектор перемещения u представим в виде ряда по собственным формам упругих колебаний Земли:

где векторы ${{{\mathbf{V}}}_{{ki}}},{{{\mathbf{W}}}_{{ki}}}$ – собственные формы, а величины ${{q}_{{ki}}},{{p}_{{ki}}}$ – нормальные координаты. Собственные формы представляют собой ортономированный базис, то есть подчиняются условиям

Здесь символ Кронекера имеет индексы (ki)(lm). В цилиндрических координатах формы запишутся в виде [11]:

Здесь через ${{U}_{{km}}}(\rho ,z)$, ${{V}_{{km}}}(\rho ,z)$, ${{W}_{{km}}}(\rho ,z)$ обозначены коэффициенты в выражениях координат собственных форм, при этом очевидно, что вообще говоря ${{V}_{{km}}}(\rho ,z) \ne \left| {{{{\mathbf{V}}}_{{km}}}} \right|$, ${{W}_{{km}}}(\rho ,z) \ne \left| {{{{\mathbf{W}}}_{{km}}}} \right|$.

Вариации тензора инерции определим из уравнений деформаций, которые согласно [9, 10], можно представить в виде:

Здесь ${{\omega }_{1}},\;{{\omega }_{2}},\;{{\omega }_{3}}$ – компоненты вектора мгновенной угловой скорости вращения Земли; $\nu _{{im}}^{2}$ – квадрат частоты собственных колебаний, которая соответствует формам ${{{\mathbf{V}}}_{{im}}},{{{\mathbf{W}}}_{{im}}}$; постоянные коэффициенты ${{c}_{{0m11}}}$, ${{c}_{{0m33}}}$, ${{c}_{{1m13}}}$, ${{c}_{{2m11}}}$, ${{b}_{{1m12}}}$, ${{b}_{{1m32}}}$ определяются геометрией области Ω, то есть фигурой Земли; χ – безразмерный диссипативный коэффициент $\chi \ll 1$; b – положительная константа, такая что χb – время релаксации.

Уравнения (2.3) описывают квазистатические деформации Земли. Предполагается, что свободные колебания уже затухли вследствие вязкого трения. Поэтому в уравнениях опущены инерционные члены со вторыми производными по времени.

Модальные переменные ${{p}_{{km}}},{{q}_{{km}}}$ при k > 2 определяются однородными уравнениями вида (2.3), поэтому в квазистатическом приближении имеем

Решение системы уравнений (2.3) можно представить в виде ряда по степеням χ [11]:

В данной работе ограничимся первым приближением и решение системы (2.3) будем искать в виде:

ограничившись двумя первыми членами.

Используя приближенные выражения для нормальных координат

из (2.1) получим вектор перемещений u в виде разложения по собственным формам.

Тензор инерции Земли J = J[u] будет зависеть от вектора перемещений u. Без учета квадратичных членов по u, представим J в виде суммы постоянной и варьируемой частей:

где ${{J}_{1}}[{\mathbf{u}}]$ – линейная по u компонента тензора инерции деформированной Земли:

С учетом (2.4) запишем выражения для центробежных моментов инерции Земли:

Здесь через dx* обозначено интегрирование по области $\Omega {\kern 1pt} *$, представляющей собой область Ω, взятую после интегрирования по цилиндрической координате φ. Интегралы в выражениях (2.6) являются константами поскольку берутся по неизменной области. Обозначив (аналогично [5]):

центробежные моменты инерции (2.6) запишем в виде:

Наибольшими по величине будут J₁₃, J₂₃, которые, подставив формулы (2.4) в (2.7), можно представить в виде:

Коэффициенты в (2.8) определяются реологией мантии Земли. Вариации центробежных моментов инерции (2.8) идентичны выражениям, полученным в работе [8]. Учет центробежных моментов инерции (2.8) приводит к наличию малых диссипативных слагаемых в уравнениях движения земного полюса.

3. Оценка параметров модели полюсного прилива. Наибольшим по величине слагаемым из разложения геопотенциала $W$в ряд по сферическим гармоникам является слагаемое ${{W}_{2}}$ [2]:

где $P_{n}^{m}(\cos \theta )$ – присоединённые функции Лежандра; G – гравитационная постоянная; ${{m}_{E}}$, ${{R}_{E}}$ – масса и радиус Земли соответственно; $R$, $\theta $, $\lambda $ – сферические координаты некоторой точки пространства.

Коэффициенты зональной (при m = 0), тессеральной (при m = 1) и секториальной (при m = 2) гармоник в ${{W}_{2}}$ известным образом выражаются через осевые и центробежные моменты инерции Земли следующим образом [2]:

Зависимость коэффициентов тессеральной гармоники геопотенциала от координат земного полюса x_p, y_p определяется общепринятой моделью полюсного прилива [1]:

Изменение центробежных моментов инерции ${{\tilde {J}}_{{13}}}$, ${{\tilde {J}}_{{23}}}$, соответствующие этой модели, согласно (3.3) и (3.2), можно представить в виде:

где a, c – коэффициенты, характеризующие величину полюсного прилива и сдвиг его фазы, возникающий вследствие вязкости подвижной среды. Коэффициент c в (3.4) определяется диссипацией и значительно меньше коэффициента a. Из (3.3) следует, что $c{\text{/}}a = 0.0115$.

Выражения (3.4) отличаются от (2.8) диссипативными слагаемыми с коэффициентами b и c. Диссипативные слагаемые в (2.8) приводят к переменному сдвигу фазы полюсного прилива относительно положения полюса, в то время как соответствующие слагаемые из (3.4) приводят к постоянному сдвигу фазы, то есть к “запаздыванию” полюсного прилива на постоянный угол.

Рассмотрим различия выражений (2.8) и (3.4) более подробно. Компоненты ω₁, ω₂ вектора мгновенной угловой скорости согласно [12, 13] содержат две основные компоненты – чандлеровское колебание и годичное колебание:

Здесь a_ch, a_h – амплитуды чандлеровского и годичного колебаний соответственно, а ${{\alpha }_{{ch}}} = 2\pi Nt + \alpha _{{ch}}^{0}$, ${{\alpha }_{h}} = 2\pi t + \alpha _{h}^{0}$ – их фазы, которым соответствуют чандлеровская (N = 0.843 цикл/год) и годичная (1 цикл/год) частоты.

В уравнениях (3.5) движения полюса перейдем к полярным координатам (амплитуде движения полюса A и полярному углу ψ), используя замену ω₁ = Acosψ, ω₂ = Asinψ. Амплитуда результирующего движения полюса дается выражением [14]:

Как следует из (3.6) амплитуда полюсного прилива пропорциональна амплитуде колебаний полюса $\sqrt {{{{({{{\tilde {J}}}_{{13}}})}}^{2}} + {{{({{{\tilde {J}}}_{{23}}})}}^{2}}} = \sqrt {{{a}^{2}} + {{c}^{2}}} A$. Таким образом, фазы амплитуды полюсного прилива согласно (3.4) и амплитуды колебаний полюса A не зависят от времени, совпадают и равны $\alpha _{{ch}}^{0} - \alpha _{h}^{0}$. Из (3.3) следует, что сдвиг фазы полюсного прилива по отношению к положению полюса – около 0.65°. От сдвига фазы полюсного прилива зависят параметры возмущения с чандлеровской частотой, необходимого для поддержания наблюдаемого колебания. Кроме того, постоянный сдвиг фазы приводит к линейной системе дифференциальных уравнений движения земного полюса. Для вариаций центробежных моментов инерции, определяемых выражениями (2.8) сдвиг фазы окажется переменной величиной.

Теперь вычислим амплитуду полюсного прилива, описываемого выражениями (2.8):

Как следует из (3.7), фаза амплитуды полюсного прилива будет сдвинута по отношению к фазе амплитуды колебаний полюса.

Предположим, что наблюдаемый полюсный прилив описывается выражениями (2.8), а (3.4) является оптимальной в среднеквадратическом смысле аппроксимацией наблюдаемого полюсного прилива с известными параметрами a и c. Для сравнения установившихся режимов колебания полюса при различных моделях полюсного прилива (2.8) и (3.2) необходимо оценить коэффициент b. Для этого найдем наименьшее отклонение модели (2.8) от модели (3.4):

Используя (3.5) выражения (2.8) перепишем в следующем виде:

Введенный в (3.9) параметр ξ позволяет в условии (3.9) минимизацию по параметру b заменить минимизацией по параметру ξ.

Теперь неизвестный коэффициент b можно найти из соответствия коэффициентов при ω₂ в выражениях (3.8) и (3.4), которое приводит к равенству $c = b\pi \left( {(1 + \xi )N + 1 - \xi } \right)$. Величина σ после предельного перехода в (3.8) оказывается независимой от параметров t, T, а оптимальное значение $\xi {\kern 1pt} *$ будет найдено из (3.8). Тогда неизвестный коэффициент b найдем из уравнения $c = b\pi \left( {(1 + \xi {\kern 1pt} *)N + 1 - \xi {\kern 1pt} *} \right)$.

Подставляя в условие (3.8) выражения ${{J}_{{13}}}$, ${{J}_{{23}}}$ из (3.9) и ${{\tilde {J}}_{{13}}}$, ${{\tilde {J}}_{{23}}}$ из (3.4) с учетом $c = b\pi \left( {(1 + \xi )N + 1 - \xi } \right)$ функция $\sigma $ окажется квадратичной по параметру ξ, минимум которой достигается при ξ*. Как следует из расчетов $\xi {\kern 1pt} * = 0.18$. Теперь, приближенно можно определить отношение ${b \mathord{\left/ {\vphantom {b a}} \right. \kern-0em} a} \cong 0.002$, которое в пределах принятой точности определения коэффициентов из (3.3), выполняется и для ξ = 0. Используя это значение найдем из (3.7) сдвиг фазы амплитудной модуляции, который составляет примерно 18 часов.

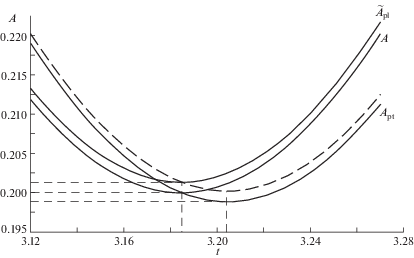
Для иллюстрации сдвига фазы амплитудной модуляции полюсного прилива приведем на рис. 1 сравнение графиков амплитуды A полюса, амплитуд A_pt, ${{\tilde {A}}_{{pt}}}$ полюсного прилива согласно моделям (2.8) и (3.4) соответственно (сплошные линии) и приближенной амплитуды (3.7) (пунктирная линия). По оси ординат на графике отложена обезразмеренная амплитуда, достигающая максимума при значении 2.2 и минимума при значении 0.2. По оси абсцисс отложено время в годах. На графике показано расхождение в фазе амплитудных модуляций в окрестности минимума амплитуды. Для улучшения наглядности на графиках рис. 1 отношение b/a было увеличено в 10 раз. Так как фазовый сдвиг приближенно пропорционален отношению b/a, что следует из выражения (3.7), то запаздывание амплитудной модуляции окажется увеличенным в 10 раз.

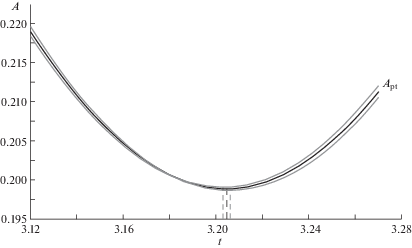
Сравнение амплитуд A_pt полюсного прилива модели (2.8) при различных параметрах ξ ($\xi = 1$, $\xi = 0$, $\xi = - 1$) показано на рис. 2 . Из рисунка видно, что среднее значение сдвига фазы амплитуды A_pt относительно амплитуды A колебаний полюса существенно больше отклонения фазы при изменении параметра $ - 1 \leqslant \xi \leqslant 1$. Если $\left| \xi \right| > 1$, то среднеквадратическое отклонение в (3.9) становится больше минимального более, чем в два раза и увеличивается по квадратичному закону при увеличении $\xi $.

Таким образом, отличие реального полюсного прилива от рекомендуемой модели (3.3) приведет к сдвигу амплитуды полюсного прилива.

4. Установившиеся чандлеровские колебания земного полюса. Рассмотрим как влияет выбор модели полюсного прилива на стационарный режим чандлеровских колебаний. Согласно [12, 13] модель движения полюса может быть получена из динамических уравнений Эйлера–Лиувилля с переменным тензором инерции

Здесь J – матрица переменного тензора инерции.

В первом приближении уравнения движения полюса представляются в виде [12]:

где $j_{{pr}}^{0}$, $j_{{qr}}^{0}$ определяются центробежными моментами инерции ${{J}_{{13}}}$, ${{J}_{{23}}}$ и им пропорциональны ($j_{{pr}}^{0}$, $j_{{qr}}^{0}$ являются диссипативными слагаемыми модели движения земного полюса), ${{\mu }_{x}}$, ${{\mu }_{y}}$ – внешнее возмущение, приводящее к наблюдаемому движению полюса с годичной и чандлеровской частотами, а ${{N}_{x}} \approx {{N}_{y}}$ – чандлеровская частота колебаний.

Рассмотрим вначале установившийся режим чандлеровских колебаний с учетом диссипативных слагаемых в $j_{{pr}}^{0}$, $j_{{qr}}^{0}$ вида (3.4) и при возмущении только с чандлеровской или близкой к ней частотами:

Положительные коэффициенты s₁, s₂ пропорциональны коэффициентам из (3.3), т.е. ${{s}_{2}}{\text{/}}{{s}_{1}} = c{\text{/}}a$. В такой постановке задачи ${{N}_{1}} = 2\pi N$ – наблюдаемая чандлеровская частота.

Перейдя к новым переменным

запишем амплитуду A и поправку в частоту $\Delta \psi $ в стационарном режиме при N₁ = N:

Так как определяемой из наблюдений является частота N₁, введем $\tilde {N} \cong {{N}_{x}} \approx {{N}_{y}}$. В предельном случае при устремлении N₁ к $\tilde {N} - {{s}_{1}}$ чувствительность амплитуды стационарного режима к коэффициенту s₂ будет возрастать и достигнет максимума.

Для приливных выступов вида (2.8)

стационарный режим чандлеровских колебаний не изменится при ${{s}_{2}} = \tilde {N}{{s}_{3}}$.

Теперь рассмотрим установившиеся чандлеровские колебания в более общем случае – при учете возмущений с близкой к чандлеровской N₁ и годичной ${{\nu }_{h}}$ частотами:

Приливные выступы вида $\begin{array}{*{20}{c}} {j_{{pr}}^{0} = {{s}_{1}}{{x}_{p}} - {{s}_{3}}{{{\dot {x}}}_{p}},}&{j_{{pr}}^{0} = - {{s}_{1}}{{y}_{p}} + {{s}_{3}}{{{\dot {y}}}_{p}}} \end{array}$ в уравнениях движения полюса (4.2) можно приближенно заменить выражениями

на интервале модуляции чандлеровской и годичной гармоник при соотношении на коэффициенты ${{\tilde {s}}_{3}}$ и ${{s}_{3}}$:

Из соотношений $c = b\pi \left( {(1 + \xi )N + 1 - \xi } \right)$ и ${{s}_{3}}{\text{/}}{{s}_{1}} = b{\text{/}}a$ при ξ = 0 коэффициент s₂ выражается через s₃:

Из (4.7) можно оценить коэффициент ${{\tilde {s}}_{3}}$:

Соотношение (4.9) показывает что, применение модели движения полюса в рамках общепринятой модели полюсного прилива может приводить к искажению параметров установившегося чандлеровского колебания. Например, если движение полюса находится интегрированием дифференциальных уравнений (4.2) по известной правой части. Причем амплитуда колебаний зависит не только от выбора модели полюсного прилива, но и от длительности интервала оценки коэффициента диссипативного слагаемого.

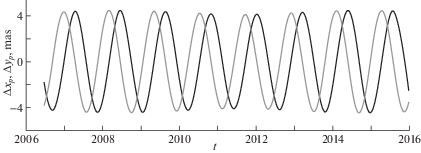
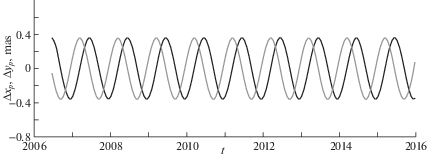
На рис. 3 приводится разность $\Delta {{x}_{p}}$, $\Delta {{y}_{p}}$ установившихся движений полюса, полученных в результате интегрирования уравнений (4.2) при учете выражений полюсного прилива (2.8) и (3.4). Величины μ_x, μ_y были найдены из уравнений (4.2), используя аппроксимацию данных наблюдений МСВЗ движения полюса с помощью выражений вида (3.5) на временном интервале с 2010 по 2017 гг. Из графика следует, что разности Δx_p, Δy_p обусловлены в основном различием в амплитудах чандлеровской компоненты решений. Если сделать замену $j_{{pr}}^{0} = {{s}_{1}}{{x}_{p}} - {{\tilde {s}}_{3}}{{y}_{p}},$ $j_{{qr}}^{0} = - {{s}_{1}}{{y}_{p}} - {{\tilde {s}}_{3}}{{x}_{p}}$ с учетом (4.9) вместо $j_{{pr}}^{0} = {{s}_{1}}{{x}_{p}} - {{s}_{3}}{{\dot {x}}_{p}},$ $j_{{qr}}^{0} = - {{s}_{1}}{{y}_{p}} + {{s}_{3}}{{\dot {y}}_{p}}$, то в разностях Δx_p, Δy_p останется только годичное колебание (рис. 4 ). Из-за того, что разность между чандлеровской и годичной частотами не мала, амплитуда годичного колебания в Δx_p, Δy_p оказывается малой. При этом, как показано на рис. 3 , амплитуда разности чандлеровского колебания двух моделей с учетом выражений полюсного прилива (2.8) и (3.4) достигает 10% по отношению к амплитуде наблюдаемого чандлеровского колебания, что является весьма существенным. В то время как невязка колебаний, вычисленных по моделям с учетом (4.5) и (4.6) содержит только годичную компоненту амплитуда которой не превышает 0.5% по отношению к амплитуде годичного колебания полюса. Таким образом, поправка в коэффициенте модели полюсного прилива (4.9) приводит к оптимальной аппроксимации чандлеровского колебания. Однако, как следует из рис. 1 и рис. 2 сдвиг амплитудной модуляции в этом случае учтен не будет и разность Δx_p, Δy_p, показанная на рис. 4 является следствием неучета сдвига амплитудной модуляции полюсного прилива.

Таким образом, если диссипативные слагаемые полюсного прилива определяются не положением полюса, а его скоростью, то оптимальная аппроксимация параметров полюсного прилива, описываемого общепринятой моделью, не приводит к оптимальной аппроксимации параметров установившегося колебания полюса.

5. Выводы. Показано, что для модели вязкоупругой Земли полюсный прилив зависит от координат полюса и от его скорости. Это приводит к сдвигу фазы (запаздыванию) амплитуды полюсного прилива относительно амплитуды колебаний полюса. Изменение структуры модели полюсного прилива в свою очередь влияет на оценку параметров установившегося чандлероского колебания, а ошибка определения амплитуды установившегося чандлеровского колебания может достигать 10%. То есть, аппроксимация параметров полюсного прилива, описываемого общепринятой моделью, не приводит к оптимальной аппроксимации параметров установившегося колебания полюса.

Корректировка установившегося чандлеровского колебания может быть выполнена изменением диссипативных слагаемых общепринятой модели полюсного прилива в уравнениях движения полюса. Однако, сдвиг амплитудной модуляции полюсного прилива в этом случае учтен не будет, что приведет к некоторому изменению амплитуды годичного колебания (на 0.5%).