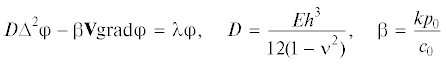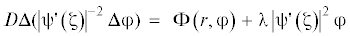Известия РАН. Механика твердого тела, 2022, № 1, стр. 153-156
ФЛАТТЕР ПЛАСТИНЫ СО СМЕШАННЫМИ КРАЕВЫМИ УСЛОВИЯМИ ПРОИЗВОЛЬНОЙ ФОРМЫ В ПЛАНЕ
a Институт проблем механики им. А.Ю. Ишлинского Российской Академии наук
Москва, Россия
* E-mail: algazinsd@mail.ru
Поступила в редакцию 16.07.2020
После доработки 24.07.2020
Принята к публикации 13.08.2020
- EDN: KBQBJX
- DOI: 10.31857/S0572329922010020
Аннотация
Методом математического моделирования исследуются флаттер пластины произвольной формы в плане. Для численного моделирования неустойчивых колебаний пластины предложен эффективный численный алгоритм без насыщения, который позволяет на редкой сетке получить приемлемую точность в приближенном решении. Стандартно критическая скорость флаттера ищется на двух сетках 9 × 15 и 15 × 31; критерием правильности расчета является близость полученных значений, возможно задать произвольную сетку. Произведены расчеты для эллиптической алюминиевой пластины для двух толщин h = 0.003 и h = 0.005 при разных направлениях вектора скорости потока. Совпадение расчетов на двух сетках удовлетворительное.
Введение. Наиболее распространенным в настоящее время методом решения задач механики деформируемого твердого тела является метод конечных элементов. Его недостатки общеизвестны: аппроксимируя перемещение кусочно-линейной функцией, мы получаем, что напряжения разрывные. Вместе с тем следует заметить, что большинство задач механики деформируемого твердого тела описывается уравнениями эллиптического типа, которые имеют гладкие решения. Представляется актуальным разработать алгоритмы, которые учитывали бы эту гладкость. Идея таких алгоритмов принадлежит К.И. Бабенко [1]. Эта идея высказана им в начале 70-х годов прошлого века. Многолетнее применение этой методики в эллиптических задачах на собственные значения автором настоящей работы доказало их высокую эффективность. В настоящей работе рассматривается флаттер пластины, обтекаемой, с одной стороны, потоком воздуха. Принятая математическая модель флаттера пластины построена А.А. Ильюшиным, И.А. Кийко [2]. Эффективный алгоритм решения задачи разработан автором и Кийко И.А. [3]. Основу программы составляет построение дискретного бигармонического оператора по методике [4]. Конформное отображение строится по программе Э.П. Казанджана [5]. Программный комплекс устроен таким образом, что если известны параметрические уравнения границы области, то возможно найти критическую скорость флаттера и построить соответствующую собственную форму. Стандартно критическая скорость флаттера ищется на двух сетках 9 × 15 и 15 × 31; критерием правильности расчета является близость полученных значений, возможно задать произвольную сетку.
1. Математическая постановка задачи. Исследование устойчивости колебаний тонкой пластины произвольной формы в плане, которая
в плоскости $x$, $y$ занимает область $G$ с границей $\partial G$ и обдувается потоком газа, приводит к спектральной задаче [2] для амплитудного значения прогибов 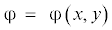 , $(x,y) \in G$.
, $(x,y) \in G$.
(1.2)
${{\left. {{\varphi }} \right|}_{{\partial G}}} = 0,\quad {{\left. {M{{\varphi }}} \right|}_{{\partial G}}} = 0$Здесь Е, ν – модуль Юнга и коэффициент Пуассона материала пластины, h – ее толщина, V = (Vx, Vy) – вектор скорости газа, р0, с0 – давление и скорость звука в невозмущенном потоке, k – показатель политропы газа.
Собственное число λ связано с частотой колебаний соотношением
в котором ρ – плотность материала пластины.Оператор М в (1.2) – это известный в теории пластин дифференциальный оператор, определяемый типом граничных условий. Методика решения спектральной задачи (1.1)–(1.3) описана для произвольного оператора М.
Колебания пластины будут устойчивыми или нет в зависимости от того, будет ли 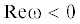 или ${\text{Re}}\omega > 0$; если ${{{{\lambda }}}_{1}} = {{{{\alpha }}}_{1}} + i{{{{\beta }}}_{1}}$ – наименьшее по модулю собственное значение, то вследствие (1.3) выписанным неравенствам
соответствуют $F\left( {{{{{\alpha }}}_{1}},{{{{\beta }}}_{1}}} \right) > 0$ или $F({{{{\alpha }}}_{1}},{{{{\beta }}}_{1}})$ < 0, где $F\left( {{{{{\alpha }}}_{1}},{{{{\beta }}}_{1}}} \right) = {{{{\alpha }}}_{1}}{{\beta }}_{1}^{2} - {{\rho }}h{{\beta }}_{1}^{2}$. Поскольку ${{{{\alpha }}}_{1}}{\text{\;}} = {\text{\;}}{{{{\alpha }}}_{1}}\left( V \right)$, ${{{{\beta }}}_{1}}{\text{\;}} = {\text{\;}}{{{{\beta }}}_{1}}\left( V \right)$ уравнение $F({{{{\alpha }}}_{1}},{{{{\beta }}}_{1}})$ = 0 определяет нейтральную кривую и соответствующую ей критическую скорость флаттера.
Речь идет, следовательно, о нахождении нулей функции $F({{{{\alpha }}}_{1}}(V),{{{{\beta }}}_{1}}(V))$ при заданном направлении вектора скорости потока.
или ${\text{Re}}\omega > 0$; если ${{{{\lambda }}}_{1}} = {{{{\alpha }}}_{1}} + i{{{{\beta }}}_{1}}$ – наименьшее по модулю собственное значение, то вследствие (1.3) выписанным неравенствам
соответствуют $F\left( {{{{{\alpha }}}_{1}},{{{{\beta }}}_{1}}} \right) > 0$ или $F({{{{\alpha }}}_{1}},{{{{\beta }}}_{1}})$ < 0, где $F\left( {{{{{\alpha }}}_{1}},{{{{\beta }}}_{1}}} \right) = {{{{\alpha }}}_{1}}{{\beta }}_{1}^{2} - {{\rho }}h{{\beta }}_{1}^{2}$. Поскольку ${{{{\alpha }}}_{1}}{\text{\;}} = {\text{\;}}{{{{\alpha }}}_{1}}\left( V \right)$, ${{{{\beta }}}_{1}}{\text{\;}} = {\text{\;}}{{{{\beta }}}_{1}}\left( V \right)$ уравнение $F({{{{\alpha }}}_{1}},{{{{\beta }}}_{1}})$ = 0 определяет нейтральную кривую и соответствующую ей критическую скорость флаттера.
Речь идет, следовательно, о нахождении нулей функции $F({{{{\alpha }}}_{1}}(V),{{{{\beta }}}_{1}}(V))$ при заданном направлении вектора скорости потока.
Обозначим через l характерный размер области G и введем безразмерные (со штрихами) координаты и параметры: $x = x{\kern 1pt} '{\kern 1pt} l$, $y = y{\kern 1pt} '$, $E = E{\kern 1pt} '{\kern 1pt} {{p}_{0}}$, $h = h{\kern 1pt} '{\kern 1pt} l$, ${{\rho }} = \frac{{{{\rho '}}{{p}_{0}}}}{{c_{0}^{2}}}$, ${{\omega }} = \frac{{{{\omega '}}{{c}_{0}}}}{l}$, V = $V{\kern 1pt} '{\kern 1pt} {{c}_{0}}$, ${{\varphi }} = {{\varphi '}}l$.
Подставив в (1.1), (1.3), убеждаемся, что в безразмерной форме система сохраняет свой вид, если параметр β заменить на безразмерный параметр k. В дальнейшем изложении штрихи будем опускать.
Введем вместо декартовых координат х, у криволинейные координаты r, θ по формулам $x{\text{\;}} = u~\left( {r,~{{\theta }}} \right)$, $y{\text{\;}} = {v}(r,~{{\theta }})$; если выполнены условия Коши–Римана
(1.4)
$\begin{gathered} ~~D\Delta ({{\left| {{{\psi '}}\left( {{\zeta }} \right)} \right|}^{{ - 2}}}\Delta {{\varphi }}) - k\left( {({{V}_{x}}{{u}_{r}} + {{V}_{y}}{{{v}}_{r}})\frac{{\partial {{\varphi }}}}{{\partial r}} + \frac{1}{r}({{V}_{y}}{{u}_{r}} - {{V}_{x}}{{{v}}_{r}})\frac{{\partial {{\varphi }}}}{{\partial {{\theta }}}}} \right) = {{\lambda }}{{\left| {{{\psi '}}\left( \zeta \right)} \right|}^{2}}{{\varphi }}~ \\ \left( {{{u}_{r}} = {\text{Re}}\left( {\frac{{{{\psi '}}\left( {{\zeta }} \right){{\zeta }}}}{r}} \right),{{{v}}_{r}} = {\text{Im}}\left( {\frac{{{{\psi '}}\left( {{\zeta }} \right){{\zeta }}}}{r}} \right)} \right) \\ \end{gathered} $Теперь очевидно, что дискретизации краевой задачи (1.5), (1.2) вполне аналогична описанной ранее [4] для бигармонического оператора.
2. Вычислительные эксперименты. Рассматриваются алгоритмы численного решения задачи (1.1) с краевыми условиями
(2.3)
${{\left. {\frac{{{{\partial }^{2}}u}}{{\partial {{n}^{2}}}} + \nu \left( {\frac{{{{\partial }^{2}}u}}{{\partial {{s}^{2}}}} + \gamma \frac{{\partial u}}{{\partial n}}} \right)} \right|}_{{\partial {{G}_{2}}}}} = 0$Здесь G – область в комплексной z – плоскости с достаточно гладкой границей $\partial G = \partial {{G}_{1}} \cup \partial {{G}_{2}}$ n – единичный вектор внешней нормали к ∂G; ∂/∂s – означает дифференцирование по длине дуги (длина отсчитывается против часовой стрелки); γ – кривизна ∂G; ν – постоянная (коэффициент Пуассона). Краевые условия (2.1) и (2.2) означают, что пластинка защемлена по краю, а краевые условия (2.1) и (2.3) означают свободное опирание по краю.
Для рассматриваемых смешанных краевых условий оператор M имеет разный вид для частей границ Gi, i = 1, 2. Возможность такой дискретизации проверяется ниже экспериментально.
Рассматривалась эллиптическая пластина с большой полуосью a = 1 и эксцентриситетом e = 0.7. Правая половина эллипса защемлена, а левая свободно оперта. Результаты расчетов представлены в таблице 1.
Таблица 1.
Результаты расчетов для эллиптической пластины
| (a = 1, e = 0.7); Al: ($E = 0.7 \times {{10}^{6}}$ кгс/см2, $\rho = 2.7 \times {{10}^{3}}$ кг/м3) | ||||
|---|---|---|---|---|
| θ | h = 0.003 | h = 0.005 | ||
| 9 × 15 | 15 × 31 | 9 × 15 | 15 × 31 | |
| 0 | 0.4255 (3) | 0.4454 (2) | 1.6984 (2) | 1.7925 (1) |
| π/8 | 0.4528 (2) | 0.4609 (2) | 1.5195 (1) | 1.5397 (1) |
| π/4 | 0.4259 (1) | 0.4199 (1) | 1.7138 (2) | 1.7989 (2) |
| 3π/8 | 0.3582 (1) | 0.3696 (1) | 1.9560 (2) | 1.9372 (2) |
| π/2 | 0.3346 (1) | 0.3438 (1) | 2.1710 (2) | 2.2268 (2) |
| 5π/8 | 0.3238 (1) | 0.3289 (1) | 2.2892 (2) | 2.2667 (2) |
| 3π/4 | 0.3117 (1) | 0.3113 (1) | 2.0261 (2) | 1.9760 (2) |
| 7π/8 | 0.2941 (1) | 0.2927 (1) | 2.2988 (2) | 2.9141 (2) |
| π | 0.2834 (1) | 0.2840 (1) | 2.5720 (2) | 2.6060 (2) |
| 9π/8 | 0.2892 (1) | 0.2900 (1) | 2.5415 (2) | 2.7088 (2) |
| 5π/4 | 0.3157 (1) | 0.3125 (1) | 2.4861 (2) | 2.0417 (2) |
| 11π/8 | 0.3704 (1) | 0.3517 (1) | 2.4607 (2) | 2.2631 (2) |
| 3π/2 | 0.4671 (1) | 0.4048 (1) | 2.6563 (2) | 2.3201 (2) |
| 13π/8 | 0.4369 (1) | 0.4676 (1) | 2.0075 (2) | 2.0203 (2) |
| 7π/4 | 0.4085 (3) | 0.4736 (2) | 1.5138 (5) | 1.8752 (1) |
| 15π/8 | 0.4042 (5) | 0.4474 (2) | 1.5576 (5) | 1.8221 (1) |
3. Выводы. Экспериментально проверено, что методика, разработанная в [6] для задач флаттера с однородными краевыми условиями, применима для смешанных краевых условий. Сравнение расчетов на двух сетках дает в большинстве случаев хорошее совпадение. Те случаи, когда совпадение плохое, выделены в таблице 1 полужирным шрифтом.
Благодарность. Работа выполнена по теме государственного задания ИПМех РАН № АААА-А20-120011690132-4.
Список литературы
Бабенко К.И. Основы численного анализа. М.: Наука, 1986. 744 с.; 2-е изд., испр. и доп. / Под ред. А.Д. Брюно. М.; Ижевск: РХД, 2002. 847 с.
Ильюшин А.А., Кийко И.А. Новая постановка задачи о флаттере пологой оболочки // ПММ. 1994. Т. 58. Вып. 3. С. 167–171.
Алгазин С.Д., Кийко И.А. Численно-аналитическое исследование флаттера пластины произвольной формы в плане // ПММ. 1997. Т. 61. Вып. 1. С. 171–174.
Алгазин С.Д. Численные алгоритмы классической матфизики. II. Спектральные задачи для бигармонического уравнения // Препр. ИПМех. М.: ИПМех, 2001. № 678. 27 с.
Казанджан Э.П. Об одном численном методе конформного отображения односвязных областей // Препр. ИПМ. М.: ИПМ, 1977. № 82. 59 с.
Алгазин С. Д., Кийко И. А. Флаттер пластин и оболочек. Издание 2-е, переработанное и дополненное. М.: “URSS”, 2016. 278 с.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика твердого тела