Известия РАН. Механика твердого тела, 2022, № 1, стр. 145-152
ВЫСОКОТОЧНАЯ ОЦЕНКА ПАРАМЕТРОВ КОЛЕБАНИЯ РЕЗОНАТОРА ВОЛНОВОГО ТВЕРДОТЕЛЬНОГО ГИРОСКОПА С ИСПОЛЬЗОВАНИЕМ МЕТОДОВ СТОХАСТИЧЕСКОЙ ФИЛЬТРАЦИИ
А. Б. Шаталов a, *, С. В. Соколов b, **, В. А. Погорелов c, ***, И. Н. Гашененко a, ****
a Российский университет дружбы народов, Институт инновационных инженерных технологий
Москва, Россия
b Московский технический университет связи и информатики
Москва, Россия
c Донской государственный технический университет
Ростов-на-Дону, Россия
* E-mail: shatalovab@yandex.ru
** E-mail: s.v.s.888@yandex.ru
*** E-mail: vadim.pogorelov.rnd@gmail.com
**** E-mail: gashenenko@mail.ru
Поступила в редакцию 10.04.2020
После доработки 12.08.2020
Принята к публикации 07.09.2020
- EDN: BXYYUX
- DOI: 10.31857/S057232992201010X
Аннотация
Для повышения точности работы волнового твердотельного гироскопа (ВТГ) построена стохастическая модель колебаний кромки резонатора и выходного сигнала чувствительного элемента (ЧЭ) ВТГ в форме “объект-наблюдатель”, учитывающая особенности динамики выходного сигнала ЧЭ и наличие широкополосных помех. Для оценки амплитуды колебаний резонатора предложено использование фильтра Калмана. Приведены результаты численного моделирования, иллюстрирующие эффективность использования предложенного метода.
Введение. Совершенствование технологий изготовления волновых твердотельных гироскопов (ВТГ) обеспечивает им все большее применение в навигационно-измерительных комплексах самого различного назначения [1–7]. Но, несмотря на резкое улучшение технических характеристик ВТГ за последние годы, их точность по-прежнему существенно уступает точности механических и лазерных гироскопов [8–11]. В связи с этим проблема повышения точности для ВТГ на сегодняшний день остается одной из основных. Ее решение осуществляется по многим направлениям, из которых следует выделить в качестве особо перспективного направление обработки выходной информации чувствительных элементов (ЧЭ) ВТГ (пьезоэлементов, оптических датчиков и др.), измеряющих амплитуду колебаний его резонатора с неизбежными и весьма интенсивными широкополосными помехами [12]. В настоящее время для фильтрации зашумленных измерений ЧЭ ВТГ применяется метод наименьших квадратов (МНК) [13]. Его основным недостатком является то, что данный метод не является алгоритмически инвариантным. Время его работы растет экспоненциально с увеличением входных данных, что существенно затрудняет его использование в алгоритмах обработки выходной информации ВТГ. Кроме того, оценки, получаемые с использованием МНК, будут точны только для небольшого интервала времени. В связи с этим возникает необходимость постоянного перерасчета уравнения регрессии по мере поступления новых измерений, осложняемого известными трудностями подбора уравнения регрессии при построении модели выходного сигнала ВТГ [14].
Подобная проблема обусловливает необходимость разработки новых методов обработки измерительной информации ВТГ, учитывающих особенности динамики выходного сигнала ВТГ и обеспечивающих заданную точность его оценки в условиях широкополосных интенсивных помех. Рассмотрим далее один из возможных вариантов решения данной проблемы.
1. Постановка задачи. Как показано в [15], динамика ВТГ может быть описана системой двух линейных обыкновенных нестационарных дифференциальных уравнений второго порядка, описывающих возбуждаемую моду (режим возбуждения) и измеряемую моду (режим чувствительности):
(1.1)
$\begin{gathered} {{{\ddot {x}}}_{1}} + 2\xi \omega {{{\dot {x}}}_{1}} + ({{\omega }^{2}} - {{\Omega }^{2}}){{x}_{1}} = {{f}_{1}} - 2K\Omega {{{\dot {x}}}_{2}} - K\dot {\Omega }{{x}_{2}} \\ {{{\ddot {x}}}_{2}} + 2\xi \omega {{{\dot {x}}}_{2}} + ({{\omega }^{2}} - {{\Omega }^{2}}){{x}_{2}} = {{f}_{2}} + 2K\Omega {{{\dot {x}}}_{1}} + K\dot {\Omega }{{x}_{1}} \\ \end{gathered} $При выполнении типичных для практики условий работы ВТГ [1, 2, 13, 15]:
– угловая скорость основания намного меньше собственной частоты резонатора $\Omega \ll \omega $;
– элементы возбуждения действуют только на координату х1, т.е. ${{f}_{2}} = 0$;
– угловая скорость основания постоянна $\dot {\Omega } = 0$;
– ускорение кромки резонатора, обусловленное действием элементов возбуждения, намного больше ускорения Кориолиса ${{f}_{1}} \gg 2K\Omega {{\dot {x}}_{2}}$;
уравнения (1.1) трансформируются в систему линейных стационарных уравнений
(1.2)
$\begin{gathered} {{{\ddot {x}}}_{1}} + \frac{\omega }{Q}{{{\dot {x}}}_{1}} + {{\omega }^{2}}{{x}_{1}} = {{f}_{1}} \\ {{{\ddot {x}}}_{2}} + \frac{\omega }{Q}{{{\dot {x}}}_{2}} + {{\omega }^{2}}{{x}_{2}} = 2K\Omega {{{\dot {x}}}_{1}} \\ \end{gathered} $При формировании возбуждения резонатора по гармоническому закону f1 = ${{f}_{0}}{\text{sin}}\nu t$, где ${{f}_{0}},\nu $ – амплитуда и частота ускорения, обусловленного действием элементов возбуждения, в установившемся режиме резонансной настройки решение первого уравнения системы (1.2) имеет вид [15]
где ${{x}_{{1r}}} = {{{{f}_{0}}Q} \mathord{\left/ {\vphantom {{{{f}_{0}}Q} {\omega \nu }}} \right. \kern-0em} {\omega \nu }}$, и, соответственно, уравнение движения кромки резонатора в режиме чувствительности может быть записано следующим образом:(1.3)
${{\ddot {x}}_{2}} + \frac{\omega }{Q}{{\dot {x}}_{2}} + {{\omega }^{2}}{{x}_{2}} = 2K\Omega {{\dot {x}}_{1}} = 2K\Omega {{x}_{{1r}}}\nu {\kern 1pt} {\kern 1pt} {\text{sin}}\nu t$Решением данного уравнения в установившемся режиме является временной сигнал, измеряемый чувствительными элементами ВТГ:
Соответственно, с выхода ЧЭ ВТГ (пьезоэлементов, оптических датчиков и др.) снимается измерительный сигнал, который с учетом неизбежных помех измерения W1 может быть записан следующим образом:
(1.4)
${{z}_{1}} = {{x}_{2}} + {{W}_{1}} = - 2K\Omega {{x}_{{1r}}}\frac{Q}{\nu }{\text{cos}}\nu t + {{W}_{1}}$Так как помехи измерения W1 обусловлены, как правило, значительным числом равномощных случайных факторов (вариациями температуры, случайными перегрузками, флуктуациями питания, конструктивными погрешностями ЧЭ и др.), то с целью сохранения общности последующих рассуждений полагаем далее помеху измерения W1 белым гауссовским шумом с нулевым средним и известной интенсивностью DW1.
В силу того, что измеряемый сигнал х2 является высокодинамичным, для его оценки по стохастическим измерениям (1.4) целесообразно использовать не традиционные методы статической обработки сигналов [14], а методы стохастической оценки динамических сигналов [18, 19]. Т.к. оцениваемый сигнал х2 описывается линейным дифференциальным уравнением второго порядка, то с точки зрения точности оценивания здесь наиболее эффективным оказывается линейный фильтр Калмана (ФК), обеспечивающий минимум среднеквадратической ошибки оценки. Но построение данного фильтра непосредственно с использованием уравнения (1.3), содержащего неизвестный параметр $\Omega $ в правой части, оказывается невозможным. В связи с этим возникает необходимость разработки нового подхода, обеспечивающего минимальную в среднеквадратическом ошибку оценки амплитуды колебания резонатора ВТГ х2 в условиях неизбежных помех измерения.
2. Решение задачи. Для решения задачи построения уравнений стохастической оценки сигнала х2 сформируем помимо сигнала х2 дополнительный сигнал х3, образованный сдвигом гармонического сигнала х2 на π/2 (например, за счет использования типовой фазосдвигающей цепи [20]):
который далее подвергается зашумленному измерению(2.1)
${{z}_{2}} = {{x}_{3}} + {{W}_{2}} = 2K\Omega {{x}_{{1r}}}\frac{Q}{\nu }{\text{sin}}\nu t + {{W}_{2}}$Из выражения сигнала измерения (2.1) может быть получено с точностью до постоянного множителя $\nu $ следующее представление правой части уравнения (1.3):
Подстановка полученного выражения в уравнение движения кромки резонатора в режиме чувствительности приводит к стохастическому дифференциальному уравнению, не содержащему параметрической неопределенности:
Для возможности дальнейшего использования методов стохастической фильтрации представим данное уравнение в векторной форме Ланжевена:
Выбирая в качестве сигнала наблюдения за координатой х2= х20 сигнал измерения z1, уравнение наблюдателя получаем в форме (1.4):
(2.2)
$\left| {\begin{array}{*{20}{c}} {{{{\hat {\dot {x}}}}_{{20}}}} \\ {{{{\hat {\dot {x}}}}_{{21}}}} \end{array}} \right| = A\left| {\begin{array}{*{20}{c}} {{{x}_{{20}}}} \\ {{{x}_{{21}}}} \end{array}} \right| + B + K\left( {{{z}_{1}} - {{{\hat {x}}}_{{20}}}} \right)$Выбор значения $M\left[ \Omega \right]$ осуществляется исходя из априорной информации о скорости вращения основания ВТГ: при нулевой скорости вращения основания значение $M\left[ \Omega \right]$ следует выбирать равным значению проекции скорости вращения Земли на ось чувствительности ВТГ.
Для увеличения наблюдаемости вектора ${{\left| {\begin{array}{*{20}{c}} {{{{\hat {x}}}_{{20}}}}&{{{{\hat {x}}}_{{21}}}} \end{array}} \right|}^{T}}$ можно использовать ранее полученное измерение сигнала х3:
которое с учетом выражения скорости кромки резонатора может быть преобразовано к измерению компоненты х21 масштабированием с коэффициентом $\nu $:В этом случае ФК, не изменяя размерности, приобретает вид
(2.3)
$K = R\left| {\begin{array}{*{20}{c}} {D_{{W1}}^{{ - 1}}}&0 \\ 0&{{{\nu }^{{ - 2}}}D_{{W2}}^{{ - 1}}} \end{array}} \right|$После процедуры оценки сигнала ${{\hat {x}}_{2}}$ вычисление значения Ω осуществляется традиционными способами [15]. Необходимо при этом отметить, что введение дополнительного наблюдения компоненты х21 хотя и увеличивает (незначительно) вычислительные затраты на реализацию ФК, но позволяет при этом существенно увеличить его сходимость, что проиллюстрировано в приведенном ниже примере.
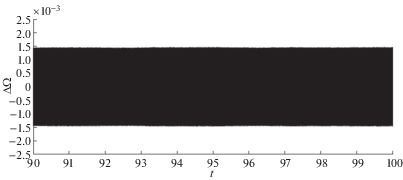
3. Имитационное моделирование. Численное моделирование работы ВТГ в режиме чувствительности осуществлялось на временном интервале [0, 1000] сек при следующих значениях параметров режима и самой конструкции: ${{f}_{0}} = 0.4$ м/с2, Q = 5000, $\omega = \nu = 4500$ Гц, K = 0.4. Интегрирование уравнения колебания кромки резонатора (1.3) осуществлялось с использованием метода Рунге–Кутты 4-го порядка с шагом 0.01 сек. Значения постоянной угловой скорости $\Omega $ выбирались в интервале [10–4, 1 ] рад/сек, помехи измерения W1, W2 моделировались центрированными гауссовскими случайными последовательностями с дисперсиями DW1= DW2 = (10–7 м)2. Оценка параметров движения кромки резонатора осуществлялась с использованием ФК (2.3). На рис. 1, 2 показаны изменения во времени ошибок оценивания амплитуды колебаний кромки резонатора фильтром (2.3) для значений скорости вращения основания: ${{\Omega }_{1}} = {{10}^{{ - 4}}}$ рад/сек, ${{\Omega }_{2}} = {{10}^{{ - 2}}}$ рад/сек, соответственно; на рис. 3, 4 – ошибки оценивания самой скорости вращения основания ${{\Omega }_{1}} = {{10}^{{ - 4}}}$ рад/сек на всем интервале моделирования (рис. 3) и в конце его (рис. 4); на рис. 5, 6 – ошибки оценивания скорости вращения основания ${{\Omega }_{2}} = {{10}^{{ - 2}}}$ рад/сек на всем интервале моделирования (рис. 5) и в конце его (рис. 6). Анализ результатов моделирования показывает высокую устойчивость процесса оценивания и существенное увеличение ее точности по сравнению с традиционным подходом – непосредственным определением угловой скорости по показаниям ЧЭ ВТГ. Так, при оценке ${{\Omega }_{1}} = {{10}^{{ - 4}}}$ рад/сек с использованием традиционного подхода ошибка имеет неустойчивый характер и достигает величины 2.8 × ${{10}^{{ - 4}}}$ рад/сек, а при оценке предложенным методом не превышает 2 × 10–5 рад/сек (рис. 4) (т.е. точнее, более чем в 10 раз). Аналогично, при оценке ${{\Omega }_{2}} = {{10}^{{ - 2}}}$ рад/сек с использованием традиционного подхода ошибка имеет также ярко выраженный неустойчивый характер и достигает величины 2 × 10–2 рад/сек, а при оценке предложенным методом не превышает 1.5 × 10–3 рад/сек (рис. 6) (т.е. также точнее на порядок).
Рис. 1.
Ошибка оценивания амплитуды колебаний кромки резонатора при ${{\Omega }_{1}} = {{10}^{{ - 4}}}$ рад/сек.
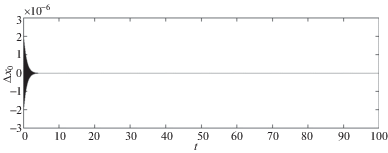
Рис. 2.
Ошибка оценивания амплитуды колебаний кромки резонатора при ${{\Omega }_{2}} = {{10}^{{ - 2}}}$ рад/сек.
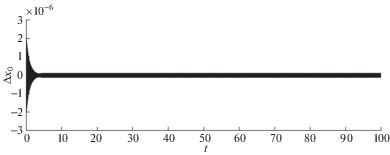
Рис. 3.
Ошибки оценивания скорости вращения основания на всем интервале моделирования при ${{\Omega }_{1}} = {{10}^{{ - 4}}}$ рад/сек.
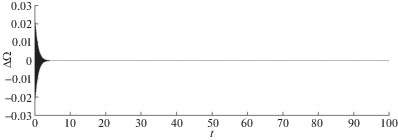
Рис. 4.
Ошибки оценивания скорости вращения основания в конце интервала моделирования при ${{\Omega }_{1}} = {{10}^{{ - 4}}}$ рад/сек.
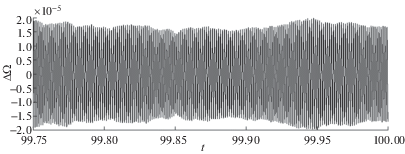
Рис. 5.
Ошибки оценивания скорости вращения основания на всем интервале моделирования при ${{\Omega }_{2}} = {{10}^{{ - 2}}}$ рад/сек.
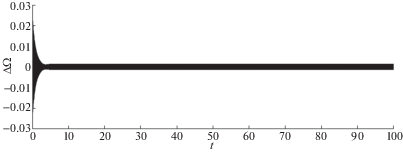
Рис. 6.
Ошибки оценивания скорости вращения основания на всем интервале моделирования при ${{\Omega }_{2}} = {{10}^{{ - 2}}}$ рад/сек.
Таким образом, результаты имитационного моделирования свидетельствуют о возможности эффективного практического применения предложенного подхода для увеличения точности обработки выходной информации ВТГ.
Заключение. В целом, построенная в работе стохастическая модель “ВТГ-ЧЭ” в форме “объект-наблюдатель”, разработанный подход к оценке ее вектора состояния и полученные результаты имитационного моделирования позволяют сделать вывод об устойчивости и высокой точности предложенного метода оценки амплитуды колебаний резонатора ВТГ. Разработанный метод может найти широкое применение при проектировании современных и перспективных ВТГ, функционирующих в условиях действия внутренних и внешних помех различной физической природы.
Список литературы
Делэйе Ф. Бортовая инерциальная система координат Spacenaute для европейской ракеты-носителя “Ариан-6” на основе волнового твердотельного гироскопа // Гироскопия и навигация. 2018. Т. 26. № 4 (103). С. 3–13.
Negri C., Labarre E., Lignon C., Brunstein E., Salaün E. A new generation of IRS with innovative architecture based on HRG for Satellite Launch Vehicle // Proceedings of the 22nd Saint Petersburg International Conference on Integrated Navigation Systems. Saint Petersburg, 2015. P. 298–306.
Джангжава Г.И., Бахонин К.А., Виноградов Г.М., Требухов А.В. Бесплатформенная инерциальная навигационная система на базе твердотельного волнового гироскопа // Сб. материалов XIV С.-Петербургской международной конференции по интегрированным навигационным системам. СПб., 2007. С. 116–125.
Delhaye, F. HRG by SAFRAN: The game-changing technology // 2018 IEEE International Symposium on Inertial Sensors and Systems (INERTIAL). 2018. P. 1–4. https://doi.org/10.1109/ISISS.2018.8358163
Современные информационные технологии в задачах навигации и наведения беспилотных маневренных летательных аппаратов / Под. ред. М.Н. Красильщикова, Г.Г. Себрякова. М.: Физматлит, 2009. 556 с.
Матвеев В.А., Лунин Б.С., Басараб М.А. Навигационные системы на волновых твердотельных гироскопах. М.: Физматлит, 2008. 240 с.
Розенберг И.Н., Соколов С.В., Уманский В.И., Погорелов В.А. Теоретические основы тесной интеграции инерциально-спутниковых навигационных систем. М.: Физматлит, 2018. 312 с.
Соколов С.В., Погорелов В.А. Стохастическая оценка, управление и идентификация в высокоточных навигационных системах. М.: Физматлит, 2016. 264 с.
Соколов С.В., Погорелов В.А. Основы синтеза многоструктурных бесплатформенных навигационных систем. М.: Физматлит, 2009. 190 с.
Аналитический обзор состояния исследований и разработок в области навигации за рубежом / Под. ред. Ривкин Б.С. СПб.: ГНЦ РФ АО “Концерн “ЦНИИ “Электроприбор”, 2017. 58 с.
Лукьянов Д.П., Распопов В.Я., Филатов Ю.В. Прикладная теория гироскопов. СПб.: ГНЦ РФ ОАО “Концерн “ЦНИИ “Электроприбор”, 2015. 316 с.
Джексон Р.Г. Новейшие датчики. М.: Техносфера, 2007. 384 с.
Распопов В.Я. и др. Волновой твердотельный гироскоп с металлическим резонатором / Под ред. Распопова В.Я. Тула: ТулГУ, 2018. 189 с.
Пугачев В.С., Синицын И.Н. Теория стохастических систем. М.: Логос, 2004. 1000 с.
Журавлев В.Ф., Климов Д.М. Волновой твердотельный гироскоп. М.: Наука, 1985. 126 с.
Журавлев В.Ф., Линч Д.Д. Электрическая модель волнового твердотельного гироскопа // Изв. РАН. МТТ. 1995. № 5. С. 12–24.
Трутнев Г.А. Модель твердотельного волнового гироскопа в медленных переменных // Вестник Удмуртского университета. 2015. Т. 25. Вып. 3. С. 421–429.
Синицын И.Н. Фильтры Калмана и Пугачева. М.: Логос, 2006. 640 с.
Соколов С.В., Ковалев С.М., Кучеренко П.А., Смирнов Ю.А. Методы идентификации нечетких и стохастических систем. М.: Физматлит, 2018. 432 с.
Харкевич А.А. Основы радиотехники. М.: Физматлит, 2007. 512 с.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика твердого тела


