Известия РАН. Механика твердого тела, 2022, № 2, стр. 135-153

1. Введение. При контактном взаимодействии твердых тел область фактического контакта, как правило, дискретна. Размеры и положение пятен фактического контакта зависят от условий контактного взаимодействия, механических характеристик тел и их поверхностной микроструктуры. Для описания дискретного (множественного) контакта твердых тел предложены различные математические модели, учитывающие параметры макро- и микрогеометрии реальных поверхностей и условия их контактного взаимодействия [1–4]. Большинство этих моделей основано на классической теории контактного взаимодействия деформируемых тел [5]. Подробный обзор современного состояния исследований в области механики дискретного контакта, включая основные подходы к постановке задач, методы аналитического и численного решения, конкретные результаты и области их практического использования, приведен в статье [6].

В настоящей работе рассматриваются задачи дискретного контакта упругой полуплоскости и жесткого штампа конечных размеров. На поверхности возможного контакта полуплоскости со штампом задаются условия одностороннего контакта, трение на площадках контакта отсутствует.

Краевые задачи для упругой полуплоскости являются классическими задачами теории упругости. Для их решения, как правило, применяются методы, основанные на использовании комплексных потенциалов [7]. При наличии в постановке задачи условий одностороннего контакта, содержащих неравенства, положение и размеры зон контакта заранее неизвестны, что значительно усложняет применение указанных методов.

Альтернативный подход к решению контактных задач теории упругости с односторонними связями состоит в применении вариационных методов [8, 9]. Вариационные формулировки контактных задач используются как для исследования проблемы существования, единственности и регулярности решения [10–12], так и для фактического построения численных решений [13, 14]. В результате дискретизации вариационных формулировок контактных задач с помощью методов конечных или граничных элементов получают задачи квадратичного программирования.

В настоящее время одними из наиболее эффективных вычислительных алгоритмов для решения контактных задач с односторонними связями при отсутствии трения считаются алгоритмы, разработанные на основе метода сопряженных градиентов (МСГ). Впервые алгоритм решения задач квадратичного программирования на основе МСГ был предложен в [15]. Идея алгоритма состояла в использовании стратегии рабочего списка активных ограничений-неравенств (активного набора) и применении МСГ для нахождения минимума на текущем рабочем подпространстве. Была доказана теоретическая сходимость алгоритма за конечное число шагов. При практическом использовании алгоритма оказалось, что скорость сходимости итерационного процесса существенно зависит от количества и вида ограничений. Поэтому впоследствии были предложены различные модификации базового алгоритма, адаптированные для решения конкретных классов прикладных задач. Описание и анализ алгоритмов на основе МСГ для решения контактных задач с односторонними связями можно найти, например, в работах [16, 17].

Один из наиболее популярных алгоритмов, приведенный в часто цитируемой статье [18], отличается от базового алгоритма [15] с учетом специфики множества ограничений решаемой задачи квадратичного программирования. При дискретизации граничной вариационной формулировки контактной задачи количество ограничений в виде неравенств (условий неположительности нормальных напряжений при одностороннем контакте) совпадает с количеством неизвестных. Поэтому в алгоритме [18] при нарушении неактивных ограничений применяется метод проекции точки на допустимое множество, позволяющий включать в рабочий список сразу несколько ограничений, что существенно снижает количество рестартов по сравнению с алгоритмом [15]. Для сокращения вычислительных затрат также допускается, в отличие от алгоритма [15], исключение ограничений из рабочего списка до нахождения минимума на текущем рабочем подпространстве.

Следует отметить, что алгоритм [18] имеет существенное ограничение. В нем учитывается только одно уравнение равновесия штампа (для сил) и, следовательно, только поступательное движение штампа. Это не позволяет использовать алгоритм для решения контактных задач при внецентренном нагружении штампа, когда необходимо учитывать его повороты. Кроме того, на каждом шаге итерационного процесса дважды выполняется операция умножения матрицы Гессе минимизируемой функции на вектор, при этом в алгоритме [15] эта операция выполняется лишь один раз. При изменении размерности рабочего подпространства рестарт алгоритма [18], как и алгоритма [15], производится с направления антиградиента, что замедляет их сходимость.

В настоящей работе на основе МСГ разработан новый алгоритм решения контактных задач с односторонними связями для упругой полуплоскости. Вводится линейное преобразование переменных, позволяющее свести ограничения в виде равенств, аппроксимирующие уравнения равновесия штампа и содержащие все переменные задачи, к простым ограничениям, содержащим только одну переменную. Такие ограничения несложно учесть в алгоритме МСГ. Этот прием позволяет рассматривать оба уравнения равновесия штампа и задавать значение момента внешних сил. В качестве направления рестарта в разработанном алгоритме используется редукция направления поиска с предыдущего шага на новое рабочее подпространство [19]. Однако, в отличие от работы [19], после рестарта для сохранения сопряженности направления поиска вычисляются по трехчленной формуле, предложенной в [20] для алгоритма с рестартами при безусловной минимизации неквадратичных функций. Отметим также, что в разработанном алгоритме операция умножения матрицы Гессе на вектор дважды выполняется только в случае уменьшения размерности рабочего подпространства.

2. Постановка задачи. Пусть в неподвижной прямоугольной системе координат $O{{x}_{1}}{{x}_{2}}$ невесомая однородная изотропная упругая полуплоскость занимает область Ω = = $\{ x = ({{x}_{1}},{{x}_{2}}) \in {{R}^{2}}:\;{{x}_{2}} \leqslant 0\} $ с границей $\Gamma $. Далее под $u(x),\;\varepsilon (x),\;\sigma (x)$ будем понимать соответственно вектор перемещений и тензоры деформаций и напряжений в точке $x \in \Omega $. Предполагается, что полуплоскость находится в условиях плоской деформации, деформации малы, а напряжения в недеформированном состоянии отсутствуют. Напряженно-деформированное состояние полуплоскости описывается системой уравнений:

где $def \equiv 1{\text{/}}2(grad + gra{{d}^{T}})$, $S$ – тензор модулей упругости.

В полуплоскость вдавливается гладкий жесткий штамп. Часть границы $\Gamma $, по которой возможен контакт полуплоскости со штампом, обозначается ${{\Gamma }_{p}}$. Положение и предельные размеры ${{\Gamma }_{p}}$, т.е. номинальная область контакта, задаются априори, исходя из геометрических соображений. Предполагается, что участок границы ${{\Gamma }_{p}}$ является конечным.

Форма основания штампа описывается функцией $\Phi {\kern 1pt} ({{x}_{1}})$, значение которой в точке $x \in {{\Gamma }_{p}}$ равно расстоянию от этой точки до поверхности штампа, измеренному вдоль направления внешней нормали к границе полуплоскости. Расстояние $\Phi {\kern 1pt} ({{x}_{1}})$ отсчитывается по отношению к недеформированному состоянию полуплоскости. Для определенности будем полагать $\mathop {min}\limits_{x \in {{\Gamma }_{p}}} \Phi {\kern 1pt} ({{x}_{1}}) = 0$. В задачах дискретного контакта функция $\Phi {\kern 1pt} ({{x}_{1}})$ является мультимодальной (многоэкстремальной). Положение штампа определяется вектором перемещений $\delta = ({{\delta }_{1}},{{\delta }_{2}})$ и углом поворота ${{\varphi }_{3}}$. Главный вектор $F = ({{F}_{1}},{{F}_{2}})$ и главный момент M₃ внешних сил, приложенных к штампу, считаются заданными. В качестве центра приведения выбирается точка ${{x}^{c}} = (x_{1}^{c},x_{2}^{c})$. Далее рассматривается задача нормального контакта полуплоскости со штампом, поэтому будем полагать ${{F}_{1}} = 0$ и ${{\delta }_{1}} = 0$.

Контактное взаимодействие упругой полуплоскости с жестким штампом описывается условиями одностороннего гладкого контакта:

Остальная часть границы полуплоскости свободна от внешних нагрузок:

Уравнения равновесия жесткого штампа имеют вид:

Отметим, что соотношения (2.4), по существу, представляют собой нелокальные граничные условия.

Для существования решения рассматриваемой контактной задачи далее будем предполагать, что внешние силы и моменты, приложенные к жесткому штампу, удовлетворяют следующим условиям:

– компонента главного вектора ${{F}_{2}}$ ограничена по абсолютной величине и ${{F}_{2}} < 0$;

– значения ${{F}_{2}}$ и M₃ согласованы между собой таким образом, что существует распределение нормальных напряжений ${{\sigma }_{{22}}}(x) \leqslant 0, x \in {{\Gamma }_{p}}$, удовлетворяющее уравнениям равновесия штампа (2.4).

Для выделения класса единственности решения в рассматриваемой контактной задаче, необходимо наложить дополнительные условия на поведение решения на бесконечности и на смещения полуплоскости как жесткого целого.

В монографии [7] рассмотрен случай, когда на бесконечности напряжения и вращение стремятся к нулю. Показано, что эти условия обеспечивают единственность поля напряжений. Если при этом отсутствуют массовые силы, а главный вектор внешних поверхностных усилий имеет ограниченную величину и отличен от нуля, то напряжения и соответствующие им перемещения имеют асимптотические представления

Перемещения $v = ({{{v}}_{1}},{{{v}}_{2}})$ полуплоскости как жесткого целого имеют вид:

где ${{\lambda }_{1}}$ и ${{\lambda }_{2}}$ – компоненты поступательного перемещения; $\omega $ – поворот полуплоскости как жесткого целого.

Значение перемещения ${{\lambda }_{1}}$ не влияет на условия нормального контакта полуплоскости со штампом, поэтому примем ${{\lambda }_{1}} = 0$. Для выполнения условий (2.5) положим $\omega = 0$. Значение ${{\lambda }_{2}}$ выбирается так, чтобы введенный далее оператор Пуанкаре–Стеклова был положительно-определенным.

Задача (в дифференциальной постановке) состоит в определении полей перемещений $u(x)$, деформаций $\varepsilon (x)$ и напряжений $\sigma (x)$, удовлетворяющих уравнениям (2.1), граничным условиям (2.2)–(2.3), уравнениям равновесия штампа (2.4), условиям на бесконечности (2.5) и дополнительным условиям на перемещения полуплоскости как жесткого целого (2.6). Подчеркнем, что фактические зоны контакта полуплоскости со штампом заранее неизвестны и подлежат определению в процессе решения задачи.

3. Функциональные пространства. Решение $u(x)$ задачи (2.1)–(2.6), принадлежащее классу функций ${{[{{C}^{2}}\left( \Omega \right)]}^{2}} \cap {{[{{C}^{1}}\left( {\bar {\Omega }} \right)]}^{2}}$, является классическим решением. Переход к вариационной формулировке задачи позволяет определить обобщенное решение. Введем необходимые функциональные пространства [21]. Учитывая условия (2.5), компоненты вектора перемещений ${{u}_{i}}(x),\;i = 1,2,$ будем рассматривать как элементы функционального пространства Соболева с весами [22]:

где $D'(\Omega )$ – пространство распределений на $\Omega $; ${{L}_{2}}(\Omega )$ – пространство (классов) функций с интегрируемым квадратом по области $\Omega $; $\rho (x) = {{(1 + {{\left| x \right|}^{2}})}^{{ - 1/2}}}{\text{/}}ln(2 + {{\left| x \right|}^{2}})$ – весовая функция.

Пространство ${{H}^{1}}(\Omega ;\rho )$ является гильбертовым со скалярным произведением

Введем далее пространство вектор-функций

Это пространство является гильбертовым со скалярным произведением

Можно показать, что при некоторых дополнительных предположениях относительно свойств гладкости функции $\Phi ({{x}_{1}})$, описывающей форму штампа, классическое решение $u(x)$ контактной задачи (2.1)–(2.6) принадлежит пространству ${{H}^{1}}(div;\Omega ;\rho )$.

Введем необходимые для построения граничной вариационной формулировки задачи пространства следов функций из ${{H}^{1}}(div;\Omega ;\rho )$.

Рассмотрим произвольную ограниченную подобласть $\Omega {\text{'}} \subset \Omega $ с границей $\Gamma '$ класса ${{C}^{{1,1}}}$, примыкающую к границе $\Gamma $ полуплоскости так, что

Известно [23, 24], что существуют линейные непрерывные операторы

определяющие для полей перемещений из ${{H}^{1}}(div;\Omega ') \equiv {{H}^{1}}(div;\Omega ';1)$ соответственно векторные функции перемещений и напряжений на $\Gamma '$. Кроме того, существует линейный непрерывный оператор такой, что для заданного $t \in {{[{{H}^{{ - 1{\text{/}}2}}}(\Gamma ')]}^{2}}$ можно построить функцию $v \in {{H}^{1}}(div;\Omega ')$, обладающую свойством $\gamma _{t}^{'}v = t$.

Введем пространство сужений на ${{\Gamma }_{p}}$ функций из ${{H}^{{1{\text{/}}2}}}(\Gamma ')$

и оснастим его нормой

Имеет место вложение пространств ${{H}^{{1{\text{/}}2}}}({{\Gamma }_{p}}) \subset {{L}_{2}}({{\Gamma }_{p}})$ [25]. Двойственным к пространству ${{H}^{{1{\text{/}}2}}}({{\Gamma }_{p}})$ является пространство ${{\tilde {H}}^{{ - 1{\text{/}}2}}}({{\Gamma }_{p}})$ – пополнение ${{L}_{2}}({{\Gamma }_{p}})$ по норме

т.е. отношение двойственности ${}_{{{{{\tilde {H}}}^{{ - 1{\text{/}}2}}}({{\Gamma }_{p}})}}{{\left\langle { \cdot , \cdot } \right\rangle }_{{{{H}^{{1{\text{/}}2}}}({{\Gamma }_{p}})}}}$ порождается продолжением стандартного скалярного произведения на ${{L}_{2}}({{\Gamma }_{p}})$ [25]. Для упрощения обозначений указанное отношение двойственности будем обозначать как $\left\langle { \cdot , \cdot } \right\rangle $, иные отношения двойственности далее не рассматриваются.

Имеет место плотное вложение пространств

Весовая функция $\rho (x)$ непрерывна и ограничена в ограниченной подобласти $\Omega {\kern 1pt} '\, \subset \,\Omega $, поэтому сужения функций из ${{H}^{1}}(div;\Omega ;\rho )$ на $\Omega '$ принадлежат пространству ${{H}^{1}}(div;\Omega ')$, для элементов которого определены операторы следа (3.2). Как следствие существуют линейные непрерывные операторы

Обратно, для любой функции $v \in {{H}^{1}}(div;\Omega ')$ существует функция $\tilde {v} \in {{H}^{1}}(div;\Omega ;\rho )$ такая, что $v$ является сужением ${\mathbf{\tilde {v}}}$ на $\Omega '$. Поэтому с учетом (3.3) существует линейный непрерывный оператор

такой, что для заданного $p \in {{\tilde {H}}^{{ - 1{\text{/}}2}}}({{\Gamma }_{p}})$ можно построить функцию $v \in {{H}^{1}}(div;\Omega ;\rho )$, обладающую свойством ${{\gamma }_{t}}{\kern 1pt} v = p$.

Можно показать, что при выполнении условия (3.1) введенные выше пространства ${{H}^{{1{\text{/}}2}}}({{\Gamma }_{p}})$ и ${{\tilde {H}}^{{ - 1{\text{/}}2}}}({{\Gamma }_{p}})$, а также операторы следа (3.5) и оператор (3.6) не зависят от выбора области $\Omega '$.

4. Интегральное представление решения. Решение контактной задачи (2.1)–(2.6) можно представить в виде [26]

где $g(x,{{\xi }_{1}})$ – поле перемещений, соответствующее решению задачи Фламана о действии сосредоточенной нормальной силы на границе упругой полуплоскости и вычисляемое с точностью до смещений полуплоскости как жесткого целого; $q \equiv {{\sigma }_{{22}}}$ – нормальные напряжения на ${{\Gamma }_{p}}$; $\lambda $ – поступательные перемещения полуплоскости как жесткого целого в соответствии с (2.6).

Из свойств решения задачи Фламана следует, что если $q \in {{L}_{2}}({{\Gamma }_{p}})$, то поле перемещений (4.1) удовлетворяет соотношениям (2.1), граничным условиям (2.3), условиям на бесконечности (2.5), а также учитывает поступательные перемещения полуплоскости как жесткого целого (2.6). Кроме того, оператор ${{G}_{f}}:q \mapsto u$, определяемый формулой (4.1), является непрерывным оператором из ${{L}_{2}}({{\Gamma }_{p}})$ в ${{H}^{1}}(div;\Omega ;\rho )$. Учитывая плотность вложения (3.4), оператор ${{G}_{f}}$ можно продолжить по непрерывности на ${{\tilde {H}}^{{ - 1{\text{/}}2}}}({{\Gamma }_{p}})$ и с учетом (3.6) рассматривать как оператор, действующий из ${{\tilde {H}}^{{ - 1/2}}}({{\Gamma }_{p}})$ в ${{H}^{1}}(div;\Omega ;\rho )$.

Таким образом, использование интегрального представления (4.1) в предположении, что $\Phi \in {{H}^{{1{\text{/}}2}}}({{\Gamma }_{p}})$, позволяет свести решение рассматриваемой контактной задачи к нахождению нормальных напряжений $q \in {{\tilde {H}}^{{ - 1{\text{/}}2}}}({{\Gamma }_{p}})$, удовлетворяющих следующей системе уравнений и неравенств:

Перемещения $u = {{G}_{f}}q$, соответствующие решению $q \in {{\tilde {H}}^{{ - 1/2}}}({{\Gamma }_{p}})$ системы (4.2)–(4.5), будем называть обобщенным решением контактной задачи (2.1)–(2.6).

5. Оператор Пуанкаре–Стеклова. Введем оператор Пуанкаре–Стеклова ${{G}_{{ps}}}\,:\,p\, \mapsto \,w$, отображающий посредством решения (4.1) нормальные напряжения $p({{x}_{1}}) \equiv {{\sigma }_{{22}}}({{x}_{1}},0)$ на части ${{\Gamma }_{p}}$ границы упругой полуплоскости в нормальные перемещения $w({{x}_{1}}) \equiv {{u}_{2}}({{x}_{1}}$, 0) на ${{\Gamma }_{p}}$. Из свойств решения задачи Фламана следует, что сужение функции $u(x)$, определяемой формулой (4.1), на область $\Omega '$ принадлежит пространству ${{H}^{1}}(div;\Omega ')$. Учитывая определения пространств ${{H}^{{1{\text{/}}2}}}({{\Gamma }_{p}})$ и ${{\tilde {H}}^{{ - 1{\text{/}}2}}}({{\Gamma }_{p}})$, а также существование операторов следа (3.2) и оператора (3.3), будем рассматривать ${{G}_{{ps}}}$ как оператор, действующий из ${{\tilde {H}}^{{ - 1{\text{/}}2}}}({{\Gamma }_{p}})$ в ${{H}^{{1{\text{/}}2}}}({{\Gamma }_{p}})$.

Соответствующий решению (4.1) оператор Пуанкаре–Стеклова ${{G}_{{ps}}}:p \mapsto w$ для $p \in {{L}_{2}}({{\Gamma }_{p}})$ имеет вид [26]:

где $D{\kern 1pt} * = 2(1 - {{\nu }^{2}}){\text{/}}(\pi E)$; $E$ и $\nu $ – модуль Юнга и коэффициент Пуассона материала полуплоскости.

Интегральный оператор (5.1) с логарифмическим ядром является непрерывным. Учитывая плотность вложения (3.4), продолжим оператор (5.1) по непрерывности на ${{\tilde {H}}^{{ - 1{\text{/}}2}}}({{\Gamma }_{p}})$.

Из формулы (5.1) следует, что оператор Пуанкаре–Стеклова ${{G}_{{ps}}}$ зависит от выбора параметра ${{\lambda }_{2}}$, определяемого из кинематических условий, задающих перемещения упругой полуплоскости как жесткого целого. Выберем значение параметра ${{\lambda }_{2}}$ таким образом, чтобы оператор ${{G}_{{ps}}}$ был положительно-определенным. С этой целью положим

где $L > 0$ – некоторая константа. Отметим, что интеграл в (5.2) равен равнодействующей внешней нагрузки.

Подставив (5.2) в (5.1), получим

Ядро интегрального представления (5.3) оператора Пуанкаре–Стеклова ${{G}_{{ps}}}:p \mapsto w$ является симметричным. Как указано в [27], интегральный оператор (5.3) будет положительно-определенным на ${{\tilde {H}}^{{ - 1{\text{/}}2}}}({{\Gamma }_{p}})$ тогда и только тогда, когда

где ${{C}_{l}}({\kern 1pt} {{\Gamma }_{p}})$ – логарифмическая емкость области ${\kern 1pt} {{\Gamma }_{p}}$.

Используя результаты расчетов, приведенные в [28], из условия (5.4) можно получить оценку

Произведем масштабирование (линейное отображение) области $\Omega \to \tilde {\Omega }$ таким образом, чтобы выполнялось условие

Тогда с учетом (5.5) в (5.3) можно положить

и использовать положительно-определенный оператор Пуанкаре–Стеклова ${{G}_{{ps}}}$ в виде:

Отметим, что условие (5.7) эквивалентно условию ${{\lambda }_{2}} = 0$.

6. Вариационная формулировка задачи. Для решения системы (4.2)–(4.5), содержащей уравнения и неравенства, используется вариационный подход [8–12]. Образуем множество статически допустимых нормальных напряжений на ${{\Gamma }_{p}}$

Нетрудно видеть, что множество $\Sigma $ является замкнутым выпуклым множеством в ${{\tilde {H}}^{{ - 1/2}}}({{\Gamma }_{p}})$. Кроме того, в соответствии со сделанными при постановке задачи предположениями это множество является непустым.

Пусть $q \in \Sigma $ – решение системы (4.2)–(4.5). Тогда для произвольного $p \in \Sigma $ получим следующую оценку

Из (6.2) следует, что искомые нормальные напряжения $q \in \Sigma $ удовлетворяют граничному вариационному неравенству

Отметим, что неравенство (6.3) не содержит неизвестных смещения ${{\delta }_{2}}$ и поворота ${{\varphi }_{3}}$ жесткого штампа. Как следует из вывода оценки (6.2), это является следствием того, что элементы множества статически допустимых нормальных напряжений $\Sigma $ удовлетворяют уравнениям равновесия штампа (4.5).

Используя известные приемы [8, 23], можно доказать обратное утверждение: решение $q$ вариационного неравенства (6.3) удовлетворяет системе уравнений и неравенств (4.2)–(4.5).

Учитывая, что оператор Пуанкаре–Стеклова ${{G}_{{ps}}}$ является положительно-определенным, а множество $\Sigma $ – непустым замкнутым выпуклым множеством в ${{\tilde {H}}^{{ - 1/2}}}({{\Gamma }_{p}})$, вариационное неравенство (6.3) эквивалентно задаче минимизации функционала: найти $q \in \Sigma $ такой, что

Кроме того, решение вариационного неравенства (6.3) и задачи минимизации (6.4) существует и единственно [8, 11, 12].

Отыскав нормальные напряжения $q \equiv {{\sigma }_{{22}}}$ на ${{\Gamma }_{p}}$ как решение задачи (6.4), можно определить напряженно-деформированное состояние всей полуплоскости при помощи приведенного в [26] интегрального представления решения (4.1), сужением которого на ${{\Gamma }_{p}}$ является (5.1).

7. Дискретизация задачи. Для дискретизации задачи (6.4) используется гранично-элементный подход [29–32]. Выберем тип граничных элементов и произведем разбиение границы ${{\Gamma }_{p}}$. Узлы сетки обозначим ${{s}_{n}},\;n \in {{I}_{N}} = \left\{ {1,2, \ldots ,N} \right\}$. Далее векторы из арифметического пространства ${{R}^{N}}$ и матрицы из пространства квадратных вещественных матриц ${{M}^{N}}$ размера N будем обозначать большими латинскими буквами, а их элементы – соответствующими малыми латинскими буквами.

В результате дискретизации получим задачу квадратичного программирования: найти вектор узловых нормальных напряжений $Q{\kern 1pt} * = (q{\kern 1pt} *({{s}_{1}}),q{\kern 1pt} *({{s}_{2}}), \ldots ,q{\kern 1pt} *({{s}_{N}})) \in V$ такой, что

где $A \in {{M}^{N}}$ – симметричная положительно определенная матрица податливости упругой полуплоскости $\Omega $, матрица Гессе минимизируемой функции $J(Q)$; $B \in {{R}^{N}}$ – вектор обобщенных узловых параметров, характеризующих форму штампа; $V \subset {{R}^{N}}$ – замкнутое выпуклое множество статически допустимых узловых нормальных напряжений.

Элементы матрицы $A$ и вектора $B$ вычисляются соответственно по формулам

где ${{\psi }_{i}}$ – базисная функция, соответствующая узлу s_i.

Следует отметить, что интегральное представление (5.3) оператора Пуанкаре–Стеклова ${{G}_{{ps}}}$ имеет разностное ядро. Вследствие этого при использовании для дискретизации области ${\kern 1pt} {{\Gamma }_{p}}$ равномерной гранично-элементной сетки матрица $A$ является теплицевой. Это позволяет существенно сократить затраты памяти на ее хранение. Достаточно хранить лишь одну строку матрицы $A$ и реализовать вычисление произведения матрицы на вектор программным путем.

Множество $V$ имеет вид

где

Выбор индексов ${{n}_{1}} \in {{I}_{N}}$ и ${{n}_{2}} \in {{I}_{N}}$ в общем случае произволен при условии, что в соответствующих узлах сетки нормальные напряжения отличны от нуля, т. е. выполняются неравенства $q_{n}^{*} < 0,\;n \in {{I}_{1}} = \left\{ {{{n}_{1}},{{n}_{2}}} \right\} \subset {{I}_{N}}$. При решении конкретной задачи такие узлы могут быть выбраны из априорных соображений. Корректность сделанного выбора проверяется путем апостериорного анализа полученного решения.

8. Преобразование переменных. Одна из сложностей, возникающих при численном решении задачи (7.1), состоит в наличии ограничений в виде равенств, содержащих все переменные задачи. Для упрощения вида ограничений выполним линейное преобразование переменных $Z = CQ$ такое, что

где коэффициенты ${{c}_{{ni}}}$ определяются по формулам (7.4).

Нетрудно видеть, что матрица C является невырожденной. Выражения для элементов матриц ${{C}^{{ - 1}}}$ и ${{C}^{{ - T}}}$ несложно получить в явном виде.

В результате преобразования переменных (8.1) получим следующую задачу квадратичного программирования: найти элемент $Z{\kern 1pt} * \in {{V}_{z}}$ такой, что

где

Задача (8.2) является задачей квадратичного программирования с простыми ограничениями. Нетрудно видеть, что матрицы $A$ и ${{A}_{z}}$ подобны, следовательно, матрица ${{A}_{z}}$ является симметричной положительно-определенной матрицей.

9. Метод сопряженных градиентов. Bведем необходимые для описания разработанного на основе МСГ алгоритма решения задачи (8.2) операторы и множества индексов. Пусть $X,Y,Z \in {{R}^{N}}$ и $I \subset {{I}_{N}}$. Определим оператор проектирования $X = PZ$ на множество V_z и оператор редукции $Y = R(Z,I)$ такие, что

Обозначим через $G(Z)$ градиент $grad{{J}_{z}}(Z) = {{A}_{z}}Z - {{B}_{z}}$. Введем следующие множества индексов:

Множество индексов ${{I}_{r}}(Z)$ определяет текущее рабочее подпространство, множество ${{I}_{a}}(Z)$ – рабочий список активных ограничений-неравенств, а множество ${{I}_{e}}(Z)$ используется при проверке условия увеличения размерности рабочего подпространства и условия остановки алгоритма.

Далее символом $\left\| {{\kern 1pt} \cdot {\kern 1pt} } \right\|$ будем обозначать норму вектора. При численной реализации алгоритма можно использовать одну из гельдеровских норм: ${{\left\| {{\kern 1pt} \cdot {\kern 1pt} } \right\|}_{1}}$, ${{\left\| {{\kern 1pt} \cdot {\kern 1pt} } \right\|}_{2}}$ или ${{\left\| {{\kern 1pt} \cdot {\kern 1pt} } \right\|}_{\infty }}$.

9.1. Инициализация алгоритма. Установим счетчик итераций $k = 0$. Далее векторы, переменные и множества индексов, соответствующие приближению ${{Z}^{k}}$, обозначаются верхним индексом k. В качестве начального приближения ${{Z}^{0}}$ выбирается проекция произвольной точки $Z \in {{R}^{N}}$ на множество ${{V}_{z}}$, т.е. ${{Z}^{0}} = PZ$. Далее вычисляется градиент ${{G}^{0}}$ и задаются направления поиска ${{D}^{0}} = - R({{G}^{0}},I_{r}^{0} \cup I_{e}^{0})$ и рестарта $E = 0$.

9.2. Вычисление следующего приближения. Аналогично методу проекции градиента следующее приближение вычисляется в два этапа. На первом этапе производится поиск в рабочем подпространстве:

где

На втором этапе производится проверка условия ${{Z}^{{k + 1/2}}} \in {{V}_{z}}$. Если это условие выполняется, то принимается ${{Z}^{{k + 1}}} = {{Z}^{{k + 1{\text{/}}2}}}$. В противном случае вычисляется проекция ${{Z}^{{k + 1}}} = P{{Z}^{{k + 1{\text{/}}2}}}$ на ${{V}_{z}}$, а индексы $n$, для которых $z_{n}^{{k + 1}} \ne z_{n}^{{k + 1{\text{/}}2}}$, включаются в рабочий список (множество) $I_{a}^{{k + 1}}$, тем самым уменьшается размерность рабочего подпространства.

9.3. Вычисление градиента. Если в точке ${{Z}^{{k + 1}}}$ не уменьшается размерность рабочего подпространства, т. е. ${{Z}^{{k + 1}}} = {{Z}^{{k + 1{\text{/}}2}}}$, то для вычисления градиента в этой точке можно использовать рекуррентную формулу

тем самым сокращая объем вычислений, т. к. матрично-векторное произведение ${{A}_{z}}{{D}^{k}}$ вычисляется ранее (см. формулу (9.1)).

9.4. Увеличение размерности рабочего подпространства. В качестве условия, при выполнении которого в точке ${{Z}^{k}}$ производится увеличение размерности рабочего подпространства, принимается условие

где $\eta > 0$ – заданный параметр алгоритма. Очевидно, что условие (9.2) может выполняться только в случае, если множество $I_{e}^{k}$ непустое. При выполнении условия (9.2) индексы, принадлежащие множеству $I_{e}^{k}$, исключаются из рабочего списка (множества) $I_{a}^{k}$, тем самым увеличивается размерность рабочего подпространства.

9.5. Вычисление направления поиска. Направление поиска ${{D}^{k}}$ в точке ${{Z}^{k}}$ вычисляется по трехчленной формуле, используемой в алгоритмах с рестартами при безусловной минимизации неквадратичных функций [20]:

где

9.6. Рестарты алгоритма. Если в точке ${{Z}^{k}}$ уменьшается размерность рабочего подпространства, т. е. ${{Z}^{k}} \ne {{Z}^{{k - 1{\text{/}}2}}}$, то перед вычислением направления поиска ${{D}^{k}}$ по формуле (9.3) производится редукция ${{D}^{{k - 1}}} \leftarrow R({{D}^{{k - 1}}},I_{r}^{k})$ и $E \leftarrow R(E,I_{r}^{k})$. Если же размерность рабочего подпространства увеличивается, т. е. выполняется условие (9.2), то в формулах (9.4) множество $I_{r}^{k}$ следует заменить на множество $I_{r}^{k} \cup I_{e}^{k}$.

Если точка ${{Z}^{{k - 1}}}$ была точкой рестарта, то перед вычислением в точке ${{Z}^{k}}$ направления поиска ${{D}^{k}}$ по формулам (9.3)–(9.4) следует последовательно выполнить присваивания $E \leftarrow {{D}^{{k - 1}}}$ и ${{D}^{{k - 1}}} \leftarrow 0$.

9.7. Условие остановки алгоритма. В качестве условия остановки алгоритма можно использовать одно из условий:

или где ${{\varepsilon }_{1}} > 0,\;{{\varepsilon }_{2}} > 0$ – параметры, определяющие погрешность приближенного решения.

Проверка этих условий не производится при рестартах или если $I_{e}^{k} \ne \emptyset $, т. е. если не для всех активных ограничений-неравенств выполняются необходимые условия минимума.

9.8. Определение нормальных напряжений. После нахождения решения $Z{\kern 1pt} *$ задачи (8.2) узловые нормальные напряжения вычисляются по формуле $Q{\kern 1pt} * = {{C}^{{ - 1}}}Z{\kern 1pt} *$.

9.9. Определение перемещения и поворота штампа. Можно показать, что перемещение и поворот штампа выражаются через компоненты градиента $G(Z{\text{*}})$ следующим образом:

10. Численные результаты. Разработанный вычислительный алгоритм реализован на языке FORTRAN 2008 в виде пакета модулей. Визуализация результатов расчетов производилась с помощью пакета научной графики Matplotlib.

Для дискретизации области ${\kern 1pt} {{\Gamma }_{p}}$ использовались равномерные сетки граничных элементов. Как отмечалось выше, в этом случае матрица A является теплицевой.

С целью проверки сходимости получаемых численных результатов вычисления проводились на нескольких сетках для двух типов граничных элементов – с постоянной и линейной аппроксимацией искомых нормальных напряжений.

Для верификации вычислительного алгоритма и разработанного программного обеспечения, а также выбора параметров гранично-элементных сеток использовалось решение [5] контактной задачи для штампа, форма основания которого описывалась функцией $\Phi ({{x}_{1}}) = x_{1}^{2}{\text{/}}(2R)$, где $R$ – радиус кривизны штампа.

Рассматривался также случай нагружения указанного штампа с эксцентриситетом относительно точки начального контакта ${{x}_{1}} = 0$. Несложно показать аналитически, что в этом случае распределение нормальных напряжений будет соответствовать решению [5], смещенному на величину эксцентриситета приложения нагрузки. Проведенные расчеты подтвердили этот вывод.

Далее приведен анализ результатов решения задач дискретного контакта, в которых область фактического контакта состояла из совокупности отдельных пятен контакта. Рассматривались задачи для гладких штампов с поверхностным рельефом, состоящим из $K$ микровыступов. Номинальная область контакта полагалась равной Γ_p = $\{ 0 \leqslant {{x}_{1}} \leqslant a$, x₂ = 0}, где $a < 4$. Форма основания штампов задавалась функцией

где ${{\Phi }_{1}}({{x}_{1}})$ – выпуклая функция, определяющая макроформу штампа; ${{\Phi }_{2}}({{\xi }_{1}})$ – строго выпуклая функция, характеризующая форму микровыступов; ${{\xi }_{1}} = \left\{ {K{{x}_{1}}{\text{/}}a} \right\}$ – “быстрая” координата, $\left\{ \cdot \right\}$ – дробная часть числа.

Для заданной пары функций ${{\Phi }_{1}}({{x}_{1}})$ и ${{\Phi }_{2}}({{\xi }_{1}})$ формула (10.1) определяет однопараметрическое семейство штампов ${{\Xi }_{K}}$, в качестве параметра которого выступает число микровыступов $K$ штампа. Два штампа, принадлежащие к одному семейству, имеют одинаковую макроформу, а их микровыступы являются подобными, при этом коэффициент подобия равен отношению чисел микровыступов штампов.

Нормальная компонента главного вектора (погонная сила) и главный момент внешних сил, приложенных к штампу, задавались в виде:

где $E{\kern 1pt} * = E{\text{/}}(1 - {{\nu }^{2}})$ – приведенный модуль упругости; $f > 0$ – безразмерный параметр; $e$ – безразмерный параметр, характеризующий эксцентриситет равнодействующей внешней нагрузки относительно центра приведения ${{x}^{c}} = (0.5\,a,0)$. При проведении расчетов значения параметров внешней нагрузки $f$ и $e$ выбирались таким образом, чтобы решение контактной задачи существовало и пятна контакта для отдельных микровыступов оставались изолированными друг от друга.

Расчеты выполнялись для следующего класса жестких штампов:

где ${{h}_{1}} \geqslant 0,{{h}_{2}} > 0,{{m}_{1}} > 1,{{m}_{2}} > 1$ – безразмерные параметры.

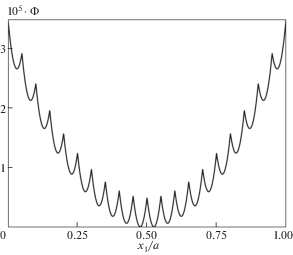
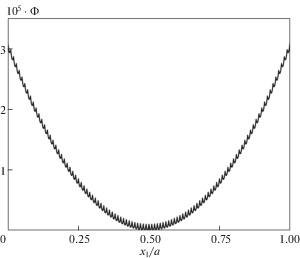
Из формул (10.1) и (10.3) следует, что однопараметрическое семейство штампов ${{\Xi }_{K}}$ определяется заданным набором параметров ${{h}_{1}},\,{{h}_{2}},\,{{m}_{1}},\,{{m}_{2}}$. Рассмотрим в качестве примера семейство штампов ${{\Xi }_{K}}$ при ${{h}_{1}} = 3 \times 1{{0}^{{ - 5}}}$, ${{h}_{2}} = 1{{0}^{{ - 4}}}$, ${{m}_{1}} = 2$, ${{m}_{2}} = 2$. На рис. 1–2 изображены профили штампов соответственно с 20 и 100 микровыступами. Следует отметить, что на обоих рисунках масштабы изображения по вертикальной и горизонтальной осям отличаются на пять порядков.

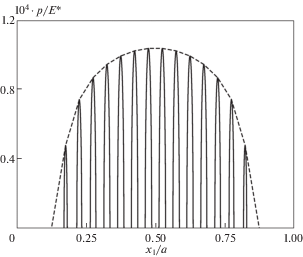
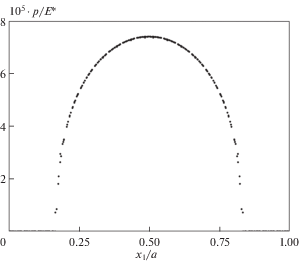
На рис. 3 приведено распределение контактного давления $p \equiv - {{\sigma }_{{22}}}$ на ${{\Gamma }_{p}}$ для штампа рассматриваемого семейства ${{\Xi }_{K}}$ при $K = 20$. Параметры внешней нагрузки в (10.2) полагались следующими: $f = 2 \times 1{{0}^{{ - 5}}}$ и $e = 0$. Сплошная кривая представляет собой график контактного давления, а пунктирная кривая соединяет локальные максимумы контактного давления на отдельных пятнах контакта. Далее такие кривые будем называть огибающими контактного давления.

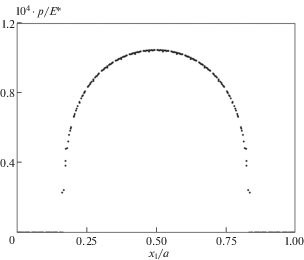
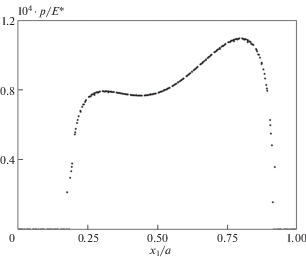
На рис. 4 приведено множество точек, соответствующих локальным максимумам контактного давления на отдельных пятнах контакта сразу для пяти штампов рассматриваемого семейства ${{\Xi }_{K}}$, имеющих 20, 40, 60, 80 и 100 микровыступов. Параметры внешней нагрузки для всех штампов были одинаковыми и равными приведенным выше. Нетрудно видеть, что в этом случае существует единая для всего указанного набора штампов огибающая контактного давления.

В результате обработки численных результатов для класса жестких штампов, форма основания которых задается формулами (10.1) и (10.3), установлена следующая закономерность: для однопараметрического семейства штампов ${{\Xi }_{K}}$ существует единая огибающая контактного давления, положение которой определяется параметрами f и $e$ внешней нагрузки.

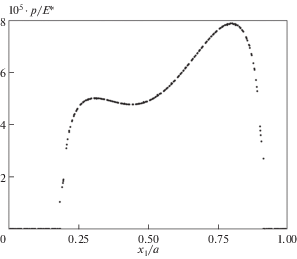
В качестве примера на рис. 5–7 приведены множества точек, аналогичные множеству точек на рис. 4, при следующих значениях параметров: рис. 5 – ${{m}_{1}} = 2$, ${{m}_{2}} = 4$ и $e = 0$; рис. 6 – ${{m}_{1}} = 4$, ${{m}_{2}} = 2$ и $e = 0.1$; рис. 7 – ${{m}_{1}} = 4$, ${{m}_{2}} = 4$ и $e = 0.1$. Значения параметров f, ${{h}_{1}}$ и ${{h}_{2}}$ принимались такими же, как для рис. 5. Несимметричные относительно центра приведения x^c множества точек на рис. 6–7 соответствуют случаям внецентренного нагружения штампа ($e = 0.1$).

Отметим также, что для каждого из рассмотренных выше однопараметрических семейств штампов Ξ_K при изменении числа микровыступов в диапазоне от 10 до 200 изменение площади фактического контакта не превышало 2.8%, а изменение перемещения штампа δ₂ – 2.4%.

Для оценки вычислительной эффективности разработанного алгоритма укажем использованные значения его параметров. При построении гранично-элементных сеток подобласть, соответствующая одному микровыступу, разбивалась на 100 граничных элементов, т. е. общее количество граничных элементов на Γ_p составляло $100 \cdot K$. В условии (9.2) полагалось $\eta $ = 10^–8. Вычисления проводились с двойной точностью до выполнения условия (9.5) для нормы || · ||₁ и параметра ε₁ = 10^–8. Учитывая немонотонную сходимость МСГ, выполнение условия (9.5) проверялось на 5 последовательных итерациях при сохранении рабочего подпространства.

В качестве метрик вычислительной эффективности алгоритма использовались средние значения ${{\bar {\mu }}_{i}}$ и ${{\bar {\mu }}_{m}}$ отношений

где $N$ – число неизвестных задачи квадратичного программирования (8.2); ${{n}_{i}}$ – требуемое число итераций; ${{n}_{m}}$ – число умножений матрицы Гессе ${{A}_{z}}$ на вектор. Усреднение проводилось для одинаковых значений параметра $N$ по всем проведенным расчетам для штампов разной формы и различных условий их нагружения.

В результате вычислительных экспериментов установлено, что значения ${{\bar {\mu }}_{i}}$ и ${{\bar {\mu }}_{m}}$ с ростом числа неизвестных N уменьшаются: для $N = 1000$ они равны ${{\bar {\mu }}_{i}} = 0.1121$ и ${{\bar {\mu }}_{m}} = 0.1401$, для $N = 5000$ – ${{\bar {\mu }}_{i}} = 0.0567$ и ${{\bar {\mu }}_{m}} = 0.0775$, для $N = 10000$ – ${{\bar {\mu }}_{i}} = 0.0366$ и ${{\bar {\mu }}_{m}} = 0.0506$, для $N = 20000$ – ${{\bar {\mu }}_{i}} = 0.0278$ и ${{\bar {\mu }}_{m}} = 0.0409$. Отметим, что приведенные данные о вычислительных затратах существенно меньше теоретических оценок, полученных для алгоритма [15].

11. Заключение. Для решения задач дискретного контакта упругой полуплоскости и жесткого штампа с заранее неизвестными площадками фактического контакта в настоящей работе применялся вариационный подход. Получена вариационная формулировка задач в виде граничного вариационного неравенства с использованием оператора Пуанкаре–Стеклова для упругой полуплоскости. Построено интегральное представление этого оператора и указаны условия его положительной определенности. Приведена эквивалентная вариационному неравенству задача минимизации, для дискретизации которой использован гранично-элементный подход. В результате получена задача квадратичного программирования с ограничениями в виде равенств и неравенств. Матрица Гессе минимизируемой функции является теплицевой, что позволяет существенно сократить затраты памяти на ее хранение. Предложено линейное преобразование переменных, позволяющее упростить вид ограничений-равенств, содержащих все переменные задачи.

Для численного решения полученной задачи квадратичного программирования с простыми ограничениями на основе МСГ разработан новый вычислительный алгоритм, учитывающий специфику множества ограничений решаемой задачи. Проведенные вычислительные эксперименты подтвердили эффективность применения разработанного алгоритма для решения рассматриваемого класса задач дискретного контакта. В отличие от известного алгоритма [18], разработанный алгоритм позволяет получать решения контактных задач для случаев внецентренного нагружения штампа, когда необходимо учитывать повороты штампа.

Построены однопараметрические семейства штампов с поверхностным рельефом, в качестве параметра которых выступает число микровыступов. Штампы, принадлежащие к одному семейству, имеют одинаковую макроформу, а их микровыступы являются подобными, при этом коэффициент подобия равен отношению чисел микровыступов штампов. В результате вычислительных экспериментов установлено существование для однопараметрического семейства штампов единой огибающей контактного давления – кривой, проходящей через локальные максимумы контактного давления на отдельных пятнах контакта. Положение огибающей контактного давления для семейства штампов зависит от параметров внешней нагрузки. Представляет интерес обобщить полученную закономерность для пространственных задач дискретного контакта упругого полупространства с жесткими штампами.