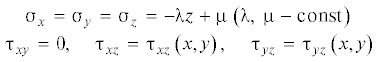Известия РАН. Механика твердого тела, 2022, № 2, стр. 82-89

К ВОПРОСУ О КРУЧЕНИИ СТЕРЖНЕЙ ИЗ УПРОЧНЯЮЩЕГОСЯ МАТЕРИАЛА, НАХОДЯЩИХСЯ ПОД ДЕЙСТВИЕМ ПЕРЕМЕННОГО ВНЕШНЕГО ДАВЛЕНИЯ, ПРИ ЛИНЕАРИЗОВАННОМ УСЛОВИИ ПЛАСТИЧНОСТИ

Б. Г. Миронов^a, *, Ю. Б. Миронов^b, **

^a Российский университет транспорта
Москва, Россия

^b Московский технический университет связи и информатики
Москва, Россия

^* E-mail: mbg.chspu@yandex.ru
^** E-mail: i.b.mironov@mtuci.ru

Поступила в редакцию 22.10.2021
После доработки 24.10.2021
Принята к публикации 25.10.2021

EDN: YUFAUS
DOI: 10.31857/S0572329922020143

Полный текст (PDF)

Аннотация

В работе исследовано кручение стержней из анизотропно упрочняющегося жесткопластического материала при линеаризованном условии пластичности. Предполагается, что стержень находится под действием внешнего давления, линейно меняющегося вдоль образующей. Определены напряженное и деформированное состояния стержня. Найдены линии разрыва напряжений.

Ключевые слова: пластичность, неоднородность, упрочнение, кручение, анизотропия, деформация, напряжение

Кручение является одним из распространенных видов деформации тел. Оно довольно часто встречается в инженерной практике. Теории кручения стержней из идеального жесткопластического материала посвящены многочисленные работы, в частности кручение изотропных и анизотропных стержней изложено в [1–3]. Работы [5, 6] и [8, 9] посвящены исследованию кручения неоднородных стержней из идеального жесткопластического материала. Кручение стержней из упрочняющегося материала приводит к определенным сложностям. В этом случае, задача не является статически определимой. Возникают трудности с точной постановкой задачи. Требует совместного рассмотрения поля напряжений и деформаций. Отдельные случаи в линеаризованной постановке рассмотрены в [4]. В [7] исследовано кручение стержней из анизотропного жесткопластического материала, находящегося под действием давления, меняющегося вдоль образующей.

Напряженно-деформированное состояние стержней из анизотропно упрочняющегося материала, находящихся под действием внешнего давления, линейно меняющегося вдоль образующей стержня, при кручении определяются из соотношений:

(1)

– уравнение равновесия

(2)

$\frac{{\partial {{{{\tau }}}_{{{\text{xz}}}}}}}{{\partial x}} + \frac{{\partial {{{{\tau }}}_{{yz}}}}}{{\partial y}} = {{\lambda }}$

– условие текучести

(3)

${{({{{{\tau }}}_{{xz}}} - c{{e}_{{xz}}})}^{2}} + {{({{{{\tau }}}_{{yz}}} - c{{e}_{{yz}}})}^{2}} = {{k}^{2}}~~\left( {k - {\text{const}}} \right)$

– соотношения ассоциированного закона течения

(4)

$\frac{{d{{e}_{{xz}}}}}{{{{{{\tau }}}_{{xz}}} - c{{e}_{{xz}}}}} = \frac{{d{{e}_{{yz}}}}}{{{{{{\tau }}}_{{yz}}} - c{{e}_{{yz}}}}},\quad {{e}_{x}} = {{e}_{y}} = {{e}_{z}} = {{e}_{{xy}}} = 0,$

где ${{e}_{{ij}}}$ – компоненты деформации, ${{{{\sigma }}}_{{ij}}}$ – компоненты напряжения, k – предел текучести.

Предполагается, что упрочнение линейное ($c - {\text{const}}$).

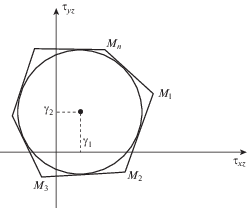
В плоскости ${{{{\tau }}}_{{xz}}},~{{{{\tau }}}_{{yz}}}$ уравнение (3) определяет окружность радиуса k (рис. 1) с центром в точке с координатами ${{{{\gamma }}}_{1}} = c{{e}_{{xz}}},~~{{{{\gamma }}}_{2}} = c{{e}_{{yz}}}.$

Рис. 1.

Линеаризованное условие пластичности.

Заменим условие текучести (3) уравнениями

(5)

${{A}_{i}}({{{{\tau }}}_{{xz}}} - c{{e}_{{xz}}}) + {{B}_{i}}({{{{\tau }}}_{{yz}}} - c{{e}_{{yz}}}) = k$

где ${{A}_{i}},~{{B}_{i}} - {\text{const}},~~{{A}_{i}}^{2} + {{B}_{i}}^{2} = 1,~~i = $ 1, 2, …, n.

Уравнения (5) на плоскости ${{{{\tau }}}_{{xz}}},~{{{{\tau }}}_{{yz}}}$ представляет собой замкнутую ломанную ${{{\text{M}}}_{1}}{{{\text{M}}}_{2}}{{{\text{M}}}_{3}} \ldots {{{\text{M}}}_{{\text{n}}}}{{{\text{M}}}_{1}}$ (рис. 1) и являются линеаризованными соотношениями условия (3). Рассмотрим (5) в качестве пластического потенциала. Тогда вместо (4) имеем соотношения

(6)

$\frac{{d{{e}_{{xz}}}}}{{{{A}_{i}}}} = \frac{{d{{e}_{{yz}}}}}{{{{B}_{i}}}}$

В начальный момент закручивания компоненты деформации ${{e}_{{ij}}}$ равны 0. Тогда из соотношений (6) и части соотношений (4) следует

(7)

$\frac{{{{e}_{{xz}}}}}{{{{A}_{i}}}} = \frac{{{{e}_{{yz}}}}}{{{{B}_{i}}}},\quad {{e}_{x}} = {{e}_{y}} = {{e}_{z}} = {{e}_{{xy}}} = 0$

Из соотношений (7) имеем

(8)

${{B}_{i}}{{e}_{{xz}}} - {{A}_{i}}{{e}_{{yz}}} = 0$

Учитывая, что компоненты перемещения $u,{v},w$ имеют вид

(9)

$u = {{\theta }}yz,\quad {v} = - {{\theta }}xz,\quad w = w\left( {x,y} \right),$

где w – депланация, θ – крутка, соотношения связи между компонентами деформации и компонентами перемещения запишем в виде

(10)

${{e}_{{xz}}} = \frac{1}{2}\left( {\frac{{\partial w}}{{\partial x}} + {{\theta }}y} \right),~\quad {{e}_{{yz}}} = \frac{1}{2}\left( {\frac{{\partial w}}{{\partial y}} - {{\theta }}x} \right)$

Из (10) получим

(11)

$\frac{{\partial {{e}_{{xz}}}}}{{\partial y}} - \frac{{\partial {{e}_{{yz}}}}}{{\partial x}} = {{\theta }}$

Согласно (8) из (11) получим

(12)

$ - {{B}_{i}}\frac{{\partial {{e}_{{xz}}}}}{{\partial x}} + {{A}_{i}}\frac{{\partial {{e}_{{xz}}}}}{{\partial y}} = {{A}_{i}}{{\theta }}$

или

(13)

$ - {{B}_{i}}\frac{{\partial {{e}_{{yz}}}}}{{\partial x}} + {{A}_{i}}\frac{{\partial {{e}_{{yz}}}}}{{\partial y}} = {{B}_{i}}{{\theta }}$

Характеристиками соотношений (12) и (13) являются прямые

(14)

${{A}_{i}}x + {{B}_{i}}y + {{C}_{i}} = 0$

Вдоль характеристик (14) имеют место интегралы соответственно соотношений (12) и (13)

(15)

$ - {{B}_{i}}{{e}_{{xz}}} = {{A}_{i}}{{\theta }}x + {{{{\alpha }}}_{{1i}}}\quad {\text{или}}\quad {{e}_{{xz}}} = {{\theta }}y + {{{{\alpha }}}_{{2i}}}$

(16)

${{e}_{{yz}}} = - {{\theta }}x + {{{{\beta }}}_{{1i}}}\quad {\text{или}}\quad {{A}_{i}}{{e}_{{yz}}} = {{B}_{i}}{{\theta }}y + {{{{\beta }}}_{{2i}}}$

${{{{\alpha }}}_{{1i}}} = {{A}_{i}}{{{{\beta }}}_{{1i}}},\quad {{{{\alpha }}}_{{1i}}} = {{\theta }}{{C}_{i}} - {{B}_{i}}{{{{\alpha }}}_{{2i}}},\quad {{{{\beta }}}_{{2i}}} = {{B}_{i}}{{{{\alpha }}}_{{2i}}},\quad {{{{\beta }}}_{{2i}}} = {{\theta }}{{C}_{i}} + A{{{{\beta }}}_{{1i}}}$

Из соотношений (3) следует

(17)

${{A}_{i}}{{{{\tau }}}_{{xz}}} + {{B}_{i}}{{{{\tau }}}_{{yz}}} = k + c({{A}_{i}}{{e}_{{xz}}} + {{B}_{i}}{{e}_{{yz}}})$

Уравнению равновесия (2) удовлетворим, полагая

(18)

${{{{\tau }}}_{{xz}}} = \frac{{\partial U}}{{\partial y}} + \frac{{{\lambda }}}{2}x,~\quad {{{{\tau }}}_{{yz}}} = - \frac{{\partial U}}{{\partial x}} + \frac{{{\lambda }}}{2}y$

Подставляя выражения (18) в условия пластичности (17), получим

(19)

${{A}_{i}}\frac{{\partial U}}{{\partial y}} - {{B}_{i}}\frac{{\partial U}}{{\partial x}} = k + c({{A}_{i}}{{e}_{{xz}}} + {{B}_{i}}{{e}_{{yz}}})$

Характеристики соотношения (19) имеют вид (14), а вдоль характеристик имеют место интегралы

(20)

$ - {{B}_{i}}U = kx - \frac{{{\lambda }}}{2}{{C}_{i}}x + c{{\theta }}\left( { - \frac{1}{2}{{B}_{i}}({{x}^{2}} + {{y}^{2}}) + c({{A}_{i}}{{{{\alpha }}}_{{2i}}} + {{B}_{i}}{{{{\beta }}}_{{1i}}})x + {{d}_{{1i}}}} \right.$

(21)

${{A}_{i}}U = ky - \frac{{{\lambda }}}{2}{{C}_{i}}y + c{{\theta }}\left( {\frac{1}{2}{{A}_{i}}({{x}^{2}} + {{y}^{2}}) + c({{A}_{i}}{{{{\alpha }}}_{{2i}}} + {{B}_{i}}{{{{\beta }}}_{{1i}}})y + {{d}_{{2i}}}} \right.$

Рассмотрим кручение стержня полигонального сечения. На контуре сечения вектор касательного напряжения ${{\vec {\tau }}} = ({{{{\tau }}}_{{xz}}},~{{{{\tau }}}_{{yz}}})$ параллелен контуру.

В случае идеально пластического материала характеристики направлены перпендикулярно контуру. В рассматриваемом случае характеристики (14) фиксированы и не зависят от величины деформации, поэтому для данного контура сечения стержня всегда можно выбрать линеаризованное условие текучести (5) таким образом, чтобы характеристики (14) оставались перпендикулярными к контуру во время всего процесса пластического деформирования.

Особо следует остановиться на линиях разрыва напряжений. Линии разрыва напряжений являются следом исчезающих жестких областей, на них всегда

(22)

${{e}_{{xz}}} = {{e}_{{yz}}} = 0$

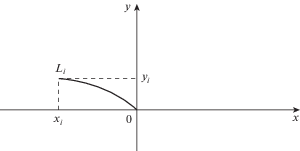
Рассмотрим область, ограниченную замкнутой ломанной $O{{x}_{i}}{{L}_{i}}{{y}_{i}}O$ (рис. 2). Пусть $O{{x}_{i}}$ и $O{{y}_{i}}$ – части контура поперечного сечения стержня. $O{{L}_{i}}$ – линия разрыва напряжений. Оси координат расположим так, как показано на рис. 2.

Рис. 2.

Линия разрыва напряжений.

Уравнения линий разрыва напряжений $O{{L}_{i}}$ запишем в виде

(23)

$y = {{{{\varphi }}}_{i}}\left( x \right)\quad {\text{или}}\quad x = {{{{\psi }}}_{i}}\left( y \right)$

Положим ${{A}_{i}} = 0,~{{B}_{i}} = 1$ для того, чтобы характеристики (14) были ортогональны к контуру $O{{y}_{i}}$. Условие (17) запишется в виде

(24)

${{{{\tau }}}_{{yz}}} = k + c{{e}_{{yz}}}$

Характеристики (14) примут вид

(25)

$y + {{C}_{i}} = 0$

Согласно (15), (16) из (22) получим

(26)

${{e}_{{xz}}} = 0,~\quad {{e}_{{yz}}} = - {{\theta }}(x - ~{{{{\psi }}}_{i}}\left( y \right))$

С учетом (26) из (24) имеем

(27)

${{{{\tau }}}_{{yz}}} = k - c{{\theta }}(x - ~{{{{\psi }}}_{i}}\left( y \right))$

В рассматриваемом случае из (20) следует

(28)

$U = - kx - \frac{{{\lambda }}}{2}xy + \frac{1}{2}c{{\theta }}({{x}^{2}} + {{y}^{2}}) - c{{\theta }}{{{{\psi }}}_{i}}\left( y \right)x + {{d}_{{1i}}}$

Полагая U = 0 на контуре поперечного сечения стержня (в данном случае O${{y}_{i}}$), из (28) получим

(29)

$U = - kx - \frac{{{\lambda }}}{2}xy + \frac{1}{2}c{{\theta }}{{x}^{2}} - c{{\theta }}{{{{\psi }}}_{i}}\left( y \right)x$

Из (18) и (29) следует

(30)

${{{{\tau }}}_{{xz}}} = ({{\lambda }} - c{{\theta \psi }}_{i}^{'}(y))x,\quad {{\psi }}_{i}^{'}\left( y \right) = \frac{{d{{{{\psi }}}_{i}}}}{{dy}}$

Для того, чтобы характеристики (14) были ортогональны к контуру $O{{x}_{i}}$, следует положить ${{A}_{i}} = 1,~{{B}_{i}} = 0.$ Условие (17) в рассматриваемом случае примет вид

(31)

${{{{\tau }}}_{{xz}}} = k + c{{e}_{{xz}}}$

Характеристики (14) запишутся в виде

(32)

$x + {{C}_{i}} = 0$

Согласно (15), (16) из (22) получим

(33)

$~{{e}_{{xz}}} = \theta (y - ~{{{{\varphi }}}_{i}}(x)),~\quad {{e}_{{yz}}} = 0$

С учетом (33) из (31) имеем

(34)

${{{{\tau }}}_{{xz}}} = k + c{{\theta }}(y - ~{{{{\varphi }}}_{i}}(x))$

В рассматриваемом случае из (20) следует

(35)

$U = ky - \frac{{{\lambda }}}{2}xy + \frac{1}{2}c{{\theta }}({{x}^{2}} + {{y}^{2}}) - c{{\theta }}{{{{\varphi }}}_{i}}\left( x \right)y + {{d}_{{2i}}}$

Полагая U = 0 на контуре поперечного сечения стержня (в данном случае O${{x}_{i}}$), из (35) получим

(36)

$U = ky - \frac{{{\lambda }}}{2}xy + \frac{1}{2}c{{\theta }}{{y}^{2}} - c{{\theta }}{{{{\varphi }}}_{i}}\left( x \right)y$

Из (18) и (36) следует

(37)

${{{{\tau }}}_{{yz}}} = ({{\lambda }} + c{{\theta \varphi }}_{i}^{'}(x))y,\quad {{\varphi }}_{i}^{'}(x) = \frac{{d{{{{\varphi }}}_{i}}}}{{dx}}$

Согласно (27), (30) и (34), (37) имеем следующее дифференциальное уравнение для определения линии разрыва напряжений $O{{L}_{i}}$

(38)

$\frac{{dy}}{{dx}} = \frac{{c{{\theta }}x - {{\lambda }}y + k}}{{{{\lambda }}x + c{{\theta }}y + k}}$

Интегрируя дифференциальное уравнение (38), получим

(39)

$c{{\theta }}({{y}^{2}} - {{x}^{2}}) + 2{{\lambda }}xy - 2k\left( {x + y} \right) = 0$

Из (39) находим

(40)

${{{{\psi }}}_{i}}\left( y \right) = \frac{1}{{c{{\theta }}}}({{\lambda }}y - k + \sqrt {{{{\left( {{{\lambda }}y - k} \right)}}^{2}} - 2kc{{\theta }}y + {{{\left( {c{{\theta }}y} \right)}}^{2}}} )$

(41)

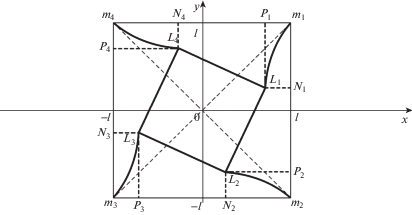
${{{{\varphi }}}_{i}}\left( x \right) = \frac{1}{{c{{\theta }}}}( - {{\lambda }}y + k - \sqrt {{{{\left( {{{\theta }}x - k} \right)}}^{2}} + 2kc{{\theta }}x + {{{\left( {c{{\theta }}x} \right)}}^{2}}} )$

Рассмотрим стержень, поперечное сечение которого есть квадрат ${{m}_{1}}{{m}_{2}}{{m}_{3}}{{m}_{4}}$ со стороной длины $2l$ (рис. 3).

Рис. 3.

Расположение линий разрыва напряжений в сечении стержня.

В рассматриваемом случае линеаризованное условие пластичности (5) выберем таким образом, чтобы отрезок ${{m}_{i}}{{m}_{{i + 1}}}$ контура поперечного сечения стержня был параллелен вектору $\overrightarrow {{{r}_{i}}} = \left( {{{A}_{i}},{{B}_{i}}} \right)$ (рис. 3).

Получим четыре линеаризованных условия текучести

(42)

${{{{\tau }}}_{{yz}}} - c{{e}_{{yz}}} = k$

(43)

${{{{\tau }}}_{{xz}}} - c{{e}_{{xz}}} = k$

(44)

${{{{\tau }}}_{{yz}}} - c{{e}_{{yz}}} = - k$

(45)

${{{{\tau }}}_{{xz}}} - c{{e}_{{xz}}} = - k$

Рассмотрим линии разрыва напряжений. Имеем следующие линии разрыва напряжений

(46)

${{m}_{1}}{{L}_{1}}:~y = {{{{\varphi }}}_{1}}\left( x \right)\quad {\text{или}}\quad x = {{{{\psi }}}_{1}}\left( y \right)$

(47)

${{m}_{2}}{{L}_{2}}:~y = {{{{\varphi }}}_{2}}\left( x \right)\quad {\text{или}}\quad x = {{{{\psi }}}_{2}}\left( y \right)$

(48)

${{m}_{3}}{{L}_{3}}:~y = {{{{\varphi }}}_{3}}\left( x \right)\quad {\text{или}}\quad x = {{{{\psi }}}_{3}}\left( y \right)~$

(49)

${{m}_{4}}{{L}_{4}}:y = {{{{\varphi }}}_{4}}\left( x \right)\quad {\text{или}}\quad x = {{{{\psi }}}_{4}}\left( y \right)$

(50)

${{L}_{i}}{{P}_{i}}:~x = {{x}_{i}}~\left( {i = 1;3} \right)~$

(51)

${{L}_{i}}{{N}_{i}}:~y = {{y}_{i}}~\left( {i = 1;3} \right)~$

(52)

${{L}_{j}}{{P}_{j}}:~y = {{y}_{j}}~\left( {j = 2;4} \right)~$

(53)

${{L}_{j}}{{N}_{j}}:~x = {{x}_{j}}~\left( {j = 2;4} \right)$

где

${{{{\psi }}}_{1}}\left( y \right) = l + \frac{1}{{c{{\theta }}}}({{\lambda }}(y - l) - k + \sqrt {{{{({{\lambda }}(y - l) - k)}}^{2}} + 2kc{{\theta }}(y - l) + {{{(c{{\theta }}(y - l))}}^{2}}} )$

${{{{\varphi }}}_{1}}\left( x \right) = l + \frac{1}{{c{{\theta }}}}( - {{\lambda }}(x - l) - k + \sqrt {{{{({{\lambda }}(x - l) + k)}}^{2}} + 2kc{{\theta }}(x - l) + {{{(c{{\theta }}(x - l))}}^{2}}} )$

${{{{\psi }}}_{2}}\left( y \right) = l + \frac{1}{{c{{\theta }}}}({{\lambda }}(y + l) - k + \sqrt {{{{({{\lambda }}(y + l) - k)}}^{2}} - 2kc{{\theta }}(y + l) + {{{(c{{\theta }}(y + l))}}^{2}}} )$

${{{{\varphi }}}_{2}}\left( x \right) = - l + \frac{1}{{c{{\theta }}}}( - {{\lambda }}(x - l) + k - \sqrt {{{{({{\lambda }}(x - l) - k)}}^{2}} + 2kc{{\theta }}(x - l) + {{{(c{{\theta }}(x - l))}}^{2}}} )$

${{{{\psi }}}_{3}}\left( y \right) = - l + \frac{1}{{c{{\theta }}}}({{\lambda }}(y + l) + k - \sqrt {{{{({{\lambda }}(y + l) + k)}}^{2}} - 2kc{{\theta }}(y + l) + {{{(c{{\theta }}(y + l))}}^{2}}} )$

${{{{\varphi }}}_{3}}(x) = - l + \frac{1}{{c{{\theta }}}}( - {{\lambda }}(x + l) + k - \sqrt {{{{({{\lambda }}(x + l) - k)}}^{2}} - 2kc{{\theta }}(x + l) + {{{(c{{\theta }}(x + l))}}^{2}}} )$

${{{{\psi }}}_{4}}\left( y \right) = - l + \frac{1}{{c{{\theta }}}}({{\lambda }}(y - l) + k - \sqrt {{{{({{\lambda }}(y - l) + k)}}^{2}} + 2kc{{\theta }}(y - l) + {{{(c{{\theta }}(y - l))}}^{2}}} )$

${{{{\varphi }}}_{4}}\left( x \right) = l + \frac{1}{{c{{\theta }}}}( - {{\lambda }}(x + l) - k + \sqrt {{{{({{\lambda }}(x + l) + k)}}^{2}} - 2kc{{\theta }}(x + l) + {{{(c{{\theta }}(x + l))}}^{2}}} )$

$c{{\theta }}\left( {{{y}_{1}} - l} \right) + {{\lambda }}\left( {{{x}_{1}} - l} \right) + k = 0$

$c{{\theta }}\left( {{{x}_{2}} - l} \right) - {{\lambda }}\left( {{{y}_{2}} + l} \right) + k = 0$

$c{{\theta }}\left( {{{y}_{3}} + l} \right) + {{\lambda }}\left( {{{x}_{3}} + l} \right) - k = 0$

$c{{\theta }}\left( {{{x}_{4}} - l} \right) - {{\lambda }}\left( {{{y}_{4}} + l} \right) - k = 0$

Согласно (46)–(53) из (26), (27), (30) и (33), (34), (37) с учетом (42)–(45) имеем следующие соотношения для компонент напряжений и деформаций:

в области ${{m}_{1}}{{L}_{1}}{{N}_{1}}$

${{e}_{{xz}}} = 0,\quad ~{{e}_{{yz}}} = - {{\theta }}\left( {x - ~{{\psi }_{1}}\left( y \right)} \right)$

${{{{\tau }}}_{{yz}}} = k - c{{\theta }}\left( {x - ~{{{{\psi }}}_{1}}\left( y \right)} \right),\quad ~{{{{\tau }}}_{{xz}}} = ({{\lambda }} - c{{\theta \psi }}_{1}^{'}\left( y \right))x$

в области ${{N}_{1}}{{L}_{1}}{{L}_{2}}{{P}_{2}}$

${{e}_{{xz}}} = 0,\quad ~{{e}_{{yz}}} = - {{\theta }}\left( {x - {{x}_{1}} - ~\frac{{{{x}_{2}} - {{x}_{1}}}}{{{{y}_{2}} - {{y}_{1}}}}\left( {y - {{y}_{1}}} \right)} \right)$

${{{{\tau }}}_{{yz}}} = k - c{{\theta }}\left( {x - {{x}_{1}} - ~\frac{{{{x}_{2}} - {{x}_{1}}}}{{{{y}_{2}} - {{y}_{1}}}}\left( {y - {{y}_{1}}} \right)} \right),~\quad {{{{\tau }}}_{{xz}}} = \left( {{{\lambda }} - c{{\theta }}\frac{{{{x}_{2}} - {{x}_{1}}}}{{{{y}_{2}} - {{y}_{1}}}}} \right)x$

в области ${{m}_{2}}{{L}_{2}}{{P}_{2}}$

${{e}_{{xz}}} = 0,~\quad {{e}_{{yz}}} = - {{\theta }}\left( {x - ~{{{{\psi }}}_{2}}\left( y \right)} \right)$

${{{{\tau }}}_{{yz}}} = k - c{{\theta }}\left( {x - ~{{{{\psi }}}_{2}}\left( y \right)} \right),\quad {{{{\tau }}}_{{xz}}} = ({{\lambda }} - c{{\theta \psi }}_{2}^{'}\left( y \right))x$

Компонента напряжения ${{{{\tau }}}_{{xz}}}$ терпит разрыв на отрезках ${{L}_{1}}{{N}_{1}},~{{L}_{2}}{{P}_{2}}$. Контактирующее напряжение ${{{{\tau }}}_{{yz}}}$ при переходе через ${{L}_{1}}{{N}_{1}},~{{L}_{2}}{{P}_{2}}$ непрерывно. Аналогично, определяются компоненты напряжений и деформаций и в других областях. В область, ограниченную ломанной ${{L}_{1}}{{L}_{2}}{{L}_{3}}{{L}_{4}}{{L}_{1}}$ решение не может быть продолжено. Вдоль ломанной L₁L₂L₃L₄L₁ действуют касательные напряжения, направленные вдоль оси z, которые уравновешивают перепад давления ${{{{\sigma }}}_{z}}$.

Таким образом, в работе

1) определено напряженное и деформированное состояние стержня из анизотропно упрочняющегося материала, находящегося под действием внешнего давления, линейно меняющегося вдоль образующей, при кручении для линеаризованного условия пластичности;

2) исследовано предельное состояние стержня из анизотропно упрочняющегося материала с квадратным поперечным сечением, находящегося под действием внешнего давления, линейно меняющегося вдоль образующей, в процессе кручения.

Список литературы

Соколовский В.В. Теория пластичности. М.: Высшая школа, 1969. 608 с.
Прагер В., Ходж Ф.Г. Теория идеально пластических тел. М.: ИЛ, 1956. 398 с.
Ивлев Д.Д. Теория идеальной пластичности. М.: Наука, 1966. 232 с.
Ивлев Д.Д. Механика пластических сред. В 2 т. Т. 2. Общие вопросы. Жесткопластическое и упругопластическое состояние тел. Упрочнение. Деформационные теории. Сложные среды. М.: Физматлит, 2002. 448 с.
Ольшак В., Рыхлевский Я., Урбановский В. Теория пластичности неоднородных тел. М.: Мир, 1964. 156 с.
Миронов Б.Г. К теории кручения неоднородных стержней // Вестник Чувашского государственного педагогического университета им. И.Я. Яковлева. Серия: Механика предельного состояния. 2014. № 4 (22). С. 236–240.
Миронов Б.Г., Козлова Л.С. Кручение призматических стержней при действии давления, линейно меняющегося вдоль образующей // Известия РАН. МТТ. 2014. № 3. С. 107–113.
Mironov B.G., Mironov Yu.B. Torsion anisotropic and composite cylindrical rod // J. Phys.: Conf. Ser. 2019. V. 1203. P. 012009. https://doi.org/10.1088/1742-6596/1203/1/012009
Mironov B.G., Mironov Yu.B. Torsion of non-uniform cylindrical and prismatic rods made of ideally plastic material under linearized yield criterion // Mech. Solids. 2020. V. 55. № 6. P. 813–819. https://doi.org/10.3103/S0025654420060102

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика твердого тела

Архивы выпусков Информация о журнале Отправить рукопись в журнал