Известия РАН. Механика твердого тела, 2022, № 2, стр. 72-81
ЭВОЛЮЦИОННАЯ МОДЕЛЬ УСТАЛОСТНОГО РАЗРУШЕНИЯ ПРИ НЕРЕГУЛЯРНОМ НАГРУЖЕНИИ
Д. С. Петухов a, *, И. Э. Келлер a, **
a Институт механики сплошных сред УрО РАН
Пермь, Россия
* E-mail: petuhovds@mail.ru
** E-mail: kie@icmm.ru
Поступила в редакцию 09.10.2021
После доработки 10.10.2021
Принята к публикации 11.10.2021
- EDN: CBBBWT
- DOI: 10.31857/S0572329922020167
Аннотация
Представлена эволюционная модель усталостного разрушения при многоцикловом нерегулярном нагружении, структура которой соответствует модели Оттосена, но уравнения перемещения поверхности выносливости и накопления повреждений существенно усовершенствованы и введена память к циклу с максимальным размахом напряжений в предшествующей истории нагружения. Определены материальные константы модели по данным времени жизни для алюминиевого сплава, включающим кривые Велера для двух значений коэффициента асимметрии, кривую Хейга, статические пределы прочности при одноосном растяжении и кручении, циклическое нагружение с периодическими перегрузками и циклическое непропорциональное нагружение. Выполнен расчет эволюции накопления поврежденности на полетном цикле и выделен критический блок нагружения, от которого зависит усталостный ресурс материала при подобном характере воздействия. Показано, что модель оставляет свободу описания различных значений этого ресурса в зависимости от данных эксперимента.
1. Введение. Многие детали машин при эксплуатации подвергаются немонотонной нерегулярной нагрузке. Подобные воздействия испытывают детали самолетов, вертолетов, экскаваторов, ветрогенераторов, наземного транспорта. Традиционным подходом к оценке усталостной прочности в подобных случаях, используемым многими конструкторскими бюро, является метод подсчета циклов, который подразумевает разбиение истории нагружения на отдельные полуциклы и определение вклада каждого из них в поврежденность без учета их очередности [1–3]. Однако очередность циклов нагрузки может значительно влиять на время до разрушения [4, 5]. Существует эволюционный подход к описанию накопления усталостных микроповреждений, который позволяет естественным образом учесть это влияние. Он заключается в записи эволюционного уравнения для параметра поврежденности в форме $\dot {D}(t) = F({\mathbf{\sigma }}(\tau ),t)$, где ${\mathbf{\sigma }}(t)$ есть история изменения тензора напряжений, F – функционал процесса. Такой подход естественным образом применим и в случае многоосного непропорционального нагружения. Данное эволюционное уравнение интегрируется по времени, пока $D$ не достигнет единицы, что означает разрушение. Некоторые эволюционные модели предложены в [6, 7]. Модель Оттосена [7] предназначена для описания многоцикловой усталости, не связана с уравнениями движения и допускает точное решение на регулярном циклическом нагружении, что существенно упрощает процедуру ее идентификации. В настоящей работе предпринимается усовершенствование этой модели для возможности учета специфических эффектов, наблюдаемых в различных программах нерегулярного циклического нагружения [5, 8, 9].
2. Модель. Предлагаются следующие уравнения:
(2.1)
$\begin{gathered} \beta = \left( {\sqrt {\frac{3}{2}} {\text{||}}{\mathbf{s}} - {\mathbf{\alpha }}{\text{||}} + g({{I}_{1}}) - r({\text{||}}{\mathbf{\alpha }}{\text{||}}) + w(\Delta {{\sigma }_{{{\text{max}}}}})} \right){\text{/}}{{\sigma }_{{ - 1}}} \\ {\mathbf{\dot {\alpha }}}\,{\text{ = }}\,{\text{||}}{\mathbf{\dot {s}}}{\text{||}}h(\beta )H(\beta )f(\angle ({\mathbf{\dot {s}}},{\mathbf{s}} - {\mathbf{\alpha }}))\frac{{{\mathbf{s}} - {\mathbf{\alpha }}}}{{{\text{||}}{\mathbf{s}} - {\mathbf{\alpha }}{\text{||}}}},\quad H(\beta ) = \left( {\begin{array}{*{20}{c}} {0,}&{\beta < 0} \\ {1,}&{\beta \geqslant 0} \end{array}} \right. \\ \dot {D} = \frac{{{\text{||}}{\mathbf{\dot {s}}}{\text{||}}}}{{{{\sigma }_{{ - 1}}}}}p(\beta )H(\beta )f(\angle ({\mathbf{\dot {s}}},{\mathbf{s}} - {\mathbf{\alpha }}))\frac{1}{{{{{\left( {1 - F({\mathbf{\sigma }})} \right)}}^{{{{L}_{4}}}}}}} \\ \end{gathered} $В основе данной модели лежит понятие поверхности выносливости в пространстве напряжений, задаваемой уравнением $\beta = 0$. Пока напряженное состояние лежит внутри поверхности ($\beta \leqslant 0$, рис. 1,a), прироста параметра поврежденности $D$ не происходит, а когда напряженное состояние выходит за ее пределы ($\beta > 0$, рис. 1,b), параметр $D$ начинает расти в зависимости от расстояния до поверхности и направления изменения напряжений. Кроме того, поверхность выносливости может менять размер и перемещаться, приспосабливаясь к нагружению. Местоположение поверхности задается тензорнозначным параметром α.
Выражение для $\beta $, приведенное в (2.1), имеет следующую структуру. Первое слагаемое определяет вклад девиаторной части напряженного состояния и является расстоянием между центром поверхности выносливости α и девиатором напряжений s = σ – – $\frac{1}{3}{{I}_{1}}{\mathbf{I}}$, где ${{I}_{1}} = {{\sigma }_{{ii}}}$ есть первый инвариант тензора напряжений, I – единичный тензор. Норма симметричного тензора определяется как ${\text{||A||}} = \sqrt {{\mathbf{A}}:{\mathbf{A}}} $. Второе слагаемое учитывает вклад гидростатической части и имеет вид материальной функции $g$ от первого инварианта тензора напряжений ${{I}_{1}}$. Третье слагаемое задает радиус поверхности выносливости, который зависит от ее положения α в пространстве напряжений. Последнее слагаемое описывает сокращение радиуса поверхности выносливости как функцию максимального размаха напряжений в течение истории нагружения до текущего момента времени $\Delta {{\sigma }_{{{\text{max}}}}}(t) = \mathop {\max }\limits_{{{t}_{1}} < {{t}_{2}} \leqslant t} \left( {{\text{||}}{\mathbf{\sigma }}({{t}_{1}}) - {\mathbf{\sigma }}({{t}_{2}}){\text{||}}} \right)$. Обезразмеривающий коэффициент σ–1 есть предел выносливости при регулярном симметричном нагружении.
Закон движения поверхности выносливости в (2.1) задается выражением для скорости ${\mathbf{\dot {\alpha }}}$ движения ее центра. Здесь $h(\beta ) \geqslant 0$ есть материальная функция, задающая скорость движения поверхности выносливости в зависимости от значения $\beta $. Функция Хевисайда $H(\beta )$ исполняет роль переключателя: пока напряженное состояние находится внутри поверхности выносливости, она не движется. Материальная функция f определяет зависимость ${\mathbf{\dot {\alpha }}}$ от угла между направлением ${{\dot {s}}}$ движения точки, изображающей напряженное состояние, и направлением ${\mathbf{s}} - {\mathbf{\alpha }}$ напряженного состояния относительно центра поверхности. Данный угол определяется как $\cos (\angle ({\mathbf{\dot {s}}},{\mathbf{s}} - {\mathbf{\alpha }}))$ = = $({\mathbf{\dot {s}}}:({\mathbf{s}} - {\mathbf{\alpha }})){\text{/}}({\text{||}}{\mathbf{\dot {s}}}{\text{||||}}{\mathbf{s}} - {\mathbf{\alpha }}{\text{||}})$; $0 \geqslant f \geqslant 1$, причем если эти направления совпадают ($\cos (\angle )$ = = 1), то f = 1 и если они противоположно направлены ($\cos (\angle ) = - 1$), то $f = 0$. Поверхность выносливости движется в направлении напряженного состояния, поскольку ${\mathbf{\dot {\alpha }}}$ пропорционально ${\mathbf{s}} - {\mathbf{\alpha }}$.
Последнее уравнение в (2.1) есть эволюционное уравнение для параметра поврежденности. Здесь $p(\beta ) \geqslant 0$ есть материальная функция, отвечающая за скорость накопления поврежденности. По структуре это уравнение отличается от уравнения для ${\mathbf{\dot {\alpha }}}$ только отсутствием тензорнозначного множителя и присутствием множителя $1{\text{/}}{{\left( {1 - F({\mathbf{\sigma }})} \right)}^{{{{L}_{4}}}}}$, где $F({\mathbf{\sigma }}) = 1$ задает поверхность прочности, а L4 – материальный параметр. Таким образом, при приближении к поверхности прочности скорость прироста поврежденности неограниченно возрастает. Скорость прироста поврежденности зависит от расстояния до поверхности выносливости (регулируется функцией $p(\beta )$) и направления изменения напряженного состояния (регулируется функцией f, той же, что и в выражении для ${\mathbf{\dot {\alpha }}}$).
Скорость прироста поврежденности принята независимой от текущей поврежденности, так как выражение с зависимостью $\dot {D} = G(D)F({\mathbf{\sigma }}(t))$ сводится к $\dot {D} = F({\mathbf{\sigma }}(t))$ заменой переменной D. Свобода такой перенормировки допускается несвязанностью модели (2.1) с уравнениями движения среды.
Модель (2.1) склерономна, т.е. независима от скорости изменения нагрузки ${\mathbf{\sigma }}(t)$, что достигается наличием множителя ${\text{||}}{\mathbf{\dot {s}}}{\text{||}}$ в правой части выражений для ${\mathbf{\dot {\alpha }}}$ и $\dot {D}$. Для уравнений (2.1) важна только форма пути в пространстве напряжений, а в случае одноосного нагружения – только значения максимумов и минимумов нагрузки.
По сравнению с моделью Оттосена
(2.2)
$\begin{gathered} \beta = \left( {\sqrt {\frac{3}{2}} {\text{||}}{\mathbf{s}} - {\mathbf{\alpha }}{\text{||}} + K{{I}_{1}} - {{\sigma }_{{ - 1}}}} \right){\text{/}}{{\sigma }_{{ - 1}}} \\ {\mathbf{\dot {\alpha }}} = \dot {\beta }h(\beta )H(\beta )H(\dot {\beta })({\mathbf{s}} - {\mathbf{\alpha }}),\quad h(\beta ) \equiv C \\ \dot {D} = \dot {\beta }p(\beta )H(\beta )H(\dot {\beta }),\quad p(\beta ) = K\exp (L\beta ) \\ \end{gathered} $1. Выражение для $\beta $ усовершенствовано, чтобы описывать одноосную и сдвиговую диаграммы Хейга произвольной формы. Модель (2.2) описывает одноосную и сдвиговую диаграммы Хейга для одноосного нагружения, а в случае сдвигового нагружения она предсказывает одинаковую амплитуду выносливости ${{\tau }_{{\text{a}}}}$ для любого среднего напряжения цикла ${{\tau }_{{\text{m}}}}$, в том числе и за пределами прочности материала.
2. Добавлено сокращение поверхности выносливости в зависимости от максимального размаха напряжений в истории. Уменьшение предела выносливости при наличии в истории нагружения циклов достаточно большой амплитуды наблюдается экспериментально [9].
3. В правой части эволюционных уравнений модели (2.2) $\dot {\beta }$ заменено на ${\text{||}}{\mathbf{\dot {s}}}{\text{||}}$. На траекториях напряжений $\beta = {\text{const}} > 0$ модель (2.2) не накапливает поврежденность, несмотря на то, что напряженное состояние все время находится за пределами поверхности выносливости.
4. В эволюционное уравнение накопления поврежденности учтена поверхность прочности, чтобы исключить неадекватный прогноз при наличии единичных циклов большой амплитуды в истории нагружения.
5. В правой части эволюционных уравнений (2.2) присутствует простой переключатель $H(\dot {\beta })$, который отключает накопление поврежденности и движение поверхности выносливости, если напряженное состояние приближается к поверхности выносливости снаружи. Он был заменен на материальную функцию $f(\angle ({\mathbf{\dot {s}}},{\mathbf{s}} - {\mathbf{\alpha }}))$, чтобы увеличить возможность модели описывать результаты экспериментов на непропорциональное нагружение.
6. Была увеличена гибкость материальных функций, регулирующих скорости накопления поврежденности и движения поверхности выносливости в зависимости от значения $\beta $, что позволяет лучше регулировать наклон кривых Велера для различных коэффициентов асимметрии нагружения.
3. Идентификация модели. Материальные функции $g({{I}_{1}})$ и $r({\text{||}}{\mathbf{\alpha }}{\text{||}})$ в выражении для $\beta $ можно идентифицировать по двум диаграммам Хейга зависимостей пределов выносливости при одноосном и сдвиговом нагружениях от среднего напряжения в цикле.
На первом этапе рассматривается регулярное сдвиговое нагружение со средним значением ${{\tau }_{m}}$ и амплитудой ${{\tau }_{a}}$. Ненулевыми компонентами тензора напряжений являются ${{\sigma }_{{12}}} = {{\sigma }_{{21}}}$; те же ненулевые компоненты ${{\alpha }_{{12}}} = {{\alpha }_{{21}}}$ имеет и тензор ${\mathbf{\alpha }}$, так как ${\mathbf{\dot {\alpha }}}$ пропорционально ${\text{s}} - {\mathbf{\alpha }}$ (2.1). Такое нагружение лежит на диаграмме Хейга, если максимальное ${{\tau }_{{{\text{max}}}}} = {{\tau }_{{\text{m}}}} + {{\tau }_{{\text{a}}}}$ и минимальное ${{\tau }_{{{\text{min}}}}} = {{\tau }_{{\text{m}}}} - {{\tau }_{{\text{a}}}}$ напряжения цикла лежат на поверхности выносливости $\beta = 0$. Тогда весь цикл лежит внутри поверхности выносливости и касается ее границ крайними значениями, подставляя которые в выражение β = 0 (2.1), получим
(3.1)
$\sqrt 3 \left( {{{\tau }_{{\text{m}}}} + {{\tau }_{{\text{a}}}} - {{\alpha }_{0}}} \right) - r(\sqrt 2 {{\alpha }_{0}}) = 0,\quad \sqrt 3 \left( { - {{\tau }_{{\text{m}}}} + {{\tau }_{{\text{a}}}} + {{\alpha }_{0}}} \right) - r(\sqrt 2 {{\alpha }_{0}}) = 0$(3.2)
${{\tau }_{a}} = \frac{1}{{\sqrt 3 }}r(\sqrt 2 {{\tau }_{{\text{m}}}})\quad {\text{или}}\quad r(x) = \sqrt 3 {{\tau }_{a}}(x{\text{/}}\sqrt 2 )$На втором этапе рассматривается регулярное одноосное нагружение со средним значением ${{\sigma }_{{\text{m}}}}$ и амплитудой ${{\sigma }_{{\text{a}}}}$. Тензор напряжений имеет единственную ненулевую компоненту ${{\sigma }_{{11}}}$, а значит тензор α имеет ненулевые диагональные элементы ${{\alpha }_{{11}}}$ и α22 = = ${{\alpha }_{{33}}} = - \frac{1}{2}{{\alpha }_{{11}}}$, что следует из пропорциональности ${\mathbf{\dot {\alpha }}}$ и ${\text{s}} - {\mathbf{\alpha }}$ (2.1). Как и ранее, нагружение лежит на диаграмме Хейга если максимальное ${{\sigma }_{{{\text{max}}}}} = {{\sigma }_{{\text{m}}}} + {{\sigma }_{{\text{a}}}}$ и минимальное ${{\sigma }_{{{\text{min}}}}} = {{\sigma }_{{\text{m}}}} - {{\sigma }_{{\text{a}}}}$ напряжения цикла лежат на поверхности выносливости $\beta = 0$, подставляя которые в выражение для $\beta $ (2.1). и обозначив ${{\alpha }_{{11}}}$ как ${{\alpha }_{0}}$, получим
(3.3)
$\begin{gathered} {{\sigma }_{{\text{m}}}} + {{\sigma }_{{\text{a}}}} - \frac{3}{2}{{\alpha }_{0}} - r\left( {\sqrt {\frac{3}{2}} {{\alpha }_{0}}} \right) + g\left( {{{\sigma }_{{\text{m}}}} + {{\sigma }_{{\text{a}}}}} \right) = 0 \\ - {{\sigma }_{{\text{m}}}} + {{\sigma }_{{\text{a}}}} + \frac{3}{2}{{\alpha }_{0}} - r\left( {\sqrt {\frac{3}{2}} {{\alpha }_{0}}} \right) + g\left( {{{\sigma }_{{\text{m}}}} - {{\sigma }_{{\text{a}}}}} \right) = 0 \\ \end{gathered} $Исключив из (3.3) ${{\alpha }_{0}}$, получим
(3.4)
${{\sigma }_{a}} + \frac{1}{2}\left( {g\left( {{{\sigma }_{{\text{m}}}} + {{\sigma }_{{\text{a}}}}} \right) + g\left( {{{\sigma }_{{\text{m}}}} - {{\sigma }_{{\text{a}}}}} \right) - r\left( {\frac{{g({{\sigma }_{{\text{m}}}} + {{\sigma }_{{\text{a}}}}) - g({{\sigma }_{{\text{m}}}} - {{\sigma }_{{\text{a}}}})}}{{\sqrt 6 }} + 2{{\sigma }_{{\text{m}}}}} \right)} \right) = 0$Если известна функция ${{\sigma }_{{\text{a}}}}({{\sigma }_{{\text{m}}}})$, задающая диаграмму Хейга для одноосного нагружения, то выражение (3.4) можно рассматривать как уравнение относительно функции $g(x)$. Это функциональное уравнение достаточно сложное, поэтому удобнее пойти другим путем. Если заданной считать функцию $g(x)$, то выражение (3.4) будет определять неявную зависимость между ${{\sigma }_{{\text{a}}}}$ и ${{\sigma }_{{\text{m}}}}$. Пусть экспериментальная диаграмма Хейга задана в формате набора из $n$ пар $\{ \sigma _{{\text{m}}}^{i},\sigma _{{\text{a}}}^{i}\} ,\;i = 1..n$. Будем искать $g(x)$ как функцию, параметризованную набором параметров ${{k}_{i}},\;i = 1..m$, достаточно гибко регулирующих ее форму. Функция g(x) должна быть монотонно возрастающей, так как повышение ${{I}_{1}}$ негативно влияет на усталостную прочность. При некотором конкретном наборе параметров ${{k}_{i}}$ выражение (3.4) сопоставляет значениям $\sigma _{{\text{m}}}^{i}$ значения $\hat {\sigma }_{{\text{a}}}^{i}$, отличающиеся от экспериментальных $\sigma _{{\text{a}}}^{i}$. Параметры ${{k}_{i}}$ подбираются так, что невязка между прогнозируемыми $\hat {\sigma }_{{\text{a}}}^{i}$ и экспериментальными $\sigma _{{\text{a}}}^{i}$ минимальна.
Модель (2.1) далее идентифицируется для алюминиевого сплава AA2024-T4. Экспериментальная диаграмма Хейга [10] (рис. 2,a) удовлетворительно описывается функциями $g({{I}_{1}}),$ $r({\text{||}}{\mathbf{\alpha }}{\text{||}})$ изображенными на рис. 3. Ввиду отсутствия сдвиговой диаграммы Хейга для данного материала была использована кривая, похожая по форме на данные по другим алюминиевым сплавам, а сдвиговой предел выносливости при симметричном нагружении был принят ${{\tau }_{{ - 1}}} = 0.55{{\sigma }_{{ - 1}}}$ [11]. Функция g искалась в виде аппроксимации, 4 параметра которой были найдены минимизацией невязки с экспериментальными данными симплекс-методом.
Рис. 2.
Диаграммы Хейга для алюминиевого сплава AA2024-T4: для одноосного нагружения (a), для сдвигового нагружения (b). По осям отложены МПа.
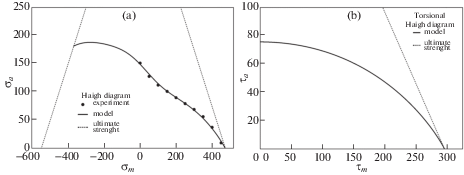
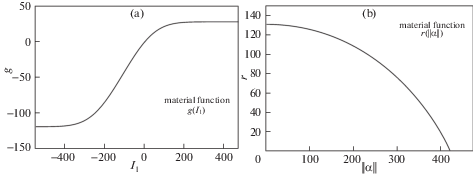
Рис. 3.
Материальные функции $g({{I}_{1}})$ (a) и $r({\text{||}}{\mathbf{\alpha }}{\text{||}})$ (b), идентифицированные для AA2024-T4. По осям отложены МПа.
В качестве критерия прочности был выбран критерий Шлейхера [12]
(3.5)
$F = \frac{{\frac{3}{2}{\mathbf{s}}:{\mathbf{s}} - {{a}_{1}}{{I}_{1}} - {{a}_{2}}I_{1}^{2}}}{{{{a}_{0}}}}$Параметры ai выражаются через пределы прочности на растяжение ${{\sigma }_{{{\text{tu}}}}}$, сжатие ${{\sigma }_{{{\text{cu}}}}} > 0$ и сдвиг ${{\tau }_{{\text{u}}}}$:
(3.6)
$\begin{gathered} {{a}_{0}} = 3{{\tau }_{{\text{u}}}} \\ {{a}_{1}} = - 3{{\tau }_{{\text{u}}}}\frac{{{{\sigma }_{{{\text{cu}}}}} - {{\sigma }_{{{\text{tu}}}}}}}{{{{\sigma }_{{{\text{cu}}}}}{{\sigma }_{{{\text{tu}}}}}}} \\ {{a}_{2}} = \frac{{3{{\tau }_{{\text{u}}}}}}{{{{\sigma }_{{{\text{cu}}}}}{{\sigma }_{{{\text{tu}}}}}}} - 1 \\ \end{gathered} $Для AA2024-T4 пределы прочности были приняты ${{\sigma }_{{{\text{tu}}}}} = 474$ МПа ${{\tau }_{{\text{u}}}} = 290$ МПа [13] и ${{\sigma }_{{{\text{cu}}}}} = 550$ МПа из оценочных соображений.
Следующую группу материальных функций предлагается искать в виде:
(3.7)
$\begin{gathered} w(x) = {{k}_{1}}\left( {\frac{1}{2}x + \frac{1}{{10}}{{b}_{1}}\ln \left( {\frac{{\cosh (5(1 - x{\text{/}}{{b}_{1}}))}}{{\cosh (5)}}} \right)} \right) \\ h(\beta ) = {{k}_{2}}{{\beta }^{{{{L}_{2}}}}} + {{b}_{2}} \\ p(\beta ) = {{k}_{3}}(\exp ({{L}_{3}}\beta ) - (1 - {{b}_{3}})) \\ \end{gathered} $Для AA2024-T4 были использованы две экспериментальные диаграммы Велера с симметричным и отнулевым одноосными нагружениями [13] (рис. 4,a), а также данные по нерегулярному одноосному нагружению [9], представляющие собой эксперименты на усталостное разрушение при наложении периодических перегрузок большой амплитуды на регулярное нагружение малой амплитуды (рис. 4,b). Сплав AA2024-T351, исследованный в [9], отличается от AA2024-T4 лишь небольшим различием в температурной обработке и имеет очень близкие механические свойства [14]. Невязка записывалась как
(3.8)
$X = \sum\limits_{i = 1}^n {{\left( {1 - \frac{{\ln ({{N}_{i}})}}{{\ln (N_{i}^{{{\text{exp}}}})}}} \right)}^{2}} + \,{\text{|}}q_{{10/50}}^{{{\text{exp}}}} - {{q}_{{10/50}}}{\text{|}}$Рис. 4.
Диаграмма Велера для AA2024-T4: результаты экспериментов и предсказание модели для симметричных ($R = - 1$) и отнулевых ($R = 0$) циклов (a) и один “такт” нерегулярного нагружения [9] (b). По вертикальной оси отложены МПа.
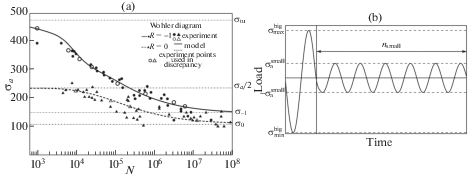
Первая часть невязки относится к диаграммам Велера; здесь $N_{i}^{{exp}}$ есть экспериментальное значение числа циклов до разрушения на i-м нагружении, ${{N}_{i}}$ – предсказание модели на том же нагружении, $n$ – общее число экспериментальных точек, использованных в невязке (обозначены полыми значками на рис. 4,a). Вторая часть невязки относится к нерегулярному нагружению [9], где $q_{{10/50}}^{{exp}} = 2.14$ есть отношение экспериментальных значений циклов до разрушения при ${{n}_{{{\text{small}}}}} = 10$ и ${{n}_{{{\text{small}}}}}$ = 50 для нагружения, изображенного на рис. 4,b при $\sigma _{{\text{a}}}^{{{\text{small}}}} = 110$ МПа, $\sigma _{{{\text{min}}}}^{{{\text{big}}}} = - 414$ МПа, $\sigma _{{{\text{max}}}}^{{{\text{big}}}}$ = = 359 МПа; ${{q}_{{10/50}}}$ – отношение, предсказываемое моделью. Путем минимизации невязки симплекс-методом были найдены значения констант для AA2024-T4:
(3.9)
$\begin{gathered} {{k}_{1}} = 1.96\,{\text{МПа}},\quad {{b}_{1}} = 804\,{\text{МПа}},\quad {{k}_{2}} = 1.68\,{\text{МПа}},\quad {{L}_{2}} = 5.94,\quad {{b}_{2}} = 0.0673\,{\text{МПа}} \\ {{k}_{3}}{{ = 10}^{{ - 5.54}}},\quad {{L}_{3}} = 2.16,\quad {{b}_{3}} = 3.09 \times {{10}^{{ - 4}}},\quad {{L}_{4}} = 1.55 \\ \end{gathered} $Этому набору констант соответствуют кривые Велера, изображенные на рис. 4,a, и ${{q}_{{10/50}}} = 2.07$.
Последняя материальная функция $f(\angle ({\mathbf{\dot {s}}},{\mathbf{s}} - {\mathbf{\alpha }}))$, отвечающая за накопление поврежденности в зависимости от направления изменения напряжений, разыскивается в виде
Материальная константа L5 определяется из экспериментов на непропорциональное циклическое нагружение.
Для AA2024-T4 использованы экспериментальные данные [8] для нагружения, состоящего из комбинации циклического одноосного растяжения–сжатия и циклического сдвига, имеющих разность фаз $\theta $:
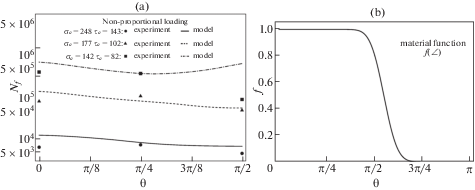
Рис. 5.
Сравнение результатов экспериментов на непропорциональное нагружение алюминиевого сплава AA2024-T4 [8] с предсказаниями модели (a), материальная функция $f(\angle )$ при ${{L}_{5}} = 1.1$, отвечающая за зависимость скорости движения поверхности выносливости от направления изменения напряженного состояния (b).
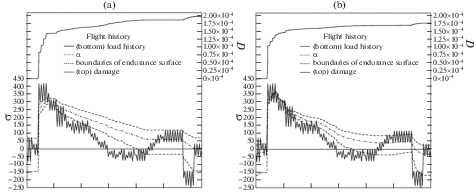
4. Пример расчета. Модель использована для прогноза накопления поврежденности при нерегулярном одноосном нагружении элемента подвески авиадвигателя в течение полетного цикла. На рис. 6 изображена динамика накопления поврежденности на этой истории нагружения, а также движение поверхности выносливости. Расчет по модели (2.1) с набором констант (3.9) показывает, что деталь выдержит ${{N}_{{\text{f}}}} = 4998$ таких полетов, тогда как метод подсчета циклов в комбинации с формулой Одинга [15] эквивалентного отнулевого цикла $\sigma _{a}^{{{\text{eq}}}} = \left( {\begin{array}{*{20}{c}} {(0.2{{\sigma }_{{\text{m}}}} + {{\sigma }_{{\text{a}}}}){\text{/}}\sqrt 2 ,}&{{{\sigma }_{{\text{m}}}} < 0} \\ {\sqrt {{{\sigma }_{{\text{a}}}}({{\sigma }_{{\text{a}}}} + {{\sigma }_{{\text{m}}}})} {\text{/}}\sqrt 2 ,}&{{{\sigma }_{{\text{m}}}} \geqslant 0} \end{array}} \right.$ и основанный на диаграмме Велера (рис. 3,a), дает результат ${{N}_{{\text{f}}}} = 8226$. Метод подсчета циклов практически не учитывает наличие циклов небольшой амплитуды в истории, даже если они имеют высокое среднее напряжение (в истории на рис. 6, большой цикл с ${{\sigma }_{{{\text{min}}}}}$ = = –234 МПа, ${{\sigma }_{{{\text{max}}}}} = 421$ МПа дает 99.7%-й вклад в накопление поврежденности).
Рис. 6.
Расчет динамики накопления поврежденности на полетном цикле с помощью модели (2.1): набор констант (3.9) (a) и набор констант (4.1) (b). Напряжения указаны в МПа.
Одного эксперимента на нерегулярное нагружение, типа изображенного на рис. 3,b, оказывается недостаточно для полной идентификации модели. Так, набор констант
(4.1)
$\begin{gathered} {{k}_{1}} = 0.55\;{\text{МПа}},\quad {{b}_{1}} = 553\;{\text{МПа}},\quad {{k}_{2}} = 1.24\;{\text{МПа}} \\ {{L}_{2}} = 1.94,\quad {{b}_{2}} = 0.0143\;{\text{МПа}} \\ {{k}_{3}}{{ = 10}^{{ - 6.16}}},\quad {{L}_{3}} = 4.59,\quad {{b}_{3}} = 0.097,\quad {{L}_{4}} = 1.36 \\ \end{gathered} $Рис. 7.
Предлагаемый эксперимент, расчет динамики накопления поврежденности с помощью модели (2.1): набор констант (3.9) (a) и набор констант (4.1) (b). Напряжения указаны в МПа.
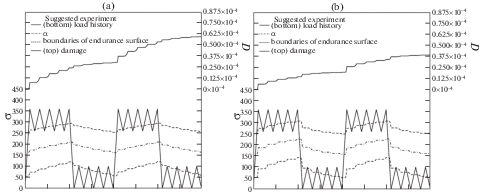
5. Заключение. Сформулированная эволюционная модель, существенно обобщающая формулировку Оттосена, способна описывать довольно широкий комплекс данных многоцикловой усталости, в том числе при нерегулярном и непропорциональном нагружениях. Предложена программа критического эксперимента, необходимого для описания моделью усталостного ресурса в полетных циклах.
Список литературы
Стрижиус В.Е. Допускаемые напряжения в машиностроении и циклическая прочность металлов. М.: Машиностроение, 2012. 271 с.
Воробьёв А.З., Олькин Б.И., Стебенев В.Н., Родченко Т.С. Сопротивление усталости элементов конструкций. М.: Машиностроение, 1990. 240 с.
Pereira H.F.S.G., DuQuesnay D.L., Jesus A.M.P. De, Silva A.L.L. Analysis of variable amplitude fatigue data of the P355NL1 steel using the effective strain damage model // ASME. J. Pressure Vessel Technol. 2009. V. 131. № 5. P. 051402. https://doi.org/10.1115/1.3147986
Schütz W., Heuler P. Miner’s rule revisited // An assessment of fatigue damage and crack growth prediction techniques. AGARD Report. 1994. № 797. P. 1.1.
Ekvall J.C., Young L. Converting fatigue loading spectra for flight-by-flight testing of aircraft and helicopter components // J. Test. Eval. 1976. V. 4. № 4. P. 231–247. https://doi.org/10.1520/JTE10207J
Волков И.А., Игумнов Л.А. Введение в континуальную механику поврежденной среды. М.: Физматлит, 2017. 304 с.
Ottosen N.S., Stenström R., Ristinmaa M. Continuum approach to high-cycle fatigue modeling // Int. J. Fatigue. 2008. V. 30. № 6. P. 996–1006. https://doi.org/10.1016/j.ijfatigue.2007.08.009
Xia T., Yao W., Zou J., Gao D. A novel accumulative fatigue damage model for multiaxial step spectrum considering the variations of loading amplitude and loading path // Fatigue Fract. Eng. Mater. Struct. 2015. V. 39. № 2. P. 194–205. https://doi.org/10.1111/ffe.12349
Jurcevic. R., DuQuesnay D.L., Topper T.H., Pompetzki M.A. Fatigue damage accumulation in 2024-T351 aluminium subjected to periodic reversed overloads // Int. J. Fatigue. 1990. V. 12. № 4. P. 259–266. https://doi.org/10.1016/0142-1123(90)90453-L
Cai X., Li X., Xu J. Fatigue limit and life evaluation formulae for compressive mean stress states // Mater. Sci. Technol. 2018. V. 34. № 17. P. 2166–2173. https://doi.org/10.1080/02670836.2018.1522100
Forrest P.G. Fatigue of metals. Oxford: Pergamon press, 1962. 436 p.
Kolupaev V.A. Equivalent stress concept for limit state analysis. Cham: Springer, 2018. 365 p.
Rice R.C., Jackson J.L., Bakuckas J., Thompson S. Metallic materials properties development and standartization – 01. Springfield: National technical information service, 2003. 1632 p.
Kaufman G.J. Introduction to aluminum alloys and tempers, Chapter 4. Materials Park: ASM International, 2000. 242 p.
Одинг И.А. Допускаемые напряжения в машиностроении и циклическая прочность металлов. М.: Машгиз, 1962. 260 с.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика твердого тела



