1. На главную
  2. Электронные версии
  3. Известия РАН. Механика твердого тела
  4. № 3, 2022

Известия РАН. Механика твердого тела, 2022, № 3, стр. 3-7

НАПРЯЖЕННОЕ СОСТОЯНИЕ КОНИЧЕСКОЙ ТРУБЫ ИЗ СТАРЕЮЩЕГО УПРУГОВЯЗКОПЛАСТИЧЕСКОГО МАТЕРИАЛА

А. В. Ковалев a, b, *, Н. В. Минаева a, **, А. И. Шашкин a, ***

a Воронежский государственный университет
Воронеж, Россия

b Военный учебно-научный центр Военно-воздушных сил “Военно-воздушная академия им. проф. Н.Е. Жуковского и Ю.А. Гагарина”
Воронеж, Россия

* E-mail: kav-mail@mail.ru
** E-mail: nminaeva@yandex.ru
*** E-mail: dean@amm.vsu.ru

Поступила в редакцию 06.10.2021
После доработки 12.10.2021
Принята к публикации 14.10.2021

Полный текст (PDF)

Аннотация

Проведено определение напряженного состояния конической трубы, близкого к осесимметричному состоянию упругопластической цилиндрической трубы из стареющего материала. Модель упруговязкопластического материала учитывает изменение свойств, связанных со старением. Принято предположение, что внешний контур мало отличается от кругового постоянного радиуса. Получены аналитические выражения для компонент напряжений, а также границы, разделяющей упругую и пластическую области.

Ключевые слова: стареющий упруговязкопластический материал, напряженное состояние, коническая труба, метод возмущений

Исследованию состояний упругопластических тел, физические свойства которых меняются со временем, посвящено множество работ [1–7]. В трудах А.В. Манжирова и его учеников [1–3] проведена постановка и исследование неклассических задач наращивания вязкоупругих тел. В работах Н.Х. Аратюняна, Д.Д. Ивлева [1, 4] была предложена модель стареющего вязкопластического материала, в которой предел текучести представляет собой интегральный оператор. На ее основе в [5, 6] изучалось развитие пластической зоны при двухосном растяжении пластин с отверстиями различной формы. В [7] проведено исследование напряженного состояния толстой плиты, имеющей т-угольную полость, которая подвержена всестороннему растяжению. Распределение поля напряжений в эксцентрической трубе из стареющего упругопластического материала, находящейся под действием внутреннего давления, изучалось в [8]. В качестве метода решения в этих работах был выбран метод малого параметра. Применение метода возмущений при решении задач деформирования упругопластических тел показано в [9]. В [10] приведены условия, при которых ряды по независимым малым параметрам будут сходящимися. В [11] методом возмущений получены решения, описывающие поведение различных цилиндрических тел из упруговязкопластических материалов.

Рассмотрим деформирование осесимметричной конической трубы под действием распределенного внутреннего давления $p(t)$. Материал трубы несжимаемый упругопластический, подвержен старению. В качестве модели упругопластической среды выбрана модель, предложенная в [1, 4].

Согласно теории малых упругопластических деформаций, напряженно-деформированное состояние будет описываться решением следующих задач:

(1)
$\frac{{\partial \sigma _{\rho }^{p}}}{{\partial \rho }} + \frac{{\partial \tau _{{\rho z}}^{p}}}{{\partial z}} + \frac{{\sigma _{\rho }^{p} - \sigma _{\theta }^{p}}}{\rho } = 0,\quad \frac{{\partial \tau _{{\rho z}}^{p}}}{{\partial \rho }} + \frac{{\partial \sigma _{z}^{p}}}{{\partial z}} + \frac{{\tau _{{\rho z}}^{p}}}{\rho } = 0$
(2)
$\frac{{\partial u_{z}^{p}}}{{\partial z}} + \frac{{\partial u_{\rho }^{p}}}{{\partial \rho }} + \frac{{u_{\rho }^{p}}}{\rho } = 0$
(3)
$\left( {\frac{{\partial u_{\rho }^{p}}}{{\partial \rho }} - \frac{{\partial u_{z}^{p}}}{{\partial z}}} \right)\tau _{{\rho z}}^{p} - \frac{1}{2}\left( {\frac{{\partial u_{\rho }^{p}}}{{\partial z}} + \frac{{\partial u_{z}^{p}}}{{\partial \rho }}} \right)\left( {\sigma _{\rho }^{p} - \sigma _{z}^{p}} \right) = 0$
(4)
$\begin{gathered} \frac{1}{4}{{\left( {\frac{{\sigma _{\rho }^{p} - \sigma _{z}^{p}}}{k} + \int\limits_0^t {(\sigma _{\rho }^{p}(\tau ) - \sigma _{z}^{p}(\tau ))K_{{}}^{*}(t,\tau )d\tau } } \right)}^{2}} + {{\left( {\frac{{\tau _{{\rho z}}^{p}}}{k} + \int\limits_0^t {\tau _{{\rho z}}^{p}K_{{}}^{*}(t,\tau )d\tau } } \right)}^{2}} = 1 \hfill \\ \frac{{\sigma _{\theta }^{p}}}{k} + \int\limits_0^t {\sigma _{\theta }^{p}(\tau )K_{{}}^{*}(t,\tau )d\tau } = \frac{1}{4}\left( {\frac{{\sigma _{\rho }^{p} + \sigma _{z}^{p}}}{k} + \int\limits_0^t {(\sigma _{\rho }^{p}(\tau ) + \sigma _{z}^{p}(\tau ))K_{{}}^{*}(t,\tau )d\tau } } \right) \pm 2k \hfill \\ \end{gathered} $
(5)
$\mathop {\left. {\sigma _{n}^{p}} \right|}\nolimits_{\rho = \alpha } = - q(t),\quad \mathop {\left. {\tau _{n}^{p}} \right|}\nolimits_{\rho = \alpha } = 0$

Здесь $\sigma _{\rho }^{p},\sigma _{\theta }^{p},\sigma _{z}^{p},\tau _{{\rho z}}^{p}$ – компоненты тензора напряжений, $u_{\rho }^{p},u_{z}^{p}$ – компоненты вектора перемещений, индекс “р” указывает на принадлежность к пластической области, $\alpha \, = \,\frac{a}{b}$, $a,b$ – внутренний и внешний радиусы цилиндрической трубы, $k = k(t)$ – переменный предел текучести, $K_{{}}^{*}(t,\tau )$ – ядро наследственного оператора [4, 5], $K_{{}}^{*}(0,\tau )\, = \,\frac{d}{{d\tau }}\left( {\frac{1}{{k(\tau )}}} \right)$.

В задачу для упругой зоны входят уравнения равновесия, условия несжимаемости, вид которых аналогичен (1), (2), а также физические соотношения:

(6)
$\begin{gathered} \frac{{\sigma _{\rho }^{e} - \sigma _{\theta }^{e}}}{{2G}} = \frac{{\partial u_{\rho }^{e}}}{{\partial \rho }} + \frac{{u_{\rho }^{e}}}{\rho } - \int\limits_0^t {(\sigma _{\rho }^{e}(\tau ) - \sigma _{\theta }^{e}(\tau ))R(t,\tau )d\tau } \\ \frac{{\sigma _{\rho }^{e} - \sigma _{z}^{e}}}{{2G}} = \frac{{\partial u_{\rho }^{e}}}{{\partial \rho }} - \frac{{\partial u_{z}^{e}}}{{\partial z}} - \int\limits_0^t {(\sigma _{\rho }^{e}(\tau ) - \sigma _{z}^{e}(\tau ))R(t,\tau )d\tau } \\ \frac{{\tau _{{\rho z}}^{e}}}{G} = \frac{{\partial u_{\rho }^{e}}}{{\partial z}} + \frac{{\partial u_{z}^{e}}}{{\partial \rho }} - \int\limits_0^t {\tau _{{\rho z}}^{e}(\tau )R(t,\tau )d\tau } \\ \end{gathered} $
где $G = G(t)$ – переменный модуль сдвига, $R(t,\tau )$ – ядро наследственного оператора [4, 5], индекс “е” указывает на принадлежность к упругой области.

На внешнем контуре выполняются граничные условия

(7)
$\mathop {\left. {\sigma _{n}^{e}} \right|}\nolimits_{\rho = 1} = \mathop {\left. {\tau _{n}^{e}} \right|}\nolimits_{\rho = 1} = 0$

К задачам (1)–(7) необходимо добавить условия сопряжения решений на упругопластической границе ${{\rho }_{s}} = {{\rho }_{s}}(t)$. Величины, имеющие размерность длины, отнесены к внешнему радиусу b цилиндрической трубы, нагруженной распределенным внутренним давлением $p(t)$.

Пусть внешний контур сечения конической трубы мало отличается от кругового радиуса b

$f(\zeta ) = 1 - \delta \zeta ,\quad 0 < \delta < 1$

Будем искать решение, характеризующее напряженное состояние в виде асимптотических рядов по малому параметру

$\sigma _{\rho }^{{}} = \sigma _{\rho }^{{0\,}} + \delta \sigma _{\rho }^{1},\quad \sigma _{\theta }^{{}} = \sigma _{\theta }^{{0\,}} + \delta \sigma _{\theta }^{1},\quad \sigma _{z}^{{}} = \sigma _{z}^{{0\,}} + \delta \sigma _{z}^{1},\quad \tau _{{\rho z}}^{{}} = \tau _{{\rho z}}^{0} + \delta \tau _{{\rho z}}^{1},\quad \rho _{s}^{{}} = \rho _{s}^{0} + \delta \rho _{s}^{1}$

В качестве нулевого приближения было выбрано осесимметричное состояние цилиндрической трубы при плоской деформации. Согласно [5, 9], получаем

$\begin{gathered} \sigma _{\rho }^{{0p}}(t) = 2k(t)\varphi (t){\text{ln}}\frac{\rho }{\alpha } - q(t),\quad \sigma _{\theta }^{{0p}}(t) = - q(t) + 2k(t)\varphi (t)\left( {{\text{1}} + {\text{ln}}\frac{\rho }{\alpha }} \right) \\ \sigma _{z}^{{0p}}\,(t) = \frac{1}{2}(\sigma _{\rho }^{{0p}}(t) + \sigma _{\theta }^{{0p}}(t)),\quad \tau _{{\rho z}}^{{0p}} = \tau _{{\rho z}}^{{0e}} \equiv 0\, \\ \sigma _{\rho }^{{0e}}(t) = \rho _{s}^{0}(t)\left( {1 - \frac{{k(t)\varphi (t)}}{{{{\rho }^{2}}}}} \right),\quad \sigma _{\theta }^{{0e}}(t) = \rho _{s}^{0}(t)\left( {1 + \frac{{k(t)\varphi (t)}}{{{{\rho }^{2}}}}} \right) \\ \sigma _{z}^{{0p}}\,(t) = \rho _{s}^{0}(t) \\ \end{gathered} $

Здесь $\rho _{s}^{0}$ находится из уравнения

$\rho {{_{s}^{0}}^{2}}(t) - 2k(t)\varphi (t)\ln \rho _{s}^{0} = k(t)\varphi (t) - q(t) + 2k(t)\varphi (t)\ln \alpha $

Функция $\varphi (t)$ является решением линейного интегрального уравнения Вольтерра II рода с ядром $K(\tau ) = k(\tau )K_{{}}^{*}(0,\tau )$.

В силу того, что внутренний контур, а также нагрузки на нем не варьируются, имеем

$\sigma _{\rho }^{{1p}} = \sigma _{\theta }^{{1p}}(t) = \sigma _{z}^{{1p}}\,(t) = \tau _{{\rho z}}^{{1p}} = 0\,$

Определим компоненты первого приближения. В упругой области в задачах для первого приближения уравнения равновесия, условие несжимаемости, физические соотношения аналогичны (1), (2), (6). А граничные условия будут такими

(8)
$\mathop {\left. {\sigma _{\rho }^{{1e}}} \right|}\nolimits_{\rho = 1} = 2\rho {{_{s}^{0}}^{2}},\quad \mathop {\left. {\tau _{{\rho z}}^{{1e}}} \right|}\nolimits_{\rho = 1} = - \rho {{_{s}^{0}}^{2}}$

К полученным задачам следует добавить условия непрерывности напряжений на границе пластической зоны $\rho = \rho _{s}^{0}$

(9)
$\mathop {\left. {\sigma _{\rho }^{{1e}}} \right|}\nolimits_{\rho = 1} = 0,\quad \mathop {\left. {\tau _{{\rho z}}^{{1e}}} \right|}\nolimits_{\rho = 1} = 0,\quad \mathop {\left. {\sigma _{\theta }^{{1e}}} \right|}\nolimits_{\rho = 1} = \frac{{4k(t)\varphi (t)}}{{\rho _{s}^{0}}}\rho _{s}^{1},\quad \mathop {\left. {\sigma _{z}^{{1e}}} \right|}\nolimits_{\rho = 1} = \frac{{2k(t)\varphi (t)}}{{\rho _{s}^{0}}}\rho _{s}^{1}$

В [1] показано, что для несжимаемого упругоползучего материала напряжения совпадают с соответствующей мгновенноупругой задачей. Тогда компоненты напряжений в первом приближении имеют вид

$\begin{gathered} \sigma _{\rho }^{{1e}}(t) = \frac{{2\rho {{{_{s}^{0}}}^{2}}}}{{1 - \rho {{{_{s}^{0}}}^{2}}}}\left( {1 - \frac{{\rho {{{_{s}^{0}}}^{2}}}}{{{{\rho }^{2}}}}} \right)z,\quad \sigma _{\theta }^{{0e}}(t) = \frac{{2\rho {{{_{s}^{0}}}^{2}}}}{{1 - \rho {{{_{s}^{0}}}^{2}}}}\left( {1 + \frac{{\rho {{{_{s}^{0}}}^{2}}}}{{{{\rho }^{2}}}}} \right)z \\ \sigma _{z}^{{0e}}(t) = \frac{{2\rho {{{_{s}^{0}}}^{2}}}}{{1 - \rho {{{_{s}^{0}}}^{2}}}}z,\quad \tau _{{\rho z}}^{{1e}}(t) = - \frac{{\rho {{{_{s}^{0}}}^{2}}}}{{1 - \rho {{{_{s}^{0}}}^{2}}}}\left( {\rho - \frac{{\rho {{{_{s}^{0}}}^{2}}}}{{{{\rho }^{2}}}}} \right) \\ \rho _{s}^{1} = \frac{{\rho {{{_{s}^{0}}}^{3}}}}{{1 - \rho {{{_{s}^{0}}}^{2}}}}\frac{1}{{k(t)\varphi (t)}}z \\ \end{gathered} $

Полученные компоненты напряжений для первого приближения при $K(t) \equiv 1$, $\varphi (t) \equiv 1$ с точностью до обозначений совпадают с результатами из [9] для конической трубы из упругопластического материала.

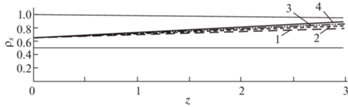
На рис. 1 изображены границы пластической зоны вдоль трубы для следующих функций [5]

$K{\text{*}}(\tau ) = \frac{{\alpha \beta (1 - \beta ){{e}^{{ - \alpha t}}}}}{{{{{(1 - \beta {{e}^{{ - \alpha t}}})}}^{2}}}},\quad \varphi (t) = \frac{{{{{(1 - \beta {{e}^{{ - \alpha t}}})}}^{2}}}}{{{{{(1 - \beta )}}^{2}}}},\quad k(t) = \frac{{1 - \beta {{e}^{{ - \alpha t}}}}}{{1 - \beta }}$
$\alpha = 0.5,\quad \beta = 0,2,\quad \delta = 0.01,\quad q(t) = 2 - 1.2{{e}^{{ - 0.1t}}}$
Рис. 1.

Граница пластической зоны $\rho _{s}^{{}}$ в различные моменты времени.

Кривая 1 соответствуют моменту времени t = 0, а кривые 2–4 – последующим относительным моментам t = 5, 10, 20.

На рис. 2 представлены кривые, показывающие изменение $\rho _{s}^{{}}(t)$ в зависимости от времени для трех сечений: 1 – $z = 0$, 2 – $z = 1$, 3 – $z = 3$.

Рис. 2.

Граница пластической зоны $\rho _{s}^{{}}(t)$.

Согласно [5, 9], в дальнейшем возможно определить и компоненты последующих приближений. Данный подход позволяет получать аналитические зависимости для модели неоднородно стареющего упруговязкопластического тела с упрочнением.

Список литературы

  1. Арутюнян Н.Х., Манжиров А.В. Контактные задачи теории ползучести. Ереван: Институт механики НАН, 1996. 320 с.

  2. Manzhirov A.V. Fundamentals of mechanical design and analysis for am fabricated parts // Proc. Manuf. 2017. V. 7. P. 59–65. https://doi.org/10.1016/j.promfg.2016.12.017

  3. Паршин Д.А. Аналитические решения задачи об аддитивном формировании неоднородного упругого шарового тела в произвольном нестационарном центральном поле сил // Изв. РАН. МТТ. 2017. № 5. С. 70–82.

  4. Арутюнян Н.Х., Ивлев Д.Д. К теории вязкопластичности неоднородно-стареющих тел // Изв. АН АрмССР. Механика. 1996. Т. 35. № 5. С. 22–26.

  5. Милявская Ф.Б. Двухосное растяжение пластины с круговым отверстием из стареющего упругопластического материала // Краевые задачи и их приложения. Чебоксары: Чуваш. Университет, 1986. С. 82–90.

  6. Милявская Ф.Б. О двухосном растяжении толстой пластины с эллиптическим отверстием из стареющего материала // Краевые задачи и их приложения. Чебоксары: Чуваш. университет, 1987. С. 169–174.

  7. Гоцев Д.В., Ковалев А.В., Яковлев А.Ю. Напряженное состояние неограниченного пространства вблизи цилиндрической полости с некруговой формой поперечного сечения для стареющих упруговязкопластических материалов // Изв. РАН. МТТ. 2020. № 6. С. 134–140. https://doi.org/10.31857/S0572329920060082

  8. Гоцев Д.В., Ковалев А.В., Шашкин А.И., Яковлев А.Ю. Об определении поля напряжений в эксцентрической трубе, из стареющего упругопластического материала // Вестник ЧГПУ им. И.Я. Яковлева. Серия: механика предельного состояния. 2020. № 4 (46). С. 93–101. https://doi.org/10.37972/chgpu.2020.46.4.005

  9. Ивлев Д.Д., Ершов Л.В. Метод возмущений в теории упругопластического тела. М.: Наука, 1978. 208 с.

  10. Минаева Н.В. Адекватность математических моделей деформируемых тел. М.: Научная книга, 2006. 236 с.

  11. Спорыхин А.Н., Ковалев А.В., Щеглова Ю.Д. Неодномерные задачи упруговязкопластичности с неизвестной границей. Воронеж: Изд-во ВГУ, 2004. 219 с.

  12. Бицено К.Б., Граммель Р. Техническая динамика. Л.: Гостехиздат, 1950. Т. 1. 900 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска содержание выпуска

Известия РАН. Механика твердого тела

Архивы выпусков Информация о журнале Отправить рукопись в журнал