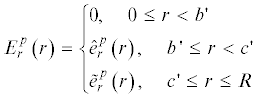Известия РАН. Механика твердого тела, 2022, № 4, стр. 70-84
ТЕРМОДЕФОРМИРОВАНИЕ ТЕЛА СО СЛОЖНОЙ РЕОЛОГИЕЙ В УСЛОВИЯХ СФЕРИЧЕСКОЙ СИММЕТРИИ
Д. А. Чернышов a, b, *, А. В. Ковалев a, c, **
a Воронежский государственный университет
Воронеж, Россия
b Воронежский государственный технический университет
Воронеж, Россия
c Военный учебно-научный центр Военно-воздушных сил «Военно-воздушная академия
им. проф. Н.Е. Жуковского и Ю.А. Гагарина»
Воронеж, Россия
* E-mail: chernyshov.danil@gmail.com
** E-mail: kav-mail@mail.ru
Поступила в редакцию 15.04.2021
После доработки 06.10.2021
Принята к публикации 07.10.2021
- EDN: IGJKZT
- DOI: 10.31857/S0572329922030059
Аннотация
Для изучения влияния реологии тела на его напряженно-деформированное состояние под действием температуры используется модель А.Н. Спорыхина (упрочняющееся упруговязкопластическое тело). Предполагается квазистатическое деформирование при отсутствии массовых и поверхностных сил. Для данной постановки задачи определены компоненты напряжений и перемещений в упругой и пластической областях, зоне разгрузки и повторной пластичности и исследована их зависимость от учета конкретных реологических особенностей тела.
1. Введение. Процессу деформирования материалов (как обратимого, так и необратимого) большое количество работ [1–11], в которых рассматриваются модели с различными свойствами. Наиболее исследованным является вопрос зависимости напряженно-деформированного состояния от выбора условий пластичности [1, 6, 10]. Однако не меньший интерес вызывает рассмотрение в рамках одной модели сразу нескольких механизмов деформирования. Следуя [5], введение в рассмотрение вязкости наделяет модель свойствами внутренней неконсервативности и связано с дополнительными вычислительными сложностями. В данной работе предложен подходов к решению задач с учетом вязких свойств материала, а также установлено влияние различных реологических свойств на процесс деформирования.
2. Постановка задачи. Сплошной шар радиуса $R$ имеет начальную температуру ${{T}_{0}}$. В течение времени он нагревается таким образом, что в каждый момент на поверхности выполнено условие
(2.1)
$\frac{{T\left( {R,t} \right) - {{T}_{0}}}}{{{{T}_{m}} - {{T}_{0}}}} = 1 - {{{\text{e}}}^{{ - xt}}}$где $T\left( {r,t} \right)$ – распределение температуры, $r$ – пространственная координата точки, $t$ – время, $x$ – скорость нагрева, ${{T}_{0}}$ – начальная температура тела, ${{T}_{m}}$ – максимальная температура нагрева. Примем, что внешняя поверхность шара свободна от усилий, массовые силы отсутствуют. Требуется определить напряженно-деформированное состояние тела. Аналогичная постановка задачи произведена в [6] для упругопластического материала.
3. Решение задачи. 3.1. Задача теплопроводности. В условиях сферической симметрии уравнение теплопроводности принимает вид
(3.1)
$\frac{{\partial T\left( {r,t} \right)}}{{\partial t}} = \vartheta \left( {\frac{2}{r}\frac{{\partial T\left( {r,t} \right)}}{{\partial r}} + \frac{{{{\partial }^{2}}T\left( {r,t} \right)}}{{\partial {{r}^{2}}}}} \right)$Начальное и граничные условия (включая (2.1)), а также условие симметрии записываются в виде:
(3.2)
$\begin{gathered} T\left( {r,0} \right) = {{T}_{0}} \\ \frac{{T\left( {R,t} \right) - {{T}_{0}}}}{{{{T}_{m}} - {{T}_{0}}}} = 1 - {{{\text{e}}}^{{ - xt}}} \\ T\left( {0,t} \right) \ne \infty \\ \end{gathered} $Таким образом, получена замкнутая система уравнений (3.1)–(3.2).
Введем замену
(3.3)
$\Psi \left( {r,t} \right) = r\frac{{T\left( {r,t} \right) - {{T}_{m}}}}{{{{T}_{0}} - {{T}_{m}}}}$Будем искать решение в виде суммы
где функция $U\left( {r,t} \right)$ подбирается так, чтобы она удовлетворяла только граничным условиям.Тогда для $V\left( {r,t} \right)$ получим систему уравнений
(3.5)
$\begin{gathered} \frac{{\partial V\left( {r,t} \right)}}{{\partial t}} = \vartheta \frac{{{{\partial }^{2}}V\left( {r,t} \right)}}{{\partial {{r}^{2}}}} - \left[ {\frac{{\partial U\left( {r,t} \right)}}{{\partial t}} - \vartheta \frac{{{{\partial }^{2}}U\left( {r,t} \right)}}{{\partial {{r}^{2}}}}} \right] \\ V\left( {r,0} \right) = r - U\left( {r,0} \right) \\ V\left( {0,t} \right) = V\left( {R,t} \right) = 0 \\ \end{gathered} $Проведем рассмотрение с выбранной функцией
Следуя [12], выпишем решение задачи (3.5)
Возвращаясь к замене (3.3)–(3.4) и вводя безразмерную функцию, получим
(3.6)
$\Theta \left( {\xi ,t} \right) = \frac{{T\left( {\xi ,t} \right) - {{T}_{0}}}}{{{{T}_{m}} - {{T}_{0}}}} = 1 - {{e}^{{ - xt}}} + \sum\limits_{n = 1}^\infty {2{{{\left( { - 1} \right)}}^{n}}\frac{{\sin \left( {\pi n\xi } \right)}}{{\pi n\xi }}\frac{x}{{x - \vartheta \frac{{{{\pi }^{2}}{{n}^{2}}}}{{{{R}^{2}}}}}}} \left[ {{{e}^{{ - \frac{{{{\pi }^{2}}{{n}^{2}}}}{{{{R}^{2}}}}\vartheta t}}} - {{e}^{{ - xt}}}} \right]$В случае рассмотрения мгновенного нагрева поверхности приходим к задаче, решение которой приводится в [13, с. 105].
3.2. Напряженно-деформированное состояние. Общие соотношения. В случае сферической симметрии все величины с индексами углов $\varphi $ и $\theta $ считаются равными между собой. Кроме того, частные производные любой функции по координатам $\varphi $ и $\theta $ будут равны нулю. Запишем основные уравнения, используемые для решения задач механики сплошной среды с учетом реологических свойств и температуры.
Уравнение равновесия:
(3.7)
$\frac{{\partial {{\sigma }_{r}}}}{{\partial r}} + \frac{2}{r}\left( {{{\sigma }_{r}} - {{\sigma }_{\varphi }}} \right) = 0$В пластической зоне свойства материала будут описываться моделью среды, предложенной А.Н. Спорыхиным [5] и учитывающей упругий, вязкий и пластический механизмы деформирования:
(3.8)
${{({{S}_{r}} - ce_{r}^{p} - \eta \dot {e}_{r}^{p})}^{2}} + 2{{({{S}_{\varphi }} - ce_{\varphi }^{p} - \eta \dot {e}_{\varphi }^{p})}^{2}} = 2{{\tilde {k}}^{2}}(r,t)$Ассоциированный закон пластического течения:
(3.9)
$\begin{gathered} {\text{d}}e_{r}^{p} = \frac{4}{3}d\psi ({{\sigma }_{r}} - {{\sigma }_{\varphi }} - c(e_{r}^{p} - e_{\varphi }^{p}) - \eta (\dot {e}_{r}^{p} - \dot {e}_{\varphi }^{p})) \\ {\text{d}}e_{\varphi }^{p} = {\text{d}}e_{\theta }^{p} = - \frac{2}{3}d\psi ({{\sigma }_{r}} - {{\sigma }_{\varphi }} - c(e_{r}^{p} - e_{\varphi }^{p}) - \eta (\dot {e}_{r}^{p} - \dot {e}_{\varphi }^{p})) \\ \end{gathered} $Следуя [6], будем считать, что ${\text{d}}e_{{ij}}^{p} = e_{{ij}}^{p} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{e} _{{ij}}^{p}$, где $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{e} _{{ij}}^{p}$ – пластические деформации в предыдущий момент времени, и существует некоторый начальный момент, для которого $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{e} _{{ij}}^{p} = 0$. Тогда (3.10) примет вид
Преобразовывая (3.8) с учетом (3.11), получим
После замены $\tilde {k}\left( {r,t} \right) = \frac{2}{{\sqrt 3 }}k\left( {r,t} \right)$ условие пластичности запишется в форме
(3.12)
${\text{|}}({{\sigma }_{r}} - ce_{r}^{p} - \eta \dot {e}_{r}^{p}) - ({{\sigma }_{\varphi }} - ce_{\varphi }^{p} - \eta \dot {e}_{\varphi }^{p}){\text{|}} = 2k\left( {r,t} \right)$Аналогичное соотношение можно получить при использовании условий пластичности Треска и Ивлева.
Аналогично [6], будем рассматривать материал, предел текучести которого линейно зависит от температуры $k\left( {r,t} \right) = {{k}_{0}}\left( {1 - \gamma \Delta \left( {r,t} \right)} \right)$, где k0 – предел текучести при начальной температуре, $\gamma $ – некоторая константа, определяемая из экспериментов, Δ(r, t) = = $\alpha \left( {T\left( {r,t} \right) - {{T}_{0}}} \right)$, $\alpha $ – коэффициент температурного расширения.
Закон Дюамеля-Неймана:
(3.13)
$\begin{gathered} {{\sigma }_{r}} = \lambda (e_{r}^{e} + 2e_{\varphi }^{e}) + 2\mu e_{r}^{e} - \left( {3\lambda + 2\mu } \right)\Delta \\ {{\sigma }_{\varphi }} = {{\sigma }_{\theta }} = \lambda (e_{r}^{e} + 2e_{\varphi }^{e}) + 2\mu e_{\varphi }^{e} - \left( {3\lambda + 2\mu } \right)\Delta \\ \end{gathered} $Уравнения для полных деформаций и соотношения Коши:
(3.14)
$\begin{gathered} e_{r}^{e} + e_{r}^{p} = {{e}_{r}} = {{u}_{{r,r}}} \\ e_{\varphi }^{e} + e_{\varphi }^{p} = e_{\theta }^{e} + e_{\theta }^{p} = {{e}_{\varphi }} = {{e}_{\theta }} = \frac{{{{u}_{r}}}}{r} \\ \end{gathered} $3.3. Построение общего алгоритма определения напряженно-деформированного состояния. Поскольку безразмерное решение для поля температур имеет вид (3.6), то все величины будем искать в форме
(3.15)
$F\left( {r,t} \right) = \sum\limits_{j = 1}^2 {\sum\limits_{n = 0}^\infty {{{F}^{{\left[ {n,j} \right]}}}\left( r \right){{e}^{{ - h\left[ {n,j} \right]t}}}} } $Очевидно, что $\Delta \left( {r,t} \right) = {{\Delta }_{m}}\Theta \left( {\frac{r}{R},t} \right)$, где ${{\Delta }_{m}} = \alpha \left( {{{T}_{m}} - {{T}_{0}}} \right)$. Кроме того, можно разложить предел текучести в ряд:
Здесь
(3.16)
${{\delta }^{{\left[ {0,1} \right]}}} = 1;\quad {{\delta }^{{\left[ {0,2} \right]}}} = 0;\quad \forall n > 0\quad {{\delta }^{{\left[ {n,1} \right]}}} = {{\delta }^{{\left[ {n,2} \right]}}} = 0$Подставив (3.15) в (3.7), (3.11), (3.12)–(3.14), получим полную систему уравнений. Очевидно, что все величины в ней представляют собой ряды, и каждое из уравнений имеет вид $\sum\limits_{j = 1}^2 {\sum\limits_{n = 0}^\infty {{{G}^{{\left[ {n,j} \right]}}}\left( r \right){{e}^{{ - h\left[ {n,j} \right]t}}}} } = 0$. Поскольку данное условие выполняется в любой точке $0 \leqslant r \leqslant R$ и для любого момента времени $t \geqslant 0$, то из него следует условие равенства нулю каждого члена ряда. В дальнейшем для удобства будем опускать индексы [n, j]. Таким образом, получим полную систему уравнений для определения всех членов разложения искомых величин в форме:
(3.17)
$\frac{{\partial {{\sigma }_{r}}}}{{\partial r}} + \frac{2}{r}\left( {{{\sigma }_{r}} - {{\sigma }_{\varphi }}} \right) = 0$(3.18)
${\text{|}}({{\sigma }_{r}} - \left( {c - \eta h} \right)e_{r}^{p}) - ({{\sigma }_{\varphi }} - \left( {c - \eta h} \right)e_{\varphi }^{p}){\text{|}} = 2k\left( r \right)$(3.20)
$\begin{gathered} {{\sigma }_{r}} = \lambda (e_{r}^{e} + 2e_{\varphi }^{e}) + 2\mu e_{r}^{e} - \left( {3\lambda + 2\mu } \right)\Delta \left( r \right) \\ {{\sigma }_{\varphi }} = {{\sigma }_{\theta }} = \lambda (e_{r}^{e} + 2e_{\varphi }^{e}) + 2\mu e_{\varphi }^{e} - \left( {3\lambda + 2\mu } \right)\Delta \left( r \right) \\ \end{gathered} $(3.21)
$\begin{gathered} e_{r}^{e} + e_{r}^{p} = {{e}_{r}} = {{u}_{{r,r}}} \\ e_{\varphi }^{e} + e_{\varphi }^{p} = e_{\theta }^{e} + e_{\theta }^{p} = {{e}_{\varphi }} = {{e}_{\theta }} = \frac{{{{u}_{r}}}}{r} \\ \end{gathered} $Предположим, что в начальный момент времени тело полностью находилось в упругом состоянии, и по мере нагревания на его поверхности возникают и двигаются по направлению к центру зоны пластического и остаточного деформирования. Для определения напряженно-деформированного состояния будем осуществлять следующую последовательность действий:
1. Из соотношений Коши (3.21) получить
2. Подставляя закон Дюамеля–Неймана (3.20) и учитывая условие пластической несжимаемости (3.19) и уравнение равновесия (3.17), записать соотношение
3. Решая полученное уравнение, выписать выражение напряжений через пластические деформации;
4. В случае пластического деформирования подставить формулы для напряжений в условие пластичности (3.18) и решить его относительно пластических деформаций;
5. Возвращаясь к закону Дюамеля–Неймана и соотношениям Коши, получить формулу для перемещений;
6. Из граничных условий и условий сопряжения найти константы интегрирования.
3.4. Решения для каждой зоны. В начальный момент времени тело находится в состоянии упругого равновесия. Поэтому во всем шаре решение записывается в виде
(3.22)
$\begin{gathered} {{\sigma }_{r}} = - \frac{{4\omega }}{{{{r}^{3}}}}\int\limits_0^r {{{\rho }^{2}}\Delta \left( \rho \right){\text{d}}\rho } + {{A}_{1}} + \frac{{{{B}_{1}}}}{{{{r}^{3}}}} \\ {{\sigma }_{\varphi }} = \frac{{2\omega }}{{{{r}^{3}}}}\int\limits_0^r {{{\rho }^{2}}\Delta \left( \rho \right){\text{d}}\rho } - 2\omega \Delta \left( r \right) + {{A}_{1}} - \frac{{{{B}_{1}}}}{{2{{r}^{3}}}} \\ u = \frac{\omega }{{\mu {{r}^{2}}}}\int\limits_0^r {{{\rho }^{2}}\Delta \left( \rho \right){\text{d}}\rho } + \frac{{r{{A}_{1}}}}{{3\lambda + 2\mu }} - \frac{{{{B}_{1}}}}{{4\mu {{r}^{2}}}} \\ \end{gathered} $Неизвестные постоянные определяются из условий свободной от усилий поверхности и отсутствия перемещений в центре:
В некоторый момент $t = {{t}_{p}}$ на поверхности шара $r = R$ начинает выполняться условие пластичности
(3.23)
$({{\sigma }_{r}} - \left( {c - \eta h} \right)e_{r}^{p}) - ({{\sigma }_{\varphi }} - \left( {c - \eta h} \right)e_{\varphi }^{p}) = 2k\left( r \right)$В связи с этим при $t > {{t}_{p}}$ в шаре одновременно существуют область $0 \leqslant r < a\left( t \right)$ обратимого и $a\left( t \right) \leqslant r \leqslant R$ необратимого деформирования. a(t) – упругопластическая граница.
В упругой зоне напряжения и перемещение определяются по формулам (3.22) с точностью до новых констант интегрирования. В пластической зоне решение принимает вид
(3.24)
$\begin{gathered} {{\sigma }_{r}} = \left\{ { - \frac{{4\omega }}{{{{r}^{3}}}}\int\limits_a^r {{{\rho }^{2}}\Delta \left( {\rho ,t} \right){\text{d}}\rho } + {{A}_{2}} + \frac{{{{B}_{2}}}}{{{{r}^{3}}}}} \right\} - \frac{{8\omega }}{{3\eta \left( {\Omega - h} \right)}}\int\limits_a^r {\frac{{k\left( \rho \right)}}{\rho }{\text{d}}\rho } + \\ + \frac{{8{{\omega }^{2}}}}{{3\eta \left( {\Omega - h} \right)}}\frac{1}{{{{r}^{3}}}}\int\limits_a^r {{{\rho }^{2}}\Delta \left( \rho \right){\text{d}}\rho } - \frac{{2\omega }}{{3\eta \left( {\Omega - h} \right)}}\frac{{{{B}_{2}}}}{{{{r}^{3}}}} \\ {{\sigma }_{\varphi }} = \left\{ {\frac{{2\omega }}{{{{r}^{3}}}}\int\limits_a^r {{{\rho }^{2}}\Delta \left( \rho \right){\text{d}}\rho } - 2\omega \Delta \left( r \right) + {{A}_{2}} - \frac{{{{B}_{2}}}}{{2{{r}^{3}}}}} \right\} - \frac{{8\omega }}{{3\eta \left( {\Omega - h} \right)}}\int\limits_a^r {\frac{{k\left( \rho \right)}}{\rho }{\text{d}}\rho } - \\ - \frac{{4{{\omega }^{2}}}}{{3\eta \left( {\Omega - h} \right)}}\frac{1}{{{{r}^{3}}}}\int\limits_a^r {{{\rho }^{2}}\Delta \left( \rho \right){\text{d}}\rho } - \frac{{4\omega }}{{3\eta \left( {\Omega - h} \right)}}k\left( r \right) + \frac{{4{{\omega }^{2}}}}{{3\eta \left( {\Omega - h} \right)}}\Delta \left( r \right) + \frac{\omega }{{3\eta \left( {\Omega - h} \right)}}\frac{{{{B}_{2}}}}{{{{r}^{3}}}} \\ u = \left\{ {\frac{\omega }{{\mu {{r}^{2}}}}\int\limits_a^r {{{\rho }^{2}}\Delta \left( {\rho ,t} \right){\text{d}}\rho } + \frac{{r{{A}_{2}}}}{{3\lambda + 2\mu }} - \frac{{{{B}_{2}}}}{{4\mu {{r}^{2}}}}} \right\} - \frac{{8\omega }}{{3\eta \left( {\Omega - h} \right)\left( {3\lambda + 2\mu } \right)}}r\int\limits_a^r {\frac{{k\left( \rho \right)}}{\rho }{\text{d}}\rho } + \\ + \frac{{8{{\omega }^{2}}}}{{3\eta \left( {\Omega - h} \right)\left( {3\lambda + 2\mu } \right)}}\frac{1}{{{{r}^{2}}}}\int\limits_a^r {{{\rho }^{2}}\Delta \left( \rho \right){\text{d}}\rho } - \frac{{2\omega }}{{3\eta \left( {\Omega - h} \right)\left( {3\lambda + 2\mu } \right)}}\frac{{{{B}_{2}}}}{{{{r}^{2}}}}, \\ \end{gathered} $Константы интегрирования для обеих зон находятся из граничных условий, а также условий сопряжения напряжений и перемещений на границе $a\left( t \right)$:
Положение a(t) определяется из отсутствия на ней пластических деформаций, выполнения условия пластичности (3.23) для напряжений (3.22) или непрерывности окружных напряжений на границе (данные условия являются эквивалентными):
По мере нагревания температурные напряжения в теле уменьшаются. Это приводит к снижению уровня пластических деформаций. Согласно ассоциированному закону, их скорость не может быть отрицательной. Пусть в некоторый момент $t = {{t}_{u}}$ на поверхности шара выполняется условие разгрузки материала
Тогда при $t > {{t}_{u}}$ возникает новая область с границей b(t). Следует заметить, что в каждой точке области $b\left( t \right) \leqslant r \leqslant R$ сохраняется уровень накопленной деформации ${{\hat {e}}^{p}}$, равный пластической деформации в этой точке в момент прохождения через нее границы b(t).
В зонах упругости и пластичности решение записывается по уже известным формулам (3.22) и (3.24). Выражения в зоне разгрузки имеют вид
(3.25)
$\begin{gathered} {{\sigma }_{r}} = \left\{ { - \frac{{4\omega }}{{{{r}^{3}}}}\int\limits_b^r {{{\rho }^{2}}\Delta \left( \rho \right){\text{d}}\rho } + {{A}_{3}} + \frac{{{{B}_{3}}}}{{{{r}^{3}}}}} \right\} + 2\omega \mathop \smallint \limits_b^r \frac{{\hat {e}_{r}^{p}\left( \rho \right)}}{\rho }{\text{d}}\rho \\ {{\sigma }_{\varphi }} = \left\{ {\frac{{2\omega }}{{{{r}^{3}}}}\int\limits_b^r {{{\rho }^{2}}\Delta \left( \rho \right){\text{d}}\rho } - 2\omega \Delta \left( r \right) + {{A}_{3}} - \frac{{{{B}_{3}}}}{{2{{r}^{3}}}}} \right\} + 2\omega \mathop \smallint \limits_b^r \frac{{\hat {e}_{r}^{p}\left( \rho \right)}}{\rho }{\text{d}}\rho + 2\omega \hat {e}_{r}^{p}\left( r \right) \\ u = \left\{ {\frac{\omega }{{\mu {{r}^{2}}}}\int\limits_b^r {{{\rho }^{2}}\Delta \left( \rho \right){\text{d}}\rho } + \frac{{r{{A}_{3}}}}{{3\lambda + 2\mu }} - \frac{{{{B}_{3}}}}{{4\mu {{r}^{2}}}}} \right\} + \frac{{2\omega }}{{3\lambda + 2\mu }}r\mathop \smallint \limits_b^r \frac{{\hat {e}_{r}^{p}\left( \rho \right)}}{\rho }{\text{d}}\rho \\ \end{gathered} $Далее необходимо воспользоваться граничными условиями и условиями сопряжения на упругопластических границах и определить из них неизвестные константы:
Положение границы b(t) при $t > {{t}_{u}}$ определяется из условия равенства нулю скорости пластических деформаций на ней
(3.26)
$\dot {e}_{r}^{p}\left( {b,t} \right) = \sum\limits_{j = 1}^2 {\sum\limits_{n = 0}^\infty {\frac{{2\omega ( - {{h}^{{\left[ {n,j} \right]}}})}}{{3\eta (\Omega - {{h}^{{\left[ {n,j} \right]}}})}}\left\{ {2{{\Delta }^{{\left[ {n,j} \right]}}}\left( b \right) - \frac{{2{{k}^{{\left[ {n,j} \right]}}}\left( b \right)}}{\omega } - \frac{6}{{{{b}^{3}}}}\int\limits_0^b {{{\rho }^{2}}{{\Delta }^{{\left[ {n,j} \right]}}}\left( \rho \right){\text{d}}\rho } } \right\}{{e}^{{ - h\left[ {n,j} \right]t}}}} } = 0$Определим уровень накопленной деформации $\hat {e}_{r}^{p}$. Поскольку b(t), вычисляемая из (3.26), непрерывна и монотонно убывает, то существует обратная ей функция s(b). Тогда накопленные деформации имеют вид
что эквивалентно поиску огибающей семейства пластических деформаций с параметром t. Так как $\hat {e}_{r}^{p}$ не зависит от времени, то будем считать, что она состоит только из одного ненулевого слагаемого вида $\hat {e}{{_{r}^{p}}^{{\left[ {0,1} \right]}}}\left( r \right) = \sum\limits_{j = 1}^2 {\sum\limits_{n = 0}^\infty {e{{{_{r}^{p}}}^{{\left[ {n,j} \right]}}}\left( r \right){{e}^{{ - h\left[ {n,j} \right]s\left( r \right)}}}} } $. Поэтому (3.25) справедливы только для напряжений и перемещений с индексом [0, 1], а для всех остальных следует делать подстановку $\hat {e}{{_{r}^{p}}^{{\left[ {n,j} \right]}}}\left( r \right) = 0$.В зависимости от уровня накопленных деформаций возможно существование момента $t = {{t}_{r}}$, при котором происходит выход на условие пластичности (3.23) с противоположным знаком:
Решение в новой области совпадает с решением (3.24) в зоне $a\left( t \right) \leqslant r < b\left( t \right)$ с точностью до новых постоянных и знака перед пределом текучести:
(3.28)
$\begin{gathered} {{\sigma }_{r}} = \left\{ { - \frac{{4\omega }}{{{{r}^{3}}}}\int\limits_c^r {{{\rho }^{2}}\Delta \left( {\rho ,t} \right){\text{d}}\rho } + {{A}_{4}} + \frac{{{{B}_{4}}}}{{{{r}^{3}}}}} \right\} + \frac{{8\omega }}{{3\eta \left( {\Omega - h} \right)}}\int\limits_c^r {\frac{{k\left( \rho \right)}}{\rho }{\text{d}}\rho } + \\ + \frac{{8{{\omega }^{2}}}}{{3\eta \left( {\Omega - h} \right)}}\frac{1}{{{{r}^{3}}}}\int\limits_c^r {{{\rho }^{2}}\Delta \left( \rho \right){\text{d}}\rho } - \frac{{2\omega }}{{3\eta \left( {\Omega - h} \right)}}\frac{{{{B}_{4}}}}{{{{r}^{3}}}} \\ {{\sigma }_{\varphi }} = \left\{ {\frac{{2\omega }}{{{{r}^{3}}}}\int\limits_c^r {{{\rho }^{2}}\Delta \left( \rho \right){\text{d}}\rho } - 2\omega \Delta \left( r \right) + {{A}_{4}} - \frac{{{{B}_{4}}}}{{2{{r}^{3}}}}} \right\} + \frac{{8\omega }}{{3\eta \left( {\Omega - h} \right)}}\int\limits_c^r {\frac{{k\left( \rho \right)}}{\rho }{\text{d}}\rho } - \\ - \frac{{4{{\omega }^{2}}}}{{3\eta \left( {\Omega - h} \right)}}\frac{1}{{{{r}^{3}}}}\int\limits_c^r {{{\rho }^{2}}\Delta \left( \rho \right){\text{d}}\rho } + \frac{{4\omega }}{{3\eta \left( {\Omega - h} \right)}}k\left( r \right) + \frac{{4{{\omega }^{2}}}}{{3\eta \left( {\Omega - h} \right)}}\Delta \left( r \right) + \frac{\omega }{{3\eta \left( {\Omega - h} \right)}}\frac{{{{B}_{4}}}}{{{{r}^{3}}}} \\ u = \left\{ {\frac{\omega }{{\mu {{r}^{2}}}}\int\limits_c^r {{{\rho }^{2}}\Delta \left( {\rho ,t} \right){\text{d}}\rho } + \frac{{r{{A}_{4}}}}{{3\lambda + 2\mu }} - \frac{{{{B}_{4}}}}{{4\mu {{r}^{2}}}}} \right\} + \frac{{8\omega }}{{3\eta \left( {\Omega - h} \right)\left( {3\lambda + 2\mu } \right)}}r\int\limits_c^r {\frac{{k\left( \rho \right)}}{\rho }{\text{d}}\rho } + \\ + \frac{{8{{\omega }^{2}}}}{{3\eta \left( {\Omega - h} \right)\left( {3\lambda + 2\mu } \right)}}\frac{1}{{{{r}^{2}}}}\int\limits_c^r {{{\rho }^{2}}\Delta \left( \rho \right){\text{d}}\rho } - \frac{{2\omega }}{{3\eta \left( {\Omega - h} \right)\left( {3\lambda + 2\mu } \right)}}\frac{{{{B}_{4}}}}{{{{r}^{2}}}} \\ \end{gathered} $Для определения констант интегрирования следует исходить из граничных условий, а также условий сопряжения напряжений и перемещений на упругопластических границах. Возможны различные варианты одновременного существования зон. Рассмотрим случай, при котором в теле присутствует каждая из рассмотренных областей. Тогда неизвестные постоянные принимают вид
Положение границы c(t) находится аналогично a(t) из уравнения
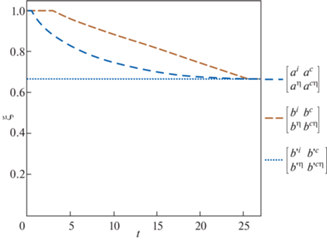
В процесс деформирования существует момент времени $t = {{t}_{k}}$, при котором положение границ $a\left( {{{t}_{k}}} \right)$ и $b\left( {{{t}_{k}}} \right)$ совпадает, то есть первая зона пластического деформирования перестает существовать. Тогда в зоне $0 \leqslant r \leqslant c\left( t \right)$ устанавливается состояние разгрузки, а упругопластические границы достигают своего предельного положения $a\left( {{{t}_{k}}} \right) = b\left( {{{t}_{k}}} \right) = b{\kern 1pt} '$. В зависимости от температурного воздействия момент $t = {{t}_{k}}$ может наступить как до, так и после возникновения зоны повторного пластического течения.
При полном нагреве до температуры ${{T}_{m}}$ в момент времени $t = {{t}_{m}}$ положение границы c(t) достигает предельного положения $c{\kern 1pt} '$, а скорость пластического деформирования становится равной нулю. Тогда в области $c{\kern 1pt} ' \leqslant r \leqslant R$ имеют место остаточные деформации $\tilde {e}_{r}^{p}$. Выражение для них записывается в виде
Так как при полном нагреве $\Theta \left( {\frac{r}{R},{{t}_{m}}} \right) = 1$, то $\Delta _{m}^{{\left[ {0,1} \right]}}\, = \,1;{\text{ }}\Delta _{m}^{{\left[ {0,2} \right]}}\, = \,0;{\text{ }}\forall n\, > \,0{\text{ }}\Delta _{m}^{{\left[ {n,1} \right]}}\, = \,\Delta _{m}^{{\left[ {n,2} \right]}}$ = 0. С учетом (3.16), выражение для остаточных деформаций принимает вид
Для простоты введем функцию остаточных деформаций
Охладим теперь шар до начальной температуры. Запишем условие полного остывания:
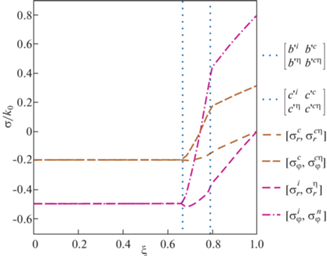
Данный процесс представляет собой разгрузку материала. С учетом (3.25) и (3.29), получим выражения для остаточных напряжений и деформаций
(3.30)
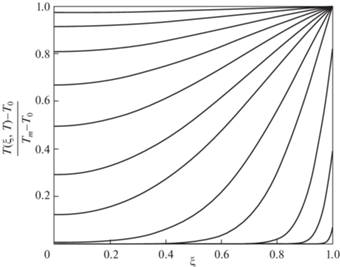
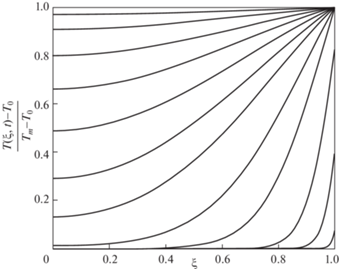
$\begin{gathered} {{\sigma }_{r}} = 2\omega \mathop \smallint \limits_R^r \frac{{E_{r}^{p}\left( \rho \right)}}{\rho }{\text{d}}\rho \\ {{\sigma }_{\varphi }} = 2\omega \mathop \smallint \limits_R^r \frac{{E_{r}^{p}\left( \rho \right)}}{\rho }{\text{d}}\rho + 2\omega E_{r}^{p}\left( r \right) \\ u = \frac{{2\omega }}{{3\lambda + 2\mu }}r\mathop \smallint \limits_R^r \frac{{E_{r}^{p}\left( \rho \right)}}{\rho }{\text{d}}\rho \\ \end{gathered} $4. Анализ решения. Обоснование применимости метода решения задачи теплопроводности приводится в [12]. Однако дополнительно необходимо проверить, что все полученные величины достаточное количество раз непрерывно дифференцируемы и интегрируемы, чтобы удовлетворять уравнениям задачи. Этот вопрос (как и выбор оптимального количества членов ряда и скорость сходимости при малых t) представляет собой отдельную тему исследования и не приводится в рамках данной работы. В дальнейшем будем рассматривать постоянное количество членов каждого из рядов. С целью определения достаточности подобранного числа членов на примере задачи теплопроводности было проведено численное интегрирование краевой задачи в программной системе конечно-элементного анализа с последующей визуальной оценкой графических зависимостей. На рис. 1 и 2 представлено распределение поля безразмерной температуры, полученное аналитически и с применением численных методов решения дифференциальных уравнений, в одни и те же моменты времени.
Для сравнения моделей, учитывающих различные свойства материала, необходимо совершить предельный переход. Для рассмотрения модели без упрочнения материала, необходимо в полученном решении задаться c = 0. Чтобы в общем случае исключить из рассмотрения вязкость, следует положить $\eta = 0$. Тогда во всех выражениях следует заменить коэффициенты вида $3\eta \left( {\Omega - h} \right)$ на $3с + 2\omega $. Если дополнительно приравнять c = 0, то получится решение для случая упругопластического материала. Можно легко убедиться, что для каждого члена ряда оно в точности совпадает с решением [6].
Проведем сравнение для четырех моделей сред. В дальнейшем будем пользоваться следующими индексами для основных величин: $i$ – упругопластический материал, c – упругопластический материал с упрочнением, $\eta $ – упруговязкопластический материал без упрочнения, $c\eta $ – упруговязкопластический материал с упрочнением. В качестве примера рассмотрим тело со следующими параметрами: $R = 0.2$ м, $x = 1$ c–1, $\vartheta = 1.172 \times {{10}^{{ - 4}}}$ м2 ⋅ с–1, ${{\Delta }_{m}} = 8.5$ × 10–3, ${{k}_{0}} = 2$ × 108 Па, $\gamma = 70.6$, $\lambda = 9.2 \times {{10}^{{10}}}$ Па, $\mu = 4.3 \times {{10}^{{10}}}$ Па, $c = 0.9 \times {{10}^{{11}}}$ Па, $\eta = 1.0 \times {{10}^{{10}}}$ Па ⋅ c.
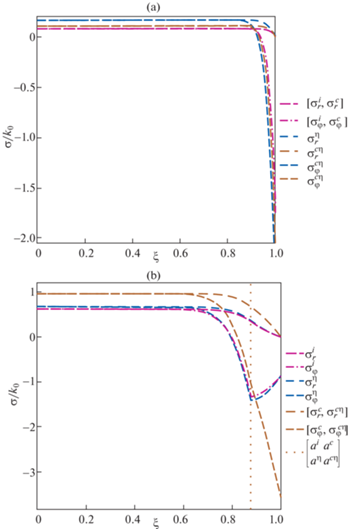
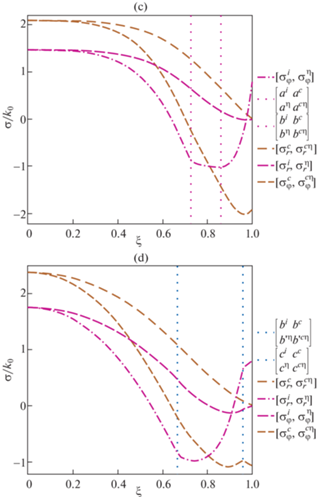
В табл. 1 приведены численные значения моментов возникновения новых зон, а также положение упругопластических границ в эти моменты. На рис. 3 представлено распределение радиальных и окружных напряжений в шаре для каждой из моделей сред в различные моменты времени: (a) – возникновение зоны пластического течения, (b) – возникновение зоны разгрузки, (c) – возникновение зоны повторного пластического течения, (d) – исчезновение первой зоны пластического течения. В случае упругопластического материала полученные графики совпадают с приведенными в [6]. То же справедливо и для остаточных напряжений в теле (см. рис. 4).
Таблица 1.
Значения моментов возникновения зон (в секундах) и положения границ (безразмерные)
| $i$ | $c$ | $\eta $ | $c\eta $ | |
|---|---|---|---|---|
| ${{t}_{p}}$ | 0.28166 | 0.28166 | 0.47532 | 0.35202 |
| ${{t}_{u}}$ | 2.98776 | 2.98776 | 3.17949 | 3.05806 |
| $a\left( {{{t}_{u}}} \right)$ | 0.87561 | 0.87561 | 0.87514 | 0.87554 |
| ${{t}_{r}}$ | 11.75536 | 11.75536 | 11.96710 | 11.82847 |
| $a\left( {{{t}_{r}}} \right)$ | 0.72574 | 0.72574 | 0.72537 | 0.72569 |
| $b\left( {{{t}_{r}}} \right)$ | 0.85930 | 0.85930 | 0.85881 | 0.85923 |
| ${{t}_{k}}$ | 25.31517 | 25.31517 | 25.48840 | 25.38286 |
| $a\left( {{{t}_{k}}} \right) = b\left( {{{t}_{k}}} \right) = b{\kern 1pt} '$ | 0.66649 | 0.66649 | 0.66650 | 0.66649 |
| $c\left( {{{t}_{k}}} \right)$ | 0.95746 | 0.95746 | 0.95752 | 0.95747 |
| $c\left( {{{t}_{m}}} \right) = c{\kern 1pt} '$ | 0.79004 | 0.79004 | 0.79006 | 0.79005 |
На рис. 5 представлен график возникновения, развития во времени и исчезновения первой зоны пластического течения.
5. Заключение. В работе было получено аналитическое решение задачи о напряженно-деформированном состоянии нагреваемого сплошного шара с реологическими свойствами; совершены предельные переходы к упругопластическому материалу, упруговязкопластическому материалу и упрочняющемуся упругопластическому материалу; проведено сравнение с уже имеющимися результатами; построены графики распределения напряжений в шаре при отличающихся механизмах деформирования.
Анализ решения позволил сформулировать следующие выводы:
1. Учет упрочнения материала оказывает существенное влияние на величину напряжений.
2. При отсутствии вязкости упрочнение не влияет на положение упругопластических границ.
3. Влияние вязкости на величину напряжений быстро уменьшается с течением времени. Остаточные деформации при полном нагреве не зависят от данного параметра.
4. Предельные положения границ для всех четырех моделей материалов можно считать одинаковыми.
Список литературы
Качанов Л.М. Основы теории пластичности. М.: Наука, 1969. 420 с.
Паркус Г. Неустановившиеся температурные напряжения. М.: Физматгиз, 1963. 252 с. = Parkus H. Instationäre Wärmespannungen. Vienna: Springer, 1959.
Боли Б., Уэйнер Дж. Теория температурных напряжений. М.: Мир, 1964. 517 c. = Boley B.A., Weiner J.H. Theory of Thermal Stresses. N. Y.: Wiley, 1960.
Спорыхин А.Н., Ковалев А.В., Щеглова Ю.Д. Неодномерные задачи упруговязкопластичности с неизвестной границей. Воронеж: ВГУ, 2004. 218 с.
Спорыхин А.Н. Метод возмущений в задачах устойчивости сложных сред. Воронеж: ВГУ. 1997. 361 с.
Дац Е.П. Неустановившиеся температурные напряжения в условиях зависимости предела текучести от температуры. Дис. канд. физ.-мат. наук. Владивосток, 2017. С. 23–48.
Буренин А.А., Ковтанюк Л.В., Лушпей А.В. Переходный процесс торможения прямолинейного вязкопластического течения при мгновенном снятии нагружающих усилий // Прикладная математика и механика. 2009. № 4. С. 663–669.
Мурашкин Е.В., Дац Е.П. Термоупругопластическое деформирование многослойного шара // Изв. РАН. МТТ. 2017. № 5. С. 30–36.
Дац Е.П., Мокрин С.Н., Мурашкин Е.В. Расчет накопленной остаточной деформации в процессе “нагрева-охлаждения” упругопластического шара // Вестн. ЧГПУ им. И.Я. Яковлева. Сер.: Мех. пред. сост. 2012. № 4. С. 123–132.
Артемов М.А., Барановский Е.С., Якубенко А.П. Альтернативные формы записи кусочно-линейных условий пластичности и их обобщения // Вестн. Воронеж. гос. ун-та. Сер.: Физ. Мат. 2015. № 1. С. 71–82.
Галанин М.П., Гузев М.А., Низкая Т.В. Численное решение задачи термопластичности с дополнительными параметрами состояния. Препринт № 8. М.: ИПМ им. М.В. Келдыша РАН, 2007. 20 с.
Карташов Э.М. Аналитические методы в теплопроводности твердых тел. М.: Высшая школа, 1979. 415 с.
Лыков А.В. Теория теплопроводности. М.: Высшая школа, 1967. 600 с.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика твердого тела