Известия РАН. Механика твердого тела, 2022, № 4, стр. 3-24
РАВНОВЕСИЕ ПОЛИМЕРНЫХ ГЕЛЕЙ В ПОЛЕ МАССОВЫХ СИЛ
a Институт механики сплошных сред Уральского отделения РАН
Пермь, Россия
* E-mail: denisyuk@icmm.ru
Поступила в редакцию 26.06.2021
После доработки 13.08.2021
Принята к публикации 13.08.2021
- EDN: OTKBWV
- DOI: 10.31857/S0572329922030072
Аннотация
На основе вариационного подхода сформулированы краевые задачи, описывающие состояние термодинамического равновесия полимерных гелей, находящихся в поле массовых сил. Полимерный гель рассматривается как смесь, представляющая собой упругий материал и растворенную в нем жидкость (растворитель). Общая теория применена для изучения деформационного поведения полимерных гелей и пластифицированных полимерных материалов в поле силы тяжести. В рамках модельной задачи, описывающей состояние равновесия геля в форме плоского слоя, установлены условия, при которых растворитель или пластификатор способен под действием силы тяжести выделяться из полимера. В частности, получены соотношения, позволяющие оценить критические значения параметров, при которых происходит выделение растворителя, а также рассчитать количество выделившейся из материала жидкости.
1. Введение. Полимерные гели – это сетчатые полимеры, содержащие жидкость (растворитель) и находящиеся в высокоэластичном состоянии. На молекулярном уровне они представляют собой пространственную полимерную сетку, состоящую из длинных и гибких макромолекулярных цепей, соединенных между собой химическими связями. Межцепное пространство полимерной сетки заполняет растворитель. Благодаря такому строению полимерные гели способны испытывать большие упругие деформации. В рамках механики сплошных сред их естественной моделью является смесь, представляющая собой упругий материал и растворенную в нем жидкость. К смесям такого рода также относятся многие пластифицированные полимеры и набухшие в растворителе эластомеры.
Благодаря свойству поглощать и удерживать в себе большие объемы жидкости, многократно (в десятки и в сотни раз) превосходящие исходный объем полимера, полимерные гели находят применение в медицине и фармакологии, в биотехнологии, в технологиях разделения жидких смесей и во многих других современных технологиях [1–17].
Растворенная в полимере жидкость оказывает существенное влияние на его упругие свойства и деформационное поведение. В частности, внешние механические нагрузки могут вызывать миграцию и перераспределение жидкости внутри материала. При этом, достаточно большие сжимающие нагрузки могут приводить к выделению части жидкости из полимера во внешнюю среду, что вызывает частичную релаксацию внутренних напряжений. Важным случаем таких нагрузок являются массовые силы, в частности, поле тяжести, в котором полимерные гели могут демонстрировать весьма сложное и нетривиальное поведение [18–21].
Данная работа посвящена формулировке краевых задач, описывающих напряженно-деформированное состояние полимерных гелей в поле массовых сил, находящихся в состоянии термодинамического равновесия. Такие состояния возникают при статическом нагружении гелей после завершения диффузионных процессов, связанных с перераспределением растворителя внутри материала и массообменом с внешней средой.
Уравнения равновесия гелей можно вывести, используя различные подходы. Например, можно обратиться к теории смесей [22], основы которой заложены Трусделлом [23]. Основная задача этой теории состоит в описании неравновесных процессов. Она также позволяет формулировать статические задачи и описывать равновесные состояния смесей. Однако в теории смесей Трусделла используются нетрадиционные (с точки зрения классической термодинамики) параметры состояния системы – парциальные тензоры напряжений, характеризующие механические напряжения, действующие в каждом из компонентов смеси, и внутренние силы, описывающие взаимодействие между компонентами. По существу, для применения теории смесей Трусделла к растворам (в частности, к полимерным растворам), требуется применять особый вариант механики и равновесной термодинамики, в котором текущее состояние смеси должно описываться в терминах этих парциальных величин. Это приводит к значительным трудностям при формулировке граничных условий, характеризующих механическое нагружение материала и его взаимодействие с внешней средой [22].
В работе [24] показано, что используя подход Трусделла в качестве отправной точки, теорию смесей можно сформулировать в терминах классической термодинамики – глобального тензора напряжений и химического потенциала растворителя. Применение предложенной в [24] теории к полимерам, позволило описать неравновесные процессы их набухания в растворителях, в частности, объяснить так называемые аномалии кинетических кривых набухания и предложить новые экспериментальные методы исследования термодинамических и диффузионных свойств сетчатых полимеров [24–27]. В качестве частных случаев из нее вытекают уравнения, описывающие состояние смеси в условиях термодинамического и механического равновесия.
В работе [28] показано, что уравнения равновесия геля можно вывести на основе вариационного подхода, используя известный в классической термодинамике факт, что свободная энергия макроскопической системы в состоянии равновесия достигает свой минимум, и равновесное состояние системы может быть определено из решения задачи минимизации функционала свободной энергии системы. В этом случае система уравнений и граничных условий, описывающая состояние равновесия геля, представляет собой уравнения Эйлера–Лагранжа соответствующей вариационной задачи. На основе вариационного подхода были сформулированы основные типы краевых задач, описывающих напряженно-деформированное состояние полимерных гелей в условиях механического и термодинамического равновесия при конечных деформациях [28] и в приближении малых деформаций [29].
В данной работе вывод уравнений равновесия гелей осуществляется с помощью второго подхода, то есть вариационного. Это делается из следующих соображений. Во-первых, при таком подходе, в отличие от теории смесей Трусделла, состояние геля сразу же удается описать в традиционных терминах глобального тензора напряжений и химического потенциала растворителя, что делает теорию более прозрачной как с точки зрения термодинамики растворов, так и механики деформируемого твердого тела. Во-вторых, удается установить связь между задачами механики полимерных гелей и статическими задачами теории упругости. Наконец, вариационный подход может оказаться более предпочтительным с математической точки зрения, так как в настоящее время он является наиболее эффективным методом исследования нелинейных краевых задач и построения численных методов их решения [30].
2. Постановка задачи. Рассмотрим образец полимерного геля в ненагруженном состоянии с однородным распределением растворителя. Это исходное состояние геля примем в качестве отсчетного. Будем полагать, что деформирование геля происходит в атмосфере. Гель будем считать химически инертным, однородным и изотропным материалом, а растворитель – нелетучей жидкостью. Последнее обстоятельство позволяет пренебречь эффектами, связанными с испарением растворителя, и делает общее количество растворителя ${{\mathcal{N}}_{1}}$ в системе (измеряемое в молях) сохраняющейся величиной.
Пусть Ω0 – ограниченная область пространства, которую занимает гель в отсчетной конфигурации. Материальную систему координат свяжем с полимерной матрицей геля. Положение материальных частиц полимерной матрицы в отсчетной конфигурации Ω0 будем задавать радиус-вектором r, а их положение в деформированной конфигурации $\Omega $ – радиус-вектором ${\mathbf{R}}({\mathbf{r}})$.
Для описания деформированного состояния геля будем использовать градиент места ${\mathbf{F}} = \mathop \nabla \limits^ \circ {\mathbf{R}}({\mathbf{r}})$, где $\mathop \nabla \limits^ \circ $ – набла-оператор, действующий в отсчетной конфигурации. Соответственно, $\nabla $ – это набла-оператор, действующий в деформированной конфигурации (здесь и далее используется система представления тензорных соотношений, принятая в [31]). Третий инвариант градиента места $J = \det {\mathbf{F}}$ описывает объемные деформации геля. В частности, с его помощью устанавливается связь между элементами объемов в деформированной dV и отсчетной dV0 конфигурациях геля: $dV = Jd{{V}^{0}}$.
Компонентный состав геля характеризуют N1 и N2 – мольные плотности (концентрации) растворителя и вещества полимерной матрицы соответственно, отнесенные к единичному объему отсчетной конфигурации. В деформированном состоянии распределение растворителя в геле может быть неоднородным, и его концентрация является функцией N1 = N2(r). Концентрация вещества полимерной матрицы N2 от материальных координат не зависит, и в этом смысле она является константой:
величина которой определяется выбором отсчетного состояния геля. Это следует из однородности отсчетного состояния геля и из закона сохранения вещества полимерной матрицы.Под действием приложенных статических нагрузок гель деформируется. При этом, в зависимости от характера действующих нагрузок и исходной концентрации растворителя в геле, часть растворителя может быть выдавлена из полимера во внешнюю среду, а оставшаяся часть неоднородным образом перераспределиться в объеме полимера. Такое перераспределение растворителя происходит в результате диффузионного процесса [24, 25]. Однако в случае статических нагрузок с течением времени диффузионный процесс завершается, и вся система переходит в состояние термодинамического равновесия.
Рассмотрим условия механического нагружения геля. Будем полагать, что положение части границы геля $\Gamma _{0}^{0}$ в деформированном состоянии задано и имеет конфигурацию Γ0. Эта конфигурация задается функцией ${\mathbf{R}} = {{{\mathbf{R}}}_{0}}({\mathbf{r}})$, которая отображает $\Gamma _{0}^{0}$ на Γ0. На остальной части границы $\Gamma _{1}^{0} = \partial {{\Omega }^{0}}{{\backslash }}\Gamma _{0}^{0}$ действуют поверхностные силы с плотностью ${{{\mathbf{g}}}^{0}}({\mathbf{r}})$. Поверхностные силы будем считать замороженными нагрузками [30, 31]. В деформированной конфигурации плотность поверхностных сил описывает функция ${\mathbf{g}}({\mathbf{R}})$. Она определена на Γ1 – деформированной конфигурации границы $\Gamma _{1}^{0}$. Плотности g и g0 связаны соотношением ${{{\mathbf{g}}}^{0}}({\mathbf{r}})d{{S}^{0}} = {\mathbf{g}}({\mathbf{R}}({\mathbf{r}}))dS$, где $d{{S}^{0}}$ и $dS$ – элементы площади в отсчетной и деформированной конфигурациях соответственно.
Гель находится в поле массовых сил b(R), которое является потенциальным:
где $\Phi ({\mathbf{R}})$ – потенциальная энергия единичной массы геля. Объемные плотности приложенных к гелю сил в деформированной и отсчетной конфигурациях равны ${{\rho }}({\mathbf{R}}){\mathbf{b}}({\mathbf{R}})$ и ${{{{\rho }}}^{0}}({\mathbf{r}}){\mathbf{b}}({\mathbf{R}}({\mathbf{r}}))$ соответственно. Здесь ρ и ρ0 – плотности геля в деформированной и отсчетной конфигурациях. Они связаны соотношением ${{{{\rho }}}^{0}} = J{{\rho }}$. Плотность геля в отсчетной конфигурации можно выразить через концентрации компонентов следующим образом: где M1, M2 – мольные массы растворителя и полимера соответственно.Также будем считать, что давление внешней среды имеет фиксированное значение и не меняется в процессе деформирования геля. Постоянной является и температура всей системы, то есть деформирование геля осуществляется в изотермических условиях.
Полимерные гели обычно рассматривают в приближении несжимаемой, аддитивной смеси. Смесь называется несжимаемой, если ее объем не зависит от внешних механических нагрузок, в частности, от давления, однако он зависит от компонентного состава и от температуры. Несжимаемая смесь называется аддитивной, если ее объем равен сумме объемов ее компонентов. Из этого определения следует, что объем несжимаемой аддитивной смеси
где ${{\mathcal{N}}_{1}}$, ${{\mathcal{N}}_{2}}$ – количество молей растворителя и полимера соответственно; ${{\bar {V}}_{1}}$, ${{\bar {V}}_{2}}$ – мольные объемы чистых компонентов геля, которые (в изотермических условиях) являются константами.Если растворитель в геле распределен однородным образом, то разделив обе части равенства (2.4) на объем геля в отсчетном состоянии V0 и учитывая, что $V{\text{/}}{{V}^{0}} = J$ = = detF, ${{N}_{1}} = {{\mathcal{N}}_{1}}{\text{/}}{{V}^{0}}$ и ${{N}_{2}} = {{\mathcal{N}}_{2}}$/V0, получим условие несжимаемости геля в локальной форме
Оно естественным образом распространяется на состояния геля с неоднородным распределением растворителя.
Компонентный состав геля в приближении несжимаемой аддитивной смеси удобно характеризовать с помощью объемных долей компонентов:
(2.6)
${{{{\varphi }}}_{1}} = {{\bar {V}}_{1}}{{N}_{1}}{\text{/}}({{\bar {V}}_{1}}{{N}_{1}} + {{\bar {V}}_{2}}{{N}_{2}}),\quad {{{{\varphi }}}_{2}} = {{\bar {V}}_{2}}{{N}_{2}}{\text{/}}({{\bar {V}}_{1}}{{N}_{1}} + {{\bar {V}}_{2}}{{N}_{2}})$(2.8)
${{{{\varphi }}}_{2}} = {{\varphi }}_{2}^{0}{\text{/}}J,\quad {{N}_{1}} = \bar {V}_{1}^{{ - 1}}(J - {{\varphi }}_{2}^{0})$Равенства (2.8) означают, что распределение растворителя в геле в приближении несжимаемой аддитивной смеси можно полностью описать в терминах объемной деформации J(r). Для этого можно также использовать объемные доли полимера ${{{{\varphi }}}_{2}}({\mathbf{r}})$ или жидкости ${{{{\varphi }}}_{1}}({\mathbf{r}})$. В частности, с помощью соотношений (2.3) и (2.6)–(2.8) плотность геля в деформированной и отсчетной конфигурациях можно представить в следующем виде:
(2.9)
${{\rho }} = {{{{\rho }}}_{{01}}}{{{{\varphi }}}_{1}} + {{{{\rho }}}_{{02}}}{{{{\varphi }}}_{2}} = {{{{\rho }}}_{{01}}} + ({{{{\rho }}}_{{02}}} - {{{{\rho }}}_{{01}}}){{{{\varphi }}}_{2}}$(2.10)
${{{{\rho }}}^{0}} = J{{\rho }} = {{{{\rho }}}_{{01}}}J + \left( {{{{{\rho }}}_{{02}}} - {{{{\rho }}}_{{01}}}} \right){{\varphi }}_{2}^{0}$(2.11)
${{{{\rho }}}_{{01}}} = {{M}_{1}}{\text{/}}{{\bar {V}}_{1}},\quad {{{{\rho }}}_{{02}}} = {{M}_{2}}{\text{/}}{{\bar {V}}_{2}}$Здесь ${{{{\rho }}}_{{01}}}$, ${{{{\rho }}}_{{02}}}$ – плотности чистой жидкости и чистого полимера соответственно.
Наша цель состоит в том, чтобы описать напряженно-деформированное состояние геля в состоянии термодинамического равновесия. В частности, требуется выяснить, при каких условиях произойдет выделение растворителя из геля во внешнюю среду, какое количество растворителя выделится из образца и каким образом оставшийся в геле растворитель распределится в его объеме. Ответы на эти вопросы можно получить из решения соответствующих уравнений, которые далее выводятся как уравнения Эйлера–Лагранжа вариационной задачи минимизации функционала свободной энергии системы. В свою очередь, эта задача минимизации вытекает из основных принципов термодинамики.
3. Уравнения равновесия геля. При макроскопическом подходе гель, растворитель и приложенные нагрузки представляют собой термодинамическую систему. В состоянии термодинамического равновесия ее свободная энергия достигает минимального значения:
(3.1)
$\begin{gathered} \int\limits_{{{\Omega }^{0}}} {f\left( {{\mathbf{F}},{{N}_{1}},{{N}_{2}}} \right)d{{V}^{0}} + {{{{\mu }}}_{L}}} \left( {{{\mathcal{N}}_{1}} - \int\limits_{{{\Omega }^{0}}} {{{N}_{1}}d{{V}^{0}}} } \right) - \\ \, - \int\limits_{\Gamma _{1}^{0}} {{{{\mathbf{g}}}^{0}} \cdot \,} {\mathbf{R}}({\mathbf{r}})d{{S}^{0}} + \int\limits_{{{\Omega }^{0}}} {{{{{\rho }}}^{0}}({\mathbf{r}})\Phi \left( {{\mathbf{R}}({\mathbf{r}})} \right)d{{V}^{0}}} \to \min \\ \end{gathered} $Здесь $f({\mathbf{F}},{{N}_{1}},{{N}_{2}})$ – плотность свободной энергии геля, отнесенная к единичному объему отсчетной конфигурации; ${{\mathcal{N}}_{1}}$ – исходное количество молей растворителя в геле; ${{{{\mu }}}_{L}}$ – константа, равная химическому потенциалу жидкой фазы чистого растворителя. Здесь также полагается, что давление внешней среды (атмосферы) постоянно, а его перепад на масштабах, отвечающих размерам образца геля, ничтожно мал.
Первое слагаемое в выражении (3.1) – это свободная энергия геля, второе – свободная энергия выделившейся из геля жидкости, третье слагаемое – потенциальная энергия поверхностных сил, и последнее слагаемое – потенциальная энергия геля в поле массовых сил. Действующее в геле давление здесь отсчитывается от давления внешней среды, и это учтено в выражении свободной энергии (3.1).
Величина, стоящая в скобках второго слагаемого левой части выражения (3.1), равна количеству выдавленного из геля растворителя. Поскольку количество растворителя ${{\mathcal{N}}_{1}}$ в системе фиксировано, и в исходном состоянии он весь содержался в геле, то количество выделившегося из геля растворителя должно удовлетворять очевидному неравенству
(3.2)
${{\mathcal{N}}_{1}} - \int\limits_{{{\Omega }^{0}}} {{{N}_{1}}({\mathbf{r}})d{{V}^{0}}} \geqslant 0$Поскольку гель рассматривается как несжимаемая, аддитивная смесь, сюда необходимо добавить условие несжимаемости
Таким образом, задача о термодинамическом равновесии геля сводится к задаче минимизации функционала свободной энергии (3.1) с ограничениями (3.2) и (3.3). Она заключается в поиске таких функций R(r) и ${{N}_{1}}({\mathbf{r}})$, которые удовлетворяют граничным условиям ${\mathbf{R}}({\mathbf{r}}) = {{{\mathbf{R}}}_{0}}({\mathbf{r}})$ на $\Gamma _{0}^{0}$, ограничениям (3.2), (3.3) и доставляют минимум функционала (3.1). Допустим, что она имеет решение. Также предположим, что это решение и все исходные данные обладают достаточной гладкостью. Опираясь на эти допущения и используя метод множителей Лагранжа, выведем соответствующие уравнения Эйлера–Лагранжа, описывающие состояние термодинамического равновесия геля. Для этого левые части соотношений (3.2) и (3.3) умножим на лагранжевы множители ${{\mu }}_{*}^{{}} - {{{{\mu }}}_{L}}$ и p соответственно, а полученные выражения прибавим к левой части (3.1). В результате получим функционал Лагранжа
(3.4)
$\begin{gathered} \mathcal{L} = \int\limits_{{{\Omega }^{0}}} {f\left( {{\mathbf{F}},{{N}_{1}},{{N}_{2}}} \right)d{{V}^{0}} + {{\mu }}_{*}^{{}}} \left( {{{\mathcal{N}}_{1}} - \int\limits_{{{\Omega }^{0}}} {{{N}_{1}}d{{V}^{0}}} } \right) - \\ \, - \int\limits_{\Gamma _{1}^{0}} {{{{\mathbf{g}}}^{0}} \cdot } \,{\mathbf{R}}d{{S}^{0}} + \int\limits_{{{\Omega }^{0}}} {{{{{\rho }}}^{0}}\Phi d{{V}^{0}}} + \int\limits_{{{\Omega }^{0}}} {p\left( {{v} - J} \right)d{{V}^{0}}} \\ \end{gathered} $Предположим, что найдутся такая функция p(r) и такое значение ${{\mu }}_{*}^{{}}$, что решение исходной задачи (3.1)–(3.3) доставляет минимум функционала (3.4). При этом величина ${{\mu }}_{*}^{{}}$ удовлетворяет дополнительным условиям
(3.5)
$({{\mu }}_{*}^{{}} - {{{{\mu }}}_{L}})\left( {{{\mathcal{N}}_{1}} - \int\limits_{{{\Omega }^{0}}} {{{N}_{1}}d{{V}^{0}}} } \right) = 0$Тогда, согласно методу Лагранжа, исходная задача минимизации с ограничениями сводится к задаче безусловной минимизации функционала (3.4). Необходимое условие минимума функционала (3.4) заключается в обращении в нуль его первой вариации. Отсюда получаем уравнения Эйлера–Лагранжа в вариационной форме
(3.7)
$\delta \mathcal{L} = \int\limits_{{{\Omega }^{0}}} {({\mathbf{P}}:\delta {{{\mathbf{F}}}^{T}} - {{{{\rho }}}^{0}}{\mathbf{b}} \cdot \delta {\mathbf{R}})d{{V}^{0}}} + \int\limits_{{{\Omega }^{0}}} {({{\mu }} + {{M}_{1}}\Phi - {{\mu }}_{*}^{{}})\delta {{N}_{1}}d{{V}^{0}}} - \int\limits_{\Gamma _{1}^{0}} {{{{\mathbf{g}}}^{0}} \cdot \delta } {\mathbf{R}}d{{S}^{0}} = 0$(3.8)
${\mathbf{P}} = {{\left( {\partial f{\text{/}}\partial {\mathbf{F}}} \right)}_{{{{N}_{1}},\,{{N}_{2}}}}} - pJ{{{\mathbf{F}}}^{{ - T}}},\quad {{\mu }} = {{\left( {\partial f{\text{/}}\partial {{N}_{1}}} \right)}_{{{\mathbf{F}},\,{{N}_{2}}}}} + {{\bar {V}}_{1}}p$Здесь $\delta {{N}_{1}}({\mathbf{r}})$, $\delta {\mathbf{R}}({\mathbf{r}})$, $\delta {\mathbf{F}} = \mathop \nabla \limits^ \circ \delta {\mathbf{R}}({\mathbf{r}})$ – вариации концентрации растворителя, векторного поля ${\mathbf{R}}({\mathbf{r}})$ и градиента места соответственно. Вариация $\delta {\mathbf{R}}$ должна удовлетворять условию $\delta {\mathbf{R}}({\mathbf{r}}) = 0$ на $\Gamma _{0}^{0}$. Соотношения (3.8) являются обобщением известных в механике [30, 31] и в термодинамике [24] выражений для тензора напряжений Пиолы P и химического потенциала μ. При выводе (3.7) учтено, что первая вариация потенциальной энергии геля в поле массовых сил
Это выражение следует из соотношений (2.1)–(2.3).
Применив в уравнении (3.7) интегрирование по частям и теорему Остроградского– Гаусса, получим (с учетом (3.5) и (3.6)) следующую краевую задачу:
(3.9)
$\mathop \nabla \limits^ \circ \, \cdot {\mathbf{P}} + {{{{\rho }}}^{0}}{\mathbf{b}} = 0,\quad {{\mu }} + {{M}_{1}}\Phi = {{\mu }}_{*}^{{}}\quad {\text{\;в области}}\quad {{\Omega }^{0}}$(3.10)
${\mathbf{R}}({\mathbf{r}}) = {{{\mathbf{R}}}_{0}}({\mathbf{r}})\quad {\text{на}}\quad \Gamma _{0}^{0}$(3.11)
${{{\mathbf{n}}}^{0}}\, \cdot {\mathbf{P}} = {{{\mathbf{g}}}^{0}}\quad {\text{на}}\quad \Gamma _{1}^{0}$(3.14)
$({{\mu }}_{*}^{{}} - {{{{\mu }}}_{L}})\left( {{{\mathcal{N}}_{1}} - \int\limits_{{{\Omega }^{0}}} {{{N}_{1}}d{{V}^{0}}} } \right) = 0$Задача (3.9)–(3.15) имеет следующую физическую интерпретацию. Первое из уравнений (3.8) – это условие механического равновесия геля, второе уравнение – условие термодинамического равновесия, которое означает, что сумма химического потенциала растворителя и потенциальной энергии массовых сил в геле является константой. Значение этой константы ${{{{\mu }}}_{*}}$ неизвестно и должно определяться из решения задачи. Граничные условия (3.10) и (3.11) задают действующие на гель внешние механические нагрузки. Уравнение (3.11) – это условие несжимаемости. Неравенство (3.13) уже обсуждалось выше. Соотношения (3.14) и (3.15) описывают условия, при которых происходит выделение части растворителя из геля во внешнюю среду. В частности, неравенство (3.15) выражает известный в термодинамике факт, что химический потенциал растворенного в смеси вещества в состоянии равновесия не может превосходить величину химического потенциала этого же вещества, находящегося в чистом состоянии. Нарушение этого неравенства означает отсутствие термодинамического равновесия, что приводит к самопроизвольному разделению смеси. Из уравнения (3.14) следует, что если имеет место строгое неравенство ${{\mu }}_{*}^{{}} < {{{{\mu }}}_{L}}$, то весь растворитель остается в геле. Но как только достигается равенство ${{\mu }}_{*}^{{}} = {{{{\mu }}}_{L}}$, что возможно при достаточно больших сжимающих нагрузках, растворитель начинает выделяться во внешнюю среду. При дальнейшем сжатии геля равенство ${{{{\mu }}}_{*}} = {{{{\mu }}}_{L}}$ остается в силе, а неравенство (3.13) становится строгим, что означает выделение растворителя из геля во внешнюю среду.
Задача (3.9)–(3.15) описывает состояние равновесия геля в отсчетной конфигурации. В деформированной конфигурации она имеет следующий вид:
(3.16)
$\nabla \, \cdot {\mathbf{T}} + {{\rho }}{\mathbf{b}} = 0,\quad {{\mu }} + {{M}_{1}}\Phi = {{\mu }}_{*}^{{}}\quad {\text{в}}\quad \Omega $(3.21)
$({{\mu }}_{*}^{{}} - {{{{\mu }}}_{L}})\left( {{{\mathcal{N}}_{1}} - \int\limits_\Omega {{{n}_{1}}dV} } \right) = 0$Обратившись к (3.8), получаем
(3.24)
${\mathbf{T}} = {{J}^{{ - 1}}}{{{\mathbf{F}}}^{T}} \cdot {{\left( {\partial f{\text{/}}\partial {\mathbf{F}}} \right)}_{{{{N}_{1}},\,{{N}_{2}}}}} - p{\mathbf{E}}$4. Осмотический тензор напряжений. Если гель находится в состоянии термодинамического равновесия, то гидростатическое давление можно определить из уравнения ${{\mu }} + {{M}_{1}}\Phi = {{\mu }}_{*}^{{}}$. Для этого, используя выражение химического потенциала (3.8), запишем его в виде $\partial f{\text{/}}\partial {{N}_{1}} + {{\bar {V}}_{1}}p + {{M}_{1}}\Phi = {{\mu }}_{*}^{{}}$. Отсюда выразим гидростатическое давление и представим его следующим образом:
Введем также величину ${{{{\pi }}}_{L}} = - \bar {V}_{1}^{{ - 1}}{{{{\mu }}}_{L}}$, которую назовем осмотическим давлением чистого растворителя. Выражение (4.1) подставим в соотношение (3.24). В результате тензор напряжений Коши примет вид
(4.4)
${\mathbf{T}} = {\mathbf{\Pi }} + {{\pi }}_{*}^{{}}{\mathbf{E}} + {{{{\rho }}}_{{01}}}\Phi {\mathbf{E}}$(4.5)
${\mathbf{\Pi }} = {{J}^{{ - 1}}}{{{\mathbf{F}}}^{T}} \cdot \partial f{\text{/}}\partial {\mathbf{F}} - {{\pi }}{\mathbf{E}}$В термодинамике растворов $\pi $ называется осмотическим давлением [32]. По аналогии тензор (4.5) назовем осмотическим тензором напряжений Коши. В отличие от тензора напряжений (3.24), согласно выражениям (4.2) и (4.5), он является функцией состояния геля. Более того, его зависимость от концентрации растворителя с помощью (2.8) можно выразить в терминах J = detF, и осмотический тензор напряжений будет иметь такую же структуру, как и тензор напряжений сжимаемого материала в нелинейной теории упругости.
Поскольку гель рассматривается как несжимаемая аддитивная смесь, количество выделившейся из геля жидкости можно выразить через изменение объема геля:
(4.6)
${{\mathcal{N}}_{1}} - \int\limits_{{{\Omega }^{0}}} {{{N}_{1}}d{{V}^{0}}} = ({{V}^{0}} - V){\text{/}}{{\bar {V}}_{1}}$Используя соотношения (2.2), (2.9) и (4.3)–(4.6), задачу (3.16)–(3.22) представим в следующем виде:
(4.7)
$\nabla \, \cdot {\mathbf{\Pi }} + ({{{{\rho }}}_{{02}}} - {{{{\rho }}}_{{01}}}){{{{\varphi }}}_{2}}{\mathbf{b}} = 0\quad {\text{в}}\quad \Omega $(4.9)
${\mathbf{n}}\, \cdot {\mathbf{\Pi }} = {\mathbf{g}} - {\mathbf{n}}{{\pi }}_{*}^{{}} - {\mathbf{n}}{{{{\rho }}}_{{01}}}\Phi \quad {\text{на}}\quad {{\Gamma }_{1}}$(4.10)
${{V}^{0}} - V = \int\limits_{{{\Omega }^{0}}} {\left( {1 - J} \right)d{{V}^{0}}} \geqslant 0$(4.11)
$({{{{\pi }}}_{L}} - {{\pi }}_{*}^{{}})\int\limits_{{{\Omega }^{0}}} {\left( {1 - J} \right)d{{V}^{0}}} = 0$В ней требуется найти функцию R(r), определяющую равновесную деформированную конфигурацию геля и равновесное значение $\pi _{*}^{{}}$ осмотического давления. Текущее распределение растворителя в геле описывает функция J(r), объем выделившегося во внешнюю среду растворителя можно рассчитать с помощью (4.10). Механические напряжения в геле определяются равенством (4.4).
Можно заметить, что уравнение равновесия (4.7), граничные условия (4.8), (4.9), а также структура тензора Π, аналогичны соответствующим уравнениям и граничным условиям, используемым в статических задачах нелинейной теории упругости сжимаемого материала. Отличие от стандартных задач теории упругости заключается в том, что “внешнее давление” ${{\pi }}_{*}^{{}}$ неизвестно и заданы дополнительные ограничения (4.10)–(4.12). С точки зрения обычной механики их можно интерпретировать следующим образом. При достаточно малых нагрузках объем геля остается постоянным. Неизменность объема обеспечивает давление ${{\pi }}_{*}^{{}}$, компенсирующее ту часть нагрузок, которые способны вызвать изменение объема геля. То есть глобально гель ведет себя как несжимаемый материал, однако локально он проявляет свойства сжимаемого материала, поскольку растворитель внутри него может перераспределяться, порождая локальные объемные деформации. Объем геля сохраняется, пока давление ${{\pi }}_{*}^{{}}$ строго больше предельного значения πL – осмотического давления жидкой фазы растворителя. Если достигается равенство ${{\pi }}_{*}^{{}} = {{{{\pi }}}_{L}}$ (это возможно при достаточно больших сжимающих нагрузках), объем геля начинает уменьшаться за счет выделения растворителя во внешнюю среду. При дальнейшем росте сжимающих нагрузок равенство ${{\pi }}_{*}^{{}} = {{{{\pi }}}_{L}}$ сохраняется, а неравенство (4.10) становится строгим, что означает дальнейшее сжатие геля.
В отсчетной конфигурации задача (4.7)–(4.12) имеет следующий вид:
(4.13)
$\mathop \nabla \limits^ \circ \, \cdot {{{\mathbf{\Pi }}}^{0}} + ({{{{\rho }}}_{{02}}} - {{{{\rho }}}_{{01}}}){{\varphi }}_{2}^{0}{\mathbf{b}} = 0\quad {\text{\;в области}}\quad {{\Omega }^{0}}$(4.14)
${\mathbf{R}}({\mathbf{r}}) = {{{\mathbf{R}}}_{0}}({\mathbf{r}})\quad {\text{на}}\quad \Gamma _{0}^{0}$(4.15)
${{{\mathbf{n}}}^{0}}\, \cdot {{{\mathbf{\Pi }}}^{0}} = {{{\mathbf{g}}}^{0}} - {{{\mathbf{n}}}^{0}} \cdot {{{\mathbf{F}}}^{{ - T}}}J{{\pi }}_{*}^{{}} - {{{\mathbf{n}}}^{0}} \cdot {{{\mathbf{F}}}^{{ - T}}}J{{{{\rho }}}_{{01}}}\Phi \quad {\text{на}}\quad \Gamma _{1}^{0}$Осмотический тензор напряжений Пиолы Π0 определяется равенством
(4.19)
${{{\mathbf{\Pi }}}^{0}} = J{{{\mathbf{F}}}^{{ - T}}} \cdot {\mathbf{\Pi }} = \partial f{\text{/}}\partial {\mathbf{F}} - {{\pi }}J{{{\mathbf{F}}}^{{ - T}}}$5. Определяющие соотношения. Поскольку гель является изотропным материалом, и рассматривается как несжимаемая смесь, плотность его свободной энергии можно записать в виде [28]
где ${{\hat {I}}_{1}}$ и ${{\hat {I}}_{2}}$ – главные инварианты меры деформации искажения формы ${\mathbf{\hat {B}}}$, которые определяются следующим образом:(5.2)
${\mathbf{\hat {B}}} = {\mathbf{B}}{\text{/}}{{J}^{{2{\text{/}}3}}},\quad {\mathbf{B}} = {{{\mathbf{F}}}^{T}} \cdot {\mathbf{F}}$(5.3)
${{\hat {I}}_{1}} = {{I}_{1}}{\text{/}}{{J}^{{2{\text{/}}3}}},\quad {{\hat {I}}_{2}} = {{I}_{2}}{\text{/}}{{J}^{{4{\text{/}}3}}}$(5.4)
${{I}_{1}} = {\mathbf{E}}:{\mathbf{B}},\quad {{I}_{2}} = \frac{1}{2}(I_{1}^{2}({\mathbf{B}}) - {{I}_{1}}({{{\mathbf{B}}}^{2}}))$Здесь B – мера деформации Фингера (левая мера деформации Коши–Грина); I1, I2 – ее первые два главных инварианта; третий инвариант $\det {\mathbf{B}} = {{J}^{2}}$. Отметим, что третий инвариант меры деформации ${\mathbf{\hat {B}}}$, согласно ее определению (5.2), тождественно равен единице: $\det {\mathbf{\hat {B}}} = 1$.
Применив формулы (3.24), (3.8), (4.2) и (4.5) к выражению (5.1), получаем следующие соотношения:
(5.5)
${\mathbf{T}} = {{{{\xi }}}_{1}}\left( {{\mathbf{\hat {B}}} - \frac{1}{3}{{{\hat {I}}}_{1}}{\mathbf{E}}} \right) - {{{{\xi }}}_{2}}\left( {{{{{\mathbf{\hat {B}}}}}^{2}} - \frac{1}{3}{{I}_{1}}({{{{\mathbf{\hat {B}}}}}^{2}}){\mathbf{E}}} \right) - p{\mathbf{E}}$(5.6)
${{{{\xi }}}_{1}} = 2{{J}^{{ - 1}}}(\partial f{\text{/}}\partial {{\hat {I}}_{1}} + {{\hat {I}}_{1}}\partial f{\text{/}}\partial {{\hat {I}}_{2}})\quad {{{{\xi }}}_{2}} = 2{{J}^{{ - 1}}}\partial f{\text{/}}\partial {{\hat {I}}_{2}}$(5.7)
${{\mu }} = {{\left( {\partial f{\text{/}}\partial {{N}_{1}}} \right)}_{{{{{\hat {I}}}_{1}},{{{\hat {I}}}_{2}},{{N}_{2}}}}} + {{\bar {V}}_{1}}p$(5.8)
${{\pi }} = - \bar {V}_{1}^{{ - 1}}{{\left( {\partial f{\text{/}}\partial {{N}_{1}}} \right)}_{{{{{\hat {I}}}_{1}},{{{\hat {I}}}_{2}},{{N}_{2}}}}}$(5.9)
${\mathbf{\Pi }} = {{{{\xi }}}_{1}}\left( {{\mathbf{\hat {B}}} - \frac{1}{3}{{{\hat {I}}}_{1}}{\mathbf{E}}} \right) - {{{{\xi }}}_{2}}\left( {{{{{\mathbf{\hat {B}}}}}^{2}} - \frac{1}{3}{{I}_{1}}({{{{\mathbf{\hat {B}}}}}^{2}}){\mathbf{E}}} \right) - {{\pi }}{\mathbf{E}}$Формулы (5.5)–(5.9) имеют общий характер и позволяют получить все необходимые определяющие соотношения для гелей, если известно конкретное выражение свободной энергии (5.1). В свою очередь, такое выражение можно получить, обратившись к существующим теориям полимерных сеток или к их эмпирическим и полуэмпирическим моделям. Одной из таких наиболее популярных теорий является теория Флори–Ренера [33], которая широко используется как при моделировании поведения сетчатых полимеров, так и при интерпретации экспериментальных данных. Согласно этой теории плотность свободной энергии геля дается выражением [28]
(5.10)
$f = RT\left( {{{N}_{1}}\ln {{{{\varphi }}}_{1}} + {{\chi }}{{N}_{1}}{{{{\varphi }}}_{2}} + \frac{1}{2}{{N}_{2}}{{\varphi }}_{2}^{{ - 2{\text{/}}3}}{{{\hat {I}}}_{1}}} \right)$Применив формулы (5.5)–(5.9) к выражению (5.10) и используя равенства (2.6)–(2.8), получим следующую систему определяющих соотношений:
(5.11)
${\mathbf{T}} = RT\bar {V}_{2}^{{ - 1}}{{\varphi }}_{2}^{{1{\text{/}}3}}\left( {{\mathbf{\hat {B}}} - \frac{1}{3}{{{\hat {I}}}_{1}}{\mathbf{E}}} \right) - p{\mathbf{E}}$(5.12)
${{\mu }} = RT\left( {\ln {{{{\varphi }}}_{1}} + {{{{\varphi }}}_{2}} + {{\chi \varphi }}_{2}^{2} + \frac{1}{3}\left( {{{{\bar {V}}}_{1}}{\text{/}}{{{\bar {V}}}_{2}}} \right){{\varphi }}_{2}^{{1{\text{/}}3}}{{{\hat {I}}}_{1}}} \right) + {{\bar {V}}_{1}}p$(5.13)
${{\pi }} = - RT\bar {V}_{1}^{{ - 1}}\left( {\ln {{{{\varphi }}}_{1}} + {{{{\varphi }}}_{2}} + {{\chi \varphi }}_{2}^{2} + \frac{1}{3}\left( {{{{\bar {V}}}_{1}}{\text{/}}{{{\bar {V}}}_{2}}} \right){{\varphi }}_{2}^{{1{\text{/}}3}}{{{\hat {I}}}_{1}}} \right)$(5.14)
${\mathbf{\Pi }} = RT\bar {V}_{1}^{{ - 1}}(\left( {{{{\bar {V}}}_{1}}{\text{/}}{{{\bar {V}}}_{2}}} \right){{\varphi }}_{2}^{{1{\text{/}}3}}{\mathbf{\hat {B}}} + (\ln {{{{\varphi }}}_{1}} + {{{{\varphi }}}_{2}} + {{\chi \varphi }}_{2}^{2}){\mathbf{E}})$(5.15)
${\mathbf{P}} = J{{{\mathbf{F}}}^{{ - T}}} \cdot {\mathbf{T}} = {{G}_{0}}\left( {{\mathbf{F}} - \frac{1}{3}{{I}_{1}}J{{{\mathbf{F}}}^{{ - T}}}} \right) - pJ{{{\mathbf{F}}}^{{ - T}}}$(5.16)
${{{\mathbf{\Pi }}}^{0}} = J{{{\mathbf{F}}}^{{ - T}}} \cdot {\mathbf{\Pi }} = {{G}_{0}}[{\mathbf{F}} + \left( {{{{\bar {V}}}_{2}}{\text{/}}{{{\bar {V}}}_{1}}} \right){{(\phi _{2}^{0})}^{{ - 1{\text{/}}3}}}(\ln {{\phi }_{1}} + {{\phi }_{2}} + \chi \phi _{2}^{2})J{{{\mathbf{F}}}^{{ - T}}}]$(5.17)
${{{{\varphi }}}_{2}} = {{\varphi }}_{2}^{0}{\text{/}}J$ ${{{{\varphi }}}_{1}} = 1 - {{\varphi }}_{2}^{0}{\text{/}}J$Здесь ${{G}_{0}} = RT\bar {V}_{2}^{{ - 1}}{{({{\varphi }}_{2}^{0})}^{{1{\text{/}}3}}}$ – модуль сдвига полимерного геля в отсчетном состоянии. Равенства (5.17) вытекают из (2.7), (2.8) и являются следствием несжимаемости смеси. Из них следует, что распределение растворителя в геле можно полностью описать в терминах объемных деформаций материала.
Приведенные выше соотношения (5.11)–(5.17), в частности, позволяют описать важное для многих приложений явление свободного набухания сетчатых полимеров, то есть набухание механически ненагруженного полимера, помещенного в растворитель. В теории Флори–Ренера химический потенциал жидкой фазы чистого растворителя полагается равным нулю:
В этом случае ${\mathbf{T}} = {\mathbf{\Pi }} = 0$, ${\mathbf{\hat {B}}} = {\mathbf{E}}$, ${{\hat {I}}_{1}} = 3$, p = 0 и выражение (5.14) дает уравнение
(5.19)
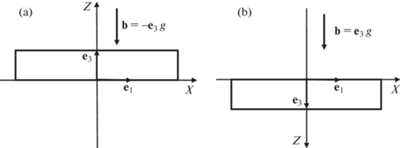
$\ln (1 - {{\varphi }}_{2}^{E}) + {{\varphi }}_{2}^{E} + {{\chi }}{{({{\varphi }}_{2}^{E})}^{2}} + \left( {{{{\bar {V}}}_{1}}{\text{/}}{{{\bar {V}}}_{2}}} \right){{({{\varphi }}_{2}^{E})}^{{1{\text{/}}3}}} = 0$6. Равновесие плоского слоя геля в поле тяжести. Для иллюстрации общей теории рассмотрим состояние равновесия плоского образца полимерного геля в поле тяжести. Гель расположен горизонтально и скреплен с жесткой подложкой. Будем полагать, что в первом случае гель находится на подложке, то есть сила тяжести действует на гель сверху вниз. Подложка проницаема для жидкости, поэтому растворитель, выделившийся из геля под действием силы тяжести, свободно просачивается через нее и удаляется из системы. Во втором случае гель находится под подложкой и выделение растворителя может осуществляться через нижнюю (свободную) поверхность образца. Оба эти случая схематически изображены на рис. 1.
Будем также полагать, что поверхностные силы отсутствуют, гель находится в атмосфере, растворитель – нелетучая жидкость, а его исходная концентрация в геле не превосходит предельного (равновесного) значения, то есть выполняется неравенство
где ${{\varphi }}_{2}^{E}$ – объемная доля полимера в равновесно набухшем состоянии геля. В отсутствие силы тяжести состояние геля (скрепленного с подложкой) является неискаженным и внутренние напряжения в нем отсутствуют. Это исходное состояние будем использовать в качестве отсчетного. Материальную систему координат выберем следующим образом: оси x и y направим вдоль образца, а ось z – в поперечном направлении. Пространственное положение частиц полимерной матрицы деформированного геля задается декартовыми координатами X, Y, Z.Считая, что продольные размеры образца намного превосходят его толщину, гель будем рассматривать как бесконечно протяженный (в горизонтальных направлениях) плоский слой. Поскольку гель скреплен с подложкой, то $X = x$, $Y = y$, и его деформированная конфигурация полностью характеризуется функцией Z(z):
где ei – декартов базис. Отсюда следует, что ${\mathbf{F}} = \sum\limits_i {{{{{\lambda }}}_{i}}} {{{\mathbf{e}}}_{i}}{{{\mathbf{e}}}_{i}}$, где главные относительные удлинения(6.3)
${{{{\lambda }}}_{1}} = {{{{\lambda }}}_{2}} = 1,\quad {{{{\lambda }}}_{3}} = {{\lambda }}(z) = Z{\kern 1pt} '(z),\quad J = {{{{\lambda }}}_{1}}{{{{\lambda }}}_{2}}{{{{\lambda }}}_{3}} = {{\lambda }}(z)$Вследствие этого все параметры, характеризующие состояние геля (напряжения, деформации, распределение растворителя), зависят только от поперечной координаты z. При этом, все тензорные величины соосны и имеют диагональный вид. В частности,
(6.4)
$\Pi _{3}^{0} = {{\Pi }_{3}},\quad \Pi _{1}^{0} = \Pi _{2}^{0} = {{\lambda }}{{\Pi }_{1}} = {{\lambda }}{{\Pi }_{2}},\quad {{P}_{3}} = {{T}_{3}},\quad {{P}_{1}} = {{P}_{2}} = {{\lambda }}{{T}_{1}} = {{\lambda }}{{T}_{2}}$Рассмотрим случай, когда гель находится на подложке. Тогда потенциальная энергия $\Phi = gZ(z)$, а массовая сила ${\mathbf{b}} = - g{{{\mathbf{e}}}_{3}}$, где g – ускорение свободного падения. На свободной поверхности геля вектор внешней нормали ${{{\mathbf{n}}}^{0}} = {{{\mathbf{e}}}_{3}}$. Далее будем считать, что химический потенциал чистого растворителя равен нулю и, следовательно, πL = 0. С учетом этого и изложенного выше, краевая задача (4.13)–(4.18) приобретает следующий вид:
(6.5)
${{\partial }_{z}}{{\Pi }_{3}} = ({{{{\rho }}}_{{02}}} - {{{{\rho }}}_{{01}}}){{\varphi }}_{2}^{0}g\quad {\text{при}}\quad z \in (0,\,\,{{h}_{0}})$(6.7)
${{\Pi }_{3}} = - {{{{\rho }}}_{{01}}}gh - {{\pi }}_{*}^{{}}\quad {\text{при}}\quad z = {{h}_{0}}$(6.8)
$\int\limits_0^{{{h}_{0}}} {\left( {{{\lambda }}(z) - 1} \right)\,dz} \leqslant 0,\quad {{\pi }}_{*}^{{}}\int\limits_0^{{{h}_{0}}} {\left( {{{\lambda }}(z) - 1} \right)\,dz} = 0,\quad {{\pi }}_{*}^{{}} \geqslant 0$(6.9)
${{\Pi }_{3}} = {{G}_{0}}[{{\lambda }} + \left( {{{{\bar {V}}}_{2}}{\text{/}}{{{\bar {V}}}_{1}}} \right){{({{\varphi }}_{2}^{0})}^{{ - 1{\text{/}}3}}}(\ln (1 - {{\varphi }}_{2}^{0}{{{{\lambda }}}^{{ - 1}}}) + {{\varphi }}_{2}^{0}{{{{\lambda }}}^{{ - 1}}} + {{\chi }}{{({{\varphi }}_{2}^{0})}^{2}}{{{{\lambda }}}^{{ - 2}}})]$Проинтегрируем (6.5) по z, и используя граничные условия (6.6) и (6.7), получаем уравнение, определяющее в неявном виде зависимость λ(z):
(6.10)
${{\Pi }_{3}}({{\lambda }}) = \left( {{{{{\rho }}}_{{02}}} - {{{{\rho }}}_{{01}}}} \right){{\varphi }}_{2}^{0}g{{h}_{0}}\left( {z{\text{/}}{{h}_{0}} - 1} \right) - {{{{\rho }}}_{{01}}}gh - {{\pi }}_{*}^{{}}$Функция λ(z) должна удовлетворять ограничениям (6.8), с помощью которых устанавливаются значения неизвестных ${{{{\pi }}}_{*}}$ и h. Если зависимость λ(z) определена, то
Введя безразмерные переменные
(6.12)
$\hat {p} = {{{{\rho }}}_{0}}g{{h}_{0}}{\text{/}}{{G}_{0}},\quad {{\gamma }} = ({{{{\rho }}}_{0}} - {{{{\rho }}}_{{01}}}){\text{/}}{{{{\rho }}}_{0}} = ({{{{\rho }}}_{{02}}} - {{{{\rho }}}_{{01}}}){{\varphi }}_{2}^{0}{\text{/}}{{{{\rho }}}_{0}}$(6.13)
$\Pi ({{\lambda }}) = {{\gamma }}\hat {p}\left( {\hat {z} - 1} \right) - \left( {1 - {{\gamma }}} \right)\hat {p}{{\bar {\lambda }}} - {{\hat {\pi }}}_{*}^{{}},\quad \hat {z} \in [0,\,\,1]$(6.14)
${{\bar {\lambda }}} - 1 \leqslant 0,\quad {{\hat {\pi }}}_{*}^{{}}({{\bar {\lambda }}} - 1) = 0,\quad {{\hat {\pi }}}_{*}^{{}} \geqslant 0$(6.16)
$\Pi = {{\lambda }} + \left( {{{{\bar {V}}}_{2}}{\text{/}}{{{\bar {V}}}_{1}}} \right){{({{\varphi }}_{2}^{0})}^{{ - 1{\text{/}}3}}}(\ln (1 - {{\varphi }}_{2}^{0}{{{{\lambda }}}^{{ - 1}}}) + {{\varphi }}_{2}^{0}{{{{\lambda }}}^{{ - 1}}} + {{\chi }}{{({{\varphi }}_{2}^{0})}^{2}}{{{{\lambda }}}^{{ - 2}}})$Единицами измерения давления здесь служит модуль сдвига полимерного геля в отсчетном состоянии ${{G}_{0}} = RT\bar {V}_{2}^{{ - 1}}{{({{\varphi }}_{2}^{0})}^{{1{\text{/}}3}}}$; $\hat {p}$ – это давление (выраженное в единицах ${{G}_{0}}$), оказываемое гелем в исходном состоянии на подложку; ${{{{\rho }}}_{0}}$ – плотность геля в исходном состоянии, которая определяется равенством
(6.17)
${{{{\rho }}}_{0}} = \left( {{{{{\rho }}}_{{02}}} - {{{{\rho }}}_{{01}}}} \right){{\varphi }}_{2}^{0} + {{{{\rho }}}_{{01}}} = {{{{\rho }}}_{{01}}}(1 - {{\varphi }}_{2}^{0}) + {{{{\rho }}}_{{02}}}{{\varphi }}_{2}^{0}$Параметр ${{\gamma }}$ может принимать как положительные, так и отрицательные значения. Из его определения (6.12) и равенства (6.17) нетрудно видеть, что ${{\gamma }} < 1$. Далее будем считать, что это неравенство всегда выполняется.
Если гель размещен на подложке, то $\hat {p} > 0$. Отрицательные значения $\hat {p}$ естественно отнести к случаю, когда гель находится под подложкой. Это хорошо видно из сравнения рис. 1, a и рис. 1, b. Нетрудно видеть, что система уравнений, описывающая состояние равновесия геля, находящегося под подложкой, получается из предыдущей путем замены $g \to - g$, в результате которой параметр $\hat {p}$ становится отрицательным. Сюда же можно включить значение $\hat {p} = 0$, считая, что ему соответствует значение $g = 0$, то есть сила тяжести отсутствует. Допуская, что параметр $\hat {p}$ может принимать любые вещественные значения, мы получаем возможность с помощью системы (6.13)–(6.16) описать обе схемы размещения геля. Непрерывное изменение $\hat {p}$, при этом, можно интерпретировать как непрерывное изменение ускорения свободного падения. Однако следует отметить, что в экспериментах варьирование $\hat {p}$ осуществляется за счет изменения толщины образца и его размещения.
Сила тяжести оказывает наиболее существенное влияние на деформационное поведение геля, когда в нем содержится большое количество растворителя. Это возможно, если растворитель для данного полимера является хорошим. Концентрация такого растворителя в геле может варьироваться в широких пределах, достигая величин 99% и выше. Далее мы будем рассматривать именно этот случай, как наиболее интересный.
В теории Флори–Ренера для хороших растворителей параметр Флори-Хаггинса χ < 1/2. При таких значениях параметра функция Π(λ), отвечающая выражению (6.16), является возрастающей и вогнутой. Она определена при всех ${{\lambda }} > {{\varphi }}_{2}^{0}$, принимает любые вещественные значения и имеет следующие асимптотические свойства:
(6.18)
$\Pi ({{\lambda }}) = {{\lambda }} - {{K}_{1}}{{{{\lambda }}}^{{ - 2}}} + O({{{{\lambda }}}^{{ - 3}}})\quad {\text{при}}\quad {{\lambda }} \to + \infty $(6.19)
$\Pi ({{\lambda }}) = {{K}_{2}}\ln ({{\lambda }} - {{\varphi }}_{2}^{0}) + O(1)\quad {\text{при}}\quad {{\lambda }} \to {{\varphi }}_{2}^{0}$Отметим также, что при ${{\varphi }}_{2}^{0} \geqslant {{\varphi }}_{2}^{E}$ величина
Причем, равенство ${{{{\pi }}}_{0}} = 0$ достигается только при ${{\varphi }}_{2}^{0} = {{\varphi }}_{2}^{E}$, то есть в предельно набухшем состоянии геля. Это следует из сравнения уравнений (6.16) и (5.19). Величина ${{{{\pi }}}_{0}}$ – это осмотическое давление растворителя в исходном состоянии геля.
Задача (6.13)–(6.16) состоит в том, чтобы для заданных $\hat {p}$ и ${{\gamma }} < 1$ найти такую функцию ${{\lambda }}(\hat {z})$ и значения переменных ${{\hat {\pi }}}_{*}^{{}}$ и ${{\bar {\lambda }}}$, которые удовлетворяют соотношениям (6.13)–(6.16).
Предположим, что переменные ${{\hat {\pi }}}_{*}^{{}}$ и ${{\bar {\lambda }}}$ определены. Тогда подставив их значения в правую часть уравнения (6.13) мы получим уравнение, в неявном виде определяющее функцию ${{\lambda }}(\hat {z})$. Поскольку функция Π(λ) возрастающая, то существует обратная к ней функция $\Lambda (\Pi )$. С ее помощью зависимость ${{\lambda }}(\hat {z})$ можно представить в виде
(6.21)
${{\lambda }}(\hat {z}) = \Lambda \left( {\bar {\Pi } + {{\gamma }}\hat {p}\left( {\hat {z} - 1{\text{/}}2} \right)} \right),\quad \hat {z} \in [0,\,\,1]$(6.22)
$\bar {\Pi } = - \frac{1}{2}{{\gamma }}\hat {p} - \left( {1 - {{\gamma }}} \right)\hat {p}{{\bar {\lambda }}} - {{\hat {\pi }}}_{*}^{{}}$Функция $\Lambda (\Pi )$ является гладкой, возрастающей и выпуклой. Она определена при всех вещественных Π, ограничена снизу и имеет следующие свойства:
(6.24)
$\Lambda (\Pi ) > {{\varphi }}_{2}^{0}\quad {\text{при всех}}\quad \Pi ;\quad \Lambda (\Pi ) \to {{\varphi }}_{2}^{0}\quad {\text{при}}\quad \Pi \to - \infty $Все эти свойства и поведение $\Lambda (\Pi )$ непосредственно вытекают из свойств функции Π(λ) и соотношений (6.18)–(6.20).
Для определения неизвестных ${{\hat {\pi }}}_{*}^{{}}$ и ${{\bar {\lambda }}}$ обратимся к уравнению (6.15). Его правую часть с помощью (6.21) представим в виде интеграла
(6.26)
$I = \int\limits_{ - 1{\text{/}}2}^{1{\text{/}}2} {\Lambda \left( {\bar {\Pi } + {{\gamma }}\hat {p}{{\zeta }}} \right)d{{\zeta }}} $Согласно равенству (6.22) он является функцией трех переменных
Эта функция непрерывна и определена при всех вещественных $\hat {p}$, ${{\hat {\pi }}}_{*}^{{}}$ и ${{\bar {\lambda }}} > {{\varphi }}_{2}^{0}$. В итоге уравнение (6.15) примет вид
Уравнение (6.28) должно решаться совместно с условиями (6.14). Ниже показано, что эта задача имеет решение при достаточно общих условиях, налагаемых на функцию $\Lambda (\Pi )$.
Предложение. Пусть задана непрерывно дифференцируемая, возрастающая функция $\Lambda (\Pi )$, определенная на всей вещественной прямой и обладающая свойствами (6.23)–(6.25), а также функция (6.27), заданная соотношениями (6.26) и (6.22) при ${{\gamma }} < 1$. Тогда:
1) существует значение ${{\hat {p}}_{c}} \geqslant 0$, являющееся единственным решением уравнения
2) существуют непрерывные функции ${{\hat {\pi }}}_{*}^{{}} = {{f}_{1}}(\hat {p})$ и ${{\bar {\lambda }}} = {{f}_{2}}(\hat {p})$ такие, что
(6.30)
${{f}_{1}}(\hat {p}) > 0\quad {\text{при}}\quad \hat {p} < \hat {p}{}_{c};\quad {{f}_{1}}({{\hat {p}}_{c}}) = 0;\quad {{f}_{1}}(\hat {p}) = 0\quad {\text{при}}\quad \hat {p} > \hat {p}{}_{c}$(6.31)
${{\varphi }}_{2}^{0} < {{f}_{2}}(\hat {p}) < 1\quad {\text{при}}\quad \hat {p} > \hat {p}{}_{c};\quad {{f}_{2}}({{\hat {p}}_{c}}) = 1;\quad {{f}_{2}}(\hat {p}) = 1\quad {\text{при}}\quad \hat {p} < \hat {p}{}_{c}$3) функции ${{{{\hat {\pi }}}}_{*}} = {{f}_{1}}(\hat {p})$ при $\hat {p} \leqslant \hat {p}{}_{c}$ и ${{\bar {\lambda }}} = {{f}_{2}}(\hat {p})$ при $\hat {p} \geqslant \hat {p}{}_{c}$ убывающие и являются решениями уравнений
соответственно;4) при любом $\hat {p}$ значения ${{\hat {\pi }}}_{*}^{{}} = {{f}_{1}}\left( {\hat {p}} \right)$ и ${{\bar {\lambda }}} = {{f}_{2}}(\hat {p})$ удовлетворяют уравнению (6.28) и условиям (6.14);
5) данное решение единственно.
Доказательство. Функция (6.27), заданная соотношениями (6.26) и (6.22), непрерывна и при всех ${{\hat {\pi }}}_{*}^{{}}$, $\hat {p}$ и ${{\bar {\lambda }}} > {{\varphi }}_{2}^{0}$ имеет непрерывные частные производные:
Используя свойства монотонности функции $\Lambda (\Pi )$, условие ${{\gamma }} < 1$ и несложные оценки, легко показать, что
(6.34)
$\partial I{\text{/}}\partial {{\pi }}_{*}^{{}} < 0,\quad \partial I{\text{/}}\partial{ \hat {p}} < 0\quad {\text{при всех}}\quad {{\hat {\pi }}}_{*}^{{}},\quad \hat {p}\quad {\text{и}}\quad {{\bar {\lambda }}} > {{\varphi }}_{2}^{0}$(6.35)
$\partial I{\text{/}}\partial {{\bar {\lambda }}} < 0\quad {\text{при всех}}\quad {{\hat {\pi }}}_{*}^{{}},\quad \hat {p} > 0,\quad {{\bar {\lambda }}} > {{\varphi }}_{2}^{0}$Отсюда видно, что при любом фиксированном ${{\bar {\lambda }}} > {{\varphi }}_{2}^{0}$ интеграл $I(\hat {p},{{\hat {\pi }}}_{*}^{{}},{{\bar {\lambda }}})$ относительно переменных $\hat {p}$ и ${{\hat {\pi }}}_{*}^{{}}$ является убывающей функцией, и согласно свойствам (6.23) и (6.24) характеризуется следующим поведением:
(6.36)
$I(\hat {p},{{\hat {\pi }}}_{*}^{{}},{{\bar {\lambda }}}) \to + \infty \quad {\text{при}}\quad \hat {p} \to - \infty \quad {\text{или}}\quad {{\hat {\pi }}}_{*}^{{}} \to - \infty \quad {\text{и любых}}\quad {{\bar {\lambda }}} > {{\varphi }}_{2}^{0}$(6.37)
$I(\hat {p},{{\hat {\pi }}}_{*}^{{}},{{\bar {\lambda }}}) \to \varphi _{2}^{0}\quad {\text{при}}\quad \hat {p} \to + \infty \quad {\text{или}}\quad {{\hat {\pi }}}_{*}^{{}} \to + \infty \quad {\text{и любых}}\quad {{\bar {\lambda }}} > {{\varphi }}_{2}^{0}$(6.38)
$I(\hat {p},{{\hat {\pi }}}_{*}^{{}},{{\bar {\lambda }}}) > {{\varphi }}_{2}^{0}\quad ~{\text{при всех}}\quad \hat {p},\quad {{\hat {\pi }}}_{*}^{{}}\quad {\text{и}}\quad {{\bar {\lambda }}} > {{\varphi }}_{2}^{0}$(6.39)
$I(0,{{\hat {\pi }}}_{*}^{{}},{{\bar {\lambda }}}) = \Lambda ( - {{\hat {\pi }}}_{*}^{{}})\quad {\text{при любых}}\quad {{\hat {\pi }}}_{*}^{{}}\quad {\text{и}}\quad {{\bar {\lambda }}} > {{\varphi }}_{2}^{0}$Равенство (6.39) вытекает из определений (6.26) и (6.22), если в них положить $\hat {p} = 0$.
Существование и единственность решения уравнения (6.29) вытекает из того, что левая часть этого уравнения представляет собой непрерывную, убывающую функцию, область значений которой, согласно свойствам (6.36) и (6.37), содержит нулевое значение. Из (6.39) и (6.25) следует, что при $\hat {p} = 0$ $I(0,\,\,0,\,\,1) = \Lambda (0) \geqslant 1$, поэтому решение уравнения (6.29) удовлетворяет неравенству ${{\hat {p}}_{c}} \geqslant 0$.
Рассмотрим уравнение (6.32). Его левая часть при любом фиксированном $\hat {p}$ есть непрерывная, убывающая функция аргумента ${{{{\hat {\pi }}}}_{*}}$, принимающая, согласно свойствам (6.36) и (6.37), как положительные, так и отрицательные значения. Следовательно, для каждого заданного $\hat {p}$ найдется единственное значение ${{{{\hat {\pi }}}}_{*}}$, при котором левая часть уравнения (6.32) обращается в нуль. Тем самым, на всей вещественной прямой определена функция ${{\hat {\pi }}}_{*}^{{}} = {{\tilde {f}}_{1}}(\hat {p})$. Она является непрерывно дифференцируемой, а ее производная $\tilde {f}_{1}^{'}(\hat {p}) < 0$ при всех $\hat {p}$. Это вытекает из непрерывной дифференцируемости функции $\Lambda (\Pi )$, соотношения $\tilde {f}_{1}^{'}(\hat {p}) = - (\partial I{\text{/}}\partial{ \hat {p}}){\text{/}}(\partial I{\text{/}}\partial {{\pi }}_{*}^{{}})$ и неравенств (6.34). Следовательно, функция ${{\hat {\pi }}}_{*}^{{}} = {{\tilde {f}}_{1}}(\hat {p})$ убывающая. При $\hat {p} = {{\hat {p}}_{c}}$ она обращается в нуль. Действительно, как показано выше, $I({{\hat {p}}_{c}},\,\,0,\,\,1) = 1$, причем, в силу монотонной зависимости I от ${{\hat {\pi }}}_{*}^{{}}$ при любом ${{{{\hat {\pi }}}}_{*}} > 0$ $I({{\hat {p}}_{c}},{{\hat {\pi }}}_{*}^{{}},1) < 1$, а при ${{{{\hat {\pi }}}}_{*}} < 0$ $I({{\hat {p}}_{c}},{{\hat {\pi }}}_{*}^{{}},1) > 1$. Следовательно, ${{\hat {\pi }}}_{*}^{{}}$ = 0 – единственное решение уравнения (6.32) при $\hat {p} = {{\hat {p}}_{c}}$. Поскольку функция ${{\hat {\pi }}}_{*}^{{}} = {{\tilde {f}}_{1}}(\hat {p})$ убывающая и ${{\tilde {f}}_{1}}({{\hat {p}}_{c}}) = 0$, то ${{\hat {\pi }}}_{*}^{{}} = {{\tilde {f}}_{1}}(\hat {p}) > 0$ при всех $\hat {p} < {{\hat {p}}_{c}}$. Функцию ${{f}_{1}}(\hat {p})$ определим, положив ${{f}_{1}}(\hat {p}) = {{\tilde {f}}_{1}}(\hat {p})$ при $\hat {p} \leqslant \hat {p}{}_{c}$ и ${{f}_{1}}(\hat {p}) = 0$ при $\hat {p} > \hat {p}{}_{c}$. Нетрудно видеть, что она удовлетворяет всем условиям, сформулированным в пунктах 2) и 3).
Теперь обратимся к уравнению (6.33). При фиксированном значении ${{\bar {\lambda }}} > {{\varphi }}_{2}^{0}$ $I(\hat {p},0,{{\bar {\lambda }}})$ является непрерывной, убывающей функцией от $\hat {p}$ и при $\hat {p} \geqslant 0$ принимает любые значения из промежутка $({{\varphi }}_{2}^{0},\Lambda (0)]$. Это следует из второго неравенства (6.34) и асимптотических свойств (6.37)–(6.39). Следовательно, для любого ${{\bar {\lambda }}}$, принадлежащего этому промежутку, найдется единственное значение $\hat {p}$, при котором $I(\hat {p},\,\,0,\,\,{{\bar {\lambda }}}) = {{\bar {\lambda }}}$ и левая часть уравнения (6.33) обращается в нуль. Это означает, что существует функция $\hat {p}({{\bar {\lambda }}})$, определяемая в неявном виде уравнением (6.33). Данная функция непрерывна, имеет непрерывную производную $\hat {p}_{{}}^{'}({{\bar {\lambda }}}) = - \left[ {\partial I{\text{/}}\partial {{\bar {\lambda }}} - 1} \right]{{\left[ {\partial I{\text{/}}\partial{ \hat {p}}} \right]}^{{ - 1}}}$, которая, согласно неравенствам (6.34) и (6.35), отрицательна при всех $\hat {p} \geqslant 0$. Отсюда следует, что функция $\hat {p}({{\bar {\lambda }}})$ строго монотонна и, следовательно, имеет обратную функцию ${{\bar {\lambda }}} = {{\tilde {f}}_{2}}(\hat {p})$, определенную при $\hat {p} \geqslant 0$. Эта функция непрерывна и имеет, согласно (6.34) и (6.35), отрицательную непрерывную производную:
Также путем непосредственной проверки нетрудно убедиться, что значения ${{\hat {\pi }}}_{*}^{{}} = {{f}_{1}}(\hat {p})$ и ${{\bar {\lambda }}} = {{f}_{2}}(\hat {p})$ при любом $\hat {p}$ удовлетворяют уравнению (6.28) и условиям (6.14). Единственность данного решения является следствием единственности решений уравнений (6.29), (6.32) и (6.33), что было показано в ходе доказательства. Предложение доказано.
Замечание. При построении решения задачи была использована только строгая монотонность функции $\Lambda (\Pi )$. В модели Флори–Ренера она также обладает свойством строгой выпуклости. Если принять во внимание это обстоятельство и применить к соотношению (6.26) неравенство Иенссена, то можно получить неравенство $\Lambda (\bar {\Pi })\, \leqslant \,I(\hat {p},{{\hat {\pi }}}_{*}^{{}},{{\bar {\lambda }}})$. Подстановка в него значений ${{\hat {\pi }}}_{*}^{{}} = 0$, $\hat {p} = \hat {p}{}_{c}$ и ${{\bar {\lambda }}} = 1$ дает неравенство для $\hat {p}{}_{c}$: $\Lambda ( - (1\, - \,{{\gamma /}}2){{\hat {p}}_{c}})\, \leqslant \,1$ (Здесь использованы равенства (6.22) и (6.29)). В терминах функции $\Pi ({{\lambda )}}$ последнее неравенство принимает вид $ - (1 - {{\gamma /}}2){{\hat {p}}_{c}} \leqslant \Pi (1)$. Учитывая (6.20), получим полезную оценку для критического значения ${{\hat {p}}_{c}}$ в случае, когда $\Lambda (\Pi )$ – выпуклая функция:
Дадим физическую интерпретацию полученного решения. Прежде всего отметим, что параметр $\hat {p}$ можно рассматривать как безразмерную толщину геля в исходном состоянии. Это следует из его определения (6.12). Тогда можно говорить о существовании критической толщины геля ${{\hat {p}}_{c}} \geqslant 0$, при превышении которой происходит выделение растворителя из геля во внешнюю среду, что приводит к уменьшению равновесной толщины геля ${{\bar {\lambda }}}$ по сравнению с исходной. Зависимость ${{\bar {\lambda }}}$ от $\hat {p}$ описывает функция ${{f}_{2}}(\hat {p})$. При этом величина ${{{{\hat {\pi }}}}_{*}}$, имеющая смысл равновесного значения осмотического давления растворителя в геле, равна нулю. Это означает, что гель в таком состоянии, не может поглощать растворитель из внешней среды, даже находясь с ним в контакте. Этому препятствует достаточно высокий уровень действующих на гель сжимающих нагрузок.
Если $\hat {p} < {{\hat {p}}_{c}}$, то ${{\bar {\lambda }}} = 1$, то есть весь растворитель остается в геле. При этом равновесное осмотическое давление растворителя в геле ${{\hat {\pi }}}_{*}^{{}} = {{f}_{1}}(\hat {p}) > 0$ и растет по мере убывания $\hat {p}$. Это означает, что гель в таком состоянии мог бы поглотить дополнительное количество растворителя из внешней среды, если бы находился с ним в контакте. Поглощение растворителя в этом случае продолжалось бы до тех пор, пока ${{{{\hat {\pi }}}}_{*}}$ не достиг бы нулевого значения. Поэтому ${{\hat {\pi }}}_{*}^{{}}$ можно рассматривать как величину, характеризующую совместимость растворителя с полимером в данных условиях.
Параметр $\hat {p}$ может принимать и отрицательные значения. Как было показано выше, это соответствует размещению геля под подложкой. В этом случае всегда $\hat {p} < {{\hat {p}}_{c}}$, ${{\bar {\lambda }}} = 1$ и ${{\hat {\pi }}}_{*}^{{}} > 0$, то есть весь растворитель остается в геле. Это объясняется тем, что здесь гель оказывается подвергнутым растягивающим нагрузкам, под действием которых его совместимость с растворителем возрастает [26].
Таким образом, при размещении геля под подложкой выделение растворителя из геля под действием силы тяжести невозможно. Однако это утверждение справедливо только при сохранении плоской геометрии геля. При достаточно большой толщине слоя состояние механического равновесия слоя становится неустойчивым, в результате чего гель может приобретать весьма сложные конфигурации [19–21]. Можно ожидать, что в этом случае растворитель способен выделяться из геля. Более того, это может влиять на порог устойчивости геля и на его конечную, равновесную конфигурацию. Такого рода эффекты пока никем не изучались. Более того, теоретическое описание явления потери устойчивости геля в поле тяжести в настоящее время обычно осуществляется в рамках модели, в которой гель рассматривается как несжимаемый упругий материал, и возможность миграции растворителя в нем не учитывается.
Сформулируем “алгоритм” решения всей задачи в целом. Он заключается в следующем. Сначала необходимо рассчитать по формулам (6.12) значения параметров ${{\gamma }}$ и $\hat {p}$. При этом знак $\hat {p}$ нужно выбрать в зависимости от способа размещения геля. Затем с помощью уравнения (6.29) определить критическое значение ${{\hat {p}}_{c}}$ и сравнить его с актуальным значением параметра $\hat {p}$. Если $\hat {p} \leqslant {{\hat {p}}_{c}}$, то следует положить ${{\bar {\lambda }}} = 1$, а величину ${{{{\hat {\pi }}}}_{*}}$ найти, решив уравнение (6.32). Если же $\hat {p} > {{\hat {p}}_{c}}$, то ${{\hat {\pi }}}_{*}^{{}}$ нужно присвоить нулевое значение, а ${{\bar {\lambda }}}$ определить из уравнения (6.33). После того, как величины ${{\hat {\pi }}}_{*}^{{}}$ и ${{\bar {\lambda }}}$ определены, по формуле (6.22) необходимо вычислить значение $\bar {\Pi }$. Затем по формуле (6.21) рассчитать функцию ${{\lambda }}(\hat {z})$ и путем ее интегрирования определить $\hat {Z}(\hat {z})$. Распределение напряжений в геле (в рамках теории Флори–Ренера) определяется с помощью соотношений
Первое вытекает из уравнений (4.4), (6.3), (6.4) и (6.13), а второе выводится с помощью равенства ${{P}_{1}} = {{P}_{2}} = {{\lambda }}{{T}_{1}} = {{\lambda }}({{T}_{1}} - {{T}_{3}}) + {{\lambda }}{{T}_{3}}$ и соотношений (5.11), (6.3), (6.4).
Данный алгоритм нетрудно реализовать, применив численные методы. Это дает возможность
получать решение задачи при любых (допустимых) значениях параметров ${{\gamma }}$ и $\hat {p}$. Однако во многих реальных ситуациях, например, в лабораторных экспериментах, типичные
значения 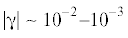 . Это объяснятся тем, что для гелей обычно ${{\varphi }}_{2}^{0} \sim {{10}^{{ - 2}}}$ и плотность такого геля мало отличается от плотности растворителя. Максимальные значения
${\text{|}}\hat {p}{\text{|}}$ обычно характеризуются числами порядка 1–10. Вследствие этого величина
. Это объяснятся тем, что для гелей обычно ${{\varphi }}_{2}^{0} \sim {{10}^{{ - 2}}}$ и плотность такого геля мало отличается от плотности растворителя. Максимальные значения
${\text{|}}\hat {p}{\text{|}}$ обычно характеризуются числами порядка 1–10. Вследствие этого величина 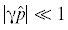 и ее можно использовать как малый параметр. Это дает возможность получить приближенное
решение задачи, которое во многих случаях хорошо описывает деформационное поведение
гелей в поле тяжести уже в линейном по ${{\gamma }}\hat {p}\,$ приближении.
и ее можно использовать как малый параметр. Это дает возможность получить приближенное
решение задачи, которое во многих случаях хорошо описывает деформационное поведение
гелей в поле тяжести уже в линейном по ${{\gamma }}\hat {p}\,$ приближении.
Полагая что 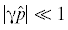 , разложим правую часть (6.21) в ряд Тейлора:
, разложим правую часть (6.21) в ряд Тейлора:
(6.41)
$\Lambda \left( {\bar {\Pi } + {{\gamma }}\hat {p}\left( {\hat {z} - 1{\text{/}}2} \right)} \right) = \Lambda \left( {\bar {\Pi }} \right) + \Lambda {\kern 1pt} '\left( {\bar {\Pi }} \right){{\gamma }}\hat {p}\left( {\hat {z} - 1{\text{/}}2} \right) + \ldots $Далее будем использовать только два первых члена этого разложения. В этом приближении, согласно (6.26), $I = \Lambda (\bar {\Pi })$ и уравнение (6.28) приобретает вид
С учетом данного равенства и разложения (6.41), соотношение (6.21) запишем в виде
(6.43)
${{\lambda }}(\hat {z}) = {{\bar {\lambda }}} + {{\left[ {\Pi {\kern 1pt} '({{\bar {\lambda }}})} \right]}^{{ - 1}}}{{\gamma }}\hat {p}\left( {\hat {z} - 1{\text{/}}2} \right)$(6.44)
$\Pi \left( {{{\bar {\lambda }}}} \right) + [{{\gamma /}}2 + (1 - {{\gamma }}){{\bar {\lambda }}}]\hat {p} + {{\hat {\pi }}}_{*}^{{}} = 0$Из него нетрудно получить аналоги уравнений (6.29) и (6.32). Из них следует, что
(6.46)
${{\hat {\pi }}}_{*}^{{}} = \left( {1 - {{\gamma /}}2} \right)\left( {{{{\hat {p}}}_{c}} - \hat {p}} \right),\quad {{\bar {\lambda }}} = 1,\quad \hat {p} \leqslant {{\hat {p}}_{c}}$Уравнение (6.33) принимает вид
Его можно решать численно. Однако при небольших отклонениях $\hat {p}$ от ${{\hat {p}}_{c}}$ можно воспользоваться приближенной формулой $\Pi ({{\bar {\lambda }}}) \approx - {{{{\pi }}}_{0}} + \Pi '(1)({{\bar {\lambda }}} - 1)$ (Здесь учтено равенство (6.20)). В результате получаем
В этом же приближении, то есть при ${\text{|}}\hat {p} - {{\hat {p}}_{c}}{\text{|}} \ll 1$
Для получения более точного решения в разложении (6.41) необходимо использовать члены более высокого порядка.
7. Заключение. В статье рассмотрены термодинамически равновесные состояния полимерных гелей в поле массовых сил. Гель рассматривается как аддитивная несжимаемая смесь, представляющая собой несжимаемый упругий материал и растворенную в нем несжимаемую жидкость (растворитель). В этом случае объем геля (при фиксированной концентрации растворителя) не зависит от приложенных механических нагрузок, а объемные деформации могут возникать только за счет поглощения или выделения растворителя. Предполагается, что растворитель – нелетучая жидкость, а деформирование геля происходит в атмосфере, поэтому поглощение растворителя из внешней среды отсутствует.
В исходном виде задача о равновесии геля формулируется как задача минимизации функционала свободной энергии системы “ полимер–растворитель” и потенциальной энергии приложенных сил с ограничениями. Приближение несжимаемой смеси дает двустороннее ограничение, а условие отсутствия поглощения растворителя из внешней среды – одностороннее ограничение в виде неравенства. Уравнения, описывающие состояние термодинамического равновесия геля, получены как уравнения Эйлера–Лагранжа задачи минимизации с помощью метода множителей Лагранжа. Вследствие этого в уравнениях в качестве дополнительных неизвестных появляются два лагранжевых множителя: гидростатическое давление и равновесное значение химического потенциала растворителя.
Показано, что равновесное напряженно-деформированное состояние геля в приближении несжимаемой смеси может быть описано в терминах осмотического тензора напряжений, который имеет такую же структуру, как и тензор напряжений сжимаемого материала в нелинейной теории упругости. В результате этого задача о равновесии геля оказывается аналогичной статическим задачам теории упругости для сжимаемого материала, но с дополнительным ограничением в форме неравенства, налагаемым на его объем.
Это ограничение приводит к тому, что гель, в зависимости от приложенных нагрузок и от исходной концентрации растворителя в нем, может демонстрировать поведение как несжимаемого, так и сжимаемого материала. В частности, при растягивающих или малых сжимающих нагрузках объем геля остается постоянным. То есть глобально гель ведет себя как несжимаемый материал, однако локально он проявляет свойства сжимаемого материала, поскольку растворитель внутри него под действием массовых сил может мигрировать, порождая локальные объемные деформации. Если уровень сжимающих нагрузок превышает некоторый порог, то происходит выделение растворителя во внешнюю среду, и гель деформируется как обычный сжимаемый упругий материал.
Общая теория и перечисленные выше эффекты проиллюстрированы на примере решения модельной задачи, описывающей деформирование плоского слоя геля под действием силы тяжести.
Сформулированные задачи можно рассматривать как нетривиальные обобщения статических задач нелинейной теории упругости. Они могут быть полезны при моделировании нелинейных явлений, наблюдаемых в полимерных гелях, а также при прогнозировании поведения полимеров с высоким содержанием пластификатора в условиях длительного хранения.
Список литературы
Bashir S. et al. Fundamental concepts of hydrogels: synthesis, properties, and their applications // Polymers. 2020. V. 12. 2702. https://doi.org/10.3390/polym12112702
Валуев Л.И., Валуева Т.А., Валуев И.Л., Платэ Н.А. Полимерные системы для контролируемого выделения биологически активных соединений // Успехи биол. хим. 2003. Т. 43. С. 307–328.
Buengera D., Topuza F., Groll J. Hydrogels in sensing applications // Prog. Polym. Sci. 2012. V. 37. № 12. P. 1678–1719. https://doi.org/10.1016/j.progpolymsci.2012.09.001
Calvert P. Hydrogels for soft machines // Adv. Mater. 2009. V. 21. № 7. P. 743–756. https://doi.org/10.1002/adma.200800534
Chyzy A., Tomczykowa M., Plonska-Brzezinska M.E. Hydrogels as potential nano-, micro- and macroscale systems for controlled drug delivery // Materials. 2020. V. 13. № 1. P. 188. https://doi.org/10.3390/ma13010188
Chai Q., Jiao Y., Yu X. Hydrogels for biomedical applications: their characteristics and the mechanisms behind them // Gels. 2017. V. 3. № 1. P. 6. https://doi.org/10.3390/gels3010006
Deligkaris K., Tadele T.S., Olthuis W., Berg A. Hydrogel-based devices for biomedical applications // Sensor Actuat. B. 2010. V. 147. № 2. P. 765–774. https://doi.org/10.1016/j.snb.2010.03.083
Ding M. et al. Multifunctional soft machines based on stimuli-responsive hydrogels: from freestanding hydrogels to smart integrated systems // Mater. Today Adv. 2020. V. 8. P. 100088.
Hlavac N., Kasper M., Schmidt C.E. Progress towardfinding the perfect match: hydrogels for treatment of central nervous system injury // Mater. Today Adv. 2020. V. 6. P. 100039. https://doi.org/10.1016/j.mtadv.2020.100088
Hoare T.R., Kohane D.S. Hydrogels in drug delivery: Progress and challenges // Polymer. 2008. V. 49. № 8. P. 1993–2007. https://doi.org/10.1016/j.polymer.2008.01.027
Kopecek J. Hydrogels: from soft contact lenses and implants to self-assembled nanomaterials // J. Polym. Sci. A Polym. Chem. 2009. V. 47. P. 5929–5946. https://doi.org/10.1002/pola.23607
Kordea J.M., Kandasubramaniana B. Naturally biomimicked smart shape memory hydrogels for biomedical functions // Chem. Eng. J. 2020. V. 379. P. 122430. https://doi.org/10.1016/j.cej.2019.122430
Lee K.Y., Mooney D.J. Hydrogels for tissue engineering // Chem. Rev. 2001. V. 101. № 7. P. 1869–1880. https://doi.org/10.1021/cr000108x
Liu X., Liu J., Lin S., Zhao X. Hydrogel machines // Mater. Today. 2020. V. 36. № 6. P. 102–124. https://doi.org/10.1016/j.mattod.2019.12.026
Nishino M., Gong J., Osada Y. Polymer gels as a chemical valve // Bioseparation. 1999. V. 7. P. 269–280. https://doi.org/10.1023/A:1008049525761
Oveissi F., Fletcher D.F., Dehghani F., Naficy S. Tough hydrogels for soft artificial muscles // Mater. Design. 2021. V. 203. P. 109609.
Peppas N.A., Hilt J.Z., Khademhosseini A., Langer R. Hydrogels in biology and medicine: from molecular principles to bionanotechnology // Adv. Mater. 2006. V. 18. № 11. P. 1345–1360. https://doi.org/10.1002/adma.200501612
Mora S., Phou T., Fromental J.-M., Pomeau Y. Gravity driven instability in elastic solid layers // Phys. Rev. Lett. 2014. V. 113. P. 178301. https://doi.org/10.1103/PhysRevLett.113.178301
Riccobelli D., Ciarletta P. Rayleigh–Taylor instability in soft elastic layers // Phil. Trans. R. Soc. A. 2017. V. 375. № 2039. P. 20160421. https://doi.org/10.1098/rsta.2016.0421
Chakrabarti A., Mora S., Richard F., Phou T., Fromental J.-M., Pomeau Y., Audoly B. Selection of hexagonal buckling patterns by the elastic Rayleigh–Taylor instability // J. Mech. Phys. Solids. 2018. V. 121. P. 234–257. https://doi.org/10.1016/j.jmps.2018.07.024
Zheng Y., Lai Y., Hu Y., Cai S. Rayleigh–Taylor instability in a confined elastic soft cylinder // J. Mech. Phys. Solids. 2019. V. 131. P. 221–229. https://doi.org/10.1016/j.jmps.2019.07.006
Rajagopal K.R., Tao L. Mechanics of mixtures. World Scientific Publishing, 1995. 195 p.
Truesdell C., Toupin R. The classical field theories // Handbuch der Phisik. Vol. III/l / Ed. S. Flugge. Berlin: Springer-Verlag, 1960. P. 226–793.
Денисюк Е.Я., Терешатов В.В. Теория механодиффузионных процессов переноса многокомпонентных жидкостей в сшитых эластомерах // ПМТФ. 1997. Т. 38. № 6. С. 113–129.
Денисюк Е.Я., Терешатов В.В. Нелинейная теория процессов набухания эластомеров в низкомолекулярных жидкостях // Высокомолек. соед. А. 2000. Т. 42. № 1. С. 71–83.
Денисюк Е.Я., Волкова Е.Р. Влияние термодинамического качества растворителя на кинетику набухания полимерных сеток // Высокомолек. соед. А. 2003. Т. 45. № 7. С. 1160–1168.
Денисюк Е.Я., Волкова Е.Р. О проницаемости полимерных сеток // Высокомолек. соед. А. 2004. Т. 46. № 5. С. 896–904.
Денисюк Е.Я. Механика и термодинамика высокоэластичных материалов, насыщенных жидкостью // Изв. РАН. МТТ. 2010. № 1. С. 118–138.
Денисюк Е.Я. Механика и термодинамика деформирования насыщенных жидкостью упругих материалов в приближении малых деформаций // Изв. РАН. МТТ. 2018. № 2. С. 54–69.
Ciarlet P. Mathematical Elasticity. Vol. I. Amsterdam: Elsevier, 1988. = Сьярле Ф. Математическая теория упругости. М.: Мир, 1992. 472 с.
Лурье А.И. Нелинейная теория упругости. М.: Наука, 1980. 512 с.
Prigogine I., Defay R. Chemical Thermodynamics. N.Y.: Longmans Green and Co, 1954. = Пригожин И., Дефэй Р. Химическая термодинамика. Новосибирск: Наука, 1966. 508 с.
Flory P.J., Rehner J. Statistical mechanics of cross-linked polymer networks // J. Chem. Phys. 1943. V. 11. P. 512–526. https://doi.org/10.1063/1.1723791
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика твердого тела