Известия РАН. Механика твердого тела, 2022, № 4, стр. 25-37

ТЕРМОУПРУГОЕ ПОВЕДЕНИЕ НЕСЖИМАЕМОГО ЭЛАСТОМЕРА ПРИ КОНЕЧНЫХ ДЕФОРМАЦИЯХ

Б. А. Жуков^a, b, *

^a Волгоградский государственный социально-педагогический университет
Волгоград, Россия

^b Волгоградский государственный технический университет
Волгоград, Россия

^* E-mail: zhukov.b.a@gmail.com

Поступила в редакцию 12.02.2021
После доработки 14.04.2021
Принята к публикации 24.05.2021

EDN: JTJIIW
DOI: 10.31857/S0572329922030138

Полный текст (PDF)

Аннотация

Детали из эластомеров обычно работают в температурном диапазоне, в котором обладают высокоэластичной деформацией. Тепловое расширение высокоэластичной деформацией не является и присутствует во всем диапазоне температур, в котором эластомер существует. Эти виды деформации по-разному реагируют на изменение температуры. Целью работы является выяснение в рамках феноменологического подхода влияния температурных зависимостей этих деформаций на температурную зависимость компонент тензора напряжений, описывающих напряженное состояние несжимаемого эластомера при конечной деформации на примере конкретной задачи. Использован вариант постановки задачи статики однородного изотропного несжимаемого материала при конечных деформациях, позволяющий учитывать тепловое расширение как самодостаточный процесс, независящий от высокоэластичной деформации. В рамках этой постановки получено новое точное решение связной задачи термоупругости о конечном продольном сдвиге длинной цилиндрической втулки с потенциалом энергии деформации Джента–Томаса в неоднородном температурном поле. Показано, что температурная зависимость касательного напряжения, вызывающего продольный сдвиг, определяется только тепловым расширением, тогда как температурная зависимость нормальных напряжений существенно определяется тепловым расширением, и слабее температурным изменением высокоэластичной деформации. Температурная зависимость сдвиговой жесткости определяется, в основном, температурным изменением высокоэластичной деформации.

Ключевые слова: термомеханика, тепловое расширение, высокоэластичная конечная деформация, неоднородное температурное поле, гиперупругость, несжимаемость, потенциал Джента–Томаса

1. Введение. Для инженерных приложений эластомеров, работающих в широком диапазоне температур, важны методы расчета температурной зависимости напряженно-деформированного состояния. Обычно эластомеры применяются в области температур, при которых проявляется высокоэластичная деформация. Тепловое расширение высокоэластичной деформацией не является и присутствует во всем диапазоне температур, в котором эластомер существует. Эти виды деформации по-разному реагируют на изменение температуры. Целью работы является выяснение в рамках феноменологического подхода влияния температурных зависимостей этих деформаций на температурную зависимость компонент тензора напряжений, описывающих напряженное состояние несжимаемого эластомера при конечной деформации на примере конкретной задачи.

В прошлом веке была разработана статистическая теория высокой эластичности полимеров. С историей вопроса можно познакомиться в [1–4]. Важным результатом этой теории, с точки зрения инженерных приложений, было существование единственного потенциала энергии деформации (потенциала Трелоара, неогуковского потенциала)

(1.1)

$W = \frac{\mu }{2}\left( {{{I}_{1}} - 3} \right),\quad \mu = \frac{{\rho \tilde {R}T}}{{{{M}_{c}}}}$

Здесь μ – модуль сдвига, ρ – плотность массы, $\tilde {R}$ – универсальная газовая постоянная, ${{M}_{c}}$ – средняя молекулярная масса, T – абсолютная температура, I₁ – первый из трех главных инвариантов деформации

(1.2)

${{I}_{1}} = \lambda _{1}^{2} + \lambda _{2}^{2} + \lambda _{3}^{2},\quad {{I}_{2}} = \lambda _{3}^{2}\lambda _{2}^{2} + \lambda _{1}^{2}\lambda _{3}^{2} + \lambda _{1}^{2}\lambda _{2}^{2},\quad {{I}_{3}} = \lambda _{1}^{2}\lambda _{2}^{2}\lambda _{3}^{2}$

где ${{\lambda }_{i}}$ – кратности растяжения вдоль главных направлений деформации. Дальнейшие эксперименты [5] показали, что $\partial W{\text{/}}\partial {{I}_{2}} \ne 0$ и уменьшается с увеличением I₂. Появилась проблема, состоящая в том, чтобы описать общую форму функции энергии деформации, объясняющую этот факт. Эта проблема не решена до сих пор, что проявляется во множестве форм функции энергии деформации, предлагаемых разными авторами [6]. Реалистичная формула, которая в достаточной степени аппроксимирует общие данные о деформациях резины, приведенные в [5], была выдвинута Джентом и Томасом [7]. Это выражение имеет вид

(1.3)

$W = {{c}_{1}}\left( {{{I}_{1}} - 3} \right) + {{c}_{2}}\ln \left( {\frac{{{{I}_{2}}}}{3}} \right),\quad {{c}_{1}},{{c}_{2}} - {\text{const}}$

Форма (1.3) была выбрана главным образом по причине математической простоты [1] и перехода при ${{с}_{2}} = 0$ и ${{с}_{1}} = \mu {\text{/}}2$ в выражение (1.1). Дифференцирование дает соотношения

$\frac{{\partial W}}{{\partial {{I}_{1}}}} = {{c}_{1}},\quad \frac{{\partial W}}{{\partial {{I}_{2}}}} = \frac{{{{c}_{2}}}}{{{{I}_{2}}}}$

соответствующие нелинейной зависимости $\partial W{\text{/}}\partial {{I}_{2}}$ от I₂. В формуле (1.1) температурная зависимость потенциала энергии деформации проявляется через зависимость модуля сдвига от температуры. Подчеркнем, что в (1.1) тепловое расширение не учитывается, то есть эта формула описывает температурную зависимость высокоэластичной деформации. Ниже будет использован этот подход для описания температурной зависимости более сложного, чем (1.1) потенциала (1.3).

Предлагаемая работа относится к феноменологическим. Использован вариант постановки задачи статики однородного изотропного несжимаемого материала при конечных деформациях, позволяющий учитывать тепловое расширение как самодостаточный процесс, независящий от высокоэластичной деформации. От других работ по термоупругости резины она отличается уточнением способа учета теплового расширения. В работе рассматривается стандартная задача о конечном продольном сдвиге полого цилиндра, но в рамках предложенной постановки получено новое точное решение связной задачи термоупругости. Приводятся решения как в неоднородном осесимметричном температурном поле, так и в отсутствии его, как с учетом теплового расширения, так и без него. Проводится сравнение с решением в рамках потенциала (1.1).

2. Основные соотношения. При рассмотрении задач термоупругости обычно полагается, чтобы напряжение, приращения свободной энергии и энтропии, вызванные деформацией, исчезали в отсчетной конфигурации [8]. При учете теплового расширения вводится разностная температура $\theta = T - {{T}_{0}}$, где T – абсолютная температура деформированной конфигурации, а T₀ – однородная абсолютная температура отсчетной конфигурации. При этом считается, что тепловое расширение при $\theta = 0$ отсутствует [8–10]. С учетом этих положений предлагается следующий вариант постановки задач статической термоупругости однородного изотропного несжимаемого материала при конечных деформациях.

Будем описывать конечную деформацию эластомера с помощью тензора градиента деформации F, задаваемого выражением

(2.1)

$d{\mathbf{r}} = {\mathbf{F}} \cdot d{\mathbf{R}}$

Здесь r и R – векторы места точек тела в деформированной (текущей) и недеформированной (отсчетной) конфигурациях соответственно. Точка означает скалярное произведение (свертку по одному тензорному индексу).

Согласно рациональной механике сплошных сред [12, 13] для простого однородного материала с массовой плотностью свободной энергии $\Psi = \Psi \left( {{\mathbf{F}},\,T} \right)$ уравнения состояния (определяющие уравнения) принимают вид

(2.2)

${\mathbf{P}} = {{\rho }_{0}}\frac{{\partial \Psi }}{{\partial {{{\mathbf{F}}}^{T}}}},\quad \hat {\eta } = - \frac{{\partial \Psi }}{{\partial T}}$

Здесь ${{\rho }_{0}}$ – плотность массы в отсчетной конфигурации, P – тензор напряжений Пиолы [12] (по [13] это транспонированный первый тензор Пиолы–Кирхгофа), $\hat {\eta }$ – массовая плотность энтропии. Если материал начально изотропен, то Ψ = Ψ$({{I}_{1}},{{I}_{2}},{{I}_{3}},T)$. Здесь ${{I}_{1}} = {\mathbf{1}} \cdot \cdot {\mathbf{B}}$, ${{I}_{2}} = 1{\text{/}}2(I_{1}^{2} - {\mathbf{1}} \cdot \cdot \,{{{\mathbf{B}}}^{2}})$, ${{I}_{3}} = {{J}^{2}} = \det {\mathbf{B}}$ – главные алгебраические инварианты тензора ${\mathbf{B}} = {\mathbf{F}} \cdot {{{\mathbf{F}}}^{T}}$ – левого тензора деформации Коши–Грина [13] (в [12] это мера деформации Фингера), 1 – единичный тензор. Значок ^T обозначает транспонирование, а пара точек – двойное скалярное произведение (имеется в виду вариант последовательного перемножения, когда скалярно перемножаются ближайшие векторы). Эти инварианты совпадают с (1.2).

Полагая, что изменение объема происходит только за счет теплового расширения, уравнение изменения объема выберем в виде [8–10]

(2.3)

$J = \det {\mathbf{F}} = g\left( \theta \right)$

Здесь g(θ) – некоторая монотонная функция приращения температуры θ, причем $g(0)$ = 1. Обычно используются выражения $g\left( \theta \right) = {{e}^{{3\alpha \theta }}}$, где α – линейный коэффициент теплового расширения. В [10] показано, что из (2.3) и (2.2) следует выражение для тензора напряжений Коши ${\mathbf{S}}$

(2.4)

${\mathbf{S}} = 2\left( {\frac{1}{{g\left( \theta \right)}}\frac{{\partial W}}{{\partial {{I}_{1}}}}\,{\mathbf{B}} - g\left( \theta \right)\frac{{\partial W}}{{\partial {{I}_{2}}}}\,{{{\mathbf{B}}}^{{ - 1}}}} \right) + \gamma {\mathbf{1}}$

где удельная энергия упругой деформации (потенциал энергии деформации) W, отнесенная к единице объема отсчетной конфигурации, связана с массовой плотностью свободной энергии соотношением $W = {{\rho }_{0}}\Psi $, γ – функция гидростатического давления. Выражения (2.3) и (2.4) учитывают тепловое расширение.

Учет температурной зависимости высокоэластичной деформации производится через температурную зависимость модулей упругости [1, 11]. Таким образом, влияние поля температур на потенциал энергии деформации проявляется двояко, через зависимость модулей упругости и, неявно, через механизм теплового расширения, влияющий на инварианты тензора В. В качестве потенциала энергии деформации принят потенциал Джента–Томаса (1.3). В [14] приводится выражение для этого потенциала в форме, переходящей в закон Гука при малых деформациях

$W = \mu \left\{ {\frac{{3 - 2\beta }}{6}\left( {{{I}_{1}} - 3} \right) + \beta \ln \left( {\frac{{{{I}_{2}}}}{3}} \right)} \right\},\quad 0 \leqslant \beta < \frac{3}{2}$

Здесь модуль сдвига μ в соответствие с [1] имеет вид

(2.5)

$\mu = \frac{{\rho \tilde {R}T}}{{{{M}_{c}}}} = \frac{{{{\rho }_{0}}\tilde {R}{{T}_{0}}}}{{{{M}_{c}}}}\frac{T}{{{{T}_{0}}J}} = \frac{{{{\mu }_{0}}}}{{g\left( \theta \right)}}\left( {1 + \frac{\theta }{{{{T}_{0}}}}} \right),\quad {{\mu }_{0}} = \frac{{{{T}_{0}}{{\rho }_{0}}\tilde {R}}}{{{{M}_{c}}}}$

Другими словами, модуль сдвига зависит от температуры как явно, так и неявно через тепловое расширение. Таким образом, получим

(2.6)

$W = \frac{{{{\mu }_{0}}}}{{g\left( \theta \right)}}\left( {1 + \frac{\theta }{{{{T}_{0}}}}} \right)\left\{ {\frac{{3 - 2\beta }}{6}\left( {{{I}_{1}} - 3} \right) + \beta \ln \left( {\frac{{{{I}_{2}}}}{3}} \right)} \right\},\quad 0 \leqslant \beta < \frac{3}{2}$

При $\beta = 0$ выражение (2.6) перейдет в потенциал Трелоара

$W = \frac{{{{\mu }_{0}}}}{{2g\left( \theta \right)}}\left( {1 + \frac{\theta }{{{{T}_{0}}}}} \right)\left( {{{I}_{1}} - 3} \right) = \frac{\mu }{2}\left( {{{I}_{1}} - 3} \right)$

В отсутствие массовых сил уравнение равновесия запишется в форме [12]

$\mathop \nabla \limits^0 \cdot {\mathbf{P}} = 0$

Здесь $\mathop \nabla \limits^0 = {{{\mathbf{R}}}^{k}}\partial {\text{/}}\partial {{q}^{k}}$ – оператор Гамильтона в отсчетной конфигурации, ${{{\mathbf{R}}}^{k}}$ – базис взаимный с базисом ${{{\mathbf{R}}}_{k}}$, то есть ${{{\mathbf{R}}}_{k}} = \partial {\mathbf{R}}{\text{/}}\partial {{q}^{k}},{{{\mathbf{R}}}^{k}} \cdot {{{\mathbf{R}}}_{p}} = \delta _{p}^{k}$, где ${{q}^{1}},{{q}^{2}},{{q}^{3}}$ – материальные координаты точек тела, $\delta _{p}^{k}$ – символ Кронекера. Это уравнение можно выразить и через тензор напряжений Коши [12] в виде

(2.7)

$\mathop \nabla \limits^0 \cdot {\mathbf{P}} = \nabla \cdot {\mathbf{S}} = 0$

Здесь $\nabla = {{{\mathbf{r}}}^{k}}\partial {\text{/}}\partial {{q}^{k}}$ – оператор Гамильтона в деформированной конфигурации, r^k – базис взаимный с базисом r_k, то есть

(2.8)

${{{\mathbf{r}}}_{k}} = {\mathbf{F}} \cdot {{{\mathbf{R}}}_{k}},\quad {{{\mathbf{r}}}^{k}} = {{({{{\mathbf{F}}}^{{ - 1}}})}^{T}} \cdot {{{\mathbf{R}}}^{k}}$

Согласно (2.7) из (2.4) получим

(2.9)

$\nabla \gamma = - 2\nabla \cdot \left[ {\frac{{{{W}_{1}}}}{{g\left( \theta \right)}}\,{\mathbf{B}} - g\left( \theta \right){{W}_{2}}\,{{{\mathbf{B}}}^{{ - 1}}}} \right]$

Здесь введены обозначения ${{W}_{1}} = \partial W{\text{/}}\partial {{I}_{1}},{{W}_{2}} = \partial W{\text{/}}\partial {{I}_{2}}$. Исключая функцию $\gamma $ в (2.9), будем иметь

(2.10)

$\nabla \times \nabla \cdot \left[ {\frac{{{{W}_{1}}}}{{g\left( \theta \right)}}\,{\mathbf{B}} - g\left( \theta \right){{W}_{2}}\,{{{\mathbf{B}}}^{{ - 1}}}} \right] = 0$

Среди простых, однородных и начально изотропных материалов будем рассматривать материалы, подчиняющиеся закону Фурье

(2.11)

${\mathbf{q}} = - \lambda \nabla T = - \lambda \nabla \theta $

Здесь q – удельный тепловой поток в актуальной конфигурации, $\lambda $ – постоянный коэффициент теплопроводности. В отсутствие внутренних источников теплоты для стационарного потока тепла уравнение теплового баланса имеет вид [12]

(2.12)

$\nabla \cdot {\mathbf{q}} = 0$

Из уравнения (2.12) и выражения (2.11) следует стационарное уравнение теплопроводности

(2.13)

$\nabla \cdot \nabla \theta = 0$

которое дополняется граничными условиями. Уравнения (2.3) и (2.13) образуют связную систему уравнений, описывающих поле температур и тепловое расширение независимо от высокоэластичной деформации.

3. Решение задачи термоупругости о конечном продольном сдвиге длинной цилиндрической втулки с потенциалом энергии деформации Джента–Томаса в неоднородном температурном поле. По внутренней боковой поверхности втулка приклеена к неподвижной жесткой обойме. На внешней боковой поверхности действует продольная сдвигающая сила с модулем Q и нулевые нормальное и окружное усилия. Полагается, что нагрузка “мертвая”, то есть вектор ${\mathbf{Q}} = Q{\mathbf{k}}$ не меняет величину и направление в процессе деформации (${{{\mathbf{e}}}_{R}},\,{{{\mathbf{e}}}_{\Phi }},\,{\mathbf{k}}$ – единичный базис цилиндрической системы координат). На внутренней боковой поверхности поддерживается температура ${{T}_{1}}$, а на внешней ${{T}_{2}}$. Через ${{R}_{1}}$ и ${{R}_{2}}$ обозначаются внутренний и внешний радиусы эластомерной втулки, а через H ее длина. Эта задача для различных потенциалов энергии деформации, как в линейной, так и в нелинейной постановке решалась многими авторами. В рамках связной термоупругости эта задача решалась в [8] с оригинальным термоупругим аналогом одноконстантного потенциала энергии деформации Джента–Томаса. Для предлагаемой постановки с двухконстантым потенциалом Джента–Томаса точное решение получено впервые.

3.1. Общая постановка задач в рамках полуобратного метода. Материальная система координат выбрана совпадающей в отсчетной конфигурации с цилиндрической системой $\left( {R,\Phi ,Z} \right)$, причем ось OZ совпадает с осью симметрии втулки. Втулка считается достаточно длинной, чтобы пренебречь торцевыми эффектами и считать напряженно-деформированное состояние независящим от Z.

В этих условиях можно использовать кинематическую гипотезу коаксиальных сечений, то есть сечения цилиндрические и коаксиальные до деформации остаются таковыми и после деформации (ось единая для всех таких сечений совпадает с осью симметрии втулки). В цилиндрической системе координат в силу осевой симметрии вектор места в деформированной (актуальной) конфигурации задается соотношением

(3.1)

${\mathbf{r}} = f\left( R \right){{{\mathbf{e}}}_{R}} + \left[ {Z + w\left( R \right)} \right]\,{\mathbf{k}}$

Здесь $r = f\left( R \right),\varphi = \Phi ,z = Z + w\left( R \right)$ – координаты точек в актуальной конфигурации в цилиндрической системе координат, а $w\left( R \right)$ и f (R) подлежащие определению функции. Граничные условия для этих функций имеют вид $f\left( {{{R}_{1}}} \right) = {{R}_{1}},w\left( {{{R}_{1}}} \right) = 0$. Температурное поле так же полагается осесимметричным $\theta = \theta \left( R \right)$. Оператор Гамильтона материальной системы координат в отсчетной конфигурации записывается в форме

(3.2)

$\mathop \nabla \limits^0 = {{{\mathbf{e}}}_{R}}\frac{\partial }{{\partial R}} + \frac{{{{{\mathbf{e}}}_{\Phi }}\,}}{R}\frac{\partial }{{\partial \Phi }} + {\mathbf{k}}\frac{\partial }{{\partial Z}}$

В актуальной конфигурации его можно записать в виде

(3.3)

$\nabla = {{{\mathbf{e}}}_{R}}\frac{\partial }{{\partial r}} + \frac{{{{{\mathbf{e}}}_{\Phi }}\,}}{r}\frac{\partial }{{\partial \varphi }} + {\mathbf{k}}\frac{\partial }{{\partial z}}$

Уравнение (2.13) в цилиндрической системе координат имеет вид

(3.4)

$\nabla \cdot \nabla \theta = \frac{\partial }{{\partial r}}\left( {r\frac{{\partial \theta }}{{\partial r}}} \right) = 0$

Транспонированный тензор градиента деформации по (3.1) и (3.2) получается в виде

(3.5)

${{{\mathbf{F}}}^{T}} = \mathop \nabla \limits^0 {\mathbf{r}} = \frac{{df\left( R \right)}}{{dR}}{{{\mathbf{e}}}_{R}}{{{\mathbf{e}}}_{R}} + \frac{{f\left( R \right)}}{R}{{{\mathbf{e}}}_{\Phi }}{{{\mathbf{e}}}_{\Phi }} + \frac{{dw\left( R \right)}}{{dR}}{{{\mathbf{e}}}_{R}}{\mathbf{k}} + {\mathbf{kk}}$

Так, что условие несжимаемости $(J = \det \mathop \nabla \limits^0 {\mathbf{r}} = B\left( R \right){\text{где}}B\left( R \right) = g\left[ {\theta \left( R \right)} \right] = {{e}^{{3\alpha \theta \left( R \right)}}})$ принимает форму дифференциального уравнения

(3.6)

$\frac{{f\left( R \right)f{\kern 1pt} '\left( R \right)}}{R} = B\left( R \right)\quad {\text{или}}\quad f{\kern 1pt} '\left( R \right) = \frac{{RB\left( R \right)}}{{f\left( R \right)}}$

где штрих означает производную по R. Уравнения (3.4) и (3.6) образуют связную систему уравнений. Эта система описывает тепловое расширение и температурное поле независимо от потенциала энергии деформации. Будем искать решение системы в параметрической форме. Решение уравнения (3.4), дополненного граничными условиями $r\left( {{{R}_{1}}} \right) = f\left( {{{R}_{1}}} \right) = {{R}_{1}},\,\,\,\theta \left( {{{R}_{1}}} \right) = \theta \left[ {f\left( {{{R}_{1}}} \right)} \right] = {{\theta }_{1}}$, имеет вид

(3.7)

$\theta \left( R \right) = \eta \ln \frac{{f\left( R \right)}}{{{{R}_{1}}}} + {{\theta }_{1}}$

Здесь $\eta \left[ {^\circ {\text{C}}} \right]$ – размерная константа интегрирования, играющая роль параметра.

По (3.7) вычисляем $B\left( R \right) = {{e}^{{3\alpha \theta \left( R \right)}}} = a{{(f(R){\text{/}}{{R}_{1}})}^{{3\alpha \eta }}},a = {{e}^{{3\alpha {{\theta }_{1}}}}}$, и подставляем в (3.6). Получаем ${{f}^{{1 - 3\alpha \eta }}}\left( R \right)f_{{}}^{'}\left( R \right) = aRR_{1}^{{ - 3\alpha \eta }}$. Решение этого уравнения с граничным условием $f\left( {{{R}_{1}}} \right) = {{R}_{1}}$ имеет выражение

(3.8)

$f\left( R \right) = {{R}_{1}}{{\left\{ {1 + \frac{{a\left( {2 - 3\alpha \eta } \right)}}{2}\left[ {{{{\left( {\frac{R}{{{{R}_{1}}}}} \right)}}^{2}} - 1} \right]} \right\}}^{{^{{\frac{1}{{2 - 3\alpha \eta }}}}}}}$

и (3.7) можно переписать

(3.9)

$\theta \left( R \right) = \frac{\eta }{{2 - 3\alpha \eta }}\ln \left\{ {1 + \frac{{a\left( {2 - 3\alpha \eta } \right)}}{2}\left[ {{{{\left( {\frac{R}{{{{R}_{1}}}}} \right)}}^{2}} - 1} \right]} \right\} + {{\theta }_{1}}$

Функции (3.8) и (3.9) описывают процесс теплового расширения и температурное поле в параметрической форме. Так же можно переписать выражение для B(R)

$B\left( R \right) = a{{\left\{ {1 + \frac{{a\left( {2 - 3\alpha \eta } \right)}}{2}\left[ {{{{\left( {\frac{R}{{{{R}_{1}}}}} \right)}}^{2}} - 1} \right]} \right\}}^{{^{{\frac{{3\alpha \eta }}{{2 - 3\alpha \eta }}}}}}}$

Используя (3.6), из (3.5) получим выражения

${{{\mathbf{F}}}^{T}} = \frac{{RB\left( R \right)}}{{f\left( R \right)}}{{{\mathbf{e}}}_{R}}{{{\mathbf{e}}}_{R}} + \frac{{f\left( R \right)}}{R}{{{\mathbf{e}}}_{\Phi }}{{{\mathbf{e}}}_{\Phi }} + w_{{}}^{'}\left( R \right){{{\mathbf{e}}}_{R}}{\mathbf{k}} + {\mathbf{kk}}$

(3.10)

${\mathbf{F}} = \frac{{RB\left( R \right)}}{{f\left( R \right)}}{{{\mathbf{e}}}_{R}}{{{\mathbf{e}}}_{R}} + \frac{{f\left( R \right)}}{R}{{{\mathbf{e}}}_{\Phi }}{{{\mathbf{e}}}_{\Phi }} + w_{{}}^{'}\left( R \right){\mathbf{k}}{{{\mathbf{e}}}_{R}} + {\mathbf{kk}}$

Обратный тензор к F вычисляется с помощью следствия из теоремы Гамильтона–Кэли

${{{\mathbf{F}}}^{{ - 1}}} = [{{{\mathbf{F}}}^{2}} - {{I}_{1}}\left( {\mathbf{F}} \right){\mathbf{F}} + {{I}_{2}}\left( {\mathbf{F}} \right){\mathbf{1}}]{{J}^{{ - 1}}}$

${{{\mathbf{F}}}^{{ - 1}}} = \frac{{f\left( R \right)}}{{RB\left( R \right)}}{{{\mathbf{e}}}_{R}}{{{\mathbf{e}}}_{R}} + \frac{R}{{f\left( R \right)}}{{{\mathbf{e}}}_{\Phi }}{{{\mathbf{e}}}_{\Phi }} - w_{{}}^{'}\left( R \right)\frac{{f\left( R \right)}}{{RB\left( R \right)}}{\mathbf{k}}{{{\mathbf{e}}}_{R}} + {\mathbf{kk}}$

(3.11)

${{({{{\mathbf{F}}}^{T}})}^{{ - 1}}} = \frac{{f\left( R \right)}}{{RB\left( R \right)}}{{{\mathbf{e}}}_{R}}{{{\mathbf{e}}}_{R}} + \frac{R}{{f\left( R \right)}}{{{\mathbf{e}}}_{\Phi }}{{{\mathbf{e}}}_{\Phi }} - w_{{}}^{'}\left( R \right)\frac{{f\left( R \right)}}{{RB\left( R \right)}}{{{\mathbf{e}}}_{R}}{\mathbf{k}} + {\mathbf{kk}}$

По этим выражениям вычисляются

(3.12)

${\mathbf{B}} = \frac{{{{R}^{2}}{{B}^{2}}\left( R \right)}}{{{{f}^{2}}\left( R \right)}}{{{\mathbf{e}}}_{R}}{{{\mathbf{e}}}_{R}} + \frac{{{{f}^{2}}\left( R \right)}}{{{{R}^{2}}}}{{{\mathbf{e}}}_{\Phi }}{{{\mathbf{e}}}_{\Phi }} + w_{{}}^{'}\left( R \right)\frac{{RB\left( R \right)}}{{f\left( R \right)}}\left( {{{{\mathbf{e}}}_{R}}{\mathbf{k}} + {\mathbf{k}}{{{\mathbf{e}}}_{R}}} \right) + (1 + w{{_{{}}^{'}}^{2}}\left( R \right)){\mathbf{kk}}$

(3.13)

${{{\mathbf{B}}}^{{ - 1}}} = \frac{{{{f}^{2}}\left( R \right)(1 + w{{{_{{}}^{'}}}^{2}}\left( R \right))}}{{{{R}^{2}}{{B}^{2}}\left( R \right)}}{{{\mathbf{e}}}_{R}}{{{\mathbf{e}}}_{R}} + \frac{{{{R}^{2}}}}{{{{f}^{2}}\left( R \right)}}{{{\mathbf{e}}}_{\Phi }}{{{\mathbf{e}}}_{\Phi }} - w_{{}}^{'}\left( R \right)\frac{{f\left( R \right)}}{{RB\left( R \right)}}\left( {{{{\mathbf{e}}}_{R}}{\mathbf{k}} + {\mathbf{k}}{{{\mathbf{e}}}_{R}}} \right) + {\mathbf{kk}}$

${{I}_{1}}\left( {\mathbf{B}} \right) = \frac{{{{R}^{2}}{{B}^{2}}\left( R \right)}}{{{{f}^{2}}\left( R \right)}} + \frac{{{{f}^{2}}\left( R \right)}}{{{{R}^{2}}}} + 1 + w{{'}^{2}}\left( R \right)$

(3.14)

${{I}_{2}}\left( {\mathbf{B}} \right) = {{B}^{2}}\left( R \right)\left( {1 + \frac{{{{R}^{2}}}}{{{{f}^{2}}\left( R \right)}}} \right) + \frac{{{{f}^{2}}\left( R \right)(1 + w{{'}^{2}}\left( R \right))}}{{{{R}^{2}}}}$

Используя (2.4), (3.12), (3.13) (функция гидростатического давления $\gamma $ считается зависящей только от R), получим

(3.15)

${\mathbf{S}} = {{S}_{{RR}}}{{{\mathbf{e}}}_{R}}{{{\mathbf{e}}}_{R}} + {{S}_{{\Phi \Phi }}}{{{\mathbf{e}}}_{\Phi }}{{{\mathbf{e}}}_{\Phi }} + {{S}_{{RZ}}}\left( {{{{\mathbf{e}}}_{R}}{\mathbf{k}} + {\mathbf{k}}{{{\mathbf{e}}}_{R}}} \right) + {{S}_{{ZZ}}}{\mathbf{kk}}$

где

${{S}_{{RR}}} = {{s}_{{RR}}}\left( R \right) + \gamma \left( R \right),\quad {{S}_{{\Phi \Phi }}} = {{s}_{{\Phi \Phi }}}\left( R \right) + \gamma \left( R \right),\quad {{S}_{{ZZ}}} = {{s}_{{ZZ}}}\left( R \right) + \gamma \left( R \right),\quad {{S}_{{RZ}}} = {{s}_{{RZ}}}\left( R \right)$

${{s}_{{RR}}}(R) = 2\left[ {{{W}_{1}}\frac{{{{R}^{2}}B(R)}}{{{{f}^{2}}(R)}} - {{W}_{2}}\frac{{{{f}^{2}}(R)(1 + w{{'}^{2}}(R))}}{{{{R}^{2}}B(R)}}} \right],\quad {{s}_{{\Phi \Phi }}}(R) = 2\left[ {{{W}_{1}}\frac{{{{f}^{2}}(R)}}{{{{R}^{2}}B(R)}} - {{W}_{2}}\frac{{{{R}^{2}}B(R)}}{{{{f}^{2}}(R)}}} \right]$

${{s}_{{ZZ}}}\left( R \right) = 2\left[ {{{W}_{1}}\frac{{1 + w{{{_{{}}^{'}}}^{2}}\left( R \right)}}{{B\left( R \right)}} - {{W}_{2}}B\left( R \right)} \right],\quad {{s}_{{RZ}}}\left( R \right) = 2\left[ {{{W}_{1}}\frac{R}{{f\left( R \right)}} + {{W}_{2}}\frac{{f\left( R \right)}}{R}} \right]w_{{}}^{'}\left( R \right)$

С помощью (3.3) и (3.15), перепишем (2.7) в компонентах

(3.16)

$\frac{\partial }{{\partial r}}\left[ {r{{S}_{{RZ}}}\left( R \right)} \right] = 0$

(3.17)

$r\frac{\partial }{{\partial r}}{{S}_{{RR}}}\left( R \right) + {{S}_{{RR}}}\left( R \right) - {{S}_{{\Phi \Phi }}}\left( R \right) = r\frac{\partial }{{\partial r}}\left[ {{{s}_{{RR}}}\left( R \right) + \gamma \left( R \right)} \right] + {{s}_{{RR}}}\left( R \right) - {{s}_{{\Phi \Phi }}}\left( R \right) = 0$

Первый интеграл уравнения (3.16) записывается в форме

(3.18)

$r{{S}_{{RZ}}}\left( R \right) = с \Leftrightarrow {{S}_{{RZ}}}\left( R \right) = \frac{c}{{f\left( R \right)}}$

Константа интегрирования c находится из силовых граничных условий на цилиндрической боковой поверхности. Вектор единичной нормали к боковой поверхности не меняется в процессе деформации и совпадает с ${{{\mathbf{e}}}_{R}}$. Главный вектор на боковой поверхности получим, используя (3.15) и (3.18), в виде

$\frac{Q}{H}{\mathbf{k}} = \int\limits_0^{2\pi } {{{{\mathbf{e}}}_{R}} \cdot {\mathbf{S}}rd\varphi } = \int\limits_0^{2\pi } {\left\{ {{{S}_{{RR}}}\left( R \right)\,{{{\mathbf{e}}}_{R}} + {{S}_{{RZ}}}\left( R \right){\mathbf{k}}\,} \right\}f\left( R \right)d\Phi } = 2\pi {{S}_{{RZ}}}\left( R \right)f\left( R \right){\mathbf{k}} = 2\pi c{\mathbf{k}}$

То есть $c = Q{\text{/}}\left( {2\pi H} \right)$. Теперь имеем выражение для продольного касательного напряжения

(3.19)

${{S}_{{RZ}}} = \frac{Q}{{2\pi H}}\frac{1}{{f\left( R \right)}}$

И из (3.15) и (3.18) получаем уравнение для нахождения продольного смещения

(3.20)

$w'\left( R \right) = \frac{Q}{{4\pi H}}\frac{1}{{f\left( R \right)\left[ {{{W}_{1}}\frac{R}{{f\left( R \right)}} + {{W}_{1}}\frac{{f\left( R \right)}}{R}} \right]}}$

Исходя из формулы (3.19), касательные напряжения не зависят от вида потенциала энергии деформации, а зависимость от температуры определяется только тепловым расширением. По формуле (3.20) от вида потенциала энергии деформации зависит продольное смещение, соответствующее касательному напряжению, и его температурная зависимость определяется не только тепловым расширением, но и температурной зависимостью высокоэластичной деформации.

Обратимся к уравнению (3.17). По (2.8), воспользовавшись (3.10) и (3.11), запишем

${{{\mathbf{r}}}_{1}} = \frac{{RB\left( R \right)}}{{f\left( R \right)}}{{{\mathbf{e}}}_{R}} + w_{{}}^{'}\left( R \right){\mathbf{k}},\quad {{{\mathbf{r}}}_{2}} = f\left( R \right){{{\mathbf{e}}}_{2}},\quad {{{\mathbf{r}}}_{3}} = {\mathbf{k}}$

${{{\mathbf{r}}}^{1}} = \frac{{f\left( R \right)}}{{RB\left( R \right)}}{{{\mathbf{e}}}_{R}},\quad {{{\mathbf{r}}}^{2}} = \frac{1}{{f\left( R \right)}}{{{\mathbf{e}}}_{\Phi }},\quad {{{\mathbf{r}}}^{3}} = - \frac{{f\left( R \right)w_{{}}^{'}\left( R \right)}}{{RB\left( R \right)}}{{{\mathbf{e}}}_{R}} + {\mathbf{k}}$

и получим оператор Гамильтона в материальной системе координат $\left( {R,\Phi ,Z} \right)$ в актуальной конфигурации

(3.21)

$\nabla = \frac{{f\left( R \right)}}{{RB\left( R \right)}}{{{\mathbf{e}}}_{R}}\frac{\partial }{{\partial R}} + \frac{1}{{f\left( R \right)}}{{{\mathbf{e}}}_{\Phi }}\frac{\partial }{{\partial \Phi }} + \left[ { - \frac{{f\left( R \right)w'\left( R \right)}}{{RB\left( R \right)}}{{{\mathbf{e}}}_{R}} + {\mathbf{k}}} \right]\frac{\partial }{{\partial Z}}$

Сравнивая (3.21) и (3.3), получим

$r\frac{\partial }{{\partial r}} = \frac{{{{f}^{2}}\left( R \right)}}{{RB\left( R \right)}}\frac{\partial }{{\partial R}} - \frac{{w'\left( R \right){{f}^{2}}\left( R \right)}}{{RB\left( R \right)}}\frac{\partial }{{\partial Z}}$

используя которое перепишем уравнение (3.17) в виде

$\frac{\partial }{{\partial R}}\left[ {\gamma \left( R \right)} \right] = - \frac{\partial }{{\partial R}}\left[ {{{s}_{{RR}}}\left( R \right)} \right] - \frac{{RB\left( R \right)\left[ {{{s}_{{RR}}}\left( R \right) - {{s}_{{\Phi \Phi }}}\left( R \right)} \right]}}{{{{f}^{2}}\left( R \right)}}$

Откуда

$\gamma \left( R \right) = - {{s}_{{RR}}}\left( R \right) - \int\limits_{{{R}_{1}}}^R {\frac{{tB\left( t \right)\left[ {{{s}_{{RR}}}\left( t \right) - {{s}_{{\Phi \Phi }}}\left( t \right)} \right]}}{{{{f}^{2}}\left( t \right)}}dt} + {{\gamma }_{0}}$

Здесь γ₀ – константа интегрирования, которая находится из граничного условия ${{S}_{{RR}}}\left( {{{R}_{2}}} \right) = 0$ или

${{\gamma }_{0}} = \int\limits_{{{R}_{1}}}^{{{R}_{2}}} {\frac{{tB\left( t \right)\left[ {{{s}_{{RR}}}\left( t \right) - {{s}_{{\Phi \Phi }}}\left( t \right)} \right]}}{{{{f}^{2}}\left( t \right)}}dt} \quad {\text{и}}\quad \gamma \left( R \right) = - {{s}_{{RR}}}\left( R \right) + \int\limits_R^{{{R}_{2}}} {\frac{{tB\left( t \right)\left[ {{{s}_{{RR}}}\left( t \right) - {{s}_{{\Phi \Phi }}}\left( t \right)} \right]}}{{{{f}^{2}}\left( t \right)}}dt} $

Подставляя (3.15) и (3.15) , будем иметь

$\begin{gathered} \gamma \left( R \right) = - 2\left[ {{{W}_{1}}\frac{{{{R}^{2}}B\left( R \right)}}{{{{f}^{2}}\left( R \right)}} - {{W}_{2}}\frac{{{{f}^{2}}\left( R \right)(1 + w{{'}^{2}}\left( R \right))}}{{{{R}^{2}}B\left( R \right)}}} \right] + \\ \, + 2\int\limits_R^{{{R}_{2}}} {{{W}_{1}}\left( {\frac{{{{t}^{3}}{{B}^{2}}\left( t \right)}}{{{{f}^{4}}\left( t \right)}} - \frac{1}{t}} \right) + {{W}_{2}}\left( {\frac{{{{t}^{3}}{{B}^{2}}\left( t \right)}}{{{{f}^{4}}\left( t \right)}} - \frac{{(1 + w{{'}^{2}}\left( t \right))}}{t}} \right)dt} \\ \end{gathered} $

Перейдем к безразмерным величинам, переменным и параметрам.

$\bar {\rho } = \frac{R}{{{{R}_{1}}}},\quad \kappa = \frac{{{{R}_{2}}}}{{{{R}_{1}}}},\quad \delta = \frac{\Delta }{{{{R}_{1}}}},\quad \omega = \frac{w}{{{{R}_{1}}}},\quad \upsilon = \frac{f}{{{{R}_{1}}}},\quad q = \frac{Q}{{2\pi {{R}_{1}}H{{\mu }_{0}}}},\quad \tilde {\gamma }\left( {\bar {\rho }} \right) = \frac{{\gamma \left( {\bar {\rho }} \right)}}{{{{\mu }_{0}}}}$

${{\sigma }_{{RZ}}} = \frac{{{{s}_{{RZ}}}}}{{{{\mu }_{0}}}},\quad {{\sigma }_{{RR}}} = \frac{{{{s}_{{RR}}}}}{{{{\mu }_{0}}}},\quad {{\sigma }_{{\Phi \Phi }}} = \frac{{{{s}_{{\Phi \Phi }}}}}{{{{\mu }_{0}}}},\quad \dot {\omega }\left( {\bar {\rho }} \right) = \frac{{\partial \omega \left( {\bar {\rho }} \right)}}{{\partial{ \bar {\rho }}}} = \frac{{\partial w\left( R \right)}}{{\partial R}} = w_{{}}^{'}\left( R \right)$

${{\Sigma }_{{RR}}} = \frac{{{{S}_{{RR}}}}}{{{{\mu }_{0}}}},\quad {{\Sigma }_{{\Phi \Phi }}} = \frac{{{{S}_{{\Phi \Phi }}}}}{{{{\mu }_{0}}}},\quad {{\Sigma }_{{ZZ}}} = \frac{{{{S}_{{ZZ}}}}}{{{{\mu }_{0}}}},\quad {{\Sigma }_{{RZ}}} = \frac{{{{S}_{{RZ}}}}}{{{{\mu }_{0}}}}$

Здесь $\Delta $ – продольное смещение внешней боковой поверхности втулки относительно внутренней. Используя эти соотношения, получим $\left( {\bar {\rho } \in \left[ {1,\kappa } \right]} \right)$

• выражение, характеризующее поле температур

(3.22)

$\theta \left( {\bar {\rho }} \right) = \frac{\eta }{{2 - 3a\eta }}\ln \left\{ {1 + \frac{{a\left( {2 - 3\alpha \eta } \right)}}{2}[{{{\bar {\rho }}}^{2}} - 1]} \right\} + {{\theta }_{1}}$

• выражения, описывающие напряженно-деформированное состояние

(3.23)

$\upsilon \left( {\bar {\rho }} \right) = {{\left\{ {1 + \frac{{a\left( {2 - 3\alpha \eta } \right)}}{2}[{{{\bar {\rho }}}^{2}} - 1]} \right\}}^{{\frac{1}{{2 - 3a\eta }}}}}$

$B\left( {\bar {\rho }} \right) = a{{\left\{ {1 + \frac{{a\left( {2 - 3\alpha \eta } \right)}}{2}[{{{\bar {\rho }}}^{2}} - 1]} \right\}}^{{\frac{{3\alpha \eta }}{{2 - 3a\eta }}}}},\quad a = {{e}^{{3\alpha {{\theta }_{1}}}}}$

(3.24)

$\dot {\omega }\left( {\bar {\rho }} \right) = \frac{{{{\mu }_{0}}q}}{2}{{\left[ {{{W}_{1}}\bar {\rho } + {{W}_{2}}\frac{{{{\upsilon }^{2}}\left( {\bar {\rho }} \right)}}{{\bar {\rho }}}} \right]}^{{ - 1}}}$

(3.25)

$\begin{gathered} {{\Sigma }_{{RR}}}\left( {\bar {\rho }} \right) = {{\sigma }_{{RR}}}\left( {\bar {\rho }} \right) + \tilde {\gamma }\left( {\bar {\rho }} \right),\quad {{\Sigma }_{{\Phi \Phi }}}\left( {\bar {\rho }} \right) = {{\sigma }_{{\Phi \Phi }}}\left( {\bar {\rho }} \right) + \tilde {\gamma }\left( {\bar {\rho }} \right) \\ {{\Sigma }_{{ZZ}}}\left( {\bar {\rho }} \right) = {{\sigma }_{{ZZ}}}\left( {\bar {\rho }} \right) + \tilde {\gamma }\left( {\bar {\rho }} \right),\quad {{\Sigma }_{{RZ}}}\left( {\bar {\rho }} \right) = {{\sigma }_{{RZ}}}\left( {\bar {\rho }} \right) \\ \end{gathered} $

где

${{\sigma }_{{RR}}}\left( {\bar {\rho }} \right) = \frac{2}{{{{\mu }_{0}}}}\left[ {{{W}_{1}}\frac{{{{{\bar {\rho }}}^{2}}B\left( {\bar {\rho }} \right)}}{{{{\upsilon }^{2}}\left( {\bar {\rho }} \right)}} - {{W}_{2}}\frac{{{{\upsilon }^{2}}\left( {\bar {\rho }} \right)(1 + {{{\dot {\omega }}}^{2}}\left( {\bar {\rho }} \right))}}{{{{{\bar {\rho }}}^{2}}B\left( {\bar {\rho }} \right)}}} \right],\quad {{\sigma }_{{RZ}}}\left( {\bar {\rho }} \right) = \frac{q}{{\upsilon \left( {\bar {\rho }} \right)}}$

${{\sigma }_{{\Phi \Phi }}}\left( {\bar {\rho }} \right) = \frac{2}{{{{\mu }_{0}}}}\left[ {{{W}_{1}}\frac{{{{\upsilon }^{2}}\left( {\bar {\rho }} \right)}}{{{{{\bar {\rho }}}^{2}}B\left( {\bar {\rho }} \right)}} - {{W}_{2}}\frac{{{{{\bar {\rho }}}^{2}}B\left( {\bar {\rho }} \right)}}{{{{\upsilon }^{2}}\left( {\bar {\rho }} \right)}}} \right],\quad {{\sigma }_{{ZZ}}}\left( {\bar {\rho }} \right) = \frac{2}{{{{\mu }_{0}}}}\left[ {{{W}_{1}}\frac{{1 + {{{\dot {\omega }}}^{2}}\left( {\bar {\rho }} \right)}}{{B\left( {\bar {\rho }} \right)}} - {{W}_{2}}B\left( {\bar {\rho }} \right)} \right]$

$\tilde {\gamma }\left( {\bar {\rho }} \right) = - {{\sigma }_{{RR}}}\left( {\bar {\rho }} \right) + \frac{2}{{{{\mu }_{0}}}}\int\limits_{\bar {\rho }}^\kappa {{{W}_{1}}\left( {\frac{{{{t}^{3}}{{B}^{2}}\left( t \right)}}{{{{\upsilon }^{4}}\left( t \right)}} - \frac{1}{t}} \right) + {{W}_{2}}\left( {\frac{{{{t}^{3}}{{B}^{2}}\left( t \right)}}{{{{\upsilon }^{4}}\left( t \right)}} - \frac{{(1 + {{{\dot {\omega }}}^{2}}\left( t \right))}}{t}} \right)dt} $

Для потенциала Джента-Томаса

(3.26)

${{W}_{1}} = \frac{{{{\mu }_{0}}}}{{B\left( R \right)}}\left[ {1 + \frac{{\theta \left( {\bar {\rho }} \right)}}{{{{T}_{0}}}}} \right]\left( {\frac{1}{2} - \frac{\beta }{3}} \right),\quad {{W}_{2}} = \frac{{{{\mu }_{0}}}}{{B\left( R \right)}}\left[ {1 + \frac{{\theta \left( {\bar {\rho }} \right)}}{{{{T}_{0}}}}} \right]\frac{\beta }{{{{I}_{2}}}}$

(3.27)

${{I}_{2}} = {{B}^{2}}\left( {\bar {\rho }} \right)\left( {1 + \frac{{{{{\bar {\rho }}}^{2}}}}{{{{\upsilon }^{2}}\left( {\bar {\rho }} \right)}}} \right) + \frac{{{{\upsilon }^{2}}\left( {\bar {\rho }} \right)(1 + {{{\dot {\omega }}}^{2}}\left( {\bar {\rho }} \right))}}{{{{{\bar {\rho }}}^{2}}}}$

и исключая I₂ в выражениях (3.24), (3.26), (3.27), получим относительно $\dot {\omega }$ кубическое уравнение

(3.28)

$\begin{gathered} {{a}_{3}}{{{\dot {\omega }}}^{3}}\left( {\bar {\rho }} \right) + {{a}_{2}}{{{\dot {\omega }}}^{2}}\left( {\bar {\rho }} \right) + {{a}_{1}}\dot {\omega }\left( {\bar {\rho }} \right) + {{a}_{0}} = 0 \\ {{a}_{3}} = \frac{{\bar {\rho }{{\upsilon }^{4}}\left( {\bar {\rho }} \right)\left( {3 - 2\beta } \right)}}{{B\left( R \right)}}\left[ {1 + \frac{{\theta \left( {\bar {\rho }} \right)}}{{{{T}_{0}}}}} \right],\quad {{a}_{2}} = - 3q{{\upsilon }^{4}}\left( {\bar {\rho }} \right) \\ {{a}_{1}} = \{ {{{\bar {\rho }}}^{3}}{{B}^{2}}\left( {\bar {\rho }} \right)[{{{\bar {\rho }}}^{2}} + {{\upsilon }^{2}}\left( {\bar {\rho }} \right)]\left( {3 - 2\beta } \right) + \bar {\rho }\left( {4\beta + 3} \right){{\upsilon }^{4}}\left( {\bar {\rho }} \right)\} {{B}^{{ - 1}}}\left( R \right)\left[ {1 + \frac{{\theta \left( {\bar {\rho }} \right)}}{{{{T}_{0}}}}} \right] \\ {{a}_{0}} = - 3q\{ {{{\bar {\rho }}}^{2}}[{{{\bar {\rho }}}^{2}} + {{\upsilon }^{2}}\left( {\bar {\rho }} \right)]{{B}^{2}}\left( {\bar {\rho }} \right) + {{\upsilon }^{4}}\left( {\bar {\rho }} \right)\} \\ \end{gathered} $

3.2. Результаты вычислений. В данной работе принят линейный коэффициент теплового расширения $\alpha = 0.0002^\circ {{{\text{C}}}^{{ - 1}}}$, характерный для эластомеров. Недеформированной конфигурации соответствует однородная температура ${{T}_{0}} = 293$ K. Значение разностной температуры на внутренней поверхности ${{\theta }_{1}} = {{T}_{1}} - {{T}_{0}}$ полагается равным 0°C. Значение разностной температуры на внешней поверхности ${{\theta }_{2}} = {{T}_{2}} - {{T}_{0}}$ полагается равным 100°C. Случаю отсутствия нагрева соответствует разностная температура на внешней поверхности ${{\theta }_{2}} = 0^\circ {\text{C}}$.

Уравнение (3.28) имеет вещественные коэффициенты и для принятых значений $\theta \in \left[ {0.100\,{\text{C}}^\circ } \right]$, $\kappa \in \left[ {1.2,2} \right],q \in \left[ {0,0.8} \right],\beta \in \left[ {0.2{\text{/}}3} \right)$ у него один вещественный и два комплексно сопряженных корня. Физический смысл имеет только вещественный корень.

Все вычисления проводились для κ = 2. Зависимости безразмерных напряжений от безразмерного радиуса вычислялись при q = 0.8.

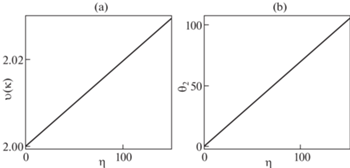
На рис. 1(а, б) представлены зависимости, $\upsilon \left( \kappa \right)$ и ${{\theta }_{2}} = \theta \left( \kappa \right)$ от $\eta $. Равенство ${{\theta }_{2}} = 100{\text{C}}^\circ $ для κ = 2 достигается при $\eta = 141.448^\circ {\text{C}}$, а ${{\theta }_{2}} = 0^\circ {\text{C}}$ при $\eta = 0$.

Рис. 1.

Зависимости $\upsilon (\kappa )$ (a) и ${{\theta }_{2}} = \theta (\kappa )$ (b) от $\eta $.

Имея аналитическое решение (3.22)–(3.25) в виде функций, зависящих от $\alpha $ и ${{\theta }_{2}}$ как от параметров, легко выяснить степень влияния теплового расширения и температурной зависимости высокоэластичной составляющей на свойства этого решения.

Ниже представлены результаты вычислений в виде графиков. На каждом рисунке представлены три кривые. Кривая 1 соответствует ${{\theta }_{2}} = 0$ (отсутствию температурного поля). Кривая 2 соответствует ${{\theta }_{2}} = 100^\circ {\text{C}},\alpha = 0^\circ {{{\text{C}}}^{{ - 1}}}$ (температурное поле присутствует, но тепловое расширение отсутствует). Кривая 3 соответствует ${{\theta }_{2}} = 100^\circ {\text{C}}$, $\alpha = 0.0002^\circ {{{\text{C}}}^{{ - 1}}}$ (температурное поле и тепловое расширение присутствуют).

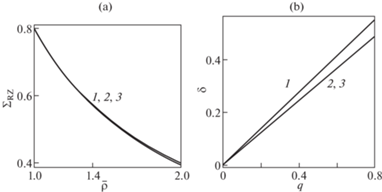
На рис. 2, а приведены зависимости ${{\Sigma }_{{RZ}}} = {{\Sigma }_{{RZ}}}\left( {\bar {\rho }} \right)$. Все три кривые визуально совпадают, поскольку температурная зависимость этого напряжения определяется только весьма слабым температурным изменением площади цилиндрической поверхности (3.24) за счет теплового расширения. На рис. 2, b для $\beta = 0.6$ приведены зависимости $\delta = \delta \left( q \right)$ (жесткостные характеристики). Повышение температуры повышает сдвиговую жесткость, а совпадение кривых 2 и 3 говорит о том, что на процесс сильнее влияет температурная зависимость высокоэластичной составляющей деформации.

Рис. 2.

Зависимости ${{\Sigma }_{{RZ}}}$ от $\bar {\rho }$ (a). Зависимости $\delta $ от $q$ при $\beta = 0.6$ (b). 1 – ${{\theta }_{2}} = 0$, 2 – ${{\theta }_{2}} = 100^\circ {\text{C}}$, $\alpha = 0$, 3 – ${{\theta }_{2}} = 100^\circ {\text{C}}$, $\alpha = 2 \times {{10}^{{ - 4}}}^\circ {{{\text{C}}}^{{ - 1}}}$.

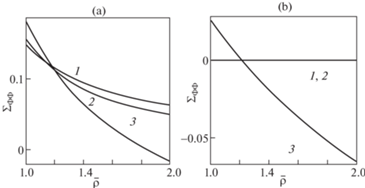
На рис. 3 (a) представлены кривые зависимости ${{\Sigma }_{{RR}}} = {{\Sigma }_{{RR}}}\left( {\bar {\rho }} \right)$ при $\beta = 0.6$. Близость кривых 1 и 2 говорит о том, что температурная зависимость высокоэластичной деформации проявляется слабо. Существенное отличие кривой 3 от кривых 1, 2 показывает, что температурная зависимость радиального напряжения определяется, в основном, тепловым расширением. На рис. 3, b представлены кривые ${{\Sigma }_{{RR}}} = {{\Sigma }_{{RR}}}\left( \rho \right)$ для $\beta = 0$ (потенциал Трелоара). Здесь высокоэластичная деформация вообще не дает вклада в ${{{\mathbf{\Sigma }}}_{{RR}}}$ и эти напряжения возникают исключительно вследствие теплового расширения. Аналогичная ситуация справедлива и для температурного поведения зависимости ${{\Sigma }_{{\Phi \Phi }}} = {{\Sigma }_{{\Phi \Phi }}}\left( {\bar {\rho }} \right)$, что иллюстрируется рис. 3, a с $\beta = 0.6$ и рис. 3, b c $\beta = 0$.

Рис. 3.

Зависимости ${{\Sigma }_{{RR}}}$ от $\bar {\rho }$ при $\beta = 0.6$ (a). Зависимости ${{\Sigma }_{{RR}}}$ от $\bar {\rho }$ при $\beta = 0$ (b). 1 – ${{\theta }_{2}} = 0$, 2 – ${{\theta }_{2}} = 100^\circ {\text{C}}$, $\alpha = 0$, 3 – ${{\theta }_{2}} = 100^\circ {\text{C}}$, $\alpha = 2 \times {{10}^{{ - 4}}}{\text{ }}^\circ {{{\text{C}}}^{{ - 1}}}$.

4. Заключение. В рамках феноменологического подхода предложен вариант постановки задач статической термоупругости однородного изотропного несжимаемого материала при конечных деформациях, позволяющий в неоднородном температурном поле учитывать как тепловое расширение, так и температурные изменения напряжений, вызванных высокоэластичной деформацией. Рассмотрена задача о конечном продольном сдвиге полого цилиндра в осесимметричном температурном поле. В рамках предложенной постановки с потенциалом Джента–Томаса получено новое аналитическое решение связной задачи термоупругости. Общим результатом термоупругого анализа является то, что температурная зависимость разных характеристик напряженно-деформированного состояния может контролироваться разными механизмами. Так температурная зависимость касательного напряжения, вызывающего продольный сдвиг, определяется только тепловым расширением, тогда как температурная зависимость сдвиговой жесткости определяется, в основном, температурным изменением высокоэластичной деформации. Температурная зависимость нормальных напряжений существенно определяется тепловым расширением, и слабее температурным изменением высокоэластичной деформации при ${{W}_{2}} \ne 0$. При W₂ = 0 высокоэластичная деформация вообще не дает вклада в нормальные напряжения, и они возникают исключительно вследствие теплового расширения. Подобная информация представляет определенный интерес при проектировании резинометаллических деталей, поскольку на тепловое расширение влияет наличие свободных поверхностей, которые можно задавать конструктивно.

Рис. 4.

Зависимости ${{\Sigma }_{{\Phi \Phi }}}$ от $\bar {\rho }$ при $\beta = 0.6$ (a). Зависимости ${{\Sigma }_{{\Phi \Phi }}}$ от $\bar {\rho }$ при $\beta = 0$ (b). 1 – ${{\theta }_{2}} = 0$, 2 – ${{\theta }_{2}} = 100^\circ {\text{C}}$, $\alpha = 0$, 3 – ${{\theta }_{2}} = 100^\circ {\text{C}}$, $\alpha = 2 \times {{10}^{{ - 4}}}{\text{ }}^\circ {{{\text{C}}}^{{ - 1}}}$.

Список литературы

Treloar L.R. The Physics of Rubber Elasticity. Oxford: Clarendon Press, 1975. 310 p.
Shen M. Elasticity and thermoelasticity of crosslinked polymer networks // Pure and Appl. Chem. 1975. V. 43. № 1–2. P. 43–55. https://doi.org/10.1351/pac197543010043
Марк Дж., Эрман Б., Эйрич Ф. Каучук и резина. Наука и технология. Долгопрудный: Издательский Дом “Интеллект”, 2011. 768 с.
Бартенев Г.М., Френкель С.Я. Физика полимеров. Л.: Химия, 1990. 432 с.
Rivlin R.S., Saunders D.W. Large elastic deformations of isotropic materials. VII. Experiments on the deformation of rubber / Phil. Trans. Roy. Soc. Lond. A. 1951. V. 243. № 865. P. 251–288. https://doi.org/10.1098/rsta.1951.0004
Hossa L., Marczakb R.J. A new constitutive model for rubber-like materials // Mech. Computat. 2010. V. 29. P. 2759–2773.
Gent A.N., Thomas A.G. Forms for the stored (strain) energy function for vulcanized rubber // J. Polymer Sci. 1958. V. XXVIII. № 118. P. 625–628. https://doi.org/10.1002/pol.1958.1202811814
Horgan C., Saccomandi G. Finite thermoelasticity with limiting chain extensibility // J. Mech. Phys. Solids. 2003. V. 51. № 6. P. 1127–1146. https://doi.org/10.1016/S0022-5096(02)00144-8
Ogden R.W. On the thermoelastic modeling of rubberlike solids // J. Therm. Stress. 1992. V. 15. № 4. P. 533–557. https://doi.org/10.1080/01495739208946155
Жуков Б.А. Влияние теплового расширения в неоднородном стационарном температурном поле на неоднородное напряженно-деформированное состояние тела из несжимаемого эластомера при статических конечных деформациях // Изв. РАН. МТТ. 2021. № 2. С. 17–30. https://doi.org/10.31857/S057232992101013X
Saccomandi G. On inhomogeneous deformations in finite thermoelasticity. // IMA Journal of Applied Mathematics. 1999. V. 63. P. 131–148. https://doi.org/10.1093/imamat/63.2.131
Лурье А.И. Нелинейная теория упругости. М.: Наука, 1980. 512 с.
Truesdell C., Noll W. The Non-linear Field Theories of Mechanics. N. Y.: Springer, 2003. 602 p.
Андреева Ю.Ю., Жуков Б.А. Точные аналитические решения одной задачи нелинейной теории упругости для двух потенциалов энергии деформации несжимаемого материала // Изв. вузов. Поволжский регион. Физико-математические науки. 2018. № 2 (46). С. 64–76. https://doi.org/10.21685/2072-3040-2018-2-7

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика твердого тела

Архивы выпусков Информация о журнале Отправить рукопись в журнал