Известия РАН. Механика твердого тела, 2022, № 4, стр. 144-162
О СПУСКЕ ЛЫЖНИКА ПО ПРЯМОЛИНЕЙНОЙ ТРАССЕ
Б. Я. Локшин a, *, В. А. Самсонов a, **
a НИИ механики МГУ имени М.В. Ломоносова
Москва, Россия
* E-mail: lokshinb@imec.msu.ru
** E-mail: samson@imec.msu.ru
Поступила в редакцию 21.09.2021
После доработки 22.11.2021
Принята к публикации 23.11.2021
- EDN: ECOMOT
- DOI: 10.31857/S0572329922040067
Аннотация
Рассматривается движение лыжника в процессе разгона на прямолинейной трассе. Предлагается лыжника представить в виде связки двух твердых тел, сцепленных между собой под некоторым установочным углом, одно из которых (“крыло”) обладает аэродинамическим качеством. Выбор желаемого режима спуска происходит за счет управляющего момента, приложенного в точке контакта корпуса с поверхностью, и за счет выбора установочного угла. Основное внимание уделяется рассмотрению вопроса о движении этой связки тел при условии, что в процессе спуска “стойка лыжника” не изменяется. Показано, что существует некоторое значение установочного угла “крыла”, при котором достигается максимальное значение скорости спуска в любой момент времени. Это экстремальное значение угла зависит только от аэродинамических характеристик силового воздействия. Тем самым установлено, что в рамках предложенной математической модели для достижения максимально возможной скорости спуска необходимо соблюдать постоянную стойку и форму корпуса. Реализация этого экстремального режима спуска ограничена только возможностью обеспечения требуемого управляющего момента. Показано, что при определенных условиях сила реакции обнуляется, происходит отрыв тела от поверхности, причем с продолжающимся ростом скорости. Установлено, что после такого отрыва возвращения на поверхность не происходит, в дальнейшем тело совершает свободный полет с выходом на режим устойчивого планирования.
1. Введение. Первым этапом в спортивных соревнованиях по прыжкам с трамплина является разгон лыжника до момента отталкивания. В процессе этого разгона лыжник принимает определенную позу и старается поддерживать ее при нарастании скорости за счет вырабатываемых моментов в суставах. Профиль поверхности спуска выполнен в виде наклонной прямой достаточно большой протяженности, которая заканчивается некоторой плавной кривой. Поэтому анализ движения лыжника именно по наклонной прямой представляет определенный интерес как с практической точки зрения, так и в качестве теоретико-механической задачи. В научной литературе имеются определенные исследования по этой теме. При этом сначала представляют лыжника как некоторый трехзвенный перевернутый маятник, но этим “рисованием” и ограничиваются, заменяя его на материальную точку [1–3]. Затем с разной степенью точности рассматриваются дифференциальные уравнения движения этой точки, ставятся и решаются разные задачи для нее. В [1] отмечается ограниченность такого подхода, в частности указывается на необходимость рассмотрения твердого тела в качестве модели лыжника, а не материальной точки, и анализа устойчивости режима спуска. В работах [2, 3] на основе все той же модели тела как материальной точки рассматриваются задачи быстродействия по переводу движения с некоторой заданной начальной скоростью на движение с заданной конечной скоростью за счет управления лобовым сопротивлением. Для решения этих оптимальных задач используют принцип максимума Понтрягина [2] или метод Миеле [3]. Вообще, научных публикаций, посвященных прыжкам лыжников с трамплина, достаточно много, но в них рассматриваются последующие этапы этих соревнований: процесс отталкивания, режим полета и приземления. По-видимому, считается, что процесс разгона лыжника во время спуска не очень интересен. На самом деле, это не совсем так, и в процессе разгона есть предмет для более подробного исследования.
В настоящей работе для простоты предлагается представить лыжника как связку двух твердых тел, жестко сцепленных в общем центре масс (рис. 1). Одно из них – это корпус, скользящий своей одной фиксированной точкой (опорной точкой) по поверхности склона и имеющий возможность совершать поворот относительно нее. Другое твердое тело (типа “крыла”) сцеплено с первым под некоторым установочным углом. Эта сцепка тел имитирует стойку и конфигурацию лыжника, которые, вообще говоря, в процессе спуска могут изменяться.
Будем считать, что аэродинамическое воздействие сосредоточено именно на втором теле, для описания этого воздействия используется хорошо зарекомендовавшая себя в ряде других задач квазистатическая модель обтекания [4, 5]. Выбор желаемого режима движения происходит за счет управляющего момента, приложенного в точке контакта корпуса с поверхностью и за счет выбора установочного угла “крыла”. Решение соответствующих дифференциальных уравнений при выбранных зависимостях управляющего момента и величине установочного угла крыла полностью определяет режим движения в процессе спуска: не только скорость спуска, как это было в предыдущих моделях с материальной точкой, но и угол наклона тела.
Основное внимание в настоящей работе уделяется рассмотрению вопроса о движении тела при условии, что в процессе спуска “стойка лыжника” не изменяется. В этом случае оказывается, что направление вектора скорости центра масс тоже не изменяется и совпадает с направлением склона. Условие постоянства угла наклона корпуса накладывает определенное ограничение на выбор изменяющегося в процессе спуска управляющего момента. Реализация желаемого режима спуска ограничена возможностью обеспечения требуемого управляющего момента.
Рассмотрен также вопрос о возможности отрыва “лыжника” от поверхности спуска и дальнейшего движения в режиме свободного полета. Такая ситуация может возникнуть, когда при достаточно большой подъемной силе сила реакции со стороны поверхности обнуляется.
Представлены результаты численного исследования некоторых примеров движения рассматриваемой конструкции.
2. Постановка задачи и математическая модель. Рассматривается задача о спуске лыжника в среде с квадратичным законом сопротивления в вертикальной плоскости по заданной наклонной прямой $y = h(x) = x \cdot {\text{tg}}\varphi $, причем по этой прямой перемещается фиксированная опорная точка корпуса лыжника. Эту задачу можно трактовать как теоретико-механическую задачу о движении в сопротивляющейся среде перевернутого маятника, точка опоры которого скользит по заданной наклонной прямой.
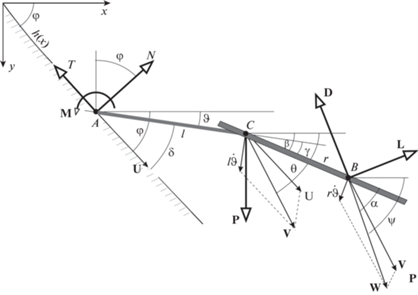
Стойку лыжника в процессе спуска будем моделировать твердым телом (корпус+крыло) с фиксированной в теле опорной точкой А, перемещающейся по склону (по указанной прямой) (рис. 2). Со стороны склона на это тело в точке А действуют нормальная сила реакции и сила сухого трения, пропорциональная силе реакции.
Со стороны воздушной среды на тело действует результирующая аэродинамических сил (силы лобового сопротивления и подъемной силы), проходящая через некоторую фиксированную точку В “крыла”, не совпадающую, вообще говоря, с центром С масс тела.
В опорной точке на тело действует управляющий момент, формируемый самим лыжником в соответствии с желаемым режимом спуска. На рис. 2 схематически представлены стойка лыжника, характеризуемая отрезками АС и СВ, а также силы и все введенные обозначения (указаны положительные значения углов).
Здесь ${\mathbf{U}}$ – скорость точки А, направлена вдоль склона,${\mathbf{V}}$ – скорость центра масс, ${\mathbf{W}}$ – скорость центра давления, $l = AC$, $r = CB$, $\varphi $ – угол наклона прямой, $\vartheta $ – угол наклона корпуса, $\theta $ – угол наклона вектора скорости центра масс, $\psi $ – угол наклона вектора скорости центра давления, $\alpha $ – угол атаки, $\gamma $ – установочный угол, $\delta = \varphi - \vartheta $, $\beta = \gamma + \vartheta $ – угол наклона “крыла”, $\alpha = \psi - \beta $. Предполагается, что величина М управляющего момента выбирается с целью поддержки определенной ориентации корпуса, а значение установочного угла $\gamma $ – для увеличения скорости спуска. Силовое воздействие на лыжника складывается из силы ${\mathbf{P}}$ тяжести, сил реакции со стороны склона: нормальной силы ${\mathbf{N}}$ и силы ${\mathbf{T}}$ сухого трения, величина которой равна $\;T = \mu \left| N \right|$, и сил аэродинамического воздействия со стороны окружающего воздуха: силы ${\mathbf{D}}$ лобового сопротивления и боковой (подъемной) силы ${\mathbf{L}}$. Кроме того, в опорной точке на корпус действует момент ${\mathbf{M}}$ (будем называть его управляющим). Все эти величины отражены на рисунке.
Рассмотрим некоторые особенности спуска при постоянном угле наклона корпуса при условии $\mu < {\text{tg}}\varphi $ (иначе спуск был бы невозможен).
Из школьного курса физики известно, что при отсутствии аэродинамических сил тело на наклонной плоскости перемещается с постоянным положительным ускорением $g(\sin \varphi - \mu \cos \varphi )$, так что скорость в процессе спуска будет неограниченно возрастать.
Другая ситуация возникает при наличии аэродинамических сил. Предположим сначала, что подъемная сила отсутствует (например, крыло в виде шара), и есть только сила лобового сопротивления. Тогда по мере нарастания скорости и соответственно силы лобового сопротивления положительное ускорение спуска будет уменьшаться, и при некоторой предельной скорости обратится в нуль; дальнейший спуск будет происходить именно с этим постоянным значением скорости.
Если к силе лобового сопротивления добавить еще и подъемную силу, то из рис. 2 видно, что эта сила приводит к уменьшению нормальной силы реакции, это в свою очередь уменьшает и силу сухого трения. Вследствие этого скорость спуска сначала увеличивается по сравнению со случаем отсутствия подъемной силы. В этом и проявляется антидиссипативное влияние подъемной силы [4]. По мере роста скорости сила лобового сопротивления увеличивается. При этом в процессе своего роста скорость может в некоторый момент времени достигнуть такого значения, при котором сила реакции обращается в ноль, и дальнейшее движение происходит уже в соответствии с другой математической моделью.
Пусть текущие координаты центра масс: $x,\;y$, точки А: ${{x}_{A}},\;{{y}_{A}} = {{x}_{A}} \cdot {\text{tg}}\varphi $. Очевидно, имеют место кинематические соотношения $x = {{x}_{A}} + l\cos \vartheta ,\;y = {{y}_{A}} + l\sin \vartheta $. Координаты скорости центра масс равны
(2.1)
$\begin{array}{*{20}{c}} {\dot {x} = {{{\dot {x}}}_{A}} - l\dot {\vartheta }\sin \vartheta = V\cos \theta } \\ {\dot {y} = {{{\dot {y}}}_{A}} + l\dot {\vartheta }\cos \vartheta = V\sin \theta } \end{array}$После несложных преобразований в (2.1), учитывая ${{\dot {y}}_{A}} = {{\dot {x}}_{A}} \cdot {\text{tg}}\varphi $, $\dot {y} = \dot {x} \cdot {\text{tg}}\theta $, имеет место уравнение связи в форме
Уравнения движения рассматриваемого тела можно представить в виде:
(2.3)
$\begin{array}{*{20}{c}} {m\dot {V} = mg\sin \theta - D\cos (\psi - \theta ) + L\sin (\psi - \theta ) - N\left[ {\sin (\theta - \varphi ) + \mu \cos (\theta - \varphi )} \right]} \\ {mV\dot {\theta } = mg\cos \theta - D\sin (\psi - \theta ) - L\cos (\psi - \theta ) - N\left[ {\cos (\theta - \varphi ) - \mu \sin (\theta - \varphi )} \right]} \\ {J\ddot {\vartheta } = lN\left[ {\cos \delta + \mu \sin \delta } \right] - r\left[ {D\sin \alpha + L\cos \alpha } \right] + M} \\ {\dot {x} = V\cos \theta } \\ {\dot {y} = V\sin \theta } \end{array}$Здесь учитывается, что нормальная сила реакции положительна и знак модуля в определении силы сухого трения можно опустить, $m$ и $J$ – масса тела и его центральный момент инерции соответственно. Величины аэродинамических сил представляются в обычном для прикладной аэродинамики виде (D – drag, сила лобового сопротивления, L – lift, подъемная сила):
(2.4)
$D = 0.5{{C}_{D}}(\alpha )\rho S{{V}^{2}},\quad L = 0.5{{C}_{L}}(\alpha )\rho S{{V}^{2}}\quad $Из уравнения (2.2) связи следует
Угол $\psi $ ориентации вектора скорости центра давления определяется через те же переменные
(2.6)
$\psi = {\text{arctg}}\frac{{V\sin \theta + r\dot {\vartheta }\cos \beta }}{{V\cos \theta - r\dot {\vartheta }\sin \beta }}$Вертикальная координата центра масс, пока опорная точка А не покидает поверхность, также выражается с помощью этих переменных:
Для исключения силы реакции снова воспользуемся равенством (2.2). После его дифференцирования имеем
Подставляя в это равенство выражения производных из (2.3), получим
(2.8)
$\begin{gathered} N[1 + (m{{l}^{2}}{\text{/}}J)\cos \delta \cdot [\cos \delta + \mu \sin \delta ]] = mg\cos \varphi - ml{{{\dot {\vartheta }}}^{2}}\sin \delta - \left( {ml{\text{/}}J} \right)M\cos \delta - \\ \, - D\left[ {\sin (\psi - \varphi ) - \left( {mlr{\text{/}}J} \right)\cos \delta \sin \alpha } \right] - L\left[ {\cos (\psi - \varphi ) - \left( {mlr{\text{/}}J} \right)\cos \delta \cos \alpha } \right] \\ \end{gathered} $Теперь в уравнениях (2.3) можно отбросить второе и пятое уравнения, так что дифференциальные уравнения движения рассматриваемого объекта могут быть представлены в следующем виде:
(2.9)
$\begin{array}{*{20}{c}} {m\dot {V} = mg\sin \theta - D\cos (\psi - \theta ) + L\sin (\psi - \theta ) - N\left[ {\sin (\theta - \varphi ) + \mu \cos (\theta - \varphi )} \right]} \\ {J\ddot {\vartheta } = lN\left[ {\cos \delta + \mu \sin \delta } \right] - r\left[ {D\sin \alpha + L\cos \alpha } \right] + M} \\ {\dot {x} = V\cos \theta } \end{array}$Система (2.4)–(2.9) образует искомую замкнутую математическую модель движения рассматриваемого объекта. Остается задать зависимости аэродинамических характеристик ${{C}_{D}}(\alpha ),\;{{C}_{L}}(\alpha )$, параметры $m,\;J,\;l,\,r$, установочный угол $\gamma $ и управляющий момент $M(t)$, после чего можно будет исследовать траектории движения центра масс корпуса и его динамику в процессе спуска.
Поскольку при выводе этих уравнений молчаливо предполагалась положительность силы реакции, определяемой из (2.8), то из этого условия следует неравенство, ограничивающее область применимости построенной математической модели
Отсюда получаем ограничение на скорость спуска в виде неравенства (${{V}_{{N0}}}$ – скорость в момент обращения нормальной реакции в ноль)
(2.10)
${{V}^{2}} < V_{{N0}}^{2} = 2\frac{{mg\cos \varphi - ml{{{\dot {\vartheta }}}^{2}}\sin \delta - \left( {ml{\text{/}}J} \right)M\cos \delta }}{{\rho S\left\{ {{{C}_{D}}\left[ {\sin (\psi - \varphi ) + {{C}_{L}}\cos (\psi - \varphi )} \right] - \left( {mlr{\text{/}}J} \right)\cos \delta \left[ {{{C}_{D}}\sin \alpha + {{C}_{L}}\cos \alpha } \right]} \right\}}}$Здесь предполагается, что числитель и знаменатель дроби положительны. Таким образом, пока выполняется неравенство (2.10), можно пользоваться построенной моделью. При $V = {{V}_{{N0}}}$ сила реакции вместе с силой трения исчезают, происходит отрыв тела от поверхности, и для рассмотрения дальнейшего движения понадобится другая математическая модель. Ниже будет рассмотрена эта ситуация, а пока продолжим анализ построенной модели, когда тело не покидает поверхность.
В качестве числового примера рассматривается спуск тела с антропоморфными параметрами: m = 70 (кг), J = 5 (кгм2), l = 0.6 (м), r = 0.1 (м). Пусть зависимости аэродинамических коэффициентов имеют вид ${{С}_{D}}(\alpha ) = 1.38 - 1.16{\kern 1pt} {\text{cos}}2\alpha ,{{С}_{L}}(\alpha ) = 1.5{\kern 1pt} {\text{sin}}2\alpha $. Угол наклона прямой спуска равен $\varphi = \pi {\text{/}}6$. Пусть “лыжник” собирается поддерживать корпус перпендикулярным склону, тогда он выбирает соответствующий начальный наклон корпуса $\vartheta (0) = - \pi {\text{/}}3$ и соответствующий управляющий момент, например, в виде отрицательной обратной связи
(2.11)
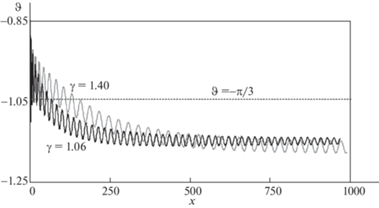
$M = M(x) = - mgl\left( {k(\vartheta (x) + \pi {\text{/}}3) + hl\dot {\vartheta }(x){\text{/}}V(x)} \right)$Параметры $k,\;h$, естественно, выбираются в зависимости от желаемого угла наклона, массовых и геометрических размеров. В данном случае для расчетов были приняты следующие значения этих параметров: $k = 1.5,\;h = 0.1$. Проведенные расчеты при начальных условиях $V(0) = 0,\vartheta (0) = - \pi {\text{/}}3 + 0.34,\dot {\vartheta }(0) = 0,x(0) = 0$ (подчеркнем, что начальный угол наклона корпуса отличается от желаемого примерно на 20°) в соответствии с уравнениями (2.4)–(2.9) показали, что задача поддержки желаемого угла наклона корпуса с помощью выбранного управляющего момента (2.11) решается не вполне удовлетворительно. При этом скорость центра масс растет монотонно от нуля до некоторого предельного значения. Зависимости скорости спуска и угла $\vartheta $ корпуса при различных значениях установочного угла $\gamma $ представлены на рис. 3 и рис. 4 соответственно.
Рис. 3.
Примеры изменения скорости при компенсирующем управляющем моменте и различных значениях установочного угла.
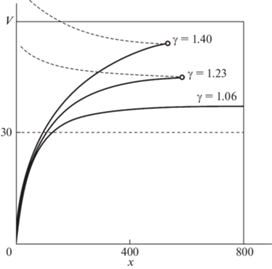
Рис. 4.
Примеры изменения угла наклона корпуса при компенсирующем управляющем моменте и различных значениях установочного угла.
На рис. 3 сплошными жирными линиями изображены графики зависимости скорости при различных значениях установочного угла. Кружочками отмечены моменты, когда сила реакции обращается в ноль. Кроме того, для наглядности пунктиром построены графики (2.10) скорости ${{V}_{{N0}}}$, при которой сила реакции могла бы обратиться в ноль при текущих значениях управляющего момента и угловых координат.
На рис. 4 представлены графики зависимости угла $\vartheta $ при двух значениях установочного угла, а также пунктиром – желаемое значение, равное $\vartheta = - \pi {\text{/}}3$. Из рисунка видно, что желаемое значение угла наклона корпуса не устанавливается. Вместо него устанавливаются слабо затухающие колебания примерно около $\vartheta = - 1.15$ при γ = 1.06 $(\alpha \approx 0.5)$ и $\vartheta = - 1.17$ при $\gamma = 1.40\;(\alpha \approx 0.1)$, так что корпус совершает небольшие затухающие колебания около положения, отклоненного примерно на 6° “назад” от вертикали к поверхности. Соответствующие колебания скорости спуска на рис. 3 не отражены ввиду их малости. При численных расчетах с другими параметрами и желаемом значении угла наклона корпуса наблюдались как более быстро затухающие колебания и выход на некоторый стационарный режим спуска, отличный от желаемого, так и, наоборот, совершенно “нефизичные” очень “размашистые” колебания с амплитудой в несколько десятков градусов около некоторого также отличного от желаемого угла наклона корпуса (с проваливанием тела “вперед” или “назад” под поверхность).
Кроме того, при расчетах установлено, что, за исключением первоначального участка $x < 0.1$ м, значения силы реакции не превосходят силы тяжести лыжника, а принятый управляющий момент находится в пределах 150 нм. Эти данные находятся в соответствии с результатами экспериментальных исследований [6], где отмечается, что максимальная сила в голеностопе наблюдалась порядка 750 н, а максимальный момент не превосходит 150 нм. На первоначальном участке $x < 0.1$ м оказалось, что сила реакции также находится в тех же допустимых пределах, а управляющий момент носит импульсный характер и достигает 210 нм. В процессе дальнейшего движения (спуска) величина управляющего момента быстро уменьшается до 50 нм и даже еще меньше.
Поскольку пример носит чисто иллюстративный характер, то не имеет особого смысла добиваться более удовлетворительного совпадения с желаемым режимом спуска. Отметим лишь, что это совпадение определяется, прежде всего, выбранным управляющим моментом.
3. Движение тела с неизменяемой стойкой. В этом и последующих разделах будем считать, что движение тела происходит с неизменяемой фиксированной стойкой. Это означает, что управляющий момент M выбирается таким образом, что угол наклона корпуса остается постоянным: $\vartheta (t) \equiv \bar {\vartheta } = {\text{const}}$, так что и $\delta (t) \equiv \bar {\delta } = {\text{const}}$, причем установочный угол также не изменяется в процессе спуска, так что $\gamma (t) \equiv \gamma = {\text{const}}$. Отметим, что по физическому смыслу угол $\gamma $ выбирается из интервала $\gamma \in (0,\;\;\varphi - \bar {\vartheta })$. При этом, в соответствии с (2.5), угол наклона вектора скорости центра масс также не изменяется и выполняется равенство:
Последнее равенство означает, что вектор V скорости центра масс параллелен прямой спуска. Также, в соответствии с (6) сохраняется ориентация и вектора W скорости центра давления:
Вследствие этого угол атаки $\alpha = \psi - \beta $ также остается постоянным:
Для краткости записи чертой сверху будем обозначать и соответствующие значения аэродинамических сил, так что
Для осуществления такого режима движения следует выбрать подходящую величину управляющего момента. Примем его, например, в виде компенсирующего момента ${{M}_{k}}$:
(3.1)
$M = {{M}_{k}} = - lN\left[ {\cos \bar {\delta } + \mu \sin \bar {\delta }} \right] + r\left[ {\bar {D}\sin \bar {\alpha } + \bar {L}\cos \bar {\alpha }} \right]$При этом, как это следует из (2.8), сила реакции (тоже отметим ее чертой сверху) равна:
Уравнения (2.9) преобразуются к виду
(3.3)
$\begin{array}{*{20}{c}} {m\dot {V} = mg(\sin \varphi - \mu \cos \varphi ) - (\bar {D} - \mu \bar {L})} \\ {\dot {x} = V\cos \varphi } \end{array}$Переходя в (3.3) к независимой переменной х, получим одно уравнение (штрихом обозначена производная по х):
где введены обозначения константЧтобы не терялся физический смысл задачи, будем считать, что $\mu < {\text{tg}}\varphi $, так что $B > 0$. Величина А при некоторых значениях угла атаки может быть, вообще говоря, и отрицательной, и даже нулевой. В зависимости от знака А решение уравнения (3.4) при нулевом начальном значении $V(0) = 0$ удобно представить в виде (хотя, очевидно, после раскрытия модуля выражения (3.5) и (3.6) совпадают):
(3.6)
${{V}^{2}}(x) = B\left( {\exp \left| A \right|x - 1} \right){\text{/}}\left| A \right|,\quad {\text{если}}\quad А < 0$Видно, что скорость монотонно растет, но формулы (3.5)–(3.7) справедливы лишь до тех пор, пока выполняется условие (2.10), т.е. пока сила реакции положительна. Значение ${{V}_{{N0}}}$ скорости, при которой эта сила обращается в ноль, с учетом (3.1) равно
Если в процессе спуска скорость достигает этого “критического” характерного значения, то происходит отрыв тела от поверхности, и для рассмотрения дальнейшего движения понадобится другая математическая модель.
В случае положительного значения $A > 0$ существует еще одно характерное значение скорости – это ее предельное (очевидно, максимальное) значение $V_{\infty }^{2}$ при спуске по наклонной прямой при $x \to \infty $, которое равно
(3.9)
$V_{\infty }^{2} = \frac{B}{A} = \frac{{2mg(\sin \varphi - \mu \cos \varphi )}}{{\rho S({{C}_{D}}(\bar {\alpha }) - \mu {{C}_{L}}(\bar {\alpha }))}}$Примечание. Выражение (3.9) несколько уточняет полученное ранее выражение предельной скорости лыжника в процессе спуска при прыжках с трамплина [1], где лыжник рассматривался как материальная точка.
При этом возможны две ситуации в зависимости от соотношения этих двух характерных значений скорости.
Если $V_{\infty }^{2} < V_{{N0}}^{2}$, то скорость спуска изменяется по закону (3.5) на всем протяжении спуска и не достигает значения (3.8), сила реакции в процессе спуска остается положительной. Это как-бы “стандартная” ситуация. В этом случае выполняется неравенство $(\sin \varphi - \mu \cos \varphi ){\text{/}}\left( {{{C}_{D}}(\bar {\alpha }) - \mu {{C}_{L}}(\bar {\alpha })} \right) < \cos \varphi {\text{/}}{{C}_{L}}(\bar {\alpha })$, что приводит к неравенствам
(3.10)
${{C}_{L}}(\bar {\alpha })\sin \varphi < {{C}_{D}}(\bar {\alpha })\cos \varphi \quad {\text{или}}\quad K(\bar {\alpha }) < {\text{ctg}}\varphi $Если же при выбранном угле атаки выполняются неравенства $K(\bar {\alpha }) > {\text{ctg}}\varphi $ и ${{C}_{L}}(\bar {\alpha })\sin \varphi - {{C}_{D}}(\bar {\alpha })\cos \varphi > 0$, то в процессе спуска (возрастания скорости) сначала достигается значение $V_{{N0}}^{{}}$, сила реакции исчезает, контакт тела с поверхностью теряется, и тело как бы взлетает, переходит в режим свободного полета. Эта ситуация будет обсуждаться ниже отдельно.
Учитывая полученные соотношения (3.8)–(3.10), последовательно прокомментируем физическую сторону формальных решений (3.5)–(3.7).
Правая часть первого из уравнений (2.14) представляет собой разность двух сил: тянущей силы $mg(\sin \varphi - \mu \cos \varphi )$, положительной при $\mu < {\text{tg}}\varphi $, и силы $\bar {D} - \mu \bar {L}$ = = $0.5\rho S\left[ {{{C}_{D}}(\bar {\alpha }) - \mu {{C}_{L}}(\bar {\alpha })} \right]{{V}^{2}}$ аэродинамического воздействия (положительной, отрицательной или даже нулевой). Баланс этих сил и определяет предельную скорость $V_{\infty }^{2}$ (3.9) при $A > 0$. С другой стороны, это уравнение можно представить и в виде двух других слагаемых: разгоняющей силы $(mg\sin \varphi - \bar {D})$ и тормозящей силы $\mu (mg\cos \varphi - \bar {L})$. Понятно, что, во-первых, тормозящая сила – это просто сила сухого трения, $\mu (mg\cos \varphi - \bar {L}) = \mu \bar {N}$, и во-вторых, разгоняющая сила будет, действительно, разгоняющей только в том случае, когда сила $\bar {D}$ лобового сопротивления не превосходит проекции силы тяжести $mg\sin \varphi $. Это означает, что когда сила $(mg\sin \varphi - \bar {D})$, действительно, разгоняющая, скорость спуска не превосходит некоторой константы Vf, так что ${{V}^{2}} < V_{f}^{2} = \frac{{2mg\sin \varphi }}{{\rho S{{C}_{D}}(\bar {\alpha })}}$.
Теперь рассмотрим все три случая знакоопределенности величины А в соответствии с (3.5)–(3.7), считая, что сила реакции $\bar {N}$ строго положительна.
Пусть $A > 0,\;\;{{C}_{D}}(\bar {\alpha }) - \mu {{C}_{L}}(\bar {\alpha }) > 0$. а) Пусть при этом $V_{\infty }^{2} < V_{{N0}}^{2}$, а значит из (3.10), ${{C}_{D}}(\bar {\alpha }){\text{/}}{{C}_{L}}(\bar {\alpha }) > {\text{tg}}\varphi $, отрыв тела от поверхности не происходит, скорость тела монотонно возрастает, стремясь к своему предельному значению $V_{\infty }^{2}$ (3.9). Остается удостовериться, что она не превышает и значения $V_{f}^{2}$, чтобы разгоняющая сила $(mg\sin \varphi - \bar {D})$ оставалась положительной. Действительно, из неравенства $V_{\infty }^{2} < V_{f}^{2}$ следует то же самое неравенство (3.10). Заметим, что при этом коэффициент сухого трения должен удовлетворять неравенству $\mu < {\text{tg}}\varphi < {{C}_{D}}(\bar {\alpha }){\text{/}}{{C}_{L}}(\bar {\alpha })\;$. б) Пусть, наоборот, $V_{{N0}}^{2} < V_{\infty }^{2}$, так что ${{C}_{D}}(\bar {\alpha }){\text{/}}{{C}_{L}}(\bar {\alpha }) < {\text{tg}}\varphi $, скорость тела не достигает своего предельного значения $V_{\infty }^{2}$, отрыв тела происходит раньше, при скорости $V_{{N0}}^{{}}$. При этом так же выполняется неравенство $V_{{N0}}^{2} < V_{f}^{2}$, которое сводится к условию $V_{{N0}}^{2} < V_{\infty }^{2}$. Коэффициент сухого трения в этом случае должен удовлетворять неравенству $\mu < {{C}_{D}}(\bar {\alpha }){\text{/}}{{C}_{L}}(\bar {\alpha })\; < {\text{tg}}\varphi $.
Пусть теперь $A = 0,\;\;{{C}_{D}}(\bar {\alpha }) = \mu {{C}_{L}}(\bar {\alpha })$. В этом случае разгоняющая сила равна $(mg\sin \varphi - \mu \bar {L})$, а тормозящая – $\mu (mg\cos \varphi - \bar {L})$. Происходит своего рода “нейтрализация” аэродинамического воздействия, и скорость тела изменяется так, словно оно перемещается по поверхности в пустоте. В этом случае складывается такая ситуация, что на сколько уменьшается сила реакции за счет подъемной силы, ровно на столько же уменьшается и разгоняющая сила за счет силы лобового сопротивления. Тело перемещается с постоянным ускорением $g(\sin \varphi - \mu \cos \varphi )$. Коэффициент сухого трения в этом случае удовлетворяет неравенству $\mu = {{C}_{D}}(\bar {\alpha }){\text{/}}{{C}_{L}}(\bar {\alpha })\; < {\text{tg}}\varphi $.
И, наконец, пусть $A < 0,\;\;{{C}_{D}}(\bar {\alpha }) - \mu {{C}_{L}}(\bar {\alpha }) < 0$. Коэффициент сухого трения в этом случае должен удовлетворять двойному неравенству ${{C}_{D}}(\bar {\alpha }){\text{/}}{{C}_{L}}(\bar {\alpha })\; < \mu < {\text{tg}}\varphi $. В этом случае обе силы: тянущая сила и сила аэродинамического воздействия действуют как бы в одну сторону – на рост скорости. Этот рост продолжается до величины $V_{{N0}}^{{}}$, после чего происходит отрыв тела от поверхности.
4. Максимизация скорости при движении с неизменяемой стойкой. При движении с неизменяемой стойкой, когда выбраны значения $\bar {\vartheta } = {\text{const}}$ и $\gamma = {\text{const}}$, угол атаки также не изменяется: $\bar {\alpha } = \varphi - \bar {\vartheta } - \gamma $. При А = 0 скорость (3.7) спуска не зависит от этих углов, поскольку параметр В не зависит от выбранных значений углов, а определяется только углом $\varphi $ наклона поверхности и коэффициентом $\mu $ сухого трения. Поэтому в этом случае задача максимизации скорости не возникает.
Но при А, отличном от нуля, величина скорости спуска зависит от выбранных углов $\bar {\vartheta }$, γ ориентации стойки, точнее от их суммы (через $\bar {\alpha }$). В этом случае представляет интерес рассмотреть задачу о выборе стойки, определяемой этими углами, при которой достигается максимальное значение скорости в процессе спуска. Рассмотрим совместно ситуации (3.5) и (3.6), пользуясь выражением (3.5). Покажем, что скорость спуска является убывающей функцией от А. Для этого вычислим производную $\partial ({{V}^{2}}){\text{/}}\partial A$
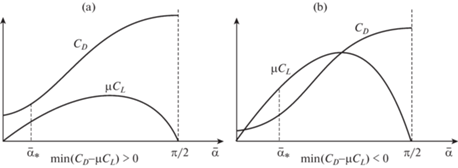
Следовательно, для максимального значения скорости надо выбирать минимальное значение величины А. Из (3.5) видно, что этот минимум достигается при минимальном значении разности ${{С}_{D}}(\bar {\alpha }) - \mu {{С}_{L}}(\bar {\alpha })$ (положительной или отрицательной). Обозначим соответствующее значение угла атаки через $\bar {\alpha }_{*}^{{}}$, так что
(4.1)
${{С}_{D}}(\bar {\alpha }_{*}^{{}}) - \mu {{С}_{L}}(\bar {\alpha }_{*}^{{}}) = \mathop {\min }\limits_{\bar {\alpha }} \left[ {{{С}_{D}}(\bar {\alpha }) - \mu {{С}_{L}}(\bar {\alpha })} \right]$Отметим важное обстоятельство: видно, что оптимальное значение угла атаки определяется только зависимостью аэродинамических коэффициентов от угла атаки и не зависит ни от каких других аргументов: ни от скорости спуска, ни от выбранного угла наклона корпуса, ни от массовых и геометрических параметров. Отсюда следует, что именно этот угол надо выбирать на всем пути спуска в любой момент времени. Чтобы это осуществить, надо установить постоянным угол $\bar {\beta }_{*}^{{}} = (\bar {\vartheta } + \gamma )_{*}^{{}} = \varphi - \bar {\alpha }_{*}^{{}}$.
Таким образом, для получения максимального значения скорости независимо от знака ненулевого значения А углы $\bar {\vartheta },\gamma $ ориентации “лыжника” следует выбирать так, чтобы угол атаки ${{\bar {\alpha }}_{*}}$ определялся условием (4.1). В частности, если зафиксирован угол $\bar {\vartheta }$, то установочный угол следует выбрать равным $\gamma = \varphi - \bar {\vartheta } - {{\bar {\alpha }}_{*}}$.
Для иллюстрации рассмотрим пример, приведенный выше в конце п.2. Минимальное значение разности ${{С}_{D}}(\bar {\alpha }) - \mu {{С}_{L}}(\bar {\alpha })$ для $\mu = 0.1$ достигается при ${{\bar {\alpha }}_{*}} \approx 0.065\;( \approx 4^\circ )$. Значения аэродинамических коэффициентов равны ${{С}_{D}}(\bar {\alpha }_{*}^{{}}) = 0.221,{{С}_{L}}(\bar {\alpha }_{*}^{{}}) = 0.195$. Углы $\bar {\vartheta }$, γ связаны соотношением $\bar {\vartheta } + \;\gamma = \varphi - {{\bar {\alpha }}_{*}} = 0.458\;( \approx 26^\circ )$. Например, могут быть выбраны значения $\bar {\vartheta } = - 60^\circ ,\gamma = 86^\circ $ или $\bar {\vartheta } = - 45^\circ ,\gamma = 71^\circ $ и т.д. Характерные значения скоростей приближенно равны $V_{\infty }^{{}} \approx 68.4$ (м/с) и $V_{{N0}}^{{}} \approx 100.8$ (м/с).
Вывод. При спуске по наклонной прямой в течение всего процесса спуска (в любой момент времени) максимальная скорость спуска достигается при фиксированном значении угла атаки ${{\bar {\alpha }}_{*}}$ (4.1). При этом максимальное значение скорости спуска не зависит от угла $\bar {\vartheta }$ наклона корпуса при подходящем выборе угла $\gamma = \varphi - \bar {\vartheta } - {{\bar {\alpha }}_{*}}$ наклона второго звена.
На рис. 5 представлены типичные зависимости аэродинамических характеристик от угла атаки для тела типа крыла. На рис. 5,а представлен случай, когда неравенство ${{С}_{D}}(\alpha ) - \mu {{С}_{L}}(\alpha ) > 0$ справедливо для всех значений угла атаки, а на рис. 5,b – когда на некотором диапазоне значений угла атаки выполняется противоположное неравенство ${{С}_{D}}(\alpha ) - \mu {{С}_{L}}(\alpha ) < 0$. Очевидно, в любом случае всегда существует значение ${{\alpha }_{*}}$, при котором достигается минимум разности ${{С}_{D}}(\alpha ) - \mu {{С}_{L}}(\alpha )$. Это значение отмечено на рисунке.
Напомним, что при $\bar {\alpha } = {{\bar {\alpha }}_{*}}$ возрастание скорости продолжается либо до выхода на предельное значение $V_{\infty }^{2}$, либо до достижения величины $V_{{N0}}^{2}$, при которой сила реакции обращается в ноль, и происходит отрыв тела от поверхности. Отметим, что левому фрагменту рис. 5 могут отвечать как первая ситуация, так и вторая. Правому фрагменту отвечает рост скорости только до $V_{{N0}}^{2}$, после чего начинается другой режим движения.
5. Об устойчивости движения тела с неизменяемой стойкой. Пусть выбрано некоторое желаемое значение $\vartheta (t) \equiv \bar {\vartheta } = {\text{const}}$ угла наклона корпуса. Для осуществления движения с таким углом наклона выбран соответствующий компенсирующий управляющий момент ${{M}_{k}}$(3.1)
(5.1)
$M = {{M}_{k}} = - lN\left[ {\cos \bar {\delta } + \mu \sin \bar {\delta }} \right] + r\left[ {\bar {D}\sin \bar {\alpha } + \bar {L}\cos \bar {\alpha }} \right].$При этом $\theta (t) \equiv \varphi = {\text{const}}$, и сила реакции равна $\bar {N} = mg\cos \varphi - \bar {L}$.
Представляет интерес анализ устойчивости такого режима спуска. При этом следует иметь в виду, что исследуемый режим не является стационарным, хотя $\vartheta (t) \equiv \bar {\vartheta }$ = = const, так как скорость в процессе спуска изменяется в соответствии с (3.5)–(3.7). Поэтому уравнения первого приближения содержат переменные коэффициенты, и проведение аналитического исследования устойчивости этого режима спуска тела оказывается затруднительным. Поэтому ограничимся результатами численных расчетов.
Эти расчеты показали, что рассматриваемый режим движения с заданным желаемым углом наклона и выбранным управляющим моментом в виде (5.1) неустойчив. Более того, было обнаружено, что при управляющем моменте (5.1), выбранном специально для реализации угла наклона $\bar {\vartheta } = {{\bar {\vartheta }}_{1}}$, может существовать режим спуска с другим углом наклона (обозначим его через ${{\bar {\vartheta }}_{2}}$), тоже неустойчивый. Необходимо разобраться с этой двойственностью.
Пусть выбраны значения $\bar {\vartheta }_{1}^{{}}$ (удобнее будет иметь дело с углом ${{\bar {\delta }}_{1}} = \varphi - \bar {\vartheta }_{1}^{{}}$) и управляющего момента ${{M}_{k}}({{\bar {\delta }}_{1}})$ (5.1), а искать будем другое тоже постоянное значение ${{\bar {\delta }}_{2}}$, при котором второе уравнение системы (2.9) принимает вид
(5.2)
$l(mg\cos \varphi - L)(\cos \delta + \mu \sin \delta ) - r(D\sin \alpha + L\cos \alpha ) + {{M}_{k}}({{\bar {\delta }}_{1}}) = 0$(5.3)
$\begin{gathered} l(mg\cos \varphi - L)(\cos \delta + \mu \sin \delta ) - r(D\sin \alpha + L\cos \alpha ) = \hfill \\ = l(mg\cos \varphi - \bar {L})(\cos {{{\bar {\delta }}}_{1}} + \mu \sin {{{\bar {\delta }}}_{1}}) - r(\bar {D}\sin \bar {\alpha } + \bar {L}\cos \bar {\alpha }) \hfill \\ \end{gathered} $Для каждого значения скорости правая часть этого уравнения – это некоторое заданное число, левая часть – функция неизвестной переменной $\delta $. Одно решение очевидно: оно отвечает исходному режиму ${{\bar {\delta }}_{2}} = {{\bar {\delta }}_{1}}$. Но в зависимости от параметров и аэродинамических характеристик левая часть уравнения (5.3) может быть равна правой и при других значениях $\delta \ne {{\bar {\delta }}_{1}}$. При этом, как и полагается в рассматриваемом случае, ${{M}_{k}}({{\bar {\delta }}_{1}}) = {{M}_{k}}({{\bar {\delta }}_{2}})$. Отметим, что режим спуска с постоянным углом наклона может быть реализован только при $ - \pi + \varphi < \bar {\vartheta } < \varphi $ (иначе тело “провалится” под поверхность).
Ввиду сложной зависимости левой части от $\delta $ ограничимся парой числовых примеров, полученных графическим решением уравнения (5.3). Рассмотрим то же тело с антропоморфными параметрами, которое рассматривалось выше. Угол наклона прямой спуска $\varphi = 30^\circ = \pi {\text{/}}6$. Пусть “лыжник” сохраняет неизменной стойку, в которой корпус наклонен к склону, так что $\vartheta (t) = {{\bar {\vartheta }}_{1}} = - 0.78 \approx - 45^\circ $, а установочный угол γ = 0.9 $( \approx 52^\circ )$. Тогда ${{\bar {\delta }}_{1}}\, = \,\varphi - {{\bar {\vartheta }}_{1}}\, = \,1.303( \approx {\kern 1pt} 75^\circ )$, угол атаки ${{\bar {\alpha }}_{1}}\, = \,{{\bar {\delta }}_{1}} - \gamma \, = \,0.403( \approx \,23^\circ )$. При этих значениях параметров уравнение (5.3) имеет еще ровно одно решение ${{\bar {\delta }}_{2}} = 1.239( \approx {\kern 1pt} 71^\circ )$, которому отвечают ${{\bar {\vartheta }}_{2}} = - 0.716 \approx - 41^\circ $ и ${{\bar {\alpha }}_{2}} = {{\bar {\delta }}_{2}} - \gamma = 0.339\left( { \approx 19^\circ } \right)$. При этом величина управляющего момента для обоих установившихся режимов совпадает и равна 86.43 нм. Очевидно, оба значения ${{\bar {\vartheta }}_{1}}\;,\;{{\bar {\vartheta }}_{2}}$ отрицательны, не превосходят угла $\varphi $, так что оба режима могут быть реализованы. Но, как и все режимы с неизменной стойкой и с управляющим моментом в виде компенсирующего (5.1), они оба неустойчивы.
В случае $\gamma = 0.8( \approx 46^\circ )$ при неизменных всех остальных параметров существует только одно решение уравнения (5.3) ${{\bar {\delta }}_{1}} = 1.303$.
В ходе многократных численных экспериментов выяснилось, что для обеспечения надежной устойчивости режима спуска с желаемым углом ${{\vartheta }_{{des}}}$ (designed) наклона корпуса только компенсирующего управляющего момента в виде (5.1) не достаточно. Поэтому в дальнейшем в качестве управляющего момента целесообразно использовать, наряду с компенсирующим ${{M}_{k}}({{\vartheta }_{{des}}})$, еще и следящий момент в виде отрицательной обратной связи, так что управляющий момент примет вид
(5.4)
$M = {{M}_{k}}({{\vartheta }_{{des}}}) - k(\vartheta - {{\vartheta }_{{des}}}) - h\dot {\vartheta }$Как показывают проведенные расчеты, использование управляющего момента в виде (5.4) может обеспечить устойчивость желаемого режима спуска.
Вывод. Чтобы обеспечить устойчивый спуск с желаемым (designed) углом наклона корпуса ${{\vartheta }_{{des}}}$, надо кроме компенсирующего момента (5.1) приложить дополнительный управляющий момент в виде отрицательной обратной связи, отслеживающий отклонение от желаемого режима спуска.
6. Движение тела в случае отрыва от поверхности. Рассмотрим теперь случай, когда в процессе спуска скорость достигает такого значения $V_{{N0}}^{2}$ (3.8), при котором сила N реакции обращается в ноль (тело теряет контакт с поверхностью и может вообще от нее оторваться).
В этом случае справедливо неравенство, противоположное (3.10)
(6.1)
${{C}_{L}}(\bar {\alpha })\sin \varphi - {{C}_{D}}(\bar {\alpha })\cos \varphi > 0,\quad {\text{или\;}}\quad K(\bar {\alpha }) = {{C}_{L}}(\bar {\alpha }){\text{/}}{{C}_{D}}(\bar {\alpha }) > {\text{ctg}}\varphi $При выполнении этого условия и достижения скорости значения $V_{{N0}}^{{}}$ сила реакции исчезает, и тело как бы взлетает, переходит в режим свободного полета. Уравнения движения тела в этом случае принимают вид
(6.2)
$\begin{array}{*{20}{c}} {m\dot {V} = mg\sin \theta - D} \\ {mV\dot {\theta } = mg\cos \theta - L} \\ {J\ddot {\vartheta } = - r(D\sin \alpha + L\cos \alpha )} \end{array}$При этом угол атаки, фигурирующий в определении аэродинамических сил, уже не постоянный и изменяется в соответствии с соотношением α(t) = ψ(t) – β(t) = = $\psi (t) - (\vartheta (t)$ + γ).
В начальный момент $(t = 0)$ отрыва от поверхности имеем
Отметим, что $\dot {V}(0) > 0$, так как
Таким образом, в течение некоторого времени после отрыва скорость продолжает возрастать. Этого можно было и ожидать, поскольку исчезновение силы реакции и вместе с ней силы трения должно было привести к некоторому росту скорости спуска.
Продифференцировав второе уравнение системы (6.2), получим, что в начальный момент угол наклона вектора скорости убывает, так как вторая производная $\ddot {\theta }(0) < 0$ (а первая производная $\dot {\theta }(0) = 0$). Действительно,
Это тоже ожидаемый результат: достаточно большой коэффициент подъемной силы обеспечивает поворот вектора скорости центра масс против часовой стрелки. Итак, по крайней мере, в течение некоторого времени после отрыва потеря контакта с поверхностью спуска продолжается, угол $\theta (t) < \varphi $.
Таким образом, в течение некоторого интервала времени после отрыва скорость центра масс тела продолжает возрастать, а угол наклона вектора скорости центра масс уменьшаться, в результате чего на этом интервале времени центр масс удаляется от поверхности. Остается разобраться с ориентацией этого тела. При $r \ne 0$ на тело действует ничем не скомпенсированный момент аэродинамических сил. Из третьего уравнения системы (6.2) видно, что при $r \ne 0$ и пока угол атаки положителен, угол $\vartheta (t)$ наклона корпуса уменьшается, то есть происходит поворот тела против часовой стрелки. При этом не исключено, что своим “хвостом” – бывшей опорной точкой А тело снова коснется поверхности. Тем не менее, до тех пор, пока выполнено неравенство $x\cos \varphi - y\sin \varphi > l\sin \delta $, тело будет совершать свободный полет, точка А будет выше поверхности спуска. Следует иметь в виду, что если возобновляется контакт с поверхностью, то скорее всего, этот выход на поверхность будет сопровождаться ударом. Эта ситуация является предметом отдельного исследования и выходит за рамки настоящей работы.
Рассмотрим подробнее более простой случай, когда центр давления и центр масс тела совпадают, то есть r = 0. Тогда из третьего уравнения системы (6.2) с учетом начальных условий следует, что угол наклона после отрыва от поверхности не изменяется, так что $\vartheta (t) \equiv \bar {\vartheta }$, $\psi (t) \equiv \theta (t)$. При этом угол атаки равен α(t) = $\theta (t) - (\bar {\vartheta } + \gamma ) = \theta (t) - \bar {\beta }$.
Первые два уравнения системы (6.2) в этом случае определяют единственный устойчивый стационарный режим движения $({{V}_{s}},{{\theta }_{s}},\alpha {}_{s})$ – (s – state, стационарный режим) режим планирования [4], где
(6.3)
${\text{ctg}}{{\theta }_{s}} = {\text{ctg}}({{\alpha }_{s}} + \bar {\beta }) = {{C}_{L}}({{\alpha }_{s}}){\text{/}}{{C}_{D}}({{\alpha }_{s}}) = K(\alpha {}_{s}),\quad {{V}_{s}}^{2} = 2mg{\text{/}}(\rho S\sqrt {C_{D}^{2}({{\alpha }_{s}}) + C_{L}^{2}({{\alpha }_{s}})} )$Представим соотношения (6.1) и (6.3), связывающие углы $\bar {\vartheta },\;\bar {\alpha },\;{{\alpha }_{s}}$, в несколько ином виде:
(6.4)
$1{\text{/}}K(\bar {\alpha }) = {{C}_{D}}(\bar {\alpha }){\text{/}}{{C}_{L}}(\bar {\alpha }) < {\text{tg}}\varphi $(6.5)
$1{\text{/}}K({{\alpha }_{s}}) = {{C}_{D}}(\alpha {}_{s}){\text{/}}{{C}_{L}}({{\alpha }_{s}}) = {\text{tg}}({{\alpha }_{s}} + \bar {\beta })\,\,(\bar {\beta } = \bar {\vartheta } + \gamma )$Первое из этих соотношений является условием отрыва от поверхности, а второе определяет угол атаки в режиме планирования. Для реализации режима планирования должно быть выполнено еще одно условие:
(6.6)
${\text{tg}}({{\alpha }_{s}} + \bar {\beta }) = {\text{tg}}{{\theta }_{s}} < {\text{tg}}\varphi $Тут уместно вспомнить понятия высокого и низкого аэродинамического качества [4]. В обоих случаях, начиная с некоторого характерного значения $\tilde {\alpha }$ угла атаки справедливо приближенное равенство $K(\alpha ) \approx {\text{ctg}}\alpha $ при $\alpha \in (\tilde {\alpha },\,\;\pi {\text{/}}2)$. Известно также, что функция $K(\alpha )$ унимодальна, так что ее график имеет единственный максимум, а график функции $1{\text{/}}K(\alpha ) = {{C}_{D}}(\alpha ){\text{/}}{{C}_{L}}(\alpha )$ имеет единственный минимум.
Имея в виду моделирование спуска лыжника, более вероятно считать, что лыжник обладает скорее низким аэродинамическим качеством, чем высоким, то есть $K(\alpha ) \leqslant {\text{ctg}}\alpha $ во всем диапазоне значений угла атаки. Итак, рассмотрим сначала случай низкого аэродинамического качества.
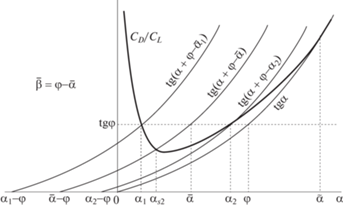
На рис. 6 представлены график функция ${{C}_{D}}(\alpha ){\text{/}}{{C}_{L}}(\alpha )$ жирной линией и ниже ее – график ${\text{tg}}\alpha $ тонкой линией. Поскольку условие (6.4) отрыва считается выполненным, то заведомо существует диапазон $({{\alpha }_{1}},{{\alpha }_{2}})$ значений угла атаки, на котором эта функция принимает значения, меньшие, чем ${\text{tg}}\varphi $. На этом же рисунке указано также некоторое произвольное значение $\bar {\alpha }$ из этого диапазона. Графическое решение уравнения (6.5) относительно ${{\alpha }_{s}}$ представлено графиком функции ${\text{tg(}}\alpha + \varphi - \bar {\alpha })$ (графика функции ${\text{tg}}\alpha $, сдвинутого влево на положительную величину $\bar {\beta } = \varphi - \bar {\alpha }$ ($\bar {\beta } = \bar {\vartheta } + \gamma > 0$). Пересечение графика этой функции с графиком функции ${{C}_{D}}(\alpha ){\text{/}}{{C}_{L}}(\alpha )$ определяет значение ${{\alpha }_{s}}$ угла атаки в режиме планирования, где ${{C}_{D}}(\alpha ){\text{/}}{{C}_{L}}(\alpha ) = {\text{tg}}({{\alpha }_{s}} + \bar {\beta })$. Для отрицательных значений $\bar {\beta } = \varphi - \bar {\alpha }$ такого пересечения нет. Кроме того, из этого рисунка ясно, что пересечение графика этой функции с графиком функции ${{C}_{D}}(\alpha ){\text{/}}{{C}_{L}}(\alpha )$ возможно только внутри интервала $({{\alpha }_{1}},\bar {\alpha })$. Это означает, что угол ${{\theta }_{s}}$ планирования удовлетворяет условию ${{\theta }_{s}} = {{\alpha }_{s}}{\text{ + }}\bar {\beta } = {{\alpha }_{s}}{\text{ + }}\varphi - \bar {\alpha } = \varphi - (\bar {\alpha } - {{\alpha }_{s}}) < \varphi $, то есть выполнено неравенство (6.6), режим планирования реализуется, и тело, раз оторвавшись от поверхности, на нее уже не возвращается, а выходит на режим планирования, более пологий, чем наклон поверхности.
Рис. 6.
Определение угла планирования после отрыва от поверхности для тела с низким аэродинамическим качеством.
Рассмотрим для общности и случай тела с высоким аэродинамическим качеством. Для такого тела характерно наличие диапазона значений углов атаки, в котором $K(\alpha ) > {\text{ctg}}\alpha $. На рис. 7, как и на предыдущем рисунке, схематически представлены графики функции ${{C}_{D}}(\alpha ){\text{/}}{{C}_{L}}(\alpha )$ и ${\text{tg}}\alpha $, и на оси абсцисс отмечен квадратными скобками указан диапазон, где ${{C}_{D}}(\alpha ){\text{/}}{{C}_{L}}(\alpha ) < {\text{tg}}\alpha $. Отметим, что все представленные кривые для наглядности изображены без соблюдения масштаба, но с сохранением топологической картины в целом.
Рис. 7.
Определение угла планирования после отрыва от поверхности для тела с высоким аэродинамическим качеством.
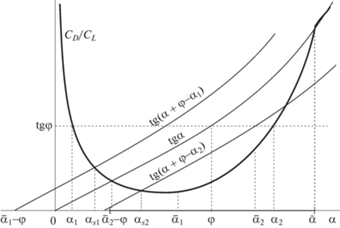
Так же выделен интервал $({{\alpha }_{1}},\;\;{{\alpha }_{2}})$, на котором ${{C}_{D}}(\alpha ){\text{/}}{{C}_{L}}(\alpha ) < {\text{tg}}\varphi $, для некоторого положительного значения величины $\bar {\beta } = \varphi - \bar {\alpha }$, отмечено значение ${{\bar {\alpha }}_{1}} \in ({{\alpha }_{1}},\;\;\varphi )$, построена кривая ${\text{tg(}}\alpha + \varphi - {{\bar {\alpha }}_{1}})$ и отмечено значение ${{\alpha }_{s}}_{1}$ точки пересечения этой кривой с графиком функции ${{C}_{D}}(\alpha ){\text{/}}{{C}_{L}}(\alpha )$. Это значение отвечает углу атаки в режиме планирования. Поскольку ${{\alpha }_{s}}_{1} < {{\bar {\alpha }}_{1}}$, то угол ${{\theta }_{s}} = {{\alpha }_{{s1}}} + \varphi - {{\bar {\alpha }}_{1}} < \varphi $, так что режим планирования реализуется. Пока что все обстоит так же, как было в случае низкого аэродинамического качества. Но в отличие от него, существует диапазон отрицательных значений величины $\bar {\beta } = \varphi - \bar {\alpha }$ ($\bar {\vartheta } + \gamma < 0$), для которых также возможен режим планирования. На том же рис. 7 отмечено значение ${{\bar {\alpha }}_{2}} \in (\varphi ,{{\alpha }_{2}})$, построена кривая ${\text{tg(}}\alpha + \varphi - {{\bar {\alpha }}_{2}})$ и отмечено значение ${{\alpha }_{s}}_{2}$ точки пересечения этой кривой с графиком функции ${{C}_{D}}(\alpha ){\text{/}}{{C}_{L}}(\alpha )$. И в этом случае ${{\alpha }_{s}}_{2} < {{\bar {\alpha }}_{2}}$, угол ${{\theta }_{s}} = {{\alpha }_{{s2}}} + \varphi - {{\bar {\alpha }}_{2}} < \varphi $, так что условие реализации режима планирования выполняется.
Таким образом, независимо от того, обладает ли “лыжник” высоким или низким аэродинамическим качеством, в случае отрыва его от поверхности спуска он уже не возвращается (в рамках принятой модели) на поверхность.
В качестве числового примера рассмотрим то же тело с антропоморфными параметрами, которое рассматривалось выше. Принятая зависимость аэродинамических коэффициентов означает, что лыжник обладает низким аэродинамическим качеством. Соответствующее характерное значение угла атаки равно $\tilde {\alpha } \approx 0.6$. Пусть “лыжник” сохраняет неизменной стойку, в которой корпус перпендикулярен склону, так что $\vartheta (t) = \bar {\vartheta } = - 60^\circ = - \pi {\text{/}}3$, а установочный угол $\gamma = 70^\circ $, $\bar {\beta } = 10^\circ \;( \approx 0.1745)$. Тогда угол атаки $\bar {\alpha } = 20^\circ \approx 0.349$ и ${{С}_{D}}(\bar {\alpha }) = 0.489,\,\,{{С}_{L}}(\bar {\alpha }) = 0.964$. Для реализации этого режима с неизменяемой стойкой необходимый управляющий момент примем в виде:
Нетрудно проверить, что при таком моменте и начальном условии $\vartheta (0) = - \pi {\text{/}}3$ решение уравнений (2.9) описывается формулой (3.5) для изменения скорости и $\vartheta (t) \equiv \bar {\vartheta } = - \pi {\text{/}}3$, то есть неизменность стойки обеспечивается. При этом угол $\theta $ наклона вектора скорости центра масс совпадает с углом $\varphi $ наклона поверхности: $\theta (t) \equiv \bar {\theta }$ = φ. Более того, при разумных отклонениях начального значения угла $\vartheta (0)$ наклона корпуса от значения $\vartheta (0) = - \pi {\text{/}}3$ желаемый режим спуска с неизменяемой стойкой восстанавливается.
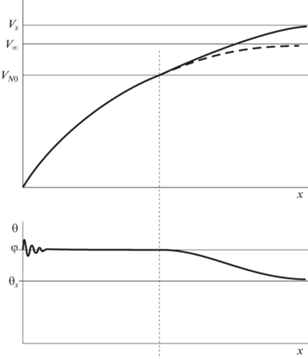
Отметим, что предельное значение (3.9) скорости равно ${{V}_{\infty }} = 53.3\,({\text{м/с}})$. Однако, в соответствии с (3.8) при скорости ${{V}_{{N0}}} = 49.7\,({\text{м/с}})$, меньшей этого предельного значения, происходит отрыв тела и начинается этап свободного полета в соответствии с уравнениями (6.2). Расчеты по формулам (6.3) показывают, что устанавливается режим планирования со скоростью ${{V}_{s}} = 55.1$ (м/с) и углом наклона вектора скорости, равным ${{\theta }_{s}} \approx 0.46$, меньшим угла $\bar {\theta } = \varphi = 0.523$, так что раз оторвавшись от поверхности, “лыжник” обратно на поверхность уже не возвращается.
В результате численных расчетов при $\vartheta (0) \ne \bar {\vartheta } = - \pi {\text{/}}3$ получены перечисленные зависимости, которые схематически представлены на рис. 8, для наглядности в несколько искаженном масштабе. На рисунке вертикальным пунктиром отмечен также момент, когда сила реакции обращается в нуль, происходит отрыв от поверхности и выход на устойчивый режим планирования. Жирным пунктиром отмечена нереализуемая часть зависимости (3.9).
Для полноты картины рассмотрим того же лыжника на том же склоне, но обладающего высоким аэродинамическим качеством. Соответствующие зависимости аэродинамических коэффициентов имеют вид ${{С}_{D}}(\alpha ) = 0.69 - 0.58\cos 2\alpha $, ${{С}_{L}}(\alpha ) = 1.5\sin 2\alpha $ + + sin4α, а характерное значение угла атаки равно $\tilde {\alpha } \approx 0.96$.
Пусть установочный угол будет тот же $\gamma = 70^\circ $, тогда $\bar {\beta } = 10^\circ $, $\bar {\alpha } = 20^\circ $ и ${{С}_{D}}(\bar {\alpha }) = 0.246,\,\,{{С}_{L}}(\bar {\alpha })$ = 1.945. Предельное значение (3.9) скорости равно ${{V}_{\infty }} = 91.9$ (м/с) . Однако, при скорости ${{V}_{{N0}}} = 34.9$ (м/с) уже происходит отрыв тела и начинается этап свободного полета в соответствии с уравнениями (6.2). В соответствии с формулами (6.3) получаем, что устанавливается режим планирования со скоростью ${{V}_{s}} = 37.4$ (м/с) и углом наклона вектора скорости, равным ${{\theta }_{s}} \approx 0.126$, меньшим угла $\bar {\theta } = \varphi = 0.523$, так что и в этом случае, раз оторвавшись от поверхности, “лыжник” обратно на поверхность уже не возвращается.
Видно, что угол планирования для тел с высоким аэродинамическим качеством, как и следовало ожидать, меньше, чем для тел с низким аэродинамическим качеством. Напомним, что эти выводы получены для случая, когда центр давления совпадает с центром масс тела.
Таким образом, приведенные численные результаты подтверждают ранее полученные качественные выводы.
7. Заключение. В настоящей работе рассматривается первый этап спортивных соревнований по прыжкам с трамплина, а именно: разгон лыжника на прямолинейном участке спуска. В процессе этого разгона лыжник принимает определенную позу и старается поддерживать ее при нарастании скорости за счет вырабатываемых моментов в суставах. Анализ движения лыжника именно по наклонной прямой представляет определенный интерес как с практической спортивной точки зрения, так и в качестве самостоятельной теоретико-механической задачи.
Ранее в научной литературе рассматривалась математическая модель такого лыжника в виде материальной точки, движение которой происходит под действием силы реакции со стороны поверхности и аэродинамического воздействия в виде только силы лобового сопротивления, без учета боковой (подъемной) силы.
В настоящей работе предлагается новая математическая модель лыжника в виде связки двух твердых тел. Одно из них, тяжелое, скользит своей фиксированной точкой (опорной точкой) по поверхности склона и имеет возможность совершать поворот относительно нее. Другое тело, типа крыла, установлено под некоторым углом к первому, так что в целом образуется своеобразный перевернутый маятник сложной формы. Эти два тела в совокупности имитируют стойку и конфигурацию лыжника, которая, вообще говоря, в процессе спуска может изменяться. Считается, что центр масс системы находится на фиксированном расстоянии от опорной точки. На втором теле (крыле) сосредоточено все аэродинамическое воздействие: сила лобового сопротивления и подъемная сила, для описания этих сил используется квазистатическая модель обтекания. При этом центр давления, вообще говоря, не совпадает с центром масс. Выбор желаемого режима движения происходит за счет управляющего момента, приложенного в точке контакта корпуса с поверхностью и за счет изменения ориентации (установочного угла) крыла.
Построена соответствующая система дифференциальных уравнений, из которой при заданных зависимостях управляющего момента и величины установочного угла полностью определяется режим движения в процессе спуска: не только переменная скорость спуска, как это было в предыдущих моделях с материальной точкой, но и изменяющийся угол ориентации корпуса.
Основное внимание уделено рассмотрению вопроса о движении тела при условии, что в процессе спуска “стойка лыжника” не изменяется. В этом случае происходит своеобразная “игра” сил трения и аэродинамических сил, в которых существенную роль играет именно подъемная сила. Найдены характерные значения скорости спуска, определяемые в значительной мере величиной подъемной силы. Показано, что существует фиксированное значение установочного угла крыла, при котором достигается максимальное значение скорости спуска в любой момент времени. Это экстремальное значение угла не зависит ни от геометрических размеров, ни от площади корпуса и крыла, ни от скорости спуска, ни от выбранного угла наклона корпуса, ни от времени – оно зависит только от соотношения аэродинамических коэффициентов силы лобового сопротивления и подъемной силы. Таким образом, в рамках предложенной математической модели движения лыжника для достижения максимально возможной скорости спуска необходимо соблюдать определенную постоянную стойку и форму корпуса. Реализация этого экстремального режима спуска ограничена только возможностью обеспечения требуемого управляющего момента.
Рассмотрен также вопрос о возможности отрыва “лыжника” от поверхности спуска и дальнейшего движения в режиме свободного полета. Установлено, что при достаточно большой величине подъемной силы сила реакции может обнулиться, происходит отрыв тела от поверхности, причем с продолжающимся ростом скорости. В случае совпадения центра давления с центром масс показано, что после такого отрыва от поверхности не происходит возвращения на поверхность, в дальнейшем тело совершает свободный полет с выходом на режим устойчивого планирования.
Таким образом, в рамках принятой модели установлено значительное влияние подъемной силы, носящей “антидиссипативный” характер.
Для иллюстрации полученных выводов приведены результаты численных расчетов применительно к телу с антропоморфными параметрами. Используемые при этом величины управляющего момента и сил реакции находятся в разумных “человеческих” пределах.
Список литературы
Подгаец А.Р., Рудаков Р.Н. Биомеханические проблемы прыжка на лыжах с трамплина // Russ. J. Biomech. 2000. V. 4. № 2. С. 1–11.
Remizov L.P. Optimal running on skis in downhill // J. Biomech. 1980. V. 13. № 11. P. 941–945.
Maronski R. On optimal running downhill on skis // J. Biomech. 1990. V. 23. № 5. P. 435–439.
Локшин Б.Я., Самсонов В.А. Задача о движении тела в сопротивляющейся среде. Качественный анализ. М.: Изд-во Моск. ун-та, 2012. 237 с.
Локшин Б.Я., Самсонов В.А. Особенности движения тела-вертушки // Изв. РАН. МТТ. 2018. № 1. С. 64–71.
Воронов А.В., Хуснутдинова Д.Р. Теоретическая и экспериментальная оценка силы головок трехглавой мышцы голени при разгибании голеностопного сустава // Вестн. спорт. науки. 2011. № 4. С. 44–55.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика твердого тела