Известия РАН. Механика твердого тела, 2022, № 4, стр. 130-143

1. Введение. Аэроупругие системы с одной поступательной и одной вращательной степенями свободы привлекают к себе внимание исследователей в течение достаточно длительного времени. Интерес к ним связан, в частности, с тем, что они позволяют смоделировать явление флаттера крыла. Изучению этого эффекта посвящено огромное количество работ, как классических (в частности, [1–3]), так и новых (например, [4–6]).

С точки зрения динамики летательных аппаратов самовозбуждающиеся колебания, возникающие в рамках флаттера, считают нежелательными, поскольку они могут привести к износу и разрушению конструкции. В то же время, автоколебания (в том числе, и флаттер) можно рассматривать и в другом ключе: как способ преобразования энергии потока в полезные формы.

Один из первых патентов на ветроэнергетическую установку, использующую явление флаттера, был подан в 1924 году [7]. В работах [8] и [9] также изучались системы подобного типа и отмечено, что они обладают достаточно хорошим потенциалом с точки зрения выработки энергии. В [10] проанализированы динамика и эффективность (в терминах вырабатываемой мощности) колеблющегося крыла в потоке с линейным сдвигом и даны оценки влияния положения центра масс.

Достаточно подробный обзор ветроэнергетических установок колебательного типа, в которых рабочие элементы совершают флаттерные колебания, представлен в статьях [11] и [12].

Энергию колебаний аэроупругой системы в конечном счете требуется преобразовать в электричество. Использовать для этого обычные электрогенераторы, по-видимому, нецелесообразно, поскольку для этого потребуется преобразовывать колебания во вращение ротора генератора, что связано с дополнительными потерями энергии. Поэтому активно изучается возможность применения пьезоэлементов. В [13] предложена модель пьезоаэроупругой системы и проведено экспериментальное и теоретическое исследование ее динамики. В статье [14] исследованы колебания консольно закрепленной упругой балки с прикрепленными на ней пьезоэлектрическими пластинками и даны оценки критической скорости потока. В [15] рассмотрена миниатюрная пьезоэлектрическая балка, которая может колебаться поперек набегающего потока. В [16] изучено влияние нагрузочного электрического сопротивления и нелинейной жесткости пружин крепления на характеристики предельных циклов в пьезоэлектрической флаттерной системе.

При обсуждении флаттерных колебаний предполагается, что ось вращения лежит на хорде крыла. Влияние ее положения на характеристики предельных циклов исследовано, в частности, в [17]. Однако интересно проанализировать случай, когда эта ось расположена вне крыла. Такую систему можно рассматривать как аэродинамический маятник с упруго закрепленной точкой подвеса.

Систематическое исследование поведения аэродинамического маятника с фиксированной точкой подвеса проведено, в частности, в [18, 19]. В то же время, можно ожидать, что упругое закрепление точки подвеса и ее расположение вне хорды крыла приведет к возникновению новых эффектов, которые не наблюдались ни в динамике аэродинамического маятника, ни в динамике обычных флаттерных систем.

В настоящей работе рассматривается аэродинамический маятник с упруго закрепленной точкой подвеса. Исследуется устойчивость “флюгерного” положения равновесия и периодические режимы, возникающие в этой системе. Обсуждается возможность использования этого объекта в качестве рабочего элемента ветроэнергетической установки. При этом механизм отбора энергии потока моделируется демпфированием в пружине крепления. Исследовано влияние параметров системы на амплитуды и частоты колебаний, возникающих в системе, а также на величину вырабатываемой мощности.

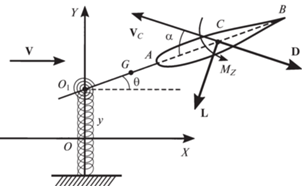
2. Постановка задачи. Рассмотрим механическую систему, состоящую из тонкого крыла с симметричным профилем AB, прикрепленного к жесткому стержню ${{O}_{1}}A$ таким образом, что хорда крыла параллельна стержню (рис. 1). Предположим, что центр масс G системы лежит на прямой ${{O}_{1}}B$. Стержень вместе с крылом может вращаться вокруг вертикальной оси, проходящей через точку ${{O}_{1}}$, причем данная точка может перемещаться вдоль некоторой неподвижной оси $OY$, перпендикулярной этой оси.

Пусть система помещена в горизонтальный стационарный поток среды, скорость которого ${\mathbf{V}}$ перпендикулярна оси $OY$.

Будем считать, что маятник находится в упругом закреплении, которое будем моделировать с помощью пружины растяжения/сжатия и спиральной пружины (см. рис. 1). Будем считать, что спиральная пружина не напряжена, когда державка ${{O}_{1}}A$ направлена вдоль скорости потока.

Введем неподвижную систему координат $OXY$, начало которой поместим в точку, в которой пружина растяжения/сжатия не деформирована, а ось абсцисс направим вдоль скорости набегающего потока.

Очевидно, рассматриваемая механическая система имеет две степени свободы. Ее положение будем характеризовать двумя обобщенными координатами: y – координата точки G и $\theta $ – угол между стержнем ${{O}_{1}}A$ и скоростью потока.

Предположим, что поток действует только на крыло, и воспользуемся квазистатическим подходом для описания этого воздействия. Будем считать, что оно сводится к подъемной силе ${\mathbf{L}}$, силе лобового сопротивления ${\mathbf{D}}$ (обе они приложены в середине C хорды), а также к моменту ${{M}_{z}}$ относительно этой точки. Направления силы лобового сопротивления и подъемной силы определяются воздушной скоростью ${{{\mathbf{V}}}_{C}}$ точки C, т.е. ее скоростью относительно набегающего потока: вектор ${\mathbf{D}}$ направлен против ${{{\mathbf{V}}}_{C}}$, а вектор ${\mathbf{L}}$ составляет с ним прямой угол. Как и в [18], будем считать, что величины аэродинамических сил и момента имеют следующую структуру:

Здесь $\rho $ – плотность среды, $S = lb$ – площадь крыла ($l$ – размах крыла, а $b$ – хорда, т.е. расстояние $AB$), $\alpha $ – эффективный угол атаки, под которым будем понимать угол между воздушной скоростью и хордой крыла, ${{C}_{l}}$, ${{C}_{d}}$ и ${{C}_{m}}$ – безразмерные коэффициенты подъемной силы, лобового сопротивления и аэродинамического момента, соответственно. Как и в [20, 21], будем считать, что эти коэффициенты зависят только от угла атаки, и зависимости эти такие же, как и в случае крыла, закрепленного в стационарном потоке. Отметим, что эти зависимости являются нелинейными. В литературе представлены соответствующие данные для профилей различной формы, полученные как в результате экспериментов с круговыми обдувками крыльев, так и расчетов, (например, [22, 23]).

Чтобы связать угол атаки и воздушную скорость с обобщенными координатами и скоростями системы, запишем кинематические соотношения:

Здесь $r$ обозначает расстояние ${{O}_{1}}C$.

Тогда уравнения движения системы можно представить в следующем виде:

Здесь $m$ – масса подвижных частей системы, ${{r}_{0}}$ – радиус инерции крыла вместе со стержнем относительно центра масс G, $\xi $ – расстояние от точки подвеса до центра масс, ${{K}_{y}}(y)$ – жесткость пружины растяжения/сжатия, ${{K}_{\theta }}(\theta )$ – жесткость спиральной пружины; $h$ и $\delta $ – коэффициенты демпфирования, соответствующие линейному перемещению и вращению, соответственно. Будем считать, что пружина растяжения/сжатия обладает нелинейной жесткостью, а коэффициент жесткости спиральной пружины постоянен:

Величины $k$, ${{k}_{3}}$ и $\kappa $ являются положительными.

Таким образом, в нашей системе имеется два источника нелинейности: аэродинамика и жесткость пружины растяжения/сжатия в креплении.

Чтобы уменьшить число параметров, введем безразмерное время $\bar {t} = t\sqrt {k{\text{/}}m} $ и следующие безразмерные величины:

С учетом соотношений (2.4) и (2.5), безразмерные уравнения движения и кинематические соотношения можно записать в следующем виде:

Уравнения (2.6)–(2.7) образуют замкнутую систему.

Далее для упрощения записи будем опускать черту над безразмерными величинами и обозначать производную по безразмерному времени точкой.

3. Положения равновесия и их устойчивость. Теперь найдем положения равновесия $\theta \equiv {{\theta }_{*}} = {\text{const}}$, $y \equiv {{y}_{*}} = {\text{const}}$ нашей системы. Из (2.7) следует, что в равновесии $\alpha = \theta _{*}^{{}}$ и ${{V}_{C}} = V$. Следовательно, уравнения равновесия принимают вид

Здесь ${{C}_{n}}(\alpha ) = {{C}_{l}}(\alpha )\cos \alpha + {{C}_{d}}(\alpha ){\text{sin}}\alpha $ – так называемый коэффициент нормальной силы.

Для симметричного профиля ${{C}_{l}}(\alpha )$ и ${{C}_{m}}(\alpha )$ – нечетные функции, а ${{C}_{d}}(\alpha )$ – четная и положительная при всех $\alpha $. Поэтому система имеет тривиальное равновесие ${{y}_{*}} = 0$, $\theta _{*}^{{}} = 0$.

Из статических экспериментов известно, что для тонких симметричных профилей $\left| {{{C}_{m}}(\alpha ){\text{/}}{{C}_{n}}(\alpha )} \right| \leqslant 0.3$ для всех значений угла атаки, причем эта величина стремится к максимуму при $\alpha \to 0$. Кроме того, ${{C}_{n}}(\alpha )\sin \alpha \geqslant 0$ при всех $\alpha $, и ${{C}_{n}}(\alpha )$ обращается в нуль только при $\alpha = n\pi $ ($n \in \mathbb{Z}$). Следовательно, при выполнении условия

где $C_{n}^{\alpha } = {{\left. {d{{C}_{n}}{\text{/}}d\alpha } \right|}_{{\alpha = 0}}}$, $C_{m}^{\alpha } = {{\left. {d{{C}_{m}}{\text{/}}d\alpha } \right|}_{{\alpha = 0}}}$, знак выражения ${{C}_{m}}({{\theta }_{*}}) - {{C}_{n}}({{\theta }_{*}})r$ определяется знаком ${{C}_{n}}({{\theta }_{*}})$, а значит, второе уравнение (3.1) имеет единственный корень на интервале $[ - \pi ,\pi ]$, а именно, $\theta _{*}^{{}} = 0$. Таким образом, если державка достаточно длинная, то у системы имеется только одно положение равновесия на этом интервале. Однако следует отметить, что в случае, когда $\kappa $ мало или $V$ велико, имеются положения равновесия, в которых ${\text{|}}{{\theta }_{*}}{\text{|}} > \pi $. В частности, при $\kappa = 0$ равновесиями будут все точки $y_{*}^{{}} = 0$, ${{\theta }_{*}} = n\pi $ ($n \in \mathbb{Z}$).

В дальнейшем мы будем считать, что условие (3.2) выполнено.

Исследованию влияния различных видов сил на устойчивость равновесия систем, в том числе, с двумя степенями свободы посвящено огромное количество работ (в частности, [24–26]). Однако, как нетрудно показать, аэродинамические силы вносят вклад сразу во все виды сил (диссипативные, гироскопические, потенциальные и позиционные неконсервативные), с чем связана определенная специфика аэроупругих систем.

Чтобы исследовать устойчивость тривиального равновесия, линеаризуем уравнения движения в его окрестности, учитывая кинематические соотношения. Получим:

Здесь $C_{l}^{\alpha } = {{\left. {d{{C}_{l}}{\text{/}}d\alpha } \right|}_{{\alpha = 0}}}$. Заметим, что $C_{n}^{\alpha } = C_{l}^{\alpha } + {{C}_{{d0}}}$, где ${{C}_{{d0}}} = {{C}_{d}}(0) > 0$. Для тонких профилей величины $C_{n}^{\alpha }$, $C_{l}^{\alpha }$ и $C_{m}^{\alpha }$ положительны, а величина ${{C}_{{d0}}}$ мала.

Характеристическое уравнение можно представить в следующем виде:

Здесь $\zeta = C_{n}^{\alpha }r - C_{m}^{\alpha }$. С учетом (3.2) имеем $\zeta > 0$.

Для того чтобы рассматриваемый маятник можно было использовать в качестве рабочего элемента ветроэнергетической установки, необходимо, чтобы он мог совершать автоколебания под действием аэродинамических сил. Поэтому ситуация, когда тривиальное равновесие асимптотически устойчиво, представляется нежелательной.

Достаточным условием асимптотической устойчивости является положительность всех коэффициентов характеристического полинома и третьего минора ${{H}_{3}}$ матрицы Гурвица. Выражение для ${{H}_{3}}$ в общем случае сравнительно громоздкое. Рассмотрим ситуацию, когда демпфирование отсутствует: $\delta = h = 0$. При этом

Пусть $r < \xi $. Тогда $\zeta - C_{n}^{\alpha }\xi < 0$ и ${{u}_{1}} < 0$. С учетом того, что ${{C}_{{d0}}} = 1$, получаем, что ${{u}_{2}} > 0$. Нетрудно показать, что при $V < \sqrt {{{u}_{2}}} $ третий минор Гурвица положителен. В данной ситуации все коэффициенты характеристического полинома также положительны, и равновесие асимптотически устойчиво. При $V > \sqrt {{{u}_{2}}} $ имеет место неустойчивость.

Пусть $\xi < r < \xi + {{r_{0}^{2}} \mathord{\left/ {\vphantom {{r_{0}^{2}} \xi }} \right. \kern-0em} \xi }$ и $r < \xi + {{C_{m}^{\alpha }} \mathord{\left/ {\vphantom {{C_{m}^{\alpha }} {C_{n}^{\alpha }}}} \right. \kern-0em} {C_{n}^{\alpha }}}$. Тогда $\zeta - C_{n}^{\alpha }\xi < 0$ и ${{u}_{1}} < 0$. Если, кроме того, $\kappa < r(r_{0}^{2} + {{\xi }^{2}} - r\xi ){{\left( {r - \xi } \right)}^{{ - 1}}}$, то ${{u}_{2}} > 0$, и, как и ранее, асимптотическая устойчивость имеет место при $V < \sqrt {{{u}_{2}}} $. Если $\kappa $ больше этой величины, то ${{u}_{2}} < 0$, и равновесие неустойчиво при всех положительных значениях скорости потока.

Пусть $\xi < r < \xi + {{r_{0}^{2}} \mathord{\left/ {\vphantom {{r_{0}^{2}} \xi }} \right. \kern-0em} \xi }$ и $r > \xi + {{C_{m}^{\alpha }} \mathord{\left/ {\vphantom {{C_{m}^{\alpha }} {C_{n}^{\alpha }}}} \right. \kern-0em} {C_{n}^{\alpha }}}$. Тогда $\zeta - C_{n}^{\alpha }\xi > 0$, и при малых $\kappa $ имеем ${{u}_{1}} > 0$ и ${{u}_{2}} > 0$. Соответственно, в промежутке $\min (\sqrt {{{u}_{1}}} ,\sqrt {{{u}_{2}}} ) < V < \max (\sqrt {{{u}_{1}}} ,\sqrt {{{u}_{2}}} )$ имеет место неустойчивость, а вне него (при положительных V) – место асимптотическая устойчивость. Таким образом, в этой ситуации увеличение скорости потока вначале приводит к потере устойчивости, но когда V превышает некоторое критическое значение, устойчивость восстанавливается.

Пусть $r > \xi + {{r_{0}^{2}} \mathord{\left/ {\vphantom {{r_{0}^{2}} \xi }} \right. \kern-0em} \xi }$ и $r < \xi + {{C_{m}^{\alpha }} \mathord{\left/ {\vphantom {{C_{m}^{\alpha }} {C_{n}^{\alpha }}}} \right. \kern-0em} {C_{n}^{\alpha }}}$. Тогда $\zeta - C_{n}^{\alpha }\xi < 0$ и ${{u}_{1}} < 0$. Если при этом ${{u}_{2}} > 0$, то положение равновесия неустойчиво при $V < \sqrt {{{u}_{2}}} $ и устойчиво при $V > \sqrt {{{u}_{2}}} $. Если же ${{u}_{2}} < 0$, то положение равновесия неустойчиво при всех $V$.

Пусть $r > \xi + {{r_{0}^{2}} \mathord{\left/ {\vphantom {{r_{0}^{2}} \xi }} \right. \kern-0em} \xi }$ и $\xi + {{C_{m}^{\alpha }} \mathord{\left/ {\vphantom {{C_{m}^{\alpha }} {C_{n}^{\alpha }}}} \right. \kern-0em} {C_{n}^{\alpha }}} < r < \xi + {{C_{m}^{\alpha }} \mathord{\left/ {\vphantom {{C_{m}^{\alpha }} {C_{n}^{\alpha }}}} \right. \kern-0em} {C_{n}^{\alpha }}} + {{r_{0}^{2}} \mathord{\left/ {\vphantom {{r_{0}^{2}} {(\xi + \kappa C_{n}^{\alpha })}}} \right. \kern-0em} {(\xi + \kappa C_{n}^{\alpha })}}$. Тогда ${{u}_{2}} < 0$ и ${{u}_{1}}$ > 0. При $V < \sqrt {{{u}_{1}}} $ имеет место неустойчивость, а при $V > \sqrt {{{u}_{1}}} $ асимптотическая устойчивость.

Таким образом, при определенном выборе значений параметров тривиальное равновесие неустойчиво в области малых скоростей потока, а рост V приводит к стабилизации. Этот эффект может быть полезен с прикладной точки зрения, поскольку при больших скоростях ветра ветроэнергетические системы, как правило, требуется “останавливать”, чтобы избежать их разрушения вследствие чрезмерных нагрузок.

Пусть, наконец, $r > \xi + {{r_{0}^{2}} \mathord{\left/ {\vphantom {{r_{0}^{2}} \xi }} \right. \kern-0em} \xi }$ и $r > \xi + {{C_{m}^{\alpha }} \mathord{\left/ {\vphantom {{C_{m}^{\alpha }} {C_{n}^{\alpha }}}} \right. \kern-0em} {C_{n}^{\alpha }}} + {{r_{0}^{2}} \mathord{\left/ {\vphantom {{r_{0}^{2}} {(\xi + \kappa C_{n}^{\alpha })}}} \right. \kern-0em} {(\xi + \kappa C_{n}^{\alpha })}}$. Тогда ${{u}_{2}} < 0$ и ${{u}_{1}} < 0$. В этой ситуации асимптотическая устойчивость имеет место при любых значениях скорости потока. Иными словами, увеличение расстояния от крыла до точки подвеса маятника ведет к стабилизации равновесия.

Обсудим теперь влияние демпфирования. Нетрудно показать, что в отсутствие потока тривиальное положение маятника асимптотически устойчиво, если $\xi \ne 0$, $\kappa \ne 0$ и хотя бы один из коэффициентов демпфирования не равен нулю. Соответственно, при выполнении этих условий асимптотическая устойчивость имеет место и при достаточно малых скоростях потока.

Выражение для ${{H}_{3}}$ представляет собой кубический полином относительно как $\delta $, так и $h$, причем коэффициент при ${{\delta }^{3}}$ имеет вид $C_{n}^{\alpha }\mu V + h > 0$, а коэффициент при ${{h}^{3}}$ представляет собой выражение $(\zeta \mu {{V}^{2}} + \kappa )\left( {rV\mu \zeta + \delta } \right)(r_{0}^{2} + {{\xi }^{2}}) > 0$. Значит, при достаточно больших значениях $\delta $ и/или $h$ тривиальное равновесие, как и следовало ожидать, асимптотически устойчиво.

На рис. 2 изображена область неустойчивости тривиального равновесия на плоскости $(h,V)$ при разных значениях $\delta $ и $\kappa $. Для расчетов использованы следующие значения остальных безразмерных параметров:

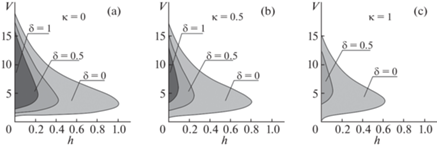
Видно, что эффект двукратного изменения характера устойчивости при увеличении скорости потока и стабилизации при больших значениях V сохраняется в некотором диапазоне значений коэффициентов демпфирования.

Увеличение жесткости спиральной пружины ведет к уменьшению области неустойчивости.

Вообще говоря, выражение ${{H}_{3}}$, рассматриваемое как полином относительно $\delta $ или $h$, может иметь три действительных положительных корня. В таком случае характер устойчивости равновесия будет изменяться 3 раза при изменении соответствующего коэффициента демпфирования от нуля до бесконечности.

Это проиллюстрировано на рис. 3, где серым цветом показана область неустойчивости на плоскости $(V,\ln \delta )$ при разных значениях $\kappa $. Пунктирными линиями отмечены значения скорости, соответствующие изменению характера устойчивости (бифуркации Андронова–Хопфа) при $\delta = 0$. Для расчетов использованы следующие значения:

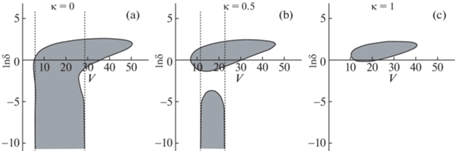
Для остальных параметров приняты те же значения, что и ранее.

Видно, что можно выбрать значения параметров таким образом, что при увеличении $\delta $ от нуля до бесконечности будет наблюдаться “чередование” характера устойчивости равновесия: неустойчивость при малых $\delta $, стабилизация при некотором увеличении $\delta $, дестабилизация при дальнейшем увеличении $\delta $, и, наконец, снова стабилизация. Этот эффект наиболее отчетливо выражен на рис. 3, b.

Возможна также ситуация, когда ${{H}_{3}}$ обращается в нуль при двух положительных значениях $\delta $. В частности, на рис. 3, с тривиальное равновесие при $\delta = 0$ асимптотически устойчиво при всех скоростях потока. Однако если V не слишком мало, то увеличение $\delta $ приводит к дестабилизации положения равновесия. Устойчивость восстанавливается, только когда $\delta $ становится больше некоторого критического значения, зависящего от скорости потока.

Надо отметить, что и при маленьких, и при больших значениях V асимптотическая устойчивость имеет место при всех $\delta $.

Найти физически осмысленные значения параметров системы, при которых подобные эффекты наблюдались бы при изменении коэффициента $h$, не удалось.

4. Периодические решения. Исследуем периодические решения, существующие в рассматриваемой системе. Будем считать, что спиральная пружина и трение в шарнире отсутствуют: $\kappa = \delta = 0$. Кроме того, предположим, что пружина растяжения/сжатия имеет характеристику с упрочнением, так что коэффициент ${{k}_{3}}$ велик: ε = $1{\text{/}}\sqrt {{{k}_{3}}} \ll 1$.

Будем искать периодические решения вида

Для поиска периодических решений автономных динамических систем существует множество методов (например, [27]). Мы воспользуемся методом гармонического баланса.

Из статических экспериментов известно, что в области малых углов атаки имеют место следующие соотношения: ${{C}_{l}}(\alpha ) = C_{l}^{\alpha }\alpha $, ${{C}_{m}}(\alpha ) = C_{m}^{\alpha }\alpha $, ${{C}_{d}}(\alpha ) = {{C}_{{d0}}} + {{C}_{{d2}}}{{\alpha }^{2}}$.

Тогда, подставив (4.1) в уравнения (2.6) и (2.7) и оставляя только члены первого порядка малости, получим следующие уравнения для неизвестных ${{y}_{1}}$, ${{\theta }_{1}}$, ${{\theta }_{2}}$ и $\omega $:

Из (4.2) получаем формулу для частоты:

Здесь

Таким образом, в системе может существовать до 2 циклов данного типа.

Величины ${{y}_{1}}$, ${{\theta }_{1}}$, ${{\theta }_{2}}$ для периодического решения, отвечающего корню $\omega $ уравнения (4.2), имеют следующий вид:

Вообще говоря, не каждой величине $\omega $, определяемой выражением (4.3), соответствует периодический режим, даже если она положительна: необходимо еще, чтобы величина ${{y}_{1}}$ была действительной и отличной от нуля.

Рассмотрим случай, когда спиральная пружина отсутствует ($\kappa = \delta = 0$) и демпфирование h равно нулю, решения уравнение (4.3) имеют следующий вид:

Формулы (4.4) при этом упрощаются:

Как отмечалось выше, величина ${{C}_{{d0}}}$ для тонких крыльев мала. Поэтому подкоренное выражение в формуле для ${{y}_{{12}}}$ отрицательно. Соответственно, в системе существует только один цикл указанного типа. Разумеется, эта ситуация сохраняется и в случае, когда коэффициент h отличен от нуля, но достаточно мал.

Проведем численное моделирование динамики системы, чтобы изучить поведение предельных циклов в более широком диапазоне значений параметров. Для расчетов выберем следующие значения параметров:

Эволюция амплитуд ${{A}_{\theta }}$ (по углу) и ${{A}_{y}}$ (по положению), а также частоты $\omega $ цикла при изменении коэффициента демпфирования в пружине растяжения/сжатия при различных значениях параметра $\xi $ представлена на рис. 4. Кружками и квадратами изображены результаты, полученные путем численного интегрирования уравнений движения (2.6)–(2.7). Сплошными и пунктирными линиями представлены результаты расчетов по формулам (4.3)–(4.4).

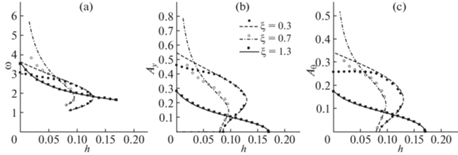
Видно, что в тех случаях, когда амплитуды циклов не слишком велики, качество аппроксимации достаточно хорошее (причем как для притягивающих, так и для отталкивающих циклов).

При всех рассмотренных значениях $\xi $ положение равновесия неустойчиво при $h \in [0,{{h}_{*}})$. При достаточно больших расстояниях $\xi $ от центра масс до оси вращения бифуркация Андронова–Хопфа, происходящая при $h = {{h}_{*}}$, является суперкритической. В системе наблюдается только один цикл (притягивающий) указанного типа. При уменьшении $\xi $ эта бифуркация становится субкритической. Появляется интервал значений h, в котором существует притягивающий и отталкивающий циклы.

В определенном диапазоне $\xi $ (и, в частности, при $\xi = 0.7$) в области малых $h$ цикла рассматриваемого типа не существует. Вместо этого в системе наблюдаются два симметричных относительно начала координат притягивающих цикла. Ни при $\xi = 1.3$, ни при $\xi = 0.3$ эти циклы не наблюдаются. Этот эффект требует отдельного исследования.

5. Оценка мощности. В качестве оценки эффективности данной системы как устройства преобразования энергии потока представляется естественным использовать безразмерный коэффициент мощности. Предположим, что в системе существует притягивающий цикл с периодом $T$. Как и в работе [28], определим коэффициент мощности для этого предельного цикла как отношение мощности, вырабатываемой системой, к мощности потока, проходящей через сечение, ометаемое крылом в ходе колебаний. В терминах введенных выше безразмерных величин получаем следующую формулу:

Здесь $P$ – безразмерная мощность, а ${{Y}_{w}}$ – максимум на множестве ординат всех точек крыла, взятый на периоде, т.е.

В ряде случаев (например, если система сопряжена с линейным генератором) можно считать, что полезная мощность, вырабатываемая генератором, определяется силой вязкого трения в линейной пружине. Тогда для мощности, вырабатываемой на рассматриваемом цикле, имеет место следующая формула:

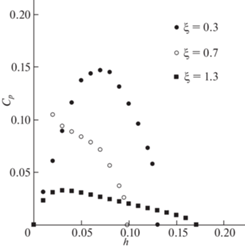
Зависимость коэффициента мощности от коэффициента демпфирования h при различных значениях $\xi $ и V = 2 представлена на рис. 5. Видно, что для каждого $\xi $ существует некоторое “оптимальное” значение демпфирования h, при котором ${{C}_{p}}$ достигает максимума.

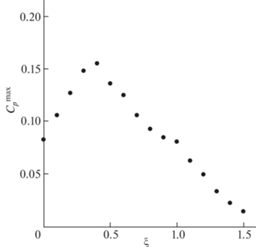
На рис. 6 проиллюстрировано влияние положения центра масс на максимальное значение $C_{p}^{{\max }}$ коэффициента мощности. Расчеты выполнены при безразмерной скорости потока V = 2. Зависимость ${{C}_{p}}$ от $\xi $ немонотонная, и выбор величины $\xi $ может существенно повлиять на вырабатываемую мощность.

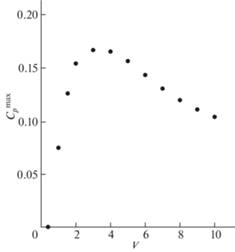
На рис. 7 приведена зависимость максимума ${{C}_{p}}$ от скорости потока. Расчеты проведены при $\xi = 0.4$. Интересно, что зависимость максимума коэффициента мощности от скорости потока также немонотонная: при малых значениях V циклы отсутствуют, с ростом скорости величина $C_{p}^{{\max }}$ возрастает, а затем начинает убывать.

6. Заключение. Рассмотрена динамика аэродинамического маятника с упруго закрепленной точкой подвеса. Построены области устойчивости положения равновесия, в котором маятник ориентирован по потоку, в пространстве параметров. В частности, найдены условия на параметры, при которых увеличение скорости потока приводит к стабилизации равновесия. Кроме того, показано, что при определенных условиях характер устойчивости этого равновесия меняется три раза при изменении коэффициента демпфирования спиральной пружины, установленной в точке подвеса, от нуля до бесконечности.

Получены аппроксимационные формулы для циклов, существующих в системе. Проведено численное моделирование динамики системы. Даны оценки коэффициента, характеризующего мощность, которая может быть отобрана у потока с помощью данной механической системы. Продемонстрирована немонотонная зависимость этого коэффициента от расстояния между центром масс и точкой подвеса, а также от скорости потока.

Исследование выполнено при поддержке Междисциплинарной научно-образовательной школы Московского университета “Фундаментальные и прикладные исследования космоса”.