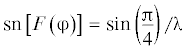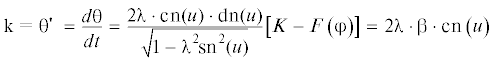Известия РАН. Механика твердого тела, 2022, № 5, стр. 47-57

1. Введение. Изгиб консоли тонкого упругого горизонтального стержня длиной $L$, жестко защемленного одним (левым) концом в центре координат $xOy$, возникает при воздействии на другой свободный конец поперечной вертикальной статической силы $P$ (рис. 1). При этом, как известно, уравнение равновесия такого стержня имеет вид [1, 2]

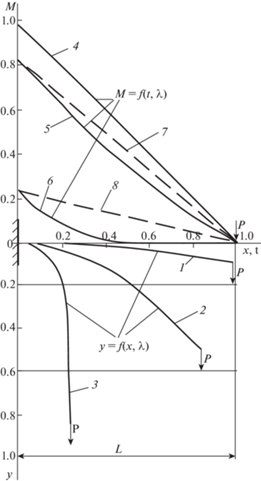
в котором $E$ – модуль упругости (модуль Юнга); J – момент инерции; $EJ$ – изгибная жесткость стержня; l и ${{\theta }}\left( l \right)$ – текущие значения длины (неизменной) дуги стержня и угла между касательной к текущей точке стержня и осью $0x$.

Выражение (1.1) преобразовывается в нелинейное уравнение маятника [1–4]

где ${{\beta }} = \sqrt {\frac{{P{{L}^{2}}}}{{EJ}}} $ – силовой коэффициент подобия; ${{\gamma }}\left( t \right) = \frac{{{\pi }}}{2} + {{\theta }}$ – угол между касательной к текущей точке и осью $0y$; $t = \frac{l}{L}$ – приведенная длина стержня.

2. Постановка задачи. Решение уравнения (1.2) представляется в виде зависимостей [1–3]

в которых значения модуля ${{\lambda }}$, равного ${{\lambda }} = \sin {{\alpha }}$ (α – модулярный угол), и неполного эллиптического интеграла 1 рода $F\left( {{{\varphi ,\lambda }}} \right) \equiv F\left( {{\varphi }} \right)$ (${{\varphi }}$ – амплитуда интеграла) зависят от величины силы P. Здесь и далее (см. ниже) обозначение модуля ${{\lambda }}$ в эллиптических интегралах и эллиптических функциях опущено для упрощения записей, то есть: $K\left( {{\lambda }} \right) \equiv K$, $K{\kern 1pt} '\left( {{\lambda }} \right) \equiv K{\kern 1pt} '$, $E\left( {{\lambda }} \right) \equiv E$, $E\left( {{{\varphi ,\lambda }}} \right) \equiv E\left( {{\varphi }} \right)$, ${\text{sn}}(u,{{\lambda }}) \equiv {\text{sn}}\left( u \right)$, ${\text{cn}}(u,{{\lambda }}) \equiv {\text{cn}}\left( u \right)$, ${\text{dn}}(u,{{\lambda }}) \equiv {\text{dn}}\left( u \right)$

При этом с учетом граничных условий, равных: $t = 0$ → ${{\theta }}\left( 0 \right) = 0$, ${{\gamma }}\left( 0 \right) = \frac{{{\pi }}}{2}$ и $t = 1$ → → $\frac{{d{{\theta }}\left( L \right)}}{{dl}} = 0$, $\frac{{d{{\gamma }}\left( 1 \right)}}{{dt}} = 0$ из зависимостей (2.1) после преобразований следует значение эллиптического синуса Якоби, равное

откуда выразим зависимости [2, 3, 5, 6] для определения значений амплитуды и неполного эллиптического интеграла 1 рода а также нижеследующее равенство (2.3) для силового коэффициента подобия где $K$ – полный эллиптический интеграл 1 рода при модуле ${{\lambda }}$ и модулярном угле ${{\alpha }}$, изменяющихся в интервалах $\frac{{\sqrt 2 }}{2} \leqslant {{\lambda }} < 1$, $\frac{{{\pi }}}{4} \leqslant {{\alpha }} < \frac{{{\pi }}}{2}$.

В вышеприведенных формулах (2.1)–(2.3) значения ${{\lambda }}$ и $F\left( {{\varphi }} \right)$ находятся в зависимости от силовой нагрузки ${{\beta }}$ методом подбора при известном $P$ – задаваясь ${{\lambda }}$ в формуле для определения критической нагрузки [2, 3]:

где ${{P}_{c}} = {{\left( {\frac{{{\pi }}}{2}} \right)}^{2}}\frac{{EJ}}{{{{L}^{2}}}}$ – эйлерова критическая сила.

По результатам интегрирования соотношений $\frac{{dx}}{{dl}} = \cos {{\theta }}$, $\frac{{dy}}{{dl}} = \sin {{\theta }}$ и преобразований представлены следующие расчетные зависимости (2.5) для описания очертания упругого стержня [1–3] при L = 1 (в усл. ед.):

в которых $E\left( {{\varphi }} \right)$ и $E\left[ {am\left( u \right)} \right]$ – неполные эллиптические интегралы 2 рода с модулем ${{\lambda }}$, соответственно, при амплитуде ${{\varphi }} = \arcsin \left( {\frac{{\sqrt 2 }}{{2{{\lambda }}}}} \right)$ и эллиптической амплитуде Якоби [5, 6] $am(u) = \arcsin \left[ {{\text{sn}}\left( u \right)} \right]$. При этом значение угла $u$ в эллиптических функциях Якоби – синусе ${\text{sn}}(u)$ и косинусе ${\text{cn}}(u)$, определяется по зависимости [2, 3]

3. Метод и построение решения. Следует отметить, что аналитическое решение различных прикладных задач механики с эллиптическими функциями Якоби и эллиптическими интегралами 1 и 2 рода (не выражающимися через элементарные функции) представляет собой значительные математические трудности, связанные, в том числе, с использованием специальных графиков и таблиц и необходимостью нелинейного, перекрестного и обратного интерполирования их данных. В то же время, используемые в настоящее время математические программы позволяют на основе численных решений находить значения эллиптических функций и интегралов с заданной точностью – однако, при этом результаты получаются в “цифрах” и только для отдельных дискретных точек. Указанное не позволяет получить общее аналитическое решение в элементарных функциях более сложной и многокомпонентной задачи, в которую отдельными “фрагментами” могут входить специальные функции, что ограничивает возможности выявления причинно-следственных связей исходных факторов и их влияние на итоговые результаты решаемых задач [7–10].

При этом известные аппроксимации указанных интегралов [11] не охватывают всю область их определения и представлены достаточно громоздкими приближенными формулами с большим числом интервалов их разбиения и т.д.

Другим направлением исследований является получение на основе результатов теоретических исследований упрощенных аналитических зависимостей для решения прикладных инженерных задач. В частности, в работах [12, 13] выполнены такие исследования для представления в элементарных функциях параметров прогиба стержня при изгибе от воздействия продольной нагрузки.

Аналогичные упрощенные зависимости для определения прогиба консоли от действия поперечной силы на свободном конце получены на основе “модифицированного линейного решения” [14, 15] (с численным решением алгебраических уравнений), а также путем разложения эллиптических интегралов в ряды [16] (с результатами близкими к точным). Вместе с тем, следует указать на недостаточность таковых исследований для оценки “укорочения” консоли при прогибе, то есть по определению абсциссы ее конца, что имеет важное значение при проектировании гибких стержневых систем.

Ниже приводятся расчетные зависимости для аналитического представления эллиптических интегралов 1 и 2 рода: $K$, $F\left( {{\varphi }} \right)$, $E\left( {{\varphi }} \right)$, $E\left[ {am\left( u \right)} \right]$ и эллиптических функций Якоби: ${\text{sn}}(u)$, ${\text{cn}}(u)$ в элементарных функциях, полученные на основе результатов гидромеханических решений (с погрешностью ≪1–2%) для заданных значений модуля $\frac{{\sqrt 2 }}{2} \leqslant {{\lambda }} < 1$.

При этом неполный эллиптический интеграл 1 рода $F\left( {{\varphi }} \right)$ для рассматриваемых случаев $\frac{{\sqrt 2 }}{2} \leqslant {{\lambda }} < 1$ рекомендуется определять по новой расчетной зависимости (3.1), основанной на результатах ранее полученных гидромеханических решений [7, 8, 17],

где величины ${{{{\varepsilon }}}_{1}}$, ${{{{\varepsilon }}}_{2}}$, $r$ находятся по формулам в которых $K$ и $K{\kern 1pt} _{{}}^{'}$ ($K_{{}}^{'}$ – полный эллиптический интеграл 1 рода при дополнительном модуле ${{\lambda }}_{{}}^{'} = \sqrt {1 - {{{{\lambda }}}^{2}}} $) определяются по зависимостям [7–10, 17]:

При этом получена новая аналитическая зависимость (3.4) в элементарных функциях для прямого определения значений эллиптического синуса Якоби ${\text{sn}}(u)$ (основанная на работах [7, 8, 17]), в виде:

где значения угла $u$ подсчитываются по формулам (2.6), (3.1)–(3.3) для заданных значений $t$ и ${{\lambda }}$.

Величина эллиптического косинуса Якоби ${\text{cn}}(u)$ определяется по формуле [6]

Значения же неполного эллиптического интеграла 2 рода $E\left( {{\varphi }} \right)$ находятся для двух интервалов в зависимости от заданных величин модулярного угла ${{{{\alpha }}}_{0}} = \frac{{{\alpha }}}{{{\pi }}} \cdot 180^\circ $ и амплитуды ${{\varphi }} = \arcsin \left( {\frac{{\sqrt 2 }}{{2{{\lambda }}}}} \right)$ по следующим усовершенствованным формулам [10]:

где $E$ – полный эллиптический интеграл 2 рода, определяемый в виде [9, 10]:

Значения $E\left( {{\varphi }} \right)$, полученные по зависимостям (3.6), близко (~1%) согласуются с графиками точного решения [5], а для частных случаев (граничных участков) значения $E\left( {{\varphi }} \right)$ полностью совпадают с точными формулами, в частности, при ${{{{\alpha }}}_{0}} = 0;$ $\frac{{{\pi }}}{2}$ и ${{\varphi }} = 0;$ $\frac{{{\pi }}}{2}$, соответственно, $E\left( {{{\varphi }},0} \right) = {{\varphi }}$; $E\left( {{{\varphi }},1} \right) = \sin {{\varphi }}$ и $E\left( {0,{{\lambda }}} \right) = 0$; $E\left( {\frac{{{\pi }}}{2},{{\lambda }}} \right) = E$.

Величина интеграла $E\left[ {am\left( u \right)} \right]$ в зависимости (2.5) также находится по формулам (3.6), принимая в них вместо ${{\varphi }}$ величину эллиптической амплитуды am(u) = $\arcsin [{\text{sn}}(u)]$, в котором значение эллиптического синуса Якоби ${\text{sn}}(u)$ рассчитывается по (3.4).

Таким образом, подставляя рекомендуемые расчетные зависимости, выраженные в элементарных функциях (3.1)–(3.7), в формулы (2.5), строятся очертания линии изогнутой консоли для заданных значений модуля ${{\lambda }}$.

Кроме этого, по подсчитанным по формуле (2.6) значениям угла $u$, определяются также по нижеследующим зависимостям [1] значения изгибающих моментов

и углов ${{\theta }}$ между касательной к текущей точке консоли и осью $0x$которые для концевой точки (при $t = 1$) будут равны $M = 0$; ${{\theta }} = 2{{\alpha }} - 0.5{{\pi }}$.

Кривизна изгиба консоли k вдоль длины стержня определится производной

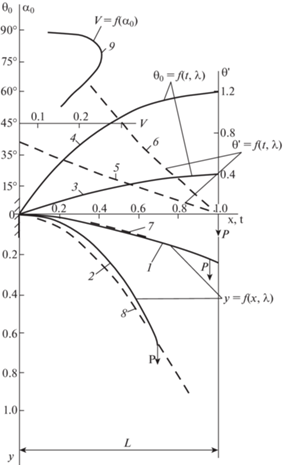
в которой ${\text{dn}}\left( u \right) = \sqrt {1 - {{{{\lambda }}}^{2}}{\text{s}}{{{\text{n}}}^{2}}\left( u \right)} $ – дельта амплитуды Якоби (рис. 2).

Внутренняя энергия изгиба консоли $V$ находится по формуле [1]

характер изменения которой в зависимости от значений модулярного угла ${{{{\alpha }}}_{0}}$ (в градусах) показан на рис. 2.

Для расчетов прикладных задач (с погрешностью <1.5–2.5%) аналитическую взаимосвязь между значениями ${{\beta }}$ и ${{\lambda }}$ в формуле (2.4), можно выразить через значения модулярного угла ${{{{\alpha }}}_{0}}$ в виде зависимостей (3.11) и (3.12), полученных на основе [9]:

в которых величины модуля ${{\lambda }}$ и амплитуды ${{\varphi }}$, соответственно, равны ${{\lambda }} = \sin {{{{\alpha }}}_{0}}$ и ${{\varphi }} = \arcsin \left( {\frac{{\sqrt 2 }}{{2{{\lambda }}}}} \right)$, а полные эллиптические интегралы 1 рода $K$ и $K_{{}}^{'}$ определяются по формулам (3.2) и (3.3).

4. Анализ результатов и примеры. На рис. 1 приведена расчетная схема изгиба горизонтальной консоли от действия поперечной вертикальной силы $P$, на которой для заданных значений модуля λ, равных $\sqrt {0.6} $, $\sqrt {0.85} $, $\sqrt {0.99999} $, показаны:

– линии изгибов консоли (кривые 1–3), практически совпадающих с очертаниями кривых, построенных численным методом [2, рис. 2, с. 128];

– эпюры изгибающих моментов сил по длине консоли с учетом нелинейности (кривые 4–6) и для случая линейной задачи (кривые 7, 8).

Из рис. 1 также следует, что при силовых нагрузках с модулем ${{\lambda }} > \sqrt {0.85} $ завышение “линейных” моментов сил над “нелинейными” составляет от 20% до кратных значений.

В табл. 1 дается сравнение значений координат (при $L = 1$) изогнутой консоли, подсчитанных по рекомендуемым зависимостям (2.5), (2.6), (3.1)–(3.7) с данными численного (точного) решения Попова Е.П. [1, табл. 9.4 и 9.5 , с. 231] для силовых нагрузок ${{{{\beta }}}^{2}} = 0.7305,3.4055$ при соответствующих значениях модуля ${{\lambda }} = 0.8192,0.9659$.

Как следует из табл. 1, результаты подсчетов координат изогнутой консоли для модулей ${{\lambda }} = 0.8192,0.9659$, подсчитанные по предлагаемым зависимостям на основе элементарных функций (2.5), (2.6), (3.1)–(3.7), весьма близко (<1.0–1.7%) согласуются с данными численного (точного) решения [1] по всей длине консоли (рис. 2, кривые 1 и 2).

На рис. 2 для указанных модулей ${{\lambda }} = 0.8192,0.9659$ показаны также графики углов изгиба ${{{{\theta }}}_{0}}$ (в градусах), равные ${{{{\theta }}}_{0}} = \frac{{{\theta }}}{{{\pi }}}180^\circ $ – (кривые 3, 4) и кривизны консоли, определяемые производной 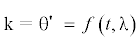(кривые 5, 6).

Для сравнительной оценки результатов полученного решения нелинейной задачи представлены также очертания изгибов консолей при решении линейной задачи (кривые 7, 8). Как видно из последнего, “линейное” очертание кривой 7 для модуля ${{\lambda }} = 0.8192$ достаточно близко совпадает с точной кривой (без учета горизонтального смещения на ~3%), однако же, для повышенных значений модуля ${{\lambda }} = 0.9659$ линейная задача с очертанием кривой 8 дает неприемлемые результаты с завышением прогибов консоли до 50–80%, не учитывая при этом и горизонтальное смещение на ~30%.

Из рассмотренного общего решения задачи следуют отдельные результаты, в частности, по определению координат свободного конца консоли. Последние выразятся из (2.5), (2.6), (3.4) и (3.5) при значении $t = 1$ в виде:

Для нахождения значений указанных координат в зависимости от действующей силовой нагрузки ${{\beta }}$ предлагаются также следующие упрощенные зависимости для соответствующих интервалов нагрузки:

– для абсциссы $x = f\left( {{\beta }} \right)$

– для ординаты $y = f\left( {{\beta }} \right)$

В нижеследующей табл. 2 дается сравнение значений координат $x = f\left( {{\beta }} \right)$ и $y\, = \,f{\text{(}}\beta {\text{)}}$ для свободного конца изогнутой консоли, подсчитанных по рекомендуемым зависимостям (4.2)–(4.6) с точными данными (в том числе, заимствованными из [1, 16]) для интервала силовых нагрузок $0 < {{\beta }} \leqslant 4.85$.

Как следует из табл. 2, значения координат $x = f\left( {{\beta }} \right)$ и $y = f\left( {{\beta }} \right)$ для свободного конца изогнутой консоли, подсчитанных по рекомендуемым зависимостям (4.2)–(4.6) весьма близко (~1–2%) согласуются с точными данными, в том числе, заимствованными из [1, 16], для всего интервала действия силовых нагрузок $0 < {{\beta }} \leqslant 4.85$.

Кроме этого, на рис. 2 представлено изменение характера внутренней энергии изгиба $V = f\left( {{{{{\alpha }}}_{0}}} \right)$ в зависимости от модулярного угла ${{{{\alpha }}}_{0}}$ (кривая 9), из которого следует, что консоль обладает наибольшей внутренней энергией при значениях ${{{{\alpha }}}_{0}} = 75^\circ ...80^\circ $, соответствующих силовому коэффициенту подобия ${{\beta }} = 1.845...2.284$.

Заключение. В работе рассматривается классическая нелинейная задача изгиба консоли от действия вертикальной силы. При этом получены расчетные зависимости в элементарных функциях для прямого аналитического определения основных параметров изгибаемой консоли, таких как – координаты очертания консоли, изгибаемые углы и кривизна по длине консоли, моменты сил и внутренняя энергия изгиба, а также упрощенные формулы для нахождения координат свободного конца консоли. Сравнение полученных расчетных значений с графическими и табличными данными известных численных (точных) решений дало достаточно высокую сходимость результатов (<1–2%), приведены примеры расчета, в том числе со сравнением с результатами линейного расчета. Полученные результаты могут быть использованы, в частности, при определении (обратным методом) жесткости стержней консолей произвольного поперечного сечения, а также модуля упругости материала консоли при известных сечениях, в том числе при конструировании защитных сооружений от опасных склоновых геофизических процессов и др.