1. На главную
  2. Электронные версии
  3. Известия РАН. Механика твердого тела
  4. № 5, 2022

Известия РАН. Механика твердого тела, 2022, № 5, стр. 32-46

О ТЕПЛОТВОРНОЙ СПОСОБНОСТИ ПРЯМОЛИНЕЙНОГО УПРУГОВЯЗКОПЛАСТИЧЕСКОГО ТЕЧЕНИЯ ПРИ УЧЕТЕ ПРОИЗВОДСТВА ТЕПЛА ЗА СЧЕТ ТРЕНИЯ МАТЕРИАЛА О ЕГО ГРАНИЧНУЮ ШЕРОХОВАТУЮ ПОВЕРХНОСТЬ

А. А. Буренин a, *, Л. В. Ковтанюк b, **, Г. Л. Панченко b, c, ***

a Институт машиноведения и металлургии ДВО РАН
Комсомольск-на-Амуре, Россия

b Институт автоматики и процессов управления ДВО РАН
Владивосток, Россия

c Владивостокский государственный университет экономики и сервиса
Владивосток, Россия

* E-mail: burenin@iacp.dvo.ru
** E-mail: lk@iacp.dvo.ru
*** E-mail: panchenko@iacp.dvo.ru

Поступила в редакцию 20.05.2022
После доработки 22.05.2022
Принята к публикации 23.05.2022

Полный текст (PDF)

Аннотация

Приводятся расчеты распределения деформаций, напряжений и температуры в процессе деформирования упруговязкопластического материала, зажатого между коаксиальными цилиндрическими поверхностями и удерживаемого первоначально за счет сухого трения о граничные поверхности. За счет задаваемого переменного продвижения внешней из них происходит проскальзывание материала и наступает (не одновременно) его вязкопластическое течение. Рассматривается процесс развития течения с его последующим торможением до остановки, разгрузки материала и остывания до комнатной температуры. Тепло производится за счет трения скольжения о граничную шероховатую поверхность и за счет необратимого деформирования (связанная задача теории больших деформаций). Деформируемый материал считается механически несжимаемым, когда изменение его объема связывается только с температурным расширением, предел текучести полагается зависящим от температуры.

Ключевые слова: термоупругость, вязкопластическое течение, большие деформации, деформационное теплопроизводство, теплопроводность

1. Введение. Прямолинейные движения жестковязкопластических сред изучены достаточно подробно [1–6]. Если отказаться от принимаемого в рамках жесткопластического анализа положения о недеформируемости материала застойных зон и продвигающихся ядер, то с неизбежностью приходим к необходимости постановок таких задач в рамках теории больших упруговязкопластических деформаций [7–9]. В областях вязкопластического течения деформации положить малыми невозможно, а в областях упругого деформирования они существенно зависят от параметров протекающего вязкопластического течения. Прямолинейные движения упруговязкопластической среды посредством постановок задач теории больших деформаций рассматривались в [8, 10–13]. Современная технологическая практика заставляет считать [14], что в областях застойных зон и продвигающихся ядер происходит не только обратимое (упругое) деформирование, но и необратимое в форме роста деформаций ползучести. На продвигающихся границах областей вязкопластического течения в таком случае одномоментно меняется механизм производства необратимых деформаций (меняются определяющие законы) с вязкого (ползучесть) на пластический (течение) при активном процессе деформирования и наоборот при разгрузке. Задачи, учитывающие такие обстоятельства, ставились и решались в рамках теории больших деформаций в [15–18].

Учет теплотворной способности процесса необратимого деформирования (связанности задач теории больших деформаций) только усложняет математическое моделирование процесса деформирования, постановки и методы решения соответствующих краевых задач [19–24]. Производство тепла за счет необратимого деформирования в прямолинейных движениях упруговязкопластических сред рассматривалось в [25–28]. В таких задачах теории больших деформаций также считалось, что тепло производится еще и за счет трения материала о шероховатые поверхности, его ограничивающие. Здесь рассмотрим еще одну связанную задачу о прямолинейном движении упруговязкопластического материала, зажатого в зазоре между коаксиальными цилиндрическими поверхностями при заданном переменном движении внешней из них.

В качестве математической модели упруговязкопластического деформирования выбираем предложение [8, 29], когда обратимые и необратимые деформации определяются дифференциальными уравнениями их переноса [30, 31]. Отметим при этом, что именно в рамках такой модели было получено большинство численно-аналитических, включая точные, решений краевых задач теории больших упругопластических или упруговязкопластических деформаций. На часть их ссылаемся в настоящей публикации.

2. Основные зависимости модели деформирования. Дифференциальные уравнения изменения (переноса) тензоров обратимых m и необратимых p деформаций запишем, следуя [8], в виде

(2.1)
$\frac{{D{\mathbf{m}}}}{{Dt}} = {\mathbf{\varepsilon }} - {{{\mathbf{\varepsilon }}}^{p}} - \frac{1}{2}(({\mathbf{\varepsilon }} - {{{\mathbf{\varepsilon }}}^{p}} + {\mathbf{z}}) \cdot {\mathbf{m}} + {\mathbf{m}} \cdot ({\mathbf{\varepsilon }} - {{{\mathbf{\varepsilon }}}^{p}} - {\mathbf{z}}))$
(2.2)
$\frac{{D{\mathbf{p}}}}{{Dt}} = \frac{{d{\mathbf{p}}}}{{dt}} - {\mathbf{\psi }} \cdot {\mathbf{p}} + {\mathbf{p}} \cdot {\mathbf{\psi }} = {{{\mathbf{\varepsilon }}}^{p}} - {\mathbf{p}} \cdot {{{\mathbf{\varepsilon }}}^{p}} - {{{\mathbf{\varepsilon }}}^{p}} \cdot {\mathbf{p}}$
$\begin{gathered} {\mathbf{m}} = {\mathbf{e}} + \alpha {{T}_{0}}\theta {\mathbf{I}},\quad {\mathbf{\psi }} = {\mathbf{\omega }} + {\mathbf{z}}\left( {{\mathbf{\varepsilon }},{\mathbf{m}}} \right) \\ {\mathbf{\varepsilon }} = \frac{1}{2}(\nabla {\mathbf{v}} + {{\nabla }^{T}}{\mathbf{v}}),\quad {\mathbf{\omega }} = \frac{1}{2}(\nabla {\mathbf{v}} - {{\nabla }^{T}}{\mathbf{v}}),\quad \theta = \left( {T - {{T}_{0}}} \right)T_{0}^{{ - 1}} \\ \end{gathered} $

Здесь ${\mathbf{v}}$ – вектор скорости; $T,\,\,{{T}_{0}}$ – температура и температура недеформированного состояния (комнатная температура); e – тензор, задающий упругие деформации; I – единичный тензор, составленный из символов Кронекера; ${\mathbf{z}}\left( {{\mathbf{\varepsilon }},{\mathbf{m}}} \right)$ – нелинейная часть тензора вращений ${\mathbf{\psi }}$ $({\mathbf{\psi }} = - {{{\mathbf{\psi }}}^{T}})$, здесь ее не приводим, в [8] она полностью записана; ${{{\mathbf{\varepsilon }}}^{p}}$ – скорость изменения необратимых деформаций, $\alpha $ – коэффициент линейного расширения.

Соотношением (2.2) вводится объективная производная по времени, с помощью которой задается взаимодействие между обратимыми и необратимыми деформациями в процессе деформирования, обеспечивающее геометрическую корректность в построениях кинематики среды. При ${\mathbf{z}}\left( {{\mathbf{\varepsilon }},{\mathbf{m}}} \right) = {\mathbf{0}}$ такая производная оказывается производной Зарембы–Яумана. Когда ${{{\mathbf{\varepsilon }}}^{p}} = {\mathbf{0}}$ тензор необратимых деформаций неизменен и согласно (2.2) изменяются только компоненты этого тензора, что характерно для процесса разгрузки.

Для тензора полных деформаций Альманси d из (2.1) и (2.2) следует

(2.3)
${\mathbf{d}} = {\mathbf{m}} + {\mathbf{p}} - \frac{1}{2}{\mathbf{m}} \cdot {\mathbf{m}} - {\mathbf{m}} \cdot {\mathbf{p}} - {\mathbf{p}} \cdot {\mathbf{m}} + {\mathbf{m}} \cdot {\mathbf{p}} \cdot {\mathbf{m}}$

Тензор m, следовательно, является только главной линейной частью тензора обратимых деформаций ${\mathbf{c}} = {\mathbf{m}} - 0.5{\mathbf{m}} \cdot {\mathbf{m}}$. Его использование в качестве меры обратимых деформаций оправдано удобствами в записи уравнения его изменения (2.1) и не только. Так следствием уравнения баланса внутренней энергии (закона сохранения энергии) можно [8] получить

(2.4)
${\mathbf{\sigma }} = \rho \frac{{\partial \Psi }}{{\partial {\mathbf{m}}}} \cdot ({\mathbf{I}} - {\mathbf{m}})$
(2.5)
$\frac{{\partial (\rho s)}}{{\partial t}} = - div{\mathbf{J}} - {{T}^{{ - 2}}}{\mathbf{q}} \cdot \nabla T + {{T}^{{ - 1}}}{\mathbf{\sigma }} \cdot \cdot {{{\mathbf{\varepsilon }}}^{p}}$

В (2.4) и (2.5) $\Psi = \Psi \left( {{\mathbf{m}},\theta } \right)$ – плотность распределения внутренней энергии; ${\mathbf{\sigma }}$ – тензор напряжений; s – плотность энтропии; ${\mathbf{q}}$ – поток тепла; ${\mathbf{J}} = \rho {\mathbf{v}}s + {\mathbf{q}}$ – поток энтропии; $\rho $ – плотность среды; принята гипотеза о независимости термодинамического потенциала $\Psi \left( {{\mathbf{m}},\theta } \right)$ от необратимых деформаций ${\mathbf{p}}$, что позволяет разделить процесс деформирования на его консервативную и диссипативную составляющие. Такая упрощающая математическая гипотеза является обычной в теории больших деформаций [32, 33].

Далее считаем, что деформируемый материал механически несжимаем; все изменение его объема сводится к тепловому расширению (сжатию). В этом случае из (2.4) следует

(2.6)
${\mathbf{\sigma }} = \left\{ \begin{gathered} - {{P}_{1}}{\mathbf{I}} + {{\left( {1 + 3\alpha {{T}_{0}}\theta } \right)}^{{ - 1}}}\frac{{\partial W}}{{\partial {\mathbf{d}}}} \cdot ({\mathbf{I}} - 2{\mathbf{d}}){\text{,}}\quad {\mathbf{p}} \equiv {\mathbf{0}} \hfill \\ - {{P}_{2}}{\mathbf{I}} + {{\left( {1 + 3\alpha {{T}_{0}}\theta } \right)}^{{ - 1}}}\frac{{\partial W}}{{\partial {\mathbf{m}}}} \cdot \left( {{\mathbf{I}} - {\mathbf{m}}} \right),\quad {\mathbf{p}} \ne {\mathbf{0}} \hfill \\ \end{gathered} \right.$

В (2.6) ${{P}_{1}}$ и ${{P}_{2}}$ – неизвестные функции добавочного давления; $W = {{\rho }_{0}}\Psi ({\mathbf{m}},\theta )$ – упругий потенциал; ${{\rho }_{0}}$ – плотность материала в его свободном состоянии. Полагая деформируемый материал изотропным, представим упругий потенциал его разложением в ряд Тейлора относительно свободного состояния [34]

(2.7)
$\begin{gathered} W = W\left( {{{J}_{1}},{{J}_{2}},\theta } \right) = - 2\mu {{J}_{1}} - \mu {{J}_{2}} + bJ_{1}^{2} + (b - \mu ){{J}_{1}}{{J}_{2}} - \chi J_{1}^{3} + {{\nu }_{1}}{{J}_{1}}\theta + \\ \, + {{\nu }_{2}}{{\theta }^{2}} - {{\nu }_{3}}{{J}_{1}}{{\theta }^{2}} - {{\nu }_{4}}J_{1}^{2}\theta - {{\nu }_{5}}{{J}_{2}}\theta - {{\nu }_{6}}{{\theta }^{3}} + ... \\ {{J}_{k}} = \left\{ \begin{gathered} {{L}_{k}}{\text{,}}\quad {\mathbf{p}} = {\mathbf{0}} \hfill \\ {{I}_{k}},\quad {\mathbf{p}} \ne {\mathbf{0}} \hfill \\ \end{gathered} \right.\quad {{L}_{1}} = tr{\mathbf{d}},\quad {{L}_{2}} = {\mathbf{d}} \cdot \cdot {\mathbf{d}},\quad {{I}_{1}} = tr{\mathbf{c}},\quad {{I}_{2}} = {\mathbf{c}} \cdot \cdot {\mathbf{c}} \\ \end{gathered} $

Здесь $\mu $ – модуль сдвига, b, $\chi $, ${{\nu }_{m}}$ ($m = 1,2,...,6$) – иные термомеханические постоянные. Если принять закон теплопроводности в простейшей форме Фурье, то из (2.5) и (2.7) следуют уравнения теплопроводности, имеющие разный вид в зависимости от режима деформирования:

в областях обратимого деформирования, которое предшествует вязкопластическому течению

(2.8)
$\begin{gathered} \left( {1 + {{\beta }_{1}}\theta + {{\beta }_{2}}tr{\mathbf{d}}} \right)\frac{{\partial \theta }}{{\partial t}} + {{\beta }_{3}}{\mathbf{\varepsilon }} \cdot \cdot {\mathbf{d}} = g\Delta \theta \\ {{\beta }_{1}} = \frac{{{{\nu }_{2}}\left( {1 - 3\alpha {{T}_{0}}} \right) - 3{{\nu }_{6}}}}{{{{\nu }_{2}}}},\quad {{\beta }_{2}} = - \frac{{{{\nu }_{3}}}}{{{{\nu }_{2}}}},\quad {{\beta }_{3}} = - \frac{{{{\nu }_{1}} + {{\nu }_{5}}}}{{{{\nu }_{2}}}} \\ \end{gathered} $

в области течения

(2.9)
$\left( {1 + {{\beta }_{1}}\theta + {{\beta }_{2}}tr{\mathbf{c}}} \right)\frac{{\partial \theta }}{{\partial t}} + {{\beta }_{3}}({\mathbf{\varepsilon }} - {{{\mathbf{\varepsilon }}}^{p}}) \cdot \cdot \,{\mathbf{c}} = g\Delta \theta - \frac{1}{{2{{\nu }_{2}}}}{\mathbf{\sigma }} \cdot \cdot \,{{{\mathbf{\varepsilon }}}^{p}}$

в областях разгрузки или повторного вязкопластического течения

(2.10)
$\left( {1 + {{\beta }_{1}}\theta + {{\beta }_{2}}tr{\mathbf{c}}} \right)\frac{{\partial \theta }}{{\partial t}} + {{\beta }_{3}}{\mathbf{\varepsilon }} \cdot \cdot \,{\mathbf{c}} = g\Delta \theta $

В (2.8)–(2.10) g – коэффициент температуропроводности.

В качестве пластического потенциала (уравнения поверхности нагружения) далее принимается [35] обобщенное условие пластического течения Треска–Сен-Венана

(2.11)
$\begin{array}{*{20}{c}} {F({\mathbf{\sigma }},\,{{{\mathbf{\varepsilon }}}^{p}}) = k,}&{F({\mathbf{\sigma }},\,{{{\mathbf{\varepsilon }}}^{p}}) = \frac{1}{2}\max \left| {{{\sigma }_{i}} - {{\sigma }_{j}}} \right| - \eta \max \left| {\varepsilon _{k}^{p}} \right|} \end{array}$
со следованием ассоциированного закона пластического течения [35, 36]

(2.12)
${{{\mathbf{\varepsilon }}}^{p}} = \zeta \frac{{\partial F}}{{\partial {\mathbf{\sigma }}}},\quad \zeta > 0$

В (2.11) и (2.12) ${{\sigma }_{i}}$, $\varepsilon _{k}^{p}$ – главные значения тензоров напряжений и скоростей пластических деформаций; k – предел текучести; $\eta $ – коэффициент вязкого сопротивления пластическому течению.

3. Постановка задачи. Обратимое деформирование. Пусть несжимаемый упруговязкопластический материал расположен в зазоре между двумя жесткими коаксиальными цилиндрами с радиусами ${{r}_{0}}$ и $R$ (${{r}_{0}} < R$). При этом внутренний цилиндр жестко закреплен, а внешний цилиндр движется равноускоренно. Решение задачи будем искать в классе функций $u = {{u}_{z}}\left( {r,t} \right)$, ${v} = {{{v}}_{z}}\left( {r,t} \right)$ в цилиндрической системе координат r, $\varphi $, z. Тогда граничные условия задачи можно записать в следующем виде

(3.1)
${{\left. {{{{v}}^{ + }}} \right|}_{{r = {{r}_{0}}}}} = {{\left. {{{u}^{ + }}} \right|}_{{r = {{r}_{0}}}}} = 0,\quad {{\left. {{{{v}}^{ + }}} \right|}_{{r = R}}} = {{{v}}_{R}} = {{a}_{1}}t,\quad {{\left. {{{u}^{ + }}} \right|}_{{r = R}}} = {{u}_{R}} = {{{{a}_{1}}{{t}^{2}}} \mathord{\left/ {\vphantom {{{{a}_{1}}{{t}^{2}}} 2}} \right. \kern-0em} 2},\quad {{\left. {{{\sigma }_{{rr}}}} \right|}_{{r = {{r}_{0}}}}} = {{a}_{0}}$

В условиях (3.1) знаком “+” обозначены скорости и перемещения граничных цилиндров, a0 и a1 – заданные постоянные, ${{\sigma }_{{rr}}}$ – радиальная компонента тензора напряжений. Последнее условие (3.1) задает напряженное состояние, вызванное начальным поджатием.

Также предполагаем, что пока выполняется условие

(3.2)
$\left| {{{\sigma }_{{rz}}}} \right| - f\left| {{{\sigma }_{{rr}}}} \right| < 0$
материал на границах $r = {{r}_{0}}$ и $r = R$ удерживается за счет сухого трения с коэффициентом f, то есть на граничных поверхностях выполняются условия прилипания.

Из соотношения (2.3) следует, что в рассматриваемом случае отличные от нуля компоненты тензора деформаций имеют вид

(3.3)
${{d}_{{rr}}} = - \frac{1}{2}u{\kern 1pt} {{'}^{2}},\quad {{d}_{{rz}}} = \frac{1}{2}u{\kern 1pt} ',\quad u{\kern 1pt} ' = \frac{{\partial u}}{{\partial r}}$

Считаем, что материал начинает деформироваться из свободного состояния и первоначально обратимо. Полагая обратимые деформации достаточно малыми и учитывая только слагаемые до второго порядка по $u{\kern 1pt} '$ включительно, из зависимостей (2.6) и (2.7) для компонент тензора напряжений получим

(3.4)
$\begin{gathered} {{\sigma }_{{rr}}} = {{\sigma }_{{\varphi \varphi }}} = - ({{P}_{1}} + 2\mu ) - \frac{1}{2}(b + \mu ){{(u{\kern 1pt} ')}^{2}} = - {{p}_{1}} \\ {{\sigma }_{{zz}}} = - {{p}_{1}} + \mu {{(u{\kern 1pt} ')}^{2}},\quad {{\sigma }_{{rz}}} = \mu u{\kern 1pt} ' \\ \end{gathered} $

Будем рассматривать задачу в рамках квазистатического подхода. Тогда из уравнений равновесия

(3.5)
$\frac{{\partial {{\sigma }_{{rr}}}}}{{\partial r}} + \frac{{\partial {{\sigma }_{{rz}}}}}{{\partial z}} + \frac{{{{\sigma }_{{rr}}} - {{\sigma }_{{\varphi \varphi }}}}}{r} = 0,\quad \frac{{\partial {{\sigma }_{{rz}}}}}{{\partial r}} + \frac{{\partial {{\sigma }_{{zz}}}}}{{\partial z}} + \frac{{{{\sigma }_{{rz}}}}}{r} = 0$
следует, что переменная ${{p}_{1}}$ является функцией только координаты z, так что p1 = = ${{l}_{0}}z - {{a}_{0}}$, где ${{l}_{0}}$ – неизвестная постоянная. Положим ${{l}_{0}} = 0$ для того, чтобы компоненты тензора напряжений ${{\sigma }_{{rr}}}$, ${{\sigma }_{{\varphi \varphi }}}$ и ${{\sigma }_{{zz}}}$ были конечными при $z \to \infty $. Таким образом, для граничных условий (3.1) решение упругой задачи примет форму

(3.6)
$\begin{gathered} {{\sigma }_{{rz}}} = \frac{c}{r},\quad {{\sigma }_{{rr}}} = {{\sigma }_{{\varphi \varphi }}} = {{a}_{0}},\quad {{\sigma }_{{zz}}} = {{a}_{0}} + \frac{{{{c}^{2}}}}{{\mu {{r}^{2}}}},\quad c = c(t) = \mu {{u}_{R}}{{\ln }^{{ - 1}}}\frac{R}{{{{r}_{0}}}} \\ u = \frac{c}{\mu }\ln \frac{r}{{{{r}_{0}}}},\quad v = \frac{{\dot {c}}}{\mu }\ln \frac{r}{{{{r}_{0}}}},\quad {{e}_{{rz}}} = \frac{c}{{2\mu r}},\quad {{e}_{{rr}}} = - \frac{3}{2}e_{{rz}}^{2},\quad {{e}_{{zz}}} = \frac{1}{2}e_{{rz}}^{2} \\ \end{gathered} $

Так как величина a0 влияет только на распределение компонент нормальных напряжений, положим ${{a}_{0}} < {k \mathord{\left/ {\vphantom {k f}} \right. \kern-0em} f}$. Тогда проскальзывание материала в окрестности внутреннего цилиндра начнется раньше, чем пластическое течение.

Увеличение со временем скорости движения внешнего цилиндра приведет к тому, что в некоторый момент времени $t = {{t}_{1}}$ на внутренней границе $r = {{r}_{0}}$ неравенство (3.2) обратится в равенство и с этого момента времени материал начнет проскальзывать в окрестности внутреннего цилиндра. В таком случае примем условие

(3.7)
${{\left. {\left( {\left| {{{\sigma }_{{rz}}}} \right| - f\left| {{{\sigma }_{{rr}}}} \right| - \xi v} \right)} \right|}_{{r = {{r}_{0}}}}} = 0,\quad t > {{t}_{1}} = \sqrt {\frac{{2f{{a}_{0}}{{r}_{0}}}}{{\mu {{a}_{1}}}}\ln \frac{{{{r}_{0}}}}{R}} $

Здесь $\xi $ – коэффициент вязкого трения. С момента времени $t = {{t}_{1}}$ материал начинает нагреваться из-за трения о жесткий внутренний цилиндр. В этом случае следует принять начальное и граничные условия для температуры

(3.8)
$\theta \left( {r,{{t}_{1}}} \right) = 0,\quad \theta ({{r}_{0}},t) = \gamma u({{r}_{0}},t),\quad \theta (R,t) = 0$

В условиях (3.8) $\gamma $ – постоянная теплопроизводства за счет трения. Будем дополнительно предполагать, что температура $\theta $ не достигнет температуры плавления в процессе деформирования.

Из соотношений (2.6) и (2.7) следуют зависимости для компонент тензора напряжений

(3.9)
$\begin{gathered} {{\sigma }_{{\varphi \varphi }}} = - \left( {{{P}_{1}} + 2\mu } \right) - {{\left( {b + \mu } \right){{{\left( {u{\kern 1pt} '} \right)}}^{2}}} \mathord{\left/ {\vphantom {{\left( {b + \mu } \right){{{\left( {u{\kern 1pt} '} \right)}}^{2}}} 2}} \right. \kern-0em} 2} + \left( {{{\nu }_{1}} + 6\mu \beta } \right)\theta - ({{\nu }_{3}} + 3\beta {{\nu }_{1}} + 18\mu {{\beta }^{2}}){{\theta }^{2}} + \\ \, + \left( {{{\nu }_{4}} + 3b\beta } \right)\theta {{\left( {u{\kern 1pt} '} \right)}^{2}} = - {{p}_{1}},\quad {{\sigma }_{{rr}}} = - {{p}_{1}} + b\theta {{\left( {u{\kern 1pt} '} \right)}^{2}},\quad {{\sigma }_{{zz}}} = - {{p}_{1}} + \mu {{\left( {u{\kern 1pt} '} \right)}^{2}} \\ {{\sigma }_{{rz}}} = \left( {\mu - l\theta } \right)u{\kern 1pt} ',\quad \beta = \alpha {{T}_{0}},\quad l = {{\nu }_{1}} + {{\nu }_{5}} + 3\mu \beta \\ \end{gathered} $

Интегрируя уравнения равновесия (3.5) и учитывая последнее условие (3.1), получим, что

(3.10)
${{\sigma }_{{rr}}} = \frac{{{{a}_{0}}{{r}_{0}}}}{r} - \frac{1}{r}\int\limits_{{{r}_{0}}}^r {{{p}_{1}}dr} $
а компонента ${{\sigma }_{{rz}}}$ удовлетворяет первой зависимости (3.6). Из соотношений (3.9), (3.10) и первой зависимости (3.6) следует формула для вычисления ${{p}_{1}}$

(3.11)
${{p}_{1}} = l{{c}^{2}}\int\limits_{{{r}_{0}}}^r {\left( {\theta {\kern 1pt} '\; - \frac{\theta }{r} + \frac{{2l\theta \theta {\kern 1pt} '}}{{\mu - l\theta }}} \right)} \frac{{dr}}{{{{{\left( {\mu - l\theta } \right)}}^{2}}{{r}^{2}}}} + \frac{{l\theta \left( {{{r}_{0}}} \right){{c}^{2}}}}{{{{{\left( {\mu - l\theta \left( {{{r}_{0}}} \right)} \right)}}^{2}}r_{0}^{2}}} - {{a}_{0}}$

Согласно соотношениям (2.3) и (3.9) компоненты обратимых деформаций и градиент перемещений имеют вид

(3.12)
${{m}_{{rz}}} = \frac{c}{{2\left( {\mu - l\theta } \right)r}},\quad {{m}_{{rr}}} = - \frac{3}{2}m_{{rz}}^{2},\quad {{m}_{{zz}}} = \frac{1}{2}m_{{rz}}^{2},\quad u{\kern 1pt} ' = \frac{c}{{\left( {\mu - l\theta } \right)r}}$

Уравнение теплопроводности (2.8) с учетом зависимостей (3.3) и (3.12) примет форму

(3.13)
$\left( {1 + {{\beta }_{1}}\theta + \frac{{{{\beta }_{3}}l{{c}^{2}}}}{{2{{{\left( {\mu - l\theta } \right)}}^{3}}{{r}^{2}}}}} \right)\dot {\theta } + \frac{{{{\beta }_{3}}c\dot {c}}}{{2{{{\left( {\mu - l\theta } \right)}}^{2}}{{r}^{2}}}} = g\left( {\theta {\kern 1pt} '{\kern 1pt} '\; + \frac{1}{r}\theta {\kern 1pt} '} \right) + {{h}_{1}}(r,t),\quad {{h}_{1}}(r,t) = 0$

Из последнего уравнения (3.12) при граничном условии (3.7) получим компоненты векторов перемещений и скорости

(3.14)
$\begin{gathered} u = c\int\limits_{{{r}_{0}}}^r {\frac{{dr}}{{\left( {\mu - l\theta } \right)r}}} + u\left( {{{r}_{0}}} \right),\quad u\left( {{{r}_{0}}} \right) = \frac{1}{{\xi {{r}_{0}}}}\int\limits_{{{t}_{1}}}^t {cdt} + \frac{{f{{a}_{0}}}}{\xi }\left( {t - {{t}_{1}}} \right) \\ v = \dot {c}\int\limits_{{{r}_{0}}}^r {\frac{{dr}}{{\left( {\mu - l\theta } \right)r}}} + lc\int\limits_{{{r}_{0}}}^r {\frac{{\dot {\theta }dr}}{{{{{\left( {\mu - l\theta } \right)}}^{2}}r}}} + \frac{c}{{\xi {{r}_{0}}}} + \frac{{f{{a}_{0}}}}{\xi } + {{h}_{2}}\left( {r,t} \right),\quad {{h}_{2}}\left( {r,t} \right) = 0 \\ \end{gathered} $

Изменение граничного условия на границе $r = {{r}_{0}}$ с (3.2) на (3.7) приводит и к изменению функции $c$ в первой зависимости (3.6) для компоненты тензора напряжений ${{\sigma }_{{rz}}}$. Используя первое соотношение (3.14), а также условие прилипания на границе $r = R$, получим уравнение для функции $c$

(3.15)
$c\int\limits_{{{r}_{0}}}^R {\frac{{dr}}{{\left( {\mu - l\theta } \right)r}}} + \frac{1}{{\xi {{r}_{0}}}}\int\limits_{{{t}_{1}}}^t {cdt} + \frac{{f{{a}_{0}}}}{\xi }\left( {t - {{t}_{1}}} \right) = {{u}_{R}} + {{h}_{3}}\left( t \right),\quad {{h}_{3}}\left( t \right) = 0$

Система уравнений (3.13) и (3.15) при условиях (3.8), а также при условии непрерывности функции c в момент времени $t = {{t}_{1}}$ решается численно с использованием конечно-разностного метода.

При дальнейшем увеличении скорости внешнего цилиндра в некоторый момент времени $t = {{t}_{2}}$ неравенство (3.2) перестает выполняться и на границе r = R. Этот момент времени можно найти из уравнения $c\left( {{{t}_{2}}} \right) = - fR{{\sigma }_{{rr}}}\left( {R,{{t}_{2}}} \right)$. Теперь материал начинает проскальзывать и соответственно разогреваться в окрестности внешнего цилиндра. Граничное условие (3.2) при r = R заменим на условие проскальзывания в виде

(3.16)
${{\left. {\left( {\left| {{{\sigma }_{{rz}}}} \right| - f\left| {{{\sigma }_{{rr}}}} \right| - \xi \left[ v \right]} \right)} \right|}_{{r = R}}} = 0,\quad \left[ v \right] = {{v}^{ + }} - v$

Также изменим второе граничное условие (3.8) на следующее

(3.17)
$\theta (R,t) = \gamma {{\left. {\left[ u \right]} \right|}_{{r = R}}},\quad \left[ u \right] = {{u}^{ + }} - u$

Изменение граничного условия на границе r = R приводит к изменению функции c, для которой из первой зависимости (3.14) и условия (3.16) следует уравнение вида (3.15) с функцией

${{h}_{3}}\left( t \right) = \frac{1}{\xi }\int\limits_{{{t}_{2}}}^t {\left( {f{{p}_{1}}\left( R \right) - \frac{c}{R} - \frac{{fl\theta \left( R \right){{c}^{2}}}}{{{{{\left( {\mu - l\theta \left( R \right)} \right)}}^{2}}{{R}^{2}}}}} \right)dt} $

Решение системы уравнений (3.11), (3.13) и (3.15) с учетом первого граничного условия (3.8), условия (3.17) и условий непрерывности температуры $\theta $ и функций ${{p}_{1}}$ и c в момент времени $t = {{t}_{2}}$ находится численно с помощью конечно-разностного метода. Перемещение и скорость точек деформируемого материала вычисляются из зависимостей (3.14) при известных функциях $\theta $ и $c$.

Найденное решение упругой неизотермической задачи при растущей скорости внешнего цилиндра будет справедливым до некоторого момента времени $t = {{t}_{3}}$, в который на внутренней границе $r = {{r}_{0}}$ впервые выполнится условие пластического течения (2.11) в следующем виде

(3.18)
${{\left. {{{\sigma }_{{rz}}}} \right|}_{{r = {{r}_{0}}}}} = k\left( {{{t}_{3}}} \right)$

В соотношении (3.18) предел текучести является зависящим от температуры. Введем эту зависимость в форме

(3.19)
$k = {{k}_{0}}{{\left( {1 - {\theta \mathord{\left/ {\vphantom {\theta {{{\theta }_{m}}}}} \right. \kern-0em} {{{\theta }_{m}}}}} \right)}^{2}},\quad {{\theta }_{m}} = {{\left( {{{T}_{m}} - {{T}_{0}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{T}_{m}} - {{T}_{0}}} \right)} {{{T}_{0}}}}} \right. \kern-0em} {{{T}_{0}}}}$

Здесь ${{T}_{m}}$ – температура плавления материала.

Момент начала пластического течения $t = {{t}_{3}}$ вычисляется из уравнения c(t3) = = $k({{t}_{3}}){{r}_{0}}$.

4. Вязкопластическое течение при возрастающей и постоянной скорости внешнего цилиндра. С момента времени $t = {{t}_{3}}$ в материале растет область вязкопластического течения ${{r}_{0}} \leqslant r \leqslant {{r}_{1}}(t)$. Здесь $r = {{r}_{1}}(t)$ – движущаяся граница, отделяющая область течения от области ${{r}_{1}}(t) \leqslant r \leqslant R$, в которой материал продолжает деформироваться обратимо и для напряжений выполняются зависимости (3.9).

Из соотношений (2.6) и (2.7) в области вязкопластического течения ${{r}_{0}} \leqslant r \leqslant {{r}_{1}}(t)$ следуют зависимости для компонент тензора напряжений

${{\sigma }_{{\varphi \varphi }}} = - \left( {{{P}_{2}} + 2\mu } \right) + 2b\left( {{{m}_{{rr}}} + {{m}_{{zz}}}} \right) - 2\mu m_{{rz}}^{2} + \left( {{{\nu }_{1}} + 6\mu \beta } \right)\theta - $
(4.1)
$\begin{gathered} \, - ({{\nu }_{3}} + 3\beta {{\nu }_{1}} + 18\mu {{\beta }^{2}}){{\theta }^{2}} - 2\left( {{{\nu }_{4}} + 3b\beta } \right)({{m}_{{rr}}} + {{m}_{{zz}}} - m_{{rz}}^{2})\theta = - {{p}_{1}} \\ {{\sigma }_{{rz}}} = 2\left( {\mu - l\theta } \right){{m}_{{rz}}},\quad {{\sigma }_{{rr}}} = - {{p}_{1}} + 2\left( {\mu - l\theta } \right){{m}_{{rr}}} + \left( {3\mu + l\theta } \right)m_{{rz}}^{2} \\ \end{gathered} $
${{\sigma }_{{zz}}} = - {{p}_{1}} + 2\left( {\mu - l\theta } \right){{m}_{{zz}}} + \left( {3\mu + l\theta } \right)m_{{rz}}^{2}$

Из уравнений равновесия (3.5) следует, что для компонент напряжений ${{\sigma }_{{rz}}}$ и ${{\sigma }_{{rr}}}$ продолжают выполняться первое соотношение (3.6) и зависимость (3.10) соответственно. Используя их и соотношения (4.1), в области пластического течения ${{r}_{0}} \leqslant r \leqslant {{r}_{1}}(t)$ получим уравнение для изменившейся функции p1

(4.2)
${{p}_{1}}r - \int\limits_{{{r}_{0}}}^r {{{p}_{1}}dr} = 2\left( {\mu - l\theta } \right)r{{m}_{{rr}}} + \frac{{\left( {3\mu + l\theta } \right){{c}^{2}}}}{{4{{{\left( {\mu - l\theta } \right)}}^{2}}r}} - {{a}_{0}}{{r}_{0}}$

В области обратимого деформирования ${{r}_{1}}(t) \leqslant r \leqslant R$ из (3.9), (3.10) и условия непрерывности напряжений следует уравнение

(4.3)
${{p}_{1}}r - \int\limits_{{{r}_{0}}}^r {{{p}_{1}}dr} = \frac{{l\theta {{c}^{2}}}}{{{{{\left( {\mu - l\theta } \right)}}^{2}}r}} - {{a}_{0}}{{r}_{0}}$

Из ассоциированного закона пластического течения (2.12) следует, что условие пластичности (2.11) в рассматриваемом случае (${{\sigma }_{{rz}}} > 0$, $\varepsilon _{{rz}}^{p} > 0$) примет вид

${{\sigma }_{{rz}}} = k + \eta \varepsilon _{{rz}}^{p}$

Отсюда с использованием первой зависимости (3.6) получаем соотношение для компоненты тензора скоростей пластических деформаций

(4.4)
$\varepsilon _{{rz}}^{p} = {{\eta }^{{ - 1}}}\left( {{c \mathord{\left/ {\vphantom {c r}} \right. \kern-0em} r} - k} \right)$

Из непрерывности напряжений следует равенство нулю компоненты $\varepsilon _{{rz}}^{p}$ на упругопластической границе $r = {{r}_{1}}(t)$. Таким образом, из (4.4) имеем

(4.5)
$c = {{r}_{1}}k\left( {{{r}_{1}}} \right)$

В рассматриваемом случае, согласно зависимостям (2.1)–(2.3), кинематика течения задается соотношениями

(4.6)
$\begin{gathered} {{d}_{{rz}}} = {{m}_{{rz}}} + {{p}_{{rz}}},\quad \frac{{d{{d}_{{rz}}}}}{{dt}} = \frac{{\partial {{d}_{{rz}}}}}{{\partial t}} = \frac{1}{2}v{\kern 1pt} ',\quad {{r}_{{rz}}} = - {{r}_{{zr}}} = \frac{{2{{\varepsilon }_{{rz}}}\left( {1 - {{m}_{{zz}}}} \right)}}{{{{m}_{{rr}}} + {{m}_{{zz}}} - 2}} \\ \varepsilon _{{rr}}^{p} = \frac{{d{{p}_{{rr}}}}}{{dt}} + 2{{p}_{{rz}}}({{r}_{{zr}}} + \varepsilon _{{rz}}^{p}),\quad \varepsilon _{{zz}}^{p} = \frac{{d{{p}_{{zz}}}}}{{dt}} + 2{{p}_{{rz}}}({{r}_{{rz}}} + \varepsilon _{{rz}}^{p}) \\ {{\varepsilon }_{{rz}}} = \frac{1}{2}v{\kern 1pt} ' = \varepsilon _{{rz}}^{e} + \varepsilon _{{rz}}^{p} = \frac{{\partial {{m}_{{rz}}}}}{{\partial t}} + \frac{{\partial {{p}_{{rz}}}}}{{\partial t}},\quad \varepsilon _{{rr}}^{p} = - \varepsilon _{{zz}}^{p} = \frac{{\varepsilon _{{rz}}^{p}}}{2}\frac{{{{m}_{{rr}}} - {{m}_{{zz}}}}}{{{{m}_{{rz}}}}} \\ \end{gathered} $

В области обратимого деформирования ${{r}_{1}}(t) \leqslant r \leqslant R$ уравнение теплопроводности имеет вид (3.13). В области вязкопластического течения ${{r}_{0}} \leqslant r \leqslant {{r}_{1}}(t)$ уравнение теплопроводности (2.9) с учетом первой зависимости (3.6), соотношений (4.1) и (4.4) примет форму (3.13) со следующей функцией ${{h}_{1}}(r,t)$

(4.7)
${{h}_{1}}(r,t) = - c\nu _{2}^{{ - 1}}{{\eta }^{{ - 1}}}{{r}^{{ - 1}}}\left( {{c \mathord{\left/ {\vphantom {c r}} \right. \kern-0em} r} - k} \right)$

Из зависимостей (4.6) и граничного условия (3.7) следует, что в области течения ${{r}_{0}} \leqslant r \leqslant {{r}_{1}}(t)$ компонента вектора скорости удовлетворяет второй зависимости (3.14) с функцией

(4.8)
${{h}_{2}}\left( {r,t} \right) = \frac{2}{\eta }\int\limits_{{{r}_{0}}}^r {\left( {\frac{c}{r} - k} \right)} dr$

С учетом непрерывности скорости на упругопластической границе получаем, что в области обратимого деформирования ${{r}_{1}}(t) \leqslant r \leqslant R$ скорость имеет вид второго соотношения (3.14) с функцией ${{h}_{2}}\left( {{{r}_{1}},t} \right)$, вычисляемой из (4.8).

Развивающаяся область течения приводит к изменению функции c, для которой из второй зависимости (3.14) и граничного условия (3.16) следует уравнение

(4.9)
$\begin{gathered} \dot {c}\int\limits_{{{r}_{0}}}^R {\frac{{dr}}{{\left( {\mu - l\theta } \right)r}}} + lc\int\limits_{{{r}_{0}}}^R {\frac{{\dot {\theta }dr}}{{{{{\left( {\mu - l\theta } \right)}}^{2}}r}}} + {{h}_{2}}\left( {{{r}_{1}},t} \right) = - \frac{c}{{\xi {{r}_{0}}}} - \frac{{f{{a}_{0}}}}{\xi } + {{v}_{R}} + {{h}_{4}}(t) \\ {{h}_{4}}(t) = - \frac{c}{{\xi R}} + \frac{{f{{p}_{1}}\left( R \right)}}{\xi } - \frac{{fl{{c}^{2}}\theta \left( R \right)}}{{\xi {{{\left( {\mu - l\theta \left( R \right)} \right)}}^{2}}{{R}^{2}}}} \\ \end{gathered} $

Из соотношений (4.6) при условии отсутствия необратимых деформаций в момент времени $t = {{t}_{3}}$ следует выражение для компоненты тензора пластических деформаций

(4.10)
${{p}_{{rz}}} = \int\limits_{{{t}_{3}}}^t {\varepsilon _{{rz}}^{p}dt} $

Для неизвестных компонент тензоров обратимых деформаций ${{m}_{{rr}}}$, mzz и необратимых деформаций ${{p}_{{rr}}}$, ${{p}_{{zz}}}$ в области ${{r}_{0}} \leqslant r \leqslant {{r}_{1}}(t)$ из соотношений (3.3) и (4.6) получим систему уравнений

(4.11)
$\begin{gathered} \frac{{\partial {{p}_{{zz}}}}}{{\partial t}} = \varepsilon _{{rz}}^{p}\left( {{{m}_{{rz}}} - \frac{{{{p}_{{zz}}}}}{{{{m}_{{rz}}}}}} \right) + \frac{{4(\varepsilon _{{rz}}^{e} + \varepsilon _{{rz}}^{p}){{p}_{{rz}}}}}{{2 + m_{{rz}}^{2}}}\left( {1 + {{p}_{{zz}}} - \frac{{m_{{rz}}^{2}}}{2} - 2{{m}_{{rz}}}{{p}_{{rz}}}} \right) \\ {{p}_{{rr}}} = - {{p}_{{zz}}} - 2p_{{rz}}^{2},\quad {{m}_{{zz}}} = - {{p}_{{zz}}} + \frac{{m_{{rz}}^{2}}}{2} + 2{{m}_{{rz}}}{{p}_{{rz}}},\quad {{m}_{{rr}}} = - {{m}_{{zz}}} - m_{{rz}}^{2} \\ \end{gathered} $

Уравнения (3.13), (4.2), (4.3), (4.5), (4.9) и (4.11) для неизвестных функций $\theta $, ${{p}_{1}}$, ${{r}_{1}}$, c, ${{m}_{{rr}}}$, ${{m}_{{zz}}}$, ${{p}_{{rr}}}$ и ${{p}_{{zz}}}$ решаются одновременно с использованием второго условия (3.8) и условия (3.17). Также предполагается непрерывность функций $\theta $, ${{p}_{1}}$ и c в момент времени $t = {{t}_{3}}$ и непрерывность температуры и теплового потока на упругопластической границе $r = {{r}_{1}}(t)$. Для решения этой системы разработана конечно-разностная схема первого порядка по времени и второго – по пространству, учитывающая движущуюся упругопластическую границу и изменяющиеся области необратимого и обратимого деформирования.

Из (4.6) следует, что градиент перемещений в области пластического течения ${{r}_{0}} \leqslant r \leqslant {{r}_{1}}(t)$ имеет вид

(4.12)
$u{\kern 1pt} ' = 2\left( {{{m}_{{rz}}} + {{p}_{{rz}}}} \right)$

Интегрируя это уравнение при втором условии (3.14), найдем компоненту вектора перемещений в области течения. В области обратимого деформирования ${{r}_{1}}(t) \leqslant r \leqslant R$ также выполняется уравнение (4.12) при условии равенства нулю компоненты ${{p}_{{rz}}}$. Из этого уравнения находим перемещения с учетом их непрерывности на упругопластической границе $r = {{r}_{1}}(t)$.

Пусть с момента времени $t = {{t}_{4}}$ скорость внешнего цилиндра становится постоянной, т.е. ${{v}_{R}} = {{a}_{1}}{{t}_{4}}$. Такое изменение граничного условия не приводит к качественному изменению деформационного процесса. В материале по-прежнему присутствуют область обратимого деформирования и развивающаяся область вязкопластического течения. Все соотношения данного раздела остаются верными и в данном случае.

5. Течение при убывающей скорости внешнего цилиндра. Разгрузка среды и охлаждение. В некоторый момент времени $t = {{t}_{5}} > {{t}_{4}}$ начнем снижать скорость внешнего цилиндра по закону ${{v}_{R}} = {{a}_{1}}{{t}_{4}} - {{a}_{2}}\left( {t - {{t}_{5}}} \right)$. Поначалу такое изменение в режиме нагружения не вносит никаких качественных изменений в процесс деформирования. Все соотношения предыдущего раздела продолжают выполняться. Область вязкопластического течения продолжает увеличиваться, однако скорость движения упругопластической границы $r = {{r}_{1}}(t)$ падает и в некоторый расчетный момент времени $t = {{t}_{6}}$ становится равной нулю.

С момента времени $t = {{t}_{6}}$ упругопластическая граница $r = {{r}_{1}}(t)$ начинает двигаться в обратную сторону к внутреннему цилиндру $r = {{r}_{0}}$. В деформируемом материале появляется новая область ${{r}_{1}}(t) \leqslant r \leqslant {{r}_{1}}\left( {{{t}_{6}}} \right)$, в которой компонента тензора скоростей пластических деформаций $\varepsilon _{{rz}}^{p}$ равна нулю, и, следовательно, компонента тензора пластических деформаций ${{p}_{{rz}}}$ не изменяется в этой области. В сужающейся области ${{r}_{0}}\, \leqslant \,r\, \leqslant \,{{r}_{1}}(t)$ по-прежнему продолжается вязкопластическое течение, а в области ${{r}_{1}}({{t}_{6}})\, \leqslant \,r\, \leqslant \,R$ материал деформируется обратимо.

Для компонент тензора напряжений в области обратимого деформирования ${{r}_{1}}({{t}_{6}}) \leqslant r \leqslant R$ продолжают выполняться соотношения (3.9), а в областях ${{r}_{0}} \leqslant r \leqslant {{r}_{1}}(t)$ и ${{r}_{1}}(t) \leqslant r \leqslant {{r}_{1}}\left( {{{t}_{6}}} \right)$ компоненты напряжений удовлетворяют зависимостям (4.1). С другой стороны, следуя уравнениям равновесия (3.5) с учетом условия непрерывности напряжений, получим, что для компонент ${{\sigma }_{{rz}}}$ и ${{\sigma }_{{rr}}}$ остаются справедливыми первое соотношение (3.6) и зависимость (3.10) во всех трех областях. Сравнив соотношения для напряжений, получим, что функция ${{p}_{1}}$ в областях ${{r}_{0}} \leqslant r \leqslant {{r}_{1}}(t)$ и ${{r}_{1}}(t) \leqslant r \leqslant {{r}_{1}}\left( {{{t}_{6}}} \right)$ имеет вид (4.2), а в области ${{r}_{1}}\left( {{{t}_{6}}} \right) \leqslant r \leqslant R$ – (4.3).

Уравнение (4.5) для упругопластической границы $r = {{r}_{1}}(t)$ также остается верным. Уравнение теплопроводности во всех трех областях имеет вид (3.13), причем, в областях ${{r}_{1}}(t) \leqslant r \leqslant {{r}_{1}}\left( {{{t}_{6}}} \right)$ и ${{r}_{1}}\left( {{{t}_{6}}} \right) \leqslant r \leqslant R$ функция ${{h}_{1}}(r,t) = 0$, а в области течения ${{r}_{0}} \leqslant r \leqslant {{r}_{1}}(t)$ функция ${{h}_{1}}(r,t)$ имеет вид (4.7). Функция $c$ по-прежнему удовлетворяет уравнению (4.9).

Для определения неизвестных компонент тензоров обратимых деформаций ${{m}_{{rr}}}$, mzz и необратимых деформаций ${{p}_{{rr}}}$, pzz в области течения ${{r}_{0}} \leqslant r \leqslant {{r}_{1}}(t)$ служит система уравнений (4.11), в которой $\varepsilon _{{rz}}^{p}$ и ${{p}_{{rz}}}$ определяются из зависимостей (4.4) и (4.10). В области ${{r}_{1}}(t) \leqslant r \leqslant {{r}_{1}}\left( {{{t}_{6}}} \right)$ неизвестные компоненты тензоров обратимых деформаций ${{m}_{{rr}}}$, mzz и необратимых деформаций ${{p}_{{rr}}}$, pzz также удовлетворяют системе уравнений (4.11), в которой $\varepsilon _{{rz}}^{p} = 0$, а для компоненты тензора необратимых деформаций ${{p}_{{rz}}}$ следует уравнение

(5.1)
$\frac{{\partial {{p}_{{rz}}}}}{{\partial t}} = 0$

Градиент перемещений в областях ${{r}_{0}} \leqslant r \leqslant {{r}_{1}}(t)$ и ${{r}_{1}}(t) \leqslant r \leqslant {{r}_{1}}\left( {{{t}_{6}}} \right)$ имеет вид (4.12). В области обратимого деформирования ${{r}_{1}}\left( {{{t}_{6}}} \right) \leqslant r \leqslant R$ градиент перемещений также удовлетворяет уравнению (4.12) при ${{p}_{{rz}}} = 0$.

В некоторый момент времени $t = {{t}_{7}}$ на внешней поверхности материала $r = R$ выполнится равенство ${{\left. {\left( {\left| {{{\sigma }_{{rz}}}} \right| - f\left| {{{\sigma }_{{rr}}}} \right|} \right)} \right|}_{{r = R}}} = 0$. Условие проскальзывания (3.16) далее не выполняется, напряжения вновь связаны неравенством (3.2). Нагревание материала за счет трения прекращается, поскольку снова выполняется условие прилипания внешней граничной поверхности материала с жестким цилиндром. Поэтому граничное условие для температуры (3.17) заменим следующим:

(5.2)
${{\left. {\left( {\delta \theta {\kern 1pt} '\; + h\theta } \right)} \right|}_{{r = R}}} = 0$
в котором $\delta $ и h – коэффициент теплопроводности и коэффициент теплоотдачи материала соответственно.

Изменение граничного условия на внешней границе r = R приводит к изменению функции $c$, для которой из второго соотношения (3.14) и условия прилипания следует уравнение (4.9) с функцией ${{h}_{4}}(t) = 0$.

При дальнейшем уменьшении скорости внешнего цилиндра в расчетный момент времени $t = {{t}_{8}}$ упругопластическая граница $r = {{r}_{1}}(t)$ совпадает с внутренней поверхностью $r = {{r}_{0}}$. С этого момента времени в материале остается две области: область обратимого деформирования ${{r}_{1}}\left( {{{t}_{6}}} \right) \leqslant r \leqslant R$ и область ${{r}_{0}} \leqslant r \leqslant {{r}_{1}}\left( {{{t}_{6}}} \right)$, в которой не изменяется компонента тензора необратимых деформаций ${{p}_{{rz}}}$. В этих областях уравнение теплопроводности имеет вид (3.13), функция ${{p}_{1}}$ в области ${{r}_{0}} \leqslant r \leqslant {{r}_{1}}\left( {{{t}_{6}}} \right)$ удовлетворяет соотношению (4.2), а в области ${{r}_{1}}\left( {{{t}_{6}}} \right) \leqslant r \leqslant R$ – (4.3). Для функции $c$ выполняется уравнение (4.9) при ${{h}_{4}}(t) = 0$. В области ${{r}_{0}} \leqslant r \leqslant {{r}_{1}}\left( {{{t}_{6}}} \right)$ компоненты ${{m}_{{rr}}}$, ${{m}_{{zz}}}$, ${{p}_{{rr}}}$, ${{p}_{{zz}}}$ и ${{p}_{{rz}}}$ вычисляются из зависимостей (4.11) и (5.1). Для нахождения перемещений в области ${{r}_{0}} \leqslant r \leqslant {{r}_{1}}\left( {{{t}_{6}}} \right)$ служит уравнение (4.12). Из этого же уравнения можно найти перемещения в области обратимого деформирования при ${{p}_{{rz}}} = 0$.

Расчеты проводились в безразмерных переменных $x = {r \mathord{\left/ {\vphantom {r R}} \right. \kern-0em} R}$ и $\tau = t\sqrt {{{{{a}_{1}}} \mathord{\left/ {\vphantom {{{{a}_{1}}} R}} \right. \kern-0em} R}} $ при следующих значениях постоянных: ${{{{r}_{0}}} \mathord{\left/ {\vphantom {{{{r}_{0}}} R}} \right. \kern-0em} R} = 0.1$, ${{{{a}_{0}}} \mathord{\left/ {\vphantom {{{{a}_{0}}} \mu }} \right. \kern-0em} \mu } = - 4.08 \times {{10}^{{ - 4}}}$, ${{{{k}_{0}}} \mathord{\left/ {\vphantom {{{{k}_{0}}} \mu }} \right. \kern-0em} \mu } = 2.63$ × 10–3, $f = 0.2$, ${{\beta }_{1}} = 0.379$, ${{\beta }_{3}} = - 0.558$, ${{\theta }_{m}} = 2.18$, $q{{R}^{{ - 1}}}\sqrt {a_{1}^{{ - 1}}{{R}^{{ - 1}}}} = 21.06$, $\mu {{\xi }^{{ - 1}}}\sqrt {a_{1}^{{ - 1}}{{R}^{{ - 1}}}} = 219.13$, $\mu {{\eta }^{{ - 1}}}\sqrt {a_{1}^{{ - 1}}R} $ = 525.9, ${l \mathord{\left/ {\vphantom {l \mu }} \right. \kern-0em} \mu } = 0.3$, ${{{{v}_{2}}} \mathord{\left/ {\vphantom {{{{v}_{2}}} \mu }} \right. \kern-0em} \mu } = 0.5$, $\gamma R = 10$, ${{{{a}_{2}}} \mathord{\left/ {\vphantom {{{{a}_{2}}} {{{a}_{1}}}}} \right. \kern-0em} {{{a}_{1}}}} = 2$, ${{hR} \mathord{\left/ {\vphantom {{hR} \delta }} \right. \kern-0em} \delta } = 12$.

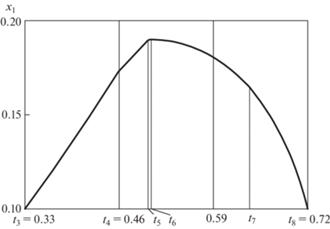
На рис. 1 представлен график изменения упругопластической границы ${{x}_{1}} = {{{{r}_{1}}} \mathord{\left/ {\vphantom {{{{r}_{1}}} R}} \right. \kern-0em} R}$ в зависимости от безразмерного времени τ в интервале от τ3 до τ8.

Рис. 1.

График упругопластической границы.

В момент времени $t = {{t}_{9}} = {{a}_{1}}a_{2}^{{ - 1}}{{t}_{4}} + {{t}_{5}}$ внешний цилиндр останавливается. Для функции $c$ в данном случае следует уравнение (4.9), в котором ${{h}_{4}}(t) = 0$ и ${{v}_{R}} = 0$.

Далее в момент времени $t = {{t}_{{10}}}$ теперь уже и на внутренней границе $r = {{r}_{0}}$ выполнится равенство ${{\left. {\left( {\left| {{{\sigma }_{{rz}}}} \right| - f\left| {{{\sigma }_{{rr}}}} \right|} \right)} \right|}_{{r = {{r}_{0}}}}} = 0$. Скорость во всем деформируемом слое становится равной нулю, а функция $c$ перестает изменяться. Теперь материал начинает остывать во всем слое. Уравнение теплопроводности во всем слое примет вид

$\left( {1 + {{\beta }_{1}}\theta + \frac{{{{\beta }_{3}}l{{c}^{2}}}}{{2{{{\left( {\mu - l\theta } \right)}}^{3}}{{r}^{2}}}}} \right)\dot {\theta } = g\left( {\theta {\kern 1pt} '{\kern 1pt} '\; + \frac{1}{r}\theta {\kern 1pt} '} \right)$

Первое граничное условие из (3.8) для этого уравнения изменим на условие

${{\left. {\theta {\kern 1pt} '} \right|}_{{r = {{r}_{0}}}}} = 0$

А на границе $r = R$ по-прежнему выполняется граничное условие (5.2). С течением времени материал полностью остынет. После полного остывания напряжения, деформации и перемещения перестают изменяться. Дальнейшая разгрузка связана с уменьшением напряжения ${{\sigma }_{{rr}}}$ на границе $r = {{r}_{0}}$ до нуля.

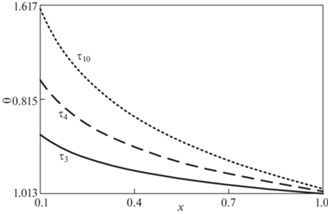
Распределения температуры $\theta $ в момент начала пластического течения ${{\tau }_{3}}$, в момент времени ${{\tau }_{4}}$, когда скорость внешнего цилиндра становится постоянной, и в момент времени ${{\tau }_{{10}}} = 0.8$, когда на внутренней границе снова выполняется условие прилипания, показаны на рис. 2.

Рис. 2.

Распределение температуры по слою в разные моменты времени.

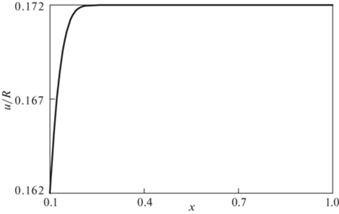
Рис. 3 иллюстрирует перемещения точек деформируемого слоя в конечный момент времени.

Рис. 3.

Перемещения точек материала в конечный момент времени.

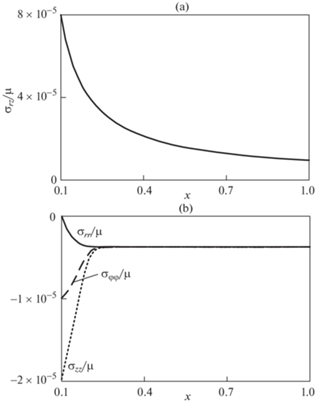
Компонента остаточных напряжений ${{{{\sigma }_{{rz}}}} \mathord{\left/ {\vphantom {{{{\sigma }_{{rz}}}} \mu }} \right. \kern-0em} \mu }$ показана на рис. 4, a. На рис. 4, b представлены остаточные напряжения ${{{{\sigma }_{{rr}}}} \mathord{\left/ {\vphantom {{{{\sigma }_{{rr}}}} \mu }} \right. \kern-0em} \mu }$, ${{{{\sigma }_{{\phi \phi }}}} \mathord{\left/ {\vphantom {{{{\sigma }_{{\phi \phi }}}} \mu }} \right. \kern-0em} \mu }$ и ${{{{\sigma }_{{zz}}}} \mathord{\left/ {\vphantom {{{{\sigma }_{{zz}}}} \mu }} \right. \kern-0em} \mu }$ сплошной, штриховой и пунктирной линиями соответственно.

Рис. 4.

Распределение по слою остаточных напряжений.

6. Заключение. Здесь рассмотрен процесс развития и торможения вязкопластического течения материала с учетом его обратимого деформирования и теплопередачи в нем вне области течения. Учитывается теплотворная способность деформирования и разогрев материала в условиях его проскальзывания по граничной поверхности. Добиться результатов таких расчетов существенно помогли дифференциальные уравнения изменения тензоров обратимых и необратимых деформаций. С их помощью в расчетах удалось избежать достаточно трудных алгоритмических приемов, связанных, например, с проецированием (радиальным вращением) напряжений на поверхность нагружения [32]. Используемый здесь подход не ограничивает в задании иных определяющих законов, не вводит новые постоянные или функции модели, ограничиваясь преимущественно классическими. При необходимости расширения модели это можно сделать. Для этого следует ввести кроме обратимых и необратимых деформаций и температуры новые термодинамические параметры состояния, например, повреждаемость, и сформулировать для них соответствующие дифференциальные уравнения изменения.

В названии статьи [29], где впервые на основе [30, 31] были записаны дифференциальные уравнения изменения обратимых и необратимых деформаций вида (2.1) и (2.2), включено “простая модель”. Представлялось, что эти уравнения будут записаны по-иному, для разных случаев, посредством других подходов. Этого до настоящего времени не произошло, надеемся, что все же произойдет. Представляемые возможности для решения краевых задач теории больших необратимых деформаций, примером чему является настоящая статья, обязаны привлечь внимание к развитию данного подхода.

Список литературы

  1. Мясников В.П. Некоторые точные решения для прямолинейных движений вязкопластической среды // ПМТФ. 1961. № 2. С. 79–86.

  2. Мосолов П.П., Мясников В.П. Вариационные методы в теории течений жестковязкопластических сред. М.: МГУ, 1971. 163 с.

  3. Огибалов П.М., Мирзаджанзаде А.Х. Нестационарные движения вязкопластических сред. М.: МГУ, 1970. 415 с.

  4. Мосолов П.П., Мясников В.П. Механика жесткопластических сред. М.: Наука, 1981. 208 с.

  5. Быковцев Г.И., Чернышов А.Д. О вязкопластическом течении в некруговых цилиндрах при наличии перепада давления // ПМТФ. 1964. № 4. С. 94–96.

  6. Георгиевский Д.В. Жесткие зоны в статически определимых и неопределимых задачах вязкопластического течения // Проблемы механики деформируемых твердых тел и горных пород. Сб. статей к 75-летию Е.И. Шемякина. М.: Физматлит, 2006. С. 135–141.

  7. Левитас В.И. Большие упругопластические деформации материалов при высоком давлении. Киев: Наукова думка, 1987. 232 с.

  8. Буренин А.А., Ковтанюк Л.В. Большие необратимые деформации и упругое последействие. Владивосток: Дальнаука, 2013. 312 с.

  9. Роговой А.А. Формализованный подход к построению моделей механики деформируемого твердого тела. Часть 1. Основные соотношения механики сплошных сред. Пермь: УрО РАН, 2020. 288 с.

  10. Ковтанюк Л.В. О продавливании упруговязкопластического материала через жесткую круговую цилиндрическую матрицу // ДАН. 2005. Т. 400. № 6. С. 764–766.

  11. Буренин А.А., Ковтанюк Л.В., Мазелис А.Л. Развитие и торможение прямолинейного осесимметричного вязкопластического течения и упругое последействие после его остановки // ПМТФ. 2010. Т. 51. № 2. С. 140–147.

  12. Буренин А.А., Ковтанюк Л.В. Об упругих деформациях и вязкопластическом течении в тяжелом слое, помещенном на наклонной плоскости // Изв. РАН. МТТ. 2010. № 2. С. 158–170.

  13. Буренин А.А., Ковтанюк Л.В., Лушпей А.В. Переходный процесс торможения прямолинейного вязкопластического течения при мгновенном снятии нагружающих усилий // ПММ. 2009. Т. 73. № 3. С. 494–500.

  14. Олейников А.И., Пекарш А.И. Интегрированное проектирование процессов изготовления монолитных панелей. М.: Эком, 2009. 109 с.

  15. Бегун А.С., Буренин А.А., Ковтанюк Л.В. Большие необратимые деформации в условиях изменяющихся механизмов их производства и проблема задания пластических потенциалов // ДАН. 2016. Т. 470. № 3. С. 275–278. https://doi.org/10.7868/S0869565216270086

  16. Prokudin A.N., Firsov S.V.  Antiplane strain of hardening elastoviscoplastic medium // J. Siber. Federal Uni. Math. Phys. 2018. V. 11. I. 4. P. 399–410. https://doi.org/10.17516/1997-1397-2018-11-4-399-410

  17. Begun A.S., Burenin A.A., Kovtanyuk L.V., Lemza A.O. On the mechanisms of production of large irreversible strains in materials with elastic, viscous and plastic properties // Arch. Appl. Mech. 2020. V. 90. I. 4. P. 829–845. https://doi.org/10.1007/s00419-019-01641-x

  18. Kovtanyuk L.V., Panchenko G.L. Mathematical modelling of the production process of irreversible strains under the heating and cooling of a flat heavy layer on an inclined surface // Lobachevskii J Math. 2021. V. 42. I. 8. P. 1998–2005. https://doi.org/10.1134/S1995080221080163

  19. Ковтанюк Л.В. Моделирование больших упругопластических деформаций в неизотермическом случае // Дальневост. мат. ж. 2004. № 1. С. 107–117.

  20. Xiao H., Bruhns O. T., Meyers A. Thermodynamic laws and consistent Eulerian formulation of finite elastoplasticity with thermal effects // J. Mech. Phys. Solids. 2007. V. 55. I. 2. P. 338–365. https://doi.org/10.1016/j.jmps.2006.07.005

  21. Canadija M., Mosler J. On the thermomechanical coupling in finite strain plasticity theory with non-linear kinematic hardening by means of incremental energy minimization // Int. J. Solids Struct. 2011. V. 48. I. 7–8. P. 1120–1129.

  22. Junker P., Hackl K. A thermo-mechanically coupled field model for shape memory alloys // Contin. Mech. Thermodyn. 2014. V. 26. I. 6. P. 859–877. https://doi.org/10.1007/s00161-014-0345-x

  23. Zhu Y., Kang G., Kan Q., Bruhns O.T., Liu Y. Thermo-mechanically coupled cyclic elasto-viscoplastic constitutive model of metals: Theory and application // Int. J. Plasticity. 2016. V. 79. P. 111–152. https://doi.org/10.1016/j.ijplas.2015.12.005

  24. Буренин А.А., Ковтанюк Л.В., Панченко Г.Л. Моделирование больших упруговязкопластических деформаций с учетом теплофизических эффектов // Изв. РАН. МТТ. 2010. № 4. С. 107–120.

  25. Буренин А.А., Ковтанюк Л.В., Панченко Г.Л. Неизотермическое движение упруговязкопластической среды в трубе в условиях изменяющегося перепада давления // ДАН. 2015. Т. 464. № 3. С. 284–287. https://doi.org/10.7868/S0869565215270080

  26. Буренин А.А., Ковтанюк Л.В., Панченко Г.Л. Развитие и торможение вязкопластического течения в слое при его нагреве за счет трения о шероховатую плоскость // ПМТФ. 2015. Т. 56. № 4 (332). С. 101–111. https://doi.org/10.15372/PMTF20150410

  27. Буренин А.А., Ковтанюк Л.В., Панченко Г.Л. Деформирование и разогрев упруговязкопластического цилиндрического слоя при его движении за счет изменяющегося перепада давления // Изв. РАН. МТТ. 2018. № 1. С. 6–18.

  28. Буренин А.А., Ковтанюк Л.В., Панченко Г.Л. Движение упруговязкопластической среды в круглой трубе при ее нагреве за счет пристеночного трения // ПММ. 2016. Т. 80. № 2. С. 265–275.

  29. Буренин А.А., Быковцев Г.И., Ковтанюк Л.В. Об одной простой модели для упругопластической среды при конечных деформациях // Докл. РАН. 1996. Т. 347. № 2. С. 199–201.

  30. Быковцев Г.И., Шитиков А.В. Конечные деформации упругопластических сред // Докл. АН СССР. 1990. Т. 311. № 1. С. 59–62.

  31. Мясников В.П. Уравнения движения упругопластических материалов при больших деформациях // Вестн. ДВО РАН. 1996. № 4. С. 8–13.

  32. Голованов А.И., Султанов Л.У. Математические модели вычислительной нелинейной механики деформируемых сред. Казань: Изд-во КГУ, 2009. 465 с.

  33. Чернышов А.Д. Определяющие уравнения для упругопластического тела при конечных деформациях // Изв. РАН. МТТ. 2000. № 1. С. 120–128.

  34. Лурье А.И. Нелинейная теория упругости. М.: Наука, 1980. 512 с.

  35. Ишлинский А.Ю., Ивлев Д.Д. Математическая теория пластичности. М.: Физматлит, 2001. 704 с.

  36. Быковцев Г.И., Ивлев Д.Д. Теория пластичности. Владивосток: Дальнаука, 1998. 528 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика твердого тела

Архивы выпусков Информация о журнале Отправить рукопись в журнал