Известия РАН. Механика твердого тела, 2022, № 6, стр. 28-40

УЧЕТ НЕЛИНЕЙНОСТИ КОЛЕБАНИЙ РЕЗОНАТОРОВ ПРИ ИДЕНТИФИКАЦИИ ПАРАМЕТРОВ ВОЛНОВЫХ ТВЕРДОТЕЛЬНЫХ ГИРОСКОПОВ РАЗНЫХ ТИПОВ

А. А. Маслов^a, *, Д. А. Маслов^a, **, И. В. Меркурьев^a, ***

^a Национальный исследовательский университет “МЭИ”
Москва, Россия

^* E-mail: MaslovAlA@mpei.ru
^** E-mail: MaslovDmA@mpei.ru
^*** E-mail: MerkuryevIV@mpei.ru

Поступила в редакцию 24.12.2021
После доработки 26.12.2021
Принята к публикации 27.12.2021

EDN: BWSHFH
DOI: 10.31857/S0572329922050099

Аннотация

Рассматривается учет нелинейности колебаний резонаторов в методиках идентификации параметров волновых твердотельных гироскопов. Определяемыми являются параметры, характеризующие демпфирование, анизотропию демпфирования, разночастотность, а также коэффициенты нелинейности математических моделей динамики резонаторов волновых твердотельных гироскопов. В зависимости от типа резонаторов и датчиков управления предлагаются методики идентификации параметров в режимах свободного выбега и вынужденных колебаний с учетом разных типов нелинейностей: нелинейностей третьей, пятой степени, нелинейности, влияющей на управление. Даны алгоритмы определения оценок параметров и их доверительных интервалов при случайных погрешностях измерений. По результатам обработки данных показано, что учет нелинейности колебаний резонаторов существенно повышает точность определения параметров волновых твердотельных гироскопов. Приведены уравнения, показывающие влияние коэффициентов нелинейности и параметров, характеризующих разночастотность и анизотропию демпфирования, на угловую скорость дрейфа гироскопа.

Ключевые слова: волновой твердотельный гироскоп, идентификация параметров, нелинейные колебания, дрейф гироскопа

1. Введение. В настоящее время волновые твердотельные гироскопы (ВТГ) находят широкое применение в качестве датчиков инерциальной информации навигационных систем, причем масштаб исследований и разработок ВТГ в ближайшее время будет расширяться, способствуя повышению точности гироскопов [1, 2]. Задача идентификации параметров резонатора ВТГ является одной из задач, решение которой направленно на повышение точности ВТГ.

Основы теории ВТГ заложены в работах Д.М. Климова и В.Ф. Журавлева [3–7]. В [4, 7] показано, что погрешность, вызванная нелинейными свойствами колебательной системы, присуща всем ВТГ, а исследование динамики может проводиться в рамках одних и тех же уравнений, аналогичных уравнениям классического маятника Фуко. Вопросы идентификации погрешностей изготовления резонаторов ВТГ рассмотрены в [4, 7–13]. В указанных работах при определении параметров гироскопа использовались линейные уравнения малых колебаний резонатора. В [14–16] отмечено, что при экспериментальных исследованиях динамики вибрационных гироскопов были обнаружены явления, характерные для нелинейных систем, например, срыв колебаний в режиме вынужденных колебаний. Пренебрежение нелинейностью возможно лишь при малых амплитудах колебаний, при которых отношение сигнала к шуму недостаточно высокое. Для его повышения следует увеличивать амплитуду колебаний, однако при этом возрастают погрешности, вызванные нелинейностью. В [17–22] предложены методики определения параметров ВТГ с кольцевым и цилиндрическим резонаторами при учете нелинейности. Идентификация может выполняться в режиме свободного выбега, в режиме вынужденных колебаний и в режиме управляемой прецессии [23]. У кварцевых полусферических и цилиндрических резонаторов, обладающих высокой добротностью, ширина резонанса мала для снятия данных при регулировании частотной настройки, а время затухания колебаний велико и достаточно для снятия данных в режиме свободного выбега. Для резонаторов с меньшей добротностью, например, кольцевых резонаторов микромеханических ВТГ, время затухания мало, но есть возможность снимать данные при разных значениях частотной настройки в режиме вынужденных колебаний.

В данной статье уточняются и обобщаются результаты предшествующих работ по учету нелинейности в методиках идентификации параметров ВТГ путем введения коэффициентов нелинейности в определяемые параметры [17–22]. Ставятся задачи обобщить учет нелинейностей третьей и пятой степени на методику идентификации параметров в режиме свободного выбега, определить классы гироскопов и типы нелинейностей для применения методик идентификации параметров, показать влияние определяемых параметров на угловую скорость дрейфа ВТГ.

Найденные при идентификации параметры, включая технологические погрешности изготовления резонатора и коэффициенты нелинейности, могут использоваться для повышения точности определения угловой скорости в методиках компенсации погрешностей [24] или для повышения точности балансировки резонаторов [25, 26].

2. Определение параметров ВТГ в режиме свободного выбега. Рассматривается ВТГ с кварцевым резонатором, представленным упругой осесимметричной оболочкой вращения. Обычно подобные резонаторы изготавливаются в виде полусферы или цилиндра и обладают малыми потерями на внутреннее трение, соответственно, имеют высокую добротность. Поэтому для ВТГ с кварцевым резонатором в виде оболочки вращения рассмотрим идентификацию параметров в режиме свободного выбега.

В [27] выведены уравнения динамики цилиндрического резонатора ВТГ с учетом нелинейных свойств электростатических датчиков управления, которые представляют собой конденсаторы, образованные металлизированной поверхностью резонатора и электродами, расположенными вблизи свободной кромки резонатора,

(2.1)

$\begin{gathered} \ddot {f} + {{\omega }^{2}}f = - \gamma \dot {f} + {v}\dot {g} + \\ + \;\eta \left( {3({{f}^{2}} + {{g}^{2}})f + \frac{{15}}{4}{{{({{f}^{2}} + {{g}^{2}})}}^{2}}f + (1 + 3{{f}^{2}})( - {{u}_{1}}\sin {{\omega }_{0}}t + {{u}_{2}}\cos {{\omega }_{0}}t)} \right) - \\ - \;\frac{\eta }{2}((u_{1}^{2} - u_{2}^{2})\cos 2{{\omega }_{0}}t + 2{{u}_{1}}{{u}_{2}}\sin 2{{\omega }_{0}}t)f \\ \ddot {g} + {{\omega }^{2}}g = - \gamma \dot {g} - {v}\dot {f} + \\ + \;\eta \left( {3({{f}^{2}} + {{g}^{2}})g + \frac{{15}}{4}{{{({{f}^{2}} + {{g}^{2}})}}^{2}}g + (1 + 3{{g}^{2}})( - {{u}_{3}}\sin {{\omega }_{0}}t + {{u}_{4}}\cos {{\omega }_{0}}t)} \right) - \\ - \;\frac{\eta }{2}((u_{3}^{2} - u_{4}^{2})\cos 2{{\omega }_{0}}t + 2{{u}_{3}}{{u}_{4}}\sin 2{{\omega }_{0}}t)g \\ \end{gathered} $

где f, g – обобщенные координаты второй основной формы колебаний резонатора; ω – характерная частота собственных колебаний; γ – коэффициент демпфирования; v – параметр, характеризующий угловую скорость основания гироскопа; η – коэффициент, характеризующий нелинейность, вызванную электростатическими датчиками управления [27]; ${{u}_{1}}$, ${{u}_{2}}$, ${{u}_{3}}$, ${{u}_{4}}$ – нормализованные управляющие напряжения, ω₀ – частота внешнего гармонического возбуждения колебаний резонатора. Заметим, что слагаемые с кубической нелинейностью свойственны уравнениям динамики резонаторов гироскопов класса обобщенного маятника Фуко [7] и были получены в [7] для классического маятника Фуко, а в [13] в предположении о том, что для материала резонатора справедлив нелинейный закон упругости. Поэтому введем единые коэффициенты ξ и $\kappa $ при, соответственно, нелинейностях третьей и пятой степени, обусловленных различными факторами. Так как рассматривается режим свободного выбега, положим в (2.1) нулевое управление. Получим уравнения

(2.2)

$\begin{gathered} \ddot {f} + {{\omega }^{2}}f = - \gamma \dot {f} + {v}\dot {g} + \xi ({{f}^{2}} + {{g}^{2}})f + \kappa {{({{f}^{2}} + {{g}^{2}})}^{2}}f \\ \ddot {g} + {{\omega }^{2}}g = - \gamma \dot {g} - {v}\dot {f} + \xi ({{f}^{2}} + {{g}^{2}})g + \kappa {{({{f}^{2}} + {{g}^{2}})}^{2}}g \\ \end{gathered} $

В [4, 7, 8] проведен анализ сил, являющихся следствием разнообразных дефектов резонатора, и вызываемой этими силами эволюции формы колебаний резонатора. С учетом наиболее общего [4] представления действующих на резонатор возмущений, нелинейные уравнения динамики (2.2) могут быть записаны в следующем виде:

(2.3)

$\begin{gathered} \ddot {f} + {{\omega }^{2}}f = - (\gamma + {{b}_{c}})\dot {f} - ( - \nu + {{b}_{s}})\dot {g} - ({{c}_{m}} + {{h}_{c}})f - (n + {{h}_{s}})g + \\ + \;\xi ({{f}^{2}} + {{g}^{2}})f + \kappa {{({{f}^{2}} + {{g}^{2}})}^{2}}f \\ \ddot {g} + {{\omega }^{2}}g = - (\gamma - {{b}_{c}})\dot {g} - (\nu + {{b}_{s}})\dot {f} - ({{c}_{m}} - {{h}_{c}})g - ( - n + {{h}_{s}})f + \\ \, + \xi ({{f}^{2}} + {{g}^{2}})g + \kappa {{({{f}^{2}} + {{g}^{2}})}^{2}}g \\ \end{gathered} $

где с_m и n – параметры позиционных сил; ${{h}_{s}} = {{h}_{m}}\sin 4\alpha $, ${{h}_{c}} = {{h}_{m}}\cos 4\alpha $ и ${{b}_{s}} = {{b}_{m}}\sin 4\beta ,$ ${{b}_{c}} = {{b}_{m}}\cos 4\beta $ – параметры, характеризующие разночастотность и анизотропию демпфирования соответственно, h_m, b_m – модули разночастотности и анизотропии демпфирования, α и β – углы ориентации главных осей жесткости и диссипации относительно отсчетных осей.

Используя метод осреднения Крылова–Боголюбова [28] и переменные Ван-дер-Поля, с помощью замены

(2.4)

$\begin{gathered} f = {{p}_{1}}\sin \omega t + {{q}_{1}}\cos \omega t,\quad \dot {f} = \omega ({{p}_{1}}\cos \omega t - {{q}_{1}}\sin \omega t) \\ g = {{p}_{2}}\sin \omega t + {{q}_{2}}\cos \omega t,\quad \dot {g} = \omega ({{p}_{2}}\cos \omega t - {{q}_{2}}\sin \omega t) \\ \end{gathered} $

можно получить из (2.3), осредненную систему дифференциальных уравнений в медленных переменных:

(2.5)

$\begin{gathered} 2{{{\dot {q}}}_{1}} = - \gamma {{q}_{1}} - {{b}_{c}}{{q}_{1}} + \nu {{q}_{2}} - {{b}_{s}}{{q}_{2}} + {{{\tilde {c}}}_{m}}{{p}_{1}} + {{{\tilde {h}}}_{c}}{{p}_{1}} + \tilde {n}{{p}_{2}} + {{{\tilde {h}}}_{s}}{{p}_{2}} + \tilde {\xi }{{k}_{1}} + \tilde {\kappa }{{k}_{5}} \\ 2{{{\dot {p}}}_{1}} = - \gamma {{p}_{1}} - {{b}_{c}}{{p}_{1}} + \nu {{p}_{2}} - {{b}_{s}}{{p}_{2}} - {{{\tilde {c}}}_{m}}{{q}_{1}} - {{{\tilde {h}}}_{c}}{{q}_{1}} - \tilde {n}{{q}_{2}} - {{{\tilde {h}}}_{s}}{{q}_{2}} + \tilde {\xi }{{k}_{2}} + \tilde {\kappa }{{k}_{6}} \\ 2{{{\dot {q}}}_{2}} = - \gamma {{q}_{2}} + {{b}_{c}}{{q}_{2}} - \nu {{q}_{1}} - {{b}_{s}}{{q}_{1}} + {{{\tilde {c}}}_{m}}{{p}_{2}} - {{{\tilde {h}}}_{c}}{{p}_{2}} - \tilde {n}{{p}_{1}} + {{{\tilde {h}}}_{s}}{{p}_{1}} + \tilde {\xi }{{k}_{3}} + \tilde {\kappa }{{k}_{7}} \\ 2{{{\dot {p}}}_{2}} = - \gamma {{p}_{2}} + {{b}_{c}}{{p}_{2}} - \nu {{p}_{1}} - {{b}_{s}}{{p}_{1}} - {{{\tilde {c}}}_{m}}{{q}_{2}} + {{{\tilde {h}}}_{c}}{{q}_{2}} + \tilde {n}{{q}_{1}} - {{{\tilde {h}}}_{s}}{{q}_{1}} + \tilde {\xi }{{k}_{4}} + \tilde {\kappa }{{k}_{8}} \\ \end{gathered} $

где $\tilde {\xi } = \xi {\text{/}}\omega $, $\tilde {\kappa } = \kappa {\text{/}}\omega $, ${{\tilde {h}}_{c}} = h_{c}^{{}}{\text{/}}\omega $, ${{\tilde {h}}_{s}} = {{h}_{s}}{\text{/}}\omega $, ${{\tilde {c}}_{m}} = {{c}_{m}}{\text{/}}\omega $, $\tilde {n} = n{\text{/}}\omega $, осредненные нелинейные выражения ${{k}_{1}} - {{k}_{8}}$ заданы формулами:

$k_{1}^{{}} = - {{p}_{1}}E - {{q}_{2}}X,\quad {{k}_{2}} = {{q}_{1}}E - {{p}_{2}}X,\quad {{k}_{3}} = - {{p}_{2}}E + {{q}_{1}}X,\quad {{k}_{4}} = {{q}_{2}}E + {{p}_{1}}X$

$E = 3(q_{1}^{2} + p_{1}^{2} + q_{2}^{2} + p_{2}^{2}){\text{/}}4,\quad X = ({{p}_{2}}{{q}_{1}} - {{p}_{1}}{{q}_{2}}){\text{/}}2$

$\begin{gathered} {{k}_{5}} = - \frac{1}{{16}}(5p_{1}^{5} + 12p_{1}^{2}{{p}_{2}}{{q}_{1}}{{q}_{2}} + 4{{p}_{2}}{{q}_{1}}{{q}_{2}}(p_{2}^{2} + q_{1}^{2} + q_{2}^{2}) + 2p_{1}^{3}(5(p_{2}^{2} + q_{1}^{2}) + q_{2}^{2}) + \\ + \;{{p}_{1}}\left. {(5p_{2}^{4} + 6p_{2}^{2}q_{1}^{2} + 5q_{1}^{4} + 6(p_{2}^{2} + q_{1}^{2})q_{2}^{2} + q_{2}^{4})} \right) \\ \end{gathered} $

$\begin{gathered} {{k}_{6}} = \frac{1}{{16}}(5p_{1}^{4}{{q}_{1}} + 4p_{1}^{3}{{p}_{2}}{{q}_{2}} + 4{{p}_{1}}{{p}_{2}}{{q}_{2}}(p_{2}^{2} + 3q_{1}^{2} + q_{2}^{2}) + \\ + \;2p_{1}^{2}{{q}_{1}}(3p_{2}^{2} + 5q_{1}^{2} + 3q_{2}^{2}) + {{q}_{1}})(p_{2}^{4} + 5{{(q_{1}^{2} + q_{2}^{2})}^{2}} + 2p_{2}^{2}(q_{1}^{2} + 3q_{2}^{2})) \\ \end{gathered} $

$\begin{gathered} {{k}_{7}} = - \frac{1}{{16}}({{p}_{2}}(5{{(p_{1}^{2} + p_{2}^{2})}^{2}} + 2(3p_{1}^{2} + p_{2}^{2})q_{1}^{2} + q_{1}^{4}) + 4{{p}_{1}}{{q}_{1}}(p_{1}^{2} + 3p_{2}^{2} + q_{1}^{2}){{q}_{2}} + \\ + \;2{{p}_{2}}(3p_{1}^{2} + 5p_{2}^{2} + 3q_{1}^{2})q_{2}^{2} + 4{{p}_{1}}{{q}_{1}}q_{2}^{3} + 5{{p}_{2}}q_{2}^{4}) \\ \end{gathered} $

$\begin{gathered} {{k}_{8}} = \frac{1}{{16}}(4p_{1}^{3}{{p}_{2}}{{q}_{1}} + p_{1}^{4}{{q}_{2}} + 2p_{1}^{2}{{q}_{2}}(3(p_{2}^{2} + q_{1}^{2}) + q_{2}^{2}) + 4{{p}_{1}}{{p}_{2}}{{q}_{1}}(p_{2}^{2} + q_{1}^{2} + 3q_{2}^{2}) + \\ + \;{{q}_{2}}(5p_{2}^{4} + 5{{(q_{1}^{2} + q_{2}^{2})}^{2}} + 2p_{2}^{2}(3q_{1}^{2} + 5q_{2}^{2}))) \\ \end{gathered} $

Заметим, что в электронном контуре гироскопа физически реализуется схема осреднения [13]: с помощью емкостной системы электродов измеряются высокочастотные функции времени f(t), g(t) и с помощью контуров обработки сигналов выделяются огибающие ${{q}_{1}}(t),$ ${{p}_{1}}(t),$ ${{q}_{2}}(t),$ ${{p}_{2}}(t)$. Таким образом, медленные переменные ${{q}_{1}}(t),$ ${{p}_{1}}(t),$ ${{q}_{2}}(t),$ ${{p}_{2}}(t)$ системы (2.5) являются измеряемыми.

Запишем систему (2.5) в векторно-матричном виде:

(2.6)

$\dot {q} = \frac{1}{2}{\mathbf{D}} \cdot z$

где вектор медленных переменных

$q(t) = {{\left( {{{q}_{1}}(t),{{p}_{1}}(t),{{q}_{2}}(t),{{p}_{2}}(t)} \right)}^{{\text{т}}}}$

матрицу D и вектор определяемых параметров z задаем в блочной форме:

${\mathbf{D}} = \left( {{{{\mathbf{D}}}_{\gamma }}\left| {{{{\mathbf{D}}}_{\xi }}} \right|{{{\mathbf{D}}}_{\kappa }}} \right)$

${\mathbf{D}}_{\gamma }^{{}} = \left( {\begin{array}{*{20}{c}} { - {{q}_{1}}}&{{{q}_{2}}}&{ - {{q}_{1}}}&{ - {{q}_{2}}}&{{{p}_{1}}}&{{{p}_{2}}}&{{{p}_{1}}}&{{{p}_{2}}} \\ { - {{p}_{1}}}&{{{p}_{2}}}&{ - {{p}_{1}}}&{ - {{p}_{2}}}&{ - {{q}_{1}}}&{ - {{q}_{2}}}&{ - {{q}_{1}}}&{ - {{q}_{2}}} \\ { - {{q}_{2}}}&{ - {{q}_{1}}}&{{{q}_{2}}}&{ - {{q}_{1}}}&{{{p}_{2}}}&{ - {{p}_{1}}}&{ - {{p}_{2}}}&{{{p}_{1}}} \\ { - {{p}_{2}}}&{ - {{p}_{1}}}&{{{p}_{2}}}&{ - {{p}_{1}}}&{ - {{q}_{2}}}&{{{q}_{1}}}&{{{q}_{2}}}&{ - {{q}_{1}}} \end{array}} \right),\quad {\mathbf{D}}_{\xi }^{{}} = \left( {\begin{array}{*{20}{c}} {{{k}_{1}}} \\ {{{k}_{2}}} \\ {{{k}_{3}}} \\ {{{k}_{4}}} \end{array}} \right),\quad {\mathbf{D}}_{\kappa }^{{}} = \left( {\begin{array}{*{20}{c}} {{{k}_{5}}} \\ {{{k}_{6}}} \\ {{{k}_{7}}} \\ {{{k}_{8}}} \end{array}} \right)$

${\mathbf{z}} = {{({\mathbf{z}}_{\gamma }^{{\text{т}}}\;\tilde {\xi }\;\tilde {\kappa })}^{{\text{т}}}},\quad {{{\mathbf{z}}}_{\gamma }} = {{(\gamma ,\nu ,{{b}_{c}},{{b}_{s}},{{\tilde {c}}_{m}},\tilde {n},{{\tilde {h}}_{c}},{{\tilde {h}}_{s}})}^{{\text{т}}}}$

С помощью данной записи, в зависимости от количества блоков, мы можем записать как линейную математическую модель, так и обе нелинейные математические модели: с кубической нелинейностью (коэффициент нелинейности $\tilde {\xi }$, k = 9 параметров) и с нелинейностью пятой степени (два коэффициента нелинейности $\tilde {\xi }$ и $\tilde {\kappa }$, k = 10 параметров).

Начальным моментом съема данных является момент отключения управляющего напряжения в режиме стационарных колебаний. Для обработки данных, берется массив значений затухающих медленных переменных так, чтобы в конце процесса была достаточная амплитуда колебаний для отличия их от случайных помех. Лучше брать начальный участок процесса затухания колебаний, на котором наибольшим образом изменяются медленные переменные. Обозначим отрезок времени наблюдений [0, T] и разобьем его на N равных частей: ${{t}_{i}} = i \cdot {{h}_{t}},$ ${{h}_{t}} = T{\text{/}}N$ – шаг по времени, $i = 0 \ldots N$. Определяемые параметры считаем постоянными на [0, T].

Интегрируем левую и правую часть (2.6) на отрезках $\left[ {{{t}_{{i - 1}}},{{t}_{{i + 1}}}} \right]$:

(2.7)

$q({{t}_{{i + 1}}}) - q({{t}_{{i - 1}}}) = \frac{1}{2}{{{\mathbf{D}}}_{i}} \cdot z,\quad i = 1,\;2,\; \ldots ,\;N - 1$

где интегралы, обозначенные как

${{{\mathbf{D}}}_{i}} = \int\limits_{{{t}_{{i - 1}}}}^{{{t}_{{i + 1}}}} {{\mathbf{D}}\left( {q(t)} \right)} dt,\quad i = 1,\;2,\; \ldots ,\;N - 1$

вычисляются от элементов матриц численно, например по формуле Симпсона. Таким образом, систему (2.6), дискретизированную на отрезке [0, T] и представленную системами (2.7), записываем в виде переопределенной системы линейных алгебраических уравнений:

(2.8)

${\mathbf{y}} = {\mathbf{\bar {D}}} \cdot z + {\mathbf{e}}{\text{ }}$

где введены составные матрица ${\mathbf{\bar {D}}}$ и вектор y:

$\begin{gathered} {\mathbf{\bar {D}}} = {{({\mathbf{D}}_{1}^{{\text{т}}},{\mathbf{D}}_{2}^{{\text{т}}},\; \ldots ,\;{\mathbf{D}}_{{N - 1}}^{{\text{т}}})}^{{\text{т}}}},\quad {\mathbf{y}} = {{({\mathbf{y}}_{1}^{{\text{т}}},{\mathbf{y}}_{2}^{{\text{т}}},\; \ldots ,\;{\mathbf{y}}_{{N - 1}}^{{\text{т}}})}^{{\text{т}}}} \\ {{{\mathbf{y}}}_{i}} = q({{t}_{{i + 1}}}) - q({{t}_{{i - 1}}}),\quad i = 1,\;2,\; \ldots ,\;N - 1 \\ \end{gathered} $

${\mathbf{e}} \sim N({\mathbf{0}},\sigma _{e}^{2}{\mathbf{E}})$ – вектор некоррелированных случайных ошибок измерений, подчиняющихся нормальному закону распределения с нулевым средним и одинаковыми дисперсиями.

Рассмотрим сначала оценку вектора параметров z по методу наименьших квадратов. Тогда для линейной регрессии (2.8) получим оценку:

(2.9)

${\mathbf{\hat {z}}} = {{({{{\mathbf{\bar {D}}}}^{{\text{т}}}}{\mathbf{\bar {D}}})}^{{ - 1}}}{{{\mathbf{\bar {D}}}}^{{\text{т}}}}{\mathbf{y}}$

при условии, что матрица ${{{\mathbf{\bar {D}}}}^{{\text{т}}}}{\mathbf{\bar {D}}}$ не является вырожденной.

Оценка (2.9) минимизирует сумму квадратов отклонений $S = {{({\mathbf{y}} - {\mathbf{\bar {D}\hat {z}}})}^{{\text{т}}}}({\mathbf{y}} - {\mathbf{\bar {D}\hat {z}}}).$ Оценка среднеквадратического отклонения:

(2.10)

$\hat {\sigma } = \sqrt {\frac{S}{{n - k}}} $

где n = 4(N – 2) – размерность вектора измерений y, k – число определяемых параметров.

Доверительные интервалы для определяемых параметров оцениваем по формуле [29]:

(2.11)

${{\hat {z}}_{j}} - {{s}_{p}}\hat {\sigma }\sqrt {{{c}_{{jj}}}} \leqslant {{z}_{j}} \leqslant {{\hat {z}}_{j}} + {{s}_{p}}\hat {\sigma }\sqrt {{{c}_{{jj}}}} ,\quad j = 1\; \ldots \;k$

где ${{c}_{{jj}}}$ – диагональные элементы матрицы ${\mathbf{C}} = {{({{{\mathbf{\bar {D}}}}^{{\text{т}}}}{\mathbf{\bar {D}}})}^{{ - 1}}}$, s_p – квантиль порядка p = = $(1 + {{P}_{0}}){\text{/}}2$ распределения Стьюдента c n – k степенями свободы, ${{P}_{{\text{0}}}}$ – доверительная вероятность. Если число n – k мало, то s_p выбирают по таблице распределения Стьюдента, если n – k > 30, то s_p можно выбирать из таблицы функций Лапласа.

Получаемые в результате измерений данные поступают последовательно, поэтому целесообразно рассмотреть для данной методики применение рекуррентного метода наименьших квадратов.

Пусть на некотором начальном этапе измерений выбран отрезок времени $[0,{{t}_{m}}]$, где m много меньше N. Для инициализации рекуррентного метода наименьших квадратов определяем оценку параметров по методу наименьших квадратов (2.10):

${{{\mathbf{\hat {z}}}}_{{(m)}}} = {{{\mathbf{P}}}_{{(m)}}}{\mathbf{D}}_{{(m)}}^{{\text{т}}}{\mathbf{y}}$

где введены ${{{\mathbf{P}}}_{{(m)}}} = {{({\mathbf{D}}_{{(m)}}^{{\text{т}}}{{{\mathbf{D}}}_{{(m)}}})}^{{ - 1}}}$ – матрица размера $k \cdot k$, ${{{\mathbf{D}}}_{{(m)}}} = {{({\mathbf{D}}_{1}^{{\text{т}}},{\mathbf{D}}_{2}^{{\text{т}}},\; \ldots ,\;{\mathbf{D}}_{m}^{{\text{т}}})}^{{\text{т}}}}$ – матрица размера $4m \cdot k$, ${{{\mathbf{y}}}_{{(m)}}} = {{({\mathbf{y}}_{1}^{{\text{т}}},{\mathbf{y}}_{2}^{{\text{т}}},\; \ldots ,\;{\mathbf{y}}_{m}^{{\text{т}}})}^{{\text{т}}}}$ – вектор размерности $4m$, ${{{\mathbf{\hat {z}}}}_{{(m)}}}$ – вектор размерности k. После инициализации первого приближения к решению и ковариационной матрице, определяем последующие приближения итерационным алгоритмом:

(2.12)

$\begin{gathered} {{{\mathbf{S}}}_{{i + 1}}} = {{{\mathbf{P}}}_{i}}{{{\mathbf{r}}}_{i}}({\mathbf{E}} - {{({\mathbf{E}} + {\mathbf{r}}_{i}^{{\text{т}}}{{{\mathbf{P}}}_{i}}{{{\mathbf{r}}}_{i}})}^{{ - 1}}}{\mathbf{r}}_{i}^{{\text{т}}}{{{\mathbf{P}}}_{i}}{{{\mathbf{r}}}_{i}}) \\ {{{{\mathbf{\hat {z}}}}}_{{i + 1}}} = {{{{\mathbf{\hat {z}}}}}_{i}} + {{{\mathbf{S}}}_{{i + 1}}} \cdot \left( {{{{\mathbf{y}}}_{{i + 1}}} - {{{{\mathbf{\hat {y}}}}}_{{i + 1}}}} \right) \\ {{{\mathbf{P}}}_{{i + 1}}} = {{{\mathbf{P}}}_{i}} - {{{\mathbf{S}}}_{{i + 1}}}{\mathbf{r}}_{i}^{{\text{т}}}{{{\mathbf{P}}}_{i}} \\ \end{gathered} $

${\text{ }}i = m,m + 1,\; \ldots ,\;N - 1$

где Е – единичная матрица размера $4 \times 4$, ${{{\mathbf{r}}}_{i}} = {\mathbf{D}}_{i}^{{\text{т}}}$ – матрица размера $k \cdot 4$, ${{{\mathbf{P}}}_{i}}$ – матрица размера $k \cdot k$, ${{{\mathbf{S}}}_{{i + 1}}}$ – матрица размера $k \cdot 4$, ${{{\mathbf{\hat {y}}}}_{{i + 1}}} = {{{\mathbf{D}}}_{i}}{{{\mathbf{\hat {z}}}}_{i}}$ – вектор размерности 4. Данный алгоритм, в котором на каждой итерации ${{{\mathbf{r}}}_{i}}$ является матрицей, а не вектором, обусловлен использованием на каждом шаге измерений четырех медленных переменных. Поэтому в данном случае результат произведения ${\mathbf{r}}_{i}^{{\text{т}}}{{{\mathbf{P}}}_{i}}{{{\mathbf{r}}}_{i}}$ является матрицей, а не скаляром и оценку среднеквадратичного отклонения вычисляем по следующей формуле:

$\hat {\sigma }_{{}}^{2} = \sigma _{e}^{2} \cdot \left( {1 + \mathop {\max }\limits_{1 \leqslant j \leqslant k} \sqrt {{{\lambda }_{j}}({{{{\mathbf{\tilde {P}}}}}^{{\text{т}}}}{\mathbf{\tilde {P}}})} } \right)$

где σ_e – среднеквадратическое отклонение случайных погрешностей измерений медленных переменных, ${{\lambda }_{j}}({{{\mathbf{\tilde {P}}}}^{{\text{т}}}}{\mathbf{\tilde {P}}})$ – собственные значения произведения матриц ${{{\mathbf{\tilde {P}}}}^{{\text{т}}}}$ и ${\mathbf{\tilde {P}}}$, $j = 1\; \ldots \;k$, обозначаем ${\mathbf{\tilde {P}}} = {\mathbf{r}}_{i}^{{\text{т}}}{{{\mathbf{P}}}_{i}}{{{\mathbf{r}}}_{i}}$. Для расчета доверительных интервалов параметров могут использоваться формулы (2.11), с матрицей C = P.

3. Определение параметров ВТГ в режиме вынужденных колебаний. Значения добротности у кольцевых резонаторов микромеханических ВТГ значительно ниже, чем у рассмотренных ранее полусферических и цилиндрических резонаторов прецизионных ВТГ. Поэтому продолжительность свободного выбега микромеханического ВТГ недостаточна для проведения идентификации параметров, и нужно рассматривать данные, полученные в режиме вынужденных колебаний при разных значениях частотной настройки вблизи резонанса. Волновые твердотельные гироскопы в микромеханическом исполнении обычно имеют кольцевой резонатор с магнитоэлектрическими датчиками управления, реже – с электростатическими датчиками управления [13]. Предлагаемая методика может использоваться для определения параметров ВТГ и с другими типами резонаторов в случае, если есть возможность провести достаточное количество измерений медленных переменных на резонансном пике при изменении частотной настройки.

При использовании в ВТГ электростатических датчиков управления, уравнения вынужденных колебаний имеют вид аналогичный (2.1), запишем их с коэффициентами, учитывающими разные типы нелинейностей:

(3.1)

$\begin{gathered} \ddot {f} + {{\omega }^{2}}f = - \gamma \dot {f} + {v}\dot {g} + \xi ({{f}^{2}} + {{g}^{2}})f + \\ + \;\kappa {{({{f}^{2}} + {{g}^{2}})}^{2}}f + \eta (1 + 3\mu {{f}^{2}})( - {{u}_{1}}\sin {{\omega }_{0}}t + {{u}_{2}}\cos {{\omega }_{0}}t) \\ \ddot {g} + {{\omega }^{2}}g = - \gamma \dot {g} - {v}\dot {f} + \xi ({{f}^{2}} + {{g}^{2}})g + \\ + \;\kappa {{({{f}^{2}} + {{g}^{2}})}^{2}}g + \eta (1 + 3\mu {{g}^{2}})( - {{u}_{3}}\sin {{\omega }_{0}}t + {{u}_{4}}\cos {{\omega }_{0}}t) \\ \end{gathered} $

При использовании магнитоэлектрических датчиков управления введенный параметр μ = 0, коэффициенты ξ, $\kappa $, η определяются не нелинейностью, вызванной электростатическими датчиками управления, а другими факторами [13]. Поэтому предложим методику идентификации с возможностью учитывать разные типы нелинейностей.

Аналогично (2.3) вводя в (3.1) возмущения, вызванные дефектами резонатора, и осредняя полученные уравнения, выведем уравнения в медленных переменных:

(3.2)

$\begin{gathered} 2{{{\dot {p}}}_{1}} = - \gamma {{p}_{1}} - {{b}_{c}}{{p}_{1}} + \nu {{p}_{2}} - {{b}_{s}}{{p}_{2}} - {{{\tilde {c}}}_{m}}{{q}_{1}} - {{{\tilde {h}}}_{c}}{{q}_{1}} - \tilde {n}{{q}_{2}} - {{{\tilde {h}}}_{s}}{{q}_{2}} + \hfill \\ ~~~~~~~~~~~~~~~~ + \;2\lambda {{q}_{1}} + \tilde {\xi }{{k}_{2}} + \tilde {\kappa }{{k}_{6}} + {{{\tilde {u}}}_{2}}\left( {1 + \mu {{k}_{{12}}}} \right) + \mu {{{\tilde {u}}}_{1}}{{k}_{9}} \hfill \\ 2{{{\dot {q}}}_{2}} = - \gamma {{q}_{2}} + {{b}_{c}}{{q}_{2}} - \nu {{q}_{1}} - {{b}_{s}}{{q}_{1}} + {{{\tilde {c}}}_{m}}{{p}_{2}} - {{{\tilde {h}}}_{c}}{{p}_{2}} - \tilde {n}{{p}_{1}} + {{{\tilde {h}}}_{s}}{{p}_{1}} - \hfill \\ ~~~~~~~~~~~~~~~~ - \;2\lambda {{p}_{2}} + \tilde {\xi }{{k}_{3}} + \tilde {\kappa }{{k}_{7}} + {{{\tilde {u}}}_{3}}\left( {1 + \mu {{k}_{{13}}}} \right) + \mu {{{\tilde {u}}}_{4}}{{k}_{{10}}} \hfill \\ \end{gathered} $

$\begin{gathered} 2{{{\dot {p}}}_{2}} = - \gamma {{p}_{2}} + {{b}_{c}}{{p}_{2}} - \nu {{p}_{1}} - {{b}_{s}}{{p}_{1}} - {{{\tilde {c}}}_{m}}{{q}_{2}} + {{{\tilde {h}}}_{c}}{{q}_{2}} + \tilde {n}{{q}_{1}} - {{{\tilde {h}}}_{s}}{{q}_{1}} + \\ ~ + \;2\lambda {{q}_{2}} + \tilde {\xi }{{k}_{4}} + \tilde {\kappa }{{k}_{8}} + {{{\tilde {u}}}_{4}}\left( {1 + \mu {{k}_{{14}}}} \right) + \mu {{{\tilde {u}}}_{3}}{{k}_{{10}}} \\ \end{gathered} $

где $\lambda = {{\omega }_{0}} - \omega $ − частотная настройка, ${{\tilde {u}}_{i}} = \eta {{u}_{i}}{\text{/}}\omega $, $i = 1,2,3,4$; $k_{9}^{{}} = - 3{{q}_{1}}{{p}_{1}}{\text{/}}2$, k₁₀ = = $ - 3{{q}_{2}}{{p}_{2}}{\text{/}}2$

$\begin{gathered} k_{{11}}^{{}} = 3(3p_{1}^{2} + q_{1}^{2}){\text{/}}4,\quad {{k}_{{12}}} = 3(p_{1}^{2} + 3q_{1}^{2}){\text{/}}4 \\ {{k}_{{13}}} = 3(3p_{2}^{2} + q_{2}^{2}){\text{/}}4,\quad {{k}_{{14}}} = 3(p_{2}^{2} + 3q_{2}^{2}){\text{/}}4 \\ \end{gathered} $

Остальные обозначения в (3.2) аналогичны введенным после уравнений (2.5) и (2.6).

Запишем (3.2) в векторно-матричном виде:

(3.3)

$\dot {q} = \frac{1}{2}({\mathbf{D}} \cdot z - {\mathbf{y}})$

$q(t) = {{\left( {{{q}_{1}}(t),{{p}_{1}}(t),{{q}_{2}}(t),{{p}_{2}}(t)} \right)}^{{\text{т}}}}$

${\mathbf{z}} = {{({\mathbf{z}}_{\gamma }^{T}\,\,{\mathbf{z}}_{u}^{T}\,\,\tilde {\xi }\,\,\,\tilde {\kappa }\,)}^{T}},\,\,$ ${{{\mathbf{z}}}_{\gamma }} = {{(\gamma ,\,\,\nu ,\,\,{{b}_{c}},\,\,{{b}_{s}},\,\,{{\tilde {c}}_{m}},\,\,\tilde {n},\,\,{{\tilde {h}}_{c}},\,\,{{\tilde {h}}_{s}})}^{T}},$ ${{{\mathbf{z}}}_{u}} = {{({{\tilde {u}}_{1}},\,\,{{\tilde {u}}_{2}},\,\,{{\tilde {u}}_{3}},\,\,{{\tilde {u}}_{4}})}^{T}}$

${\mathbf{D}} = \left( {{{{\mathbf{D}}}_{\gamma }}|{{{\mathbf{D}}}_{u}}|{{{\mathbf{D}}}_{\xi }}|{{{\mathbf{D}}}_{\kappa }}} \right)$, ${{{\mathbf{D}}}_{u}} = {\mathbf{E}} + \alpha \cdot {{{\mathbf{D}}}_{n}},\,$ ${\mathbf{E}} = {\text{diag}}\{ 1,\;1,\;1,\;1\} $ – единичная матрица

${\mathbf{D}}_{\gamma }^{{}} = \left( {\begin{array}{*{20}{c}} { - {{q}_{1}}}&{{{q}_{2}}}&{ - {{q}_{1}}}&{ - {{q}_{2}}}&{{{p}_{1}}}&{{{p}_{2}}}&{{{p}_{1}}}&{{{p}_{2}}} \\ { - {{p}_{1}}}&{{{p}_{2}}}&{ - {{p}_{1}}}&{ - {{p}_{2}}}&{ - {{q}_{1}}}&{ - {{q}_{2}}}&{ - {{q}_{1}}}&{ - {{q}_{2}}} \\ { - {{q}_{2}}}&{ - {{q}_{1}}}&{{{q}_{2}}}&{ - {{q}_{1}}}&{{{p}_{2}}}&{ - {{p}_{1}}}&{ - {{p}_{2}}}&{{{p}_{1}}} \\ { - {{p}_{2}}}&{ - {{p}_{1}}}&{{{p}_{2}}}&{ - {{p}_{1}}}&{ - {{q}_{2}}}&{{{q}_{1}}}&{{{q}_{2}}}&{ - {{q}_{1}}} \end{array}} \right),\quad {\mathbf{D}}_{n}^{{}} = \left( {\begin{array}{*{20}{c}} {{{k}_{{11}}}}&{{{k}_{9}}}&0&0 \\ {{{k}_{9}}}&{{{k}_{{12}}}}&0&0 \\ 0&0&{{{k}_{{13}}}}&{{{k}_{{10}}}} \\ 0&0&{{{k}_{{10}}}}&{{{k}_{{14}}}} \end{array}} \right)$

${\mathbf{D}}_{\xi }^{{}} = \left( {\begin{array}{*{20}{c}} {{{k}_{1}}} \\ {{{k}_{2}}} \\ {{{k}_{3}}} \\ {{{k}_{4}}} \end{array}} \right),\quad {\mathbf{D}}_{\kappa }^{{}} = \left( {\begin{array}{*{20}{c}} {{{k}_{5}}} \\ {{{k}_{6}}} \\ {{{k}_{7}}} \\ {{{k}_{8}}} \end{array}} \right),\quad {\mathbf{y}} = 2\lambda \cdot \left( {\begin{array}{*{20}{c}} {{{p}_{1}}} \\ { - {{q}_{1}}} \\ {{{p}_{2}}} \\ { - {{q}_{2}}} \end{array}} \right)$

Для идентификации параметров рассмотрим стационарные режимы вынужденных колебаний резонатора, ${{\dot {q}}_{1}} = \,{{\dot {p}}_{1}} = {{\dot {q}}_{2}} = {{\dot {p}}_{2}} = 0$. Стационарные значения медленных переменных ${{q}_{1}}(t),$ ${{p}_{1}}(t),$ ${{q}_{2}}(t),$ ${{p}_{2}}(t)$ являются измеряемыми и соответствуют разным значениям частотной настройки $\lambda = {{\lambda }_{j}}$, где $j = 1,\; \ldots ,\;N$, N – число стационарных режимов колебаний резонатора. Соответствующие ${{\lambda }_{j}}$ стационарные системы уравнений (3.3) являются алгебраическими и имеют вид

(3.4)

${{{\mathbf{y}}}_{j}} = {{{\mathbf{D}}}_{j}} \cdot {\mathbf{z}} + {{{\mathbf{e}}}_{j}},\quad j = 1,\; \ldots ,\;N$

где ${{{\mathbf{e}}}_{j}} \sim N({\mathbf{0}},\sigma _{e}^{2}{\mathbf{E}})$.

Далее составим переопределенную систему линейных алгебраических уравнений из N блоков (3.4), соответствующих заданным частотным настройкам

(3.5)

${\mathbf{y}} = {\mathbf{\bar {D}z}} + {\mathbf{e}}$

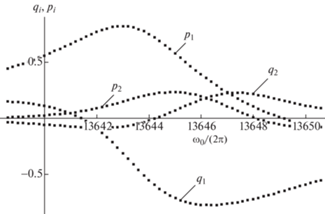
${\mathbf{\bar {D}}} = {{({\mathbf{D}}_{1}^{{\text{т}}},{\mathbf{D}}_{2}^{{\text{т}}},\; \ldots ,\;{\mathbf{D}}_{N}^{{\text{т}}})}^{{\text{т}}}},y = {{(y_{1}^{{\text{т}}},y_{2}^{{\text{т}}},\; \ldots ,\;y_{N}^{{\text{т}}})}^{{\text{т}}}},e = {{(e_{1}^{{\text{т}}},e_{2}^{{\text{т}}},\; \ldots ,\;e_{N}^{{\text{т}}})}^{{\text{т}}}}$. Размерность векторов ${\mathbf{y}}$ и ${\mathbf{e}}$ равняется числу уравнений переопределенной системы $n = 4N,$ размерность вектора z равняется числу идентифицируемых параметров k. Минимальное число измерений, необходимое для определения возможного числа k < 15 параметров, N = 4 задает 16 уравнений в системе (3.5). Оценка вектора параметров z может быть найдена по методу наименьших квадратов (2.9), оценки доверительных интервалов для параметров – по формуле (2.11).

4. Обработка экспериментальных данных. Рассматривались вынужденные колебания кольцевого резонатора микромеханического ВТГ с магнитоэлектрическими датчиками управления. Считаем, что динамика резонатора описывается уравнениями, имеющими вид (3.1) при μ = 0. В результате экспериментального наблюдения вынужденных колебаний резонатора [18, 30] получены стационарные значения медленных переменных ${{q}_{i}} = {{q}_{i}}({{\omega }_{{0j}}})$, ${{p}_{i}} = {{p}_{i}}({{\omega }_{{0j}}})$, $i = 1,\;2$, соответствующие частотам вынужденных колебаний ${{\omega }_{0}} = {{\omega }_{{0j}}},$ $j = 1\; \ldots $ N, N = 61 (рис. 1). Для нормализации величин ${{q}_{i}}$, ${{p}_{i}}$, $i = 1,\;2$, использовалось максимальное значение амплитуды колебаний резонатора. Характерная частота собственных колебаний резонатора ω = 85732 c^–1 (13645 Гц).

Рис. 1.

Зависимости медленных переменных ${{p}_{1}}$, q₁, ${{p}_{2}}$, q₂ от частоты колебаний $\frac{{{{\omega }_{0}}}}{{2\pi }}$ [Гц].

Определяем оценку вектора параметров по математической модели, содержащей только кубическую нелинейность (ξ ≠ 0, $\kappa $= 0, μ = 0). Получен результат:

$\begin{gathered} {\mathbf{\hat {z}}}{\text{ = (43}}.029{\text{;}}\;{\text{2}}.0{\text{29}};\;{\text{1}}.{\text{332;}}\; - {\text{1}}.{\text{389;}}\;{\text{24}}.{\text{358;}}\;{\text{1}}.{\text{173;}}\; - {\text{12}}.{\text{797}};\;{\text{11}}.{\text{588}}; \\ {\text{32}}.{\text{159;}}\;{\text{3}}0.{\text{597;}}\;{\text{1}}.{\text{415;}}\; - 0.{\text{6}}0{\text{5}};\;{\text{18}}.{\text{217}}{{{\text{)}}}^{{\text{т}}}} \\ \end{gathered} $

По полученной оценке вектора запишем параметры ВТГ. Коэффициент демпфирования $\gamma = 43.029$ c^–1, добротность $Q = \omega {\text{/}}\gamma = 1992$. Для кольцевого резонатора масштабный коэффициент $K = 0.4$, поэтому абсолютное значение нулевого сигнала $\Omega \, = \,1.268$ c^–1. Погрешность характерной частоты собственных колебаний $\Delta \omega = {{\tilde {c}}_{m}}{\text{/2}}$ = = 12.179 c^–1 (1.94 Гц). Расщепление частот ${{\omega }_{{\max }}} - {{\omega }_{{\min }}} = \sqrt {{{{({{{\tilde {h}}}_{c}})}}^{2}} + {{{({{{\tilde {h}}}_{s}})}}^{2}}} $ = 17.264 c^–1 (2.748 Гц). Анизотропия демпфирования ${{\gamma }_{{\max }}} - {{\gamma }_{{\min }}} = 2\sqrt {b_{s}^{2} + b_{c}^{2}} $ = 3.848 c^–1. Углы главных осей жесткости и диссипации равны соответственно $\alpha = 0.601$ рад (34.4°) и $\beta = - 0.201$ рад (–11.5°). Полученные результаты для невакуумированного несбалансированного кольцевого резонатора соответствуют известным данным [31].

При идентификации параметров по предложенной методике оценка среднеквадратического отклонения составила $\hat {\sigma } = 0.0926$. В случае идентификации параметров по линейной математической модели [30] получаем $\hat {\sigma } = 0.295$. Таким образом, учет коэффициента нелинейности ξ позволил уменьшить среднеквадратическое отклонение в 3.2 раза, что указывает на значительное повышение точности определения параметров ВТГ при учете нелинейности колебаний. Учет обоих коэффициентов нелинейности ξ и $\kappa $ позволил уменьшить среднеквадратическое отклонение в 1.4 раза по сравнению с результатами, полученными при учете только кубической нелинейности, $\hat {\sigma }$ = = 0.0656.

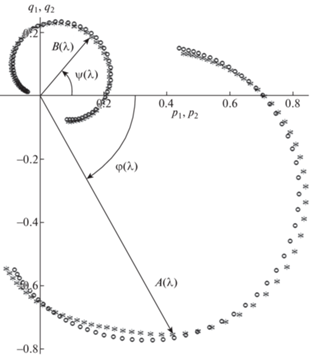
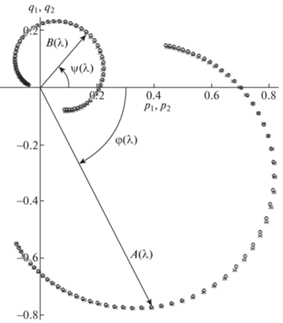
По найденным параметрам математической модели были рассчитаны невязки между модельными значениями и экспериментальными измерениями. На рисунках 2 и 3 представлено сравнение экспериментальных и расчетных амплитудно-фазочастотных характеристик (АФЧХ). Модули радиус-векторов равны амплитудам $A = \sqrt {q_{1}^{2} + p_{1}^{2}} $ и $B = \sqrt {q_{2}^{2} + p_{2}^{2}} $, а фазы колебаний φ и ψ определяются положением этих векторов на плоскости. В первом случае (рис. 2) оценка параметров ВТГ проводилась по линейной математической модели, ξ = 0, $\kappa $ = 0. Во втором случае (рис. 3) оценка параметров ВТГ проводилась по нелинейной математической модели с учетом кубической нелинейности ξ ≠ 0, $\kappa $ = 0. Из сравнения (рис. 2) экспериментальных и расчетных данных, полученных по результатам идентификации параметров линейной математической модели ВТГ, следует, что имеется систематическая погрешность. На рис. 3 экспериментальная и расчетная АФЧХ, полученная по результатам идентификации параметров по нелинейной математической модели ВТГ, практически совпадают. Учет нелинейности пятой степени, ξ ≠ 0, $\kappa $ ≠ 0, на АФЧХ визуально неотличим от рис. 3. Поэтому существенным является учет кубической нелинейности при идентификации параметров ВТГ, учет нелинейности пятой степени дает дополнительное повышение точности.

Рис. 2.

АФЧХ, о – экспериментальные данные; * – значения, рассчитанные по линейной модели.

Рис. 3.

АФЧХ, о – экспериментальные данные; * – значения, рассчитанные по нелинейной модели.

5. Зависимость угловой скорости дрейфа ВТГ от параметров резонатора и коэффициентов нелинейности. Исследование угловой скорости дрейфа ВТГ будем проводить при нулевых управляющих напряжениях ${{u}_{1}} = {{u}_{2}} = {{u}_{3}} = {{u}_{4}} = 0$, то есть, рассмотрим уравнения (2.3). Перейдем к переменным, называемым элементами орбиты [7]: $r(t)$ и $k(t)$ − амплитуды основной и квадратурной волн колебаний, $\theta (t)$ − угол прецессии, $\chi (t)$ − временная фаза,

(5.1)

$\begin{gathered} f = r\cos (\omega t + \chi )\cos 2\theta - k\sin (\omega t + \chi )\sin 2\theta {\text{ }} \\ g = r\cos (\omega t + \chi )\sin 2\theta + k\sin (\omega t + \chi )\cos 2\theta \\ \end{gathered} $

Чтобы перейти от переменных ${{q}_{1}}(t),$ ${{p}_{1}}(t),$ ${{q}_{2}}(t),$ ${{p}_{2}}(t)$ в осредненных уравнениях (2.5) к $r(t)$, $k(t)$, $\theta (t)$, $\chi (t)$, будем использовать замену переменных:

(5.2)

$\begin{gathered} {{q}_{1}}{\text{ = }}r{\text{ cos}}2\theta {\text{ cos}}\chi - k{\text{ sin}}2\theta {\text{ sin}}\chi {\text{,}}\quad {{p}_{1}}{\text{ = }} - r{\text{ cos}}2\theta {\text{ sin}}\chi - k{\text{ sin}}2\theta {\text{ cos}}\chi \\ {{q}_{2}}{\text{ = }}r{\text{ sin}}2\theta {\text{ cos}}\chi + k{\text{ cos}}2\theta {\text{ sin}}\chi {\text{,}}\quad {{p}_{2}}{\text{ = }} - r{\text{ sin}}2\theta {\text{ sin}}\chi + k{\text{ cos}}2\theta {\text{ cos}}\chi \\ \end{gathered} $

В результате преобразований получаем систему

(5.3)

$\dot {r} = \frac{1}{2}( - \gamma r + \tilde {n}k + ({{\tilde {h}}_{s}}k - {{b}_{c}}r)\cos 4\theta - ({{\tilde {h}}_{c}}k + {{b}_{s}}r)\sin 4\theta )$

(5.4)

$\dot {k} = \frac{1}{2}( - \gamma k + \tilde {n}r - ({{\tilde {h}}_{s}}r - {{b}_{c}}k)\cos 4\theta + ({{\tilde {h}}_{c}}r + {{b}_{s}}k)\sin 4\theta )$

(5.5)

$\begin{gathered} \dot {\theta } = - \frac{1}{4}\nu + \frac{{\tilde {\xi }}}{8}rk + \frac{{\tilde {\kappa }}}{8}rk({{r}^{2}} + {{k}^{2}}) - \\ - \;\frac{{rk}}{{2({{r}^{2}} - {{k}^{2}})}}\left( {{{{\tilde {h}}}_{c}}\cos 4\theta + {{{\tilde {h}}}_{s}}\sin 4\theta } \right) - \frac{{{{r}^{2}} + {{k}^{2}}}}{{4({{r}^{2}} - {{k}^{2}})}}\left( {{{b}_{s}}\cos 4\theta - {{b}_{c}}\sin 4\theta } \right) \\ \end{gathered} $

(5.6)

$\begin{gathered} \dot {\chi } = \frac{1}{2}\tilde {c} - \frac{{3\tilde {\xi }}}{8}({{k}^{2}} + {{r}^{2}}) - \frac{{\tilde {\kappa }}}{{16}}(5{{k}^{4}} + 6{{k}^{2}}{{r}^{2}} + 5{{r}^{4}}) + \\ + \;\frac{{{{r}^{2}} + {{k}^{2}}}}{{2({{r}^{2}} - {{k}^{2}})}}({{{\tilde {h}}}_{c}}\cos 4\theta + {{{\tilde {h}}}_{s}}\sin 4\theta ) + \frac{{rk}}{{{{r}^{2}} - {{k}^{2}}}}\left( {{{b}_{s}}\cos 4\theta - {{b}_{c}}\sin 4\theta } \right) \\ \end{gathered} $

Подставляя обозначения ${{\tilde {h}}_{s}} = {{\tilde {h}}_{m}}\sin 4\alpha $, ${{\tilde {h}}_{c}} = {{\tilde {h}}_{m}}\cos 4\alpha $, ${{b}_{s}} = {{b}_{m}}\sin 4\beta $, ${{b}_{c}} = {{b}_{m}}\cos 4\beta $ и используя тригонометрические формулы, преобразуем (5.3)−(5.6) к виду

(5.7)

$\dot {r} = \frac{1}{2}( - \gamma r + \tilde {n}k - {{\tilde {h}}_{m}}k\sin 4(\theta - \alpha ) - {{b}_{m}}r\cos 4(\theta - \alpha ))$

(5.8)

$\dot {k} = \frac{1}{2}( - \gamma k + \tilde {n}r + {{\tilde {h}}_{m}}r\sin 4(\theta - \alpha ) + {{b}_{m}}k\cos 4(\theta - \alpha ))$

(5.9)

$\begin{gathered} \dot {\theta } = - \frac{1}{4}\nu + \frac{{\tilde {\xi }}}{8}rk + \frac{{\tilde {\kappa }}}{8}rk({{r}^{2}} + {{k}^{2}}) - \\ - \;\frac{{rk}}{{2({{r}^{2}} - {{k}^{2}})}}{{{\tilde {h}}}_{m}}\cos 4(\theta - \alpha ) + \frac{{{{r}^{2}} + {{k}^{2}}}}{{4({{r}^{2}} - {{k}^{2}})}}{{b}_{m}}\sin 4(\theta - \alpha ) \\ \end{gathered} $

(5.10)

$\begin{gathered} \dot {\chi } = \frac{1}{2}\tilde {c} - \frac{{3\tilde {\xi }}}{8}({{k}^{2}} + {{r}^{2}}) - \frac{{\tilde {\kappa }}}{{16}}(5{{k}^{4}} + 6{{k}^{2}}{{r}^{2}} + 5{{r}^{4}}) + \\ + \;\frac{{{{r}^{2}} + {{k}^{2}}}}{{2({{r}^{2}} - {{k}^{2}})}}{{{\tilde {h}}}_{m}}\cos 4(\theta - \alpha ) - \frac{{rk}}{{{{r}^{2}} - {{k}^{2}}}}{{b}_{m}}\sin 4(\theta - \alpha ) \\ \end{gathered} $

Уравнения (5.7)−(5.10) соответствуют теории эволюций траектории резонатора ВТГ под воздействием возмущений, вызванных дефектами резонатора [7], но при этом учитывают влияние нелинейности колебаний. Из уравнения (5.9) следует, что угловая скорость дрейфа ВТГ зависит от коэффициентов ${{h}_{m}}$, ${{b}_{m}}$, характеризующих разночастотность и анизотропию демпфирования, а также от параметров $\tilde {\xi }$ и $\tilde {\kappa }$, характеризующих нелинейность колебаний резонатора.

6. Заключение. Разработаны методики идентификации параметров ВТГ с учетом разных типов нелинейности колебаний в двух режимах: свободного выбега и вынужденных колебаний. В режиме свободного выбега проводится идентификация параметров прецизионных ВТГ с кварцевыми резонаторами, обладающими высокой добротностью. Так как отключено управление, то для них учитывается только кубическая нелинейность и нелинейность пятой степени. В режиме вынужденных колебаний проводится идентификация параметров ВТГ с меньшей добротностью, позволяющей снимать данные в области резонансного пика при изменении частотной настройки. Проведена обработка экспериментальных данных, полученных для микромеханического ВТГ с кольцевым резонатором и магнитоэлектрическими датчиками управления. Показано, что учет кубической нелинейности существенно повышает точность определения параметров, учет нелинейности пятой степени дополнительно повышает точность определения параметров. Сделан вывод о необходимости учета кубической нелинейности путем введения коэффициента нелинейности в определяемые параметры ВТГ. Показано влияние определяемых параметров, включая коэффициенты нелинейностей, на угловую скорость дрейфа ВТГ.

Список литературы

Переляев С.Е. Обзор и анализ направлений создания бесплатформенных инерциальных навигационных систем на волновых твердотельных гироскопах // Новости навигации. 2018. № 2. С. 21–27.
Пешехонов В.Г. Перспективы развития гироскопии // Гироскопия и навигация. Т. 28. № 2 (109), 2020. С. 3–10. https://doi.org/10.17285/0869-7035.0028
Журавлев В.Ф., Климов Д.М. Волновой твердотельный гироскоп. М.: Наука, 1985. 125 с.
Климов Д.М., Журавлев В.Ф., Жбанов Ю.К. Кварцевый полусферический резонатор (волновой твердотельный гироскоп). М.: Изд-во “Ким Л.А.”, 2017. 194 с.
Журавлев В.Ф. Теоретические основы волнового твердотельного гироскопа (ВТГ) // Изв. РАН. МТТ. 1993. № 3. С. 6–19.
Журавлев В.Ф. О глобальных эволюциях состояния обобщенного маятника Фуко // Изв. РАН. МТТ. 1998. № 6. С. 5–11.
Журавлев В.Ф. Управляемый маятник Фуко как модель одного класса свободных гироскопов // Изв. РАН. МТТ. 1997. № 6. С. 27–35.
Журавлев В.Ф. Задача идентификации погрешностей обобщенного маятника Фуко // Изв. РАН. МТТ. 2000. № 5. С. 5–9.
Жбанов Ю.К., Журавлев В.Ф. О балансировке волнового твердотельного гироскопа // Изв. РАН. МТТ. 1998. № 4. С. 4–16.
Жбанов Ю.К. Контур управления амплитудой в волновом твердотельном гироскопе с автоматической компенсацией разнодобротности // Изв. РАН. МТТ. 2008. № 3. С. 17–22. https://doi.org/10.3103/S0025654408030035
Каленова Н.В. Определение параметров поверхностного дебаланса резонатора волнового твердотельного гироскопа по его реакции на угловую вибрацию основания // Изв. РАН. МТТ. 2004. № 2. С. 3–7.
Матвеев В.А., Липатников В.И., Алехин А.В. Проектирование волнового твердотельного гироскопа. М.: Изд-во МГТУ им. Н.Э. Баумана, 1997. 167 c.
Меркурьев И.В., Подалков В.В. Динамика микромеханического и волнового твердотельного гироскопов. М.: Физматлит, 2009. 228 с.
Астахов С.В. Нелинейные эффекты в динамике волнового твердотельного и микромеханического гироскопов в условиях медленно меняющихся параметров. Дисс. … канд. техн. наук. Москва, 2012. 157 с.
Sudipto K.De., Aluru N.R. Complex nonlinear oscillations in electrostatically actuated microstructures // J. Microelectromech. Sys. 2005. V. 15. № 2. P. 355–369. https://doi.org/10.1109/JMEMS.2006.872227
Rhoads J., Shaw S., Tunner K., Moehlis J., DeMartiniB., Zhang W. Generalized parametric resonance in electrostatically actuated microelectromechanical oscillators // J. Sound Vibr. 2006. V. 296. P. 797–829. https://doi.org/10.1016/j.jsv.2006.03.009
Маслов Д.А. Влияние нелинейных свойств электростатических и электромагнитных датчиков управления на динамику цилиндрического резонатора волнового твердотельного гироскопа. Дисс. … канд. техн. наук. Москва, 2019. 127 с.
Маслов А.А., Маслов Д.А., Меркурьев И.В. Идентификация параметров волнового твердотельного гироскопа с учетом нелинейности колебаний резонатора // Приборы и системы. Управление, контроль, диагностика. 2014. № 5. С. 18–23.
Маслов А.А., Маслов Д.А., Меркурьев И.В. Способ определения параметров волнового твердотельного гироскопа // Патент RU 2544308 C9. 2015. Бюл. № 14.
Маслов Д.А. Идентификация параметров гироскопа с цилиндрическим резонатором при учете влияния нелинейности на амплитуду вынуждающего воздействия // Машиностроение и инженерное образование. 2017. № 1 (50). С. 24–31.
Maslov D.A., Merkuryev I.V. Increase in the Accuracy of the Parameters Identification for a Vibrating Ring Microgyroscope Operating in the Forced Oscillation Mode with Nonlinearity Taken into Account // Rus. J. Nonlin. Dyn. 2018. V. 14. № 3. P. 377–386. https://doi.org/10.20537/nd180308
Маслов А.А., Маслов Д.А., Меркурьев И.В., Подалков В.В. Разработка методов идентификации параметров нелинейной математической модели волнового твердотельного гироскопа // ХXVII Санкт-Петербургская международная конференция по интегрированным навигационным системам. Сборник материалов. IEEE, 2020. С. 244–248. https://doi.org/10.23919/ICINS43215.2020.9133967
Журавлев В.Ф. Волновой твердотельный гироскоп: современное состояние, некоторые аспекты // Актуальные проблемы авиационных и аэрокосмических систем: процессы, модели, эксперимент. 2011. № 2 (33). Т. 16. С. 118–123.
Маслов Д.А., Меркурьев И.В. Компенсация погрешностей и учет нелинейности колебаний вибрационного кольцевого микрогироскопа в режиме датчика угловой скорости // Нелинейная динамика. 2017. Т. 13. № 2. С. 227–241. https://doi.org/10.20537/nd1702006
Лунин Б.С., Басараб М.А., Юрин А.В., Чуманкин Е.А. Цилиндрический резонатор из кварцевого стекла для недорогих вибрационных гироскопов // Сборник материалов юбилейной XXV Санкт-Петербургской международной конференции по интегрированным навигационным системам. IEEE, 2018. С. 204–207. https://doi.org/10.23919/ICINS.2018.8405896
Басараб М.А., Лунин Б.С., Матвеев В.А., Чуманкин Е.А. Балансировка полусферических резонаторов волновых твердотельных гироскопов методом химического травления // Гироскопия и навигация. 2015. № 1. С. 61–70. doi.org/10.1134/S2075108715030025
Маслов Д.А., Меркурьев И.В. Влияние нелинейных свойств электростатических датчиков управления на динамику цилиндрического резонатора волнового твердотельного гироскопа // Изв. РАН. МТТ. 2021. № 6. С. 88–110. https://doi.org/10.3103/S002565442106011X
Журавлев В.Ф., Климов Д.М. Прикладные методы в теории колебаний. М.: Наука, 1988. 328 с.
Ивченко Г.И., Медведев Ю.И. Введение в математическую статистику. М.: ЛКИ, 2010. 600 с.
Гавриленко А.Б., Меркурьев И.В., Подалков В.В., Сбытова Е.С. Динамика микромеханических систем. М.: Издательство МЭИ, 2016. 60 с.
Тимошенков С.П., Симонов Б.М., Бритков О.М., Анчутин С.А., Тимошенков А.С. Балансировка кремниевых датчиков угловой скорости в процессе изготовления // Изв. вузов. Электроника. 2015. Том 20. № 1. С. 58–67.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика твердого тела

Архивы выпусков Информация о журнале Отправить рукопись в журнал