Известия РАН. Механика твердого тела, 2023, № 1, стр. 76-94
ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ КИНЕТИЧЕСКИМ МОМЕНТОМ ТВЕРДОГО ТЕЛА (КОСМИЧЕСКОГО АППАРАТА) ПРИ ВЫПОЛНЕНИИ ПРОСТРАНСТВЕННОГО РАЗВОРОТА
a Научно-исследовательский институт космических систем им. А.А. Максимова –
филиал Государственного космического научно-производственного центра им. М.В. Хруничева
Королев, Россия
* E-mail: levskii1966@mail.ru
Поступила в редакцию 31.10.2021
После доработки 08.02.2022
Принята к публикации 09.03.2022
- EDN: KGUTWN
- DOI: 10.31857/S0572329922060137
Аннотация
Представлено кватернионное решение динамической задачи оптимального разворота твердого тела (например, космического аппарата) из известного начального в заданное конечное угловое положение. Оптимизация программы управления проводится с использованием комбинированного показателя, сочетающего квадратичный критерий качества и время разворота, минимизируемый функционал объединяет в заданной пропорции энергетические затраты и длительность маневра. На основе принципа максимума и кватернионных моделей и методов исследования управляемого движения твердого тела (космического аппарата) получено решение поставленной задачи. Построение оптимального вращения основано на дифференциальном уравнении, связывающем кинетический момент и кватернион ориентации твердого тела. В аналитической форме записаны условия оптимальности и изучены свойства оптимального движения. Представлены аналитические уравнения и расчетные формулы для нахождения оптимального управления. Закон управления сформулирован в виде явной зависимости управляющих переменных от фазовых координат. Даны ключевые соотношения, определяющие оптимальные значения параметров алгоритма управления кинетическим моментом. В случае динамически симметричного тела дается полное решение задачи разворота в замкнутой форме: получены аналитические зависимости как явные функции времени для управляющих переменных и соотношения для расчета параметров закона управления. Приводятся численный пример и результаты математического моделирования вращения космического аппарата как твердого тела при оптимальном управлении, демонстрирующие практическую реализуемость предложенного метода управления.
Введение. Решается задача перевода твердого тела (в частности, космического аппарата (КА)) из исходного углового положения в положение заданной ориентации. Главное отличие рассматриваемой задачи и предлагаемого решения состоит в оптимизации на основе нового критерия качества. Построение оптимальной программы разворота основывается на кватернионных моделях и принципе максимума.
Управляемые вращения твердого тела и соответствующие оптимизационные задачи исследовались неоднократно [1–28 ]. Большое количество работ соответствуют вращению вокруг неподвижной оси [1–8]; при этом принципы оптимизации и алгоритмы управления различны (в том числе на базе нечеткой логики [2], обратных задач динамики [3] или с помощью прогнозирующих моделей [4]). Проблема разработки высокоэффективных алгоритмов управления ориентацией КА остается актуальной и сегодня. Большой практический интерес представляют аналитические решения задачи оптимального разворота в замкнутой форме, поскольку они дают готовые законы программного управления и изменения оптимальной траектории движения КА, которые могут непосредственно применяться на борту КА. Для плоских вращений КА вокруг одной из главных центральных осей инерции и пространственного вращения сферически-симметричного тела оптимальные управления угловым движением изучены достаточно подробно [1, 5, 6, 9]. Также известны решения для осесимметричных КА [10–13], задачи оптимального по времени разворота [1, 7, 11–18], и кинематические задачи разворота в различных постановках [18–22]. В работе [19] минимизировался модуль кинетического момента во время разворота, что крайне важно при использовании инерционных исполнительных органов, которые в настоящее время широко применяют для управления КА [23–25]. В [20, 21] рассматриваются задачи построения с помощью принципа максимума оптимальных законов изменения вектора кинетического момента твердого тела для разворота за фиксированное время [20] (с минимизацией интегрального квадратичного функционала качества с подынтегральным выражением, являющимся взвешенной суммой квадратов проекций вектора кинетического момента) или разворота динамически симметричного тела, используя комбинированные функционалы качества, один из которых объединяет в заданной пропорции время и интеграл от квадрата модуля вектора кинетического момента, а другой – расход времени и импульса модуля вектора кинетического момента на разворот твердого тела [21]. Причем в обеих работах управлением считается вектор кинетического момента твердого тела [20, 21].
Для КА с произвольным соотношением моментов инерции и произвольными начальным и конечным угловыми положениями аналитического решения задачи пространственной переориентации не найдено; рассматривались только специфические случаи решения задачи разворота (например, [1, 6]). Ниже приводится кватернионное решение задачи управления угловым движением КА, когда фазовыми переменными являются кватернион ориентации связанной системы координат относительно инерциального базиса и кинетический момент КА (как твердого тела), а оптимизация выполнена на основе комбинированного показателя качества, который объединяет в заданной пропорции энергетические затраты на переориентацию КА и время разворота; фактор времени позволяет ограничить длительность маневра, а наличие интеграла от квадратичной свертки по силовым моментам ограничивает максимальный управляющий момент в процессе разворота. Вопросы экономичности при управлении движением КА остаются до сих пор актуальными, из-за чего решаемая ниже задача управления является практически важной. В отличие от упомянутых исследований [20, 21], в статье решается динамическая задача оптимального разворота, когда управлением является силовой момент, действующий на корпус КА. Представленное решение отличается от ранее известных.
1. Уравнения углового движения и постановка задачи управления. Движение КА (как твердого тела) относительно центра масс описывается известным уравнением [1, 5]:
где L – кинетический момент твердого тела (КА), I – тензор инерции твердого тела, М – главный момент сил М (символ × означает векторное произведение векторов). Управление движением КА относительно центра масс производится за счет изменения силового момента М. Особенностью управления во время космического полета является малость возмущающих моментов, вызванных сопротивлением среды и взаимодействием КА с внешними полями.Пространственное движение КА вокруг центра масс будем описывать с помощью кватернионов (параметров Родрига–Гамильтона). Ориентацию связанного базиса относительно опорного базиса зададим кватернионом Λ (для удобства кватернион Λ считается нормированным ||Λ|| = 1) [1]. Опорный базис полагаем инерциальным. Кинематическое уравнение, связывающее кинетический момент L и кватернион ориентации Λ твердого тела, имеет вид [1]:
где символ “$ \circ $” – знак умножения кватернионов [1, с. 11–20] (под кватернионным умножением на вектор понимается умножение на кватернион с нулевой скалярной частью).Задачи, когда разворот выполняется из состояния покоя в состояние покоя, встречаются достаточно часто и имеют практическое значение. Выпишем краевые условия задачи оптимального управления для динамической системы (1.1), (1.2):
где Т – время окончания поворотного маневра. Кватернионы Λin и Λf, отражающие ориентацию связанных с КА осей в начальный и конечный моменты времени, имеют произвольные наперед заданные значения, удовлетворяющие условию ||Λin|| = ||Λf|| = 1 (предполагается, что Λf ≠ Λin).Полагаем, что управление угловым положением КА осуществляется относительно главных центральных осей инерции КА (т.е. оси связанного базиса параллельны главным центральным осям инерции КА). Эффективность управления оценивается интегральной величиной
(1.5)
$G = \int\limits_0^T {(М_{1}^{2}{\text{/}}{{J}_{1}} + М_{2}^{2}{\text{/}}{{J}_{2}} + М_{3}^{2}{\text{/}}{{J}_{3}})dt} + {{k}_{0}}T$Принятый критерий качества позволяет найти программу вращения (переориентации) с минимальными затратами управляющих ресурсов и времени. Сформулированная задача управления отличается от решаемых ранее задач видом функционала (1.5), при котором управляющие переменные не могут быть неограниченно большими (даже в отсутствие ограничений на управление). Фактор времени, присутствующий в критерии оптимальности (1.5), ограничивает длительность Т оптимального разворота некоторым конечным значением Тopt (коэффициент k0 ≠ 0). И еще одна особенность – поскольку время Т не фиксировано, то требуемый поворотный маневр реализуется при любых условиях разворота Λin, Λf и заданных значениях J1, J2, J3, k0. Задача оптимального изменения кинетического момента во время разворота КА, когда качество программы управления определяется характеристикой (1.5), достаточно актуальна (подынтегральное выражение в (1.5) отражает энергию управляющих ускорений, а коэффициент k0 определяет максимальный управляющий момент в ходе разворота).
2. Применение принципа максимума Л.С. Понтрягина. Рассматриваемая задача оптимального управления (1.1)–(1.5) есть задача динамического оптимального разворота твердого тела [1], в которой L и Λ – фазовые переменные, а управляющими функциями являются моменты Мi ($i = \overline {1,\;3} $). Поставленную задачу решаем на основе необходимых условий оптимальности в форме принципа максимума Л.С. Понтрягина [29].
2.1. Функция Гамильтона и сопряженная система уравнений. Введем сопряженные переменные ${{\varphi }_{i}}$, соответствующие проекциям кинетического момента на оси связанного базиса Li. Критерий оптимальности (1.5) не содержит позиционных координат (элементов кватерниона ориентации Λ), поэтому вместо сопряженных переменных ψj, которые соответствуют компонентам λj кватерниона Λ (j = $\overline {0,\;3} $), используем следующие переменные ri, i = $\overline {1,3} $ [26]:
Впервые такую замену переменных предложили В.Н. Бранец, И.П. Шмыглевский и М.Б. Черток, Ю.В. Казначеев [1, 11]; позднее аналогичный прием использовали многие авторы [9, 10, 13, 18–24], в том числе при решении задач оптимального разворота твердого тела в постановках (1.1)–(1.4), но с другими функционалами оптимизации – чистые быстродействие и минимум энергозатрат (в частности, когда они содержат модуль вектора управляющего момента) [11, 27]. Оптимальные функции ri, как компоненты вектора r, и вектор r удовлетворяют уравнениям [26]:
(2.1)
${{\dot {r}}_{1}} = {{L}_{3}}{{r}_{2}}{\text{/}}{{J}_{3}} - {{L}_{2}}{{r}_{3}}{\text{/}}{{J}_{2}},\quad {{\dot {r}}_{2}} = {{L}_{1}}{{r}_{3}}{\text{/}}{{J}_{1}} - {{L}_{3}}{{r}_{1}}{\text{/}}{{J}_{3}},\quad {{\dot {r}}_{3}} = {{L}_{2}}{{r}_{1}}{\text{/}}{{J}_{2}} - {{L}_{1}}{{r}_{2}}{\text{/}}{{J}_{1}}$Запишем функцию Гамильтона для задачи оптимального управления (1.1)–(1.5) [26]:
Согласно принципу максимума уравнения для сопряженных функций φi имеют вид [29]:
В результате получим следующую сопряженную систему уравнений:
(2.2)
$\begin{gathered} {{{\dot {\varphi }}}_{1}} = {{L}_{3}}{{\varphi }_{2}}(1{\text{/}}{{J}_{3}} - 1{\text{/}}{{J}_{1}}) + {{L}_{2}}{{\varphi }_{3}}(1{\text{/}}{{J}_{1}} - 1{\text{/}}{{J}_{2}}) - {{r}_{1}}{\text{/}}{{J}_{1}} \\ {{{\dot {\varphi }}}_{2}} = {{L}_{1}}{{\varphi }_{3}}(1{\text{/}}{{J}_{1}} - 1{\text{/}}{{J}_{2}}) + {{L}_{3}}{{\varphi }_{1}}(1{\text{/}}{{J}_{2}} - 1{\text{/}}{{J}_{3}}) - {{r}_{2}}{\text{/}}{{J}_{2}} \\ {{{\dot {\varphi }}}_{3}} = {{L}_{2}}{{\varphi }_{1}}(1{\text{/}}{{J}_{2}} - 1{\text{/}}{{J}_{3}}) + {{L}_{1}}{{\varphi }_{2}}(1{\text{/}}{{J}_{3}} - 1{\text{/}}{{J}_{1}}) - {{r}_{3}}{\text{/}}{{J}_{3}} \\ \end{gathered} $Вектор r является постоянным относительно инерциального базиса и |r∣= const ≠ 0. Решение r(t) системы (2.1) зависит от начальной Λin и конечной Λf ориентаций КА. Оптимальная функция r(t) определяется кватернионом Λ(t) [1, 26]:
2.2. Условия максимума гамильтониана и структура оптимального управления. Гамильтониан Н – квадратичная функция вектора управления М, и ее максимум определяется необходимыми условиями экстремума ${{\partial Н} \mathord{\left/ {\vphantom {{\partial Н} {\partial {{M}_{i}}}}} \right. \kern-0em} {\partial {{M}_{i}}}} = 0$, которым удовлетворяют значения
Замкнутая система уравнений (1.1), (1.2), (2.1)–(2.3) определяет оптимальное решение. Задача построения оптимальной программы управления сводится к решению системы уравнений углового движения КА (1.1), (1.2), сопряженных уравнений (2.2) и уравнений (2.1) при условии, что управляющие функции Mi вычисляются в соответствии с (2.3) (системой уравнений (2.1)–(2.3) формализуются необходимые условия оптимальности для исходной задачи оптимального управления (1.1)–(1.5)).
Обозначим r0 = |r(t)∣, Lm = |L∣. С учетом условия L(0) = L(Т) = 0 система уравнений (1.1), (2.1)–(2.3) имеет единственное решение, которое удовлетворяет соотношениям:
где ρ = const > 0 – скалярная величина (факт соответствия (2.5) уравнениям (2.1) легко проверить, подставив равенства (2.5) в уравнения движения (1.1) с учетом (2.3) и (2.4)).Значение r(0) таково, чтобы в результате интегрирования уравнений (1.1), (1.2), (2.1)–(2.3) с начальными условиями Λ(0) = Λin для траектории вращения Λ(t ) выполнялось равенство Λ(Т) = Λf. Если рассматривать нормированный вектор р = r/|r∣, то краевая задача принципа максимума заключается в определении значения вектора р0 = р(0) и положительной величины r0, при которых решение системы дифференциальных уравнений (1.1), (1.2), (2.1), (2.2), (2.4) с одновременным выполнением (2.3) удовлетворяло условиям разворота (1.3), (1.4) (с учетом соотношений ri = r0pi). В оптимальном решении сопряженные переменные φi подчиняются уравнениям (2.4), и оптимальный управляющий момент М имеет значение
Как видно из (2.1), (2.6), при оптимальном управлении силовой момент М действует вдоль прямой, неподвижной в инерциальной системе координат. Поэтому при нулевом начальном и конечном кинетическом моментах решение системы (1.1), (2.1)–(2.3) описывает движение, при котором кинетический момент КА L имеет постоянное направление в инерциальной системе координат, причем это решение единственное (так как L(0) = L(T) = 0).
Истинность решения (2.4), (2.5) для системы дифференциальных уравнений (1.1), (2.1)–(2.3) подтверждается последовательной подстановкой зависимостей (2.4) в уравнения (2.2) с учетом соотношений (2.1), (2.5) для всех i = 1, 2, 3 (равенства (2.5) непосредственно следуют из системы (1.1), (2.1), (2.6)). Если обозначить φ – вектор, компонентами которого являются сопряженные функции φi, то система (2.2) принимает вид
(2.7)
${\mathbf{\dot {\varphi }}} = {\mathbf{\varphi }} \times ~({{I}^{{--1}}}{\mathbf{L}}) + {{I}^{{--1}}}({\mathbf{L}} \times {\mathbf{\varphi }}--{\mathbf{r}})$Подставим значения φ и L, рассчитанные в соответствии с найденным решением (2.4), (2.5), в уравнение (2.7). Вычисление левой части (2.7) с учетом (2.1), (2.4) дает следующее:
Подстановка (2.4), (2.5) в правую часть уравнения (2.7) дает следующий результат:
В итоге убедились, что соотношения (2.4), (2.5) превращают уравнение (2.7) в тождество. Следовательно, зависимости (2.4), (2.5) есть решение системы уравнений (1.1), (2.1)–(2.3).
2.3. Свойства оптимального управления. Поскольку вращение с минимальным значением (1.5) одновременно удовлетворяет уравнениям (2.1) и (2.5), то оптимальное изменение кинетического момента описывается следующим дифференциальным уравнением:
Для исследования свойств оптимального решения M(t) введем скалярную функцию m(t), равную скалярному произведению векторов М и р. Тогда М = m(t)р. В начальный момент времени t = 0 модуль |M(0)∣ = m0 = r0ρ/2. Значение константы ρ = Т/2 = 2m0/r0. Следовательно, m(t) = m0 – r0t/2 = m0(1 – 2t/Т). Перепишем закономерность (2.6) в следующем виде
Управление (2.8) динамической системой (1.1), (1.2), когда модуль момента М изменяется как кусочно-линейная функция времени, удовлетворяет необходимым условиям оптимальности для критерия (1.5) (направление момента М параллельно прямой, неподвижной относительно инерциального базиса). Так как разворот выполняется из состояния покоя в состояние покоя, то такое управление кинетическим моментом всегда можно осуществить (замкнутая система (1.1), (2.1)–(2.3) имеет решение при любых значениях Λin и Λf).
Изучим свойства функции Lm(t). Подстановка (2.5) в (1.1) с учетом (2.1) дает M = = ${{\dot {L}}_{m}}{\mathbf{r}}{\text{/}}{{r}_{0}}$. После сравнения с соотношениями (2.8) заключаем, что ${{\dot {L}}_{m}}$ = m(t) = m0 – r0t/2. Из (2.3) получим φ =2I–1М = $2{{\dot {L}}_{m}}$I–1p, что совпадает с (2.4), если (ρ – t)r0 = $2{{\dot {L}}_{m}}$ и ${{\ddot {L}}_{m}}$ = = –r0/2. На концах траектории вращения (в точках t = 0 и t = T) имеем Lm(0) = Lm(T) = 0 (поскольку по условиям разворота L(0) = L(T) = 0). В точке t = T/2 кинетический момент максимален и M(T/2) = 0. Скалярная функция Lm(t) в оптимальном решении имеет вид: Lm(t) = m0t(1 – t/Т), а время разворота и максимальный модуль силового момента связаны соотношением m0 = r0Т/4. Оптимальный закон изменения кинетического момента выглядит следующим образом:
Оптимальные функции Li(t), φi(t), ri(t) соответствуют требованиям (2.4), (2.5), в которых переменные ri (t) являются решением системы (2.1). Оптимальные управления определяются выражениями (2.8). Оптимальным (в смысле минимума функционала (1.5)) является вращение, при котором направление кинетического момента КА остается неизменным относительно инерциальной системы координат (векторы М и L параллельны на всем интервале управления). Управление (2.6) оптимально, потому что оно – единственное решение системы уравнений (1.1), (2.1)–(2.3), которая отражает необходимые условия оптимальности.
Еще одним основным свойством оптимального разворота КА является постоянство соотношения кинетической энергии вращения Е к квадрату модуля кинетического момента КА во все время движения (на всем отрезке времени [0, T ] ). Докажем сделанное утверждение. Найдем Е = $L_{m}^{2}(r_{1}^{2}{\text{/}}{{J}_{1}} + {{r_{2}^{2}} \mathord{\left/ {\vphantom {{r_{2}^{2}} {{{J}_{2}}}}} \right. \kern-0em} {{{J}_{2}}}} + {{r_{3}^{2}} \mathord{\left/ {\vphantom {{r_{3}^{2}} {{{J}_{3}}}}} \right. \kern-0em} {{{J}_{3}}}}){\text{/}}(2r_{0}^{2})$ и E/|L2| = $({{r_{1}^{2}} \mathord{\left/ {\vphantom {{r_{1}^{2}} {{{J}_{1}}}}} \right. \kern-0em} {{{J}_{1}}}} + {{r_{2}^{2}} \mathord{\left/ {\vphantom {{r_{2}^{2}} {{{J}_{2}}}}} \right. \kern-0em} {{{J}_{2}}}} + {{r_{3}^{2}} \mathord{\left/ {\vphantom {{r_{3}^{2}} {{{J}_{3}}}}} \right. \kern-0em} {{{J}_{3}}}}){\text{/}}(2r_{0}^{2})$ = = const (напомним, r0 = |r(t)∣ = const). Нетрудно показать, что у оптимального вращения, которое подчиняется уравнениям (2.1), (2.5), наблюдается закономерность ${{r_{1}^{2}} \mathord{\left/ {\vphantom {{r_{1}^{2}} {{{J}_{1}} + {{r_{2}^{2}} \mathord{\left/ {\vphantom {{r_{2}^{2}} {{{J}_{2}} + {{r_{3}^{2}} \mathord{\left/ {\vphantom {{r_{3}^{2}} {{{J}_{3}}}}} \right. \kern-0em} {{{J}_{3}}}}}}} \right. \kern-0em} {{{J}_{2}} + {{r_{3}^{2}} \mathord{\left/ {\vphantom {{r_{3}^{2}} {{{J}_{3}}}}} \right. \kern-0em} {{{J}_{3}}}}}}}}} \right. \kern-0em} {{{J}_{1}} + {{r_{2}^{2}} \mathord{\left/ {\vphantom {{r_{2}^{2}} {{{J}_{2}} + {{r_{3}^{2}} \mathord{\left/ {\vphantom {{r_{3}^{2}} {{{J}_{3}}}}} \right. \kern-0em} {{{J}_{3}}}}}}} \right. \kern-0em} {{{J}_{2}} + {{r_{3}^{2}} \mathord{\left/ {\vphantom {{r_{3}^{2}} {{{J}_{3}}}}} \right. \kern-0em} {{{J}_{3}}}}}}}} = {\text{const}}$. Для проверки этого утверждения достаточно продифференцировать по времени левую часть указанного равенства с учетом зависимостей (2.1), (2.5) и убедиться, что полученная производная равна нулю после подстановки ${{\dot {r}}_{i}}$ по формулам (2.1) и затем Li по выражениям (2.5).
Обозначим Lmax – максимальное значение функции Lm(t). При оптимальном изменении кинетического момента L(t) вращение имеет свойство симметрии и характеризуется следующими закономерностями:
Максимальный управляющий момент m0 = |M(0)| = |M(T)|. Свойство оптимального решения m(T) = –m(0) следует из структуры функции Lm(t), а именно
2.4. Подтверждение единственности оптимального решения. Пусть q – орт, параллельный моменту М, причем в начальный момент времени t = 0 направления векторов М и q совпадают. Тогда φ = f I–1q, где f – скалярная функция, у которой f(0) > 0. В окрестности точки t = 0 имеем М $||$ L и L = χq, где χ – скалярная величина. Подставим φ = f I–1q в уравнения М = Iφ/2 и (1.1) с учетом условия L = χq и соотношений (2.1). Получим следующее уравнение
(2.10)
${\mathbf{q}}\dot {\chi } + {\mathbf{\dot {q}}}\chi + (\chi {{I}^{{ - 1}}}{\mathbf{q}}) \times {\mathbf{q}}\chi = m(t){\mathbf{q}}$Сумма ${\mathbf{\dot {q}}}\chi + (\chi {{I}^{{ - 1}}}{\mathbf{q}}) \times {\mathbf{q}}\chi $ ортогональна орту q или равна нулю (всегда q ⋅ ${\mathbf{\dot {q}}}$ = 0, так как |q| = 1); символ ⋅ означает скалярное произведение векторов. Уравнение (2.10) будет выполнено в единственном случае, если $\dot {\chi } = m(t)$ и ${\mathbf{\dot {q}}} = - (\chi {{I}^{{ - 1}}}{\mathbf{q}}) \times {\mathbf{q}}$. Теперь подставим равенства φ = f (t)I–1q и L = χq в правую и левую части уравнения (2.7). Рассмотрим левую часть (2.7)
Приравняв левую и правую части уравнения (2.7) получаем $\dot {f}$q = –r, из чего заключаем: $\dot {f}$ = –r0 и q ≡ р = r/r0 (так как f (0) > 0, а f (T ) < 0, и потому $\dot {f}$ < 0). Учитывая, что ω = I–1L есть угловая скорость, приходим к следующему выводу: если существует момент времени t, когда угловая скорость ω и вектор сопряженных переменных φ параллельны, то они параллельны на всем интервале управления 0 < t < T. По условиям задачи управления L(0) = 0 и L(T) = 0, из-за чего векторы φ и ω параллельны как минимум два раза – в самом начале разворота и в самом конце разворота (ω = htφ при t → 0, и ω = –h (Т – t) φ при t → T). Поэтому заключаем, что при оптимальном управлении на всем отрезке времени t ∈ [0, T] имеет место свойство L $||$ r. Следовательно, оптимальное вращение обязательно удовлетворяет соотношениям (2.4), (2.5).
Доказано, что зависимости (2.4), (2.5) – единственное решение системы уравнений (1.1), (2.1)–(2.3) при условии L(0) = 0, L(T) = 0. В момент времени t = T/2 силовой момент М обнуляется M(T/2) = 0, а кинетический момент КА принимает максимальное значение.
3. Нахождение основных констант оптимального управления. Поскольку гамильтониан Н не зависит от времени в явном виде и время окончания маневра T не фиксировано, то на оптимальной траектории Н = const = 0 [30]. Поэтому
На основании необходимого условия оптимальности Н = 0 найдем время разворота, максимальную величину управляющего момента и максимальный кинетический момент. Из структуры гамильтониана условие H(T) = 0 принимает вид
Если Lm = 0, то гамильтониан равен H = $m_{0}^{2}$C2 – k0 = 0.
Если t = T/2, то m(t) = |M| = 0 и H(T/2) = r0LmaxC2 – k0 = 0, откуда Lmax = k0/(r0C2).
Значение r0 для оптимального решения равно r0 = $4{{\sqrt {{{k}_{0}}} } \mathord{\left/ {\vphantom {{\sqrt {{{k}_{0}}} } {(CT)}}} \right. \kern-0em} {(CT)}}$ и связано с максимальным управляющим моментом m0 и временем разворота T зависимостью r0 = = 4m0/T. Максимальный модуль кинетического момента определяется параметром m0. Длительность оптимального разворота T зависит от максимального управляющего момента m0 и значения интеграла
и составляет $T = \sqrt {6F{\text{/}}{{m}_{0}}} $, или $T = \sqrt {{{6S} \mathord{\left/ {\vphantom {{6S} {\sqrt {{{k}_{0}}} }}} \right. \kern-0em} {\sqrt {{{k}_{0}}} }}} $, где S – функционал пути [22]:Соответственно, ${{r}_{0}} = 4{{m}_{0}}\sqrt {{{m}_{0}}{\text{/}}(6F)} $, ${{L}_{{{\text{max}}}}} = \sqrt {3F\sqrt {{{k}_{0}}} {\text{/}}(8C)} $, так как Lmax = m0T/4 = = $\sqrt {3{{m}_{0}}F{\text{/}}8} $ (напомним, что m0 = ${{\sqrt {{{k}_{0}}} } \mathord{\left/ {\vphantom {{\sqrt {{{k}_{0}}} } C}} \right. \kern-0em} C}$). Максимальная энергия вращения Emax = = ${{3FC\sqrt {{{k}_{0}}} } \mathord{\left/ {\vphantom {{3FC\sqrt {{{k}_{0}}} } {16}}} \right. \kern-0em} {16}}$ = ${{3S\sqrt {{{k}_{0}}} } \mathord{\left/ {\vphantom {{3S\sqrt {{{k}_{0}}} } {16}}} \right. \kern-0em} {16}}$.
Значения F и S не зависят от характера изменения модуля |L(t)∣ и определяются исключительно кватернионом разворота ${{\Lambda }_{{\text{t}}}} = {{\tilde {\Lambda }}_{{{\text{in}}}}} \circ {{\Lambda }_{{\text{f}}}}$ и моментами инерции КА J1, J2, J3 [22]. Нетрудно доказать, что найденные значения времени T, а также остальных характеристик разворота действительно оптимальны по критерию (1.5). Вычислим значение G для закона (2.8).
G = ${{k}_{0}}T + m_{0}^{2}{{C}^{2}}T{\text{/}}3 = {{k}_{0}}T + 12{{F}^{2}}{{C}^{2}}{\text{/}}{{T}^{3}}$, потому что F = m0T 2/6, а значит m0 = 6F/T 2
Минимум G достигается в точке T = $\sqrt {{{6FC} \mathord{\left/ {\vphantom {{6FC} {\sqrt {{{k}_{0}}} }}} \right. \kern-0em} {\sqrt {{{k}_{0}}} }}} $, при котором m0 = ${{\sqrt {{{k}_{0}}} } \mathord{\left/ {\vphantom {{\sqrt {{{k}_{0}}} } C}} \right. \kern-0em} C}$.
Как видим, время оптимального разворота T зависит только от коэффициента k0 минимизируемого функционала. Величина (1.5) при оптимальном управлении равна G = 4k0T/3.
Если рассматривать приведенные управления ${{{{u}_{i}} = {{M}_{i}}} \mathord{\left/ {\vphantom {{{{u}_{i}} = {{M}_{i}}} {\sqrt {{{J}_{i}}} }}} \right. \kern-0em} {\sqrt {{{J}_{i}}} }}$ [11], то |u|2 характеризует энергетику управляющих воздействий, интеграл
соответствует энергетическим затратам на разворот, где T – время, затраченное на перевод КА из положения (1.3) в положение (1.4); u – приведенный вектор управления, компонентами которого являются ui. Значение показателя качества (1.5) таково G = Q + k0T.В переменных ui гамильтониан в начальный и конечный моменты времени равен H = |u|2 – k0 = 0, так как при оптимальном управлении φi = ${{2{{u}_{i}}} \mathord{\left/ {\vphantom {{2{{u}_{i}}} {\sqrt {{{J}_{i}}} }}} \right. \kern-0em} {\sqrt {{{J}_{i}}} }}$ и L(0) = L(T) = 0. Отсюда следует важный вывод: модуль приведенного управления в начальный и конечный моменты времени одинаковый и не зависит от начального и конечного положений КА и его моментов инерции, а определяется только коэффициентом k0 минимизируемого функционала; |u(0)| = |u(T)| = $\sqrt {{{k}_{0}}} $. Максимальная величина силового момента для оптимального вращения не зависит от значения “функционала пути” S и от интеграла (3.1).
Решение задачи оптимального управления (в смысле минимума (1.5)) описывается уравнениями (2.1), (2.4), а управляющие функции Мi и компоненты кинетического момента Li изменяются по законам (2.8), (2.9). Решение (2.8), (2.9) оптимально, так как оно является единственным, что соответствует необходимым условиям оптимальности. Параметр m0 в законах (2.8), (2.9) определяет максимальную величину управляющего момента и максимальный модуль кинетического момента. Константы r0, m0 полностью определяют траекторию вращения во время оптимального управления кинетическим моментом.
Оптимальный управляющий момент М связан с кватернионом Λ следующим образом:
(3.2)
${\mathbf{М}} = {{m}_{0}}(1--2t{\text{/}}Т)\tilde {\Lambda } \circ {{\Lambda }_{{{\text{in}}}}}{{{\mathbf{р}}}_{0}} \circ {{\tilde {\Lambda }}_{{{\text{in}}}}} \circ \Lambda $Любое отличное от (3.2) управление заведомо хуже (в смысле минимума показателя качества (1.5)), потому что не является решением системы уравнений (1.1), (2.1)–(2.3) и не отвечает необходимым условиям оптимальности, сформулированным системой (2.1)–(2.3).
Задача построения оптимального управления М(t) состоит главным образом в нахождении такого значения m0 и вектора р0 = р(0), чтобы в результате вращения твердого тела в соответствии с уравнениями (1.2), (2.1), (2.9) выполнялись равенства Λ(Т ) = Λf и ω(Т) = 0. Для получения функциональной зависимости управлений от фазовых координат необходимо решить уравнения (2.1), которые для закона (2.5) с учетом формул ri = r0pi принимают следующий вид
(3.3)
${{\dot {p}}_{1}} = \frac{{{{J}_{2}} - {{J}_{3}}}}{{{{J}_{2}}{{J}_{3}}}}{{L}_{m}}{{p}_{2}}{{p}_{3}},\quad {{\dot {p}}_{2}} = \frac{{{{J}_{3}} - {{J}_{1}}}}{{{{J}_{1}}{{J}_{3}}}}{{L}_{m}}{{p}_{1}}{{p}_{3}},\quad {{\dot {p}}_{3}} = \frac{{{{J}_{1}} - {{J}_{2}}}}{{{{J}_{1}}{{J}_{2}}}}{{L}_{m}}{{p}_{1}}{{p}_{2}}$Общее решение приведенной системы уравнений найти практически невозможно. Трудность заключается в нахождении граничных значений p(0) и p(T), связанных выражением
Для синтеза оптимального управления кинетическим моментом требуется знание времени оптимального разворота Т и значений постоянных параметров m0,r0, определяющих темп приближения к заданному конечному положению Λ(Т) = Λf, L(Т) = 0. Конкретные положительные величины r0 и m0, а также длительность разворота определяются коэффициентом k0 функционала качества и вектором р0. Убедимся, что найденные ранее постоянные параметры m0, Т для закона управления (3.2) действительно оптимальны. Приняв во внимание соотношение m0Т2 = 6F, запишем значение функционала (1.5) в следующем виде:
илиФункция (3.4) минимальна, если m0 = ${{\sqrt {{{k}_{0}}} } \mathord{\left/ {\vphantom {{\sqrt {{{k}_{0}}} } C}} \right. \kern-0em} C}$. Минимум функции (3.5) соответствует времени разворота T = $\sqrt {{{6S} \mathord{\left/ {\vphantom {{6S} {\sqrt {{{k}_{0}}} }}} \right. \kern-0em} {\sqrt {{{k}_{0}}} }}} $. При этом величина (1.5) для оптимального управления (3.2) равна G = 4k0T/3, т.е. $G = 4\sqrt {{{2{{k}_{0}}S\sqrt {{{k}_{0}}} } \mathord{\left/ {\vphantom {{2{{k}_{0}}S\sqrt {{{k}_{0}}} } 3}} \right. \kern-0em} 3}} $.
4. Некоторые частные случаи оптимального управления. Функции φi(t), ri(t), Li(t) будут оптимальными тогда и только тогда, когда они удовлетворяют уравнениям (2.1), (2.4), (2.5). Ключевой проблемой в решении задачи оптимального управления кинетическим моментом является нахождение значения вектора р0 и времени разворота Т. Постоянная m0 = |М(0)| оптимального закона изменения кинетического момента определяется значением коэффициента k0 минимизируемого показателя качества (р0 зависит исключительно от кватерниона разворота Λt и моментов инерции J1, J2, J3 и не зависит от времени Т). Если р0 известно, то
Управляющие переменные рассчитываются в соответствии с законом (2.8), для исполнения которого надо в каждый текущий момент времени t знать все три переменные р1, р2, р3. Система (1.2), (2.1), (2.5) имеет аналитическое решение только для динамически симметричного и сферического тел. Для сферически-симметричного тела (J1 = J2 = J3) решение следующее:
В случае динамически симметричного тела (например, если J2 = J3) задача оптимального управления кинетическим моментом решается до конца (при дальнейших рассуждениях продольной осью считается ось ОХ). В этом частном, но достаточно распространенном случае оптимальным решением является одновременное вращение твердого тела (например, КА) вокруг некоторого направления η, неподвижного относительно инерциального базиса, и вокруг продольной оси ОХ, которая образует с осью η постоянный угол ϑ. Угловые скорости относительно осей η и ОХ изменяются пропорционально с постоянным коэффициентом пропорциональности, и поэтому можем записать [11, 16]
(4.1)
$\begin{gathered} {{р}_{1}} = {{р}_{{10}}} = {\text{cos}}\vartheta ,\quad {{p}_{2}} = {{p}_{{20}}}\cos \kappa + {{p}_{{30}}}\sin \kappa ,\quad {{p}_{3}} = - {{p}_{{20}}}\sin \kappa + {{p}_{{30}}}\cos \kappa \\ {\text{и}}\quad \kappa = \frac{{J - {{J}_{1}}}}{{{{J}_{1}}J}}\int\limits_0^t {{{L}_{1}}(t)dt} \\ \end{gathered} $(4.2)
$\alpha = \frac{{J - {{J}_{1}}}}{{{{J}_{1}}}}{{p}_{{10}}}\beta ,\quad \cos \frac{\beta }{2}\cos \frac{\alpha }{2} - {{p}_{{10}}}\sin \frac{\beta }{2}\sin \frac{\alpha }{2} = {{\nu }_{0}},\quad \cos \frac{\beta }{2}\sin \frac{\alpha }{2} + {{p}_{{10}}}\sin \frac{\beta }{2}\cos \frac{\alpha }{2} = {{\nu }_{1}}$Функции Li (проекции оптимального кинетического момента L на оси связанной системы координат) рассчитываются по уравнениям (4.1) и (2.9). Искомое решение Mi(t), Li(t) представим в аналитическом виде:
Заметим, что в работе [27] также выписаны все предварительные выражения общего решения задачи оптимального разворота твердого тела (но для другого функционала качества) и до конца доведено решение для случая динамической симметрии тела. Авторы работы [11], решая задачу разворота при условии динамической симметричности твердого тела (из-за чего оптимальное управление обеспечивает вращение КА с постоянным углом отклонения кинетического момента от продольной оси), показали, что решение системы (4.2) существует при любых значениях кватерниона Λt и моментах инерции динамически симметричного тела.
Для динамически симметричного тела параметры закона управления r0, m0, T находятся намного проще (также упрощается определение интеграла F и показателя G). У динамически симметричных тел с продольной осью ОХ |L| = J2${{\dot {\beta }}}$ и F = J2 β, где J2 – момент инерции относительно поперечной оси (J2 = J3); ${{\dot {\beta }}}$ – скорость вращения вокруг кинетического момента L; β – угол поворота КА вокруг вектора L (из физического смысла β ≥ 0). Чтобы показатель (1.5) был минимальным, необходимо чтобы угол β был как можно меньше, для чего потребуем β ≤ π (отсюда понятно, почему система (4.2) включает условие 0 ≤ β ≤ π). Значения r0, Т, Lmax, G зависят только от угла поворота вокруг кинетического момента L и, соответственно, таковы:
Для несимметричного КА (${{J}_{1}} \ne {{J}_{2}} \ne {{J}_{3}}$) решение системы уравнений (1.2), (2.1), (2.5) в аналитическом виде не существует и определяется численными методами (например, методом последовательных приближений или как описано в [16]). Расчет значения p0 осуществляется в процессе решения краевой задачи р(0) = р0, р(Т) = ${{\tilde {\Lambda }}_{{\text{t}}}} \circ {{{\mathbf{p}}}_{0}} \circ {{\Lambda }_{{\text{t}}}}$ для системы (3.3). Как известно [22], решение р0 не зависит от характера изменения функции Lm, которая присутствует в уравнениях (3.3), в силу чего искомый вектор р0 рассчитываем в предположении, что Lm = const ≠ 0, что значительно упрощает решение краевой задачи; так как в этом случае кинетический момент изменяется согласно уравнению
Если кинетический момент изменяется в соответствии с уравнениями (2.1), (2.5), то вне зависимости от характера поведения параметра Lm значение (3.1) следующее [22]:
где Kav – известный отличный от нуля модуль кинетического момента (Kav > 0); tpr – прогнозируемое время достижения условия Λ = Λf для решения Λ(t) системы уравнений (1.2), (2.1), (2.5) с учетом Lm = Kav и Λ(0) = Λin (очевидно, что если Lm(t) = const = Kav, то интеграл (3.1) составляет F = ${{K}_{{{\text{av}}}}}{{t}_{{{\text{pr}}}}}$). Каждому конкретному Kav соответствует свое значение tpr (время tpr обратно пропорционально величине Kav). Приняв какое-то Kav ≠ 0 и интегрируя уравнения (1.2), (4.3) с начальными условиями Λ(0) = Λin, L(0) = Kavр0, получим прогнозируемое время tpr, а затем F.В отличие от известного решения [11], применимого исключительно для тел с осевой симметрией, в представленном оптимальном управлении отсутствуют отрезки времени с постоянным модулем управляющего момента. Кроме того, в предложенном оптимальном решении все управляющие переменные Мi (t) – непрерывные гладкие функции времени.
5. Результаты математического моделирования. Для примера рассмотрим разворот международной космической станции (МКС) из положения, при котором связанные оси совпадают по направлению с одноименными осями инерциального базиса, в положение, соответствующее кватерниону Λf = {0.258819, 0.683013, 0.591506, 0.341506}. Приведем численное решение задачи оптимального управления кинетическим моментом в процессе разворота с минимальной величиной (1.5). Разворот выполняется из положения покоя в положение покоя. Определим оптимальную программу управления М(t), которая переводит МКС из состояния (1.3) в состояние (1.4). Инерционные характеристики МКС полагаем равными [31]: J1 = 4 853 000 кг ⋅ м2, J2 = 23 601 000 кг ⋅ м2, J3 = 26 278 000 кг ⋅ м2. Считаем, что коэффициент k0 = 0.1 Вт/с. Элементы кватерниона разворота Λt имеют следующие значения: ν0 = 0.258819; ν1 = 0.683013; ν2 = 0.591506; ν3 = 0.341506. Вектор р0 находим в результате решения краевой задачи принципа максимума. Из соотношения моментов инерции J1, J2, J3 следует, что ось ОХ – продольная ось КА. При решении краевой задачи принципа максимума в уравнениях (2.5) полагаем Lm = const (и, соответственно, |L| = const), так как искомое значение p0 не зависит от характера изменения функции Lm(t) [22]. Расчет вектора p0 происходит методом последовательных приближений, где в качестве первого приближения берется решение той же краевой задачи для динамически симметричного тела с моментами инерции J1 и J, где J – момент инерции относительно поперечной оси, равный среднему значению между J2 и J3 (принцип осреднения нередко используется исследователями [32]). Было принято значение
При сделанном допущении о динамической симметричности решение p0 находится из уравнений (4.2). В результате получили следующее значение: ${\mathbf{p}}_{0}^{{(0)}}$ = {0.283154; 0.113225; 0.952368}. Рассчитанные в соответствии с системой (4.2) значения p0 и β являются начальным приближением к истинному решению. Они уточняются до тех пор, пока не будут удовлетворять требованиям Λ(0) = Λin, Λ(tpr) = Λf для решения системы уравнений (1.2), (4.3) с начальным кинетическим моментом Lst, определяемым вектором p0 и углом β по формулам:
(5.1)
${{L}_{{1{\text{st}}}}} = \frac{{J\beta }}{T}{{p}_{{10}}},\quad {{L}_{{2{\text{st}}}}} = \frac{{J\beta }}{T}{{p}_{{20}}},\quad {{L}_{{3{\text{st}}}}} = \frac{{J\beta }}{T}{{p}_{{30}}}$Описанная схема итераций аналогична итерационному методу решения уравнения вида x = g(x) для скалярной функции g(x) скалярного (одномерного) аргумента x. При уточнении p0 аргументом является гиперкомплексное число (кватернион) Λt, а функцией – кватернион ${{\Lambda }_{{\text{t}}}} \circ {{\tilde {\Lambda }}_{{\text{f}}}} \circ {{\Lambda }_{{{\text{pr}}}}}$, где Λf – постоянный кватернион, не зависящий от аргумента Λt, а Λpr зависит от аргумента Λt через систему уравнений (4.2), (5.1) посредством модели движения (1.2), (4.3). После изменения Λt меняются вектор p0 (в соответствии с (4.2)) и начальный кинетический момент Lst, и поэтому обновится значение Λpr, что приведет к изменению функции ${{\Lambda }_{{\text{t}}}} \circ {{\tilde {\Lambda }}_{{\text{f}}}} \circ {{\Lambda }_{{{\text{pr}}}}}$. Как только sqal(${{\tilde {\Lambda }}_{{{\text{pr}}}}} \circ {{\Lambda }_{{\text{f}}}}$) ≥ εth, итерационный процесс прекращается, и решение p0 получено. Отмечаем, что |vect(${{\tilde {\Lambda }}_{{\text{f}}}} \circ \Lambda _{{{\text{pr}}}}^{{(k)}}$)| < |vect$\Lambda _{{\text{t}}}^{{(k)}}$| для любого k, поэтому процесс приближения p0 к оптимальному значению сходится. Аналогичный метод нахождения оптимального вектора р0 в решении краевой задачи принципа максимума применялся в задаче максимального быстродействия [16], как один из возможных (хотя и не единственный) итерационных алгоритмов расчета вектора р0 для оптимального управления.
После решения краевой задачи разворота из положения Λ(0) = Λin в положение Λ(Т) = Λf определили основные параметры: p0 = {0.310532; 0.105396; 0.944702}, F = = 38 957 кН ⋅ м ⋅ с2. Соответственно, “функционал пути” составил S = 9078.5 м ⋅ кг1/2. Максимальный модуль управляющего момента m0 = 1357 Н ⋅ м. Время оптимального разворота Т = 415 с, а ρ = 207.5 с. Максимальный модуль кинетического момента составил Lmax = 140.8 кН ⋅ м ⋅ с, а максимальная энергия вращения за время разворота оказалась равной Emax = 538 Дж. Значение константы r0 будет r0 = 4m0/T = 13.08 Н ⋅ м/с. Оптимальный вектор φ(0) = {173.66 × 10–6; 12.12 × 10–6; 97.57 × 10–6}.
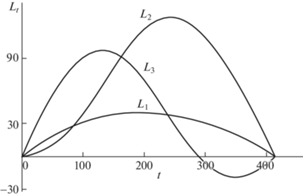
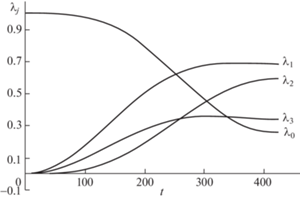
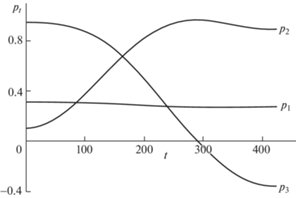
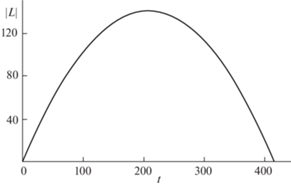
Данные математического моделирования оптимального вращения приведены рис. 1–5. На рис. 1 даны графики изменения проекций кинетического момента на оси связанного базиса L1(t), L2(t), L3(t) по времени (переменные Li приведены в кН ⋅ м ⋅ с, время t дано в секундах). Проекция L1, соответствующая продольной оси КА, не меняет знак, и характер ее изменения повторяет поведение модуля кинетического момента (в отличие от L2 и L3). На рис. 2 представлены графики изменения компонент кватерниона Λ(t), отражающего текущую ориентацию КА во время разворота: λ0(t), λ1(t), λ2(t), λ3(t). На рис. 3 дано изменение составляющих р1(t), р2(t), р3(t) орта р во времени. Отмечаем, что во время оптимального разворота проекция р1 меняется незначительно. На рис. 4 изображены графики изменения управляющих функций М1(t), М2(t), М3(t) (переменные Мi приведены в Н⋅м, время t дано в секундах). Значение (1.5), характеризующее экономичность программы М (t) управления кинетическим моментом, равно G = 4k0T/3 = 55.3 Дж/с. Рис. 5 демонстрирует поведение модуля кинетического момента КА во время разворота (величина |L| дана в кН ⋅ м ⋅ с, время t приведено в секундах). При оптимальном управлении переменные рi и λj являются гладкими функциями времени; переменные Li – гладкие функции времени (за исключением моментов времени t = 0 и t = Т).
Необходимо заметить, что чем больше коэффициент k0, тем меньше время разворота Т и больше энергия Emax, максимальный момент |M(0)| и максимальный модуль кинетического момента Lmax. Значение коэффициента k0 в минимизируемом функционале (1.5) выбрано из условия Emax < 540 Дж (при этом желательно, чтобы время разворота T < 450 с).
Заключение. Исследуется кватернионное решение динамической задачи оптимального управления пространственным разворотом твердого тела (в частности, КА) из произвольного начального в заданное конечное угловое положение. Рассматривается случай, когда в начальный и конечный моменты времени кинетический момент равен нулю. Принятый нами критерий качества объединяет в заданной пропорции энергетические затраты и время, затраченные на переориентацию КА. Вопросы экономичности управления движением КА актуальны и сегодня, а потому предложенная задача управления практически важная. В аналитической форме описаны отличительные свойства оптимального движения. Для нахождения оптимального управления и закономерностей вращения во время перевода КА в заданную ориентацию применялись кватернионные модели движения твердого тела и принцип максимума Л.С. Понтрягина. Выписаны функция Гамильтона, сопряженная система уравнений для исходной оптимизационной задачи и выражения для оптимального управления, отражающие связь управляющих и фазовых переменных. Структура полученной системы дифференциальных уравнений такова, что закономерности оптимального изменения кинетического момента L(t) и оптимального движения Λ(t) обнаруживаются в явном виде. Доказано, что в течение всего разворота отношение кинетической энергии вращения к квадрату модуля кинетического момента КА есть величина постоянная. Сформулированы необходимые условия оптимальности и определена структура оптимального управления; приведены аналитические зависимости для программной траектории движения КА. Поскольку на управляющий момент и на время разворота не наложено никаких ограничений, то маневр переориентации можно выполнить для любых начального и конечного положений. Расчетные формулы для вычисления ключевых характеристик маневра переориентации представлены в явном виде.
Была изложена процедура реализации оптимального программного управления и описана конструктивная схема решения краевой задачи принципа максимума при произвольных моментах инерции КА и условиях разворота. Поведение параметров движения КА в процессе разворота иллюстрируют результаты математического моделирования.
Основное отличие рассмотренной задачи управления состоит в использовании нового критерия оптимальности. Введение в минимизируемый функционал времени, затраченного на разворот (со своим коэффициентом пропорциональности), определяет максимальную величину управляющего момента |M(0)|, максимальный кинетический момент Lmax и, соответственно, длительность маневра T. В течение всего разворота управляющий момент действует вдоль прямой, неподвижной относительно инерциального базиса, абсолютная скорость изменения управляющего момента (как векторная величина) имеет постоянное значение относительно инерциальной системы координат. В отличие от [11], где оптимальным является релейное управление, когда возможен участок вращения по инерции, минимизация принятого показателя качества (1.5) приводит к непрерывному управлению. В оптимальном по критерию (1.5) решении отсутствуют интервалы вращения с постоянным модулем силового момента.
Для динамически симметричного КА получено законченное решение задачи оптимального управления в замкнутой форме. Даны зависимости в виде явных функций времени для оптимальной траектории вращения и соотношения для нахождения ключевых параметров закона управления, поэтому предложенное решение имеет практическое значение. В аналитическом виде записана система уравнений (4.2), позволяющая решить краевую задачу принципа максимума и полностью определить константы алгоритма управления (для расчета оптимальных значений указанных параметров используется разработанное ранее устройство [33]).
Список литературы
Бранец В.Н., Шмыглевский И.П. Применение кватернионов в задачах ориентации твердого тела. М.: Наука, 1973. 320 с.
Алексеев К.Б., Малявин А.А., Шадян А.В. Экстенсивное управление ориентацией космического аппарата на основе нечеткой логики // Полет. 2009. № 1. С. 47–53.
Велищанский М.А., Крищенко А.П., Ткачев С.Б. Синтез алгоритмов переориентации космического аппарата на основе концепции обратной задачи динамики // Изв. РАН. ТиСУ. 2003. № 5. С. 156–163.
Ваньков А.И. Адаптивное робастное управление угловым движением КА с использованием прогнозирующих моделей // Космич. исслед. 1994. Т. 32. Вып. 4–5. С. 13–21.
Раушенбах Б.В., Токарь Е.Н. Управление ориентацией космических аппаратов. М.: Наука, 1974. 600 с.
Levskii M.V. About method for solving the optimal control problems of spacecraft spatial orientation // Probl. Nonlin. Anal. Eng. Sys. 2015. V. 21. № 2. P. 61–75.
Решмин С.А. Пороговая абсолютная величина релейного управления при наискорейшем приведении спутника в гравитационно-устойчивое положение // Доклады Академии наук. 2018. Том 480. № 6. С. 671–675. https://doi.org/10.1134/S1028335818060101
Junkins J. L., Turner J. D. Optimal Spacecraft Rotational Maneuvers. Elsevier. USA, 1986. 515 p.
Молоденков A.В., Сапунков Я.Г. Особые режимы управления в задаче оптимального разворота сферически-симметричного космического аппарата // Изв. РАН. ТиСУ. 2009. № 6. С. 47–54. https://doi.org/10.1134/S1064230709060057
Молоденков А.В., Сапунков Я.Г. Решение задачи оптимального разворота осесимметричного космического аппарата с ограниченным и импульсным управлением при произвольных граничных условиях // Изв. РАН. ТиСУ. 2007. № 2. С. 152–165. https://doi.org/10.1134/S1064230707020189
Бранец В.Н., Черток М.Б., Казначеев Ю.В. Оптимальный разворот твердого тела с одной осью симметрии // Космич. исслед. 1984. Т. 22. Вып. 3. С. 352–360.
Shen H., Tsiotras P. Time-optimal Control of Axi-symmetric Rigid Spacecraft with two Controls // AIAA J. Guid. Contr. Dyn. 1999. V. 22. № 5. P. 682–694. https://doi.org/10.2514/2.4436
Молоденков A.В., Сапунков Я.Г. Аналитическое решение задачи оптимального по быстродействию разворота осесимметричного космического аппарата в классе конических движений // Изв. РАН. ТиСУ. 2018. № 2. С. 131–147. https://doi.org/10.7868/S0002338818020117
Scrivener S., Thompson R. Survey of Time-optimal Attitude Maneuvers // J. Guid. Contr. Dyn. 1994. V. 17. № 2. P. 225–233.
Zhou H., Wang D., Wu B., EK Poh. Time-optimal reorientation for rigid satellite with reaction wheels // Int. J. Contr. 2012. V. 85. № 10. P. 1–12. https://doi.org/10.1080/00207179.2012.688873
Левский М.В. Применение принципа максимума Л.С. Понтрягина к задачам оптимального управления ориентацией космического аппарата // Изв. РАН. ТиСУ. 2008. № 6. С. 144–157. https://doi.org/10.1134/S1064230708060117
Решмин С.А. Пороговая абсолютная величина релейного управления при наискорейшем приведении спутника в желаемое угловое положение // Изв. РАН. ТиСУ. 2018. № 5. С. 30–41. https://doi.org/10.1134/S106423071805012X
Левский М.В. Кинематически оптимальное управление переориентацией космического аппарата // Изв. РАН. ТиСУ. 2015. № 1. С. 119–136. https://doi.org/10.1134/S1064230714050116
Левский М.В. Об одном случае оптимального управления пространственной ориентацией космического аппарата // Изв. РАН. ТиСУ. 2012. № 4. С. 115–130. https://doi.org/10.1134/S1064230712020086
Бирюков В.Г., Челноков Ю.Н. Построение оптимальных законов изменения вектора кинетического момента твердого тела // Изв. РАН. МТТ. 2014. № 5. С. 3–21.
Зелепукина О.В., Челноков Ю.Н. Построение оптимальных законов изменения вектора кинетического момента динамически симметричного твердого тела // Изв. РАН. МТТ. 2011. № 4. С. 31–49. https://doi.org/10.3103/S0025654411040030
Левский М.В. Синтез оптимального управления терминальной ориентацией космического аппарата с использованием метода кватернионов // Изв. РАН. МТТ. 2009. № 2. С. 7–24. https://doi.org/10.3103/S0025654409020022
Левский М.В. Особенности управления ориентацией космического аппарата, оборудованного инерционными исполнительными органами // Мехатроника, автоматизация, управление. 2015. Т. 16. № 3. С. 188–195. https://doi.org/10.17587/mau.16.188-195
Levskii M.V. Special Aspects in Attitude Control of a Spacecraft, Equipped with Inertial Actuators // J. Comp. Sci. Appl. Informat. Technol. 2017. V. 2. № 4. P. 1–9. https://doi.org/10.15226/2474-9257/2/4/00121
Quang M. Lam. Robust and adaptive reconfigurable control for satellite attitude control subject to under-actuated control condition of reaction wheel assembly // Math. Eng. Sci. Aerosp. 2018. V. 9. № 1. P. 47–63.
Левский М.В. Использование универсальных переменных в задачах оптимального управления ориентацией космических аппаратов // Мехатроника, автоматизация, управление. 2014. № 1. С. 53–59.
Стрелкова Н.А. Об оптимальной переориентации твердого тела // Проблемы механики управляемого движения. Нелинейные динамические системы. Пермь: ПГУ, 1990. С. 115–133.
Зубов Н.Е., Ли М.В., Микрин Е.А., Рябченко В.Н. Терминальное построение орбитальной ориентации космического аппарата // Изв. РАН. ТиСУ. 2017. № 4. С. 154–173. https://doi.org/10.1134/S1064230717040190
Понтрягин Л.С., Болтянский В.Г., Гамкрелидзе Р.В., Мищенко Е.Ф. Математическая теория оптимальных процессов. M.: Наука, 1983. 392 с.
Янг Л. Лекции по вариационному исчислению и теории оптимального управления. М.: Мир, 1974. 488 с.
Банит Ю.Р., Беляев М.Ю., Добринская Т.А., Ефимов Н.И., Сазонов В.В., Стажков В.М. Определение тензора инерции международной космической станции по телеметрической информации. Препринт ИПМ им. М.В. Келдыша РАН. № 57. М.: ИПМ, 2002.
Журавлев В.Ф., Климов Д.М. Прикладные методы в теории колебаний. М.: Наука, 1988. 328 с.
Левский М.В. Устройство формирования параметров регулярной прецессии твердого тела. Патент на изобретение РФ № 2146638 // Бюллетень “Изобретения. Заявки и патенты”. 2000. № 8. С. 148.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика твердого тела