1. На главную
  2. Электронные версии
  3. Известия РАН. Механика твердого тела
  4. № 1, 2023

Известия РАН. Механика твердого тела, 2023, № 1, стр. 95-101

К СТАТИЧЕСКОЙ УСТОЙЧИВОСТИ ФОРМЫ ПОПЕРЕЧНОГО СЕЧЕНИЯ ТРУБОПРОВОДА, ЦИЛИНДРИЧЕСКОЙ ОБОЛОЧКИ, УГЛЕРОДНОЙ НАНОТРУБКИ

А. Г. Хакимов a, *

a Институт механики им. Р.Р. Мавлютова УФИЦ РАН
Уфа, Россия

* E-mail: hakimov@anrb.ru

Поступила в редакцию 17.02.2022
После доработки 21.04.2022
Принята к публикации 26.04.2022

Полный текст (PDF)

Аннотация

На основе предположения о начальной деформированной форме поперечного сечения трубопровода, цилиндрической оболочки, углеродной нанотрубки (УНТ) без начальных напряжений определяются критические давления внутри и вне этих элементов конструкций. Изучено статическое взаимодействие неустойчивостей под действием вышеуказанных факторов.

Ключевые слова: трубопровод, цилиндрическая оболочка, УНТ, жидкость, газ, плотность, давление

1. Введение. Актуальность работы заключается в том, что до сих пор не учитывается влияние среднего давления на устойчивость кругового поперечного сечения трубопровода, цилиндрической оболочки, УНТ. Эти элементы конструкций широко применяются в нефте–газо–продуктопроводах, в ракетных и авиационных двигателях, в воздушной и гидравлической системах самолетов и т.д. В гидроупругих системах одновременно происходит взаимодействие упругих и гидродинамических неустойчивостей. Внешние воздействия могут быть как независимыми друг от друга, так и связанными [1]. Этой теме посвящена обширная литература. К ней примыкает также серия работ по колебаниям тонкостенных тел, не контактирующих с внешней средой. Работа [2] посвящена аналитическому и численному исследованиям свободных колебаний цилиндрических оболочек с акустической средой. Сравнительный анализ результатов расчетов, полученных для моделей сжимаемой и несжимаемой среды, показывает, что при решении задачи определения параметров свободных колебаний оболочки сжимаемостью среды можно пренебречь. В то же время для решения практических задач, требующих учета полного спектра собственных частот системы оболочка–среда, должна использоваться модель сжимаемой среды, в рамках которой получены результаты о влиянии жесткости оболочки на спектр частот объема среды. Некоторые результаты решений для цилиндрических оболочек, в том числе взаимодействующих со средой, представлены в статьях [3–5].

В [6] представлен метод, позволяющий определять частоты колебаний цилиндрических оболочек бесконечной длины в акустической среде. Полученные результаты показывают, что существует низкая частота, когда излучение не происходит, и высокая частота, когда внешний источник обеспечивает передачу энергии, которая излучается. Резонанс возникает только в диапазоне низких частот. Метод требует только модификации для учета эффекта статического давления в окружающей среде.

Среди многочисленных видов применения микро- и нанопленок, нанопроволок, нанотрубок может быть указано также использование их в качестве детекторов и сенсоров в химии, биологии и т.д [7–9].

Моделируя микротрубки тонкими упругими цилиндрическими оболочками [10], получены собственные частоты и собственные моды ограниченных упругих колебаний в системе оболочка–жидкость. Метод молекулярной механики (MM) применяется для определения частот и форм собственных колебаний, а также для определения критических параметров выпучивания и послекритических форм деформирования закрученных по торцам однослойных УНТ [11].

Обзор инженерных микро- и наноматериалов для биомедицинского применения приводится в [12], который дает представление об уникальных свойствах технологии микроигл и ее способности к эффективному трансдермальному транспорту терапевтических соединений.

Однако во всех этих работах влияние среднего давления сред и разности площадей выпуклой и вогнутой поверхностей не учитывается. Это взаимодействие принимается во внимание в статьях [13, 14] в случае легких газов, когда присоединенная масса сред мала. В [15] определяется спектр частот двухопорного резонатора с учетом взаимодействия среднего избыточного давления на поверхности резонатора и кривизны, а также действия осевой нагрузки.

В данной работе определяются критические давления внутри и вне трубопровода, цилиндрической оболочки, УНТ с учетом действия среднего избыточного давления на их поверхностях.

Например, ввиду одинакового давления по всей поверхности УНТ объектом исследования может быть принято кольцо с эффективными значениями радиуса R, толщины h, ширины b, плотности по площади ρh, модуля упругости Е и коэффициента Пуассона ν. Кольцо образуется зигзагообразным рядом атомов углерода [16, 17]. Если ось x направлена вдоль трубки, ось y = Rθ по окружности (θ – центральный угол), то расстояние по y равно a = lcos30○ = 0.123 нм. На рис. 1, a в виде равностороннего треугольника показана площадь S, приходящаяся на один атом. При $4S = 3\sqrt 3 {{l}^{2}}$ эффективная ширина кольца равна $b = S{{a}^{{ - 1}}}$ = 0.213 нм. Так как масса атома углерода равна m = 1.99 × 10–26 кг, то эффективная плотность по площади

(1.1)
$\rho h = m{{S}^{{ - 1}}} = {\text{ }}0.76 \times {{10}^{{--6}}}\,\,{\text{кг}} \cdot {{{\text{м}}}^{{ - 2}}}$
Рис. 1.

(a) Кольцо шириной b, образованное двумя поперечными сечениями углеродной нанотрубки. Площадь, приходящаяся на один атом С, показана пунктирными линиями (равносторонний треугольник). (b) Поперечное сечение УНТ хиральности зигзаг (K, 0) на плоскости (x, y). Показан случай K = 15, при этом поперечное сечение характеризуется N = 2K = 30 атомами углерода. (c) Первая гармоника изгибных колебаний УНТ, соответствующая номеру n = 2 в выражении (3.1). Показано на примере УНТ (27.0), для которой N = 54 и радиус R = 9.47 Å.

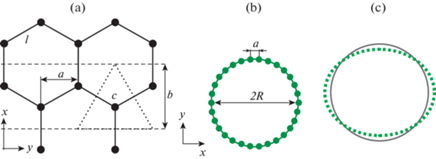
Во многих работах (в том числе в обзорных статьях [18–20]) приводятся значения модуля упругости Е = (1–5) × 106 МПа, толщины однослойного графена h = 0.07–0.34 нм. Эти данные получены экспериментально, а также с привлечением теоретического моделирования. Разброс значений Е и h объясняется разными образцами для испытаний, аппаратурой, методами определения и т.д. Эффективный радиус R определяется через число атомов N, образующих кольцо рис. 1, b.

(1.2)
$2\pi R = aN$

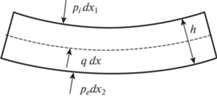
2. Постановка задачи. На внутреннюю и внешнюю поверхности элемента конструкции действуют давления pi и pe жидкостей с плотностями ρi и ρe (рис. 2). Здесь pi, pe – избыточные давления. При определении нагрузки q исходим из предположения, что ρi, ρe и pi, pe остаются постоянными при изменении формы поперечного сечения. Предполагается идеальность и несжимаемость жидкостей. Давления внутри и вне трубопровода pi, pe изменяются независимо друг от друга. Интенсивность их возрастания от нуля будем считать такой, чтобы инерционные силы в системе были малы.

Рис. 2.

Элемент dx срединной поверхности изогнутой оболочки.

При pi = 0, pe = 0 поперечное сечение конструкции имеет малое отклонение от круговой формы в виде (рис. 1, c)

(2.1)
${{w}_{0}} = {{W}_{{0n}}}\cos n{{\theta ,}}\quad n = 2,3,...$
где W0n – амплитуда малого начального отклонения; радиальные перемещения считаем положительными, если они происходят в направлении к центру поперечного сечения конструкции. При этом остаточные напряжения в нем отсутствуют, например, в результате отжига [1].

Уравнение радиальной статики тонкого кольца относительно функции прогиба в предположении о нулевой деформации срединной поверхности имеет вид [21]

(2.2)
$\frac{{{{\partial }^{6}}w}}{{\partial {{\theta }^{6}}}} + 2\frac{{{{\partial }^{4}}w}}{{\partial {{\theta }^{4}}}} + \frac{{{{\partial }^{2}}w}}{{\partial {{\theta }^{2}}}} - \frac{{T{{R}^{2}}}}{D}\left( {\frac{{{{\partial }^{4}}\left( {{{w}_{0}} + w} \right)}}{{\partial {{\theta }^{4}}}} + \frac{{{{\partial }^{2}}\left( {{{w}_{0}} + w} \right)}}{{\partial {{\theta }^{2}}}}} \right) = \frac{{{{R}^{4}}}}{D}\frac{{{{\partial }^{2}}q}}{{\partial {{\theta }^{2}}}}$
где q – давление, приведенное к срединной поверхности, T – кольцевое растягивающее усилие при pi > pe, которое находится по формуле

(2.3)
$T = {{p}_{i}}\int\limits_0^{{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}} {\left( {R - \frac{h}{2}} \right)} \cos \theta d\theta - {{p}_{e}}\int\limits_0^{{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}} {\left( {R + \frac{h}{2}} \right)} \cos \theta d\theta = \left( {{{p}_{i}} - {{p}_{e}}} \right)R - \left( {{{p}_{i}} + {{p}_{e}}} \right)\frac{h}{2}$

Линейное уравнение (2.2) получено преобразованием дифференциальных уравнений равновесия элемента кольца в проекциях на касательную и нормаль с учетом изменения кривизны линии поперечного сечения [21].

Распределенная сила q определяется по формуле [13, 14]

(2.4)
$q = {{p}_{e}} - {{p}_{i}} + \frac{{\left( {{{p}_{i}} + {{p}_{e}}} \right)h}}{{2R}}$

Уравнение статики элемента конструкции (2.2) с учетом (2.3), (2.4) для рi, рe, R не зависящих от θ, записывается

(2.5)
$\frac{{{{\partial }^{6}}w}}{{\partial {{\theta }^{6}}}} + 2\frac{{{{\partial }^{4}}w}}{{\partial {{\theta }^{4}}}} + \frac{{{{\partial }^{2}}w}}{{\partial {{\theta }^{2}}}} - \left[ {\left( {{{p}_{i}} - {{p}_{e}}} \right)R - \left( {{{p}_{i}} + {{p}_{e}}} \right)\frac{h}{2}} \right]\frac{{{{R}^{2}}}}{D}\left( {\frac{{{{\partial }^{4}}\left( {{{w}_{0}} + w} \right)}}{{\partial {{\theta }^{4}}}} + \frac{{{{\partial }^{2}}\left( {{{w}_{0}} + w} \right)}}{{\partial {{\theta }^{2}}}}} \right) = 0$

3. Изгиб оболочки. Примем частное решение уравнения (2.5) в виде

(3.1)
$w = {{W}_{n}}\cos n{{\theta ,}}\quad n = 2,3,...$.
где Wn – амплитуда малого отклонения. Подставляя (2.1), (3.1) в уравнение (2.5), получаем отношение амплитуды текущего прогиба к амплитуде начального прогиба

(3.2)
$\frac{{{{W}_{n}}}}{{{{W}_{{0n}}}}} = \frac{{3\left( {{{\alpha }_{1}} - \alpha } \right)}}{{{{n}^{2}} - 1 - 3\left( {{{\alpha }_{1}} - \alpha } \right)}},\quad {{\alpha }} = \frac{{\left( {{{p}_{i}} - {{p}_{e}}} \right){{R}^{3}}}}{{3D}},\quad {{{{\alpha }}}_{1}} = \frac{{\left( {{{p}_{i}} + {{p}_{e}}} \right)}}{2}\frac{{{{R}^{2}}h}}{{3D}}$

Здесь параметр α учитывает перепад давления pi – pe, а параметр α1 учитывает действие среднего давления (pi + pe)/2. Из (3.2) видно, что прогиб тем больше, чем меньше величина давления внутри оболочки pi и больше давление вне оболочки pe. При α1 – α = (n2 – 1)/3 прогиб в рассматриваемом линейном приближении растет неограниченно. Причем это выражение представляет собой критическую комбинацию внешних воздействий pi, pe, для системы с заданными параметрами материалов и размерами E, h, R. С возрастанием внешних воздействий рост прогиба (3.2) происходит наиболее быстро при n = 2. Указанная критическая комбинация внешних воздействий по (3.2) является минимальной при n = 2. Таким образом, получено условие устойчивости кругового поперечного сечения трубопровода, цилиндрической оболочки, УНТ с учетом действия среднего давления.

4. Анализ результатов и примеры. При α = 0, α1 = 1 происходит потеря устойчивости круговой формы поперечного сечения конструкции в виде эллипса (n = 2), причем, критическое давление потери устойчивости равно

${{p}_{{ecr}}} = {{p}_{{icr}}} = \frac{{3D}}{{{{R}^{2}}h}} = \frac{{E{{h}^{2}}}}{{4{{R}^{2}}(1 - {{\nu }^{2}})}}$
откуда следует, что оболочка может потерять устойчивость даже при нулевом перепаде давления вследствие действия среднего давления. Например, при E = 2 × 105 МПа, ν = = 0.3, R = 0.1 м, h = 0.002 м и при нулевом перепаде давления критическое давление потери устойчивости pecr равно 21.9 МПа.

Для одностенной УНТ с хиральностью кресло (10, 10), радиусом R = 0.678 нм [22] для модуля упругости E = 0.972 · 106 МПа, коэффициента Пуассона ν = 0.278 [18] и толщине h, принятой равной 0.052 нм, при нулевом перепаде давления критическое давление потери устойчивости pecr равно 1.55 ГПа [22], что соответствует давлению перехода круговой формы поперечного сечения к эллиптической или потере устойчивости кругового поперечного сечения одностенной УНТ.

При n = 2 из условия устойчивости кругового поперечного сечения трубопровода, цилиндрической оболочки, УНТ с учетом действия среднего давления следует выражение для критического внешнего давления pecr

${{p}_{{ecr}}} = {{p}_{i}}\frac{{2R - h}}{{2R + h}} + \frac{{6D}}{{{{R}^{2}}\left( {2R + h} \right)}}$

Если оболочка или трубопровод находятся в море, то критическая глубина погружения Hcr определяется

$\,{{H}_{{cr}}} = - \frac{{{{p}_{{ecr}}}}}{{\rho g}}$
где ρ, g – плотность воды и ускорение свободного падения.

Конструкция трубопроводов, состоящих из слоистых (концентрических) труб, обеспечивает хорошие балластные, теплоизоляционные и антикоррозионные свойства [23–25], частично защищает от механических повреждений, пластических деформаций, трещинообразования.

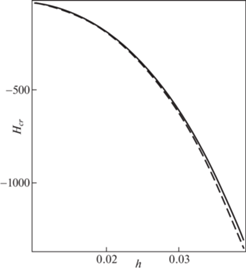
На рис. 3 приводятся зависимости критической глубины погружения Hcr (м) от суммарной толщины стенки h (м) трубопровода, состоящего из слоистых (концентрических) труб, обеспечивающих хорошие балластные, теплоизоляционные и антикоррозионные свойства [23–25] для внутреннего давления pi = 0.1 МПа, приведенного модуля упругости слоистого трубопровода E = 1.5 × 105 МПа, коэффициента Пуассона ν = 0.3, радиуса R = 0.57 м, плотности воды ρ = 1000 кг/м3, ускорения свободного падения g = 9.8 м/с без учета и с учетом действия среднего давления (штриховая, сплошная линии соответственно). Видно, что учет среднего давления приводит к уменьшению критической глубины погружения.

Рис. 3.

Зависимости критической глубины погружения Hcr (м) от толщины трубопровода h (м).

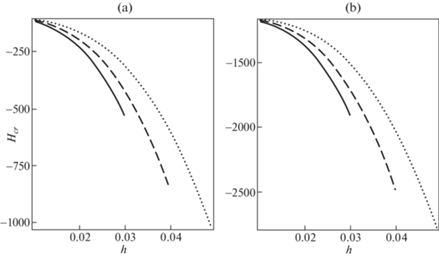
На рис. 4 приводятся зависимости критической глубины погружения Hcr (м) от суммарной толщины стенки h (м) трубопровода, состоящего из слоистых (концентрических) труб, для коэффициента Пуассона ν = 0.3, плотности воды ρ = 1000 кг/м3, ускорения свободного падения g = 9.8 м/с и разных значений приведенного модуля упругости слоистого трубопровода E = 2.0, 1.5, 1.0 × 105 МПа (сплошная, штриховая, пунктирная линии соответственно): (a) радиус R равен 0.7 м, внутреннее давление pi = = 1 МПа; (b) радиус R равен 0.57 м, внутреннее давление pi = 11.5 МПа. Предполагается, что плавучесть трубопровода отрицательная. Видно, что с увеличением толщины стенки трубопровода и уменьшением его радиуса критическая глубина погружения увеличивается.

Рис. 4.

Зависимости критической глубины погружения Hcr (м) от толщины трубопровода h (м).

5. Заключение. Оболочка может потерять устойчивость даже при нулевом перепаде давления вследствие действия среднего давления.

Получено условие устойчивости кругового поперечного сечения трубопровода, цилиндрической оболочки, УНТ с учетом действия среднего давления.

Эти результаты могут быть использованы при моделировании деформирования оболочек, контактирующих с жидкостью и газом, в том числе микро- и наноразмеров. Исследование выполнено за счет гранта Российского научного фонда № 22-21-00578.

Список литературы

  1. Ильгамов М.А. Взаимодействие неустойчивостей Эйлера, Гельмгольца, Релея // ЖТФ. 2018. Т. 63. № 2. С. 163–167. https://doi.org/10.21883/JTF.2018.02.45401.2144

  2. Дяченко И.А., Миронов А.А. Аналитические и численные исследования свободных колебаний цилиндрических оболочек с акустической средой // Проблемы прочности и пластичности. 2021. Т. 83. № 1. С. 35–48. https://doi.org/10.32326/1814-9146-2021-83-1-35-48

  3. Leizerovich G.S., Taranukha N.A. Nonobvious features of dynamics of circular cylindrical shells // Mech. Solids. 2008. V. 43. № 2. P. 246–253. https://doi.org/10.3103/S0025654408020106

  4. Rawat A., Matsagar V., Nagpal A. Finite element analysis of thin circular cylindrical shells // Proc. Indian Nat. Sci. Acad. 2016. V. 82. № 2. P. 349–355. https://doi.org/10.16943/ptinsa/2016/48426

  5. Farshidianfar A., Oliazadeh P. Free vibration analysis of circular cylindrical shells: comparison of different shell theories // Int. J. Mech. Appl. 2012. V. 2. № 5. P. 74–80. https://doi.org/10.5923/j.mechanics.20120205.04

  6. Bleich H.H., Baron M.L. Free and Forced vibration of an infinitely long cylindrical shell in an infinite acoustic medium // J. Appl. Mech. Trans. ASME. 1954. V. 21. № 2. P. 167–177.

  7. O’Connell A.D., Hofheinz M., Ansmann Mю et al. Quantum ground state and single-phonon control of a mechanical resonator // Nature. 2010. V. 464. P. 697–703. https://doi.org/10.1038/nature08967

  8. Burg T.P., Godin M., Knudsen S.M. et al. Weighing of biomolecules, single cells and single nanopar- ticles in f luid // Nature. 2007. V. 446. P. 1066–1069. https://doi.org/10.1038/nature05741

  9. Husale S., Persson H.H.J., Sahin O. DNA nanomechanics allows direct digital detection of comple- mentary DNA and microRNA targets // Nature. 2009. V. 462. P. 1075–1078. https://doi.org/10.1038/nature08626

  10. Sirenko Y.M., Stroscio M.A., Kim K.W. Elastic vibrations of microtubules in a fluid // Phys. Rev. V. 53. № 1. 1996. P. 1003–1010.

  11. Аннин Б.Д., Алехин В.В., Бабичев А.В., Коробейников С.Н. Применение метода молекулярной механики к задачам устойчивости и собственных колебаний однослойных углеродных нанотрубок // Изв. РАН. МТТ. 2012. № 5. С. 65–83.

  12. Chen Y., Alba M., Tieu T., Tong Z., Minhas R.S., Rudd D., Voelcker N.H., Cifuentes-Rius A., and Elnathan R. Engineering Micro-Nanomaterials for Biomedical Translation // Adv. NanoBiomed Res. 2021. № 1. P. 2100002. https://doi.org/10.1002/anbr.202100002

  13. Ильгамов М.А. Влияние давления окружающей среды на изгиб тонкой пластины и пленки // ДАН. 2017. Т. 476. № 4. С. 402–405.

  14. Ильгамов М.А. Влияние поверхностных эффектов на изгиб и колебания нанопленок // ФТТ. 2019. Т. 61. № 10. С. 1825–1830.

  15. Ilgamov M.A., Khakimov A.G. Influence of pressure on the frequency spectrum of micro and nanoresonators on hinged supports // J. Appl. Comput. Mech. 2021. V. 7. № 2. P. 977–983. https://doi.org/10.22055/JACM.2021.36470.2848

  16. Дмитриев С.В., Сунагатова И.Р., Ильгамов М.А., Павлов И.С. Собственные частоты радиальных колебаний углеродных нанотрубок // ЖТФ. 2021. Т. 91. Вып. 11. С. 1732–1737. https://doi.org/10.21883/JTF.2021.11.51536.127-21

  17. Dmitriev S.V., Semenov A.S., Savin A. ., Ilgamov M.A., Bachurin D.V. Rotobreather in a carbon nanotube bundle // Journal of Micromechanics and Molecular Physics 2021, 2050010. https://doi.org/10.1142/S2424913020500101

  18. Елецкий А.В. Механические свойства углеродных нанотрубок и материалов на их основе // Усп. физ.наук. 2007. Т. 177. № 3. С. 233–274.

  19. Harik V.M. Ranges of applicability for the continuum beam model in the mechanics of carbon nanotubes and nanorods // Solid State Commun. 2001. V. 120. P. 331–335. https://doi.org/10.1016/S0038-1098(01)00383-0

  20. Qian D., Wagner G.J., Lin W.K., Ju M.F., Ruoff R.S. Mechanics of carbon nanotubes // Appl. Mech. Rev. 2002. V. 55. № 6. P. 495–532. https://doi.org/10.1115/1.1490129

  21. Timoshenko S.P., Young D.H., Weaver W. Vibration Problems in Engineering. New York: John Wiley & Sons, 1974.

  22. Wu J., Zang J., Larade B., Guo H., Gong X.G., Liu F. Computational design of carbon nanotube electromechanical pressure sensors // Phys. Rev. B. 2004. V. 69. P. 153406. https://doi.org/10.1103/PhysRevB.69.153406

  23. Bi K., Hao H. Using pipe-in-pipe systems for subsea pipeline vibration control // Eng. Struct. 2016. V. 109. P. 75–84. https://doi.org/10.1016/j.engstruct.2015.11.018

  24. Davaripour F., Quinton B.W.T., Pike K. Effect of damage progression on the plastic capacity of a subsea pipeline // Ocean Eng. 2021. V. 234. https://doi.org/10.1016/j.oceaneng.2021.109118

  25. Cheng A., Chen N.-Z. Corrosion fatigue crack growth modelling for subsea pipeline steels // Ocean Eng. 2017. V. 142. P. 10–19. https://doi.org/10.1016/j.oceaneng.2017.06.057

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика твердого тела

Архивы выпусков Информация о журнале Отправить рукопись в журнал