Известия РАН. Механика твердого тела, 2023, № 1, стр. 3-32

1. Устранение особенностей типа сингулярности (деления на ноль) в классических уравнениях небесной механики и астродинамики, записанных во вращающихся системах координат и использующих углы Эйлера (угловые оскулирующие элементы орбиты) для описания орбитального движения изучаемого тела. Эффективность аналитического исследования и численного решения задач небесной механики и механики космического полета (астродинамики) во многих случаях повышается за счет использования уравнений орбитального движения, записанных в той или иной вращающейся (промежуточной (intermediate)) системе координат с помощью использования таких понятий как форма, размеры и ориентация мгновенной орбиты изучаемого движущегося тела (например, космического аппарата (КА), астероида). В уравнениях движения такого рода присутствуют переменные, характеризующие угловое движение используемой вращающейся системы координат или ориентацию мгновенной орбиты, или плоскости орбиты движущегося тела.

В качестве таких переменных в механике и астродинамике традиционно используются углы Эйлера (угловые оскулирующие элементы орбиты) или направляющие косинусы. Использование углов Эйлера позволяет записать уравнения орбитального движения в наглядной форме, но приводит к появлению в уравнениях движения громоздких тригонометрических выражений и дополнительных особых точек (деление на ноль), в которых уравнения вырождаются. Так, в состав широко используемых уравнений Ньютона–Эйлера для оскулирующих элементов (медленно изменяющихся переменных) [1, 2] входят дифференциальные уравнения для угловых элементов: долготы восходящего узла, наклона (наклонения) орбиты, углового расстояния перицентра от узла. Эти уравнения вырождаются, когда угол наклона мгновенной орбиты изучаемого тела становится равным нулю или 180 градусам. Использование направляющих косинусов позволяет устранить тригонометрические выражения и указанную особенность уравнений движения изучаемого тела, однако приводит к существенному повышению размерности системы уравнений движения и к потере геометрической наглядности.

Этих недостатков использования углов Эйлера и направляющих косинусов удается избежать, если в качестве параметров ориентации используемой вращающейся системы координат или мгновенной орбиты изучаемого тела, или плоскости его орбиты выбрать параметры Эйлера (Родрига–Гамильтона). В этом случае для описания ориентации этой системы координат и орбиты изучаемого тела удобно использовать гиперкомплексную переменную – кватернион поворота Гамильтона, компонентами которого являются вещественные параметры Эйлера. При этом в составе уравнений траекторного (орбитального) движения появляется дифференциальное кватернионное уравнение углового движения используемой вращающейся системы координат или мгновенной орбиты, или плоскости орбиты изучаемого тела, имеющее компактную, симметричную и невырождающуюся структуру. Эти уравнения в настоящее время стали широко использоваться в небесной механике и астродинамике, также как и кватернионные уравнения в четырехмерных переменных Кустаанхеймо–Штифеля и параметрах Эйлера, регулярные для орбитального движения тела в гравитационных и других центральных силовых полях (в этих регулярных кватернионных уравнениях устраняются другие особенности (деление на ноль), порождаемые действием гравитационных сил).

Параметры Эйлера (Родрига–Гамильтона) и кватернионы поворотов Гамильтона давно и успешно используются в механике, навигации и управлении движением для описания углового (вращательного) движения твердого тела, в частности, космического аппарата. Использование параметров Эйлера и кватернионов для описания орбитального (поступательного, траекторного) движения и для построения кватернионных динамических уравнений такого движения стало распространенным сравнительно недавно.

В первой части нашей работы [3] дан обзор и анализ известных нам регулярных моделей небесной механики и астродинамики, построенных с использованием вещественных параметров Эйлера (Родрига–Гамильтона) и кватернионов поворота Гамильтона на основе дифференциальных уравнений возмущенной пространственной задачи двух тел с помощью их записи в той или иной вращающейся системе координат. В этих моделях устранены особенности (деление на ноль), порождаемые использованием в классических уравнениях углов Эйлера. Рассмотрены приложения этих моделей в задачах оптимального управления орбитальным движением космического аппарата, решаемых с использованием принципа максимума Понтрягина. Показано, что эффективность аналитического исследования и численного решения краевых задач оптимального управления траекторным (орбитальным) движением космических аппаратов может быть кардинально повышена за счет использования указанных регулярных кватернионных моделей астродинамики.

Также дан обзор и анализ публикаций, в которых используются дуальные параметры Эйлера (Родрига–Гамильтона) с комплексностью Клиффорда s, обладающей свойством s² = 0, и дуальные кватернионы (бикватернионы Клиффорда) для решения задач управления общим пространственным движением твердого тела (космического аппарата), представляющим собой композицию углового (вращательного) и траекторного (орбитального) движений, с использованием принципа обратной связи (с использованием дуальных обратных связей).

В этой (второй) части работы нами получены новые регулярные кватернионные уравнения небесной механики и механики космического полета. Уравнения построены в рамках возмущенной пространственной ограниченной задачи трех тел. К ним относятся уравнения траекторного движения, записанные в неголономной или в орбитальной, или в идеальной системах координат. Для описания вращательного движения этих систем координат использованы вещественные параметры Эйлера (Родрига–Гамильтона) и кватернионы поворотов (вращений) Гамильтона. Из полученных уравнений следуют, как частные, регулярные модели небесной механики и астродинамики, построенные ранее автором статьи и другими исследователями с использованием параметров Эйлера и кватернионов Гамильтона на основе дифференциальных уравнений возмущенной пространственной задачи двух тел. Полученные в статье уравнения целесообразно использовать для решения в рамках возмущенной пространственной ограниченной задачи трех тел (Земля, Луна, космический аппарат) такой актуальной задачи механики космического полета, как полет космического аппарата на Луну.

В статье также выведены другие новые регулярные кватернионные уравнения возмущенной пространственной ограниченной задачи трех тел. Уравнения построены с использованием двухмерных идеальных прямоугольных координат Ганзена, параметров Эйлера и кватернионных переменных, а также комплексных композиций параметров Эйлера (параметров Кейли–Клейна) (используемая в них традиционная комплексность i обладает свойством i² = –1).

2. Исходные дифференциальные уравнения возмущенной пространственной ограниченной задачи трех тел. Задачи регуляризации уравнений. Рассмотрим три материальные точки M₀, M₁ и M₂ с массами m₀, m₁ и m₂, взаимно притягивающие друг друга по закону всемирного тяготения. Неограниченная задача трех тел состоит [1, 2] в определении и изучении всевозможных движений материальных точек M₀, M₁ и M₂. Ограниченная задача трех тел – это задача [1, 2] о движении материальной точки M₂ = M с нулевой массой m₂ = 0 (точнее с массой m₂, пренебрежимо малой по сравнению с массами m₀ и m₁), притягиваемой по закону Ньютона двумя другими материальными точками M₀ и M₁, имеющими отличные от нуля массы m₀ и m₁.

Ограниченная задача трех тел представляет собой [1, 2] предельный вариант неограниченной задачи трех тел. Она нашла широкое применение как в классической небесной механике (например, теория движения Луны), так и в механике космического полета (например, задача достижения Луны). Дифференциальные уравнения ограниченной задачи трех тел получаются из уравнений неограниченной задачи трех тел (5.1.04) [1], если в них положить m₂ = 0, и имеют вид

Здесь ξ₀, η₀, ζ₀; ξ₁, η₁, ζ₁ и ξ₂, η₂, ζ₂ – декартовы координаты материальных точек M₀, M₁ и M₂ в инерциальной системе координат Oξηζ (т.е. в системе координат, в которой выполняются законы Ньютона); ${{\Delta }_{{01}}}$, ${{\Delta }_{{02}}}$, ${{\Delta }_{{12}}}$ – взаимные расстояния между точками M₀ и M₁, M₀ и M₂, M₁ и M₂ соответственно;  f – гравитационная постоянная.

Отметим, что в уравнениях (2.1), (2.2) в отличие от уравнений (5.1.04) [1], дополнительно введены проекции p_ξ, p_η и p_ζ на оси инерциальной системы координат Oξηζ возмущающего ускорения p материальной точки M₂ от других действующих на точку M₂ = M сил, не вызванных силами гравитационного притяжения, действующими со стороны точек M₀ и M₁.

Введем векторы r₀ = $\overrightarrow {{{M}_{0}}M} $, r₁ = $\overrightarrow {{{M}_{1}}M} $, r₀₁ = ${{\overrightarrow {{{M}_{0}}M} }_{1}}$, r₁₀ = ${{\overrightarrow {{{M}_{1}}M} }_{0}}$ = –r₀₁. Проекции векторов r₀ и r₁ на оси инерциальной системы координат Oξηζ соответственно равны ξ₂ – ξ₀, η₂ – η₀, ζ₂ – ζ₀ и ξ₂ – ξ₁, η₂ – η₁, ζ₂ – ζ₁.

Используя введенные векторы r₀ и r₁ в качестве новых векторных переменных, из дифференциальных уравнений (2.1) получим следующую векторную форму дифференциальных уравнений возмущенной ограниченной задачи трех тел:

Дифференциальное уравнение (2.3) описывает движение точки M₂ = M в системе координат M₀X₀Y₀Z₀, имеющей начало в точке M₀ и координатные оси M₀X₀, M₀Y₀, M₀Z₀, параллельные одноименным осям инерциальной системы координат Oξηζ, а дифференциальное уравнение (2.4) – движение этой же точки в системе координат M₁X₁Y₁Z₁, имеющей начало в точке M₁ и координатные оси M₁X₁, M₁Y₁, M₁Z₁, также параллельные одноименным инерциальным осям Oξ, Oη, Oζ.

Дифференциальное уравнение (2.3) может рассматриваться независимо от дифференциального уравнения (2.4), если в нем использовать соотношение r₁ = r₀ – r₀₁ и учесть, что вектор r₀₁ удовлетворяет дифференциальному уравнению

невозмущенной задачи двух тел (M₀ и M₁), которое, как известно, интегрируется. Поэтому можно считать, что вектор r₀₁, фигурирующий в уравнении (2.3), является известной функцией времени: r₀₁ = r₀₁(t). Аналогично, дифференциальное уравнение (2.4) может рассматриваться независимо от дифференциального уравнения (2.3), если в нем использовать соотношение r₀ = r₁ – r₁₀ и учесть, что вектор r₁₀ = –r₀₁ является известной функцией времени.

Уравнения (2.3) и (2.4) могут также рассматриваться как система двух дифференциальных уравнений с неизвестными векторными переменными r₀ и r₁.

Отметим, что координатная запись уравнения (2.3) совпадает (при p = 0) с уравнениями ограниченной задачи трех тел (6.1) [2].

Уравнения (2.3) и (2.4) можно также записать в виде

Векторные уравнения (2.3) и (2.4) или (2.6) и (2.7) возмущенной пространственной ограниченной задачи трех тел содержат особые точки r₀ = 0, r₁ = 0, в которых эти уравнения вырождаются. Такого рода особенности (сингулярности) создают не только теоретические, но и практические (вычислительные) трудности в небесной механике и астродинамике, в особенности при изучении движения небесных и космических тел по сильно вытянутым орбитам.

Проблема устранения этих особенностей (как отдельное исключение одной из этих особенностей, так и одновременное исключение обеих особенностей) и составляет предмет классической регуляризации дифференциальных уравнений возмущенной пространственной ограниченной задачи трех тел.

Отметим, что одновременное выполнение условий r₀ = 0 и r₁ = 0 в большинстве задач небесной механики и астродинамики не возможно. Тем не менее, представляет как теоретический, так и практический интерес (с точки зрения построения эффективных высокоточных алгоритмов численного интегрирования дифференциальных уравнений задачи трех тел, необходимых для высокоточного прогноза движения небесных и космических тел) получение таких регулярных уравнений, которые не вырождаются при одновременном выполнении этих условий.

В наших работах [4–8] даны краткие обзоры и анализ кватернионных методов и моделей регулярной небесной механики и механики космического полета, в которых используются четырехмерные переменные Кустаанхеймо–Штифеля и параметры Эйлера, чаще называемые в России параметрами Родрига–Гамильтона, для регуляризации дифференциальных уравнений возмущенной пространственной задачи двух тел, возмущенной пространственной ограниченной задачи трех тел и возмущенного пространственного центрального движения материальной точки, а также даны обзоры их приложений к решению задач оптимального управления орбитальным движением космического аппарата (КА). С помощью этих методов и моделей устраняются особенности (деление на ноль), порождаемые гравитационными силами и возникающие в уравнениях этих задач при соударении тел.

Наряду с указанными особенностями другие особенности типа сингулярности (деления на ноль) имеют классические модели небесной механики и астродинамики [1, 2], записанные во вращающихся системах координат и использующие углы Эйлера для описания углового движения этих систем координат, а также модели, описывающие в угловых переменных мгновенную ориентацию орбиты или плоскости орбиты небесного тела, космического аппарата. Отметим, что этих особенностей не имеют классические модели орбитального движения, записанные в декартовых координатах или в векторной форме. Такие модели обладают большой компактностью и наглядностью. Однако во многих случаях они оказываются малоэффективными как для аналитического, так и численного исследования движения небесных тел и космических аппаратов, а также для решения задач оптимального управления траекторным движением КА.

Задачей настоящей статьи является регуляризация (устранение особенностей типа деления на ноль) классических дифференциальных уравнений возмущенной пространственной ограниченной задачи трех тел, записанных в той или иной используемой вращающейся системе координат и порождаемых использованием углов Эйлера для описания ориентации этих систем координат или ориентации орбиты изучаемого тела. В статье построены новые регулярные кватернионные дифференциальные уравнения возмущенной пространственной ограниченной задачи трех тел, полученные из классических векторных дифференциальных уравнений (2.3) и (2.4) или (2.6) и (2.7) этой задачи в декартовых координатах с помощью их записи в неголономной или в орбитальной, или в идеальной системе координат и использования для описания углового (вращательного) движения этих систем координат параметров Эйлера (Родрига–Гамильтона) и кватернионов поворотов Гамильтона.

3. Энергетические соотношения и уравнения в пространственной ограниченной задаче трех тел. Интеграл Якоби. При построении регулярных уравнений небесной механики и астродинамики используются энергетические характеристики движения тел и дифференциальные уравнения для этих характеристик.

Введем в рассмотрение приведенную энергию h₀ движения точки M₂ = M в системе координат M₀X₀Y₀Z₀ и приведенную энергию h₁ движения этой точки в системе координат M₁X₁Y₁Z₁:

где v₀ и v₁ – векторы скоростей движения точки M в системах координат M₀X₀Y₀Z₀ и M₁X₁Y₁Z₁ соответственно.

Дифференцируя соотношения (3.1) по времени и учитывая уравнения (2.3) и (2.4), получаем различные формы дифференциальных уравнений для энергий h₀ и h₁ [9]:

Здесь центральная точка – символ скалярного произведения векторов.

Отметим, что уравнения энергий (3.2) и (3.3) справедливы для общей возмущенной ограниченной задачи трех тел и что особенности (сингулярности) этих уравнений обусловлены ненулевой скоростью v₀₁ движения тела M₁ относительно тела M₀.

Отметим также, что для задачи двух тел

и уравнения для энергий h₀ и h₁ принимают вид

Здесь и далее верхняя точка – символ дифференцирования по времени.

При p = 0 (отсутствии возмущающего ускорения p) они интегрируются, давая первые интегралы задачи двух тел

Для задачи двух неподвижных центров r₀₁ = – r₁₀ = const, v₀₁ = – v₁₀ = 0. Поэтому в уравнениях (3.2) и (3.3) исчезают слагаемые с множителями $r_{0}^{{ - 3}}$ и $r_{1}^{{ - 3}}$. Уравнения для энергий h₀ и h₁ принимают вид

(становятся регулярными).

Эти уравнения могут быть записаны в виде

и при p = 0 интегрируются, давая первые интегралы задачи двух неподвижных центров

Как известно, для уравнений невозмущенной ограниченной круговой задачи трех тел (когда p = 0) существует первый интеграл, называемый интегралом Якоби [1, 2].

Обозначим через x₀, y₀, z₀ декартовые координаты точки M в системе координат M₀X₀Y₀Z₀ (проекции вектора r₀ на оси этой системы координат), а через x₀₁, y₀₁, z₀₁ – проекции вектора r₀₁ на оси этой же системы координат (координаты точки M₁ в системе координат M₀X₀Y₀Z₀). Проектируя уравнение (2.6) на оси системы координат M₀X₀Y₀Z₀, получим скалярные уравнения возмущенной ограниченной задачи трех тел в следующем виде:

Здесь x₁, y₁, z₁ и p_x = p_ξ, p_y = p_η, p_z = p_ζ – проекции векторов r₁ и p на оси системы координат M₀X₀Y₀Z₀ (они равны соответствующим проекциям этих векторов на оси системы координат M₁X₁Y₁Z₁).

Уравнения (3.4) и (3.5) при p_x = 0, p_y = 0, p_z = 0 совпадают с уравнениями (6.1) и (6.2) [2].

Проектируя уравнение (2.7) на оси системы координат M₁X₁Y₁Z₁, получим скалярные уравнения возмущенной ограниченной задачи трех тел в следующем виде:

Здесь x₁, y₁, z₁ – декартовые координаты точки M в системе координат M₁X₁Y₁Z₁ (проекции вектора r₁ на оси этой системы координат, равные проекциям этого вектора на оси системы координат M₀X₀Y₀Z₀), x₁₀ = –x₀₁, y₁₀ = –y₀₁, z₁₀ = –z₀₁ – проекции вектора r₁₀ = –r₀₁ на оси системы координат M₁X₁Y₁Z₁ (координаты точки M₀ в системе координат M₁X₁Y₁Z₁).

Рассмотрим частный случай ограниченной задачи трех тел – круговую ограниченную задачу трех тел. Будем считать, что материальная точка M₀ – Земля, вокруг которой по круговой орбите движется по законам Кеплера материальная точка M₁ – Луна. Будем также считать, что плоскость круговой орбиты Луны совпадает с координатной плоскостью M₀X₀Y₀Z₀. Тогда для координат x₀₁, y₀₁, z₀₁ Луны будем иметь следующие выражения [2]:

При этом полагается, что ось M₀X₀ проходит через начальное положение Луны (этот момент времени принят за начальную эпоху отсчета времени).

Радиус круговой орбиты Луны a и угловая скорость n движения ее по круговой орбите связаны известным соотношением

Проекции вектора скорости Луны в системе кординат M₀X₀Y₀Z₀ получим, дифференцируя соотношения (3.8) по времени:

Соотношения (3.8)–(3.10) могут быть также получены интегрированием уравнения (2.5) с учетом выше сделанных предположений о движении тела M₁ (Луны) и о выборе системы координат M₀X₀Y₀Z₀.

Из уравнений (3.4) и (3.6) можно получить [9] следующие дифференциальные уравнения для энергий h₀ и h₁ движения точки M в системах координат M₀X₀Y₀Z₀ и M₁X₁Y₁Z₁ в случае возмущенной круговой ограниченной задачи трех тел:

где скалярные произведения

Уравнения (3.11) и (3.12) можно записать в следующем виде:

где

Величины (функции времени) H₀ и H₁ отличаются на константу:

Для равных масс H₁ = H₀.

Отметим, что величины

присутствующие в соотношениях (3.15) и (3.16) с обратными знаками, являются моментами векторов скоростей v₀ и v₁ точки M относительно координатных осей M₀Z₀ и M₁Z₁ соответственно, а величины x₀p_y – y₀p_x и x₁p_y – y₁p_x, присутствующие в уравнениях (3.13) и (3.14) также с обратными знаками, являются моментами относительно этих осей вектора возмущающего ускорения p.

Уравнения возмущенной ограниченной круговой задачи трех тел получаются из уравнений (2.3) и (2.4) или (2.6) и (2.7) при задании проекций вектора r₀₁ в системе координат M₀X₀Y₀Z₀ соотношениями (3.8) и при задании проекций вектора r₁₀ в системе координат M₁X₁Y₁Z₁ соотношениями

соответственно. Из уравнений (3.13) и (3.14) следует, что уравнения невозмущенной ограниченной круговой задачи трех тел, когда возмущающее ускорение p = 0, имеют первые интегралы

Отметим, что интеграл (3.17) совпадает с интегралом (6.9) [2] невозмущенной ограниченной круговой задачи трех тел (интегралом Якоби).

4. Дифференциальные уравнения возмущенной пространственной ограниченной задачи трех тел, записанные во вращающихся системах координат. Введение в уравнения движения параметров Эйлера (Родрига–Гамильтона) и кватернионов поворотов. Введем в рассмотрение две вращающиеся системы координат $M_{0}^{'}X_{0}^{'}Y_{0}^{'}Z_{0}^{'}$ и $M_{1}^{'}X_{1}^{'}Y_{1}^{'}Z_{1}^{'}$, оси которых $M_{0}^{'}X_{0}^{'}$ и $M_{1}^{'}X_{1}^{'}$ направлены по радиус-векторам r₀ и r₁ соответственно. Направления двух других осей в общем случае может быть произвольным. Обозначим через ${{{\mathbf{\omega }}}_{0}}$ и ${{{\mathbf{\omega }}}_{1}}$ векторы абсолютных угловых скоростей вращения систем координат $M_{0}^{'}X_{0}^{'}Y_{0}^{'}Z_{0}^{'}$ и $M_{1}^{'}X_{1}^{'}Y_{1}^{'}Z_{1}^{'}$, а через ${{\omega }_{{0i}}}$ и ${{\omega }_{{1i}}}$ (i = 1, 2, 3) – проекции этих векторов на оси систем координат $M_{0}^{'}X_{0}^{'}Y_{0}^{'}Z_{0}^{'}$ и $M_{1}^{'}X_{1}^{'}Y_{1}^{'}Z_{1}^{'}$ соответственно.

Для описания ориентации (углового положения) системы координат $M_{0}^{'}X_{0}^{'}Y_{0}^{'}Z_{0}^{'}$ в системе координат M₀X₀Y₀Z₀ (а, следовательно, и в инерциальной системе координат Oξηζ) будем использовать нормированный кватернион поворота ${{{\mathbf{\lambda }}}_{0}}$, а для описания ориентации системы координат $M_{1}^{'}X_{1}^{'}Y_{1}^{'}Z_{1}^{'}$ в системе координат M₁X₁Y₁Z₁ (а, следовательно, и в инерциальной системе координат Oξηζ) будем использовать нормированный кватернион поворота ${{{\mathbf{\lambda }}}_{1}}$:

где i, j, k – векторные мнимые единицы Гамильтона; ${{\lambda }_{{ij}}}$ (j = $\overline {0,3} $) – компоненты кватерниона ориентации ${{{\mathbf{\lambda }}}_{i}}$ (параметры Родрига–Гамильтона (Эйлера) [10–13]), характеризующие ориентацию системы координат $M_{i}^{'}X_{i}^{'}Y_{i}^{'}Z_{i}^{'}$ в инерциальной системе координат.

Запишем векторное дифференциальное уравнение (2.3) во вращающейся системе координат $M_{0}^{'}X_{0}^{'}Y_{0}^{'}Z_{0}^{'}$, а векторное дифференциальное уравнение (2.4) во вращающейся системе координат $M_{1}^{'}X_{1}^{'}Y_{1}^{'}Z_{1}^{'}$:

Здесь и далее символ ◦ (центральный кружок) означает кватернионное умножение.

В уравнениях возмущенной пространственной ограниченной задачи трех тел (4.1)–(4.3) и (4.4)–(4.6) в качестве переменных выступают расстояния r₀ и r₁ от точки M до точек M₀ и M₁, производные от них ${{\dot {r}}_{0}}$ и ${{\dot {r}}_{1}}$ (проекции векторов скоростей v₀ и v₁ точки M в системах координат M₀X₀Y₀Z₀ и M₁X₁Y₁Z₁ соответственно на направления радиус-векторов r₀ и r₁), проекции ${{\omega }_{{02}}}$, ${{\omega }_{{03}}}$ и ${{\omega }_{{12}}}$, ${{\omega }_{{13}}}$ векторов абсолютных угловых скоростей ${{{\mathbf{\omega }}}_{0}}$ и ${{{\mathbf{\omega }}}_{1}}$ вращения систем координат $M_{0}^{'}X_{0}^{'}Y_{0}^{'}Z_{0}^{'}$ и $M_{1}^{'}X_{1}^{'}Y_{1}^{'}Z_{1}^{'}$ на оси этих же систем координат $M_{0}^{'}X_{0}^{'}Y_{0}^{'}Z_{0}^{'}$ и $M_{1}^{'}X_{1}^{'}Y_{1}^{'}Z_{1}^{'}$ соответственно и параметры Родрига–Гамильтона ${{\lambda }_{{0j}}}$ и ${{\lambda }_{{1j}}}$ (j = 0, 1, 2, 3) (компоненты кватернионов ${{{\mathbf{\lambda }}}_{0}}$ и ${{{\mathbf{\lambda }}}_{1}}$), характеризующие ориентацию систем координат $M_{0}^{'}X_{0}^{'}Y_{0}^{'}Z_{0}^{'}$ и $M_{1}^{'}X_{1}^{'}Y_{1}^{'}Z_{1}^{'}$ в инерциальной системе координат Oξηζ. Фигурирующие в уравнениях проекции ${{\omega }_{{01}}}$ и ${{\omega }_{{11}}}$ векторов угловых скоростей ${{{\mathbf{\omega }}}_{0}}$ и ${{{\mathbf{\omega }}}_{1}}$ на направления радиус-векторов r₀ и r₁ соответственно являются произвольно задаваемыми параметрами. Величины $x_{1}^{'}$, $y_{1}^{'}$, $z_{1}^{'}$; $x_{{01}}^{'}$, $y_{{01}}^{'}$, $z_{{01}}^{'}$ и $p_{1}^{'}$, $p_{2}^{'}$, $p_{3}^{'}$ в этих уравнениях являются проекциями радиус-векторов r₁, r₀₁ и вектора возмущающего ускорения p на оси вращающейся системы координат $M_{0}^{'}X_{0}^{'}Y_{0}^{'}Z_{0}^{'}$, а величины $x_{0}^{{''}}$, $y_{0}^{{''}}$, $z_{0}^{{''}}$; $x_{{01}}^{{''}}$, $y_{{01}}^{{''}}$, $z_{{01}}^{{''}}$ и $p_{1}^{{''}}$, $p_{2}^{{''}}$, $p_{3}^{{''}}$ – проекциями радиус-векторов r₀, r₀₁ и вектора ускорения p на оси вращающейся системы координат $M_{1}^{'}X_{1}^{'}Y_{1}^{'}Z_{1}^{'}$.

Декартовые координаты x₀, y₀, z₀ и x₁, y₁, z₁ точки M в системах координат M₀X₀Y₀Z₀ и M₁X₁Y₁Z₁ находятся через указанные переменные по формулам

которые в кватернионной записи принимают вид

Здесь и далее верхняя черта – сопряженный кватернион, например, ${{{\mathbf{\bar {\lambda }}}}_{0}}$ = ${{\lambda }_{{00}}}$ – ${{\lambda }_{{01}}}$i – ‒ ${{\lambda }_{{02}}}$j – ${{\lambda }_{{03}}}$k; дифференцирование кватерниона выполняется в предположении неизменности ортов i, j, k.

Проекции ${v}_{{0k}}^{'}$ и ${v}_{{1k}}^{'}$ векторов скоростей v₀ и v₁ точки M в системах координат M₀X₀Y₀Z₀ и M₁X₁Y₁Z₁ на оси систем координат $M_{0}^{'}X_{0}^{'}Y_{0}^{'}Z_{0}^{'}$ и $M_{1}^{'}X_{1}^{'}Y_{1}^{'}Z_{1}^{'}$ соответственно находятся по формулам

Проекции ${{{v}}_{{0k}}}$ и ${{{v}}_{{1k}}}$ векторов скоростей v₀ и v₁ точки M на оси систем координат M₀X₀Y₀Z₀ и M₁X₁Y₁Z₁ соответственно, совпадающие с их проекциями на оси инерциальной системы координат, находятся по кватернионным формулам

Проекции p₁ = p_x, p₂ = p_y, p₃ = p_z вектора p на оси системы координат M₀X₀Y₀Z₀, совпадающие с его проекциями на оси системы координат M₁X₁Y₁Z₁, связаны с его проекциями $p_{k}^{'}$ и $p_{k}^{{''}}$ на оси систем координат $M_{0}^{'}X_{0}^{'}Y_{0}^{'}Z_{0}^{'}$ и $M_{1}^{'}X_{1}^{'}Y_{1}^{'}Z_{1}^{'}$ кватернионными соотношениями перепроектирования

Проекции $x_{1}^{'}$, $y_{1}^{'}$, $z_{1}^{'}$; $x_{0}^{{''}}$, $y_{0}^{{''}}$, $z_{0}^{{''}}$ и $x_{{01}}^{'}$, $y_{{01}}^{'}$, $z_{{01}}^{'}$; $x_{{01}}^{{''}}$, $y_{{01}}^{{''}}$, $z_{{01}}^{{''}}$ радиус-векторов r₁, r₀ и r₀₁, присутствующие в уравнениях (4.1), (4.2) и (4.4), (4.5), определяются через новые переменные кватернионными соотношениями

5. Дифференциальные уравнения возмущенной пространственной ограниченной задачи трех тел, записанные в неголономных (азимутально свободных) сопровождающих координатных трехгранниках с использованием параметров Эйлера (Родрига–Гамильтона) и кватернионов поворотов. Введем в рассмотрение векторы c₀ и c₁ моментов скоростей v₀ и v₁ точки M в системах координат M₀X₀Y₀Z₀ и M₁X₁Y₁Z₁ относительно точек M₀ и M₁ соответственно:

Проекции c_ik (k = 1, 2, 3) вектора c_i на оси вращающейся системы координат $M_{i}^{'}X_{i}^{'}Y_{i}^{'}Z_{i}^{'}$ определяются соотношениями

Доопределим движение системы координат $M_{i}^{'}X_{i}^{'}Y_{i}^{'}Z_{i}^{'}$, полагая произвольно задаваемую проекцию ${{\omega }_{{i1}}}$ вектора ее абсолютной угловой скорости ${{{\mathbf{\omega }}}_{i}}$ на направление радиус-вектора r_i (ось $M_{i}^{'}X_{i}^{'}$) равной нулю:

Система координат $M_{i}^{'}X_{i}^{'}Y_{i}^{'}Z_{i}^{'}$ в этом случае, как это следует из (5.1), (5.2), вращается с абсолютной угловой скоростью ${{{\mathbf{\omega }}}_{i}}$, коллинеарной вектору момента скорости c_i:

Такая система координат называется неголономным (азимутально свободным) сопровождающим координатным трехгранником.

Дифференциальные уравнения ограниченной задачи трех тел (4.1)–(4.6) с учетом (5.2) принимают следующий вид:

Эти уравнения с учетом (5.1) принимают вид

Уравнения (5.5) и (5.8) запишем в кватернионном виде

или в другом кватернионном виде

В уравнениях возмущенной пространственной ограниченной задачи трех тел (5.4)–(5.6) и (5.7)–(5.9), записанных в неголономных (азимутально свободных) координатных трехгранниках, в качестве переменных выступают расстояния r₀ и r₁ от точки M до точек M₀ и M₁, производные от них ${{\dot {r}}_{0}}$ и ${{\dot {r}}_{1}}$ (проекции векторов скоростей v₀ и v₁ точки M в системах координат M₀X₀Y₀Z₀ и M₁X₁Y₁Z₁ соответственно на направления радиус-векторов r₀ и r₁), проекции c₀₂, c₀₃ и c₁₂, c₁₃ векторов c₀ и c₁ моментов скоростей v₀ и v₁ точки M в системах координат M₀X₀Y₀Z₀ и M₁X₁Y₁Z₁ относительно точек M₀ и M₁ на оси вращающихся систем координат$M_{0}^{'}X_{0}^{'}Y_{0}^{'}Z_{0}^{'}$ и $M_{1}^{'}X_{1}^{'}Y_{1}^{'}Z_{1}^{'}$ соответственно и параметры Родрига–Гамильтона (Эйлера) ${{\lambda }_{{0j}}}$ и ${{\lambda }_{{1j}}}$ (j = 0, 1, 2, 3) (компоненты кватернионов ${{{\mathbf{\lambda }}}_{0}}$ и ${{{\mathbf{\lambda }}}_{1}}$), характеризующие ориентацию систем координат $M_{0}^{'}X_{0}^{'}Y_{0}^{'}Z_{0}^{'}$ и $M_{1}^{'}X_{1}^{'}Y_{1}^{'}Z_{1}^{'}$ в инерциальной системе координат Oξηζ.

Декартовые координаты x₀, y₀, z₀ и x₁, y₁, z₁ точки M в системах координат M₀X₀Y₀Z₀ и M₁X₁Y₁Z₁ находятся через указанные переменные по формулам (4.7), а проекции ${v}_{{0k}}^{'}$ и ${v}_{{1k}}^{'}$ векторов скоростей v₀ и v₁ точки M в системах координат M₀X₀Y₀Z₀ и M₁X₁Y₁Z₁ на оси систем координат $M_{0}^{'}X_{0}^{'}Y_{0}^{'}Z_{0}^{'}$ и $M_{1}^{'}X_{1}^{'}Y_{1}^{'}Z_{1}^{'}$ соответственно находятся по формулам

Проекции ${{{v}}_{{0k}}}$ и ${{{v}}_{{1k}}}$ векторов скоростей v₀ и v₁ точки M на оси систем координат M₀X₀Y₀Z₀ и M₁X₁Y₁Z₁ соответственно, совпадающие с их проекциями на оси инерциальной системы координат, находятся по кватернионным формулам (4.10), (4.11).

Из уравнений (5.4)–(5.6) при m₁ = 0 и уравнений (5.7)–(5.9) при m₀ = 0 следуют дифференциальные уравнения возмущенной пространственной задачи двух тел, записанные в неголономном (азимутально свободном) координатном трехграннике, полученные автором статьи в [14–16]. Другие варианты вывода и примеры использования этих уравнений задачи двух тел приводятся в работах автора статьи [4, 5, 17–19]. Из этих уравнений задачи двух тел, как показано автором статьи, наиболее просто выводятся регулярные кватернионные уравнения пространственной задачи двух тел в четырехмерных переменных Кустаанхеймо–Штифеля.

6. Дифференциальные уравнения возмущенной пространственной ограниченной задачи трех тел, записанные в орбитальных координатных трехгранниках с использованием параметров Эйлера (Родрига–Гамильтона) и кватернионов поворотов. Полагая, по-прежнему, оси $M_{0}^{'}X_{0}^{'}$ и $M_{1}^{'}X_{1}^{'}$ вращающихся систем координат $M_{0}^{'}X_{0}^{'}Y_{0}^{'}Z_{0}^{'}$ и $M_{1}^{'}X_{1}^{'}Y_{1}^{'}Z_{1}^{'}$ направленными по радиус-векторам r₀ и r₁ соответственно, направим их оси $M_{0}^{'}Z_{0}^{'}$ и $M_{1}^{'}Z_{1}^{'}$ вдоль векторов ${{{\mathbf{c}}}_{0}} = {{{\mathbf{r}}}_{0}} \times {{{\mathbf{v}}}_{0}}$ и ${{{\mathbf{c}}}_{1}} = {{{\mathbf{r}}}_{1}} \times {{{\mathbf{v}}}_{1}}$ моментов скоростей v₀ и v₁ точки M в системах координат M₀X₀Y₀Z₀ и M₁X₁Y₁Z₁ относительно точек M₀ и M₁ соответственно.

В этом случае проекции c_ik (k = 1, 2, 3) вектора c_i на оси вращающейся системы координат $M_{i}^{'}X_{i}^{'}Y_{i}^{'}Z_{i}^{'}$ определяются соотношениями

Проектируя векторное равенство ${{{\mathbf{c}}}_{i}} = {{{\mathbf{r}}}_{i}} \times {{{\mathbf{\dot {r}}}}_{i}} = {{{\mathbf{r}}}_{i}} \times {{{\mathbf{v}}}_{i}}$ на оси орбитальной системы координат $M_{i}^{'}X_{i}^{'}Y_{i}^{'}Z_{i}^{'}$ (i = 0, 1) будем иметь:

где, напомним, ${v}_{{ik}}^{'}$ – проекции вектора скорости v_i точки M в системе координат M_iX_iY_iZ_i на оси системы координат $M_{i}^{'}X_{i}^{'}Y_{i}^{'}Z_{i}^{'}$.

Таким образом, в рассматриваемом случае проекции ${v}_{{ik}}^{'}$ вектора скорости v_i точки M на оси орбитальной системы координат $M_{i}^{'}X_{i}^{'}Y_{i}^{'}Z_{i}^{'}$ определяются соотношениями

Из (4.9) и (6.3) находим:

Подставляя равенства (6.4) в уравнения (4.1), (4.2) и (4.4), (4.5), получим

Из уравнений (6.7) и (6.10) с учетом второго соотношения (6.4) находим

Таким образом, проекции ω_ik вектора абсолютной угловой скорости ${{{\mathbf{\omega }}}_{i}}$ орбитальной системы координат $M_{i}^{'}X_{i}^{'}Y_{i}^{'}Z_{i}^{'}$ на ее же координатные оси имеют вид соотношений (6.11), (6.12) и (6.4), в которых ${{c}_{i}} = \left| {{{{\mathbf{r}}}_{i}} \times {{{\mathbf{v}}}_{i}}} \right|$, i = 0, 1.

Кватернионное кинематическое уравнение, описывающее вращательное движение орбитальной системы координат $M_{i}^{'}X_{i}^{'}Y_{i}^{'}Z_{i}^{'}$ в инерциальной системе координат Oξηζ, в соответствии с уравнениями (4.3) и (4.6) имеет вид

где проекция угловой скорости ω_i1 для i = 0 описывается соотношением (6.11), а для i = 1 – соотношением (6.12).

В полученных уравнениях возмущенной пространственной ограниченной задачи трех тел (6.5), (6.6), (6.13) (при i = 0), (6.11) и (6.8), (6.9), (6.13) (при i = 1), (6.12), записанных в орбитальных системах координат $M_{0}^{'}X_{0}^{'}Y_{0}^{'}Z_{0}^{'}$ и $M_{1}^{'}X_{1}^{'}Y_{1}^{'}Z_{1}^{'}$, в качестве переменных выступают расстояния r₀ и r₁ от точки M до точек M₀ и M₁, модули c₀ и c₁ векторов c₀ и c₁ моментов скоростей v₀ и v₁ точки M в системах координат M₀X₀Y₀Z₀ и M₁X₁Y₁Z₁ относительно точек M₀ и M₁ и параметры Родрига–Гамильтона ${{\lambda }_{{0j}}}$ и ${{\lambda }_{{1j}}}$ (j = 0, 1, 2, 3) (компоненты кватернионов ${{{\mathbf{\lambda }}}_{0}}$ и ${{{\mathbf{\lambda }}}_{1}}$), характеризующие ориентации орбитальных систем координат в инерциальной системе координат Oξηζ.

Декартовые координаты x₀, y₀, z₀ и x₁, y₁, z₁ точки M в системах координат M₀X₀Y₀Z₀ и M₁X₁Y₁Z₁ находятся через указанные переменные по формулам (4.7), а проекции ${v}_{{0k}}^{'}$ и ${v}_{{1k}}^{'}$ векторов скоростей v₀ и v₁ точки M в системах координат M₀X₀Y₀Z₀ и M₁X₁Y₁Z₁ на оси систем координат $M_{0}^{'}X_{0}^{'}Y_{0}^{'}Z_{0}^{'}$ и $M_{1}^{'}X_{1}^{'}Y_{1}^{'}Z_{1}^{'}$ соответственно находятся по формулам (6.3).

Проекции ${{{v}}_{{0k}}}$ и ${{{v}}_{{1k}}}$ векторов скоростей v₀ и v₁ точки M на оси систем координат M₀X₀Y₀Z₀ и M₁X₁Y₁Z₁ соответственно, совпадающие с их проекциями на оси инерциальной системы координат, находятся по кватернионным формулам

Отметим появление в кватернионном кинематическом уравнении (6.13) движения сопровождающего (орбитального) трехгранника $M_{i}^{'}X_{i}^{'}Y_{i}^{'}Z_{i}^{'}$ (в выражении для проекции ${{\omega }_{{i1}}}$ вектора абсолютной угловой скорости орбитальной системы координат) слагаемого, содержащего массу m₁ или m₀ и проекцию $p_{3}^{'}$ или $p_{3}^{{''}}$ вектора возмущающего ускорения р на ось $M_{0}^{'}Z_{0}^{'}$ или $M_{1}^{'}Z_{1}^{'}$ вращающейся системы координат $M_{0}^{'}X_{0}^{'}Y_{0}^{'}Z_{0}^{'}$ или $M_{1}^{'}X_{1}^{'}Y_{1}^{'}Z_{1}^{'}$ соответственно (на направление, ортогональное плоскости мгновенной орбиты точки M в системе координат M₀X₀Y₀Z₀ или M₁X₁Y₁Z₁).

Компоненты λ_ij кватерниона ${{{\mathbf{\lambda }}}_{i}}$ ориентации орбитальной системы координат $M_{i}^{'}X_{i}^{'}Y_{i}^{'}Z_{i}^{'}$ связаны с угловыми элементами орбиты точки M в системе координат M_iX_iY_iZ_i соотношениями

в которых Ω_iu – долгота восходящего узла, I_i – наклон (наклонение) орбиты, Σ_i – аргумент широты, равный сумме углового расстояния перицентра от узла и истинной аномалии.

Таким образом, кватернион ориентации ${{{\mathbf{\lambda }}}_{i}}$ орбитальной системы координат $M_{i}^{'}X_{i}^{'}Y_{i}^{'}Z_{i}^{'}$ характеризует собой одновременно ориентацию плоскости мгновенной орбиты точки M в системе координат M_iX_iY_iZ_i и положение точки на этой орбите.

Из уравнений (6.5), (6.6), (6.13) (при i = 0), (6.11) при m₁ = 0 и уравнений (6.8), (6.9), (6.13) (при i = 1), (6.12) при m₀ = 0 следуют дифференциальные уравнения возмущенной пространственной задачи двух тел, записанные в орбитальной системе координат, полученные автором статьи в [16] (1992). Различные варианты вывода и использования этих уравнений приводятся в других работах автора статьи [18, 4, 5 ]. Кватернионное уравнение ориентации орбитальной системы координат в задаче двух тел было также получено и использовалось для описания орбитального движения космического аппарата Брагазиным, Бранцем и Шмыглевским (1986, 1992) [20, 11 ]. Уравнения возмущенного кеплеровского движения, записанные в рамках задачи двух тел в орбитальной системе координат и состоящие из уравнений для расстояния r, модуля момента орбитальной скорости с и уравнений для угловых переменных, описывающих движение орбитальной системы, были получены Andoyer (1923) [21].

7. Дифференциальные уравнения возмущенной пространственной ограниченной задачи трех тел, записанные в орбитальных и идеальных системах координат с использованием параметров Эйлера (Родрига–Гамильтона) и кватернионов поворотов. Введем новую кватернионную переменную ${{{\mathbf{\Lambda }}}_{i}}$, связанную с кватернионом ${{{\mathbf{\lambda }}}_{i}}$ ориентации орбитальной системы координат $M_{i}^{'}X_{i}^{'}Y_{i}^{'}Z_{i}^{'}$ соотношением (формулой, вытекающей из формулы сложения двух конечных поворотов)

где φ_i – угловая переменная, удовлетворяющая дифференциальному уравнению

Кватернион ${{{\mathbf{\Lambda }}}_{i}}$ характеризует собой ориентацию идеальной системы координат ${{M}_{i}}X_{i}^{{id}}Y_{i}^{{id}}Z_{i}^{{id}}$ [21] в системе координат M_iX_iY_iZ_i, оси которой параллельны одноименным осям инерциальной системы координат Oξηζ. Ось $Z_{i}^{{id}}$ этой системы координат параллельна вектору c_i момента скорости v_i точки M в системе координат M_iX_iY_iZ_i относительно точки M_i, а координатные оси $X_{i}^{{id}}$ и $Y_{i}^{{id}}$ лежат в плоскости координатных осей $X_{i}^{'}$ и $Y_{i}^{'}$ и получаются из них поворотом вокруг оси $Z_{i}^{'}$ на угол ${{\varphi }_{i}}$ по ходу часовой стрелки.

Вектор Ω_i абсолютной угловой скорости идеальной системы координат ${{M}_{i}}X_{i}^{{id}}Y_{i}^{{id}}Z_{i}^{{id}}$ параллелен радиус-вектору r_i точки M_i и определяется формулой

где ${\mathbf{x}}_{i}^{'}$ – орт координатной оси $M_{i}^{'}X_{i}^{'}$, ω_i1 – проекция вектора абсолютной угловой скорости орбитальной системы координат $M_{i}^{'}X_{i}^{'}Y_{i}^{'}Z_{i}^{'}$ на ось $M_{i}^{'}X_{i}^{'}$, определяемая соотношением (6.11) при i = 0 и соотношением (6.12) при i = 1.

Проекции ${{\Omega }_{{ik}}}$ (k = 1, 2, 3) вектора Ω_i на оси идеальной системы координат ${{M}_{i}}X_{i}^{{id}}Y_{i}^{{id}}Z_{i}^{{id}}$ в соответствии с формулами (6.11) и (6.12) имеют вид

Отметим, что введенная система координат ${{M}_{i}}X_{i}^{{id}}Y_{i}^{{id}}Z_{i}^{{id}}$, проекция вектора угловой скорости которой ${{\Omega }_{{i3}}}$ = 0, была названа Deprit [21] идеальной системой координат.

Переходя в уравнениях (6.5), (6.6), (6.13) (при i = 0), (6.11) и (6.8), (6.9), (6.13) (при i = 1), (6.12) к новым переменным Λ_i по формулам (7.1) и учитывая уравнение (7.2) и соотношения (7.4), (7.5), получим уравнения

Уравнения (7.6)–(7.8), (7.12) и (7.13) (при i = 0), (7.14) и уравнения (7.9)–(7.11), (7.12) и (7.13) (при i = 1), (7.15) являются дифференциальными уравнениями возмущенной пространственной ограниченной задачи трех тел, записанными в двух вращающихся системах координат: в орбитальной системе координат $M_{i}^{'}X_{i}^{'}Y_{i}^{'}Z_{i}^{'}$ (уравнения (7.6)–(7.8) и (7.9)–(7.11)) и в идеальной системе координат ${{M}_{i}}X_{i}^{{id}}Y_{i}^{{id}}Z_{i}^{{id}}$(уравнения (7.12), (7.13) (при i = 0), (7.14) и уравнения (7.12), (7.13) (при i = 1), (7.15)). В этих уравнениях переменными являются расстояния r₀ и r₁ от точки M до точек M₀ и M₁, модули c₀ и c₁ векторов c₀ и c₁ моментов скоростей v₀ и v₁ точки M в системах координат M₀X₀Y₀Z₀ и M₁X₁Y₁Z₁ относительно точек M₀ и M₁, угловые переменные ${{\varphi }_{0}}$ и ${{\varphi }_{1}}$, и параметры Родрига–Гамильтона (Эйлера) ${{\Lambda }_{{0j}}}$ и ${{\Lambda }_{{1j}}}$ (j = 0, 1, 2, 3) (компоненты кватернионов ${{{\mathbf{\Lambda }}}_{0}}$ и ${{{\mathbf{\Lambda }}}_{1}}$), характеризующие ориентации идеальных систем координат ${{M}_{0}}X_{0}^{{id}}Y_{0}^{{id}}Z_{0}^{{id}}$ и ${{M}_{1}}X_{1}^{{id}}Y_{1}^{{id}}Z_{1}^{{id}}$ в инерциальной системе координат Oξηζ соответственно. Величины $x_{1}^{'}$, $y_{1}^{'}$, $z_{1}^{'}$, $x_{{01}}^{'}$, $y_{{01}}^{'}$, $z_{{01}}^{'}$ и $p_{1}^{'}$, $p_{2}^{'}$, $p_{3}^{'}$ в этих уравнениях являются проекциями радиус-векторов r₁, r₀₁ и вектора возмущающего ускорения p на оси орбитальной системы координат $M_{0}^{'}X_{0}^{'}Y_{0}^{'}Z_{0}^{'}$, а величины $x_{0}^{{''}}$, $y_{0}^{{''}}$, $z_{0}^{{''}}$; $x_{{01}}^{{''}}$, $y_{{01}}^{{''}}$, $z_{{01}}^{{''}}$ и $p_{1}^{{''}}$, $p_{2}^{{''}}$, $p_{3}^{{''}}$ – проекциями радиус-векторов r₀, r₀₁ и вектора ускорения p на оси орбитальной системы координат $M_{1}^{'}X_{1}^{'}Y_{1}^{'}Z_{1}^{'}$.

Декартовые координаты x₀, y₀, z₀ и x₁, y₁, z₁ точки M в системах координат M₀X₀Y₀Z₀ и M₁X₁Y₁Z₁ находятся через указанные переменные по формулам (4.7), в которых параметры Эйлера ${{\lambda }_{{ij}}}$, являющиеся в рассматриваемом случае компонентами кватерниона ${{{\mathbf{\lambda }}}_{i}}$ ориентации орбитальной системы координат, предварительно должны быть найдены через переменные ${{\Lambda }_{{ij}}}$ (компоненты кватерниона ${{{\mathbf{\Lambda }}}_{i}}$) в соответствии с кватернионной формулой сложения двух конечных поворотов

Проекции ${v}_{{0k}}^{'}$ и ${v}_{{1k}}^{'}$ векторов скоростей v₀ и v₁ точки M в системах координат M₀X₀Y₀Z₀ и M₁X₁Y₁Z₁ на оси систем координат $M_{0}^{'}X_{0}^{'}Y_{0}^{'}Z_{0}^{'}$ и $M_{1}^{'}X_{1}^{'}Y_{1}^{'}Z_{1}^{'}$ соответственно находятся по формулам (6.3), а проекции ${{{v}}_{{0k}}}$ и ${{{v}}_{{1k}}}$ векторов скоростей v₀ и v₁ точки M на оси систем координат M₀X₀Y₀Z₀ и M₁X₁Y₁Z₁ соответственно, совпадающие с их проекциями на оси инерциальной системы координат, находятся по кватернионным формулам (6.14), (7.16).

Из уравнений (7.6)–(7.8), (7.12) и (7.13) (при i = 0), (7.14) при m₁ = 0 и уравнений (7.9)–(7.11), (7.12) и (7.13) (при i = 1), (7.15) при m₀ = 0 следуют дифференциальные уравнения возмущенной пространственной задачи двух тел, записанные в орбитальной и идеальной системах координат, полученные автором статьи в [16, 22], а также в [5, 23]. В случае невозмущенной пространственной задачи двух тел, когда вектор возмущающего ускорения p = 0, из этих уравнений следуют первые интегралы ${{c}_{i}}$ = const, ${{{\mathbf{\Lambda }}}_{i}}$ = const. Поэтому в возмущенной пространственной задаче двух тел переменные ${{c}_{i}}$ = c и ${{{\mathbf{\Lambda }}}_{i}}$ = ${\mathbf{\Lambda }}$ являются медленно изменяющимися переменными (оскулирующими элементами).

Отметим, что уравнения возмущенного кеплеровского движения, записанные в идеальной системе координат и состоящие из уравнений для полярных координат и уравнений для угловых переменных, описывающих ориентацию идеальной системы координат, были получены Andoyer (1923), а также Musen (1959) [21].

8. Дифференциальные уравнения возмущенной пространственной ограниченной задачи трех тел, записанные в идеальных системах координат с использованием идеальных прямоугольных координат Ганзена, параметров Эйлера (Родрига–Гамильтона) и кватернионов. Введем идеальные прямоугольные координаты Ганзена ${{X}_{i}}$, ${{Y}_{i}}$ и ${{Z}_{i}}$ = 0 (i = 0, 1), являющиеся проекциями радиус-вектора r_i точки M в системе координат M_iX_iY_iZ_i на оси идеальной системы координат ${{M}_{i}}X_{i}^{{id}}Y_{i}^{{id}}Z_{i}^{{id}}$, связанные с переменными r_i = $\left| {{{{\mathbf{r}}}_{i}}} \right|$ (расстояниями) и φ_i (полярными координатами) соотношениями

Дифференцируя соотношения (8.1) дважды по времени и используя уравнения (7.6)–(7.8) и (7.9)–(7.11), получим вместо уравнений (7.6)–(7.8), (7.12) и (7.13) (при i = 0), (7.14) и уравнений (7.9)–(7.11), (7.12) и (7.13) (при i = 1), (7.15) следующие уравнения:

Величины $X_{{01}}^{'}\, = \,x_{{01}}^{'}{\text{cos}}{{\varphi }_{{\text{0}}}}\, - \,y_{{01}}^{'}{\text{sin}}{{\varphi }_{{\text{0}}}},Y_{{01}}^{'} = - x_{{01}}^{'}{\text{sin}}{{\varphi }_{{\text{0}}}}\, + \,y_{{01}}^{'}{\text{cos}}{{\varphi }_{{\text{0}}}}$ и $P_{x}^{'} = p_{1}^{'}{\text{cos}}{{\varphi }_{{\text{0}}}}$ – $p_{2}^{'}{\text{sin}}{{\varphi }_{{\text{0}}}}$, $P_{y}^{'} = - p_{1}^{'}{\text{sin}}{{\varphi }_{{\text{0}}}} + p_{2}^{'}{\text{cos}}{{\varphi }_{{\text{0}}}}$ в этих уравнениях являются проекциями радиус-вектора r₀₁ = = $\overrightarrow {{{M}_{0}}{{M}_{1}}} $ и вектора возмущающего ускорения p на оси ${{M}_{0}}X_{0}^{{id}}$ и ${{M}_{0}}Y_{0}^{{id}}$ идеальной системы координат ${{M}_{0}}X_{0}^{{id}}Y_{0}^{{id}}Z_{0}^{{id}}$, а величины $X_{{01}}^{{''}} = x_{{01}}^{{''}}{\text{cos}}{{\varphi }_{{\text{1}}}} - y_{{01}}^{{''}}{\text{sin}}{{\varphi }_{{\text{1}}}}$, $Y_{{01}}^{{''}} = - x_{{01}}^{{''}}{\text{sin}}{{\varphi }_{{\text{1}}}}$ + + $y_{{01}}^{{''}}{\text{cos}}{{\varphi }_{{\text{1}}}}$ и $P_{x}^{{''}} = p_{1}^{{''}}{\text{cos}}{{\varphi }_{{\text{1}}}} - p_{2}^{{''}}{\text{sin}}{{\varphi }_{{\text{1}}}}$, $P_{y}^{{''}} = - p_{1}^{{''}}{\text{sin}}{{\varphi }_{{\text{1}}}} + p_{2}^{{''}}{\text{cos}}{{\varphi }_{{\text{1}}}}$ – проекциями радиус-вектора r₀₁ и вектора ускорения p на оси ${{M}_{1}}X_{1}^{{id}}$ и ${{M}_{1}}Y_{1}^{{id}}$ идеальной системы координат ${{M}_{1}}X_{1}^{{id}}Y_{1}^{{id}}Z_{1}^{{id}}$. Отметим, что $Z_{{01}}^{'}$ = $z_{{01}}^{'}$ и $Z_{{01}}^{{''}}$ = $z_{{01}}^{{''}}$, а также, что $P_{z}^{'}$ = $p_{3}^{'}$ и $P_{z}^{{''}}$ = $p_{3}^{{''}}$, т.е. проекции радиус-вектора r₀₁ и вектора ускорения p на оси ${{M}_{0}}Z_{0}^{{id}}$ и ${{M}_{1}}Z_{1}^{{id}}$ идеальных систем координат ${{M}_{0}}X_{0}^{{id}}Y_{0}^{{id}}Z_{0}^{{id}}$ и ${{M}_{1}}X_{1}^{{id}}Y_{1}^{{id}}Z_{1}^{{id}}$ совпадают с их проекцими на оси ${{M}_{0}}Z_{0}^{'}$ и ${{M}_{1}}Z_{1}^{'}$ орбитальных систем координат $M_{0}^{'}X_{0}^{'}Y_{0}^{'}Z_{0}^{'}$ и $M_{1}^{'}X_{1}^{'}Y_{1}^{'}Z_{1}^{'}$.

Уравнения (8.2), (8.4)–(8.6), (8.8) (при i = 0) и уравнения (8.3)–(8.5), (8.7), (8.8) (при i = 1) являются дифференциальными уравнениями возмущенной пространственной ограниченной задачи трех тел, записанными в идеальных системах координат ${{M}_{0}}X_{0}^{{id}}Y_{0}^{{id}}Z_{0}^{{id}}$ и ${{M}_{1}}X_{1}^{{id}}Y_{1}^{{id}}Z_{1}^{{id}}$ соответственно. Уравнения (8.2), (8.4)–(8.6), (8.8) (при i = 0) описывают движение точки M в системе координат M₀X₀Y₀Z₀, а уравнения (8.3)–(8.5), (8.7), (8.8) (при i = 1) – в системе координат M₁X₁Y₁Z₁. Начала этих систем координат находятся в точках M₀ и M₁, а их координатные оси параллельны одноименным осям инерциальной системы координат Oξηζ. В этих уравнениях переменными являются идеальные прямоугольные координаты Ганзена ${{X}_{i}}$, ${{Y}_{i}}$, ${{Z}_{i}}$ = 0 (i = 0, 1), их первые производные по времени и параметры Эйлера (Родрига–Гамильтона) ${{\Lambda }_{{0j}}}$ и ${{\Lambda }_{{1j}}}$ (j = 0, 1, 2, 3) (компоненты кватернионов ${{{\mathbf{\Lambda }}}_{0}}$ и ${{{\mathbf{\Lambda }}}_{1}}$), характеризующие ориентации идеальных систем координат ${{M}_{0}}X_{0}^{{id}}Y_{0}^{{id}}Z_{0}^{{id}}$ и ${{M}_{1}}X_{1}^{{id}}Y_{1}^{{id}}Z_{1}^{{id}}$ в инерциальной системе координат Oξηζ соответственно.

Отметим, что уравнения (8.2) и (8.3) можно также записать в другом виде:

Величины $X_{1}^{'}$ и $Y_{1}^{'}$ в этих уравнениях являются проекциями радиус-вектора r₁ на оси ${{M}_{0}}X_{0}^{{id}}$ и ${{M}_{0}}Y_{0}^{{id}}$ идеальной системы координат ${{M}_{0}}X_{0}^{{id}}Y_{0}^{{id}}Z_{0}^{{id}}$, а величины $X_{0}^{{''}}$ и $Y_{0}^{{''}}$ – проекциями радиус-вектора r₀ на оси ${{M}_{1}}X_{1}^{{id}}$ и ${{M}_{1}}Y_{1}^{{id}}$ идеальной системы координат ${{M}_{1}}X_{1}^{{id}}Y_{1}^{{id}}Z_{1}^{{id}}$.

Отметим также, что уравнения возмущенной пространственной ограниченной задачи трех тел (8.2), (8.4)–(8.6), (8.8) (при i = 0) могут рассматриваться независимо от уравнений (8.3)–(8.5), (8.7), (8.8) (при i = 1), если модуль r₁ радиус-вектора r₁, фигурирующий в этих уравнениях, представить, используя соотношение r₁ = r₀ – r₀₁, в следующем виде:

Аналогично, уравнения возмущенной пространственной ограниченной задачи трех тел (8.3)–(8.5), (8.7), (8.8) (при i = 1) могут рассматриваться независимо от уравнений (8.2), (8.4)–(8.6), (8.8) (при i = 0), если модуль r₀ радиус-вектора r₀, фигурирующий в этих уравнениях, представить, используя соотношение r₀ = r₁ + r₀₁, в следующем виде:

Отметим, наконец, что уравнения (8.2), (8.3) или (8.9), (8.10) возмущенной пространственной ограниченной задачи трех тел в идеальных прямоугольных координатах Ганзена ${{X}_{i}}$, ${{Y}_{i}}$ и ${{Z}_{i}}$ = 0 (i = 0, 1) имеют вид дифференциальных уравнений возмущенной плоской ограниченной задачи трех тел.

Декартовые координаты x_i, y_i, z_i (i = 0, 1) точки M в системе координат M_iX_iY_iZ_i, оси которой параллельны одноименным осям инерциальной системы координат Oξηζ, и проекции ${{{v}}_{{ik}}}$ (k = 1, 2, 3) вектора скорости v_i точки M в системе координат M_iX_iY_iZ_i на ее же координатные оси находятся через идеальные координаты и их первые производные по времени по формулам

Проекции $P_{x}^{'}$, $P_{y}^{'}$, $P_{z}^{'}$ = $p_{3}^{'}$ вектора возмущающего ускорения p на оси идеальной системы координат ${{M}_{0}}X_{0}^{{id}}Y_{0}^{{id}}Z_{0}^{{id}}$ связаны с его проекциями p₁ = p_x, p₂ = p_y, p₃ = p_z на оси системы координат M₀X₀Y₀Z₀ соотношениями

Проекции $P_{x}^{{''}}$, $P_{y}^{{''}}$, $P_{z}^{{''}}$ = $p_{3}^{{''}}$ вектора возмущающего ускорения p на оси идеальной системы координат ${{M}_{1}}X_{1}^{{id}}Y_{1}^{{id}}Z_{1}^{{id}}$ связаны с его проекциями p₁ = p_x, p₂ = p_y, p₃ = p_z на оси системы координат M₁X₁Y₁Z₁ аналогичными соотношениями, в правых частях которых вместо первого нижнего индекса “0”, стоящего в правых частях соотношений (8.15), будет стоять индекс “1”.

Соотношения (8.13)–(8.15) и соотношения для проекций $P_{x}^{{''}}$, $P_{y}^{{''}}$, $P_{z}^{{''}}$ = $p_{3}^{{''}}$ можно записать в следующем кватернионом виде:

Обратим внимание на то, что в соответствии со свойствами идеальных координат в формулах (8.14) и (8.17) для проекций ${{{v}}_{{ik}}}$ вектора скорости точки M в системе координат M_iX_iY_iZ_i отсутствуют слагаемые с производными ${{\dot {\Lambda }}_{{ij}}}$ от параметров Эйлера ${{\Lambda }_{{ij}}}$, которые, казалось, должны были бы появиться при дифференцировании соотношений (8.13) и (8.16) (для получения формул (8.14) и (8.17)). Покажем, что в действительности эти слагаемые обращаются в ноль.

Дифференцируя соотношение (8.16) по времени и учитывая уравнение (8.4), получим после преобразований

Но в силу формулы (8.5) кватернион ${\mathbf{\Omega }}_{i}^{{id}}$ = (${{\omega }_{{i1}}}{\text{/}}{{r}_{i}}$)$\left( {{{X}_{i}}{\mathbf{i}} + {{Y}_{i}}{\mathbf{j}}} \right)$, поэтому в последнем соотношении выражение в квадратной скобке обращается в ноль, и в итоге получается формула ${{{\mathbf{\dot {R}}}}_{i}}$ = ${{{\mathbf{V}}}_{i}}$ = ${{{\mathbf{\Lambda }}}_{i}} \circ \left( {{{{\dot {X}}}_{i}}{\mathbf{i}} + {{{\dot {Y}}}_{i}}{\mathbf{j}}} \right) \circ {{{\mathbf{\bar {\Lambda }}}}_{i}}$, совпадающая с формулой (8.17).

Дифференциальные уравнения возмущенной пространственной ограниченной задачи трех тел в комплексных переменных. Уравнения (8.2), (8.3) и система четырех скалярных уравнений, эквивалентная кватернионному уравнению (8.4), могут быть записаны в комплексной форме. Введем комплексные переменные

Здесь нижний индекс i = 0, 1; основная буква i – мнимая (комплексная) единица: i² = – 1.

В комплексных переменных (8.19) (параметрах Кейли–Клейна) кватернионное кинематическое уравнение (8.4) в переменных Эйлера с учетом (8.5) эквивалентно системе скалярных дифференциальных уравнений

В комплексных переменных (8.18) и (8.19) дифференциальные уравнения возмущенной пространственной ограниченной задачи трех тел (8.2)–(8.8) в идеальных прямоугольных координатах Ганзена с учетом уравнений (8.20) принимают вид

Здесь, по-прежнему, нижний индекс i = 0, 1; основная буква i – мнимая единица.

Вместо уравнений (8.21) и (8.22) могут быть использованы другие комплексные уравнения, вытекающие из уравнений (8.9) и (8.10)

Уравнения (8.21)–(8.25) или (8.26), (8.27), (8.23) могут оказаться удобными в численных и аналитических исследованиях возмущенной пространственной ограниченной задачи трех тел. Так, известно [24], что в численных расчетах перспективно использование системы остаточных классов – непозиционной системы кодирования цифровой информации, позволяющей по остаткам осуществлять переход из пространства комплексных чисел в область целых действительных чисел, распараллеливать вычислительные операции на арифметическом уровне, повышать надежность вычислений, эффективно использовать микропроцессорную аппаратуру в вычислительных устройствах.

Интегралы Якоби уравнений невозмущенной пространственной ограниченной круговой задачи трех тел в идеальных координатах Ганзена и параметрах Эйлера. Запишем первые интегралы (3.17) и (3.18) уравнения невозмущенной пространственной ограниченной круговой задачи трех тел (интегралы Якоби), когда возмущающее ускорение p = 0, в идеальных координатах Ганзена и параметрах Эйлера. Учитывая равенства

получим эти интегралы в следующем виде:

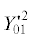Дифференциальные уравнения возмущенной пространственной задачи двух тел в идеальных координатах Ганзена и параметрах Эйлера. Эти уравнения получаются из выше полученных уравнений возмущенной пространственной ограниченной задачи трех тел и имеют следующий вид

Здесь X, Y и Z = 0 – идеальные координаты Ганзена изучаемого тела, ${\mathbf{\Lambda }}$ – кватернион ориентации идеальной системы координат, в которой записаны уравнения движения изучаемого тела, ${{{\mathbf{\Omega }}}^{{id}}}$ – кватернион абсолютной угловой скорости этой системы координат, m – сумма масс тел, $P_{x}^{{id}}$, $P_{y}^{{id}}$, $P_{z}^{{id}}$ – проекции возмущающего ускорения на оси идеальной системы координат.

Отметим, что эти уравнения задачи двух тел были получены автором статьи в работе [25], скалярные уравнения возмущенного кеплеровского движения в ганзеновских координатах и параметрах Эйлера, записанные в идеальной системе координат, ранее были получены в других формах и другими способами Deprit (1976) [21] и Брумбергом (1980) [26].

9. Обсуждение полученных уравнений и их приложений. Отметим основные особенности полученных уравнений и их возможные приложения.

1) В статье получены различные новые регулярные кватернионные уравнения небесной механики и механики космического полета (астродинамики), построенные в рамках возмущенной пространственной ограниченной задачи трех тел (например, Земля, Луна (или Солнце), космический аппарат (или астероид)). Уравнения записаны или в неголономной, или в орбитальной, или в идеальной системах координат. В этих уравнениях возмущенного орбитального движения одна группа (подсистема) уравнений описывает изменение размеров и формы мгновенной орбиты изучаемого тела (например, космического аппарата или астероида), имеющего пренебрежимо малую массу в сравнении с двумя другими гравитирующими телами, а другая группа (подсистема) уравнений, имеющая вид кватернионных кинематических уравнений в параметрах Эйлера (Родрига–Гамильтона), описывает изменение ориентации мгновенной орбиты или плоскости орбиты изучаемого движущегося тела в инерциальной системе координат, или изменение ориентации вращающейся системы координат, в которой записаны уравнения орбитального движения тела. Предложенные уравнения не имеют особенностей (деления на ноль), порождаемых использованием в моделях орбитального движения углов Эйлера, и имеют аналитические и вычислительные преимущества перед классическими уравнениями небесной механики и механики космического полета, состоящими из уравнений орбитального движения, описывающих изменение размеров и формы мгновенной орбиты изучаемого тела, и из уравнений, имеющих вид кинематических уравнений в углах Эйлера и описывающих изменение ориентации мгновенной орбиты или плоскости орбиты изучаемого движущегося тела или используемой вращающейся системы координат. Преимущество предлагаемых уравнений обусловливается хорошо известными преимуществами входящих в их состав кватернионных кинематических уравнений в параметрах Эйлера перед кинематическими уравнениями в углах Эйлера.

Из полученных уравнений следуют, как частные, широко используемые в настоящее время уравнения орбитального движения, построенные в рамках возмущенной пространственной задачи двух тел. Обзор этих известных уравнений и их приложений в задачах управления орбитальным движением космического аппарата дан в первой обзорной части нашей работы [3].

Полученные в статье уравнения орбитального движения могут быть эффективно использованы в силу их свойств для изучения орбитального движения небесных и космических тел и космических аппаратов, для прогноза их движения, а также для решения задач инерциальной навигации в космосе, задач управления орбитальным движением космических аппаратов, в частности, для решения в рамках возмущенной пространственной ограниченной задачи трех тел (Земля, Луна, космический аппарат) таких актуальных задач механики космического полета, как полет на Луну, а также задач оптимальной переориентации орбиты космического аппарата, плоскости орбиты, коррекции угловых элементов орбиты КА (в частности, КА спутниковой навигационной группировки “Глонасс”) с учетом влияния Луны.

2) В наших работах [5, 23, 27, 28] с использованием принципа максимума Понтрягина и различных вариантов регулярных кватернионных уравнений орбитального движения, записанных во вращающихся системах координат с использованием параметров Родрига–Гамильтона (Эйлера) и кватернионных переменных для описания ориентаций этих систем координат и орбиты КА, решены в рамках возмущенной пространственной задачи двух тел в различных постановках задачи оптимального управления о мягкой или жесткой встрече в ньютоновском гравитационном поле управляемого космического аппарата с неуправляемым аппаратом, движущимся по кеплеровской орбите.

В этих работах отмечено, что кватернионные регулярные уравнения орбитального движения центра масс КА, в состав которых входят уравнения в параметрах Эйлера, в отличие от классических уравнений орбитального движения в угловых оскулирующих элементов, содержащих особые точки (деление на ноль), этих особых точек не имеют. Эти кватернионные уравнения позволили кардинально повысить эффективность аналитического исследования и численного решения задач об оптимальной мягкой или жесткой встрече в ньютоновском гравитационном поле управляемого космического аппарата с неуправляемым аппаратом, улучшить сходимость итерационных процессов численного решения полученных краевых задач оптимизации. Нами с использованием параметров Эйлера установлены новые свойства оптимального управления орбитальным движением космических аппаратов и новые кватернионные первые интегралы полученных пространственных краевых задач оптимального управления, содержащие параметры Эйлера и сопряженные к ним переменные. Использование найденных кватернионных первых интегралов позволило понизить размерности кватернионных дифференциальных уравнений краевых задач оптимального управления на 5 единиц с одновременным их упрощением. Было показано, что известные векторные первые интегралы этих задачах, справедливые для оптимального управления, являются частными случаями найденных нами кватернионных первых интегралов, справедливых для любого управления, и что эти векторные первые интегралы не позволяют эффективно понизить размерности получаемых векторных дифференциальных уравнений краевых задач оптимизации, записанных с использованием декартовых координат, из-за равенства нулю определителя трехмерного кососимметрического матричного коэффициента в матричном уравнении, соответствующем известным векторным первым интегралам.

Эти достоинства решения задач оптимального управления орбитальным движением, обусловленные наличием в уравнениях орбитального движения кватернионных кинематических уравнений в параметрах Эйлера (Родрига–Гамильтона), могут быть использованы для решения задач оптимальных полетов на Луну в рамках возмущенной пространственной ограниченной задачи трех тел с использованием предложенных в статье уравнений.

3) В наших работах [29–37] решены (в рамках возмущенной пространственной задачи двух тел) задачи оптимальной переориентации орбиты космического аппарата, плоскости орбиты, коррекции угловых элементов орбиты посредством реактивного ускорения или реактивной тяги (для КА с переменной массой), ортогональных плоскости орбиты КА, с использованием принципа максимума Понтрягина и кватернионных дифференциальных уравнений ориентации орбитальной системы координат или орбиты КА в параметрах Эйлера в непрерывной (с ограниченным по модулю управлением) или в импульсной постановке. При таком управлении форма и размеры орбиты КА остаются в процессе управляемого движения неизменными, а сама орбита поворачивается в инерциальной системе координат как неизменяемая (недеформируемая) фигура, что важно, например, при управлении спутниковой навигационной группировкой.

Решены задачи быстродействия, минимизации импульса реактивного ускорения или реактивной тяги, характеристической скорости КА, а также задачи минимизации комбинированных функционалов качества: времени и суммарного импульса величины ускорения или тяги, затраченных на процесс управления, времени и характеристической скорости КА.

Решение задач оптимальной переориентации орбиты и плоскости орбиты космического аппарата, коррекции угловых элементов орбиты КА посредством реактивного ускорения или реактивной тяги, ортогональных плоскости оскулирующей орбиты, с помощью уравнений в классических угловых элементах орбиты [38–43] в строгой нелинейной постановке достаточно сложно в силу нелинейности этих уравнений, наличия в них особых точек, в которых угол наклона орбиты i = 0, π, а также в силу громоздкости уравнений для сопряженных переменных. Поэтому для решения этих задач вместо угловых элементов орбиты целесообразно использовать параметры Эйлера (Родрига–Гамильтона).

Нами для решения указанных задач в рамках возмущенной пространственной задачи двух тел использовано кватернионное дифференциальное уравнение, описывающее ориентацию орбитальной системы координат в параметрах Эйлера, или кватернионное дифференциальное уравнение мгновенной ориентации орбиты КА в параметрах Эйлера и скалярное дифференциальное уравнение для истинной аномалии, характеризующей положение центра масс КА на орбите. Использование кватернионного дифференциального уравнения ориентации орбитальной системы координат более удобно при аналитическом исследовании задачи оптимальной переориентации орбиты КА в непрерывной постановке (с использованием малой тяги реактивного двигателя), однако использование кватернионного дифференциального уравнения ориентации орбиты КА имеет преимущество при численном решении задач оптимальной переориентации орбиты КА и ее плоскости и коррекции угловых элементов орбиты, так как кватернион ориентации орбиты КА является оскулирующим (медленно изменяющимся) элементом орбиты. Кватернион ориентации орбитальной системы координат таким свойством не обладает, так как является быстро меняющейся переменной.

Отметим, что проблема вырожденности классических орбитальных элементов орбиты движущегося тела (например, КА) частично решается в механике космического полета за счет использования так называемых “невырожденных” орбитальных элементов (иногда для них используют термин “equinoctial elements”) и соответствующих уравнений ориентации орбиты Battin [44]. Эти уравнения, также как и предложенные нами кватернионные уравнения ориентации орбиты КА в параметрах Эйлера, не имеют особой точки (деления на ноль при равенстве нулю угла наклона орбиты), однако в этих уравнениях сохраняется особое значение угла наклона орбиты, равное 180 град. К тому же уравнения Battin и сопряженные к ним уравнения задач оптимального управления орбитальным движением КА, решаемых с использованием принципа максимума, значительно сложнее предложенных нами кватернионных регулярных фазовых и сопряженных уравнений в задачах оптимального управления орбитальным движением КА (например, в задачах оптимальной переориентации орбиты КА), как с аналитической, так и вычислительной точек зрения.

Кроме этого, кватернионное уравнение ориентации орбиты КА в параметрах Эйлера обладает свойством самосопряженности: оно с точностью до обозначения кватернионной переменной совпадает с кватернионным сопряженным ему уравнением, что позволяет понизить размерность краевых задач оптимизации (с одновременным их упрощением) на четыре единицы с использованием новой кватернионной переменной, являющейся мультипликативной композицией кватернионных фазовой и сопряженной переменных (в виде их кватернионного произведения). Таким свойством классические дифференциальные уравнения ориентации орбиты в угловых элементах орбиты и уравнения Battin не обладают, причем соответствующие им сопряженные уравнения гораздо сложнее фазовых. Отметим, что эти интегралы для оптимального орбитального движения аналогичны кватернионным первым интегралам, существующим в задачах оптимального управления вращательным движением твердого тела, установленным впервые Бранцем и Шмыглевским [11].

Полученные в статье уравнения орбитального движения целесообразно использовать для решения задач оптимальной переориентации орбиты космического аппарата, плоскости орбиты, коррекции угловых элементов орбиты в более общей постановке: в рамках возмущенной пространственной ограниченной задачи трех тел (Земля, Луна, космический аппарат), учитывающей влияние Луны.

4) В статье также получены новые регулярные кватернионные уравнения возмущенной пространственной ограниченной задачи трех тел, построенные с использованием двухмерных идеальных прямоугольных координат Ганзена, параметров Эйлера и кватернионных переменных, а также с использованием комплексных композиций координат Ганзена и параметров Эйлера (параметров Кейли–Клейна), в которых используется обычная комплексность i, обладающая свойством i² = –1. Получены интегралы Якоби уравнений невозмущенной пространственной ограниченной круговой задачи трех тел в идеальных координатах Ганзена и параметрах Эйлера. Уравнения в комплексных переменных целесообразно использовать для численного решения задач небесной механики и механики космического полета с использованием системы остаточных классов – непозиционной системы кодирования цифровой информации [24], позволяющей, распараллеливать вычислительные операции на арифметическом уровне, повышать надежность вычислений, эффективно использовать микропроцессорную аппаратуру в вычислительных устройствах.

5) Другие особенности типа деления на ноль классических уравнений небесной механики и механики космического полета, порождаемые гравитационными силами, также эффективно устраняются с помощью использования параметров Эйлера и кватернионов Гамильтона. Так, нами показано [45, 46], что из дифференциальных уравнений возмущенной пространственной задачи двух тел, записанных в неголономной системе кординат с использованием параметров Эйлера и кватернионов поворотов, (т.е. из уравнений, которые получаются из уравнений (5.4)–(5.6) при m₁ = 0 или из уравнений (5.7)–(5.9) при m₀ = 0), наиболее просто и наглядно получаются регулярные кватернионные уравнения пространственной задачи двух тел в четырехмерных переменных Кустаанхеймо–Штифеля [47], широко используемые в настоящее время в астродинамике. Обзор работ по кватернионной регуляризации особенностей классических уравнений небесной механики и механики космического полета, порождаемых гравитационными и другими центральными силами, в рамках возмущенной пространственной задачи двух тел с помощью использования параметров Эйлера (Родрига–Гамильтона), четырехмерных переменных Кустаахеймо–Штифеля и других модифицированных четырехмерных переменных, предложенных нами, двухмерных переменных Леви-Чивита, а также с помощью использования в качестве дополнительных переменных энергетических переменных и регуляризующего преобразования времени дан в нашей недавней работе [48].

Использование полученных в нашей статье уравнений позволяет эффективно решить проблему устранения особенностей уравнений небесной механики и механики космического полета, порождаемых гравитационными силами, в рамках возмущенной пространственной ограниченной задачи трех тел и построить различные новые регулярные кватернионные уравнения небесной механики и механики космического полета с помощью перехода в полученных уравнениях от параметров Эйлера к четырехмерным переменным Кустаахеймо–Штифеля и другим четырехмерным переменным, использования двухмерных переменных Леви-Чивита, а также с помощью использования в качестве дополнительных переменных энергетических переменных и регуляризующего преобразования времени.