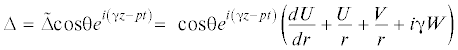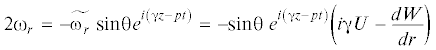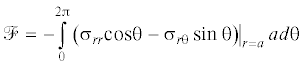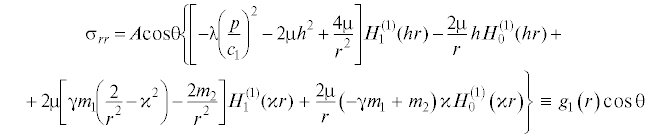Известия РАН. Механика твердого тела, 2023, № 1, стр. 33-46
РЕШЕНИЕ ВНЕШНЕЙ ЗАДАЧИ ПОХГАММЕРА–КРИ И ИЗГИБНЫЕ СЕЙСМИЧЕСКИЕ КОЛЕБАНИЯ ТРУБОПРОВОДА В БЕСКОНЕЧНОЙ УПРУГОЙ СРЕДЕ
a Комплексный НИИ РАН
Грозный, Россия
* E-mail: israiler@hotmail.com
Поступила в редакцию 01.11.2021
После доработки 09.11.2021
Принята к публикации 29.11.2021
- EDN: KFYKWF
- DOI: 10.31857/S0572329922060083
Аннотация
Доказана возможность частичного расщепления динамических уравнений линейной теории упругости для объемного расширения и компонент вектора вращения частиц среды в цилиндрических координатах в общем случае нестационарной задачи. Этот результат является обобщением аналогичного факта, установленного А. Лявом при простой гармонической зависимости названных функций от времени и двух пространственных координат. Дано точное аналитическое решение задачи об изгибных колебаниях упругого пространства с круговой цилиндрической полостью (внешней задачи Похгаммера–Кри). Показано, что опубликованное К. Токи и Ш. Такада исследование по этому вопросу не дает решения названной задачи. На основе полученного решения внешней задачи Похгаммера–Кри изучены изгибные колебания подземного трубопровода, вызванные действием сейсмической волны. Полученные при этом результаты дают, по-видимому, первое теоретическое обоснование широко используемой в нормативных документах по сейсмостойкому строительству инженерной теории жесткого защемления трубопровода в грунте для случая изгибных колебаний.
1. Введение. Теме изгибных колебаний протяженных подземных сооружений, в частности, трубопроводов посвящено значительно меньшее число работ, чем изучению продольных сейсмических движений таких сооружений в направлении их протяженности. На то существуют, по крайней мере, два объяснения ([1], гл. 9). Первое из них состоит в том, что при землетрясениях деформации в осевом направлении трубы, как правило, заметно превышают ее деформации от изгиба. Второе объяснение связано с многократно подтвержденным на практике наблюдением о примерно одинаковых поперечных колебаниях трубопроводов и грунта, за исключением случаев очень сильных землетрясений. Даже когда трубопроводы соединяются со смотровыми колодцами, то как трубопроводы, так и колодцы колеблются одинаково с грунтом. Последнее положение служит экспериментальным обоснованием простейшей инженерной теории “жесткого защемления” трубы в грунте (согласно которой движения грунта и трубопровода совпадают) для случая изгибных колебаний трубопровода. Считается, что названная теория дает верхнюю границу для сейсмических нагрузок, и потому, она до сих пор широко используется в качестве расчетной базы в принятых нормах по сейсмостойкому строительству (см., например, [2]).
Более сложное взаимодействие трубопровода с грунтом при изгибных колебаниях описывается моделью “балки на упругом основании”. Достаточно полный обзор работ этого направления содержится в монографии О’Рурке [3].
Т. Рашидов и соавторы предложили модель взаимодействия с грунтом, в которой силы взаимодействия при изгибных колебаниях (так же, как и при продольных) считаются пропорциональными относительному перемещению, равному разности между перемещением грунта в сейсмической волне (вдали от трубопровода) и перемещением самого трубопровода. Описание метода и ссылки на предшествующие работы содержатся в монографии [4]. Дифференциальные уравнения изгибных колебаний выписываются в предположении, что изгибные колебания трубы и “грунтового стержня”, замещающего трубопровод, одинаковы, если совпадают их погонные массы. Такое предположение будет верным, если изгибная жесткость трубы совпадает с “изгибной жесткостью” грунтового стержня, что может реализоваться в весьма редких случаях.
Изгибные колебания протяженных подземных трубопроводов, рассматриваемых как тонкостенные цилиндрические оболочки изучались методом конечных элементов в работах [5, 6] (здесь же можно найти ссылки и на другие работы авторов по этому предмету). Однако в них динамика взаимодействия между трубопроводом и грунтом полностью игнорируется и считается, что сейсмические волны без искажения падают на оболочку.
Попытка решения задачи об изгибных колебаниях трубопровода под воздействием сейсмических волн, рассматривая совместные движения трубы и окружающего его упругого грунта, была предпринята К. Токи и Ш. Такада в статье [7], опубликованной в малоизвестном издании (“Бюллетене Института предупреждения катастроф” Киотского университета). Однако допущенные авторами ошибки не дают возможности считать, что задача для грунта решена и цель авторов достигнута.
Настоящая статья посвящена рещению этой задачи (названной нами внешней задачей Похгаммера – Кри) и исследованию на основе этого решения изгибных сейсмических колебаний подземного трубопровода. В соответствующих местах ниже указано в чем состоят принципиальные упущения работы [7].
2. Преобразование динамических уравнений Ламе в отдельные уравнения для объемного расширения и компонент вектора вращения в цилиндрических координатах. Уравнения движения упругой среды в перемещениях (уравнения Ламе), записанные в векторной форме [8]
(2.1)
${{\rho }}\frac{{{{\partial }^{2}}{\mathbf{u}}}}{{\partial {{t}^{2}}}} = \left( {{{\lambda }} + 2{{\mu }}} \right){\text{grad}}\left( {{\text{div}}{\mathbf{u}}} \right) - {{\mu rot}}\left( {{\text{rot}}~{\mathbf{u}}} \right)$В цилиндрической системе координат $\left( {r,~{{\theta }},~z} \right)$, в которой компоненты вектора перемещений u частиц среды обозначены через ${{u}_{r}}$, ${{u}_{{{\theta }}}}$, ${{u}_{z}}$, векторное уравнение (2.1) записывается в виде системы уравнений (А. Ляв [9], гл. XII):
(2.2)
${{\rho }}\frac{{{{\partial }^{2}}{{u}_{r}}}}{{\partial {{t}^{2}}}} = \left( {{{\lambda }} + 2{{\mu }}} \right)\frac{{\partial \Delta }}{{\partial r}} - \frac{{2{{\mu }}}}{r}\frac{{\partial {{{{\omega }}}_{z}}}}{{\partial {{\theta }}}} + 2{{\mu }}\frac{{\partial {{{{\omega }}}_{{{\theta }}}}}}{{\partial z}}$(2.3)
$\Delta \equiv {\text{div}}{\mathbf{u}} = \frac{1}{r}\frac{{\partial \left( {r{{u}_{r}}} \right)}}{{\partial r}} + \frac{1}{r}\frac{{\partial {{u}_{{{\theta }}}}}}{{\partial {{\theta }}}} + \frac{{\partial {{u}_{z}}}}{{\partial z}}$(2.4)
$2{{{{\omega }}}_{r}} = \frac{1}{r}\frac{{\partial {{u}_{z}}}}{{\partial {{\theta }}}} - \frac{{\partial {{u}_{{{\theta }}}}}}{{\partial z}},2{{{{\omega }}}_{{{\theta }}}} = \frac{{\partial {{u}_{r}}}}{{\partial z}} - \frac{{\partial {{u}_{z}}}}{{\partial r}},2{{{{\omega }}}_{z}} = \frac{1}{r}\left( {\frac{{\partial \left( {r{{u}_{{{\theta }}}}} \right)}}{{\partial r}} - \frac{{\partial {{u}_{r}}}}{{\partial {{\theta }}}}} \right)$При этом компоненты (2.4) удовлетворяют тождественно равенству div(2ω) = = ${\text{div(rot}}~{\mathbf{u}}{\text{)}} \equiv 0$, т.е. равенству
(2.5)
$\frac{1}{r}\frac{{\partial \left( {r{{{{\omega }}}_{r}}} \right)}}{{\partial r}} + \frac{1}{r}\frac{{\partial {{{{\omega }}}_{{{\theta }}}}}}{{\partial {{\theta }}}} + \frac{{\partial {{{{\omega }}}_{z}}}}{{\partial z}} = 0$Таким образом, только две компоненты вектора ${\mathbf{\omega }}$ являются независимыми и, следовательно, компоненты вектора перемещений могут быть выражены через объемное расширение и любые две из компонент вектора вращения.
Векторное уравнение (2.1) или связанная система уравнений (2.2) могут быть приведены в цилиндрических координатах к частично разделенной системе отдельных уравнений для Δ и компонент ${{{{\omega }}}_{z}}$, ${{{{\omega }}}_{r}}$. После того как эти функции найдены, компонента вращения ${{{{\omega }}}_{{{\theta }}}}$ может быть найдена (при необходимости) из тождества (2.5). Действительно, применяя сначала к уравнению (2.1) операцию ${\text{div}}$ и пользуясь известным из векторного анализа тождеством ${\text{div}}\left( {{\text{rot}}~{\mathbf{a}}} \right) \equiv 0$ (для любого вектора a), получаем, что
(2.6)
$\frac{\rho }{{{{\lambda }} + 2{{\mu }}}}\frac{{{{\partial }^{2}}\Delta }}{{\partial {{t}^{2}}}} = {\text{div}}\left( {{\text{grad}}~\Delta } \right) \equiv {{\nabla }^{2}}\left( \Delta \right)~$(2.7)
${{\nabla }^{2}} \equiv \frac{{{{\partial }^{2}}}}{{\partial {{r}^{2}}}} + \frac{1}{r}\frac{\partial }{{\partial r}} + \frac{1}{{{{r}^{2}}}}\frac{{{{\partial }^{2}}}}{{\partial {{{{\theta }}}^{2}}}} + \frac{{{{\partial }^{2}}}}{{\partial {{z}^{2}}}}$Применим теперь к уравнению (2.1) операцию rot. Тогда, пользуясь тождеством ${\text{rot}}\left( {{\text{grad}}{\mathbf{a}}} \right) \equiv 0$, имеем
(2.8)
${{\rho }}\frac{{{{\partial }^{2}}{\mathbf{\omega }}}}{{\partial {{t}^{2}}}} = - {{\mu rot}}\left( {{\text{rot}}~{\mathbf{\omega }}} \right)$Выпишем уравнение (2.8) для компоненты ${{{{\omega }}}_{z}}$ в цилиндрических координатах, пользуясь определением ротора,
Выражая сумму двух последних слагаемых в правой части этого уравнения через ${{{{\omega }}}_{z}}$ при помощи тождества (2.5) получаем окончательно отдельное волновое уравнение для этой компоненты
(2.9)
$\frac{{{\rho }}}{{{\mu }}}\frac{{{{\partial }^{2}}{{{{\omega }}}_{z}}}}{{\partial {{t}^{2}}}} = {{\nabla }^{2}}{{{{\omega }}}_{z}}$Запишем теперь проекцию уравнения (2.8) на ось r, т.е. уравнение для компоненты ${{{{\omega }}}_{r}}$:
Если из правой части этого уравнения исключить с помощью тождества (2.5) члены, содержащие ${{{{\omega }}}_{{{\theta }}}}$, приходим к уравнению
(2.10)
$\frac{{{\rho }}}{{{\mu }}}\frac{{{{\partial }^{2}}{{{{\omega }}}_{r}}}}{{\partial {{t}^{2}}}} = \frac{1}{{{{r}^{2}}}}\frac{\partial }{{\partial r}}\left[ {r\frac{{\partial \left( {r{{{{\omega }}}_{r}}} \right)}}{{\partial r}}} \right] + \frac{1}{{{{r}^{2}}}}\frac{{{{\partial }^{2}}{{{{\omega }}}_{r}}}}{{\partial {{{{\theta }}}^{2}}}} + \frac{{{{\partial }^{2}}{{{{\omega }}}_{r}}}}{{\partial {{z}^{2}}}} + \frac{2}{r}\frac{{\partial {{{{\omega }}}_{z}}}}{{\partial z}}$Уравнение (2.10) упрощается введением новой неизвестной функции ${{{{\Omega }}}_{r}} = r{{{{\omega }}}_{r}}$ и приводится к виду в котором часть, зависящая от ${{{{\omega }}}_{r}}$, сводится к волновому оператору
(2.11)
$\frac{{{\rho }}}{{{\mu }}}\frac{{{{\partial }^{2}}{{{{\Omega }}}_{r}}}}{{\partial {{t}^{2}}}} = {{\nabla }^{2}}{{{{\Omega }}}_{r}} + 2\frac{{\partial {{{{\omega }}}_{z}}}}{{\partial z}}$Таким образом, связанная система динамических уравнений Ламе (2.2) сведена к отдельным волновым уравнениям (2.6), (2.9) для объемного расширения Δ и третьей компоненты вектора вращения ${{{{\omega }}}_{z}}$ и к уравнению (2.10) или (2.11) для компоненты вращения ${{{{\omega }}}_{r}}$, содержащему еще и функцию ${{{{\omega }}}_{z}}$. Уравнение (2.11) может быть проинтегрировано как неоднородное волновое уравнение после того, как функция ${{{{\omega }}}_{z}}$ определена из отдельного уравнения (2.9). Нахождение трех функций Δ, ${{{{\omega }}}_{z}}$ и ${{{{\omega }}}_{r}}$ достаточно для вычисления компонент вектора перемещений частиц среды, поскольку функция ${{{{\omega }}}_{{{\theta }}}}$ может быть определена из тождества (2.5) при известных ${{{{\omega }}}_{z}}$ и ${{{{\omega }}}_{r}}$.
Полученный выше результат хотя и является простым обобщением изложения, данного в трактате А. Лява (для случая, когда все упомянутые функции являются элементарными гармоническими функциями t и $z$ и зависимость их от θ дается простыми функциями $\cos {{\theta }}~$ или $\sin {{\theta }}$), однако он, по-видимому, не был известен до сих пор в общем случае произвольной зависимости названных функций от всех переменных и может представлять интерес при решении нестационарных динамических задач теории упругости в цилиндрических координатах.
3. Постановка и точное решение внешней задачи Похгаммера–Кри. По аналогии с постановкой задачи об изгибных колебаниях упругого кругового цилиндра сформулируем задачу об изгибных колебаниях неограниченной упругой среды, занимающей пространственную область, внешнюю по отношению к круговому цилиндру.
Первоисточниками по первой задаче (которую будем называть внутренней задачей) являются работы Похгаммера [10] (1876 г.) и Кри [11] (1886 г.). Предельно ясное решение внутренней задачи дано А. Лявом в его трактате по математической теории упругости [9]. Поэтому, отсылая за подробностями к трактату [9], ограничимся кратким изложением постановки внешней задачи, обращая, прежде всего, внимание на существующие отличия в этих постановках.
Чтобы прийти к стационарным изгибным колебаниям области, внешней по отношению к круговому цилиндру, рассмотрим, как и в случае кругового цилиндра [9], класс решений динамических уравнений теории упругости, выписанных в п. 2, в которых все компоненты вектора перемещений являются гармоническими функциями времени $t$ и координаты z (измеряемой вдоль оси цилиндра), принимая, кроме того, что ${{u}_{r}}$ и ${{u}_{z}}$ пропорциональны $\cos {{\theta }}$, а ${{u}_{{{\theta }}}}$ пропорционально $\sin {{\theta }}$, т.е.
(3.1)
${{u}_{r}} = U\cos {{\theta }}~{{e}^{{i\left( {{{\gamma }}z - pt} \right)}}},\quad {{u}_{{{\theta }}}} = V\sin {{\theta }}~{{e}^{{i\left( {{{\gamma }}z - pt} \right)}}},\quad {{u}_{z}} = W~\cos {{\theta }}~{{e}^{{i\left( {{{\gamma }}z - pt} \right)}}}$(3.3)
$\frac{{{{d}^{2}}\tilde {\Delta }}}{{d{{r}^{2}}}} + \frac{1}{r}\frac{{d\tilde {\Delta }}}{{dr}} - \left( {\frac{1}{{{{r}^{2}}}} - {{h}^{2}}} \right)\tilde {\Delta } = 0$(3.4)
$\frac{{{{d}^{2}}\widetilde {{{{{\omega }}}_{z}}}}}{{d{{r}^{2}}}} + \frac{1}{r}\frac{{d\widetilde {{{{{\omega }}}_{z}}}}}{{dr}} - \left( {\frac{1}{{{{r}^{2}}}} - {{{{\kappa }}}^{2}}} \right)\widetilde {{{{{\omega }}}_{z}}} = 0~$(3.5)
$\frac{{{{d}^{2}}{{{{\Omega }}}_{r}}}}{{d{{r}^{2}}}} + \frac{1}{r}\frac{{d{{{{\Omega }}}_{r}}}}{{dr}} - \left( {\frac{1}{{{{r}^{2}}}} - {{{{\kappa }}}^{2}}} \right){{{{\Omega }}}_{r}} + \frac{2}{r}i{{\gamma }}~\widetilde {{{{{\omega }}}_{z}}} = 0,\quad {{{{\Omega }}}_{r}} \equiv r\widetilde {{{{{\omega }}}_{r}}}$(3.6)
${{h}^{2}} = \frac{{{{\rho }}{{p}^{2}}}}{{{{\lambda }} + 2{{\mu }}}} - {{{{\gamma }}}^{2}} = {{\left( {\frac{p}{{{{c}_{1}}}}} \right)}^{2}} - {{{{\gamma }}}^{2}},\quad {{{{\kappa }}}^{2}} = \frac{{{{\rho }}{{p}^{2}}}}{{{\mu }}} - {{{{\gamma }}}^{2}} = {{\left( {\frac{p}{{{{c}_{2}}}}} \right)}^{2}} - {{{{\gamma }}}^{2}}$В соотношениях (3.6) c1 и c2 есть скорости распространения продольных и поперечных волн в упругой среде. Предполагается,
что правые части этих соотношений положительны, т.е. что фазовая скорость 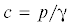 распространения возмущений (3.1) вдоль оси z больше скоростей ${{c}_{1}}$ и ${{c}_{2}}$ (это условие не оговорено А. Лявом [9], однако подразумевается выполненным). Такая ситуация реализуется, например, при
падении наклонной волны на подземный трубопровод [12]. Если это не так, то возможен только случай, когда ${{h}^{2}} < 0$, т.е. ${{c}_{2}} < c < {{c}_{1}}$. Тогда решение уравнения (3.3)$~$должно быть взято не в виде функции Ханкеля, как ниже, а в виде функции Бесселя от
чисто мнимого аргумента (т.е. в виде модифицированной функции).
распространения возмущений (3.1) вдоль оси z больше скоростей ${{c}_{1}}$ и ${{c}_{2}}$ (это условие не оговорено А. Лявом [9], однако подразумевается выполненным). Такая ситуация реализуется, например, при
падении наклонной волны на подземный трубопровод [12]. Если это не так, то возможен только случай, когда ${{h}^{2}} < 0$, т.е. ${{c}_{2}} < c < {{c}_{1}}$. Тогда решение уравнения (3.3)$~$должно быть взято не в виде функции Ханкеля, как ниже, а в виде функции Бесселя от
чисто мнимого аргумента (т.е. в виде модифицированной функции).
Уравнения (3.3), (3.4) являются уравнениями Бесселя, а (3.5) сводится к уравнению Бесселя после подстановки в него решения (3.4) для $\widetilde {{{{{\omega }}}_{z}}}$ и нахождения частного решения полученного таким образом неоднородного уравнения.
А. Лявом показано, что ограниченные на оси цилиндра r = 0 решения уравнений (3.3)–(3.5) в виде бесселевых функций первого рода приводят к изгибным колебаниям кругового цилиндра.
При решении задачи о стационарных колебаниях в области, внешней по отношению к круговому цилиндру, требуется, для обеспечения единственности, искать решения уравнений (3.3)–(3.5), удовлетворяющие условиям излучения Зоммерфельда на бесконечности (см., например, [8, 13])
(3.7)
$\mathop {\lim }\limits_{r \to \infty } r\left( {\frac{{d\tilde {\Delta }}}{{dr}} - ih\tilde {\Delta }} \right) = 0,\quad \mathop {\lim }\limits_{r \to \infty } r\left( {\frac{{d\widetilde {{{{{\omega }}}_{{{\beta }}}}}}}{{dr}} - i{{\kappa }}\widetilde {{{{{\omega }}}_{{{\beta }}}}}} \right) = 0\,\,\,~\left( {{{\beta }} = z,r} \right)$Физически условия (3.7) означают, что для выделения единственных решений недостаточно требования убывания их при $r \to \infty $ (все функции Бесселя, кроме модифицированных первого рода, исчезают на бесконечности), а необходимо, чтобы они образовывали волны, уходящие на бесконечность. Решения же уравнений (3.3)–(3.5) в виде функций Бесселя первого и второго рода (используемые во внутренней задаче) образуют стоячие волны и не удовлетворяют условиям (3.7), а из решений этих уравнений в виде функций Ханкеля, образующих бегущие волны, только функции первого рода $H_{1}^{{\left( 1 \right)}}\left( {hr} \right)$ и $H_{1}^{{\left( 1 \right)}}\left( {{{\kappa }}r} \right)$ образуют волны уходящие на бесконечность, при умножении на принятую выше для всех функций Δ, ${{{{\omega }}}_{{{\beta }}}}$ экспоненциальную зависимость по времени в виде ${{e}^{{ - ipt}}}$ (формулы (3.2)). Последнее утверждение легко устанавливается с помощью известных асимптотических представлений функций Ханкеля для больших значений аргумента [14] (функции Ханкеля второго рода образуют волны, приходящие из бесконечности).
Замечание 1. Отметим, что если, как и в книге А. Лява, взять временную зависимость для функций в (3.2) в виде ${{e}^{{ + ipt}}}$, то условия излучения (3.7) должны быть записаны со знаком плюс перед вторыми слагаемыми и решения уравнений (3.3)–(3.5), удовлетворяющие таким условиям, будут функции Ханкеля второго рода $H_{1}^{{\left( 2 \right)}}\left( {hr} \right)$ и $H_{1}^{{\left( 2 \right)}}\left( {{{\kappa }}r} \right)$.
Учитывая сказанное, имеем решения уравнений (3.3) и (3.4), удовлетворяющие условиям излучения (3.7), в следующем виде:
(3.8)
$\tilde {\Delta } = - {{\left( {\frac{p}{{{{c}_{1}}}}} \right)}^{2}}A~H_{1}^{{\left( 1 \right)}}\left( {hr} \right)$(3.9)
$2\widetilde {{{{{\omega }}}_{z}}} = {{{{\kappa }}}^{2}}C~H_{1}^{{\left( 1 \right)}}\left( {{{\kappa }}r} \right)~$В этих решениях для удобства в дальнейших вычислениях произвольные константы A и C взяты с множителями ${{\left( {p{\text{/}}{{c}_{1}}} \right)}^{2}}$ и ${{{{\kappa }}}^{2}}$.
Подставляя выражение (3.9) для $\widetilde {{{{{\omega }}}_{z}}}$ в уравнение (3.5) и интегрируя полученное таким образом неоднородное уравнение Бесселя, приходим к решению
(3.10)
$2~\widetilde {{{{{\omega }}}_{r}}} = i{{\gamma }}C\frac{{d~H_{1}^{{\left( 1 \right)}}\left( {{{\kappa }}r} \right)}}{{dr}} + iB{{\left( {\frac{p}{{{{c}_{2}}}}} \right)}^{2}}\frac{{~H_{1}^{{\left( 1 \right)}}\left( {{{\kappa }}r} \right)}}{r}$Найденные значения для $\tilde {\Delta }$, $\widetilde {{{{{\omega }}}_{z}}}~$, $\widetilde {{{{{\omega }}}_{r}}}$ (формулы (3.8)–(3.10)) приводят к следующим соотношениям для перемещений
(3.11)
$U = A\frac{{d~H_{1}^{{\left( 1 \right)}}\left( {hr} \right)}}{{dr}} + B{{\gamma }}\frac{{d~H_{1}^{{\left( 1 \right)}}\left( {{{\kappa }}r} \right)}}{{dr}} + C\frac{{~H_{1}^{{\left( 1 \right)}}\left( {{{\kappa }}r} \right)}}{r}$Подставляя эти выражения в формулы (3.1), мы получим решения уравнений (2.2).
Решение внутренней задачи Похгаммера–Кри, аналогичное (3.11), вместо функций Ханкеля содержит функции Бесселя первого рода (и первого порядка) [9] и потому, в силу равенства ${{J}_{1}}\left( 0 \right) = 0$, на оси r = 0 перемещение W (или uz) равно нулю. Поэтому точки цилиндра, лежащие на оси r = 0 движутся в плоскости, перпендикулярной оси (совершают изгибные колебания). Причем это положение имеет место при произвольных константах A и B, входящих в выражение для W. Но точки вне оси не остаются в процессе движения в перпендикулярной к оси цилиндра плоскости, т.е. $W \ne 0$ при $r \ne 0$. Или, иначе, имеет место дилатация (нарушение закона плоских сечений). Однако, поскольку аргументы Бесселевых функций определены равенствами
(3.12)
$hr = 2{{\pi }}\frac{r}{{{\Lambda }}}\sqrt {{{{\left( {\frac{c}{{{{c}_{1}}}}} \right)}}^{2}} - 1} ,\quad {{\kappa }}r = ~2{{\pi }}\frac{r}{{{\Lambda }}}\sqrt {{{{\left( {\frac{c}{{{{c}_{2}}}}} \right)}}^{2}} - 1} ,$ фазовая скорость распространения их вдоль оси z, то $W \approx 0$, если
фазовая скорость распространения их вдоль оси z, то $W \approx 0$, если 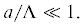 Следовательно, во внутренней задаче Похгаммера–Кри колебания цилиндра будут тем ближе
к чисто изгибным, чем меньше радиус цилиндра в сравнении с длиной волны.
Следовательно, во внутренней задаче Похгаммера–Кри колебания цилиндра будут тем ближе
к чисто изгибным, чем меньше радиус цилиндра в сравнении с длиной волны.
В решении рассматриваемой внешней задачи Похгаммера–Кри можно добиться равенства W = 0 на поверхности цилиндра (полости) r = a, что, согласно решению (3.11), выполнено, если константы A и $B$ связаны соотношением
(3.13)
$B = A~\frac{{{\gamma }}}{{{{{{\kappa }}}^{2}}}}\frac{{~H_{1}^{{\left( 1 \right)}}\left( {ha} \right)}}{{~H_{1}^{{\left( 1 \right)}}\left( {{{\kappa }}a} \right)}}~$Однако (так же, как и в описанной выше ситуации во внутренней задаче Похгаммера–Кри)
невозможно добиться, чтобы W = 0 при всех $r > a$. Но, в силу непрерывности функций Ханкеля при любом конечном значении аргумента,
будет выполнено приближенное равенство $W \approx 0$, если  .
.
Следовательно, при выполнении соотношения (3.13), точки среды, находящиеся в окрестности цилиндрической поверхности малой по размеру в сравнении с длиной волны, будут при движениях, подчиняющихся законам (3.11), мало отклоняться от плоскости, перпендикулярной оси цилиндрической полости (т.е. будут совершать приближенно изгибные колебания).
Потребуем теперь, чтобы эти изгибные колебания происходили (приближенно) в одном каком-нибудь направлении, скажем, в направлении прямой, от которой отсчитывается угол ${{\theta }}$. Это направление примем за ось x декартовой системы координат $\left( {x,y,z} \right)$, вводимой здесь наряду с цилиндрической. Указанное требование выполнено, если точки поверхности цилиндра r = a движутся в направлении x, т.е. когда
(3.14)
${{\left. {{{V}_{y}}} \right|}_{{r = a}}} = \cos {{\theta }}~\sin {{\theta }}{{\left. {\left( {U + V} \right)} \right|}_{{r = a}}} = 0$Подставляя в условие (3.14) перемещения U и $V$ из (3.11), получаем, что оно будет выполнено, если
(3.15)
$C = A\frac{{P\left( {ha} \right)}}{{Q\left( {{{\kappa }}a} \right)}} + B{{\gamma }} = A\left[ {\frac{{P\left( {ha} \right)}}{{Q\left( {{{\kappa }}a} \right)}} + \frac{{{{{{\gamma }}}^{2}}}}{{{{{{\kappa }}}^{2}}}}\frac{{~H_{1}^{{\left( 1 \right)}}\left( {ha} \right)}}{{~H_{1}^{{\left( 1 \right)}}\left( {{{\kappa }}a} \right)}}} \right]$(3.16)
$P\left( {ha} \right) = \frac{{d~H_{1}^{{\left( 1 \right)}}\left( {ha} \right)}}{{da}} - \frac{{H_{1}^{{\left( 1 \right)}}\left( {ha} \right)}}{a},\quad ~Q\left( {{{\kappa }}a} \right) = \frac{{d~H_{1}^{{\left( 1 \right)}}\left( {{{\kappa }}a} \right)}}{{da}} - \frac{{H_{1}^{{\left( 1 \right)}}\left( {{{\kappa }}a} \right)}}{a}$Таким образом, формулы (3.11), в которых константы B и $C$ выражены соотношениями (3.13), (3.15) через единственную константу A, дают решение внешней задачи Похгаммера–Кри об изгибных колебаниях внешности кругового цилиндра. Неизвестная константа A определяется из дополнительного краевого условия на цилиндрической поверхности r = a. Так, в задаче о совместных изгибных колебаниях бесконечной упругой среды и трубопровода, таким условием служит условие непрерывности (равенства) перемещений трубы и точек среды, примыкающих к поверхности трубы, в направлении изгиба (т.е. в направлении оси $x$).
Во внутренней задаче Похгаммера–Кри соотношение (3.14) так же, как и условие W = 0, выполнено при произвольных константах, входящих в выражения для перемещений, подобных (3.11). Однако, равенство (3.14) даже для точек, лежащих на оси r = 0, так же, как и во внешней задаче выполнено уже только приближенно, когда радиус цилиндра мал в сравнении с длиной волны (это обстоятельство не отмечено А. Лявом [9]).
Указанное выше различие, состоящее в том, что во внутренней задаче Похгаммера–Кри все три константы в выражениях для перемещений остаются неопределенными при изгибных колебаниях, связано с тем что в ней существуют собственные колебания только при определенных (собственных) частотах, выводимых из условий отсутствия напряжений на боковой поверхности цилиндра. В то время как во внешней задаче (с неограниченной областью) все частоты являются собственными.
Замечание 2. К. Токи и Ш. Такада утверждают в работе [7], что они нашли решение рассмотренной в настоящем пункте задачи, в котором во всех точках области (внешности кругового цилиндра) перемещения в направлении оси цилиндра равны нулю (W = 0). Как показано выше такого решения не существует. Можно добиться только, чтобы названные перемещения были равны нулю на цилиндрической поверхности (при выполнении соотношения (3.13) между константами) и малости W в окрестности этой поверхности, размер (диаметр) которой мал в сравнении с длиной сейсмической волны (ситуация здесь вполне аналогична той, что возникает во внутренней задаче Похгаммера–Кри, как отмечено выше). Токи и Такада сразу выписывают свое решение в виде первых двух соотношений из (3.11), полагая в них B = 0. Такое предположение заметно упрощает последующие выкладки (нахождение оставшихся двух констант), однако полученные авторами результаты не дают решения внешней задачи Похгаммера–Кри, поскольку, как видно из третьего уравнения (3.11) перемещения W в их решении остаются произвольными.
4. Вычисление поперечной силы при заданном поперечном перемещении границы полости во внешней задаче Похгаммера–Кри. Прежде всего установим, что при выполнении всех условий п. 3 и при одной, пока произвольной, константе A в решении внешней задачи Похгаммера–Кри, перемещения всех точек сечения $z = {\text{const}}$ цилиндрической поверхности $r = a$ в направлении оси x, т.е. в направлении изгиба, одинаковы (не зависят от угла ${{\theta }}$). Действительно, поскольку, в силу принятых соотношений (3.1), перемещения вдоль осей r и ${{\theta }}$ равны ${{U}_{r}} = U$$\cos {{\theta }}$, ${{V}_{{{\theta }}}} = V$$\sin {{\theta }}$, то
Используя теперь в полученном выражении для ${{U}_{x}}$ условие (3.14), получаем
(4.1)
${{\left. {{{U}_{x}}} \right|}_{{r = a}}} = {{\left. U \right|}_{{r = a}}} = - {{\left. V \right|}_{{r = a}}}$Выражения (4.1) представляют собой одно условие, а не два, поскольку, в силу найденных выше зависимостей между A, $B$ и $C$ ((3.13), (3.15)), $U$ и $ - V$ совпадают при $r = a$.
Если в цилиндрическую полость помещены цилиндрический стержень или труба, то полученный результат (4.1) позволяет обеспечить условие прилипания, т.е. условие непрерывности перемещений среды и стержня на его поверхности. Отсюда и находится последняя неопреденная константа A в полученном в п. 3 решении. Действительно, пусть перемещение стержня/трубы в произвольном сечении в направлении оси x (в направлении изгиба) есть ${{\mathcal{U}}_{1}}$ (или ${{u}_{1}} = {{\mathcal{U}}_{1}}{{e}^{{i\left( {{{\gamma }}z - pt} \right)}}}$). Следовательно, сагласно (4.1) и (3.11),
(4.2)
${{\mathcal{U}}_{1}} = {{\left\{ {A\frac{{d~H_{1}^{{\left( 1 \right)}}\left( {hr} \right)}}{{dr}} + B\gamma \frac{{d~H_{1}^{{\left( 1 \right)}}\left( {{{\kappa }}r} \right)}}{{dr}} + C\frac{{~H_{1}^{{\left( 1 \right)}}\left( {{{\kappa }}r} \right)}}{r}} \right\}}_{{r = a}}}~$Записывая равенства (3.13) и (3.15) в виде $B = {{m}_{1}}A$, $C = {{m}_{2}}A$, где обозначено
(4.3)
${{m}_{1}} = \frac{{{\gamma }}}{{{{{{\kappa }}}^{2}}}}\frac{{~H_{1}^{{\left( 1 \right)}}\left( {ha} \right)}}{{~H_{1}^{{\left( 1 \right)}}\left( {{{\kappa }}a} \right)}},\quad {{m}_{2}} = ~\frac{{P\left( {ha} \right)}}{{Q\left( {{{\kappa }}a} \right)}} + \frac{{{{{{\gamma }}}^{2}}}}{{{{{{\kappa }}}^{2}}}}\frac{{~H_{1}^{{\left( 1 \right)}}\left( {ha} \right)}}{{~H_{1}^{{\left( 1 \right)}}\left( {{{\kappa }}a} \right)}}~$(4.4)
$A = \frac{{{{\mathcal{U}}_{1}}}}{{\frac{{d~H_{1}^{{\left( 1 \right)}}\left( {ha} \right)}}{{da}} + {{\gamma }}{{m}_{1}}\frac{{d~H_{1}^{{\left( 1 \right)}}\left( {{{\kappa }}a} \right)}}{{da}} + {{m}_{2}}\frac{{~H_{1}^{{\left( 1 \right)}}\left( {{{\kappa }}a} \right)}}{a}}}~$Вычислением константы A по формуле (4.4) завершается окончательное решение внешней задачи Похгаммера–Кри, сформулированной в п. 3. Радиальные и тангенциальные перемещения точек среды в этом решении принимают, в соответствии с представлениями (3.1), вид
(4.5)
${{u}_{r}} = A\left[ {\frac{{d~H_{1}^{{\left( 1 \right)}}\left( {hr} \right)}}{{dr}} + {{\gamma }}{{m}_{1}}\frac{{d~H_{1}^{{\left( 1 \right)}}\left( {{{\kappa }}r} \right)}}{{dr}} + {{m}_{2}}\frac{{~H_{1}^{{\left( 1 \right)}}\left( {{{\kappa }}r} \right)}}{r}} \right]\cos {{\theta }}~{{e}^{{i\left( {{{\gamma }}z - pt} \right)}}}~~$В формулах (4.5) величины ${{m}_{1}}$, ${{m}_{2}}$ и $A$ определены выражениями (4.3) и (4.4).
Легко установить, что сила, действующая стержень или трубопровод при перемещении его в направлении оси x, дается равенством (напомним, что угол ${{\theta }}$ отсчитывается против часовой стрелки от этой оси)
Здесь ${{\sigma }_{{rr}}}$ и ${{\sigma }_{{r{{\theta }}}}}$ представляют собой физические компоненты тензора напряжений в цилиндрической системе координат; они выражаются через физические компоненты тензора малых деформаций так же, как компоненты тензора напряжений выражаются через компоненты тензора деформаций в декартовой системе координат (однако, при записи закона Гука в компонентах тензоров напряжений и деформаций в цилиндрической системе координат, как и в любой криволинейной ортогональной системе, необходимо в шаровой части единичный тензор Кронекера заменить на метрический тензор системы координат, на что, иногда, ошибочно не обращается внимания [15]).
При вычилении физических компонент напряжений по закону Гука используем полученное выше выражение для объемного расширения (3.8). Кроме того, при вычислении физических компонент деформаций по известным формулам [16]
(4.7)
${\text{\;}}\frac{{\partial H_{1}^{{\left( 1 \right)}}\left( {{\xi }} \right)}}{{\partial {{\xi }}}} = H_{0}^{{\left( 1 \right)}}\left( {{\xi }} \right) - \frac{{H_{1}^{{\left( 1 \right)}}\left( {{\xi }} \right)}}{{{\xi }}}$Упрощенные таким образом выражения для физических компонент напряжений приводятся после простых, но несколько длинных выкладок, к следующему виду
Подставляя найденные напряжения (4.8) в формулу (4.6), получаем
Следовательно, принимая во внимание значение константы A из (4.4), имеем для погонной силы (силы, действующей на поверхности элемента трубы единичной длины) окончательный результат
где(4.10)
$f = \left\{ {\left[ {\left( {{{{\left( {\frac{{{{c}_{1}}}}{{{{c}_{2}}}}} \right)}}^{2}} - 2} \right){{{\left( {\frac{{ap}}{{{{c}_{1}}}}} \right)}}^{2}} + 2{{{\bar {h}}}^{2}}} \right]H_{1}^{{\left( 1 \right)}}(\bar {h}) + \left( {2{{\gamma }}{{m}_{1}} + {{m}_{2}}} \right){{{{{\bar {\kappa }}}}}^{2}}H_{1}^{{\left( 1 \right)}}\left( {{{\bar {\kappa }}}} \right)} \right\} \times \frac{1}{\mathcal{Z}}$В формулах (4.10) введены безразмерные параметры $\bar {h} \equiv ha$, $~{{\bar {\kappa }}} \equiv \kappa a$, а безразмерная величина $\mathcal{Z}$ есть умноженный на $a$ знаменатель правой части соотношения (4.4) для коэффициента A, после исключения из него производных функций Ханкеля по формуле (4.7).
5. Изгибные колебания трубопровода в неограниченной упругой среде при воздействии сейсмическх волн. Пусть цилиндрическую полость в рассмотренной в предыдущих пунктах задаче занимает трубопровод круглого сечения (с внешним радисом a и внутренним радиусом b). И пусть поперечные колебания трубопровода совершаются из-за воздействия на него сейсмической волны
в которой перемещения частиц направлены в направлении оси x.Обозначим возникающие при падении волны (5.1) поперечные перемещения трубопровода в направлении оси x через $\hat {u} = \hat {\mathcal{U}}{{e}^{{i(\gamma z - pt)}}}$. Получаемая при этом задача для грунта (среды) отличается от рассмотренной выше тем, что ее решение на бесконечности ($r \to \infty $) должно стремиться к волне (5.1). Поскольку не существует функций Бесселя, принимающих конечные значения на бесконечности (они либо стремятся к нулю, либо не ограничены), представим $\hat {u}$ в виде
(5.2)
$\hat {u} = {{u}_{0}} + u = ({{\mathcal{U}}_{0}} + \mathcal{U}){{e}^{{i\left( {{{\gamma }}z - pt} \right)}}}$Тогда u должно исчезать на бесконечности и задача ее нахождения совпадает с внешней задачей Похгаммера–Кри, рассмотренной в пп. 3,4. Только при записи условия прилипания на поверхности трубы (при нахождении константы A) и в в выражении (4.9) для силы, действующей на трубопровод, необходимо в п. 4 положить ${{\mathcal{U}}_{1}}\, = \,\mathcal{U}\, = \, - {\kern 1pt} {{\mathcal{U}}_{0}}\, + \,\hat {\mathcal{U}}$.
Следовательно, сила, действующая на трубопровод в задаче для u, согласно (4.9), равна
(5.3)
$\hat {\mathcal{F}} = {{\pi \rho }}c_{2}^{2}f~( - {{\mathcal{U}}_{0}} + \hat {\mathcal{U}}),\quad \hat {\mathcal{F}}{{e}^{{i\left( {\gamma z - pt} \right)}}} = {{\pi \rho }}c_{2}^{2}f~\left( { - {{u}_{0}} + \hat {u}} \right)$Эта же сила (5.2) действует на трубопровод и в полной задаче (для $\hat {u}$), поскольку если бы трубопровод двигался по закону падающей волны (5.1), то никаких сил на него со стороны грунта не действовало бы. Ситуация здесь аналогична той, что возникает в хорошо изученной задаче о продольных колебаниях трубопровода под воздействием сейсмических волн. В обоих случаях сила, действующая на трубопровод со стороны упругого грунта, пропорциональна относительному перемещению трубы (или, вернее, “глобальному” относительному перемещению, под которым понимается разность между перемещениями частиц грунта в сейсмической волне вдали от трубопровода и перемещениями самого трубопровода).
Уравнение поперечных (изгибных) колебаний трубопровода составляется как обычно (см., например, [18]), рассматривая динамическое равновесие дифференциального (малого) элемента трубы между произвольными сечениями z и $z + dz$). Это уравнение, выражающее равновесие суммы перерезывающих сил, действующих в сечениях z и $z + dz$, силы инерции и распределенной поперечной силы (5.3), записывается следующим образом:
(5.4)
$EI\frac{{{{\partial }^{4}}\hat {u}}}{{\partial {{z}^{4}}}} + S{{\rho '}}\frac{{{{\partial }^{2}}\hat {u}}}{{\partial {{t}^{2}}}} = {{\pi \rho }}c_{2}^{2}f~\left( { - {{u}_{0}} + \hat {u}} \right)~$Здесь ${{\rho '}}$ и E соответственно плотность и модуль Юнга материала трубопровода, $~S = \pi ({{a}^{2}} - {{b}^{2}})$ площадь его поперечного сечения, а I – момент инерции сечения трубы относительно нейтрального (не деформированного) диаметра, расположенного в данном случае вдоль оси y, так что I = Iy (I равен моменту инерции сечения относительно оси y).
Подставляя в уравнение (5.4) выражения для перемещений (5.1), (5.2), получаем для безразмерной амплитуды изгибных колебаний трубопровода (амплитуды, отнесенной к амплитуде падающей сейсмической волны) соотношение
(5.5)
$\frac{{\hat {\mathcal{U}}}}{{{{\mathcal{U}}_{0}}}} = \frac{{\frac{{{{\rho }}c_{2}^{2}f}}{{{{\rho '}}({{a}^{2}} - {{b}^{2}}){{p}^{2}}}}}}{{ - ~\frac{{EI{{{{\gamma }}}^{4}}}}{{{{\rho '\pi }}({{a}^{2}} - {{b}^{2}}){{p}^{2}}}} + 1 + \frac{{{{\rho }}c_{2}^{2}f}}{{{{\rho '}}({{a}^{2}} - {{b}^{2}}){{p}^{2}}}}}}$Тот же результат можно получить составляя уравнение относительного движения трубопровода (движения относительно среды, возмущенной падающей волной), путем введения функции ${v} = \hat {u} - {{u}_{0}}$. Такой путь принят в упомянутой выше работе К. Токи и Ш. Такады [7]. Однако полученное ими уравнение содержит неточность так же, как и уравнение для относительных продольных колебаний, приведенное там же [19]. Эта неточность связана с тем, что переносное движение, представляемое падающей волной (5.1), не является движением грунта как абсолютно твердого тела и потому в уравнении относительного движения трубопровода необходимо учесть не только силу инерции переносного движения, но и член, содержащий четвертую производную u0 по z.
6. Анализ решения и выводы. Изучим поведение полученного решения (5.5) в наиболее естественном для сейсмической задачи случае, когда длина сейсмической волны значительно (на порядок или несколько порядков) превосходит радиус трубопровода. Для этого используем известные (см., например, [20]) представления функций Ханкеля
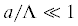 :
:
(6.1)
${{\gamma }}{{m}_{1}}{\text{\;}}\sim 1{\text{/}}\left( {\sqrt {{{{\left( {\frac{c}{{{{c}_{1}}}}} \right)}}^{2}} - 1} ~\sqrt {{{{\left( {\frac{c}{{{{c}_{2}}}}} \right)}}^{2}} - 1} ~} \right)~$Обозначая через ${{c}_{0}} = \sqrt {E{\text{/}}\rho '} $ стержневую скорость распространения волн в трубе и имея ввиду, что момент инерции его кольцевого поперечного сечения относительно диаметра $I = \pi ({{a}^{4}} - {{b}^{4}}){\text{/}}4$, получаем при помощи соотношений (6.1) окончательное выражение для безразмерной (относительной) амплитуды изгибных колебаний трубопровода
(6.2)
$Y \equiv \frac{{\hat {\mathcal{U}}}}{{{{\mathcal{U}}_{0}}}} = \frac{{G\left( {{\xi }} \right)}}{{ - {{{\left( {{{c}_{0}}{\text{/}}c} \right)}}^{2}}[1 + {{{(b{\text{/}}a)}}^{2}}]{{{{\xi }}}^{{ - 2}}} + 1 + G\left( {{\xi }} \right)}}$(6.3)
$G\left( {{\xi }} \right) \equiv \left( {\frac{{{\rho }}}{{{{\rho '}}}}} \right)\frac{{{{{{\xi }}}^{2}}}}{{[1 - {{{(b{\text{/}}a)}}^{2}}]\left( {2\ln {{\xi }} - {\text{ln}}\sqrt {{{{\left( {\frac{c}{{{{c}_{1}}}}} \right)}}^{2}} - 1} ~\sqrt {{{{\left( {\frac{c}{{{{c}_{2}}}}} \right)}}^{2}} - 1} ~} \right)}},\quad {{\xi }} \equiv \frac{{{\Lambda }}}{{{{\pi }}a}}$Отметим, что теми же соотношениями (6.2), (6.3) определяются амплитуды (а значит, максимальные значения) изгибающего момента $M = - EI{{\partial }^{2}}\hat {u}{\text{/}}\partial {{z}^{2}}$ и перерезывающей силы $Q = \partial M{\text{/}}\partial z$, отнесенные к соответствующим значениям, которые они имели бы, если бы движение трубопровода происходило по закону падающей волны (5.1).
На рис. 1 приведен график относительной амплитуды Y в функции от аргумента ξ (отношения длины сейсмической волны к примерно полутора диаметрам трубы) для железного трубопровода, когда окружающий его грунт является сухой глиной. При построении графика приняты следующие численные значения параметров: $b{\text{/}}a = 0.9$, ${{\rho }} \approx 1.64$ г/см3, ${{\rho '}} \approx 7.87$ г/см3, ${{c}_{1}} = 2.0 \times {{10}^{3}}$ м/с, ${{c}_{2}} = 0.4 \times {{10}^{3}}$ м/с, $c = 2.4 \times {{10}^{3}}$ м/с, ${{c}_{0}} = 5.17 \times {{10}^{3}}$ м/с (числовые значения для глины взяты из справочника [21]).
Рис. 1.
Графики относительных амплитуд изгибных колебаний трубопровода в зависимости от относительной длины падающей волны: сплошная линия соответствует решению (6.2), а штриховая – результату теории жесткого защемления.

Интервал изменения аргумента ${{\xi }}$ принят от 10 и выше, что охватывает практически весь имеющий интерес интервал изменения этого аргумента в сейсмической задаче. Дело в том, что при длинах волн сравнимых и, тем более, меньших диаметра трубопровода его движение не может описываеться уравнением изгибных колебаний стержня.
Главный вывод, следующий из рассмотренного примера, а также и из общей формулы (5.5), состоит в том, что амплитуды поперечных перемещений трубопровода (а также амплитуды моментов и перерезывающих сил) не превышают амплитуд, вычисленных на основе простейшей инженерной теории, в которой поперечные перемещения считаются совпадающими с перемещениями в сейсмической волне (на рис. 1 решение этой теории изображено линией). Тем самым, полученный результат дает, по-видимому, первое теоретическое обоснование и оценку точности инженерной теории “жесткого защемления” подземного трубопровода в грунте для случая его изгибных колебаний.
Отметим, что полученный К. Токи и Ш. Такада результат в [7] не может считаться достоверным из-за неверного решения внешней задачи Похгаммера–Кри и пропущенного члена в уравнении относительного движения трубопровода. Авторы также не обратили внимания на то, что в их решении амплитуда колебаний трубопровода всегда больше амплитуды падаюшей сейсмической волны, что физически никак не обосновано.
В знаменателе формулы (5.5) первый член пропорционален квадрату отношения радиуса трубы к длине сейсмической
волны ( ), а третий член – обратной величине ${{({{\Lambda /}}a)}^{2}}$. Поэтому влияние жесткости трубопровода на изгиб будет сказываться в случае сравнительно
коротких сейсмических волн, в случае же длинных волн трубопровод будет следовать колебаниям
грунта в сейсмической волне.
), а третий член – обратной величине ${{({{\Lambda /}}a)}^{2}}$. Поэтому влияние жесткости трубопровода на изгиб будет сказываться в случае сравнительно
коротких сейсмических волн, в случае же длинных волн трубопровод будет следовать колебаниям
грунта в сейсмической волне.
Благодарности. Результаты работы доложены на семинаре “Прочность и разрушение материалов и конструкций” в Институте проблем механики РАН. Автор выражает благодарность руководителю семинара профессору Е.И. Шифрину и участникам семинара за обсуждение результатов и полезные замечания.
Работа выполнена при финансовой поддержке РФФИ в рамках научного проекта № 20-08-00024.
Список литературы
Окамото Ш. Сейсмостойкость инженерных сооружений. М.: Стройиздат, 1980. 272 с.
Нормы проектирования атомных станций: НП 031–01. Приложение 6. Основные положения расчета линейно-протяженных конструкций. Москва, 2001. С. 23–25.
O'Rourke M.J., Liu X. Response of buried pipelines subject to earthquake effects. Buffalo: Univ. of Buffalo, 1999. 250 p.
Рашидов T. Динамическая теория сейсмостойкости сложных систем подземных сооружений. Ташкент: Изд-во “ФАН”, 1973. 180 с.
Kouretzis G.P., Bouckovalas G.D., Gantes C.J. 3-D shell analysis of cylindrical underground structures under seismic shear (S) wave action // Soil Dyn. Earthquake Eng. 2006. V. 26. P. 909–921. https://doi.org/10.1016/j.soildyn.2006.02.002
Kouretzis G.P., Bouckovalas G.D., Karamitros D.K. Seismic verification of long cylindrical underground structures considering Rayleigh wave effects // Tunneling Underground Space Technol. 2011. V. 26. P. 789–794. https://doi.org/10.1016/j.tust.2011.05.001
Toki T., Takada S. Earthquake response of underground tubular structure // Bull. Disaster Preventation Res. Inst. Kyoto Univ. 1974. V. 24. Pt. 2. № 221. P. 107–125.
Исраилов М.Ш. Динамическая теория упругости и дифракция волн. М.: Изд-во Моск. ун-та. 1992, 206 с.
Ляв А. Математическая теория упругости. М.: ОНТИ НКТП СССР, 1935. 674 с.
Pochhammer L. Ueber die Fortpflanzungsgeschwindigkeiten kleiner Schwingungen in einem unbegrenzten isotropen Kreiscylinder // J. Reine Angew. Math. 1876. V. 81. P. 324–336.
Chree C. Longitudinal vibrations of a circular bar // Quart. J. Pure Appl. Math. 1886. V. XXI. P. 287–298.
Исраилов М.Ш. Действие наклонной сейсмической волны на подземный трубопровод // Известия РАН. МТТ. 2022. № 5. С. 58–69.
Трехмерные задачи математической теории упругости и термоупругости / Под ред. В.Д. Купрадзе. М.: Наука, 1976. 664 с.
Bell W.W. Special functions for scientists and engineers. London: Van Nostrand, 1968. 248 p.
Поручиков В.Б. Методы динамической теории упругости. М.: Наука, 1986. 328 с.
Eringen A.C. Mecanics of continua. N. Y.: Wiley, 1967. 592 p.
Magnus W., Oberhettinger F., Soni R.P. Formulas and theorems of the special functions of mathematical physics. 3-d ed. N. Y.: Springer, 1966. 508 p.
Miklowitz J. The theory of elastic waves and waveguides. Amsterdam: North-Holland Publ., 1978. 618 p.
Исраилов М.Ш. Связанные сейсмические колебания трубопровода в бесконечной упругой среде // Изв. РАН. МТТ. 2016. № 1. С. 57–66.
Лебедев Н.Н. Специальные функции и их приложения. М.: ГИТТЛ, 1963. 380 с.
Берч Ф., Шерер Дж., Спайсер Г. Справочник для геологов по физическим константам. М.: Изд-во иностр. лит., 1949. 304 с.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика твердого тела