1. На главную
  2. Электронные версии
  3. Известия РАН. Механика твердого тела
  4. № 1, 2023

Известия РАН. Механика твердого тела, 2023, № 1, стр. 166-180

АУКСЕТИКИ СРЕДИ ДВУХСЛОЙНЫХ КОМПОЗИТОВ ИЗ КРИСТАЛЛОВ С КУБИЧЕСКОЙ СИММЕТРИЕЙ. АНАЛИТИЧЕСКИЙ И ЧИСЛЕННЫЙ АНАЛИЗ

А. И. Демин a, М. А. Волков a, *, В. А. Городцов a, Д. С. Лисовенко a, **

a Институт проблем механики им. А.Ю. Ишлинского РАН
Москва, Россия

* E-mail: volkovmikhl@ipmnet.ru
** E-mail: lisovenk@ipmnet.ru

Поступила в редакцию 02.10.2022
После доработки 08.10.2022
Принята к публикации 10.10.2022

Полный текст (PDF)

Аннотация

Представлены результаты расчетов эффективного модуля Юнга продольно растягиваемых двухслойных пластин из одинаково ориентированных кубических кристаллов на основе аналитического анализа и численного метода конечных элементов. Приведены аналитические зависимости эффективного модуля Юнга от модулей Юнга и коэффициентов Пуассона кристаллов в слоях. Определены комбинации пар кристаллов со значительным отклонением эффективных характеристик, найденных по правилу смесей. Установлены зависимости эффективных модулей Юнга от экстремальных значений модулей Юнга и коэффициентов Пуассона кристаллов в слоях, которые представлены графически, и в ряде случаев отражены в виде таблицы.

Ключевые слова: кубические кристаллы, ауксетики, двухслойные пластины, модуль Юнга, коэффициент Пуассона

1. Введение. Экспериментальное обнаружение ряда материалов с отрицательным коэффициентом Пуассона (ауксетиков) во второй половине 20 столетия в работах [1–15] вызвал бурный рост исследований ауксетиков среди кристаллов, сплавов, полимеров, пен, текстиля, цеолитов, керамик, пористых материалов, мета- и наноматериалов, композитов (см. обзоры за последние 7 лет [16–52 ]). Большое количество ауксетиков найдено среди кристаллов различных кристаллических систем (точнее говоря частичных ауксетиков, имеющих отрицательный коэффициент Пуассона при определенных ориентациях кристаллов). При этом, наибольшее количество из них обнаружено среди кристаллов с кубической анизотропией (более трехсот). В связи с этим, анализу ауксетиков среди них и их композитов посвящена значительная литература [5, 8, 15, 53–104 ]. Многие простые вещества с кубической симметрией из периодической системы элементов, например, литий Li, калий K, натрий Na, медь Cu, железо Fe, никель Ni, кальций Ca, кобальт Co, цезий Cs, барий Ba, свинец Pb, серебро Ag, золото Au, рубидий Rb, стронций Sr, иттербий Yb, талий Tl, палладий Pd оказываются частичными ауксетиками.

Аналитически упругие свойства растягиваемых двухслойных пластин из одинаково ориентированных кубических кристаллов ранее анализировались в статье [105]. Здесь он будет продолжен наряду с численным анализом методом конечных элементов при учете изгиба слоев пластины. Иллюстрацией таких упругих характеристик некоторых кубических кристаллов, как модули Юнга и коэффициенты Пуассона, служит табл. 1. Среди указанных в ней кристаллов, растягиваемых в направлении [100], имеются ауксетики Sm0.75Y0.25S, TmS, Sm0.65La0.35S и неауксетики CuAl (14at%Al), AgAu (50at%Au), CoFe (12at%Fe).

Таблица 1.

Модули Юнга и коэффициенты Пуассона для некоторых кубических кристаллов, растягиваемых вдоль направления [100]

Кристаллы E, ГПа $\nu $
Sm0.75Y0.25S 55.6 –0.67
TmSe 114.7 –0.54
Sm0.65La0.35S 50.8 –0.35
SnTe 98 –0.09
AuNi(24.20at%Ni) 54.3 0.45
CuAl(14at%Al) 55.2 0.43
Diaflex 114.5 0.45
Co-beta 113.5 0.40
CuNi(82.2at%Ni) 113.5 0.39
CuAu(80at%Au) 50.8 0.45
CuAu(50at%Au) 54.9 0.44
AgAu(50at%Au) 50.8 0.43
NbZr(69.6at%Zr) 50.0 0.42
Ni50.4Al(quenched) 97.6 0.42
NiAl(PE16H) 97.8 0.40
CoFe(12at%Fe) 97.0 0.41
Fe 130.38 0.37
W 408.16 0.28
Cs 0.84 0.38

Ниже приводится ряд результатов исследования эффективных модулей Юнга для двухслойных композитов из одинаково ориентированных кубических кристаллов в слоях как с помощью методов теории упругости анизотропного тела, так и метода конечных элементов. В качестве упругих характеристик слоев использованы экспериментальные значения упругих констант, приведенные в известном справочнике [106] и в статье [107].

2. Продольное растяжение тонкой двухслойной пластины, составленной из кубических кристаллов. 2.1. Аналитический анализ. Пользуясь результатами анализа продольного растяжения тонких двухслойных композитных пластин из кубических кристаллов, полученными в статье [105], мы продолжим обсуждение упругих характеристик пластин из одинаково ориентированных кубических кристаллов. Количество двухслойных композитов из кубических кристаллов, упругие характеристики которых указаны в [106], составляет несколько сотен тысяч. Многие из них обладают эффективными характеристиками, превосходящими характеристики исходных пар кристаллов. Таким композитам в дальнейшем уделяется основное внимание.

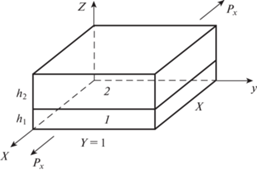
Пусть продольное растяжение плоскости тонкой двухслойной пластины из одинаково ориентированных кубических кристаллов, составленной из нижнего слоя 1 толщиной h1 и верхнего слоя 2 толщиной h2 (рис. 1), происходит в направлении оси x.

Рис. 1.

Растяжение удельной продольной силой Px пластины из двух слоев толщиной $h = {{h}_{1}} + {{h}_{2}}$.

Упругие свойства пары кубических кристаллов в слоях определяются наборами шести матричных коэффициентов податливости $s_{{11}}^{1},s_{{12}}^{1},s_{{44}}^{1}$ и $s_{{11}}^{2},s_{{12}}^{2},s_{{44}}^{2}$. Верхний индекс здесь и далее соответствует номеру слоя. Деформирование растягиваемых слоев тонкой пластины в условиях однородного плоского напряженного состояния $\sigma _{z}^{1} = \sigma _{z}^{2} = 0$ описывается упрощенным законом Гука для нормальных напряжений и деформаций

$\begin{gathered} \varepsilon _{x}^{k} = s_{{11}}^{k}\sigma _{x}^{k} + s_{{12}}^{k}\sigma _{y}^{k}, \hfill \\ \varepsilon _{y}^{k} = s_{{11}}^{k}\sigma _{y}^{k} + s_{{12}}^{k}\sigma _{x}^{k},\quad (k = 1,\;2) \hfill \\ \varepsilon _{z}^{k} = s_{{12}}^{k}\sigma _{x}^{k} + s_{{12}}^{k}\sigma _{y}^{k} \hfill \\ \end{gathered} $

Эти соотношения в предположении жесткого контакта слоев $\varepsilon _{x}^{1} = \varepsilon _{x}^{2}$, $\varepsilon _{у}^{1} = \varepsilon _{у}^{2}$ при учете условий равновесия дают следующий результат для эффективной деформации растягиваемой двухслойной пластины из кубических кристаллов (поперечную ширину тонкой пластины Y полагаем равной единице, рис. 1)

$\varepsilon _{x}^{{{\text{eff}}}} = \varepsilon _{x}^{{{\text{1eff}}}} = \varepsilon _{x}^{{{\text{2eff}}}} = \alpha {{P}_{x}},\quad \varepsilon _{y}^{{{\text{eff}}}} = \varepsilon _{y}^{{{\text{1eff}}}} = \varepsilon _{y}^{{{\text{2eff}}}} = \beta {{P}_{x}},\quad \varepsilon _{z}^{{{\text{1eff}}}} = {{\gamma }_{1}}{{P}_{x}},\quad \varepsilon _{z}^{{{\text{2eff}}}} = {{\gamma }_{2}}{{P}_{x}}$
$\alpha = \frac{{s_{{11}}^{2}{{h}_{2}}{{A}_{1}} + s_{{11}}^{1}{{h}_{1}}{{A}_{2}}}}{B},\quad \beta = \frac{{s_{{12}}^{2}{{h}_{2}}{{A}_{1}} + s_{{12}}^{1}{{h}_{1}}{{A}_{2}}}}{B}$
${{\gamma }_{1}} = s_{{12}}^{1}\frac{{{{h}_{1}}{{A}_{2}} + {{h}_{2}}({{C}_{1}} + {{C}_{2}})}}{B},\quad {{\gamma }_{2}} = s_{{12}}^{2}\frac{{{{h}_{2}}{{A}_{1}} + {{h}_{1}}({{C}_{1}} - {{C}_{2}})}}{B}$
${{A}_{k}} \equiv {{(s_{{11}}^{k})}^{2}} - {{(s_{{12}}^{k})}^{2}},\quad B \equiv {{({{h}_{2}}s_{{11}}^{1} + {{h}_{1}}s_{{11}}^{2})}^{2}} - {{({{h}_{2}}s_{{12}}^{1} + {{h}_{1}}s_{{12}}^{2})}^{2}}$
${{С}_{1}} \equiv s_{{11}}^{1}s_{{11}}^{2} - s_{{12}}^{1}s_{{12}}^{2},\quad {{С}_{2}} \equiv s_{{11}}^{1}s_{{12}}^{2} - s_{{12}}^{1}s_{{11}}^{2}$

Эффективный модуль Юнга продольного растяжения Eeff находится через отношение удельной растягивающей силы к продольной деформации двухслойной пластины

${{E}^{{{\text{eff}}}}} = \frac{1}{{\alpha ({{h}_{1}} + {{h}_{2}})}}$

Упругие характеристики кубических кристаллов, как и других анизотропных материалов, изменяются с изменением их ориентации. В итоге возникают различия в угловых зависимостях модулей Юнга и коэффициентов Пуассона при растяжениях кристаллов [108], которые в некоторых ситуациях обнаруживают определенные взаимосвязи. Так в [109] при осреднении по всем поперечным направлениям коэффициента Пуассона продольно растягиваемых кубических кристаллов установлена простая линейная связь такого среднего коэффициента Пуассона с модулем Юнга. В рассматриваемой здесь статье о продольном растяжении двухслойных композитов из кубических кристаллов также изучены некоторые связи эффективных модулей Юнга с экстремальными значениями модулей Юнга и коэффициентов Пуассона.

При растяжении однослойного кубического кристалла в направлении [100] модуль Юнга E и коэффициент Пуассона $\nu $ связаны с парой коэффициентов податливости ${{s}_{{11}}},{{s}_{{12}}}$, так что в каждом из двух одинаково ориентированных слоев имеем

$s_{{11}}^{k} = \frac{1}{{{{E}^{k}}}},\quad s_{{12}}^{k} = - \frac{{{{\nu }^{k}}}}{{{{E}^{k}}}}\quad (k = 1,2)$

Подобными заменами коэффициентов податливости на модули Юнга и коэффициенты Пуассона в полученных выше формулах для эффективных коэффициентов будем иметь

${{E}^{{eff}}} = \frac{{{{{(1 + \lambda )}}^{2}} - {{{({{\nu }^{1}} + \lambda {{\nu }^{2}})}}^{2}}}}{{[1 - {{{({{\nu }^{1}})}}^{2}}] + \lambda [1 - {{{({{\nu }^{2}})}}^{2}}]}}\frac{{{{E}^{2}}}}{{1 + \eta }},\quad \lambda \equiv \frac{{{{h}_{1}}{{E}^{1}}}}{{{{h}_{2}}{{E}^{2}}}} = \eta \mu ,\quad \eta \equiv \frac{{{{h}_{1}}}}{{{{h}_{2}}}},\quad \mu \equiv \frac{{{{E}^{1}}}}{{{{E}^{2}}}}$

Численный анализ двухслойных пластин из различных одинаково ориентированных кубических кристаллов с помощью этих соотношений и экспериментальных данных из [106, 107] выявил некоторую зависимость эффективного модуля Юнга Eeff от экстремальных значений их модулей Юнга max$({{E}^{1}},{{E}^{2}})$, min$({{E}^{1}},{{E}^{2}})$ и коэффициентов Пуассона max$({{\nu }^{1}},{{\nu }^{2}}),$ min$({{\nu }^{1}},{{\nu }^{2}})$ (рис. 2). Из рисунка видно, что эффективный модуль Юнга может превосходить максимальные значения модулей Юнга слоев двухслойных пластин более чем на 40%. Из рис. 2 также видно, что отношение эффективного модуля Юнга к максимальному модулю Юнга слоев больше для пары слоев из ауксетика и неауксетика и слоев с близкими значениями модулей Юнга. Такое отношение принимает значение большее 1.2 для почти девяти сотен двухслойных пластин с самарием Sa или тулием Tm, имеющих наименьшие значения коэффициентов Пуассона среди кубических кристаллов. Значения эффективного модуля Юнга некоторых пар материалов собраны в табл. 2. Значения модуля Юнга и коэффициента Пуассона исходных материалов можно найти в табл. 1. Среди этих кристаллов ауксетиками являются Sm0.75Y0.25S, Sm0.65La0.35S, SnTe, TmSe. Данные об упругих свойствах 3-х парных для них неауксетиков в двухслойных пластинах также приведены в этой таблице.

Рис. 2.

Зависимость эффективного модуля Юнга от экстремальных значений модулей Юнга и разности экстремальных значений коэффициентов Пуассона исходных пар кубических кристаллов.

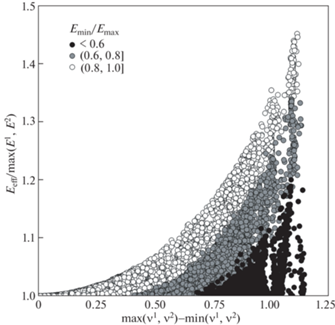
Таблица 2.

Значения эффективного модуля Юнга Eeff двухслойных пластин и отношение эффективного модуля Юнга к максимальному модулю Юнга max$({{E}^{1}},{{E}^{2}})$ при равной толщине слоев

Материал 1 Материал 2 Eeff, ГПа $\frac{{{{E}^{{{\text{eff}}}}}}}{{\max ({{E}^{1}},{{E}^{2}})}}$
Sm0.75Y0.25S CuAu(50at%Au) 80.6 1.45
Sm0.75Y0.25S AuNi(24.20at%Ni) 80.4 1.45
Sm0.75Y0.25S CuAl(14at%Al) 80 1.44
TmSe Diaflex 151.8 1.32
TmSe Co-beta 146.7 1.28
TmSe CuNi(82.2at%Ni) 146.3 1.28
Sm0.65La0.35S CuAu(80at%Au) 60.4 1.19
Sm0.65La0.35S AgAu(50at%Au) 59.9 1.18
Sm0.65La0.35S NbZr(69.6at%Zr) 59.1 1.16
SnTe Ni50.4Al(quenched) 104.7 1.07
SnTe NiAl(PE16H) 104.3 1.06
SnTe CoFe(12at%Fe) 104.2 1.06
W Fe 269.7 0.66
Cs Fe 65.6 0.50

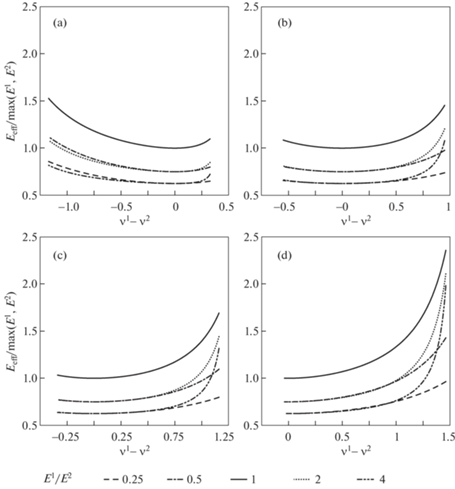
Дополнительно анализировалось поведение эффективного модуля Юнга в зависимости от разницы коэффициентов Пуассона слоев. В рамках данного анализа свойства одного из слоев фиксировались, а второго – варьировались в некотором диапазоне. Для первого слоя были выбраны кубические кристаллы различной жесткости и величины коэффициентов Пуассона: Sm0.75Y0.25S (ν = –0.67, E1 = 55.6 ГПа), Ba (ν = –0.05, E = 8 ГПа), Cr (ν = 0.16, E = 327 ГПа), Au (ν = 0.46, E = 42.7 ГПа). Коэффициент Пуассона второго материала менялся от –1 до 0.5, а модуль Юнга принимал фиксированные значения 0.25E1, 0.5E1, E1, 2E1, 4E1. Результаты анализа представлены на рис. 3. Полученные зависимости показывают, что отношение эффективного модуля Юнга пластины к модулю Юнга самого жесткого слоя максимально, если модули Юнга слоев равны и растет с увеличением модуля разности коэффициентов Пуассона слоев и может превышать значение 2.4 для ауксетиков с коэффициентом Пуассона близким к –1. При равном модуле Юнга слоев, у всех проанализированных пластин эффективный модуль Юнга превышает единицу для всех значений коэффициента Пуассона второго слоя. Минимальное значение эффективного модуля Юнга всегда достигалось при равных коэффициентах Пуассона слоев. Кроме того, при больших значениях коэффициента Пуассона второго слоя эффективный модуль Юнга растет существенно быстрее в случае второго слоя большей жесткости.

Рис. 3.

Отношение эффективного модуля Юнга к модулю Юнга наиболее жесткого слоя в зависимости от разности коэффициентов Пуассона слоев для Sm0.75La0.25S (E = 55.6 ГПа, ν = –0.67) (a), Ba (E = 8 ГПа, ν = = –0.05) (b), Cr (E = 327 ГПа, ν = 0.16) (c) и Au (E = 42.7 ГПа, ν = 0.46) (d).

2.2. Численный анализ. В аналитическом подходе, рассмотренном выше, предполагается, что пластина в процессе растяжения остается плоской. Для проверки полученных аналитически результатов и оценки влияния на результат принятых допущений об отсутствии изгиба в пластине были проведены численные эксперименты продольного растяжения двухслойной пластины из кубических кристаллов методом конечных элементов.

Трехмерная модель квадратной пластины со сторонами a и общей толщиной h из двух слоев с толщинами h1 и h2 была разбита на объемные 8-узловые конечные элементы с поддержкой упругой анизотропии. Пластина считается тонкой, отношение толщины к ширине h/a составляет 0.01. Задача решалась в перемещениях со следующими граничными условиями: плоскости x = 0 и y = 0 являются плоскостями симметрии, на которых запрещались нормальные перемещения, на задней грани (x = a) задавались нормальные перемещения, соответствующие продольной деформации 0.01. Контакт элементов на границе раздела считался абсолютно жестким.

По результатам расчета определялись эффективный модуль Юнга. Эффективный модуль Юнга пластины Eeff рассчитывался как отношение суммарной силы реакции на грани $F_{x}^{{x~ = ~0}}$ к произведению площади поверхности соответствующей грани ${{S}^{{x~ = ~0}}}$ на продольную деформацию ${{\varepsilon }_{x}}$.

${{E}^{{{\text{eff}}}}} = \frac{{F_{x}^{{x~ = ~0}}}}{{{{S}^{{x~ = ~0}}}{{\varepsilon }_{x}}}}$

Используя данную модель, были проведены две серии расчетов. В первой серии расчетов, для соответствия условиям из раздела 2.1, задавался запрет на нормальные перемещения пластины. Во второй серии расчетов запрет на нормальные перемещения отсутствовал, что позволяет пластине изгибаться.

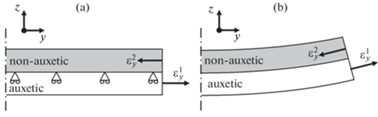
Изгиб пластины возникает вследствие различий в коэффициентах Пуассона слоев, что ярко выражено для пар неауксетик-ауксетик. При продольном растяжении в слое неауксетика возникают сжимающие поперечные деформации, а в слое ауксетика растягивающие, что приводит к возникновению изгибающего момента в поперечном сечении и к изгибу пластины (рис. 4).

Рис. 4.

Граничные условия и деформации поперечного сечения при продольном растяжении по оси x в первой (a) и во второй (b) серии расчетов методом конечных элементов.

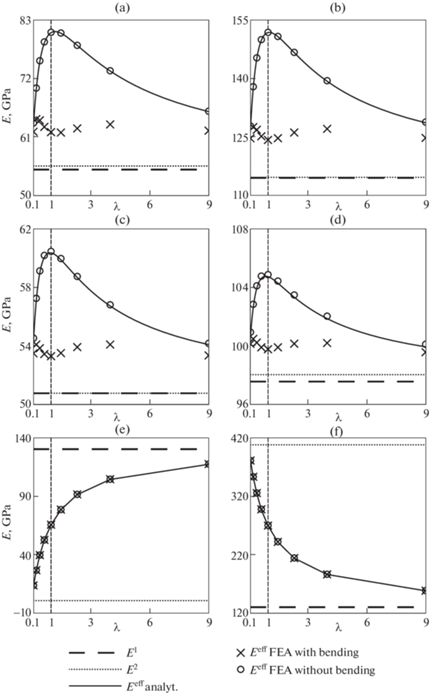
Результаты первой серии расчетов (без изгиба), практически не отличаются от аналитических. Для рассмотренных пластин отличие составило менее 1%. На рис. 5 представлены результаты аналитических и численных расчетов для нескольких кубических пластин. Сплошная линия соответствует аналитическому подходу, численные значения первой серии обозначены кругом, второй – крестом. Из зависимостей видно, что учет изгиба сильно влияет на значения эффективного модуля Юнга. Даже при значительном уменьшении эффективного модуля Юнга, для рассмотренных комбинаций его величина все еще превосходит модули Юнга слоев на существенную величину (от 3 до 12 процентов). В случае пластин из двух неауксетичских кристаллов, поведение модуля Юнга обеих серий расчетов практически не отличаются, что видно на рис. 5.e, f.

Рис. 5.

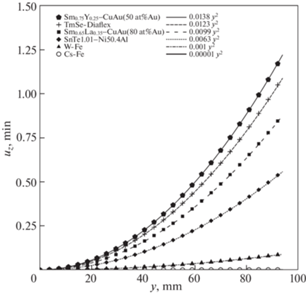
Результаты расчетов значений эффективных модулей Юнга слоистых пластинок для CuAu(50at%Au)-Sm0.75Y0.25S (a), Diaflex-TmSe (b), CuAu(80at%Au)-Sm0.65La0.35S (c), Ni50.4Al(quenched)-SnTe (d), Fe-Cs (e) и Fe-Wf (f).

На рис. 6 приводятся графики узловых перемещений в поперечном сечении пластины для нескольких комбинаций материалов, полученные во второй серии расчетов. На рисунке численные значения отмечены символами (круг, крест, квадрат и пр.), а их аппроксимация квадратичной функцией – линиями. Изгиб пластины ρ характеризуется кривизной, которая определяется второй производной аппроксимирующей поперечные узловые перемещения uzфункции:

$\rho = \frac{{{{d}^{2}}}}{{d{{y}^{2}}}}f({{u}_{z}})$
Рис. 6.

Графики узловых перемещений поперечного сечения пластины на границе раздела слоев.

Наибольшая кривизна соответствует пластинам с ауксетическим слоем (Sm0.75Y0.25S, TmSe, SnTe, Sm0.65La0.35S), в то время как для пластин из пары неауксетиков кривизна существенно меньше.

3. Заключение. В работе проведен анализ эффективных упругих характеристик при растяжении слоистых пластин из кубических кристаллов с ауксетическим слоем с применением аналитического метода и метода конечных элементов. Численные расчеты выполнены для всех возможных комбинаций кубических кристаллов. Определены пластины, у которых эффективные упругие характеристики существенно отличаются от правила смесей. Для ряда пластин выполнены численные расчеты с применением метода конечных элементов. Проведено сравнение полученных результатов с аналитическими расчетами. Результаты моделирования подтверждают эффекты, выявленные при анализе аналитических расчетов. По результатам численных расчетов методом конечных элементов показано, что изгиб пластины существенно влияет на значение эффективного модуля Юнга пластины.

Работа выполнена при поддержке гранта Российского научного фонда (проект № 22-29-01200).

Список литературы

  1. Зубов В.Г., Фирсова М.М. Об особенностях упругого поведения кварца в области α–β-перехода // Кристаллография. 1962. Т. 7. № 3. С. 469–471.

  2. Garber A.M. Pyrolytic materials for thermal protection systems // Aerospace Eng. 1963. V. 22. P. 126–137.

  3. Поперека М.Я., Балагуров В.Г. Ферромагнитные пленки с отрицательным коэффициентом Пуассона // ФТТ. 1969. Т. 11. № 12. С. 2507–3513.

  4. Gunton D.J., Saunders G.A. Stability limits on the Poisson ratio: application to a martensitic transformation // Proc. R. Soc. Lond. Ser. A. 1975. V. 343. № 1632. P. 63–83. https://doi.org/10.1098/rspa.1975.0052

  5. Milstein F., Huang K. Existence of a negative Poisson ratio in fcc crystals // Phys. Rev. B. 1979. V. 19. № 4. P. 2030–2033. https://doi.org/10.1103/PhysRevB.19.2030

  6. Lakes R.S. Foam structures with a negative Poisson’s ratio // Science. 1987. V. 235. № 4792. P. 1038–1040. https://doi.org/10.1126/science.235.4792.1038

  7. Fies F.A., Lakes R.S., Park J.B. Negative Poisson’s ratio polymeric and metallic foams // J. Mater. Sci. 1988. V. 23. № 12. P. 4406–4414. https://doi.org/10.1007/BF00551939

  8. Светлов И.Л., Епишин А.И., Кривко А.И. и др. Анизотропия коэффициента Пуассона монокристаллов никелевого сплава // ДАН СССР. 1988. Т. 302. № 6. С. 1372–1375.

  9. Caddock B.D., Evans K.E. Microporous materials with negative Poisson’s ratios. 1. Microstructure and mechanical properties // J. Phys. D. 1989. V. 22. № 22. P.1877–1882. https://doi.org/10.1088/0022-3727/22/12/012

  10. Alderson K.L., Evans K.E. The fabrication of microporous polyethylene having a negative Poisson’s ratio // Polymer 1992. V. 33. № 20. P. 4435–4438. https://doi.org/10.1016/0032-3861(92)90294-7

  11. Yeganeh-Haeri A., Weidner D.J., Parisc J.B. Elasticity of $\alpha $-cristobalite: a silicon dioxide with a negative Poisson’s ratio // Science. 1992. V. 257. № 5070. P. 650–652. https://doi.org/10.1126/science.257.5070.65010.1126/science.257.5070.650

  12. Choi J.B., Lakes R.S. Non-linear polymer properties of polymer cellular materials with a negative Poisson’s ratio // J. Mater. Sci. 1992. V. 27. № 17. P. 4678–4684. https://doi.org/10.1007/BF01166005

  13. Scharer U., Wachter P. Negative elastic constants in intermediate valent SmxLa1 – xS // Solid State Commun. 1995. V. 96. № 17. P. 497–501. https://doi.org/10.1016/0038-1098(95)00418-1

  14. Prall D., Lakes R.S. Properties of a chiral honeycomb with a Poisson’s ratio of –1 // Int. J. Mech. Sci. 1997. V. 39. № 3. P. 305–314. https://doi.org/10.1016/S0020-7403(96)00025-2

  15. Baughman R.H., Shacklette J.M., Zakhidov A.A., Stafström S. Negative Poisson’s ratios as a common feature of cubic metals // Nature. 1998. V. 392. № 6674. P. 362–363. https://doi.org/10.1038/32842

  16. Lim T.-C. Auxetic Materials and Structures. Singapore: Springer, 2015. http: //dx.doi.org/https://doi.org/10.1007/978-981-287-275-3

  17. Sanami M. Auxetic materials for biomedical applications // Thesis for the degree of Doctor of Philosophy. 2015. P. 1–252.

  18. Bhular S.K. Three decades of auxetic polymers. Review // e-Polymers. 2015. V. 15. № 4. P. 205–215. https://doi.org/10.1515/epoly-2014-0193

  19. Hou X., Silberschmidt V.V. Metamaterials with negative Poisson’s ratio. A review of mechanical properties and deformation mechanisms // In: Silberschmidt V., Matveenko V. (eds) Mechanics of Advanced Materials. Engineering Materials. Springer, Cham. 2015. P. 155–179. https://doi.org/10.1007/978-3-319-17118-0_7

  20. Hu H., Zulifgar A. Auxetic textile materials – A review // J. Textile Eng. Fashion Technolog. 2016. V. 1. № 1. P. 00001. https://doi.org/10.15406/jteft.2017.01.00002

  21. Saxena K.K., Das R., Calius E.P. Three Decades of Auxetics Research-Materials with Negative Poisson’s Ratio: A Review // Adv. Eng. Mater. 2016. V. 18. № 11. P. 1847–1870. https://doi.org/10.1002/adem.201600053

  22. Jiang J.-W., Kim S.Y., Park H.S. Auxetic Nanomaterials: Recent Progress and Future Development, Appl. Phys. Rev., 2016. V. 3. № 4. P. 041101. https://doi.org/10.1063/1.4964479

  23. Novak N., Vesenjak M., Ren Z. Auxetic cellular materials-a review // Strojniški vestnik - Journal of Mechanical Engineering. 2016. V. 62. № 9. P. 485–493. https://doi.org/10.5545/sv-jme.2016.3656

  24. Kolken H.M.A., Zadpoor A.A. Auxetic Mechanical Metamaterials // RSC Adv. 2017. V. 7. № 9. P. 5111–5129. https://doi.org/10.1039/C6RA27333E

  25. Lakes R.S. Negative-Poisson’s-ratio materials: auxetic solids //Ann. Rev. Mater. Res. 2017. V. 47. P. 63–81. https://doi.org/10.1146/annurev-matsci-070616-124118

  26. Ma P., Chang Y., Boakae A., Jiang G. Review on the knitted structures with auxetic effect // J. Textile Inst. 2017. V. 108. № 6. P. 947–961. https://doi.org/10.1080/00405000.2016.1204901

  27. Lim T.-C. Analogies across auxetic models based on deformation mechanism // Phys. Status Solidi (RRL). 2017. T. 11. № 6. P. 1600440. https://doi.org/10.1002/pssr.201770330

  28. Duncan O., Shepherd T., Moroney C. et al. Review of Auxetic Materials for Sports Applications: Expanding Options in Comfort and Protection // Appl. Sci. 2018. V. 8. № 6. P. 941. https://doi.org/10.3390/app8060941

  29. Ren X., Das R., Tran P. et al. Auxetic Metamaterials and Structures: A Review // Smart Mater. Struct. 2018. V. 27. № 2. P. 023001. https://doi.org/10.1088/1361-665X/aaa61c

  30. Gunel O., Ranjbar M. Review of auxetic materials // 1-st International Conference on Advances in Mechanical and Mechatronics Engineering “ICAMMEN-2018”. 10 p.

  31. Yu X., Zhou J., Liang H., Jiang Z., Wu L. Mechanical metamaterials associated with stiffness, rigidity and compressibility: A brief review // Progr. Mater. Sci. 2018. V. 94. P. 114–175. https://doi.org/10.1016/j.pmatsci.2017.12.003

  32. Hosseinkhani A., Yjunesian D., Ranjbar M. A short review on vibro-acoustic behavior of auxetic two-dimensional structures // 1-st International Conference on Advances in Mechanical and Mechatronics Engineering “ICAMMEN-2018”. 2018. 9 p.

  33. Duffy T.S. Single-crystal elastic properties of minerals and related materials with cubic symmetry// Amer. Mineralog. 2018. V. 103. № 6. P. 977–988. https://doi.org/10.2138/am-2018-6285

  34. Peng R., Ma Y., Wu Q., Huang B., Dai Y. Two-dimensional materials with intrinsic auxeticity: Progress and perspectives // Nanoscale. 2019. V. 11. № 24. P. 1413–1428. https://doi.org/10.1039/C9NR03546J

  35. Wu W., Hu W., Qian G. et al. Mechanical design and multifunctional applications of chiral mechanical metamaterials: A review // Mater. Des. 2019. V. 180. P. 107950. https://doi.org/10.1016/j.matdes.2019.107950

  36. Yoo S., Park Q.-H. Metamaterials and chiral sensing: A review of fundamentals and applications // Nanophotonics. 2019. V. 8. № 2. P. 249–261. https://doi.org/10.1515/nanoph-2018-0167

  37. Sayed U., Samarth A. Auxetic polymers in textiles. Review // Int. J. Adv. Sci. Eng. 2019. V. 5. № 3. P. 1056–1063. https://doi.org/10.29294/IJASE.5.3.2019.1056-1063

  38. Lim T.-C. Mechanics of Metamaterials with Negative Parameters. Singapore: Springer. 2020.

  39. Kelkar P.U., Kim H.S., Cho K.-H. et al. Cellular Auxetic Structures for Mechanical Metamaterials: A Review // Sensors. 2020. V. 20. № 11. P. 3132. https://doi.org/10.3390/s20113132

  40. Mardling P., Alderson A., Jordan-Mahy N., Le Maitre C. The use of auxetic materials in tissue engineering // Biomater. Sci. 2020. V. 8. № 8. P. 2074–2983. https://doi.org/10.1039/C9BM01928F

  41. Zang J., Lu G., You Z. Large deformation and energy absorption of additively manufactured auxetic materials and structures: A review // Compos. B. Engineering. 2020. V. 201. P. 108340. https://doi.org/10.1016/j.compositesb.2020.108340

  42. Wang P., Luan C., Liao G. et al. Progress in auxetic mechanical metamaterials: structures, characteristics, manufacturing methods and applications // Adv. Eng. Mater. 2020. V. 22. № 10. P. 2000312. https://doi.org/10.1002/adem.202000312

  43. Dugad R., Radhakrishna G., Gandhi A. Recent advancements in manufacturing technologies of microcellular polymers. A review // J. Polymer Res. 2020. V. 27. № 7. P. 1–23.

  44. Tang H., Jiang X., Ling L. et al. Highly tailorable electromechanical properties of auxetic piezoelectric ceramics with ultra-low porosity // J. Americ. Ceramic Soc. 2020. V. 103. № 11. P. 6330–6347. https://doi.org/10.1111/jace.17356

  45. Joseph A., Manesh V., Harursampath D. On the application of additive manufacturing methods for auxetic structures: A review // Adv. Manuf. 2021. V. 9. № 3. P. 342–368. https://doi.org/10.1007/s40436-021-00357-y

  46. Luo C., Han C.Z., Ren X. et al. Design, manufacturing and applications of auxetic tubular structures. A review // Thin-Walled Struct. 2021. V. 163. P. 107682. https://doi.org/10.1016/j.tws.2021.107682

  47. Francisco M.B., Pereira J.L.J., Oliver G.A. et. al. A review on the energy absorption response and structural applications of auxetic structures // Mech. Adv. Mater. Struct. 2021. P. 1–20. https://doi.org/10.1080/15376494.2021.1966143

  48. Raistrick T., Zhang Z., Mistry D. et al. Understanding the physics of the auxetic response in a liquid crystal elastomer // Phys. Rev. Res. 2021. V. 3 № 2. P. 023191. https://doi.org/10.1103/PhysRevResearch.3.023191

  49. Chang Y., Hu H. 3D fabrics with negative Poisson’s ratio. A review // Appl. Compos. Mater. 2021. № 1. P. 1–14. https://doi.org/10.1007/s10443-021-09931-w

  50. Cardoso J.O., Borges J.P., Velhinho A. Structural metamaterials with negative mechanical-thermomechanical indices. A review // Progr. Natur. Sci. Mater. Int. 2021. V. 31. № 6. P. 801–808. https://doi.org/10.1016/j.pnsc.2021.10.015

  51. Kim M.K., Kim S., Yun J.W. et al. Design and manufacturing of mechanical metamaterials. A review. Compos. Res. 2021. V. 34. № 4. P. 199–211. https://doi.org/10.7234/composres.2021.34.4.199

  52. Alomarah A. Mechanical properties novel auxetic structures // Thesis for the degree of Doctor of Philosophy. 2021. P. 1–290.

  53. Hayes M.A., Shuvalov A. On the extreme values of Young’s modulus, the shear modulus, and Poisson’s ratio for cubic materials // J. Appl. Mech. 1998. V. 65. № 3. P. 786–787. https://doi.org/10.1115/1.2789130

  54. Lubarda V.A., Meyers M.A. On the negative Poisson ratio in monocrystalline zinc // Scr. Mater. 1999. V. 40. P. 975–977. https://doi.org/10.1016/S1359-6462(99)00039-1

  55. Paczkiewicz T., Pruchnik M., Wolski S. Slowness surfaces and energy focusing patterns of auxetic cubic media // Comput. Meth. Sci. Technol. 2004. V. 10. № 2. P. 183–195. https://doi.org/10.12921/cmst.2004.10.02.183-195

  56. Tokmakova S.P. Stereographic projections of Poisson’s ratio in auxetic crystals // Phys. Status Solidi B. 2005. V. 242. № 3. P. 721–729. https://doi.org/10.1002/pssb.200460389

  57. Norris A.N. Poisson’s ratio in cubic materials // Proc. R. Soc. A. 2006. V. 462. № 2075. P. 3385–3405. https://doi.org/10.1098/rspa.2006.1726

  58. Paczkiewicz T., Wolski S. Anisotropic properties of mechanical characteristics and auxeticity of cubic crystalline media // Phys. Status Solidi B. 2007. V. 344. № 3. P. 966–977. https://doi.org/10.1002/pssb.200572715

  59. Paczkiewicz T., Wolski S. Elastic properties of cubic crystals: Every’s versus Blackman’s diagram // J. Phys. Conf. Ser. 2008. V. 104. P. 012038. https://doi.org/10.1088/1742-6596/104/1/012038

  60. Branka A.C., Wojciechowski K.W. Auxeticity of cubic materials. The role of repulsive core interaction // J. Non-Cryst. Solids. 2008. V. 354. P. 4143–4145. https://doi.org/10.1016/j.jnoncrysol.2008.06.088

  61. Branka A.C., Heyes D.M., Wojciechowski K.W. Auxeticity of cubic materials // Phys. Status Solidi B. 2009. V. 246. № 9. P. 2063–2071. https://doi.org/10.1002/pssb.200982037

  62. Hughes T.P., Marmier A., Evans K.E. Auxetic frameworks inspired by cubic crystals // Int. J. Solids Struct. 2010. V. 47. № 11–12. P. 1469–1476. https://doi.org/10.1016/j.ijsolstr.2010.02.002

  63. Branka A.C., Heyes D.M., Wojciechowski K.W. Auxeticity of cubic materials under pressure // Phys. Status Solidi B. 2011. V. 248. № 1. P. 96–104. https://doi.org/10.1002/pssb.201083981

  64. Гольдштейн Р.В., Городцов В.А., Лисовенко Д.С. Кубические ауксетики // Докл. АН 2011. Т. 439. № 2. С.184–187.

  65. Лисовенко Д.С., Городцов В.А. Кубические кристаллы с отрицательными коэффициентами Пуассона (кубические ауксетики) // Вестник Нижегородского университета им. Н.И. Лобачевского 2011. № 4 (2). С. 488–489.

  66. Гольдштейн Р.В., Городцов В.А., Лисовенко Д.С. Модуль Юнга кубических ауксетиков // Письма о материалах 2011. Т. 1. В. 3. С. 127–132. https://doi.org/10.22226/2410-3535-2011-3-127-132

  67. Branka A.C., Heyes D.M., Mackowiak Sz., et al. Cubic materials in different auxetic regions: Linking microscopic to macroscopic formulations // Phys. Status Solidi B. 2012. V. 247. № 7. P. 1373–1378. https://doi.org/10.1002/pssb.201084222

  68. Гольдштейн Р.В., Городцов В.А., Лисовенко Д.С. Модуль сдвига кубических кристаллов // Письма о материалах 2012. Т. 2. № 1. С. 21–24. https://doi.org/10.22226/2410-3535-2012-1-21-24

  69. Гольдштейн Р.В., Городцов В.А., Лисовенко Д.С. Связь среднего коэффициента Пуассона с модулем Юнга для кубических кристаллов. Ауксетики в среднем // Докл. АН. 2012. Т. 443. № 6. С. 677–681.

  70. Paes V.Z.C., Mosca D.H. Magnetostrictive contribution to Poisson ratio of galfenol // J. Appl. Phys. 2013. V. 114. № 12. P. 123915. https://doi.org/10.1063/1.4822169

  71. Tretiakov K.V., Wojciechowski K.W. Elastic properties of fcc crystals of polydisperse soft spheres // Phys. Status Solidi B. 2013. V. 250. № 10. P. 2020–2029. https://doi.org/10.1002/pssb.201384236

  72. Goldstein R.V., Gorodtsov V.A., Lisovenko D.S. Classification of cubic auxetics // Phys. Status Solidi B. 2013. V. 250. № 10. P. 2038–2043. https://doi.org/10.1002/pssb.201384233

  73. Гольдштейн Р.В., Городцов В.А., Лисовенко Д.С., Волков М.А. Отрицательный коэффициент Пуассона для кубических кристаллов и нано/микротрубок // Физ. Мезомех. 2013. Т. 16. № 6. С. 13–31.

  74. Tretiakov K.V., Wojciechowski K.W. Partially auxetic behavior in fcc crystals of hard-core repulsive Yukawa particles // Phys. Status Solidi B. 2014. V. 251. № 2. P. 383–387. https://doi.org/10.1002/pssb.201384244

  75. Krasavin V.V., Krasavin A.V. Auxetc properties of cubic metal single crystals // Phys. Status Solidi B. 2014. V. 251. № 11. P. 2314–2320. https://doi.org/10.1002/pssb.201451129

  76. Ho D.T., Park S.D., Kwon S.Y., Park K., Kim S.Y. Negative Poisson’s ratios in metal nanoplates // Nat. Commun. 2014. V. 5. № 1. P. 3255. https://doi.org/10.1038/ncomms4255

  77. Ho D.T. Mechanical response and elastic instability of cubic bulk and nanoscale materials // Thesis for the degree of Doctor of Philosophy. 2015. P. 1–232.

  78. Ho D.T., Kim H., Kwon S.Y., Kim S.Y. Auxeticity of face-centered cubic metal (001) nanoplates // Phys. Status Solidi B. 2015. V. 252. № 11. P.1492–1501.

  79. Ерофеев В.И., Павлов И.С. Параметрическая идентификация кристаллов, имеющих кубическую решетку, с отрицательными коэффициентами Пуассона // Прикл. Мех. Техн. Физ. 2015. Т. 56. № 6. С. 94–101. https://doi.org/10.15372/PMTF20150611

  80. Raghunas G., Flatan A.B. Study of magnetic domain evolution in an auxetic plane of Galfenol using Kerr microscopy // J. Appl. Phys. 2015. T. 117. № 17. C. 17E704. https://doi.org/10.1063/1.4913727

  81. Ho D.T., Park S.D., Kwon S.Y., Han T.S., Kim S.Y. Negative Poisson’s ratio in cubic materials along principal directions // Phys. Status Solidi B. 2016. V. 253. № 7. P. 1288–1294. https://doi.org/10.1002/pssb.201600017

  82. Ho D.T., Kwon S.Y., Kim S.Y. Metal [100] nanowires with negative Poisson’s ratio // Sci. Reports 2016. V. 6. № 1. P. 27560. https://doi.org/10.1038/srep27560

  83. Cabras L., Brun M. A class of auxetic three-dimensional lattices // J. Mech. Phys. Solids. 2016. V. 91. P. 56–72. https://doi.org/10.1016/j.jmps.2016.02.010

  84. Lisovenko D.S., Baimova J.A., Rysaeva L.Kh., Gorodtsov V.A., Rudskoy A.I., Dmitriev S.V. Equilibrium diamond-like carbon nanostructures with cubic anisotropy: elastic properties // Phys. Status Solidi B. 2016. V. 253. № 7. P. 1303–1309. https://doi.org/10.1002/pssb.201600049

  85. Епишин А.И., Лисовенко Д.С. Экстремальные значения коэффициента Пуассона кубических кристаллов // Ж. Техн. физ. 2016. Т. 16. № 10. С.1516–1524. http://journals.ioffe.ru/articles/43675

  86. Гольдштейн Р.В., Городцов В.А., Лисовенко Д.С., Волков М.А. Двухслойные трубки из кубических кристаллов // Докл. АН 2016. Т. 471. № 4. С. 414–420. https://doi.org/10.7868/S0869565216340077

  87. Гольдштейн Р.В., Городцов В.А., Лисовенко Д.С. Кручение цилиндрически-анизотропных нано/микротрубок из кубических материалов, полученных сворачиванием кристаллографических плоскостей (011) // Письма о материалах. 2016. Т. 6. № 4. С. 249–252. https://doi.org/10.22226/2410-3535-2016-4-249-252

  88. Goldstein R.V., Gorodtsov V.A., Lisovenko D.S., Volkov M.A. Two-layered tubes from cubic crystals: auxetic tubes // Phys. Status Solidi B. 2017. V. 254. № 12. P. 1600815. https://doi.org/10.1002/pssb.201600815

  89. Pigłowski P.M., Narojczyk J.W., Wojciechowski K.W., Tretiakov K.V. Auxeticity enhancement due to size polydispersity in fcc crystals of hard-core repulsive Yukawa particles // Soft Matter. 2017. V. 13. № 43. P. 7916–7921. https://doi.org/10.1039/C7SM01231D

  90. Гольдштейн Р.В., Городцов В.А., Лисовенко Д.С., Волков М.А. Тонкие однородные двуслойные пластины из кубических кристаллов с различной ориентацией слоев // Физ. Мезомех. 2018. Т. 21. № 2. С. 5–13. https://doi.org/10.24411/1683-805X-2018-12001

  91. Gorodtsov V.A., Lisovenko D.S., Lim T.-C. Three-layered plate exhibiting auxeticity based on stretching and bending modes // Compos. Struct. 2018. V. 194. P. 643–651. https://doi.org/10.1016/j.compstruct.2018.03.092

  92. Narojczyk J.W., Wojciechowski K.W. Poisson’s ratio of the fcc hard sphere crystals with periodically stacked (001)-nanolayers of hard spheres of another diameter // Materials. 2019. V. 12. № 5. P. 700. https://doi.org/10.3390/ma12050700

  93. Ho D.T., Nguyen C.T., Kwon S.Y., Kim S.Y. Auxeticity in metals and periodic metallic porous structures induced by elastic instabilities // Phys. Status Solidi B. 2019. V. 256. № 1. P. 1800122. https://doi.org/10.1002/pssb.201800122

  94. Bryukhanov I.A., Gorodtsov V.A., Lisovenko D.S. Chiral Fe nanotubes with both negative Poisson’s ratio and Poynting’s effect. Atomistic simulation // J. Phys.: Condens. Matter. 2019. V. 31. № 47. P. 475304. https://doi.org/10.1088/1361-648X/ab3a04

  95. Брюханов И.А., Городцов В.А., Лисовенко Д.С. Атомистическое моделирование механических свойств хиральных металлических нанотрубок // Физ. Мезомех. 2019. Т. 22. № 6. С. 48–57. https://doi.org/10.24411/1683-805X-2019-16005

  96. Городцов В.А., Лисовенко Д.С. Ауксетики среди материалов с кубической анизотропией // Изв. РАН. МТТ. 2020. № 4. С. 7–24. https://doi.org/10.31857/S0572329920040054

  97. Tretiakov K.V., Wojciechowski K.W. The influence of the soft Yukawa potential and hard core interactions on auxeticity of the face centered cubic crystal of hard-core repulsive Yukawa particles // Phys. Status Solidi B. 2020. V. 257. № 10. P. 2000194. https://doi.org/10.1002/pssb.202000194

  98. Брюханов И.А., Волков М.А., Городцов В.А., Лисовенко Д.С. Об упругих свойствах хиральных металлических нанотрубок из кубических кристаллов // Физ. Мезомех. 2021. Т. 24. № 1. С. 37–49. https://doi.org/10.24411/1683-805X-2021-11003

  99. Volkov M.A., Gorodtsov V.A., Fadeev E.P., Lisovenko D.S. Stretching of chiral tubes obtained by rolling-up plates of cubic crystals with various orientations // J. Mech. Mater. Struct. 2021. V. 16. № 2. P. 139–157. https://doi.org/10.2140/jomms.2021.16.139

  100. Gorodtsov V.A., Volkov M.A., Lisovenko D.S. Out-of-plane tension of thin two-layered plates of cubic crystals // Phys. Status Solidi B. 2021. V. 258. № 12. P. 2100184. https://doi.org/10.1002/pssb.202100184

  101. Narojczyk J.W., Wojciechowski K.W., Smardzewski J., Imre A.R., Grima J.N., Bilski M. Cancellation of auxetic properties in F.C.C. hard sphere crystals by hybrid layer-channel nanoinclusions filled by hard spheres of another diameter // Materials. 2021. V. 14. № 11. P. 3008. https://doi.org/10.3390/ma14113008

  102. Narojczyk J.W., Bilski M., Grima J.N., Kędziora P., Morozow D., Rucki M., Wojciechowski K.W. Removing auxetic properties in fcc hard sphere crystals by orthogonal nanochannels with hard spheres of another diameter // Materials. 2022. V. 15. № 3. P. 1134. https://doi.org/10.3390/ma15031134

  103. Narojczyk J.W., Tretiakov K.V., Wojciechowski K.W. Partially auxetic properties of fcc hard sphere crystals with nanochannels of different sizes, parallel to [001]-direction and filled by other hard spheres // Phys. Status Solidi B. 2022. V. 259. № 6. P. 2200006. https://doi.org/10.1002/pssb.202200006

  104. Епишин А.И., Лисовенко Д.С. Влияние кристаллической структуры и типа межатомной связи на упругие свойства одноатомных и двухатомных кубических кристаллов // Изв. РАН. МТТ. 2022. № 6. С. 79–96. https://doi.org/10.31857/S0572329922060058

  105. Goldstein R.V., Gorodtsov V.A., Lisovenko D.S. Longitudinal elastic tension of two-layered plates from isotropic auxetics-nonauxetics and cubic crystals // Eur. J. Mech. A Solids. 2017. V. 63. P. 122–127. https://doi.org/10.1016/j.euromechsol.2017.01.001

  106. Every A.G., McCurdy A.K. Second and higher order elastic constants. Nelson D.E. (editor) // Landolt-Börnstein. New Ser. Group III. Springer, 1992. V. 29a. https://doi.org/10.1007/b44185

  107. Schärer U., Jung A., Wachter P. Brillouin spectroscopy with surface acoustic waves on intermediate valent, doped SmS // Phys. B. 1998. V. 244. P. 148–153. https://doi.org/10.1016/S0921-4526(97)00478-X

  108. Сиротин Ю.И., Шаскольская М.П. Основы кристаллофизики // М.: Наука 1975. 680 с.

  109. Гольдштейн Р.В., Городцов В.А., Лисовенко Д.С. Связь среднего коэффициента Пуассона с модулем Юнга для кубических кристаллов. Ауксетики в среднем // Докл. АН 2012. Т. 443. № 6. С. 677–681.

Дополнительные материалы отсутствуют.

Инструменты

предыдущая статья выпуска содержание выпуска

Известия РАН. Механика твердого тела

Архивы выпусков Информация о журнале Отправить рукопись в журнал