Известия РАН. Механика твердого тела, 2023, № 1, стр. 156-165

ОТНОСИТЕЛЬНЫЕ РАВНОВЕСИЯ ТЯЖЕЛОЙ ТОЧКИ НА РАВНОМЕРНО ВРАЩАЮЩЕЙСЯ НАКЛОННОЙ ПЛОСКОСТИ

А. А. Буров^a, *, В. И. Никонов^a, **

^a Федеральный исследовательский центр “Информатика и управление” Российской академии наук
Москва, Россия

^* E-mail: jtm@narod.ru
^** E-mail: nikon_v@list.ru

Поступила в редакцию 15.11.2021
После доработки 07.03.2022
Принята к публикации 27.03.2022

EDN: KLKYHT
DOI: 10.31857/S0572329922600499

Аннотация

Рассматривается задача о движении тяжелой точки по наклонной плоскости, совершающей равномерное вращение вокруг вертикали. Определяется область, заполненная неизолированными относительными равновесиями, изучается ее зависимость от параметров задачи – угловой скорости, угла наклона плоскости и угла трения. Обсуждается устойчивость изучаемых относительных равновесий.

Ключевые слова: относительные равновесия, сухое трение

Введение. При движении точки по подвижным кривым и поверхностям зачастую решающую роль играет сила сухого трения. В частности, известно (см., например, [1–11]), что при таком трении относительные равновесия занимают целые области на поверхности, зависящие от поля внешних сил, геометрии поверхности тела, величины коэффициента трения, а также величины и направления вектора угловой скорости.

Классическая задача о соскальзывании материальной точки по наклонной шероховатой плоскости рассмотрена в [12–14]. Критический случай, когда угол наклона плоскости к горизонту равен углу трения, рассмотрен в [15], где выполнено точное интегрирование уравнений движения (см. также монографию [16]).

Кроме того, в [15, 16] также исследована задача о движении материальной точки на вращающейся шероховатой плоскости. С помощью теоретико-групповых методов найдены классы точных решений. Показано, что для движущейся без остановки точки предельными движениями являются движения по логарифмическим спиралям. Также показано, что такие движения являются предельными для всех движений, уходящих на бесконечность. В рамках этой же задачи в [17] построены асимптотические разложения решений уравнений движения вблизи момента остановки точки. Определены различные типы движений с остановками. Проведено численное моделирование движений, построены характерные траектории движений точки. Найдено интегральное многообразие, разделяющее в фазовом пространстве движения с остановкой и движения, при которых точка уходит на бесконечность. На этом многообразии построены фазовые траектории системы.

Если горизонтальная шероховатая плоскость равномерно вращается вокруг вертикали, то область, заполненная относительными равновесиями – круг с центром в точке пересечения плоскости и оси вращения. Возникает естественный вопрос, что будет с этим кругом относительных равновесий, если плоскость будет наклонена к горизонту на ненулевой угол. Вопросу существования относительных равновесий в такой задаче посвящена настоящая работа.

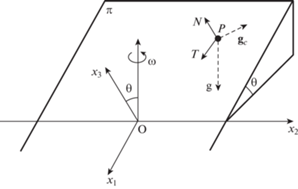
1. Постановка задачи и основные соотношения. Пусть шероховатая плоскость $\pi $ с коэффициентом трения $\mu = {\text{tg}}\alpha $, где α—т.н. угол трения, наклонена к горизонту под углом $\theta \in [0,\pi {\text{/}}2]$. Пусть ${\mathbf{e}}$ – единичный вектор восходящей вертикали, ${\mathbf{n}}$ – единичный вектор нормали к плоскости. Тогда $\cos \theta = ({\mathbf{n}},{\mathbf{e}})$. Также будем полагать, что плоскость равномерно вращается вокруг вертикали с постоянной угловой скоростью ${\kern 1pt} \omega = \omega {\mathbf{e}}$, $\omega > 0$. Ставится задача определения областей, заполненных относительными равновесиями (ОЗОР) материальной точки $P,$ соприкасающейся с данной плоскостью, и их описания в зависимости от параметров задачи. Во вращающейся вместе с плоскостью системе отсчета точка P будет находиться в равновесии под действием силы тяжести, центробежной силы, а также реакции связи, состоящей из нормальной компоненты, и силы трения. Полагая массу точки равной единице, условие равновесия запишем в виде

(1.1)

$\begin{gathered} {\mathbf{f}} + {\mathbf{N}} + {\mathbf{T}} = {\mathbf{0}} \\ {\mathbf{f}} = {{{\mathbf{g}}}_{c}} + {\mathbf{g}} \\ \end{gathered} $

где ${\mathbf{g}}$ – ускорение свободного падения, ${{{\mathbf{g}}}_{c}}$ – напряженность центробежной силы, ${\mathbf{N}} = N{\mathbf{n}}$ и ${\mathbf{T}}$ – отнесенные к массе точки нормальная реакция и сила трения. При этом на относительных равновесиях сила трения ${\mathbf{T}}$ и нормальная реакция ${\mathbf{N}}$ стеснены неравенством

(1.2)

${\text{|}}{\mathbf{T}}{\text{|}} \leqslant \mu {\text{|}}{\mathbf{N}}{\text{|}}$

выражающим закон трения Кулона–Амонтона (рис. 1). Принимая во внимание соотношение (1.1), неравенство (1.2) после преобразований может быть записано как

(1.3)

$({\mathbf{f}},{\mathbf{f}}) \leqslant (1 + {{\mu }^{2}})({\mathbf{f}},{\mathbf{n}}{{)}^{2}}$

Рис. 1.

Распределение сил и реакций связи, действующих на точку P.

На равновесиях условие напряженности связи принимает вид

(1.4)

$({\mathbf{f}},{\mathbf{n}}) < 0$

Пусть $O{{x}_{1}}{{x}_{2}}{{x}_{3}}$ – подвижная система отсчета, координатная плоскость $O{{x}_{1}}{{x}_{2}}$ которой совпадает с плоскостью $\pi $, а ось $O{{x}_{3}}$ направлена по нормали к этой плоскости. Тогда ${\mathbf{e}} = ( - \sin \theta ,0,\cos \theta {{)}^{T}}$, ${\mathbf{n}}{{ = (0,0,1)}^{T}}$, а плоскость $\pi $ задается уравнением ${{x}_{3}} = 0$. Вектор угловой скорости в проекциях на те же оси имеет вид $\omega = \omega {{( - \sin \theta ,0,\cos \theta )}^{T}}$. Кроме того, если ${{({{x}_{1}},{{x}_{2}},{{x}_{3}})}^{T}}$ – координаты радиус-вектора $\overleftarrow {OP} $ точки P, то имеем

${\mathbf{g}} = g{{(\sin \theta ,0, - \cos \theta )}^{T}},\quad {{{\mathbf{g}}}_{c}} = \omega \times ({\mathbf{x}} \times \omega ) = {{\omega }^{2}}{{({{\cos }^{2}}\theta {{x}_{1}},{{x}_{2}},\sin \theta \cos \theta {{x}_{1}})}^{T}}$

${\mathbf{f}} = {{(g\sin \theta + {{\omega }^{2}}{{\cos }^{2}}\theta {{x}_{1}},{{\omega }^{2}}{{x}_{2}},({{\omega }^{2}}\sin \theta {{x}_{1}} - g)\cos \theta )}^{T}}$

Тогда

$({\mathbf{f}},{\mathbf{f}}) = {{g}^{2}} + {{\omega }^{4}}(x_{1}^{2}{{\cos }^{2}}\theta + x_{2}^{2}),\quad ({\mathbf{f}},{\mathbf{n}}) = ({{\omega }^{2}}{{x}_{1}}{\text{sin}}\theta - g)\cos \theta $

и составляющая вектора f, направленная вдоль плоскости, имеет вид

(1.5)

${{{\mathbf{f}}}_{\tau }} = {\mathbf{f}} - ({\mathbf{f}},{\mathbf{n}}){\mathbf{n}} = {{(g\sin \theta + {{\omega }^{2}}{\text{co}}{{{\text{s}}}^{2}}\theta {{x}_{1}},{{\omega }^{2}}{{x}_{2}},0)}^{T}}$

В безразмерных координатах

${{X}_{k}} = {{x}_{k}}\frac{{{{\omega }^{2}}}}{g},\quad k = 1,2,3$

вектор (1.5) запишется как

(1.6)

${{{\mathbf{f}}}_{\tau }} = g{{(\sin \theta + {{\cos }^{2}}\theta {{X}_{1}},{{X}_{2}},0)}^{T}}$

а неравенство (1.3) примет вид

(1.7)

$1 + X_{1}^{2}{{\cos }^{2}}\theta + X_{2}^{2} \leqslant (1 + {{\mu }^{2}}){{\left( {({{X}_{1}}\sin \theta - 1)\cos \theta } \right)}^{2}}$

Замечание. Неравенство (1.7) задает физически осмысленные относительные равновесия в области, задаваемой также неравенством (1.4), гарантирующим напряженность связи. Это неравенство в данном случае принимает вид

(1.8)

${{X}_{1}} < \frac{1}{{\sin \theta }}$

Заметим что так как $\mu = {\text{tg}}\alpha $, и поэтому $1 + {{\mu }^{2}} = 1{\text{/co}}{{{\text{s}}}^{2}}\alpha $, то неравенство (1.7), определяющее ОЗОР, можно переписать как

(1.9)

$\Sigma :\,\,{{\cos }^{2}}\theta (X_{1}^{2}({{\cos }^{2}}\alpha - {{\sin }^{2}}\theta ) + 2{{X}_{1}}\sin \theta ) + X_{2}^{2}{{\cos }^{2}}\alpha + {{\cos }^{2}}\alpha - {{\cos }^{2}}\theta \leqslant 0$

ОЗОР здесь и далее обозначим $\Sigma $. Принадлежащая плоскости $\pi $ внешняя нормаль к $\partial \Sigma $ – границе области $\Sigma $ – имеет вид

${\mathbf{n}}{\kern 1pt} ' = {{({{\cos }^{2}}\theta ({{X}_{1}}({{\cos }^{2}}\alpha - {{\sin }^{2}}\theta ) + \sin \theta ),{{X}_{2}}{{\cos }^{2}}\alpha ,0)}^{T}}$

Этот вектор понадобится в разделе, посвященном устойчивости относительных равновесий.

Замечание. В отсутствии силы трения условие равновесия точки (1.1) запишем в виде

${\mathbf{f}} + {\mathbf{N}} = {{(g\sin \theta + {{\omega }^{2}}{{\cos }^{2}}\theta {{x}_{1}},{{\omega }^{2}}{{x}_{2}},({{\omega }^{2}}\sin \theta {{x}_{1}} - g)\cos \theta + N)}^{T}} = {\mathbf{0}}$

Это условие определяет равновесие

${{x}_{1}} = - \frac{g}{{{{\omega }^{2}}}}\frac{{\sin \theta }}{{{{{\cos }}^{2}}\theta }},\quad {{x}_{2}} = {{x}_{3}} = 0$

записываемое в безразмерном виде как

(1.10)

${{X}_{1}} = - \frac{{\sin \theta }}{{{{{\cos }}^{2}}\theta }},\quad {{X}_{2}} = {{X}_{3}} = 0$

При фиксированных значениях параметров это равновесие единственно, причем нормальная реакция определяется как $N = g{\text{/}}\cos \theta $.

2. Параметрический анализ основных соотношений. Для интерпретации результатов на плоскости параметров (α, θ) изобразим квадрат со стороной $\pi {\text{/}}2$ (рис. 2). Диагонали разделяют этот квадрат на четыре области, обозначенные ${{\mathcal{R}}_{1}}$, ${{\mathcal{R}}_{2}}$, ${{\mathcal{R}}_{3}}$ и ${{\mathcal{R}}_{4}}$.

Рис. 2.

Области ${{\mathcal{R}}_{1}}$, ${{\mathcal{R}}_{2}}$, ${{\mathcal{R}}_{3}}$ и ${{\mathcal{R}}_{4}}$ на плоскости параметров (α, θ).

Пусть ${{\cos }^{2}}\alpha - {{\sin }^{2}}\theta > 0$, т.е. параметры принадлежат областям ${{\mathcal{R}}_{1}}$ и ${{\mathcal{R}}_{4}}$. Тогда неравенство (1.9) задает область

(2.1)

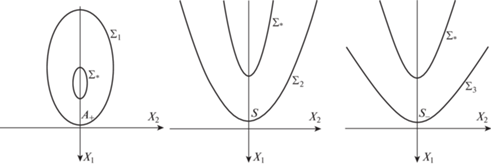
$\begin{gathered} {{\Sigma }_{1}}:\quad \frac{{{{{\left( {{{X}_{1}} - {{X}_{{10}}}} \right)}}^{2}}}}{{a_{1}^{2}}} + \frac{{X_{2}^{2}}}{{a_{2}^{2}}} - 1 \leqslant 0 \\ {{a}_{1}} = \frac{{\cos \alpha \sin \alpha }}{{\cos \theta ({{{\cos }}^{2}}\alpha - {{{\sin }}^{2}}\theta )}},\quad {{a}_{2}} = \frac{{\sin \alpha }}{{\sqrt {{{{\cos }}^{2}}\alpha - {{{\sin }}^{2}}\theta } }},\quad {{X}_{{10}}} = \frac{{\sin \theta }}{{{{{\sin }}^{2}}\theta - {{{\cos }}^{2}}\alpha }} \\ \end{gathered} $

Область (2.1) ограничена эллипсом $\partial {{\Sigma }_{1}}$ с полуосями a₁ и a₂, причем ${{a}_{1}} > {{a}_{2}}$. Центр этого эллипса – точка ${{C}_{e}}$: $\overleftarrow {O{{C}_{e}}} = ({{X}_{{10}}}{{,0,0)}^{T}}$. Она всегда располагается выше по склону, чем точка $O$. В отсутствии трения, именно эта точка и есть относительное равновесие (1.10).

Наинизшая точка эллипса – точка ${{A}_{ + }}$: $\overleftarrow {O{{A}_{ + }}} = {{\left( {{{X}_{{10}}} + {{a}_{1}},0,0} \right)}^{T}}$ – располагается по склону выше, чем точка O при $\alpha < \theta < \pi {\text{/}}2$ (область ${{\mathcal{R}}_{1}}$) и по склону ниже, чем точка O при $0 < \theta < \alpha $ (область ${{\mathcal{R}}_{4}}$). Для точек общей границы областей ${{\mathcal{R}}_{1}}$ и ${{\mathcal{R}}_{4}}$ имеем $\theta = \alpha $, и точка ${{A}_{ + }}$ совпадает с точкой O.

Фокусы эллипса – точки

${{F}_{ \pm }}:\,\,\overleftarrow {O{{F}_{ \pm }}} = {{\left( {\theta \frac{{ - \cos \theta \pm \sin \alpha \sqrt {{{{\cos }}^{2}}\alpha + {{{\cos }}^{2}}\theta } }}{{{{{\cos }}^{2}}\alpha - {{{\sin }}^{2}}\theta }},0,0} \right)}^{T}}$

Неравенство (1.8) выполнено для всех точек, расположенных внутри эллипса (2.1). Для этого достаточно убедиться в справедливости неравенства

${{X}_{{10}}} + {{a}_{1}} < \frac{1}{{\sin \theta }}$

для точки ${{A}_{ + }}$. Для $\theta > \alpha $ ОЗОР схематично представлена на рис. 3 слева.

Рис. 3.

Различные типы ОЗОР в зависимости от параметра p(α, θ) и границы их устойчивости.

Пусть теперь ${{\cos }^{2}}\alpha - {{\sin }^{2}}\theta = 0$, т.е. параметры принадлежат штриховой диагонали квадрата. Тогда неравенство (1.9) задает область

(2.2)

${{\Sigma }_{2}}:\,\,X_{2}^{2} + 2\frac{{{{{\sin }}^{2}}\alpha }}{{\cos \alpha }}\left( {{{X}_{1}} - \frac{1}{2}\frac{{{{{\sin }}^{2}}\alpha - {{{\cos }}^{2}}\alpha }}{{\cos \alpha {{{\sin }}^{2}}\alpha }}} \right) \leqslant 0$

ограниченную параболой $\partial {{\Sigma }_{2}}$. Ветви этой параболы направлены вверх по склону, а радиус-вектор $\overleftarrow {OS} $ ее вершины $S$ имеет координаты

$\overleftarrow {OS} = \left( {\frac{{{{{\sin }}^{2}}\alpha - {{{\cos }}^{2}}\alpha }}{{2\cos \alpha {{{\sin }}^{2}}\alpha }},0,0} \right)$

Вершина S располагается выше точки O по склону при $\alpha < \pi {\text{/}}4$, в точке O при $\alpha = \pi {\text{/}}4$ и ниже точки O при $\alpha > \pi {\text{/}}4$. Радиус-вектор $\overleftarrow {OF} $ фокуса параболы F имеет координаты

$\overleftarrow {OF} = {{\left( { - \frac{1}{2}\frac{{{{{\cos }}^{3}}\alpha }}{{{{{\sin }}^{2}}\alpha }},0,0} \right)}^{T}}$

Фокус F всегда располагается выше по склону по отношению к точке O. Неравенство (1.8) выполнено для всех точек, ограниченных параболой (2.2). Для этого достаточно убедиться в справедливости неравенства (1.8) для вершины параболы S. Для $\theta > \alpha $ ОЗОР схематично представлена на рис. 3 по центру.

Пусть, наконец, ${{\cos }^{2}}\alpha - {{\sin }^{2}}\theta < 0$, т.е. параметры принадлежат областям ${{\mathcal{R}}_{2}}$ и ${{\mathcal{R}}_{3}}$. Тогда неравенство (1.9) задает область

(2.3)

$\begin{gathered} {{\Sigma }_{3}}:\,\,\frac{{{{{\left( {{{X}_{1}} - {{X}_{{10}}}} \right)}}^{2}}}}{{a_{1}^{2}}} - \frac{{X_{2}^{2}}}{{a_{2}^{2}}} - 1 \geqslant 0 \\ {{a}_{1}} = \frac{{\cos \alpha \sin \alpha }}{{\cos \theta ({{{\sin }}^{2}}\theta - {{{\cos }}^{2}}\alpha )}},\quad {{a}_{2}} = \frac{{\sin \alpha }}{{\sqrt {{{{\sin }}^{2}}\theta - {{{\cos }}^{2}}\alpha } }},\quad {{X}_{{10}}} = \frac{{\sin \theta }}{{{{{\sin }}^{2}}\theta - {{{\cos }}^{2}}\alpha }} \\ \end{gathered} $

ограниченную гиперболой $\partial {{\Sigma }_{3}}$. Центр гиперболы – точка ${{C}_{h}}$: $\overleftarrow {O{{C}_{h}}} = ({{X}_{{10}}}{{,0,0)}^{T}}$. Эта точка всегда располагается ниже по склону, чем точка O. Вершины гиперболы – точки ${{S}_{ \pm }}{\text{:}}$ ${{\overleftarrow {OS} }_{ \pm }} = ({{X}_{{10}}} \pm {{a}_{1}}{{,0,0)}^{T}}$. Вершина ${{S}_{ + }}$ располагается всегда ниже по склону, чем точка O. Вершина ${{S}_{ - }}$ располагается по склону выше, чем точка O при $\alpha < \theta < \pi {\text{/}}2$ (область ${{\mathcal{R}}_{2}}$) и по склону ниже, чем точка O при $0 < \theta < \alpha $ (область ${{\mathcal{R}}_{3}}$). Для точек общей границы областей ${{\mathcal{R}}_{2}}$ и ${{\mathcal{R}}_{3}}$ имеем θ = α, и точка S₊ совпадает с точкой O. Неравенство (1.8) выполнено только для тех точек гиперболы (2.3), которые ограничены ветвью с вершиной S_–. Для θ > α ОЗОР схематично представлена на рис. 3 справа.

Замечание. Нетрудно видеть, что основным бифуркационным параметром, отличающим ОЗОР, оказывается величина

$p(\alpha ,\theta ) = {{\cos }^{2}}\alpha - {{\sin }^{2}}\theta = (\cos \alpha + \sin \theta )(\cos \alpha - \sin \theta )$

Так как первый сомножитель всегда положителен, то знак параметра $p(\alpha ,\theta )$ определяется знаком выражения $\cos \alpha - \sin \theta = \cos \alpha - \cos \left( {\pi {\text{/}}2 - \theta } \right)$. Так как в первом квадранте косинус монотонно убывает, то $p(\alpha ,\theta ) > 0,$ если $\alpha + \theta < \pi {\text{/}}2$ (области ${{\mathcal{R}}_{1}}$ и ${{\mathcal{R}}_{4}}$ на рис. 2). И наоборот, $p(\alpha ,\theta ) < 0$, если $\alpha + \theta > \pi {\text{/}}2$ (области ${{\mathcal{R}}_{2}}$ и ${{\mathcal{R}}_{3}}$ на рис. 2). Примечательно, что параметры g и ω сказываются лишь на размерах ОЗОР, но не сказываются на их типе.

3. Об устойчивости относительных равновесий. Устойчивость по Ляпунову относительных равновесий, расположенных внутри найденных областей, следует из результатов Г.К. Пожарицкого [18]. Можно, как и в [19, 20], поставить вопрос об устойчивости ОЗОР в целом.

Будем считать ОЗОР устойчивой, если для каждой точки ее границы проекция суммы активных сил и центробежной силы на плоскость, касательную к поверхности в этой точке направлена внутрь ОЗОР. Это свойство можно трактовать следующим образом. Пусть в начальный момент точка P располагается в некоторой точке Q границы ОЗОР. “Отпустим” точку P без начальной скорости, “освободив” систему от трения, т.е. предположив, что коэффициент трения обратился в нуль. В случае устойчивости ОЗОР для всех точек Q ее границы точка P начнет движение внутрь этой области или вдоль ее границы. Если найдется хотя бы одна точка Q границы ОЗОР, для которой точка P начнет движение вовне ОЗОР, то речь идет о неустойчивости этой области.

Таким образом, для анализа устойчивости вычислим скалярное произведение

(3.1)

$\begin{gathered} ({{{\mathbf{f}}}_{\tau }},{\mathbf{n}}') = g((\sin \theta + {{\cos }^{2}}\theta {{X}_{1}}){{\cos }^{2}}\theta ({{X}_{1}}({{\cos }^{2}}\alpha - {{\sin }^{2}}\theta ) + \sin \theta ) + X_{2}^{2}{{\cos }^{2}}\alpha ) = gF \\ F = {{\cos }^{4}}\theta ({{\cos }^{2}}\alpha - {{\sin }^{2}}\theta )X_{1}^{2} + {{\cos }^{2}}\theta \sin \theta ({{\cos }^{2}}\theta - {{\sin }^{2}}\theta + {{\cos }^{2}}\alpha ){{X}_{1}} + \\ \, + {{\cos }^{2}}\alpha X_{2}^{2} + {{\sin }^{2}}\theta {{\cos }^{2}}\theta \\ \end{gathered} $

Для того, чтобы ОЗОР ${{\Sigma }_{k}}$ была устойчива, она должна располагаться внутри области

(3.2)

$\Sigma {\text{:}}\quad F < 0$

ограниченной кривой второго порядка $\partial \Sigma .$

Пусть ${{\cos }^{2}}\alpha - {{\sin }^{2}}\theta > 0$. В этом случая кривая $\Sigma $ – эллипс

$\frac{{{{{\left( {{{X}_{1}} - {{X}_{{11}}}} \right)}}^{2}}}}{{b_{1}^{2}}} + \frac{{X_{2}^{2}}}{{b_{2}^{2}}} - 1 = 0$

(3.3)

${{b}_{1}} = \frac{{\sin \theta {{{\sin }}^{2}}\alpha }}{{2{{{\cos }}^{2}}\theta ({{{\cos }}^{2}}\alpha - {{{\sin }}^{2}}\theta )}},\quad {{b}_{2}} = \frac{{\sin \theta {{{\sin }}^{2}}\alpha }}{{2\cos \alpha \sqrt {{{{\cos }}^{2}}\alpha - {{{\sin }}^{2}}\theta } }}$

${{X}_{{11}}} = \frac{{\sin \theta ({{{\sin }}^{2}}\theta - {{{\cos }}^{2}}\theta - {{{\cos }}^{2}}\alpha )}}{{2{{{\cos }}^{2}}\theta ({{{\cos }}^{2}}\alpha - {{{\sin }}^{2}}\theta )}}$

с центром в точке C_ε: $O{{C}_{\varepsilon }} = {{\left( {{{X}_{{11}}},0,0} \right)}^{T}}$ и фокусами в точках

${{\mathcal{F}}_{ \pm }}:\quad \overleftarrow {O{{\mathcal{F}}_{ \pm }}} = {{\left( {{{f}_{ \pm }},0,0} \right)}^{T}}$

${{f}_{ \pm }} = {\text{tg}}\theta \frac{{\cos \alpha ({{{\sin }}^{2}}\theta - {{{\cos }}^{2}}\theta - {{{\cos }}^{2}}\alpha ) \pm \sin \theta {{{\sin }}^{2}}\alpha \sqrt {{{{\cos }}^{4}}\theta + {{{\cos }}^{2}}\theta {{{\cos }}^{2}}\alpha + {{{\cos }}^{2}}\alpha } }}{{2\cos \theta \cos \alpha ({{{\cos }}^{2}}\alpha - {{{\sin }}^{2}}\theta )}}$

Пусть угол φ – параметр обхода границы (2.1), тогда параметрически эта граница записывается как

${{X}_{1}} = {{X}_{{10}}} + {{a}_{1}}{\text{cos}}\varphi ,\quad {{X}_{2}} = {{a}_{2}}{\text{sin}}\varphi $

Подставляя эти величины в соотношение (3.3), имеем

(3.4)

$\begin{gathered} \frac{{{{{\left( {{{X}_{{10}}} - {{X}_{{11}}} + {{a}_{1}}\cos \varphi } \right)}}^{2}}}}{{b_{1}^{2}}} + \frac{{a_{2}^{2}{{{\sin }}^{2}}\varphi }}{{b_{2}^{2}}} - 1 = 4{\text{ctg}}\alpha {{\mathcal{P}}_{e}}(\cos \varphi ) \\ {{\mathcal{P}}_{e}}(z) = - {\text{ctg}}\alpha {{z}^{2}} - {\text{ctg}}\theta z + \frac{{{\text{ctg}}\alpha }}{{{{{\sin }}^{2}}\theta }},\quad z = \cos \varphi \\ \end{gathered} $

На плоскости $(z,{{\mathcal{P}}_{e}})$ соотношение (3.4) задает квадратичную параболу, ветви которой направлены вниз. Дискриминант многочлена ${{\mathcal{P}}_{e}}(z)$ положителен:

$\frac{{{{{\cos }}^{2}}\theta + 4{\text{ct}}{{{\text{g}}}^{2}}\alpha }}{{{{{\sin }}^{2}}\theta }} > 0$

Тогда так как

${{\mathcal{P}}_{e}}( \pm 1) = 4\frac{{\cos \alpha \cos \theta \cos (\alpha \pm \theta )}}{{{{{\sin }}^{2}}\alpha {{{\sin }}^{2}}\theta }} > 0,\quad 0 \leqslant \alpha + \theta < \frac{\pi }{2}$

то многочлен ${{\mathcal{P}}_{e}}(z)$ положителен на отрезке $ - 1 \leqslant z \leqslant 1$. Это означает, что эллипс (3.3) располагается внутри эллипса (2.1), и ОЗОР (2.1) неустойчива в описанном выше смысле.

Пусть теперь ${{\cos }^{2}}\alpha - {{\sin }^{2}}\theta = 0$. В этом случая кривая $\Sigma $ – парабола, определяемая уравнением

(3.5)

$X_{2}^{2} + \frac{{{{{\sin }}^{4}}\alpha }}{{\cos \alpha }}\left( {{{X}_{1}} + \frac{{\cos \alpha }}{{{{{\sin }}^{2}}\alpha }}} \right) = 0$

с фокусом в точке

$\mathcal{F}:\,\,\overleftarrow {O\mathcal{F}} = {{\left( { - \frac{{{{{\sin }}^{2}}\alpha }}{{4\cos \alpha }},0,0} \right)}^{T}}$

Для точек, принадлежащих параболе (2.2), выполнено

${{X}_{1}} = - \frac{1}{2}\frac{{\cos \alpha }}{{{{{\sin }}^{2}}\alpha }}\tilde {X}_{2}^{2} + \frac{1}{2}\frac{{{{{\sin }}^{2}}\alpha - {{{\cos }}^{2}}\alpha }}{{2\cos \alpha {{{\sin }}^{2}}\alpha }},\quad {{X}_{2}} = {{\tilde {X}}_{2}},\quad {{X}_{3}} = 0$

Подставим эти значения в соотношение (3.5). После преобразований имеем

$\frac{1}{2}[(1 + {{\cos }^{2}}\alpha )\tilde {X}_{2}^{2} + {\text{t}}{{{\text{g}}}^{2}}\alpha ] > 0,\quad 0 < \alpha < \frac{\pi }{2}$

Это означает, что парабола (3.5) располагается внутри параболы (2.2), и ОЗОР (2.2) неустойчива в описанном выше смысле.

Пусть, наконец, ${{\cos }^{2}}\alpha - {{\sin }^{2}}\theta < 0$. В этом случая кривая $\Sigma $ – гипербола

$\frac{{{{{\left( {{{X}_{1}} - {{X}_{{11}}}} \right)}}^{2}}}}{{b_{1}^{2}}} - \frac{{X_{2}^{2}}}{{b_{2}^{2}}} - 1 = 0$

(3.6)

${{b}_{1}} = \frac{{\sin \theta {{{\sin }}^{2}}\alpha }}{{2{{{\cos }}^{2}}\theta ({{{\sin }}^{2}}\theta - {{{\cos }}^{2}}\alpha )}},\quad {{b}_{2}} = \frac{{\sin \theta {{{\sin }}^{2}}\alpha }}{{2\cos \alpha \sqrt {{{{\sin }}^{2}}\theta - {{{\cos }}^{2}}\alpha } }}$

${{X}_{{11}}} = \frac{{\sin \theta ({{{\cos }}^{2}}\theta - {{{\sin }}^{2}}\theta + {{{\cos }}^{2}}\alpha )}}{{2{{{\cos }}^{2}}\theta ({{{\sin }}^{2}}\theta - {{{\cos }}^{2}}\alpha )}}$

с центром в точке ${{C}_{\mathcal{H}}}$: $O{{C}_{\mathcal{H}}} = {{\left( {{{X}_{{11}}},0,0} \right)}^{T}}$ и фокусами в точках

${{\mathcal{F}}_{ \pm }}:\,\,\overleftarrow {O{{\mathcal{F}}_{ \pm }}} = {{\left( {{{f}_{ \pm }},0,0} \right)}^{T}}$

${{f}_{ \pm }} = \frac{{\sin \theta (\cos \alpha (2{{{\cos }}^{2}}\theta - {{{\sin }}^{2}}\alpha ) \pm {{{\sin }}^{2}}\alpha \sqrt {{{{\cos }}^{4}}\theta ({{{\sin }}^{2}}\theta - {{{\cos }}^{2}}\alpha ) + {\text{co}}{{{\text{s}}}^{2}}\alpha } {\kern 1pt} )}}{{2{{{\cos }}^{2}}\theta \cos \alpha ({{{\sin }}^{2}}\theta - {{{\cos }}^{2}}\alpha )}}$

Пусть угол ψ – параметр обхода ветви гиперболы (2.3), располагающейся выше по скату. Тогда параметрически эта граница записывается как

${{X}_{1}} = {{X}_{{10}}} - {{a}_{1}}{\text{ch}}\psi ,\quad {{X}_{2}} = {{a}_{2}}{\text{sh}}\psi $

где chψ и shψ – гиперболические косинус и синус соответственно. Подставляя эти величины в соотношение (3.6), имеем

(3.7)

$\begin{gathered} \frac{{{{{\left( {{{X}_{{10}}} - {{X}_{{11}}} - {{a}_{1}}{\text{ch}}\psi } \right)}}^{2}}}}{{b_{1}^{2}}} - \frac{{a_{2}^{2}{\text{c}}{{{\text{h}}}^{2}}\psi }}{{b_{2}^{2}}} - 1 = 4\frac{{{{{\cos }}^{2}}\alpha }}{{{{{\sin }}^{2}}\theta {{{\sin }}^{2}}\alpha }}{{\mathcal{P}}_{h}}(z) \\ {{\mathcal{P}}_{h}}(z) = - {{\sin }^{2}}\theta {{z}^{2}} - \cos \theta \sin \theta {\text{tg}}\alpha z + 1,\quad z = \psi \\ \end{gathered} $

На плоскости $(z,{{\mathcal{P}}_{h}})$ соотношение (3.7) задает квадратичную параболу, ветви которой направлены вниз. Дискриминант многочлена ${{\mathcal{P}}_{h}}(z)$ положителен

${{\sin }^{2}}\theta ({{\cos }^{2}}\theta {{\tan }^{2}}\alpha + 4) > 0,$

а его корни имеют вид

${{z}_{ \pm }} = - \frac{1}{2}{\text{ctg}}\theta {\text{tg}}\alpha \pm \frac{{\sqrt {{\text{co}}{{{\text{s}}}^{2}}\theta \,{\text{t}}{{{\text{g}}}^{2}}\alpha + 4} }}{{2\sin \theta }}$

Тогда так как

${{\mathcal{P}}_{h}}(1) = \frac{{\cos \theta }}{{\cos \alpha }}\cos (\theta + \alpha ) < 0,\quad \frac{\pi }{2} < \alpha + \theta \leqslant \pi $

то многочлен ${{\mathcal{P}}_{h}}(z)$ отрицателен при $z \geqslant 1$. Это означает, что ветвь гиперболы (2.3), располагающаяся выше по скату, лежит ниже по скату соответствующей ветви гиперболы (3.6), и ОЗОР (2.3) неустойчива в описанном выше смысле.

Замечание. Неустойчивость рассматриваемых ОЗОР может быть показана проще. Для этого достаточно предъявить хотя бы одну точку границы ОЗОР, в которой данное выше определение устойчивости не выполняется. Этими точками могут являться, например, ${{A}_{ + }}$, S и ${{S}_{ - }}$ для ОЗОР ${{\Sigma }_{1}},$ ${{\Sigma }_{2}}$ и ${{\Sigma }_{3}}$ соответственно. Определяя значения величины $({{{\mathbf{f}}}_{\tau }},{\mathbf{n}}')$ в этих точках, находим

$\begin{gathered} {{\left. {({{{\mathbf{f}}}_{\tau }},{\mathbf{n}}')} \right|}_{{{{A}_{ + }}}}} = \frac{{\cos \theta \cos \alpha {{{\sin }}^{2}}\alpha \cos (\theta + \alpha )}}{{{{{\cos }}^{2}}\alpha - {{{\sin }}^{2}}\theta }} > 0,\quad 0 \leqslant \alpha + \theta < \frac{\pi }{2} \\ {{\left. {({{{\mathbf{f}}}_{\tau }},{\mathbf{n}}')} \right|}_{S}} = \frac{{{{{\sin }}^{2}}\alpha }}{2} > 0,\quad 0 < \alpha < \frac{\pi }{2} \\ {{\left. {({{{\mathbf{f}}}_{\tau }},{\mathbf{n}}')} \right|}_{{{{S}_{ - }}}}} = \frac{{\cos \theta \cos \alpha {{{\sin }}^{2}}\alpha \cos (\theta + \alpha )}}{{{{{\cos }}^{2}}\alpha - {{{\sin }}^{2}}\theta }} > 0,\quad \frac{\pi }{2} < \alpha + \theta \leqslant \pi \\ \end{gathered} $

Неравенство (3.2) не выполнятся, следовательно, обнаруженные ОЗОР неустойчивы в сформулированном выше смысле.

Заключение. Как оказалось (см., например, [21–25]) задача о неизолированных относительных равновесиях представляет интерес с точки зрения небесной механики. Так для малых небесных тел, сила притяжения на поверхности которых невелика, решение этой задачи позволяет обсудить возможности использования тех или иных частей поверхности тел для развертывания миссий. Так как зачастую поверхность малых небесных тел приближают многогранником, то изучаемую задачу можно рассматривать как частный случай общей задачи о равновесиях на поверхности гравитирующего многогранника. Для такой общей задачи естественно предположить, что сила притяжения, действующая в окрестности каждой небольшой грани постоянна, а ось вращения, вообще говоря, не параллельна линии действия этой силы. Такого рода задача представляет интерес для дальнейших исследований.

Исследование выполнено при поддержке Российского научного фонда (проект № 22-21-00297).

Список литературы

Burov A.A. On bifurcations of relative equilibria of a heavy bead sliding with dry friction on a rotating circle // Acta Mech. 2010. V. 212. № 3–4. P. 349–354. https://doi.org/10.1007/s00707-009-0265-1
Burov A.A., Shalimova E.S. On the motion of a heavy material point on a rotating sphere (dry friction case) // Regular Chaotic Dyn. 2015. V. 20. № 3. P. 225–233. https://doi.org/10.1134/S1560354715030028
Буров А.А., Шалимова Е.С. Бифуркация относительных равновесий тяжелой бусинки на вращающейся параболоидальной чаше с сухим трением // Изв. РАН. Механика твердого тела. 2016. № 4. С. 30–42.
Иванов А.П. Об устойчивости равновесия в системах с трением // ПММ. 2007. Т. 71. № 3. С. 427–438.
Иванов А.П. Бифуркации в системах с трением: основные модели и методы // Нелинейная динамика. 2009. Т. 5. № 4. С. 479–498. https://doi.org/10.20537/nd0904003
Иванов А.П. Основы теории систем с трением. Ижевск: РХД. 2011. 302 с.
Иванов А.П. О равновесии систем с сухим трением // ПММ. 2015. Т. 79. № 3. С. 317–333.
Leine R.I., van de Wouw N. Stability properties of equilibrium sets of nonlinear mechanical systems with dry friction and impact // Nonlin. Dyn. 2008. V. 51. № 4. P. 551–583. https://doi.org/10.1007/s11071-007-9244-z
Leine R.I., van de Wouw N. Stability and Convergence of Mechanical Systems with Unilateral Constraints. Berlin, Heidelberg: Springer, 2008. 236 p. https://doi.org/10.1007/978-3-540-76975-0
Leine R.I., van Campen D.H. Bifurcation phenomena in non-smooth dynamical systems // Eur. J. Mech. – A/Solids. 2006. V. 25. P. 595–616. https://doi.org/10.1016/j.euromechsol.2006.04.004
Leine R.I. Bifurcations of equilibria in non-smooth continuous systems // Phys. D: Nonlinear Phenom. 2006. V. 223. № 1. P. 121–137. https://doi.org/10.1016/j.physd.2006.08.021.10
Розе Н.В. Теоретическая механика. Ч. 1. М.; Л.: ГТТИ, 1932. 371 с.
Суслов Г.К. Теоретическая механика. М.; Л.: Гостехиздат, 1946. 655 с.
Пэнлеве П. Лекции о трении. М.: Гостехиздат, 1954. 316 с.
Журавлев В.Ф., Ишлинский А.Ю. Метод подобия в задачах динамики точки // Изв. РАН. Механика твердого тела. 1988. № 4. С. 6–12.
Андронов В.В., Журавлев В.Ф. Сухое трение в задачах механики. Серия Математика и механика. М.: Ижевск: Издательство “ИКИ”, 2010. 184 с.
Грудев А.И., Ишлинский А.Ю., Черноусько Ф.Л. О движении точки по вращающейся шероховатой плоскости // ПММ. 1989. Т. 53. № 3. С. 372–381.
Пожарицкий Г.К. Об устойчивости равновесий для систем с сухим трением // ПММ. 1962. Т. 26. № 1. С. 5–14.
Шалимова Е.С. О движении тяжелой точки по сфере, вращающейся вокруг не проходящей через ее центр вертикальной оси, при наличии сухого трения // Нелинейная динамика. 2016. Т. 12. № 3. С. 369–383. https://doi.org/10.20537/nd1603006
Буров А.А., Никонов В.И., Шалимова Е.С. Движение массивной точки по поверхности однородного шара со сферической полостью // ПММ. 2021. Т. 85. № 4. С. 528–543. https://doi.org/10.31857/S0032823521040032
Буров А.А., Косенко И.И., Шалимова Е.С. Об относительных равновесиях массивной точки на равномерно вращающемся астероиде // ДАН. 2017. № 3. С. 269–272. https://doi.org/10.7868/S0869565217210071
Guibout V., Scheeres D.J. Stability of surface motion on a rotating ellipsoid // Celest. Mech. Dyn. Astron. 2003. V. 87. P. 263–290. https://doi.org/10.1023/B:CELE.0000005720.09027.ee
Bellerose J., Girard A., Scheeres D.J. Dynamics and Control of Surface Exploration Robots on Asteroids // Optimization and Cooperative Control Strategies. Lecture Notes in Control and Information Sciences. Berlin, Heidelberg: Springer, 2009. V. 381. P. 135–150. https://doi.org/10.1007/978-3-540-88063-9_8
Scheeres D.J. Landslides and Mass shedding on spinning spheroidal asteroids // Icarus. 2015. V. 247. P. 1–17. https://doi.org/10.1016/j.icarus.2014.09.017
Jiang Y., Zhang Y., Baoyin H. Surface motion relative to the irregular celestial bodies // Planet. Space Sci. 2016. V. 127. P. 33–43. https://doi.org/10.1016/j.pss.2016.04.007

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика твердого тела

Архивы выпусков Информация о журнале Отправить рукопись в журнал