Известия РАН. Механика твердого тела, 2023, № 2, стр. 90-114
ЦИФРОВОЕ СРЕДСТВО ПРОИЗВОДСТВА – ПАКЕТ ДЛЯ ПРОЧНОСТНОГО ИНЖЕНЕРНОГО АНАЛИЗА КАК ИНСТРУМЕНТ ТРАНСФЕРА ФУНДАМЕНТАЛЬНЫХ НАУЧНЫХ РЕЗУЛЬТАТОВ В ПРОМЫШЛЕННОСТЬ НА ПРИМЕРЕ ПАКЕТА ФИДЕСИС И ТЕОРИИ МНОГОКРАТНОГО НАЛОЖЕНИЯ БОЛЬШИХ ДЕФОРМАЦИЙ
a Московский государственный университет им. М.В. Ломоносова
Москва, Россия
* E-mail: v.a.levin@mail.ru
Поступила в редакцию 18.04.2022
После доработки 26.04.2022
Принята к публикации 28.04.2022
- EDN: DFPXCA
- DOI: 10.31857/S0572329922600207
Аннотация
Отмечается, что значительно автоматизируются интеллектуальные операции при проектировании новых материалов (особенно метаматериалов, умных материалов, композитов), новых изделий, сооружений, технологических операций (включая аддитивное производство), и поэтому существенно изменилась роль специалистов в области механики деформируемого твердого тела (МДТТ). Появилась возможность полностью автоматизировать процесс решения дифференциальных уравнений, описывающих постановку задачи, включая связанные. Это осуществляется с использованием пакета для инженерного анализа (САЕ) или их комбинаций. Расчетчик, конструктор, исследователь задает конструкцию (ее СAD-модель) и внешние усилия (в терминах МДТТ граничные условия), описание материалов (в терминах МДТТ определяющие соотношения), и автоматически проводится расчет.
Отмечается, что востребованными остаются, в частности, формулировка механических и математических постановок для новых типов задач (преднагружение, междисциплинарные задачи); построение определяющих соотношений (моделей материалов) для новых материалов (композиты, метаматериалы, умные материалы) и модели с использованием дополнительных соотношений для их последующей реализации в САЕ. Также востребовано нахождение точных решений для валидации САЕ.
На примере теории многократного наложения больших деформаций и реализации этой теории и сопутствующих ей результатов в промышленном полнофункциональном пакете Фидесис демонстрируется возможность реализации результатов МДТТ для промышленности.
1. Введение. В условиях Индустрии 4.0 (и начинающегося перехода к Индустрии 5.0), когда автоматизируются не только физические, но и интеллектуальные операции при проектировании новых материалов (особенно метаматериалов, умных материалов, композитов), новых изделий, сооружений, технологических операций (включая аддитивное производство) существенно изменилась роль специалистов в области механики деформируемого твердого тела (МДТТ). Следует отметить, что МДТТ исторически была основой для проведения поверочных прочностных расчетов при проектировании новых изделий и принятия решения о ресурсе изделия на основе данных мониторинга в процессе эксплуатации.
Появилась возможность полностью автоматизировать процесс решения дифференциальных уравнений, описывающих постановку задачи, включая связанные. Эту автоматизацию выполняют с использованием пакета для инженерного анализа, который является цифровым средством производства [1, 2] (САЕ – Computer-aided engineering) или их комбинаций. И поэтому расчетчик, конструктор, исследователь задает конструкцию (ее СAD-модель) и внешние усилия (в терминах МДТТ граничные условия), описание материалов (в терминах МДТТ определяющие соотношения) и автоматически проводится расчет, если выбрана теории прочности, то определяются и “потенциальные зоны разрушения” при закритическом сценарии нагружения. То есть одна из основных функций расчетчика, исследователя автоматизирована (табл. 1).
Таблица 1.
Изменения при практическом решении задачи МДТТ и теории прочности после внедрения САЕ в расчетную практику
| До 1995 г. – до внедрения САЕ в расчетную практику | После 1995 – после внедрения САЕ в расчетную практику | |
|---|---|---|
| 1 | Механическая постановка задачи | Механическая постановка задачи (САD-модель, материал, внешние воздействия) |
| 2 | Математическая постановка задачи (в общем случае – система нелинейных дифференциальных уравнений в частных производных с граничными и начальными условиями) | Считается, что общая математическая постановка задачи есть внутри пакета и автоматически адаптируется под конкретную задачу |
| 3 | Решение системы дифференциальных уравнений (обычно одним из методов для получения приближенного решения с тем или иным обоснованием единственности и сходимости) | Расчет в пакете (обычно МКЭ), оценка инженерной сходимости средствами пакета [3–8] |
| 4 | Оценка НДС, на ее основе в соответствии с выбором критерия выделение “опасных областей” | Получение (в любом виде; обычно графическое, включая 3D) полей параметров НДС и практически автоматический вывод об “опасных областях” в соответствии с выбранными критериями |
Таким образом, произошли значительные изменения в востребованности результатов ученых-механиков как в фундаментальной, так и в прикладной науке (особенно с учетом того, что практически общепринятыми стали сквозное проектирование изделия и унификация методик проектирования, создание “цифровых двойников”, оцифровка имеющихся технических архивов и вовлечение их в моделирование):
1. С развитием промышленных пакетов для моделирования прочности механики перестали самостоятельно получать численное решение. Осталась формулировка изменений, которые вносятся в механическую модель (по сравнению со стандартной моделью), и разработка небольшого дополнения к пакету на исследовательском уровне, обычно на языке пакета (п. 4.1). Отметим, что это касается и случая использования компьютерной алгебры для решения исследовательских задач [9–13], например, при нахождении точных и приближенных аналитических решений [13–15]. Конечно, метод и алгоритм решения в этом случае выбирает исследователь.
2. С развитием использования промышленных пакетов при сквозном проектировании изделия и унификацией методик проектирования стали не востребованы работы ученых-механиков, за исключением “острых качественных решений” для описания проблемы и путей ее решения.
3. Остаются востребованными точные решения задач, в основном как верификационные задачи для тестирования промышленного ПО [14–23].
4. Остаются востребованными, на взгляд автора, классические направления МДТТ:
4.1. Построение определяющих соотношений (моделей материалов) для новых материалов (композиты, метаматериалы, умные материалы) и модели с использованием дополнительных соотношений, но и в этом случае моделирование поведения новых материалов проводится на основе промышленных пакетов.
4.2. Построение (формулировка) механических и математических постановок для новых типов задач (преднагружение, междисциплинарные задачи).
5. Экспериментальные работы, в основном для п. 4.
6. Разработка новых направлений использования МДТТ: механических моделей и механическая постановка задач (при необходимости) для систем машинного обучения на основе нейронных сетей при разработке систем искусственного интеллекта для профильных отраслей промышленности в части формирования синтетических “исходных” данных и предсказательной аналитики.
6.1. Разработка механических моделей и механическая постановка задач для систем промышленного интернета вещей для профильных отраслей промышленности, когда необходимо проводить моделирование с учетом информации, получаемой при измерении (и изменении) параметров в режиме реального времени.
6.2. Разработки в области вычислительных методов с учетом специфики задач МСС для решения прикладных задач механики сплошной среды, адаптированных под современные высокопроизводительные и облачные платформы.
6.3. Работы совместно с разработчиками САЕ для демократизации численного моделирования в задачах МСС для широкого круга пользователей-неспециалистов в данной области.
Отметим, хотя это не относится к формату статьи и направлению журнала, что такая ситуация приводит к изменению (и уменьшению) финансирования работ в области “привычного понимания МДТТ”, отнесения Механики к техническим наукам (разделу “Техника”) и т.д.
Приведем на примере реализацию теории многократного наложения больших деформаций [18–20] и сопутствующих результатов нелинейной механики в промышленном пакете Фидесис. Такая реализация позволяет расчетчикам и исследователям самостоятельно решать необходимые задачи без глубокого понимания и детальной проработки математической постановки задачи и механической в части записи уравнений равновесия (движения) граничных и начальных условий. Отметим, что часть результатов, приведенных в статье, получена самостоятельно независимыми исследователями на основе программной реализации научных разработок автора статьи и его коллег по научной группе в пакете Фидесис, созданном под руководством автора статьи. По мнению автора, реализация в САЕ фундаментальных результатов МДТТ является новым и востребованным направлением деятельности ученых – механиков, позволяющим переформатировать, сохранить и развить научные коллективы.
В работе даны некоторые примеры реализации в пакете Фидесис практически нужных научных разработок и результаты их использования для решения задач.
Теория наложения больших деформаций (рис. 1) [24–26], реализованная в пакете Фидесис, позволила рассмотреть и решить при больших деформациях принципиально новые классы статических и динамических задач, в которых дискретно (скачкообразно) или непрерывно в процессе нагружения изменяются границы (включая связность области, занимаемой телом, например образование концентраторов напряжений в нагруженном теле с большими деформациями полостей и включений), граничные условия, свойства части материала тела. При программной реализации в пакете Фидесис не использовался приближенный метод “убийства элементов” [1], а учитывалась необходимость совместного решения нескольких “не распадающихся” систем уравнений равновесия (движения).
Таблица 2.
Свойства горной породы и насыщающей жидкости
| Модуль Юнга | 1 ГПа |
| Коэффициент Пуассона | 0.25 |
| Когезия | 2 ГПа |
| Угол внутреннего трения | 20 градусы |
| Угол дилатансии | 0 градусы |
| Плотность породы | 2650 кг/м3 |
| Пористость | 0.25 |
| Проницаемость | 1 Дарси |
| Плотность жидкости | 900 кг/м3 |
| Обьемный модуль жидкости | 1 ГПа |
| Вязкость жидкости | 0.005 Па*с |
2. Моделирование процесса образования детали с помощью аддитивных технологий на примере лазерного спекания (ЛС). Постановка в рамках теории наложения больших деформаций реализована в пакете Фидесис [24–26]. Следуя терминологии и моделям данной теории, постановка краевой задачи о добавлении n-го элемента, форма которого задана в момент спекания с остальным телом, т.е. в координатах (n–1)-го промежуточного состояния, запишется следующим образом:
$\Psi _{{0,n}}^{e} = {{\Psi }_{{0,n - 1}}} \cdot {{\Psi }_{{n - 1,n}}} \cdot \Psi _{T}^{{ - 1}} \cdot \Psi _{P}^{{ - 1}}$ – мультипликативное разложение аффинора полных упругих деформаций в виде произведения аффинора накопленных деформаций (за предыдущие шаги наращивания) и аффинора дополнительных деформаций (вызванного добавлением текущего n-го элемента), а также аффиноров внутренних термических и пластических деформаций;
${{\Psi }_{T}} = \exp (\alpha {{T}^{n}})I$ – аффинор температурных деформаций, здесь α – коэффициент линейного теплового расширения, Tn – температура на n-м шаге, I – единичный тензор.
${{\Psi }_{{0,n - 1}}} = {{\left( {I - \sum\limits_{i = k}^{n - 1} {\mathop \nabla \limits^{n - 1} } {{u}_{i}}} \right)}^{{ - 1}}} = {{\left( {I - \mathop \nabla \limits^{n - 1} \sum\limits_{i = k}^{n - 1} {{{u}_{i}}} } \right)}^{{ - 1}}} = {{(I - \mathop \nabla \limits^{n - 1} U)}^{{ - 1}}}$ – представление аффинора накопленных деформаций через вектор накопленных перемещений в координатном базисе текущего (n–1)-го состояния. Здесь, как и ранее, k – номер шага, на котором элемент, содержащий текущую Лагранжеву точку, возник. В частности, для вновь добавляемого n-го элемента данный аффинор будет единичным тензором;
${{\Psi }_{{n - 1,n}}} = I + \mathop \nabla \limits^{n - 1} {{u}_{n}}$ – представление аффинора дополнительных деформаций через вектор дополнительных перемещений в координатном базисе текущего (n–1)-го состояния.Приведем для наглядности результат расчета для случая послойного изготовления изделия (крепления автомобильного руля). Материал изделия – углеродистая сталь. Температура основания 100°C, температура присоединяемого слоя 1100°C. Температура, до которой остывает слой, прежде чем к нему присоединяется следующий слой – 1000°C. Количество слоев – 121.
На рис. 2 показано распределение истинных остаточных напряжений по Мизесу в изделии после его изготовления.
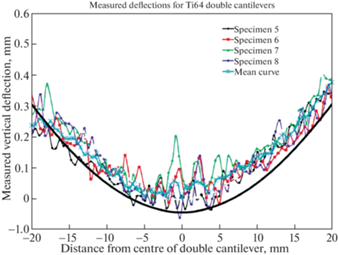
Приведем описание натурного эксперимента [27], с которым проводилось сравнение при численном моделировании послойного изготовления изделия аддитивного производства. Изделие в форме бруса размером (45 мм ⋅ 6 мм ⋅ 5 мм) с вырезами печатается на цилиндрической платформе радиусом 50 мм и высотой 20 мм. Форма вертикального сечения бруса и платформы представлена на рис. 3. Температура порошка для печати TI-6AL-4V считается равной 26°С. На основании платформы в процессе печати поддерживается постоянная температура 150°С. Мощность лазера составила 200 Вт, время воздействия лазера 40 мкс, толщина слоя печати 60 мкм. После печати изделия медленно выполняется горизонтальный разрез в его верхней части. В результате накопленных остаточных напряжений в изделии происходит вертикальный изгиб верхней надрезанной части изделия. Измеренные перемещения верхней грани изделия в процессе эксперимента [27] представлены на рис. 4.
Рис. 2.
Распределение истинных остаточных напряжений по Мизесу в изделии аддитивного производства после его изготовления.
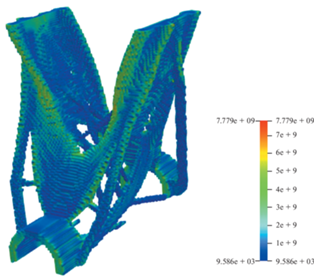
Численное моделирование проводилось в плоско-деформированном состоянии на сетке и геометрии, представленных на рис. 2. Для расчета использовались 10 слоев изготовления изделия. При моделировании несколько слоев печати объединялись в один слой изготовления, которому передавалось количество тепла, равное передаваемому лазером при печати всех слоев внутри слоя изготовления. Расчет распределения температуры в слое проводился путем решения нелинейного уравнения теплопроводности с параметрами модели (коэффициент теплопроводности, коэффициент теплового расширения и другие), зависящими от температуры. После расчета распределения температуры в слое полученные температурные деформации использовались как начальные деформации при добавлении данного слоя к телу с накопленными деформациями на предыдущих шагах печати.
На рис. 5 показаны вычисленные вертикальные перемещения в сечении изделия аддитивного производства после выполнения надреза.
Рис. 4.
Вертикальные перемещения верхней грани изделия по результатам натурного эксперимента [27] и расчета в CAE Fidesys (сплошная линия).
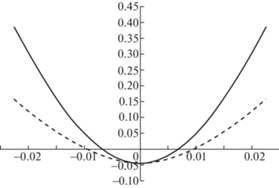
На рис. 6 приведены вычисленные вертикальные перемещения верхней грани изделия при малых деформациях (пунктирная линия) и при конечных деформациях (сплошная линия).
Рис. 5.
Вычисленные вертикальные перемещения в сечении изделия аддитивного производства после выполнения надреза.

Полученные при численном моделировании результаты хорошо согласуются с результатами натурного эксперимента, что подтверждает корректность предложенного в статье подхода к анализу напряженно-деформированного состояния и расчету остаточных напряжений в изделии аддитивного производства, изготовленного методом селективного лазерного спекания, на основе теории многократного наложения конечных деформаций.
3. Моделирование развития больших пластических деформаций во вращающемся диске [28]. Полученный механический эффект – локализованная утяжка диска, характеризующаяся развитием нелинейной упругопластической неустойчивости. Определение разрушающих частот вращения и остаточных удлинений дисков газотурбинных двигателей (ГТД) является обязательным требованием при их проектировании и сертификации. С этой целью проводятся натурные разгонные испытания дисков или роторов. Ниже приведены результаты моделирования с использованием пакета Фидесис процесса раскрутки модельного диска под действием постепенно увеличивающейся центробежной нагрузки с учетом физической и геометрической нелинейностей [28].
Моделирование выполнялось как квазистатический пошаговый расчет диска при увеличении внешней нагрузки на расчетную модель. Учитывалось, что для большинства конструкционных сплавов, используемых при изготовлении дисков ГТД, данный процесс сопровождается развитием больших пластических деформаций вплоть до разрушения. Не приводя математическую постановку задачи (она есть в пакете Фидесис, см. п. 2 таблицы 1), отметим, что для связи напряжений с деформациями используются определяющие соотношения гиперупругопластичности. Используется классический критерий пластичности Губера–Мизеса, записанный в терминах напряжений Кирхгоффа с мультилинейной функцией изотропного упрочнения. Замыкающими уравнениями являются условия Куна–Таккера, из которых определяется множитель совместности.
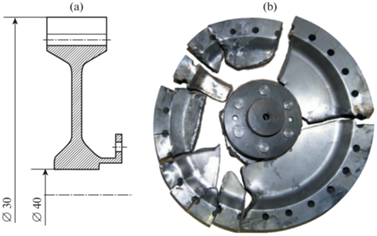
Сравнение с экспериментом (валидация). Объектами экспериментального исследования являлись две заготовки диска, отрезанные от прутка диаметром 330 мм из стали ЭИ961-ш. Из первой заготовки был изготовлен модельный диск для разгонных испытаний (рис. 7, а), а из второй – десять цилиндрических образцов для испытаний на разрыв для построения функции упрочнения.
Рис. 6.
Вычисленные вертикальные перемещения верхней грани изделия (мм) при малых деформациях (пунктирная линия) и при конечных деформациях (сплошная линия) в зависимости от расстояния до центра балки (м).
Разгонные испытания диска проводились при нормальной температуре в один этап до разрушения на фрагменты. В процессе проведения испытания выполнялись записи частоты вращения и удлинения наружного диаметра диска. Объект разрушился при частоте вращения 24 282 об/мин, при этом удлинение наружного диаметра диска в момент разрушения составило 4.4 мм. На рис. 7,b показан разрушившийся модельный диск. Первичное разрушение произошло по цилиндрическому сечению на радиусе R = 55 мм.
Оценка несущей способности диска по теории предельного равновесия показала, что разрушение диска наступает в цилиндрическом сечении на радиусе R = 56 мм при частоте вращения 23 100 об/мин, что удовлетворительно совпадает с результатами испытаний.
Результаты моделирования. Расчетная модель диска представляет собой сектор с углом в основании 90° (рис. 8). По меридиональным сечениям сектора задано граничное условие в виде равенства нулю окружных перемещений. К каждому узлу расчетной модели прикладывалась центробежная сила, пропорциональная квадрату частоты вращения и текущему радиусу, $\vec {f} = \rho {{\omega }^{2}}\vec {r}$. Для построения функции упрочнения было выполнено перестроение условной кривой деформирования в истинную в соответствии с допущением о постоянстве объема рабочей части образца до и после пластического деформирования.
Одним из характерных наблюдаемых в натурных экспериментах явлений, возникающих непосредственно перед разрушением диска, является локализованная “утяжка” диска, являющаяся аналогом “шейки” в образце и характеризующаяся развитием нелинейной упругопластической неустойчивости.
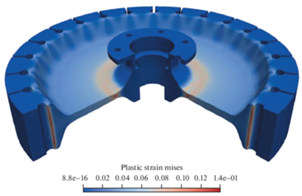
Результаты расчета удлинений наружного диаметра модельного диска и их сопоставление с экспериментальными данными представлены на рис. 9. Видно, что кривые согласуются между собой. Начиная с частоты вращения 20 000 об/мин происходит существенное изменение скорости роста удлинений модельного диска, а при приближении к разрушающей частоте вращения зависимость близка к вертикальной линии. При частоте вращения ω = 24 375 об/мин, близкой к разрушению, максимальные пластические деформации локализуются на радиусе диска R = 50–60 мм с образованием “утяжки” (рис. 10 и 11), что согласуется с зоной разрушения модельного диска.
Рис. 9.
Расчетная и экспериментальная кривые удлинения наружного диаметра модельного диска в зависимости от частоты вращения. Где 1 – результаты расчета, 2 – результаты эксперимента.
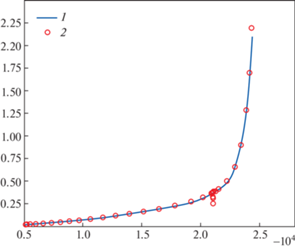
Рис. 10.
Распределение осевых перемещений в модельном диске при частоте вращения ω = 24 375 об/мин (размерность на шкале – отн. ед.).
4. Метаматериалы (на примере NTE-метаматериалов). Наукоемкие разработки [29, 30], реализованные в модуле “Композит” пакета Фидесис, позволили провести моделирование для оценки механических характеристик метаматериалов (композиционных материалов-конструкций), осуществить подбор геометрических параметров ячейки, чтобы добиться как отрицательного эффективного коэффициента теплового расширения, достаточно большого по модулю, так и близкого к нулю эффективного коэффициента [29, 30].
При моделировании учитывалось, что свойства таких материалов определяются в первую очередь их геометрической (ячеистой) микроструктурой, а не свойствами входящих в их состав компонент [31, 32]. Ниже в качестве примера приведены результаты для метаматериалов с отрицательным коэффициентом теплового расширения [33–35]. По международной терминологии такие метаматериалы называются NTE-метаматериалы (negative thermal expansion). NTE-метаматериалы при нагревании сжимаются. На взгляд автора, наибольший практический интерес представляют метаматериалы, которые при нагревании и охлаждении не меняют своих размеров. В настоящее время такие материалы, как правило, изготавливаются с помощью 3D-печати [36] из двух и более компонент с различными механическими и тепловыми свойствами: более жесткие с меньшим коэффициентом теплового расширения и более мягкие с большим коэффициентом. Следует отметить, что у компонент коэффициенты теплового расширения положительны.
Модуль “Композит” пакета Фидесис позволяет проводить оценку эффективных тепловых характеристик NTE-метаматериала на основе численного решения краевой задачи термоупругости на ячейке периодичности с заданием периодических граничных условий с осреднением по объему. Пользователь пакета в качестве результата получает эффективные коэффициенты теплового расширения.
Для построенных ячеек проведен ряд численных экспериментов [29, 30], в которых показано влияние геометрических параметров модели на коэффициент теплового расширения метаматериала. Свойства компонент при этом задавались модулем Юнга, коэффициентом Пуассона и коэффициентом теплового расширения.
В ходе исследования рассматривается модель ячейки из двух материалов: меди (жесткой, но с меньшим коэффициентом теплового расширения) и полимера (мягкого, но с большим коэффициентом теплового расширения) с большим количеством пустот. На рис. 12 приведена структура ячейки такого метаматериала. Черным цветом изображена медь (более твердая компонента с меньшим коэффициентом теплового расширения), серым – полимер (более мягкая компонента с большим коэффициентом теплового расширения).
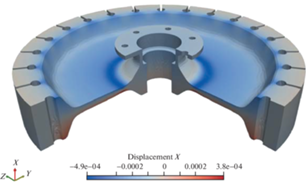
Рис. 11.
Распределение осевых перемещений в модельном диске при частоте вращения ω = 24 375 об/мин (размерность на шкале – м).
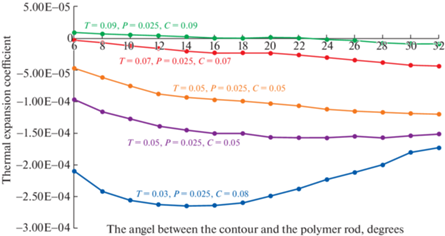
Для этой модели метаматериала построены графики зависимости эффективного коэффициента теплового расширения от геометрических параметров – угла наклона полимерных стержней к медному контуру. Эти расчеты произведены для разных комбинаций параметров исходной модели: толщины контура ячейки, толщины полимерного стержня и толщины диагональных медных стержней. Также произведен расчет на устойчивость данной ячейки к тепловым деформациям. По результатам которого был определен температурный диапазон, в пределах которого эта структура применима. Для модели, состоящей из двух материалов – меди и полимера, были построены графики зависимости коэффициента теплового расширения от угла α при определенной толщине рамки. Анализ зависимостей этих коэффициентов от параметров модели показал следующие результаты. Во-первых, существует возможность подбора параметров ячейки, при которых метаматериал имеет нулевой эффективный коэффициент теплового расширения – то есть при изменении температуры сохраняет свои размеры. Во-вторых, при определенных комбинациях параметров эффективный коэффициент – отрицательный, а модуль его достаточно большой (равен коэффициенту теплового расширения полимера). На рис. 13 представлена зависимость коэффициента теплового расширения (единица измерения K–1) от угла наклона между медным контуром и полимерным стержнем. На графике введены следующие обозначения: толщина медного контура ячейки – T, толщина полимерного стержня – Р, толщина медной диагонали – С. Размеры приведены в отношении к общему размеру ячейки. Проводились численные исследования, в которых толщина контура варьировалась в пределах от 0.03 до 0.09, толщина полимера – от 0.025 до 0.075, толщина диагонали – от 0.05 до 0.09. В расчетах задавались следующие свойства меди: модуль Юнга 1.1 × 105 МПа, коэффициент Пуассона 0.35, коэффициент теплового расширения 1.67 × 10–5 К–1. Свойства полимера: модуль Юнга 104 МПа, коэффициент Пуассона 0.45, коэффициент теплового расширения 1.5 × 10–4 К–1.
Результаты расчетов показывают, что подбор геометрических параметров ячейки указанной формы позволяет добиться как отрицательного эффективного коэффициента теплового расширения, достаточно большого по модулю, так и близкого к нулю эффективного коэффициента.
5. Оценка метанообильности угольного пласта на основе анализа НДС в этом пласте вблизи штрека. Оценка деформаций угольного пласта в зависимости от давления метана (с учетом изменения проницаемости) внутри него позволяет расширить возможности геомеханического моделирования [37] и уточнить рекомендации к параметрам горнопроходческих работ. Моделирование и расчет параметров НДС в рамках модели осуществляется в 2 этапа.
На первом этапе находятся эффективные механические характеристики [38]. Далее на основе найденных эффективных механических параметров в подобластях решается геомеханическая задача о нахождении НДС во всей области. После этого на основе рассчитанных глобальных напряжений решаются серии задач о нагружении матрицы и трещин в каждой из подобластей для определения деформаций внутри матрицы материала блоков и раскрытий трещин между ними, соответствующих текущему локальному НДС в окрестности конкретной грани блока. Рассчитанные деформации матрицы и раскрытия трещин используются при вычислении проницаемостей угольного пласта на основе подходов [39, 40]. Рассчитанные проницаемости (матрицы и межблочных трещин) передаются в газодинамический симулятор на основе модели двойной проницаемости [41, 42], который определяет поле давлений метана во всей модели. Затем на основе рассчитанных давлений в матрице и трещинах определяется среднее давление в эффективном континууме и повторяется расчет НДС и параметров геомеханической модели.
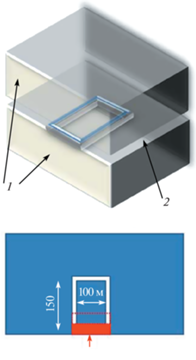
Пример расчета проницаемости для очистного забоя в угольном пласте. Данные о геометрии и свойствах модели очистного забоя приведены на рис. 14.
Рис. 13.
Зависимость коэффициента температурного расширения (K–1) от угла наклона между медным контуром и полимерным стержнем.
Параметры модели. Размер куба 500 на 500 метров. Геометрия штрекового канала – периметр прямоугольника размерами 100 на 150 метров. Внутреннее сечение штрека: 4 на 4 метра. Количество ячеек 27 ⋅ 104 ⋅ 1. Свойства газодинамической модели: проницаемость куба – 10 мД, давление в толщи угольного пласта – 200 атм, давление в штреке – 1 атм. Реализованы открытые граничные условия с постоянным давлением 200 атм и индексом продуктивности 340.56 м3/сутки/атм (поверхностные условия). Свойства геомеханической модели: коэффициент Пуассона – 0.4; модуль Юнга – 20 МПа. Продолжительность расчета 480 минут с шагом 1 минута. При расчетах на основе газодинамической модели использовался модуль ECLIPSE Compositional ESMB3. На рис. 15 приведено распределение давления на первом шаге расчетов.
Рис. 14.
Геометрия и свойства модели очистного забоя. На верхнем рисунке изображен вид на угольный пласт сверху, где 1 – аргиллит (E = 1000 МПа, µ = 500 МПа, v = 0.25, P = 2), 2 – угольный пласт (Толщина – 4 м, E = = 20–200 МПа, µ = 10 МПа, v = 0.4, P = 1.3). На нижнем рисунке изображен очистной забой с варьирующейся шириной от 4 до 50 м.
Результаты расчетов параметров газового потока приведены на рис. 16.
Графики свидетельствуют о том, что временной интервал истечения газа из зоны разгрузки в очистной забой равен примерно одному часу.
Также была решена задача о зависимости метанообильности от расстояния от штрека до угольного пласта [37, 43]. Использовалась механическая модель, приведенная на рис. 17.
Рис. 16.
Графики выделения метана в угольном пласте при различных сопряжениях. 1_step – без сопряжения. 40_steps – 60 шагов сопряжения газодинамического и геомеханического симуляторов, каждый 12 расчетный шаг газодинамического симулятора. 120_steps – 120 шагов сопряжения, 240_steps – 240 шагов сопряжения.
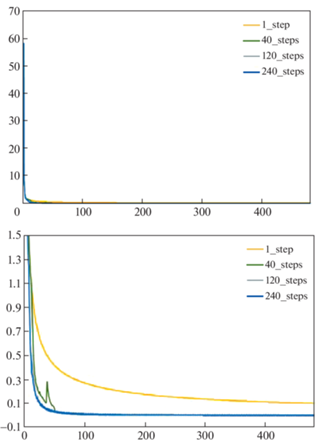
При расчетах использовались следующие значения параметров проницаемости пород (коэффициенты фильтрации Кf и проницаемости Кp и абсолютная проницаемость К):
1. Уголь. Кf = 1.2 × 10–5 м/с, Кp = 1.2 × 10–12 м2 или К = 10 мД (миллидарси)
2. Вмещающие породы: Кf = 1.2 × 10–3 м/с, Кp = 1.2 × 10–10 м2 или К = 300 мД.
Модели были просчитаны при давлении на верхнюю грань порядка 200 МПа (это соответствует глубине около 1000 м). В пласте угля начальное давление газа было принято равным 1.5 МПа (15 атм). Во вмещающей породе – 0.1 МПа (1 атм).
Для расчета была построена сопряженная трехслойная газодинамическая и геомеханическая модель угольного пласта с изменяющейся проницаемостью угля в зависимости от геомеханических напряжений и пластового давления газа.
Были произведены расчеты для четырех положений штрека относительно угольного пласта: 180 м, 80 м, 60 м и 20 м. На основе результатов расчетов был построен график зависимости метановыделения от расстояния до пласта (рис. 18). Отметим его близость к экспериментальному графику из работы [44] (рис. 19).
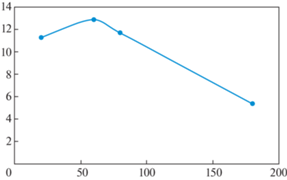
Рис. 17.
Механическая модель угольного месторождения, использованная при расчете метанообильности. Где 1 – аргиллит (E = 1000 МПа, µ = 500 МПа, v = 0.25), 2 – угольный пласт (Толщина – 4 м, E = 20 МПа, µ = 10 МПа, v = 0.4), 3 – грудь забоя, 4 – проходческий штрек 4 ⋅ 4 м в центре модели.
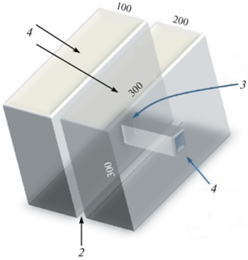
Рис. 18.
Изменение интенсивности выделения метана по мере удаления от угольного пласта. Результаты численного моделирования.
6. Расчет НДС вблизи скважины в пласте горных пород на основе модели пороупругопластичности. Верификация численной пороупругопластической модели CAE Fidesys основана на аналитическом решении Карева [45]. В [45] рассматривается распределение напряжений в окрестности вертикальной скважины радиуса RW, пробуренной на глубину $h$. Пласт считается изотропным, однородным.
Исходное напряженное состояние пласта рассматривается как состояние всестороннего сжатия горным давлением $Q = - {{\gamma }}h$, где γ – средний удельный вес вышележащих пород.
Предполагается, что коэффициент Био равен единице, ${{p}_{0}}$ – начальное пластовое давление фильтрующейся жидкости. В [45] считается, что фильтрация жидкости отсутствует, поэтому на скважине поровое давление ${{p}_{W}}$ совпадает с ${{p}_{0}}$, предполагается, что в качестве критерия пластичности используется критерий Кулона–Мора с параметрами ${{\tau }_{s}}$ – коэффициент сцепления, $\rho $ – угол внутреннего трения породы.
В пакете Фидесис используется критерий пластичности Друкера–Прагера. Поверхность Друкера–Прагера является сглаженной поверхностью Кулона–Мора (в CAE Fidesys поверхность Друкера–Прагера вписана в шестигранный конус Кулона–Мора). На основании исследования [46] предполагаем, что отличия в результатах для критериев Друкера–Прагера и Кулона–Мора должны быть незначительны.
Для сравнения результатов аналитического решения и решения в пакете CAE Fidesys использовались параметры модели: ${{\tau }_{s}} = 8$ МПа, $\rho = 30^\circ $, $Q = - 80$ МПа, ${{p}_{0}} = {{p}_{W}}$ = = 40 МПа.
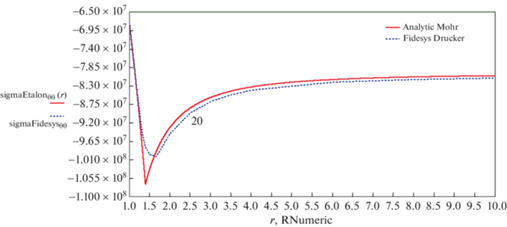
Графики зависимостей напряжений ${{\sigma }_{{rr}}}\left( R \right)$, ${{\sigma }_{{\theta \theta }}}\left( R \right)$ приведены на рис. 20, 21.
Рис. 19.
Изменение интенсивности выделения метана по мере удаления от угольного пласта. Экспериментальные данные [44].
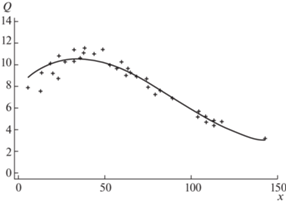
Рис. 20.
${{\sigma }_{{rr}}}\left( r \right)$ – аналитическое решение с критерием пластичности Кулона–Мора и численное решение CAE Fidesys с критерием пластичности Друкера–Прагера.
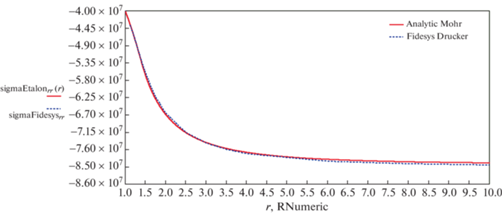
Из рис. 20, 21 следует, что результаты расчета с использованием CAE Fidesys хорошо согласуются с аналитическим решением, за исключением области в окрестности радиуса пластической зоны. Данные отличия являются следствием использования различных критериев пластичности в аналитическом решении и CAE Fidesys.
CAE Fidesys предлагает широкие возможности решения различных задач геомеханики, учитывающих уравнение пьезопроводности (закон Дарси) и упругопластическое течение с критерием пластичности Друкера–Прагера. Так, в CAE Fidesys выполнено моделирование образования и развития полос локализации пластических деформаций (полос Людерса) для модели нагружения однородной изотропной квадратной области со стороной 20 м, в центре которой расположено круговое отверстие радиуса 1 м. В силу симметрии смоделирована четверть пластины. Материал имеет следующие безразмерные параметры: модуль Юнга 109 Па, коэффициент Пуассона 0.25, плотность 2650, когезия 2 × 106 Па, угол внутреннего трения 0.349, угол дилатансии 0, коэффициент Био 0.8, пористость 0.25, проницаемость 10–12 м2, вязкость жидкости 0.005, объемный модуль упругости жидкости 109 Па.
К модели приложены следующие граничные условия: перемещения ${{\left. {{{u}_{x}}} \right|}_{{y = 0}}} = 0$, ${{\left. {{{u}_{y}}} \right|}_{{x = 0}}}$ = 0, давление ${{\left. p \right|}_{{x = 10}}} = 28$ × 106, ${{\left. p \right|}_{{y = 10}}} = 32$ × 106, давление 25 × ${{10}^{6}} - 166.67\,t$ на контуре отверстия, поровое давление $f{{{\text{|}}}_{{x = 10}}} = 25$ × 106e6, $f{{{\text{|}}}_{{y = 10}}} = 25$ × 106e6, поровое давление на контуре отверстия 25 × ${{10}^{6}} - 166.67\,t$.
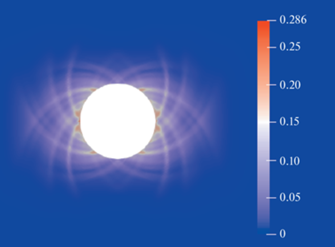
В результате динамического расчета модели в пакете CAE Fidesys получены следующие результаты: вблизи контура отверстия образуются полосы локализации пластических деформаций (полосы Людерса), к моменту времени t = 19919 с их локализация принимает вид, представленный на рис. 22.
Рис. 21.
${{\sigma }_{{\theta \theta }}}\left( r \right)$ – аналитическое решение с критерием пластичности Кулона–Мора и численное решение CAE Fidesys с критерием пластичности Друкера–Прагера.
Отметим, что проблема верификации и особенно валидации пакетов для прочностного инженерного анализа при обосновании их использования для решения нелинейных задач, особенно для задач о поэтапном нагружении тел при конечных деформациях, очень важна, и наличие точных решений позволяет ее частично решить [13–23, 47–52].
7. Многофазная пьезоупругопластическая модель скважины. Большая часть мировых запасов нефти и газа находятся в слабо консолидированных коллекторах, где, может происходить вынос песка (пескопроявление) и последующая эрозия [53]. Эрозия пласта может привести к неустойчивости ствола скважины и обрушению некоторых участков скважины. Поэтому необходима математическая модель, способная предсказать начало выноса песка и его объем.
Используется связанная модель пороупругопластичности. Критерием начала пескопроявления в рамках этой модели является возникновение областей локализации пластических деформаций. Эта модель позволяет проанализировать влияние напряжений и изменения давления на пескопроявление.
Результаты расчетов в рамках этой модели приведены на рис. 23, 24. Исходные данные для расчетов приведены в табл. 2, 3. На рис. 23 справа показана форма полости после эрозии по данным натурного эксперимента. Сопоставление данных о локализации пластических деформаций, приведенных на рис. 23 слева, с данными натурного эксперимента показывает, что зоны локализации пластических деформаций, определенные в результате расчета, расположены в тех областях, где в соответствии с данными натурного эксперимента происходит эрозия.
Рис. 23.
Полость после эрозии (справа) и локализация пластических деформаций, численный эксперимент (слева) под действием анизотропного поля напряжений.

Таблица 3.
Граничные и начальные условия
| Минимальное горизонтальное напряжение | 25 МПа |
| Максимальное горизонтальное напряжение | 32 МПа |
| Вертикальное напряжение | 35 МПа |
| Начальное поровое давление | 25 МПа |
| Падение порового давления на скважине | 0.6 МПа/ч |
Таблица 4.
Свойства породы
| Материал | Кероген | Песчаник |
|---|---|---|
| Модуль Юнга | 5000 Ма | 80 000 МПа |
| Коэффициент Пуассона | 0.3 | 0.1 |
| Когезия | 0.5 МПа | 3 МПа |
| Угол внутреннего трения | 30 | 30 |
| Угол дилатансии | 30 | 30 |
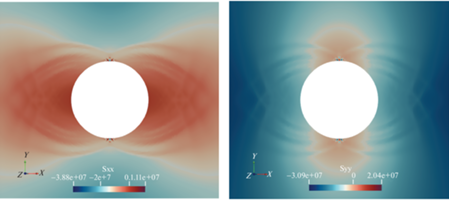
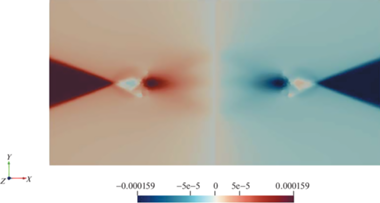
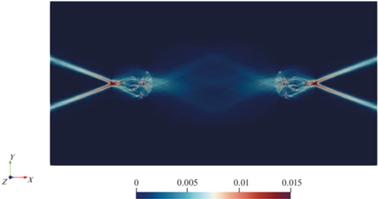
8. Пример локализации пластических деформаций в горной породе с включениями. Исследуется НДС горной породы (песчаника) с включениями из керогена. Задача решается для случая плоской деформации. Материалы считаются упругопластическими. Механические свойства материалов приведены в табл. 4 . Форма области, в которой решается задача, показана на рис. 25. На рис. 26, 27 показаны результаты расчетов. Рис. 27 показывает наличие полос скольжения (областей локализации пластических деформаций), при этом следует отметить существенный эффект взаимовлияния включений. Граничные условия: боковые грани свободны, растяжение по оси Oy.
Рис. 27.
Локализация пластических деформаций под действием растягивающих усилий, численный эксперимент.
9. Заключение. Автор отмечает, что все приведенные примеры показывают возможность ученого-механика, инженера-расчетчика проводить сложные расчеты для нелинейных задач без необходимости самостоятельно выписывать систему уравнений, описывающую постановку задачи, и решать ее. Это подтверждает значительное (возможно, кардинальное) изменение в работе специалистов и требования к их навыкам. Такие изменения происходят практически во всех отраслях научно-технической деятельности в рамках Индустрии 4.0.
Список литературы
Каплун А.Б., Морозов Е.М., Олферьева М.А. Ansys в руках инженера. М.: Едиториал УРСС, 2004. 272 с.
Морозов Е.М., Левин В.А., Вершинин А.В. Прочностной анализ. Фидесис в руках инженера. М.: URRS, 2015. 400 с.
Zienkiewicz O.C., Taylor R.L. The Finite Element Method. V. 1. The Basis. L.: Butterworth–Heinemann, 2000. 707 p.
Zienkiewicz O.C., Taylor R.L. The Finite Element Method. V. 2. Solid Mechanics. L.: Butterworth–Heinemann, 2000. 479 p.
Zienkiewicz O.C., Taylor R.L., Sherwin S.J., Peiró J. On discontinuous Galerkin methods // Int. J. Numer. Meth. Eng. 2003. V. 58. № 8. P. 1119–1148. https://doi.org/10.1002/nme.884
Zienkiewicz O.C., Taylor R.L. The Finite Element Method for Solid and Structural Mechanics. Amsterdam: Elsevier, 2005.
Zienkiewicz O.C., Taylor R.L., Zhu J.Z. The Finite Element Method: Its Basis and Fundamentals. Amsterdam: Elsevier, 2005.
Левин В.А., Вершинин А.В. Нелинейная вычислительная механика прочности. 5-томный цикл монографий. Модели и методы. Численные методы. Реализация на высокопроизводительных вычислительных системах. М.: Физматлит, 2015. Т. 2. 543 с.
Климов Д.М., Руденко В.М. Методы компьютерной алгебры в задачах механики. М.: Наука, 1989. 215 с.
Левин В.А. К использованию метода последовательных приближений в задачах теории наложения конечных деформаций // Прикладная механика. 1987. Т. 23. № 5. С. 66–71.
Левин В.А., Зингерман К.М., Санченко Е.П. Об использовании численно-аналитических вычислений на ЭВМ для оценки эффектов третьего порядка в задаче об образовании отверстий в упругом теле с начальными деформациями // ТПИ. Деп. в ВИНИТИ, 1987. 10 с. № 7993–В87.
Левин В.А., Зингерман К.М. Об одной возможности использования методов аналитических вычислений на ЭВМ в приложении к задачам теории наложения конечных деформаций // Механика эластомеров. Межвуз. сб. науч. тр. Краснодар: КПИ, 1987. С. 28–35.
Левин В.А., Зингерман К.М. Нелинейная вычислительная механика прочности. 5-томный цикл монографий. Модели и методы. Точные и приближенные аналитические решения при конечных деформациях и их наложении. М.: Физматлит, 2016. Т. 3. 393 с.
Levin V.A., Zubov L.M., Zingerman K.M. Influence of the prestressed layer on the nonlinear flexure of a rectangular beam made of compressible material // Dokl. Phys. 2015. V. 60. P. 167–170. https://doi.org/10.1134/S1028335815040023
Levin V.A., Zubov L.M., Zingerman K.M. Multiple joined prestressed orthotropic layers under large strains // Int. J. Eng Sci. 2018. V. 133. 47–59. https://doi.org/10.1016/j.ijengsci.2018.08.008
Rivlin R.S. A note on the torsion of an incompressible, highly-elastic cylinder // Proc. Cambrige Phys. Soc. 1949. V. 45. № 3. P. 485–487. https://doi.org/10.1017/S0305004100025135
Rivlin R.S. Large elastic deformations of isotropic materials. IV. Further developments of the general theory // Philos. Trans. R. Soc. Lond. Ser. A. Math. Phys. Sci. 1948. V. 241. № 835. P. 379–397. https://doi.org/10.1098/rsta.1948.0024
Rivlin R.S. Large elastic deformations of isotropic materials. V. The problem of flexture // Proc. Royal Soc. Ser A. Math Phys Sci. 1949. V. 195. № 1043. P. 463–473. https://doi.org/10.1098/rspa.1949.0004
Rivlin R.S. Large elastic deformations of isotropic materials. VI. Further results in the theory torsion, shear and flexture // Philos. Trans. Royal Soc. Ser A. Math. Phys. Sci. 1949. V. 242. № 845. P. 173–195. https://doi.org/10.1098/rsta.1949.0009
Ericksen J.L. Deformations possible in every isotropic, incompressible, perfectly elastic body // ZAMP. 1954. V. 5. P. 466–489. https://doi.org/10.1007/BF01601214
Green A.E., Shield R.T. Finite extension and torsion of cylinders // Philos. Trans. Royal Soc. Ser A. Math. Phys. Sci. 1951. V. 224. № 846. P. 47–86. https://doi.org/10.1098/rsta.1951.0015
Levin V.A., Podladchikov Y.Y., Zingerman K.M. An exact solution to the Lame problem for a hollow sphere for new types of nonlinear elastic materials in the case of large deformations // Eur. J. Mech. A/Solids. 2021. V. 90. https: //doi.org/.https://doi.org/10.1016/j.euromechsol.2021.104345
Levin V.A., Zubov L.M., Zingerman K.M. An exact solution to the problem of biaxial loading of a micropolar elastic plate made by joining two prestrained arc-shaped layers under large strains // Eur. J. Mech. A/Solids. 2021. V. 88. https: //doi.org/https://doi.org/10.1016/j.euromechsol.2021.10423
Левин В.А. Нелинейная вычислительная механика прочности. 5-томный цикл монографий. Модели и методы. Образование и развитие дефектов (предисловие академика Г.И. Марчука) М.: Физматлит, 2015. Т. 1. 454 с.
Левин В. А. Многократное наложение больших деформаций в упругих и вязкоупругих телах (предисловие академика Л.И. Седова). М.: Наука, Физматлит, 1999. 223 с.
Левин В.А. Концентрация напряжений околокругового в момент образования отверстия в теле из вязкоупругого материала // Док. ак. наук СССР. 1988. Т. 299. № 5. С. 1079–1082.
Tripathy S., Chin C., London T., Ankalkhope U., and Oancea V. Process Modeling and Validation of Powder Bed Metal Additive Manufacturing // Proc. of NAFEMS World Congress, Stockholm, 2017. URL: https://www.researchgate.net/publication/319173249
Абрамов С.М., Амелькин С.А., Клюев Л.В., Крапивин К.Ю., Ножницкий Ю.А., Серветник А.Н., Чичковский А.А. Использование программы Фидесис для моделирования развития больших пластических деформаций во вращающемся диске // Чебышев. сб. 2017. Т. 18. № 3. С. 15–27. https://doi.org/10.22405/2226-8383-2017-18-3-15-27
Яковлев М.Я., Танасевич П.С., Вершинин А.В., Левин В.А. Численный анализ эффективных теплофизических свойств и устойчивости метаматериалов с отрицательным коэффициентом теплового расширения с помощью CAE Fidesys // Тез. докл. Межд. конф. “Физическая мезомеханика. Материалы с многоуровневой иерархически организованной структурой и интеллектуальные производственные технологии.” Томск: ТГУ, 2021. С. 340–341.
Yakovlev M.Y., Tanasevich P., Vershinin A.V., Levin V.A., Zingerman K.M. Application of the finite element method to modeling the effective mechanical and thermomechanical properties of metamaterials of the 3D lattice structure // Proc. NAFEMS World Congress 2021. P. 403.
Barchiesi E., dell’Isola F., Hild F. On the validation of homogenized modeling for bi-pantographic metamaterials via digital image correlation // Int. J. Solids Struct. 2021. V. 208–209. P. 49–62. https://doi.org/10.1016/j.ijsolstr.2020.09.036
dell’Isola F., Della Corte A., Giorgio I., Scerrato D. Pantographic 2D sheets: Discussion of some numerical investigations and potential applications // Int. J. Non-Lin. Mech. 2016. V. 80. P. 200–208. https://doi.org/10.1016/j.ijnonlinmec.2015.10.010
Shubin S.N., Freidin A.B., Akulichev A.G. Elastomer composites based on filler with negative thermal expansion coefficient in sealing application // Arch. Appl. Mech. 2016. V. 86. 351–360 (2016). https://doi.org/10.1007/s00419-016-1120-1
Peng X.-L., Bargmann S. Tunable auxeticity and isotropic negative thermal expansion in three-dimensional lattice structures of cubic symmetry // Extreme Mech. Lett. 2021. V. 43. P. 101201. https://doi.org/10.1016/j.eml.2021.101201
Wang Q., Jackson J.A., Ge Q., Hopkins J.B., Spadaccini C.M., Fang N.X. Lightweight mechanical metamaterials with tunable negative thermal expansion // Phys. Rev. Lett. 2016. V. 116. P. 175901. https://doi.org/0.1103/PhysRevLett.117.175901
Bückmann T., Stenger N., Kadic M., Kaschke J., Frölich A., Kennerknecht T., Eberl C., Thiel M., Wegener M. Tailored 3D mechanical metamaterials made by dip-in direct-laser-writing optical lithography // Adv. Mater. 2012. V. 24. № 20. P. 2710–2714. https://doi.org/10.1002/adma.201200584
Лапин С.Э., Писецкий В.Б. К разработке геоинформационной панели безопасности подземных горных работ на основе связанных решений по прогнозу развития напряженного состояния массива горных пород и газовых потоков // Чебышев. сб. 2017. Т. 18. Вып. 3. С. 350–362. https://doi.org/10.22405/2226-8383-2017-18-3-350-362
Myasnikov A., Vershinin A., Sboychakov A. A generalization of geomechanical model for naturally fractured reservoirs // SPE Russian Petroleum Technology Conference and Exhibition, Moscow, Russia, October 2016. SPE, 2016. https://doi.org/10.2118/182033-MS
Gupta A., Penuela G., Avila R. An integrated approach to the determination of permeability tensors for naturally fractured reservoirs // J. Can. Pet. Technol. V. 40. № 12. P. PETSOC-01-12-02. https://doi.org/10.2118/01-12-02
Costa A. Permeability-porosity relationship: A reexamination of the Kozeny-Carman equation based on a fractal pore-space geometry assumption // Geophys. Res. Lett. V. 33. № 2. https://doi.org/10.1029/2005GL025134
Bagheri M., Settari A. Modeling of geomechanics in naturally fractured reservoirs // SPE Reservoir Simulation Symposium. Houston, 2005. SPE, 2005. P. SPE–93083–MS. https://doi.org/10.2118/93083-MS
Bagheri M., Settari A. Effects of fractures on reservoir deformation and flow modeling // Can. Geotech. J. 2006. V. 43. № 6. P. 574–586. https://doi.org/10.1139/T06-024
Писецкий В.Б., Власов В.В., Черепанов В.П. и др. Прогноз устойчивости горного массива на основе метода сейсмической локации в процессах строительства подземных сооружений // Инженерные изыскания. 2014. № 9–10. С. 46–51.
Шувалов Ю.В., Коршунов Г.И., Монтиков А.В., Истомин Р.С., Суфияров А.М., Ютяев Е.П. Геомеханические и газодинамические процессы в угленосном массиве при высоких скоростях подвигания очистных забоев // Горный информационно-аналитический бюллетень (научно-технический журнал). 2011. № 6. С. 80–88.
Журавлев А.Б., Карев В.И., Коваленко Ю.Ф., Устинов К.Б. Влияние фильтрации на напряженно-деформированное состояние породы в окрестности скважины // ПММ. 2014. Т. 78. Вып. 1. С. 86–97.
Souley M., Thoraval A. Nonlinear mechanical and poromechanical analyses: comparison with analytical solutions // COMSOL Conference 2011. Stuttgart, Germany. 2011. P. NC.ffineris00973639.
Carroll M.M., Horgan O. Finite strain solutions for compressible elastic solid // Quart. Appl. Math. 1990. V. 48. № 3. P. 767–780. https://doi.org/10.1090/qam/1079919
Ball J.M. Discontinuous equilibrium solutions and cavitation in nonlinear elasticity // Philos. Trans. Royal Soc. Ser A. 1982. V. 306. № 1496. P. 557–611. https://doi.org/10.1098/rsta.1982.0095
Zubov L.M. Universal solutions of nonlinear dislocation theory for elastic cylinder // Mech. Solids, 2020. V. 55. P. 701–709. https://doi.org/10.3103/S0025654420050167
Zubov L.M. Universal solution of nonlinear elasticity for a hollow cylinder with prestressed coatings // Acta Mech. 2019. V. 230. P. 4137–4143. https://doi.org/10.1007/s00707-018-2333-x
Еремеев В.А., Зубов Л.М. Механика упругих оболочек. М.: Наука, 2008. 280 с.
Batra R., dell’Isola F., Ruta G. Second-order solution of Saint-Venant’s problem for an elastic bar predeformed in flexure // Int. J. Non-Lin. Mech. 2005. V. 40. № 2-03. P. 411–422. https://doi.org/10.1016/j.ijnonlinmec.2004.08.002
Sharma M., Wang H. A Fully 3-D, multi-phase, poro-elasto-plastic model for sand production // SPE Annual Technical Conference and Exhibition, Dubai, UAE, September 2016. SPE, 2016. P. SPE–181566–MS. https://doi.org/10.2118/181566-MS
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика твердого тела