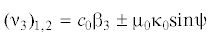Известия РАН. Механика твердого тела, 2023, № 2, стр. 115-124

Введение. Прецессионные движения твердых тел занимают особое место в классической задаче о движении тяжелого твердого тела и ее обобщениях. Прикладные задачи, связанные с изучением прецессий гироскопических приборов, рассмотрены А.Ю. Ишлинским [1]. В динамике твердого тела прецессии изучали Д. Гриоли [2], Ф. Кляйн и А. Зоммерфельд [3], автор данной статьи [4] и многие другие авторы (см. книги [5, 6]). Монография [7] посвящена исследованию условий существования прецессионных движений гиростата с переменным гиростатическим моментом. В ней приведен обзор результатов, полученных в данной задаче и сформулированы основные определения гиростата. Важное значение в постановке задачи о движении гиростата имеют подходы, которые приняты в работах Й. Виттенбурга [8], В.В. Румянцева [9], П.В. Харламова [10]. Прецессионные движения характеризуются свойством постоянства угла между двумя осями l₁, l₂, проходящими через неподвижную точку, одна из которых (l₁) связана с телом-носителем, а другая (l₂) неподвижна в пространстве. В случае, когда одна из осей подвижной системы координат содержит ось l₁, то целесообразно такую систему координат называть прецессионной системой координат [11]. Согласно [2, 4], прецессионные движения подразделяются на классы: если скорости прецессии и собственного вращения постоянны, то прецессия называется регулярной; если скорость прецессии постоянна, то прецессия называется полурегулярной первого типа; если только скорость собственного вращения постоянна, то прецессию называют полурегулярной прецессией второго типа; в других случаях прецессия называется прецессией общего типа. Наибольшее количество прецессионных движений гиростата установлено для классов регулярных и полурегулярных прецессий первого типа. Следует отметить, что уникальными случаями прецессий тяжелого твердого тела, описываемых уравнениями Эйлера–Пуассона, являются регулярные прецессии, полученные Д. Гриоли [2], относительно наклонной оси и случай А.И. Докшевича [12], для которого постоянно произведение скоростей прецессии и собственного вращения. Полурегулярные прецессии второго типа твердого тела и гиростата относятся к меньшему числу найденных прецессий. Например, в [4] доказано, что в классической задаче полурегулярные прецессии второго типа динамически невозможны. Несмотря на это, в задаче о движении гиростата с переменным гиростатическим моментом получены некоторые решения, имеющие такое свойство [7].

В данной статье исследованы условия существования полурегулярных прецессий второго типа гиростата с переменным гиростатическим моментом под действием потенциальных и гироскопических сил. Указаны условия на параметры уравнений движения и прецессии, при выполнении которых гиростат совершает прецессию второго типа.

1. Постановка задачи. При изучении уравнений движения гиростата с постоянным гиростатическим моментом следует учитывать известное свойство аналогии задачи о движении гиростата под действием потенциальных и гироскопических сил и задачи о движении тела в идеальной жидкости, которую в частном случае доказали В.А. Стеклов [13] и П.В. Харламов [14], а в общем случае – Х.М. Яхья [15]. Для случая переменного гиростатического момента ${\mathbf{\lambda }}{\text{(}}t{\text{)}}$ такой аналогии нет. Поэтому в данной статье будем использовать дифференциальные уравнения в следующей форме [6, 7, 15]:

где введены обозначения: ${\mathbf{\omega }} = {\text{(}}\omega _{1}^{{}}{\text{,}}\omega _{2}^{{}}{\text{,}}\omega _{3}^{{}}{\text{)}}$ – вектор угловой скорости; λ(t) = (λ₁(t), – вектор гиростатического момента; $A = {\text{diag(}}A_{1}^{{}},A_{2}^{{}},A_{3}^{{}}{\text{)}}$ – тензор инерции гиростата; $B = {\text{diag(}}{{B}_{1}},B_{2}^{{}},B_{3}^{{}}{\text{)}}$ – матрица, характеризующая гироскопические силы; $C = {\text{diag(}}{{C}_{1}},C_{2}^{{}},C_{3}^{{}}{\text{)}}$ – матрица, определяющая квадратичные по компонентам вектора члены; ${\mathbf{s}} = {\text{(}}{{s}_{1}}{\text{,}}\,{{s}_{2}}{\text{,}}\,{{s}_{3}}{\text{)}}$ – вектор обобщенного центра масс гиростата; точка над переменными ${\mathbf{\omega }}{\text{(}}t{\text{),}}\;{\mathbf{\lambda }}{\text{(}}t{\text{),}}\;{\mathbf{\nu }}{\text{(}}t{\text{)}}$ обозначает дифференцирование по времени t.

Уравнения (1.1), (1.2) имеют первые интегралы

где k – произвольная постоянная. Все указанные выше величины заданы в главной подвижной системе координат с единичными векторами $\,{\mathbf{i}}_{1}^{{}},\,{\mathbf{i}}_{2}^{{}},\,{\mathbf{i}}_{3}^{{}}$.

Система (1.1), (1.2) является неавтономной системой дифференциальных уравнений относительно переменных ${\mathbf{\omega }}{\text{(}}t{\text{),}}\;{\mathbf{\lambda }}{\text{(}}t{\text{),}}\;{\mathbf{\nu }}{\text{(}}t{\text{)}}$. Ее интегрирование может быть основано на нескольких подходах. В данной статье будем полагать, что ротор ${{S}_{3}}$, который несет тело-носитель ${{S}_{0}}$, лежит на третьей координатной оси, то есть ${\mathbf{\lambda }}{\text{(}}t{\text{)}} = {\text{(0,0,}}\lambda _{3}^{{}}{\text{(}}t{\text{))}}$. Тогда в силу [10] систему (1.1), (1.2) будем рассматривать совместно с уравнениями

здесь $\dot {\kappa }{\text{(}}t{\text{)}}$ – скорость вращения ротора ${{S}_{3}}$; ${\text{D}}_{{\text{3}}}^{{}}$ – момент инерции ротора ${{S}_{3}}$ относительно оси вращения $Oz$; L(t) – проекция моментов и сил на ось $Oz$ со стороны тела-носителя. Уравнения (1.4) можно изучать с помощью двух подходов: если задана функция L(t), то вначале из первого уравнения системы (1.4) находится функция ${{\lambda }}_{3}^{{}}{\text{(}}t{\text{)}}$ и интегрируются уравнения (1.1), (1.2), а затем из второго уравнения (1.4) определяется функция $\dot {\kappa }{\text{(}}t{\text{)}}$; если $\dot {\kappa }{\text{(}}t{\text{)}}$ задана и известна функция ${{\lambda }}_{3}^{{}}{\text{(}}t{\text{)}}$, то из (1.4) находится функция $L{\text{(}}t{\text{)}}$.

Задача о движении гиростата с постоянным гиростатическим моментом на основе функции Лагранжа изучалась в [16].

Исследование полурегулярных прецессий будем вести, используя метод [17, 18]. Согласно этому методу, вектор угловой скорости гиростата представим в виде

где ${{\varepsilon }}({{{{\nu }}}_{3}})$ – дифференцируемая функция; ${\mathbf{\beta }} = ({{\beta }}_{1}^{{}},{{\beta }}_{2}^{{}},{{\beta }}_{3}^{{}})$ – постоянный единичный вектор; $g_{0}^{{}}$ – постоянный параметр. Случай ${{\varepsilon }}({{{{\nu }}}_{3}}) = {{\varepsilon }}_{0}^{{}}$, где $\varepsilon _{0}^{{}}$ – постоянная, рассмотрен в [19].

Подставим значение (1.5) в уравнение (1.2):

Из уравнения (1.6) следует первый интеграл

который в векторной форме представим так: ${\mathbf{\beta }} \cdot {\mathbf{\nu }} = c_{0}^{{}}$, где $c_{0}^{{}}$ – постоянная. То есть в силу равенств ${\text{|}}{\mathbf{\beta }}| = 1$, ${\text{|}}{\mathbf{\nu }}| = 1$ параметр $c_{0}^{{}}$ удовлетворяет условию $c_{0}^{{}} < 1$. Из (1.5) следует, что скорость прецессии равна ${{\varepsilon }}({{{{\nu }}}_{3}})$, а скорость собственного вращения – $g_{0}^{{}}$. То есть прецессия гиростата относится к полурегулярной прецессии второго типа. Запишем (1.5), (1.6) в скалярной форме:

Используя равенства ${{\nu }}_{{\text{1}}}^{{\text{2}}} + {{\nu }}_{{\text{2}}}^{{\text{2}}} + {{\nu }}_{{\text{3}}}^{{\text{2}}} = 1$ и (1.7), найдем функции ${{{{\nu }}}_{{\text{1}}}}{\text{(}}{{{{\nu }}}_{3}})$, ${{{{\nu }}}_{{\text{2}}}}{\text{(}}{{{{\nu }}}_{3}})$:

где $\kappa _{0}^{2} = {{\beta }}_{{\text{1}}}^{{\text{2}}} + {{\beta }}_{{\text{2}}}^{{\text{2}}}$, а функция $F({{\nu }}_{3}^{{}})$ такова

Подставляя ${{{{\nu }}}_{{\text{1}}}}{\text{(}}{{{{\nu }}}_{3}})$, ${{{{\nu }}}_{{\text{2}}}}{\text{(}}{{{{\nu }}}_{3}})$ из (1.10) в третье уравнение системы (1.9), получим, что функцию ${{{{\nu }}}_{3}}(t)$ можно получить обращением интеграла [17]

Тогда функции ${{\nu }}_{i}^{{}}{\text{(}}t{\text{)}}$ ${\text{(}}i = 1,2{\text{)}}$, ${{\omega }}_{i}^{{}}{\text{(}}t{\text{)}}$ ${\text{(}}i = \overline {1,3} {\text{)}}$ находятся из формул (1.10), (1.8). В силу того, что функция (1.11) удовлетворяет условию $F({{\nu }}_{3}^{{}}) < 0$ при ${\text{|}}{{{{\nu }}}_{3}}{\text{|}} > 1$, то при действительном значении параметра ${{\mu }}_{0}^{{}} = \sqrt {1 - c_{0}^{2}} $ корни уравнения $F({{\nu }}_{3}^{{}}) = 0$ действительны. То есть из (1.11), (1.12) найдем

где в силу третьего уравнения из (1.9) ${{\psi }} = g_{0}^{{}}t$. Выбирая для определенности в (1.13) знак плюс, из (1.13), (1.10) получим

Здесь введены обозначения

Отметим вид решения (1.14) и обозначений (1.15) в случае ${{\beta }}_{3}^{{}} = 0$, который рассмотрен в статье [19] при изучении регулярных прецессий гиростата (${{\varepsilon }}({{{{\nu }}}_{3}}) = {{\varepsilon }}_{0}^{{}}$):

Поставим задачу: определить условия существования у уравнения (1.1) решения (1.8), (1.14).

2. Исследование уравнения (1.1). Запишем уравнение (1.1) в скалярной форме:

Подставим в (2.1)–(2.3) выражения $\omega _{i}^{{}}$ из (1.8) и воспользуемся уравнениями (1.9). Тогда получим систему трех дифференциальных уравнений

Выбор формы дифференциальных уравнений (2.4)–(2.6) связан с применяемой методикой их изучения в дальнейших преобразованиях.

В некоторых случаях целесообразно использовать уравнения (2.1), (2.2), исключив из них функцию $\lambda _{3}^{{}}{\text{(}}t{\text{)}}$:

В общем случае при подстановке функций (1.14) в уравнения (2.4), (2.5) и исключения из полученных уравнений функции $\lambda _{3}^{{}}{\text{(}}t{\text{)}}$ приходим к уравнению типа Риккати, решение которого установить не представляется возможным. Поэтому в дальнейших преобразованиях положим, что выполняются условия

Кроме этого, будем рассматривать два независимых варианта дополнительных ограничений на параметры:

где $d_{0}^{{}}$ – параметр. В случае (2.9) уравнение (2.7) на основе (1.8), (1.9) преобразуем к виду

В силу (2.8), (2.9) данные равенства можно интерпретировать, как обобщенные условия С.В. Ковалевской.

При выполнении условий (2.10) уравнение (2.7) представим следующим образом:

Аналоги первых интегралов, следующих из (2.12), рассматривались в [20]. Запишем уравнение (2.3) в случае (2.9):

где $B_{0}^{{}}$ – произвольная постоянная. Если учесть в уравнении (2.3) условия (2.10) и третье уравнение из (1.9), то получим

Здесь l₀ – произвольная постоянная. Аналогия уравнений (2.11) и (2.12), а также (2.13), (2.14) очевидна.

Рассмотрим линейную комбинацию уравнений (2.4), (2.5), умножив уравнение (2.4) на ${{\nu }_{1}}$, уравнение (2.5) – на ${{\nu }_{2}}$ и сложив левые и правые части полученных уравнений. Тогда в силу уравнения $\dot {\nu }_{3}^{{}} = g_{0}^{{}}(\beta _{2}^{{}}{{\nu }_{1}} - \beta _{1}^{{}}{{\nu }_{2}})$ найдем

В случае (2.9), (2.13) из (2.15) следует

где $E_{0}^{{}}$ – произвольная постоянная, а $E_{2}^{{}},E_{1}^{{}}$ таковы:

Распишем уравнение (2.15) при условиях (2.10), (2.14):

где $G_{0}^{{}}$ – произвольная постоянная, а $G_{2}^{{}},G_{1}^{{}}$ имеют вид

Из (2.17), (2.19) следует, что величина E₂ при $d_{0}^{{}} = 0$ примет значение G₂, а для получения из (2.17) значения G₁ необходимо положить $B_{0}^{{}} = l_{0}^{{}}$. Однако уравнения (2.11), (2.12) такой аналогией не обладают.

3. Случай (2.9). Этот случай на первом этапе будем изучать при выполнении условия

При выполнении равенства (3.1) уравнение (2.11) запишем в виде его первого интеграла

где D₀ – произвольная постоянная. В уравнении (3.2) учтены инвариантные соотношения (1.8). Подставим в равенство (3.2) значение $\varepsilon ({{\nu }_{3}})$ из формулы (2.16) и потребуем, чтобы полученное равенство было тождеством по переменной ${{\nu }_{3}}$. Тогда получим следующую алгебраическую систему на параметры задачи:

Уравнение (3.3) будем рассматривать как условие на параметры $C_{1}^{{}},C_{{\text{3}}}^{{}}$. Первое равенство из (3.4), в силу (2.17) и предположения (3.1), для которого значение E₂ имеет вид

запишем так:

На основании значения (3.8) параметр $E_{1}^{{}}$ из (2.17) выразим через параметры задачи:

Из второго уравнения системы (3.4) и уравнения (3.6) найдем значения $c_{0}^{{}},E_{0}^{{}}$:

где $\delta _{0}^{{}} = \pm 1$. Уравнение (3.6) на основании (3.10) служит для определения постоянной D₀. Изучим функцию (2.16) с учетом (3.7), (3.10). Для определенности предположим $\delta _{0}^{{}} = 1$. Тогда

Для того, чтобы функция $\varepsilon ({{\nu }_{3}})$ не принимала постоянное значение, полагаем, что выполняются условия ${{\beta }_{3}} \ne 0$, $B_{3}^{{}} - 3B_{1}^{{}} \ne 0$. Таким образом, функция $\varepsilon ({{\nu }_{3}})$ из (3.11) является дробно-линейной функцией от ${{\nu }_{3}} = a_{0}^{{}} + a_{2}^{{}}\sin g_{0}^{{}}t$. Укажем значение ${{\lambda }_{3}}({{\nu }_{3}})$ в рассматриваемом случае. Из формул (2.13), (3.11) имеем

Для окончательного решения задачи об условиях существования полурегулярных прецессий гиростата необходимо рассмотреть уравнения (1.4) совместно со значением функции (3.12), положив ${{\nu }_{3}}(t) = a_{0}^{{}} + a_{2}^{{}}\sin g_{0}^{{}}t$. В силу очевидности указанных преобразований ограничимся лишь их объяснениями.

4. Случай $d_{{\mathbf{0}}}^{{}} + g_{{\mathbf{0}}}^{{}}B_{{\mathbf{1}}}^{{}} \ne {\mathbf{0}}$. Рассмотрим уравнение (2.11) при условии $d_{0}^{{}} + g_{0}^{{}}B_{1}^{{}} \ne 0$. Функция $\varepsilon ({{\nu }_{3}})$ имеет вид (2.16) с обозначениями (2.17). Подставим в него $\omega _{1}^{{}}$, $\omega _{2}^{{}}$ из (1.8) и учтем уравнения (1.9). Тогда получим дифференциальное уравнение на функцию $\varepsilon ({{\nu }_{3}})$:

Внесем функцию (2.16) в уравнение (4.1). Результат удобно представить так:

где

Потребуем, чтобы уравнение (4.2) было тождеством по переменной ${{\nu }_{3}}$. Равенство нулю коэффициента при $\nu _{3}^{5}$ имеет вид

Для упрощения других условий выразим из равенства (4.4) величину $C_{3}^{{}} - C_{1}^{{}}$ и подставим ее в (4.2). Выпишем равенство нулю коэффициента при $\nu _{3}^{3}$. Используя формулы (4.3), получим

Покажем, что должно выполняться равенство $R_{1}^{{}} = 0$. Предположим противное; тогда из (4.5) имеем

Условие (4.6) позволяет рассмотреть уравнение (4.2) при ${v}_{3}^{{}} = \pm 1$:

Случай $E_{1}^{{}} = 0$, в силу (4.6) для функции $\varepsilon ({{\nu }_{3}})$ из (2.16), приводит к постоянному значению $\varepsilon ({{\nu }_{3}})$. Поэтому в (4.7) необходимо положить

Из равенств нулю в уравнении (4.2) коэффициентов при ${v}_{3}^{4}$ и свободного члена следует

Поскольку по предположению (4.6) $E_{0}^{{}} = - E_{2}^{{}}$, то в силу $E_{1}^{{}} \ne 0$ из (4.9) получим $R_{1}^{{}} = 0$, что и требовалось доказать. Итак, вариант, когда параметры удовлетворяют условию $d_{0}^{{}} + g_{0}^{{}}B_{1}^{{}} \ne 0$, невозможен.

5. Случай (2.10). Рассмотрим уравнения (2.11), (2.12) и функции (2.13), (2.14), (2.16), (2.18). Для того, чтобы изучить данный вариант, можно формально от уравнения (2.11) перейти к уравнению (2.12), от уравнения (2.13) перейти к уравнению (2.14), от функции (2.16) – к функции (2.18), то случай (2.10) получим из случая (2.9), положив в нем $d_{0}^{{}} = 0$ $B_{0}^{{}} = l_{0}^{{}}$ и заменив выражение $B_{1}^{{}}g_{0}^{{}}{{\beta }_{3}}$ выражением $s_{3}^{{}} + B_{1}^{{}}g_{0}^{{}}{{\beta }_{3}}$. Следовательно, уравнению (4.1) будет соответствовать уравнение, в котором $R_{1}^{{}} = B_{1}^{{}}$, а вместо последнего слагаемого в (4.1) необходимо рассматривать слагаемое $ - (s_{3}^{{}} + B_{1}^{{}}g_{0}^{{}}{{\beta }_{3}})$. Принимая во внимание результат п. 4, в данном варианте получим $R_{1}^{{}} = B_{1}^{{}} = 0$. То есть квадратичная форма $B_{1}^{{}}\nu _{1}^{2} + B_{2}^{{}}\nu _{2}^{2} + B_{3}^{{}}\nu _{3}^{2}$ становится вырожденной $B_{3}^{{}}\nu _{3}^{2}$. Данный результат не представляет интереса для динамики гиростата под действием потенциальных и гироскопических сил.

Заключение. При рассмотрении условий существования полурегулярных прецессий второго типа гиростата под действием потенциальных и гироскопических сил построено новое решение уравнений движения, в которых учтено свойство переменности гиростатического момента. Данное решение характеризуется тремя инвариантными соотношениями: (1.8) и формулами (1.14). Ключевыми условиями существования этого решения являются равенства (2.8), (2.9), характеризующие распределение масс, которое можно отнести к обобщенным условиям С.В. Ковалевской. Решение описывается элементарными функциями времени, а скорость прецессии тела-носителя является дробно-линейной функцией тригонометрической функции ${\text{sin}}\,g_{0}^{{}}t$. В общем случае решение поставленной задачи достаточно сложно. Оно может быть описано следующим образом: на первом этапе исследования условий существования на основании второго интеграла из (1.3) с помощью инвариантного соотношения (1.8) и решения (1.14), (1.15) (в частном случае вместо (1.14), (1.15) можно привлечь (1.16)) определяется функция $\lambda _{3}^{{}}{\text{(}}\psi {\text{)}}$; на втором этапе эта функция подставляется в уравнения (2.4)–(2.6) и находятся три дифференциальных уравнения на функцию $\varepsilon {\text{(}}\psi {\text{)}}$ (очевидно, что они будут зависимыми); на третьем этапе исследуется задача об условиях интегрирования полученных уравнений в квадратурах.