Известия РАН. Механика жидкости и газа, 2019, № 5, стр. 83-92
ОСРЕДНЕННАЯ АСИМПТОТИЧЕСКАЯ МОДЕЛЬ ДВУХФАЗНОЙ ФИЛЬТРАЦИИ В ТРЕЩИНОВАТО-ПОРИСТЫХ СРЕДАХ
А. А. Афанасьев *
МГУ им. М.В. Ломоносова, Научно-исследовательский институт механики
Москва, Россия
* E-mail: afanasyev@imec.msu.ru
Поступила в редакцию 23.01.2019
После доработки 27.02.2019
Принята к публикации 12.03.2019
Аннотация
Рассмотрено решение классической в теории фильтрации задачи Баклея–Леверетта, обобщенной на случай двухфазных течений в трещиновато-пористых средах. В этом случае несмешивающееся вытеснение жидкостей в пористой среде осложняется отсутствием локального капиллярного равновесия между поровыми пространствами различного масштаба, а решение задачи в случае общего положения не автомодельное. Рассмотрена фильтрация в предельном случае больших масштабов по времени, когда устанавливается капиллярное равновесие, а распределения параметров течения, как показано в работе, стремятся к автомодельной асимптотике. Получены осредненные уравнения равновесной фильтрации для эффективной одинарной пористой среды, описывающие данную асимптотику.
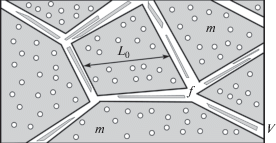
Фильтрационные течения могут осложняться наличием различных масштабов порового пространства. Например, пористая среда может содержать высокопроницаемые трещины или каналы, между которыми располагаются низкопроницаемые пористые блоки (рис. 1). Такие среды называют трещиновато-пористыми, а для прогнозирования фильтрации в них часто используют модели двойной пористости. В этих моделях трещиновато-пористая среда рассматривается в виде двух взаимопроникающих континуумов (пористых сред) – трещин, Φf, и блоков, Φm, между которыми происходит массообмен жидкостью [1]. В практических приложениях часто рассматривается предельный случай, когда ${{\Phi }^{f}}$ имеет малую пористость и высокую проницаемость, а Φm, наоборот, – высокую пористость и малую проницаемость [2–5]. В этом случае течение жидкости в основном происходит по трещинам, тогда как больший ее объем находится в блоках. В настоящей работе для общности исследования данных предположений о Φf и Φm не делается, а существенным для дальнейшего изложения является только наличие двух различных масштабов порового пространства.
Рис. 1.
Схема элементарного объема $V$ трещиновато-пористой среды. Жирные линии – границы между континуумами трещин (f) и блоков ($m$). Серым цветом выделены области, занятые скелетом пористой среды, а белым – насыщающими жидкостями.
Впервые модель двойной пористости была сформулирована в работе [1], где для случая однофазной фильтрации получено уравнение, описывающее распределение давления в Φf и Φm. В данном направлении позднее проводились исследования [2] и др. с целью интерпретации гидродинамических исследований скважин, вскрывающих трещиновато-пористые пласты. Показано, что существование пор различного размера приводит к неравновесному распределению давления в пласте, что в свою очередь влияет на забойное давление и приток жидкости к скважине. Двухфазное вытеснение в трещиновато-пористых средах рассматривалось в работах [3, 6, 7] и др., в которых были разработаны осредненные уравнения фильтрации в эффективной одинарной пористой среде. При этом предполагалось, что проницаемость в среде блоков Φm настолько низкая, что течением жидкости по Φm можно пренебречь, а исследования были сосредоточены на получении простых эффективных соотношений для перетоков между Φf и Φm в условиях отсутствия локального равновесия между средами.
В настоящей работе более подробно, по сравнению с [3, 6, 7], рассмотрен предельный случай, когда в трещиновато-пористой среде устанавливается капиллярное равновесие, а также определены критерии подобия, описывающие на больших временах стремление параметров течения к равновесной асимптотике.
1. ОСНОВНЫЕ УРАВНЕНИЯ
Поровое пространство трещиновато-пористой среды охарактеризуем параметром $\gamma = {{{{V}^{f}}} \mathord{\left/ {\vphantom {{{{V}^{f}}} V}} \right. \kern-0em} V}$ – относительным объемом среды Φf, где $V = {{V}^{f}} + {{V}^{m}}$ – полный элементарный объем среды, а Vj, $j = f,m$ – объем, относящийся к континууму Φj. Тогда относительный объем среды Φm равен $1 - \gamma $ = Vm/V. Для каждого континуума зададим пористость ${{\phi }^{j}} = {{V_{{por}}^{j}} \mathord{\left/ {\vphantom {{V_{{por}}^{j}} {{{V}^{j}}}}} \right. \kern-0em} {{{V}^{j}}}}$ и абсолютную проницаемость ${{K}^{j}}$, где $V_{{por}}^{j}$ – объем порового пространства в соответствующем континууме. Тогда поровые пространства в Φf и Φm занимают соответственно доли $\gamma {{\phi }^{f}}$ и $(1 - \gamma ){{\phi }^{m}}$ элементарного объема V.
Двухфазная фильтрация несмешивающихся несжимаемых жидкостей в тонком горизонтальном слое трещиновато-пористой среды описывается системой уравнений [2–7]
(1.1)
${{\partial }_{t}}(\gamma {{\phi }^{f}}s_{i}^{f}) + \nabla {\mathbf{w}}_{i}^{f} = q_{i}^{{mf}},\quad i = 1,2$(1.2)
${{\partial }_{t}}((1 - \gamma ){{\phi }^{m}}s_{i}^{m}) + \nabla {\mathbf{w}}_{i}^{m} = - q_{i}^{{mf}}$(1.4)
${\mathbf{w}}_{i}^{j} = - {{K}^{j}}\frac{{K_{{ri}}^{j}}}{{{{\mu }_{i}}}}\nabla P_{i}^{j},\quad j = f,m$(1.5)
$q_{i}^{{mf}} = \sigma {{K}^{m}}\frac{{K_{{ri}}^{{mf}}}}{{{{\mu }_{i}}}}(P_{i}^{m} - P_{i}^{f})$Учитывая, что плотности жидкостей постоянны, ${{\rho }_{i}} = {\text{const}}$, уравнения (1.1) и (1.2) – законы сохранения массы каждой фазы в континуумах f и m, соответственно соотношение (1.3) определяет капиллярное давление, (1.4) – закон фильтрации Дарси, а (1.5) задает массообмен между взаимопроникающими континуумами Φf и Φm.
В каждой среде насыщенности удовлетворяют соотношению
Учитывая (1.6), далее нижний индекс у насыщенности первой фазы опускаем ${{s}^{j}} \equiv s_{1}^{j}$, тогда для насыщенности второй фазы выполняется равенство $s_{2}^{j} = 1 - {{s}^{j}}$.
В настоящей работе относительные фазовые проницаемости и капиллярные давления задаются в виде следующих функций от насыщенности фазы i = 1 [10]:
(1.7)
$\begin{gathered} K_{{r1}}^{f} = {{s}^{f}},\quad K_{{r2}}^{f} = 1 - {{s}^{f}},\quad P_{c}^{f} = 0 \\ K_{{r1}}^{m} = {{({{s}^{m}})}^{{2.5}}},\quad K_{{r2}}^{m} = 0.5{{(1 - {{s}^{m}})}^{{1.5}}},\quad P_{с}^{m} = {{P}_{{\max }}}(1 - {{s}^{m}}) \\ \end{gathered} $(1.8)
$\begin{gathered} P_{i}^{f} \geqslant P_{i}^{m}{\text{:}}\quad K_{{ri}}^{{mf}} = K_{{ri}}^{f}({{s}^{f}}) \hfill \\ P_{i}^{f} < P_{i}^{m}{\text{:}}\quad K_{{ri}}^{{mf}} = K_{{ri}}^{m}({{s}^{m}}) \hfill \\ \end{gathered} $Подставляя (1.4)–(1.8) в (1.1)–(1.3), получим замкнутую систему 5 уравнений относительно неизвестных ${{s}^{f}}$, ${{s}^{m}}$, $P_{1}^{m}$, $P_{2}^{m}$ и ${{P}^{f}} = P_{1}^{f} = P_{2}^{f}$.
2. ПОСТАНОВКА ЗАДАЧИ И УРАВНЕНИЯ В БЕЗРАЗМЕРНОМ ВИДЕ
Рассмотрим одномерную задачу фильтрации в трещиновато-пористой среде, заполняющей полубесконечную область $x \geqslant 0$. В момент времени t = 0 среда насыщена фазой i = 2, т.е. ${{s}^{f}} = 0$ и ${{s}^{m}} = 0$. При t = 0 через границу x = 0 в область x > 0 начинается закачка фазы i = 1 с постоянным объемным расходом $\Omega $, т.е.
Учитывая сформулированную задачу, введем безразмерные параметры в виде
(2.1)
$x = {{x}_{ * }}L,\quad t = {{t}_{ * }}T,\quad w = {{w}_{ * }}\Omega ,\quad P = {{P}_{ * }}\Delta P$(2.2)
$\begin{gathered} L = \frac{{\Omega T}}{{\bar {\phi }}},\quad \Omega = \frac{{\bar {K}\Delta P}}{{\bar {\mu }L}},\quad \bar {\mu } = \frac{{2{{\mu }_{1}}{{\mu }_{2}}}}{{{{\mu }_{1}} + {{\mu }_{2}}}} \\ \bar {\phi } = \gamma {{\phi }^{f}} + (1 - \gamma ){{\phi }^{m}},\quad \bar {K} = {{K}^{f}} + {{K}^{m}} \\ \end{gathered} $Подставляя (1.4), (1.5), (2.1), (2.2) в уравнения (1.1)–(1.3) и всюду далее опуская символ звездочки у безразмерных величин, систему уравнений фильтрации в трещиновато-пористой среде представим в виде
(2.3)
${{( - 1)}^{{i + 1}}}\Gamma {{\partial }_{t}}{{s}^{f}} + (1 - \kappa ){{M}_{i}}\nabla ( - K_{{ri}}^{f}\nabla P_{{}}^{f}) = \frac{{{{M}_{i}}}}{B}K_{{ri}}^{{mf}}(P_{i}^{m} - P_{{}}^{f})$(2.4)
${{( - 1)}^{{i + 1}}}(1 - \Gamma ){{\partial }_{t}}{{s}^{m}} + \kappa {{M}_{i}}\nabla ( - K_{{ri}}^{m}\nabla P_{i}^{m}) = - \frac{{{{M}_{i}}}}{B}K_{{ri}}^{{mf}}(P_{i}^{m} - P_{{}}^{f})$Согласно определениям (2.2), выполняется равенство ${{M}_{1}} + {{M}_{2}} = 2$, поэтому из двух параметров подобия M1 и M2 только M1 независимый, а ${{M}_{2}} = 2 - {{M}_{1}}$.
Параметр подобия C характеризует влияние капиллярного давления на распределение насыщенности sm в среде Φm. При $C \to 0$ капиллярным давлением можно пренебречь.
Параметр подобия B характеризует интенсивность массообмена между Φf и Φm. Если $B \to 0$, то множители перед разностями давлений $P_{i}^{m} - {{P}^{f}}$ в правых частях уравнений (2.3) и (2.4) стремятся к бесконечности, а следовательно, разности давлений стремятся к нулю. Это означает, что при $B \to 0$, C = 0 давления в средах Φf и Φm быстро выравниваются. Чем больше B, тем сильнее могут различаться давления $P_{i}^{f}$ и $P_{i}^{m}$ при отсутствии локального равновесия. Таким образом, B характеризует неравновесность течения из-за различной динамики процессов в средах Φf и Φm при $С = 0$.
Для оценки влияния капиллярного давления ($C \ne 0$) на локальное равновесие, подставим соотношение (2.5) в уравнения (2.3), (2.4), исключив $P_{2}^{m}$ (или $P_{1}^{m}$). В результате получим, что в правой части (2.3), (2.4) член перед $P_{c}^{m}$ обратно пропорционален отношению
Это означает, что скорость установления капиллярного равновесия между Φf и Φm пропорциональна 1/E. При $E \to 0$ равновесие устанавливается мгновенно. Чем больше E, тем течение имеет более неравновесный характер из-за $P_{c}^{m} \ne 0$.
Складывая попарно, при $i = 1$ или 2, уравнения (2.3) и (2.4), получим следующее следствие из системы (2.3)–(2.5):
(2.6)
${{( - 1)}^{{i + 1}}}{{\partial }_{t}}\bar {s} - {{M}_{i}}\nabla ((1 - \kappa )K_{{ri}}^{f}\nabla P_{i}^{f} + \kappa K_{{ri}}^{m}\nabla P_{i}^{m}) = 0$3. АСИМПТОТИЧЕСКИЙ СЛУЧАЙ $L \to \infty $
Обозначим $X = {L \mathord{\left/ {\vphantom {L {{{L}_{0}}}}} \right. \kern-0em} {{{L}_{0}}}}$ – число вовлеченных в течение блоков в среде Φm. Рассмотрим фильтрацию на больших пространственных масштабах $X \to \infty $ ($L \to \infty $) или, что с учетом (2.2) эквивалентно, на больших временах $T \to \infty $. Далее выведем уравнения, которыми описывается течение в предельном случае $X \to \infty $, и исследуем, как происходит стремление его параметров к данной асимптотике.
Заметим, что параметры подобия $\Gamma $, ${{M}_{i}}$ и $\kappa $ не зависят от X, тогда как B, $C$ и $E$ монотонно убывают при возрастании X:
Уравнения (3.1) – условия локального равновесия между Φf и Φm, так как если выполняется (3.1), то, согласно (1.5), перетоки $q_{i}^{{mf}}$ равны нулю.
Используя систему уравнений (1.8), (3.1), определим при $C \ne 0$ равновесное распределение жидкостей $i = 1,2$ между Φf и Φm в зависимости от эффективной насыщенности $\bar {s}$. Заметим, что при $\bar {s} = 0$ насыщенности фазы i = 1 равны нулю: ${{s}^{f}} = 0$, ${{s}^{m}} = 0$. Далее, так как $P_{c}^{m} \geqslant 0$ и $P_{c}^{f} = 0$, то при возрастании $\bar {s}$ от нуля до единицы сначала фазой i = 1 заполняется среда Φm (так как из-за капиллярного давления $P_{c}^{m} \geqslant 0$ фаза i = 1 полностью впитывается в Φm из Φf) и когда Φm полностью заполнится (т.е. при ${{s}^{m}} = 1$), начнет заполняться Φf. Таким образом, учитывая (2.7), имеем:
(3.2)
$\begin{gathered} \bar {s} < 1 - \Gamma {\text{:}}\quad {{s}^{f}} = 0,\quad {{s}^{m}} = \frac{{\bar {s}}}{{1 - \Gamma }},\quad P_{1}^{m} < P_{2}^{m} = {{P}^{f}} \\ \bar {s} \geqslant 1 - \Gamma {\text{:}}\quad {{s}^{f}} = \frac{{\bar {s} - 1 + \Gamma }}{\Gamma },\quad {{s}^{m}} = 1,\quad P_{1}^{m} = P_{2}^{m} = {{P}^{f}} \\ \end{gathered} $В соответствии с (1.8), здесь учтено, что при $\bar {s} < 1 - \Gamma $ выполняются равенства $K_{1}^{{mf}} = 0$ и $q_{1}^{{mf}}$ = 0, а при $\bar {s} \geqslant 1 - \Gamma $ – равенства $K_{2}^{{mf}} = 0$ и $q_{2}^{{mf}} = 0$.
Из уравнений (2.6) следует, что полный поток каждой фазы $i = 1,2$ имеет вид
(3.3)
$ - {{M}_{i}}{{\bar {K}}_{{ri}}}\nabla {{\bar {P}}_{i}} = - {{M}_{i}}((1 - \kappa )K_{{ri}}^{f}\nabla P_{i}^{f} + \kappa K_{{ri}}^{m}\nabla P_{i}^{m})$(3.4)
$\begin{gathered} {{{\bar {K}}}_{{ri}}}(\bar {s}) = (1 - \kappa )K_{{ri}}^{f}({{s}^{f}}) + \kappa K_{{ri}}^{m}({{s}^{f}}) \\ С{{{\bar {P}}}_{c}}(\bar {s}) = {{{\bar {P}}}_{2}} - {{{\bar {P}}}_{1}} = СP_{c}^{m}({{s}^{m}}) \\ \end{gathered} $Таким образом, подставляя (3.3) в (2.6), получим, что при $B,E \ll 1$ фильтрация в трещиновато-пористой среде описывается следующей системой уравнений относительно $\bar {s}$, ${{\bar {P}}_{1}}$ и ${{\bar {P}}_{2}}$:
(3.5)
${{( - 1)}^{{i + 1}}}\bar {\phi }{{\partial }_{t}}\bar {s} - {{M}_{i}}\nabla \left( {{{{\bar {K}}}_{{ri}}}\nabla {{{\bar {P}}}_{i}}} \right) = 0,\quad {{\bar {P}}_{2}} - {{\bar {P}}_{1}} = C{{\bar {P}}_{c}}$Равновесная асимптотическая модель (3.5) проще полной модели (2.3)–(2.5), так как
она позволяет свести исследование фильтрации в трещиновато-пористой среде к решению
уравнений для эффективной одинарной среды, которые были подробно рассмотрены ранее
в литературе [12]. Если в дополнение к условиям $B,E \ll 1$ выполняется неравенство $C \ll 1$, то в уравнениях (3.5) можно пренебречь капиллярным давлением, положив $\bar {P} = {{\bar {P}}_{1}} = {{\bar {P}}_{2}}$. В этом случае исследование сводится к решению задачи Баклея–Леверетта, в которой
насыщенность имеет автомодельное распределение от переменной $\xi = x{\text{/}}t$: $\bar {s}(x,t) = \bar {s}(\xi )$ [11, 12]. В случае общего положения из-за действия капиллярных сил (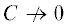 ) и неравновесных процессов (
) и неравновесных процессов (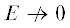 ) система уравнений (2.3)–(2.5) не имеет автомодельных решений.
) система уравнений (2.3)–(2.5) не имеет автомодельных решений.
4. ПРИМЕР РЕШЕНИЯ ЗАДАЧИ
Рассмотрим фильтрацию при следующих значениях параметров подобия
(4.1)
$\Gamma = 0.214,\quad {{M}_{1}} = 1.818,\quad \kappa = 0.7,\quad {{C}_{0}} = 26.8,\quad {{E}_{0}} = 0.04$В этом случае эффективные функции ${{\bar {K}}_{{ri}}}$ и ${{\bar {P}}_{c}}$ изображены на рис. 2. В соответствии с (3.2) и (3.4), при $\bar {s} = 1 - \Gamma $ эти функции имеют излом, что качественно согласуется с экспериментальными данными для ряда горных пород [13]. Соответствующие ${{\bar {K}}_{{ri}}}$ и $K_{{ri}}^{j}$ – функции потоков [12]:
(4.2)
$\bar {F}(\bar {s}) = \frac{{{{M}_{1}}{{{\bar {K}}}_{{r1}}}}}{{{{M}_{1}}{{{\bar {K}}}_{{r1}}} + {{M}_{2}}{{{\bar {K}}}_{{r2}}}}},\quad {{F}^{j}}({{s}^{j}}) = \frac{{{{M}_{1}}K_{{r1}}^{j}}}{{{{M}_{1}}\bar {K}_{{r1}}^{j} + {{M}_{2}}\bar {K}_{{r2}}^{j}}}$Рис. 2.
Кривые относительной фазовой проницаемости (а) и капиллярного давления (б) для эффективной модели одинарной пористости ($mf$), среды ${{\Phi }^{m}}$ ($m$) и ${{\Phi }^{f}}$ (f). Функции ${{K}_{{r1}}}$ возрастают, а ${{K}_{{r2}}}$ убывают.
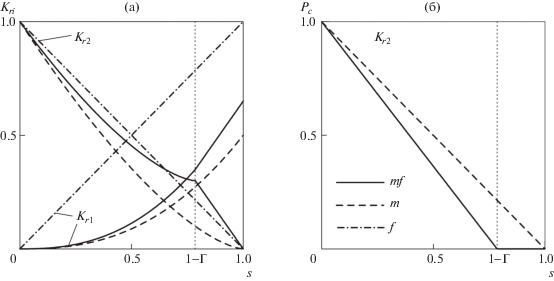
Рис. 3.
Функции потоков $F(s)$ для асимптотической модели ($mf$), среды ${{\Phi }^{m}}$($m$) и ${{\Phi }^{f}}$ (f).
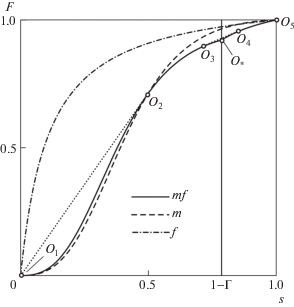
Рис. 4.
Распределение средней насыщенности $\bar {s}(\xi )$ (а), ${{s}^{f}}(\xi )$ и ${{s}^{m}}(\xi )$ (б) при $X = {{10}^{{0.6}}}$, 101, 102, 103 и 103.5 (кривые 1–5 соответственно) и волновая картина решения при $X \to \infty $ (в). Закрашены области, соответствующие волнам Римана, а жирные наклонные прямые – траектории разрывов ${{S}_{1}}$ и ${{S}_{2}}$.
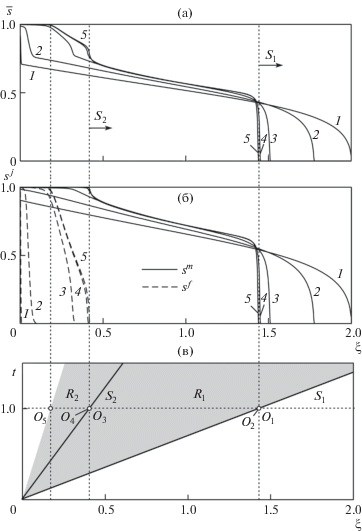
На рис. 4а,б показано стремление при возрастании X решения полной задачи к описанной автомодельной асимптотике (кривая 5). Решение получено в рамках расчета фильтрации по модели (2.3)–(2.5) в авторском комплексе программ [5], а на рис. 4 найденные распределения насыщенностей построены в зависимости от переменной $\xi = {x \mathord{\left/ {\vphantom {x t}} \right. \kern-0em} t}$. При малых X (кривые 1 и 2), когда нарушаются условия $С,E \ll 1$, решение полной задачи для трещиновато-пористой среды существенно отклоняется от асимптотического распределения. Это связано с тем, что капиллярное давление приводит как к отсутствию локального равновесия жидкости, так и влияет на распределение жидкости в пространстве. В результате вместо сильных разрывов ${{S}_{1}}$ и ${{S}_{2}}$ параметры течения изменяются непрерывно в переходных слоях (структурах разрывов [14]), определяющихся капиллярным давлением и неравновесными процессами. Протяженность данных слоев уменьшается при возрастании $X$, обращаясь в ноль при $X \to \infty $. При этом, оценивая степени $t$ и $x$ в членах уравнений (2.3), (2.4), можно показать, что протяженность слоя, образованного только капиллярным давлением ($C \ne 0$, $E = 0$) убывает с $X$ как $\sqrt {{C \mathord{\left/ {\vphantom {C X}} \right. \kern-0em} X}} $, а слоя, образованного только неравновесными процессами ($C = 0$, $E \ne 0$), как ${{\max (B,E)} \mathord{\left/ {\vphantom {{\max (B,E)} X}} \right. \kern-0em} X}$.
Так как, согласно (4.1), выполняется неравенство ${{E}_{0}} \ll {{C}_{0}}$, то при возрастании параметра X (см. рис. 4, кривые 3) сначала исчезает влияние неравновесных эффектов: ($E \ll 1$), тогда как влияние капиллярного давления на распределения в пространстве (в частности, на протяженность переходных слоев ${{S}_{1}}$ и ${{S}_{2}}$) сохраняется ($C\sim 1$). Наконец, при больших значениях X (кривые 4 и 5) выполняются условия: $С,E \ll 1$. При этом решение полной задачи для трещиновато-пористой среды слабо отличается от автомодельной асимптотики: $X \to \infty $ для эффективной одинарной среды.
5. ДИСПЕРСИОННЫЙ АНАЛИЗ И ЭВОЛЮЦИОННОСТЬ РАЗРЫВОВ
Эволюционность и структура разрывов при значениях B = 0, $C \to 0$ рассматривалась ранее в [12]. Здесь исследуем эволюционность разрывов в построенном решении (рис. 4) при $X \to \infty $, $B \to 0$, $C = 0$ в рамках двух моделей: равновесной (B = 0) и неравновесной ($B \ne 0$). Для этого сначала определим типы малых возмущений, допускаемых моделями. В случае $B \ne 0$, $C = 0$ ищем решение системы (2.3)–(2.5), соответствующее одномерному течению вдоль оси $x$, в виде простых гармонических волн
(5.1)
${{s}^{j}} = s_{0}^{j} + \delta {{s}^{j}}\theta ,\,\,\,\,\,\,\,\,{{P}^{j}} = P_{0}^{j} + ux + \delta {{P}^{j}}\theta $(5.2)
$yB{{k}^{4}}(\omega - {{c}^{f}}k)(\omega - {{c}^{m}}k) + {{k}^{2}}\left( {\omega - \bar {c}k} \right) = 0$(5.3)
${{c}^{f}} = - \frac{{1 - \alpha }}{\Gamma }\frac{{\partial {{F}^{f}}}}{{\partial {{s}^{f}}}}u,\quad {{c}^{m}} = - \frac{\alpha }{{1 - \Gamma }}\frac{{\partial {{F}^{m}}}}{{\partial {{s}^{m}}}}u,\quad \bar {c} = - \frac{{\partial{ \bar {F}}}}{{\partial{ \bar {s}}}}u$В случае равновесной фильтрации (B = 0) уравнение (5.2) упрощается к виду
В точности такое же дисперсионное уравнение имеет и эффективная модель одинарной пористости (3.5) [15]. Таким образом, при B = 0 существует одно решение эллиптического типа ${{k}^{2}}$ = 0, описывающее мгновенное распространение возмущений давления в несжимаемой среде (по одному в положительном и отрицательном направлениях оси x). При этом имеется и одно возмущение гиперболического типа (т.е. характеристика) $\omega = \bar {c}k$, описывающее распространение бесконечно малых фронтов вытеснения. При значениях B = 0 на каждом из разрывов ${{S}_{i}}$ выполняются три условия: два закона сохранения массы каждой из жидкостей $i = 1,2$ и условие непрерывности давления. В каждую сторону от разрыва ${{S}_{i}}$ уходит по малому возмущению типа ${{k}^{2}} = 0$, поэтому для эволюционности ${{S}_{i}}$ необходимо потребовать, чтобы характеристика $\bar {c}$ (как перед разрывом, так и за ним) от него не уходила [14]. Так как ${{O}_{1}}{{O}_{2}}{{O}_{3}}{{O}_{4}}{{O}_{5}}$ – огибающая к кривой $\bar {F}(\bar {s})$ (см. рис. 3), то это условие выполняется для каждого ${{S}_{i}}$ [12], т.е. при значениях B = 0 оба разрыва ${{S}_{i}}$ эволюционны.
Учитывая, что $\omega \to \infty $ и $k \to \infty $, в случае неравновесной фильтрации ($B \ne 0$) дисперсионное уравнение (5.2) сводится к виду
В этом случае существует два решения типа ${{k}^{2}} = 0$, соответствующих двум несжимаемым средам Φf и Φm и две характеристики $\omega = {{с}^{j}}k$, $j = f,m$, описывающие распространение бесконечно малых фронтов вытеснения в Φf и Φm соответственно. При $B \ne 0$ на разрывах ${{S}_{i}}$ выполняется 6 условий: в каждой среде Φf и Φm по два закона сохранения массы жидкостей $i = 1,2$ и условие непрерывности давления. В каждую сторону от ${{S}_{i}}$ уходит по два малых возмущения типа ${{k}^{2}} = 0$, поэтому для эволюционности разрыва ${{S}_{i}}$ необходимо потребовать, чтобы от него уходила только одна из характеристик cf или cm перед разрывом ${{S}_{i}}$ или за ним [14]. Используя соотношения (5.3), можно показать, что при (4.1) от каждого разрыва ${{S}_{i}}$ уходит по две характеристические скорости, т.е. при $B \ne 0$ разрывы не эволюционны. Это объясняется тем, что в рамках полной модели (2.3)–(2.5) ${{S}_{i}}$ нужно рассматривать не как разрывы, а как узкие переходные слои толщины порядка ${{\max (B,E)} \mathord{\left/ {\vphantom {{\max (B,E)} X}} \right. \kern-0em} X}$, в которых из-за неравновесных эффектов насыщенности непрерывно изменяются от значений перед разрывом до значений за ним. Разрывы ${{S}_{i}}$ – узкие, но имеют достаточно протяженные переходные слои, несмотря на то, что у модели (2.3)–(2.5) есть две характеристические скорости.
ЗАКЛЮЧЕНИЕ
В рамках обобщенной постановки задачи Баклея−Леверетта исследованы нелинейные волны при двухфазной фильтрации в трещиновато-пористых средах. Определены критерии подобия, характеризующие влияние капиллярного давления на распределение параметров течения в пространстве и на локальное равновесие между трещинами и блоками. Показано, что эти параметры убывают обратно-пропорционально характерному пространственному масштабу течения (или его характерному времени). Получены уравнения эффективной модели одинарной пористости, описывающие параметры равновесного течения в предельном случае бесконечно большого пространственного масштаба. Показано, что в условиях локального равновесия течение в трещиновато-пористой среде может сопровождаться формированием последовательности двух фронтов вытеснения. Продемонстрировано, что распределения параметров течения в переходных слоях, соответствующих данным фронтам, определяется не только капиллярным давлением, но и неравновесными перетоками между трещинами и блоками. Даны оценки влияния капиллярного давления и неравновесных процессов на протяженность переходных слоев.
Работа выполнена при финансовой поддержке Совета по грантам Президента РФ (МД-3567.2018.1).
Список литературы
Баренблатт Г.И., Желтов Ю.П., Кочина И.Н. Об основных представлениях теории фильтрации однородных жидкостей в трещиноватых породах // ПММ. 1960. Т. 24. Вып. 5. С. 852–864.
Warren J.E., Root P.J. The behavior of naturally fractured reservoirs // SPE J. 1963. V. 3. N 3. P. 245–255.
de Swaan A. Theory of waterflooding in fractured reservoirs // SPE J. 1978. V. 18. P. 117–122.
Firoozabadi A., Kent L.T. Sixth SPE comparative solution project: dual-porosity simulators // J. Pet. Tech. 1989. V. 43. № 6. P. 710–764.
Afanasyev A. Reservoir simulation with MUFITS code: Extension for double porosity reservoirs and flows in horizontal wells // Energy Proc. 2017. V. 125. P. 596–603.
Douglas J.Jr., Paes-Leme P.J., Hensley J.L. A limit form of the equations for miscible displacement in a fractured reservoir // Transp. Porous Media. 1991. V. 6. P. 549–565.
Kazemi H., Gillman J.R., Eisharkawy A.M. Analytical and numerical solution of oil recovery from fractured reservoirs with empirical transfer functions // SPE Res. Eng. 1992. V. 7. № 2. P. 219–227.
Дмитриев Н.М., Максимов В.М. Модели фильтрации в трещиновато-пористых анизотропных средах // Изв. РАН МЖГ. 2007. № 6. С. 78–84.
Kazemi H., Merill L.S., Porterfield K.L., Zeman P.R. Numerical simulation of water-oil flow in naturally fractured reservoirs // SPE J. 1976. V. 16. № 6. P. 317–326.
Brooks A.N., Corey A.T. Hydraulic properties of porous media. Hydrology Papers 3. Colorado State University, 1964.
Buckley S.E., Leverett M.C. Mechanism of fluid displacement in sands // Trans. AIME. 1942. V. 146. P. 107–116.
Баренблат Г.И., Ентов В.М., Рыжик В.М. Движение жидкостей и газов в природных пластах. М.: Недра, 1984. 211 с.
Erlich R. Relative permeability characteristics of vugular cores – their measurements and significance// 1971. SPE-paper N SPE-3553-MS.
Куликовский А.Г., Свешникова Е.И. Нелинейные волны в упругих средах. М.: Моск. лицей, 1998. 412 с.
Афанасьев A.А. Математическая модель неизотермической многофазной фильтрации бинарной смеси // Изв. РАН. МЖГ. 2011. № 1. С. 104–115.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика жидкости и газа


