1. На главную
  2. Электронные версии
  3. Известия РАН. Механика жидкости и газа
  4. № 3, 2020

Известия РАН. Механика жидкости и газа, 2020, № 3, стр. 26-35

ИССЛЕДОВАНИЕ НЕСТАЦИОНАРНЫХ ТЕЧЕНИЙ С ПОВЕРХНОСТЬЮ РАЗДЕЛА МЕТОДОМ ЧИСЛЕННОГО РЕШЕНИЯ УРАВНЕНИЙ НАВЬЕ–СТОКСА

А. И. Алексюк a, b, *, В. Я. Шкадов a, **

a Московский государственный университет им. М.В. Ломоносова
Москва, Россия

b Институт водных проблем РАН
Москва, Россия

* E-mail: aleksyuk@mech.math.msu.su
** E-mail: shkadov@mech.math.msu.su

Поступила в редакцию 07.11.2019
После доработки 17.12.2019
Принята к публикации 17.12.2019

Полный текст (PDF)

Аннотация

Рассматриваются течения двух неперемешивающихся жидкостей с учетом капиллярных сил и силы тяжести. Движение жидкостей описывается в рамках модели вязкой несжимаемой жидкости в двумерной постановке. Уравнения Навье–Стокса численно решаются расширенным методом конечных элементов (extended finite element method), который допускает наличие сильных разрывов на поверхности раздела. Положение границы раздела отслеживается с помощью метода функции уровня (level set method). Такой подход позволяет исследовать течения с меняющейся топологией поверхности раздела. Приводятся результаты решения задач о всплытии “двумерного пузыря”, о развитии неустойчивости Рэлея–Тейлора и о стекании пленки по вертикальной стенке в протяженнойобласти.

Ключевые слова: двухфазные течения, уравнения Навье–Стокса, метод функции уровня, течение пленки, двумерный пузырь, неустойчивость Рэлея–Тейлора

Сеточные методы моделирования нестационарных течений с поверхностью раздела можно разделить на методы с явным выделением границы раздела на деформируемых сетках и методы, в которых положение поверхности раздела может быть определено на неподвижных сетках. В первом классе методов во время счета граница раздела совпадает с линией сетки, что дает возможность относительно просто учитывать разрывы функций и их производных в расчетной схеме. Наиболее распространенными представителями второго класса методов являются метод объема жидкости в ячейке (volume of fluid method) и метод функции уровня (level set method). Преимуществом последнего метода является то, что граница раздела не сглаживается и может быть определена неявно с помощью вспомогательной функции – функции уровня, для которой решается уравнение переноса. Это позволяет явно рассматривать разрывы функций в математической формулировке метода. Наличие разрывов внутри ячеек может быть учтено, в частности, с помощью расширенного метода конечных элементов XFEM (extended finite element method) [1], в котором стандартные пространства пробных и весовых функций дополняются набором функций, допускающих разрывы на ячейках. Основное преимущество второго класса методов заключается в большей универсальности, например, при моделировании течений с меняющейся топологией поверхности раздела.

В настоящей статье описывается реализация метода функции уровня в сочетании с расширенным методом конечных элементов [2–5] для моделирования двухфазных течений неперемешивающихся жидкостей в протяженных областях с учетом капиллярных сил, силы тяжести и возможности сложных деформаций поверхности раздела. Представлено тестирование алгоритмов на примере задач о всплытии “двумерного пузыря”, неустойчивости Рэлея–Тейлора. Обсуждаются результаты применения этого метода к задаче о развитии течения пленки в протяженной области.

1. ПОСТАНОВКА ЗАДАЧИ

Двумерное течение двух несжимаемых вязких жидкостей, разделенных поверхностью ${{\Gamma }_{S}}(t)$, описывается уравнениями Навье–Стокса:

(1.1)
${\mathbf{u}}_{{,t}}^{\alpha } + ({{{\mathbf{u}}}^{\alpha }} \cdot \nabla ){{{\mathbf{u}}}^{\alpha }} = - \frac{1}{{{{\rho }^{\alpha }}}}\nabla \cdot {{{\mathbf{P}}}^{\alpha }} + {\mathbf{F}}$
(1.2)
$\nabla \cdot {{{\mathbf{u}}}^{\alpha }} = 0$

Здесь индекс α принимает значения 1 и 2 для параметров первой и второй жидкости соответственно; ρα – плотность; ${{{\mathbf{u}}}^{\alpha }}({\mathbf{x}},t) = (u_{1}^{\alpha },u_{2}^{\alpha })$ и ${\mathbf{F}} = (Fcos\theta ,Fsin\theta )$ – векторы скорости и массовых сил; ${{{\mathbf{P}}}^{\alpha }}({\mathbf{x}},t)$ – тензор напряжений, компоненты которого имеют следующий вид в декартовых координатах ${\mathbf{x}} = ({{x}_{1}},{{x}_{2}})$:

$P_{{ij}}^{\alpha }({\mathbf{x}},t) = - {{p}^{\alpha }}{{\delta }_{{ij}}} + {{\mu }^{\alpha }}\left( {u_{{i,j}}^{\alpha } + u_{{j,i}}^{\alpha }} \right)$
где ${{p}^{\alpha }}({\mathbf{x}},t)$ и μα – давление и коэффициент динамической вязкости; ${{\delta }_{{ij}}}$ – символ Кронекера; ${{( \cdot )}_{{,i}}} = \partial {\text{/}}\partial {{x}_{i}}$, ${{( \cdot )}_{{,t}}} = \partial {\text{/}}\partial t$.

На поверхности раздела выполняются условия

${{{\mathbf{u}}}^{1}} = {{{\mathbf{u}}}^{2}},\quad ({{{\mathbf{P}}}^{1}} - {{{\mathbf{P}}}^{2}}) \cdot {\mathbf{n}} = \sigma \kappa {\mathbf{n}},\quad {\mathbf{x}} \in {{\Gamma }_{S}}$

Здесь $\sigma $ и $\kappa ({\mathbf{x}},t){{{\text{|}}}_{{{\mathbf{x}} \in {{\Gamma }_{S}}}}}$ – постоянный коэффициент поверхностного натяжения и кривизна линии раздела двух жидкостей, n – вектор нормали. На неподвижных границах рассматриваемой области течения $\Omega $ ставятся условия Дирихле или Неймана для скорости, либо задается вектор напряжений. В начальный момент времени известно положение поверхности раздела и поле скорости.

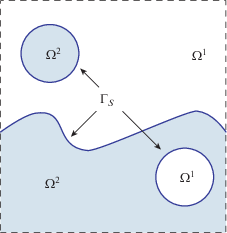
Представим $\Omega $ в виде объединения областей Ω1 и Ω2 (рис. 1), занимаемых первой и второй жидкостями, и введем общие обозначения для параметров двух сред, опуская индекс α, например, для давления: $p({\mathbf{x}},t) = {{p}^{\alpha }}({\mathbf{x}},t)$, если ${\mathbf{x}} \in {{\Omega }^{\alpha }}$.

Рис. 1.

Схема области двухфазного течения с границей раздела.

Пусть ${{L}_{0}}$, ${{U}_{0}}$, ${{\rho }_{0}}$ и ${{\mu }_{0}}$ – характерные длина, скорость, плотность и вязкость (в качестве последних двух параметров можно выбрать плотность и вязкость одной из сред). В результате обезразмеривания по формулам (штрихом ' обозначены безразмерные параметры)

$t{\text{'}} = \frac{{t{{U}_{0}}}}{{{{L}_{0}}}},\quad {\mathbf{x}}{\text{'}} = \frac{{\mathbf{x}}}{{{{L}_{0}}}},\quad {\mathbf{u}}{\text{'}} = \frac{{\mathbf{u}}}{{{{U}_{0}}}},\quad p{\text{'}} = \frac{p}{{{{\rho }_{0}}U_{0}^{2}}},\quad \rho {\text{'}} = \frac{\rho }{{{{\rho }_{0}}}},\quad \mu {\text{'}} = \frac{\mu }{{{{\mu }_{0}}}},\quad \kappa {\text{'}} = \kappa {{L}_{0}}$
в задаче возникают безразмерные комбинации, характеризующие течение:

${\text{Re}} = \frac{{{{\rho }_{0}}{{U}_{0}}{{L}_{0}}}}{{{{\mu }_{0}}}},\quad {\text{We}} = \frac{\sigma }{{{{\rho }_{0}}U_{0}^{2}{{L}_{0}}}},\quad {\text{Fr}} = \frac{{U_{0}^{2}}}{{F{{L}_{0}}}},\quad \frac{{{{\rho }^{1}}}}{{{{\rho }^{2}}}},\quad \frac{{{{\mu }^{1}}}}{{{{\mu }^{2}}}}$

Штрихи над безразмерными параметрами далее опускаем.

2. ЧИСЛЕННЫЙ МЕТОД

В разделе кратко описываются ключевые составляющие применяемого подхода. Основные идеи реализованных в работе алгоритмов для моделирования течений с границей раздела, а также другие вариации рассматриваемых методов подробно обсуждаются в работах [2–5].

Для отслеживания движения границы раздела применяется метод функции уровня [6]. Вводится функция $\varphi ({\mathbf{x}},t)$, которая обладает следующими свойствами:

1. ${{\Gamma }_{S}}(t) = \{ {\mathbf{x}}:\varphi ({\mathbf{x}},t) = 0\} $;

2. $\varphi ({\mathbf{x}},t) > 0$, если ${\mathbf{x}} \in {{\Omega }^{1}}$ и $\varphi ({\mathbf{x}},t) < 0$, если ${\mathbf{x}} \in {{\Omega }^{2}}$;

3. ${\text{|}}\varphi ({\mathbf{x}},t){\text{|}} = mi{{n}_{{{{{\mathbf{x}}}_{S}} \in {{\Gamma }_{S}}}}}{\text{|}}{\mathbf{x}} - {{{\mathbf{x}}}_{S}}{\text{|}}$.

Первые два свойства этой функции сохраняются, если она удовлетворяет уравнению переноса

(2.1)
${{\varphi }_{{,t}}} + {\mathbf{u}} \cdot \nabla \varphi = 0$

Третье условие позволяет получить направление нормали к поверхности раздела, используя соотношение ${\mathbf{n}} = \nabla \varphi $ при ${\mathbf{x}} \in {{\Gamma }_{S}}$. Однако для сохранения этого свойства необходимо периодически проводить реинициализацию функции $\varphi ({\mathbf{x}},t)$ так, чтобы выполнялось третье свойство и положение границы раздела ($\varphi ({\mathbf{x}},t) = 0$) не изменялось.

Начально-краевая задача для уравнений Навье–Стокса численно решается стабилизированным методом конечных элементов GLS (Galerkin/Least-Squares). Возможные разрывы решения и его производных на границе раздела описываются с помощью расширенного метода конечных элементов XFEM (Extended Finite Element Method) [1–5]. Расчетная область $\Omega $ представляется в виде объединения прямоугольников ${{\Omega }_{e}}$, $e = 1,...,{{n}_{e}}$, регулярной сетки с шагами ${{\Delta }_{1}}$, ${{\Delta }_{2}}$ вдоль координат x1 и x2, сетка имеет m узлов ${{{\mathbf{x}}}_{i}}$. Стандартные конечномерные аппроксимации пространств пробных и весовых функций на сетке дополняются функциями, которые допускают сильные разрывы давления внутри ячеек, содержащих границу раздела. Приближенное решение ${{{\mathbf{u}}}^{h}},{{p}^{h}}$ ищется в виде

(2.2)
${{{\mathbf{u}}}^{h}}({\mathbf{x}},t) = \sum\limits_{i = 1}^m \,{{{\mathbf{v}}}_{i}}{{N}_{i}}({\mathbf{x}});\quad {{p}^{h}}({\mathbf{x}},t) = \sum\limits_{i = 1}^m \,{{p}_{i}}{{N}_{i}}({\mathbf{x}}) + \sum\limits_{k = 1}^{m{\text{*}}} \,p_{k}^{*}{{M}_{k}}({\mathbf{x}},t)$

Здесь ${{{\mathbf{v}}}_{i}}$, ${{p}_{i}}$, $p_{k}^{*}$ – искомые коэффициенты, зависящие от времени; ${{N}_{i}}({\mathbf{x}})$ – кусочно-билинейные непрерывные функции, ${{N}_{i}}({{{\mathbf{x}}}_{j}}) = {{\delta }_{{ij}}}$; $i = 1,...,m$, $j = 1,...,m$, $k = 1,...,m{\text{*}}$. Вторая сумма в выражении для ph проводится по узлам каждой ячейки, содержащей границу раздела. Функции ${{M}_{k}}({\mathbf{x}},t)$ определяются на этих ячейках следующим образом:

${{M}_{k}}({\mathbf{x}},t) = N_{k}^{*}({\mathbf{x}})\left[ {\psi ({\mathbf{x}},t) - \psi ({{{\mathbf{x}}}_{k}},t)} \right],\quad \psi ({\mathbf{x}},t) = \left\{ \begin{gathered} - 1,\quad \varphi ({\mathbf{x}},t) < 0 \hfill \\ 0,\quad \varphi ({\mathbf{x}},t) = 0 \hfill \\ 1,\quad \varphi ({\mathbf{x}},t) > 0 \hfill \\ \end{gathered} \right.$
где $N_{k}^{*}$ – сужение функции Nk на ячейки, содержащие границу раздела ΓS. Отметим, что для скорости в (2.2) используется стандартная аппроксимация. Дискретизация по времени проводилась с помощью неявной схемы Эйлера первого порядка с постоянным шагом Δt.

Для того, чтобы избежать явного нахождения кривизны $\kappa $ при численном решении, используется подход с применением оператора Лапласа–Бельтрами, описанный, например, в [2].

Уравнение переноса (2.1) также решается стабилизированным методом конечных элементов. На каждой глобальной итерации по времени используется метод последовательных приближений, c помощью которого достигается согласованность решения уравнений движения (1.1), (1.2) и решения уравнения (2.1) для определения поверхности раздела. Система линейных алгебраических уравнений с плохо обусловленной матрицей для уравнений (1.1), (1.2) решается прямым методом LU-разложения, что позволяет избежать проблемы, связанной с плохой сходимостью итерационных методов из-за расширения пространств пробных и весовых функций [8].

Используемый в работе стабилизированный метод конечных элементов ранее успешно применялся авторами для исследования однофазных течений, возникающих при двумерном и трехмерном обтекании тел потоком вязкой жидкости (газа) [9–11]. Кроме того, в этих работах можно найти результаты тестирования метода для однофазных течений, а также детали, касающиеся реализации алгоритмов. В следующих разделах приводятся результаты применения описанного метода для трех задач с поверхностью раздела. Первые две задачи – классические примеры для тестирования численных алгоритмов расчета двухфазных потоков, см., например, [12, 13]. Третья задача является демонстрацией возможности применения метода для расчета течений в протяженных областях с перестройками волновых структур.

3. РЕЗУЛЬТАТЫ ПРИМЕНЕНИЯ МЕТОДА

3.1. Всплытие “двумерного пузыря”

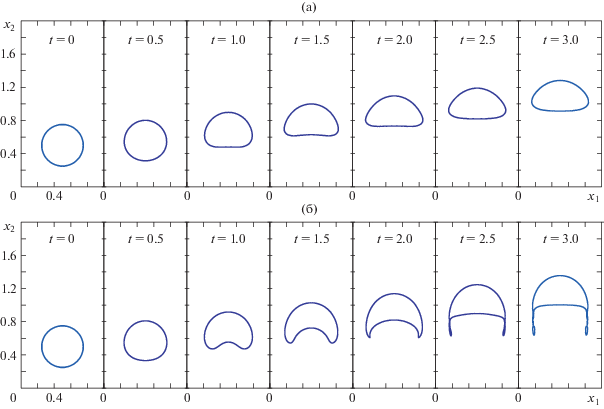
Моделируются два режима всплытия двумерного пузыря с учетом капиллярных сил (см. табл. 1). Эти режимы являются искусственными тестами [12], в первом из которых параметры подобраны так, что пузырь деформируется слабо (рис. 2а), во втором – в некоторый момент времени происходит изменение топологии поверхности раздела – от основного пузыря отделяются вторичные (рис. 2б). В [12] приведены результаты численных расчетов с использованием программных кодов трех независимых групп исследователей.

Таблица 1.

Рассматриваемые в работе режимы всплытия “двумерного” пузыря

Режим ρ1 (кг/м3) ρ2 (кг/м3) μ1 (кг/(м · с)) μ2 (кг/(м · с)) $\sigma $ (кг/c2) ${{\Delta }_{1}}( = {{\Delta }_{2}}),\Delta t$
I 1000 100 10 1 24.5 0.02, 0.002
II 1000 1 10 0.1 1.96 0.005, 0.001
Рис. 2.

Эволюция границы раздела всплывающего “двумерного пузыря” для режимов I (а) и II (б).

Далее результаты представлены в размерном виде для удобства сопоставления с [12]. В начальный момент обе жидкости покоятся, а поверхность раздела представляет собой окружность радиуса 0.25 м с центром в точке ${{x}_{1}} = 0.5$ м, ${{x}_{2}} = 0.5$ м. В поле силы тяжести $F = 0.98$ м/с2, $\theta = - \pi {\text{/}}2$ более легкая жидкость (двумерный пузырь) начинает всплывать. Область течения представляет собой прямоугольник $\{ 0 \leqslant {{x}_{1}} \leqslant 1;\;0 \leqslant {{x}_{2}} \leqslant 2\} $, у которого на границах ${{x}_{2}} = 0$, ${{x}_{2}} = 2$ ставятся условия прилипания, а на границах ${{x}_{1}} = 0$, ${{x}_{1}} = 1$ – проскальзывания.

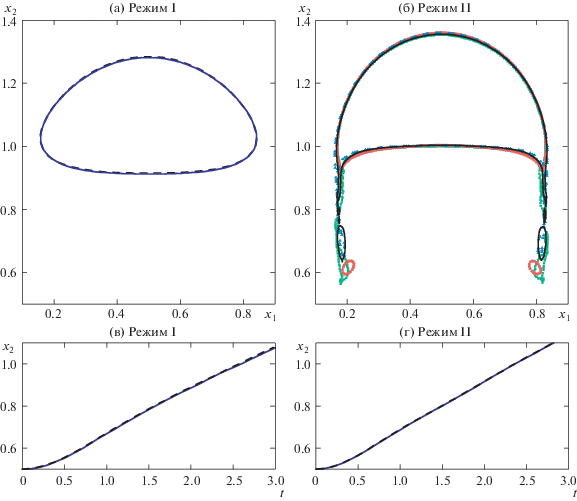
Сопоставление поверхности раздела при t = 3 c и зависимости ординаты центра масс пузыря от времени с данными [12] приведено на рис. 3. Заметное количественное отличие наблюдается только при описании процесса отделения вторичных пузырей, в остальном результаты хорошо согласуются. Авторы [12] отмечают, что во втором тесте все три рассмотренные программы также по-разному описывают процесс отделения вторичных пузырей, несмотря на полную согласованность результатов до начала этого процесса (а также для первого теста). На рисунке видно, что результаты расчета в настоящей работе оказались наиболее близки к алгоритму MooNMD, в котором использовались деформируемые сетки с узлами, перемещающимися вместе с границей раздела.

Рис. 3.

Граница раздела при t = 3 (а, б) и зависимость x2-координаты центра масс всплывающего “двумерного пузыря” от времени (в, г) для режимов I (а, в) и II (б, г). Сплошная линия – результаты настоящей работы; штриховая линия и точки – данные [12]; три разных маркера точек на рисунке (б) соответствуют расчетам по трем разным программам; на рисунках (а), (в), (г) штриховая линия соответствует расчету с использованием кода MooNMD [12] (для режима I результаты по двум другим программам в масштабе рисунков ложатся на приведенные штриховые кривые).

3.2. Неустойчивость Рэлея–Тейлора

В поле силы тяжести покоятся два слоя жидкости, разделенные горизонтальной поверхностью. Рассматривается ситуация, когда такое положение равновесия неустойчиво: жидкость сверху имеет большую плотность, чем жидкость снизу. В начальный момент времени вносятся возмущения поверхности раздела. Капиллярные силы не учитываются.

На рис. 4 приведено сопоставление с данными [13] для следующих параметров. Область течения представляет собой прямоугольник $\{ 0 \leqslant {{x}_{1}} \leqslant 1;\;0 \leqslant {{x}_{2}} \leqslant 2\} $ с условиями прилипания на границе. Возмущение поверхности раздела в начальный момент времени задается уравнением x2 = = $1 - 0.15{\text{sin}}2\pi {{x}_{1}}$. Плотности жидкостей отличаются в 1.8 раза, коэффициенты кинематической вязкости совпадают. Число Рейнольдса Re = 420 (характерный размер ${{L}_{0}}$ – длина области вдоль координаты x1, характерная скорость ${{U}_{0}} = \sqrt {{{L}_{0}}g} $, где g – величина ускорения свободного падения).

Рис. 4.

Эволюция границы раздела между тяжелой и легкой жидкостью для задачи о неустойчивости Рэлея–Тейлора. Граница раздела изображена при t = 1 (а), 3 (б), 5 (в). Сплошная линия – результаты настоящей работы на сетке 100 × 200; штриховая линия – данные [13] на сетке 312 × 624.

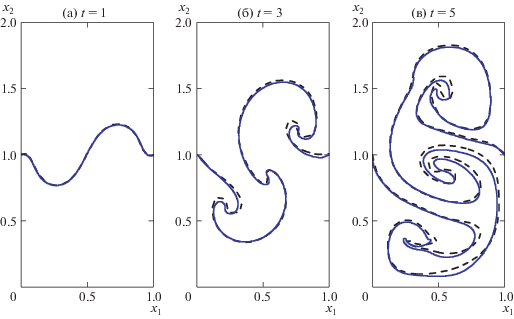
Расчеты проведены на сетке с шагами по пространству и времени ${{\Delta }_{1}} = {{\Delta }_{2}} = 0.01$, $\Delta t = 0.005$. Для сопоставления на рис. 4 представлены данные, полученные в [13] с помощью метода функции уровня на сетке 312 × 614. Несмотря на качественное совпадение, результаты имеют некоторые отличия, которые могут быть связаны с разрешением сетки.

3.3. Стекание пленки по плоской вертикальной стенке

Рассматриваются пять режимов стекания пленки по вертикальной стенке, которые представлены в табл. 2. В качестве характерных размерных параметров выбраны: плотность (${{\rho }_{0}}$), динамическая вязкость (${{\mu }_{0}}$) и толщина (${{L}_{0}}$) пленки, характерная скорость – ${{U}_{0}} = gL_{0}^{2}{{\rho }_{0}}{\text{/}}(3{{\mu }_{0}})$. Параметры второй среды выбраны таким образом, чтобы их влияние на течение было несущественным: ${{\rho }^{1}}{\text{/}}{{\rho }^{2}} = {{10}^{3}}$, ${{\mu }^{1}}{\text{/}}{{\mu }^{2}} = 5 \times {{10}^{{ - 3}}}$.

Таблица 2.

Рассматриваемые в работе режимы стекания пленки и комплексные волновые числа, которые являются решениями дисперсионных соотношений (3.1) и (3.2) с положительной фазовой скоростью и наименьшим по модулю отрицательным коэффициентом усиления ki при $\omega = f{\text{/}}2\pi $

Режим Re We f Область ${{\Delta }_{1}},{{\Delta }_{2}},\Delta t$ k – решение (3.1) k – решение (3.2)
A 16.2 46.87 0.0054 1500 × 5 1, 0.1, 0.0050 0.01138 – 0.00068i 0.01141 – 0.00082i
B 16.2 46.87 0.0252 600 × 2.2 1, 0.1, 0.0025 0.05847 – 0.01147i 0.06028 – 0.01294i
C 16.2 46.87 0.0404 1000 × 2.5 1, 0.1, 0.0020 0.10260 – 0.01787i 0.10680 – 0.01882i
D 16.2 46.87 0.0718 1500 × 5 1, 0.1, 0.0050 0.17656 – 0.00861i 0.18236 – 0.00819i
E 32.4 46.87 0.0718 1500 × 5 1, 0.1, 0.0050 0.17839 – 0.00453i 0.18390 – 0.00426i

В начальный момент времени поверхность раздела ${{\Gamma }_{S}}$ задается соотношением ${{x}_{2}} = 1$, а параметры потока соответствуют стационарному решению с параболическим профилем скорости ${{u}_{1}}({\mathbf{x}},0) = 1.5{{x}_{2}}(2 - {{x}_{2}})$, ${{u}_{2}}({\mathbf{x}},0) = 0$. На вертикальной плоской стенке (x2 = 0) ставится условие прилипания. На входной границе (${{x}_{1}} = 0$) фиксируется толщина пленки и задается периодическое изменение скорости: ${{u}_{1}}(0,{{x}_{2}},t) = 1.5{{x}_{2}}(2 - {{x}_{2}})\left[ {1 + asin(2\pi ft)} \right]$, ${{u}_{2}}(0,{{x}_{2}},t) = 0$, где a и f – заданные амплитуда и частота пульсаций скорости на входе. На выходной границе (${{x}_{1}} = L$) ставятся мягкие граничные условия ${{u}_{{1,1}}}(L,{{x}_{2}},t) = {{u}_{{2,1}}}(L,{{x}_{2}},t) = 0$. Размеры расчетной области, шаги по пространству и времени, а также значения параметров Re, We и f приведены в табл. 2 (амплитуда $a = 0.03$ для режимов B–E и $a = 0.1$ для режима A).

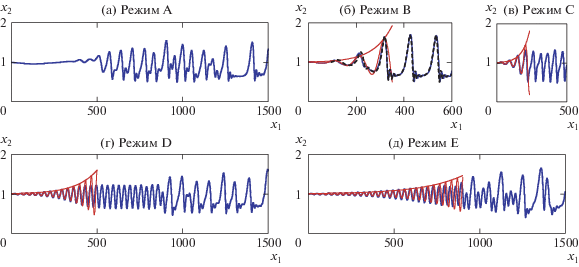
Зависимости толщины пленки от продольной координаты для режимов A-E изображены на рис. 5. Начальный этап развития волн может быть описан с помощью линейной теории устойчивости. Линеаризуя эволюционные уравнения Шкадова [14] и используя метод нормальных мод (толщина пленки разыскивается в виде $h({{x}_{1}},t) = 1 + \varepsilon expi(k{{x}_{1}} - \omega t)$), получим дисперсионное соотношение

(3.1)
$\frac{1}{3}{\text{ReWe}}{{k}^{4}} - \frac{2}{5}{\text{Re}}{{k}^{2}} + \left( {3i + \frac{4}{5}\omega {\text{Re}}} \right)k - \frac{1}{3}{\text{Re}}{{\omega }^{2}} - i\omega = 0$
Рис. 5.

Граница раздела для режимов A–E: сплошная линия (синяя) – настоящая работа; штриховая линия (черная) на рисунке (б) – данные [16]; тонкая сплошная линия (красная) – линейный этап роста возмущений, соответствующий решению уравнения (3.2).

Также рассматривается дисперсионное соотношение, полученное из уравнений второго порядка [15], в котором учитывается отклонение от параболического профиля скорости, используемого в методе Капицы–Шкадова

(3.2)
$\frac{1}{3}{\text{ReWe}}{{k}^{4}} + \frac{{12}}{5}i{{k}^{3}} - \left( {\frac{{18}}{{35}}{\text{Re}} + \frac{9}{5}i\omega } \right){{k}^{2}} + \left( {3i + \frac{{34}}{{35}}\omega {\text{Re}}} \right)k - \frac{2}{5}{\text{Re}}{{\omega }^{2}} - i\omega = 0$

В уравнениях (3.1), (3.2) разыскивается комплексное волновое число $k = {{k}_{r}} + i{{k}_{i}}$, а частота ω считается известной и связана с вынужденной частотой на входе – $f = 2\pi \omega $. Если коэффициент усиления ki отрицательный (положительный), то волны растут (затухают) по пространству. Подробный вывод дисперсионных соотношений, например, приведен в [15].

Для рассматриваемых случаев уравнения (3.1) и (3.2) имеют три корня, которые соответствуют растущим решениям, и один – затухающему. Так, например, для режима E корнями дисперсионного соотношения (3.1) являются

(3.3)
$0.1784 - 0.0045i;\quad 0.1073 - 0.2346i;\quad - 0.3558 - 0.0217i;\quad 0.0700 + 0.2609i$

Реализующимся при численном моделировании режимов A–E решениям соответствуют корни с положительной фазовой скоростью и наименьшим по модулю значением коэффициента усиления ${{k}_{i}} < 0$, т.е. первый корень в данном случае. В табл. 2 приведены соответствующие корни для каждого режима. На рис. 5б–д представлено сопоставление результатов с линейной теорией устойчивости на основе дисперсионного соотношения (3.2) – для всех рассмотренных режимов скорости роста возмущений и волновые числа согласуются. Решение классического дисперсионного соотношения (3.1) дает близкие значения (см. табл. 2): частота отличается не более чем на 4%, по коэффициенту усиления отличие доходит до 11% и 16% при низких частотах (режимы A и B). На рис. 5а не представлено сопоставление с линейной теорией, поскольку в этом случае на фоне низкочастотных волн, определяемых частотой на входе, относительно быстро начинают нарастать более неустойчивые высокочастотные возмущения (см. рис. 5а при ${{x}_{1}} \approx 400$).

Режимы B–D ранее моделировались в работе [16] (см. рис. 2a, b и d в [16]), в которой для однофазных течений применялся конечно-разностный метод маркеров в ячейках (marker-and-cell method) на сетках ${{\Delta }_{1}} = 0.436$, ${{\Delta }_{2}} = 0.08333$ и $\Delta t = 0.01$. Результаты расчетов согласуются между собой: это, например, видно при сопоставлении нелинейного этапа формирования волн и предельного волнового режима на рис. 5б. Следует отметить, что предельные режимы также хорошо воспроизводятся путем определения оптимальных волн глобального аттрактора [17], полученного на основе интегральных эволюционных уравнений [14].

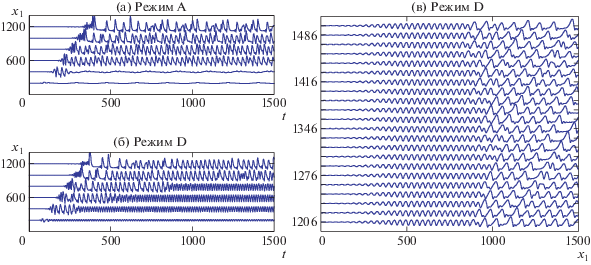
За развитием волновых структур можно проследить по графикам зависимости толщины от времени в фиксированных точках пространства и изменению поверхности раздела с течением времени, приведенным на рис. 6. Интересной особенностью, возникающей при численном моделировании, является волна, распространяющаяся в область безволнового решения. Для режимов A и D (с максимальным отличием по частоте возмущений во входном сечении) на рис. 6а, б видно, что распространение этой волны происходит с похожей скоростью, приближенно равной 4 (однако для режима A граница фронта на плоскости $(t,{{x}_{1}})$ немного смещена вправо, что связано с различием амплитуды возмущений во входном сечении). Кроме того, на протяжении некоторого интервала времени после прохождения волны зависимость толщины от времени качественно повторяется для режимов A и D. На рис. 6в наблюдаются два переходных этапа. Сначала в результате потери устойчивости безволнового режима формируются регулярные волны. Эти волны также оказываются неустойчивыми – возникает вторая область перехода к предельному волновому режиму. При этом граница существования режима с регулярными волнами может смещаться на расстояния порядка сотен толщин пленки.

Рис. 6.

Развитие границы раздела по времени и по пространству для режимов A и D: (а) и (б) – зависимости толщины пленки от времени для режимов A и D в точках x1 = 200; 400; 600; 800; 1000; 1200; (в) – граница раздела для режима D в разные моменты времени с шагом $\Delta t = 14$ (значение $1{\text{/}}\Delta t \approx 0.0714$ близко к частоте на входе, $f = 0.0718$).

ЗАКЛЮЧЕНИЕ

Представлены результаты применения метода функции уровня в сочетании с расширенным методом конечных элементов для численного решения уравнений Навье–Стокса, описывающих двухфазные течения с границей раздела. Рассмотрены три задачи о течении с поверхностью раздела: о всплытии двумерного пузыря, о развитии неустойчивости Рэлея–Тейлора и о стекании пленки по вертикальной стенке. Во всех случаях результаты согласуются с данными других авторов. Описанный подход позволяет проводить количественные расчеты нестационарных двухфазных течений с поверхностью раздела в протяженных областях, а также задач с изменяющейся топологией поверхности раздела.

Работа выполнена при финансовой поддержке РФФИ в рамках научных проектов № 18-01-00762 и № 18-51-00006.

Список литературы

  1. Moës N., Dolbow J., Belytschko T. A finite element method for crack growth without remeshing // Int. J. Numer. Meth. Eng. 1999. V. 46. № 1. P. 131–150. https://doi.org/10.1002/(SICI)1097-0207(19990910)46:1<131::AID-NME726>3.0.CO;2-J

  2. Fries T.P. The intrinsic XFEM for two-fluid flows // Int. J. Numer. Methods Fluids. 2009. V. 60. № 4. P. 437–471. https://doi.org/10.1002/fld.1901

  3. Fries T.P., Belytschko T. The extended/generalized finite element method: An overview of the method and its applications // Int. J. Numer. Meth. Eng. 2010. V. 84. № 3. P. 253–304. https://doi.org/10.1002/nme.2914

  4. Sauerland H. An XFEM Based Sharp Interface Approach for Two-Phase and Free-Surface Flows // Diss. RWTH Aachen. 2013.

  5. Sauerland H., Fries T.P. The extended finite element method for two-phase and free-surface flows: A systematic study // J. Comput. Phys. 2011. V. 230. № 9. P. 3369–3390. https://doi.org/10.1016/j.jcp.2011.01.033

  6. Osher S., Fedkiw R.P. Level set methods: An overview and some recent results // J. Comput. Phys. 2001. V. 169. № 2. P. 463–502. https://doi.org/10.1006/jcph.2000.6636

  7. Hughes T.J.R., Franca L.P., Hulbert G.M. A new finite element formulation for computational fluid dynamics: VIII. The Galerkin/least-squares method for advective-diffusive equations // Comput. Methods in Appl. Mech. Eng. 1989. V. 73. № 2. P. 173–189. https://doi.org/10.1016/0045-7825(89)90111-4

  8. Babuška I., Banerjee U. Stable Generalized Finite Element Method (SGFEM) // Comput. Methods in Appl. Mech. Eng. 2012. V. 201–204. P. 91–111. https://doi.org/10.1016/j.cma.2011.09.012

  9. Aleksyuk A.I., Shkadov V.Y. Analysis of three-dimensional transition mechanisms in the near wake behind a circular cylinder // Eur. J. Mech. B/Fluids. 2018. V. 72. P. 456–466. https://doi.org/10.1016/j.euromechflu.2018.07.011

  10. Aleksyuk A.I., Osiptsov A.N. Direct numerical simulation of energy separation effect in the near wake behind a circular cylinder // Int. J. Heat Mass Transfer. 2018. V. 119. P. 665–677. https://doi.org/10.1016/j.ijheatmasstransfer.2017.11.133

  11. Aleksyuk A.I. Influence of vortex street structure on the efficiency of energy separation // Int. J. Heat Mass Transfer. 2019. V. 135. P. 284–293. https://doi.org/10.1016/j.ijheatmasstransfer.2019.01.103

  12. Hysing S., Turek S., Kuzmin D., Parolini N., Burman E., Ganesan S., Tobiska L. Quantitative benchmark computations of two-dimensional bubble dynamics // Int. J. Numer. Methods Fluids. 2009. V. 60. № 11. P. 1259–1288. https://doi.org/10.1002/fld.1934

  13. Grenier N., Antuono M., Colagrossi A., Le Touzé, D., Alessandrini B. An Hamiltonian interface SPH formulation for multi-fluid and free surface flows // J. Comput. Phys. 2009. V. 228. № 22. P. 8380–8393. https://doi.org/10.1016/j.jcp.2009.08.009

  14. Шкадов В.Я. Волновые режимы течения тонкого слоя вязкой жидкости под действием силы тяжести // Изв. АН СССР. МЖГ. 1967. № 1. С. 43–51.

  15. Kalliadasis S., Ruyer-Quil C., Scheid B., Velarde M.G. Falling liquid films, V. 176 of Applied mathematical sciences. Springer London, London. 2012. https://doi.org/10.1007/978-1-84882-367-9

  16. Nosoko T., Miyara A. The evolution and subsequent dynamics of waves on a vertically falling liquid film // Phys. Fluids. 2004. V. 16. № 4. P. 1118–1126. https://doi.org/10.1063/1.1650840

  17. Белоглазкин А.Н., Шкадов В.Я., Кулаго А.Е. Предельные волновые режимы при пространственном и временном развитии возмущений в стекающей пленке жидкости // Вестн. Моск. ун-та. Сер. 1. Матем. Мех. 2019. № 3. С. 58–64.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал