Известия РАН. Механика жидкости и газа, 2020, № 3, стр. 12-25

КОЛЕБАНИЯ ЦИЛИНДРА В ЖИДКОСТИ ПОД ЛЕДЯНЫМ ПОКРОВОМ ВБЛИЗИ ВЕРТИКАЛЬНОЙ СТЕНКИ

Л. А. Ткачева^*

Институт гидродинамики им. М.А. Лаврентьева СО РАН
Новосибирск, Россия

Поступила в редакцию 11.12.2019
После доработки 17.12.2019
Принята к публикации 17.12.2019

DOI: 10.31857/S0568528120030135

Аннотация

Получено решение задачи о колебаниях кругового цилиндра в жидкости конечной глубины под ледяным покровом вблизи вертикальной стенки. Ледяной покров моделируется тонкой упругой полубесконечной пластиной постоянной толщины. Рассмотрены различные граничные условия на кромке пластины: свободный край и защемленный. Исследованы коэффициенты присоединенных масс и демпфирования, амплитуды прогиба и деформаций ледяного покрова, сил, действующих на стенку, в зависимости от частоты колебаний и входных параметров задачи.

Ключевые слова: тонкая упругая плавающая пластина, изгибно-гравитационные волны, преобразование Фурье, мультиполи, метод отражения, присоединенные массы, коэффициент демпфирования

Исследованию взаимодействия волн в жидкости с плавающими телами и конструкциями посвящено большое количество работ. Широкий круг математических методов решения таких задач содержится в [1]. В последнее время в связи с освоением полярных районов интерес вызывают задачи о взаимодействии волн с погруженными телами при наличии ледяного покрова. Методы, изложенные в [1], применимы и к этим задачам. Достаточно хорошо изучены задачи о колебаниях тел цилиндрической или сферической формы под бесконечным ледяным покровом. Обзор полученных результатов можно найти в работе [2]. Позднее появились работы [3–10]. В [3–6] для построения решения использован метод разложения потенциала по мультиполям – потенциалам, удовлетворяющим уравнению Лапласа и всем граничным условиям, кроме условий на теле. Ранее аналогичные мультиполи были введены для случая жидкости со свободной поверхностью [7]. В работах [8, 9] изучено движение диполя в жидкости под ледяным покровом, моделирующего движение тела. Движение подводной лодки в жидкости под ледяным покровом моделировалось с помощью системы источников и стоков в [10].

Однако в действительности ледяной покров может быть неоднородным. Он может покрывать не всю поверхность жидкости, могут быть трещины, полыньи. Влияние таких неоднородных условий на верхней границе изучалось в работах [11–19] для цилиндрического тела. В [11–14] использовался метод граничных интегральных уравнений, при этом в [11–13] функция Грина строилась методом сращивания разложений по собственным функциям, а в [14] методом Винера–Хопфа. Метод сращивания разложений по собственным функциям использован в [15] для построения решения о колебаниях цилиндрического прямоугольного тела в полынье между двумя полубесконечными ледяными пластинами. Решение задачи о колебаниях в полынье цилиндрического тела произвольной формы сечения приведено в [16] с помощью гибридного метода сращивания разложений и граничных элементов. В работе [17] в приближении широкой полыньи получено решение той же задачи на основе решений для полыньи без тела и плавающего тела без льда. Для кругового цилиндра под ледяным покровом с трещиной решение найдено в [18] с помощью мультипольных разложений. В этой работе построена функция Грина, удовлетворяющая краевым условиям на верхней и нижней границах жидкости в виде интеграла, и мультиполи получены дифференцированием функции Грина. В работе [19] приведено решение задачи о колебаниях тела в жидкости под ледяным покровом с многими трещинами, произвольно расположенными. Получена функция Грина, удовлетворяющая всем краевым условиям на верхней и нижней границах, условие на теле выполняется с помощью метода граничных интегральных уравнений. Нелинейный эффект движения тела в полынье изучался в [20] с помощью мультипольных разложений.

Взаимодействие изгибно-гравитационных волн в ледяном покрове с вертикальной стенкой (без погруженного тела) при различных краевых условиях на кромке, для неподвижной и колеблющейся стенки, изучалось в работах [21–23] с помощью преобразования Фурье. В [21] решение получено двумя методами, во втором методе используется интегральное уравнение первого рода.

В настоящей работе приведено решение задачи о колебаниях кругового цилиндра в жидкости под ледяным покровом при наличии неподвижной вертикальной стенки. Используются метод мультипольных разложений, метод отражения. Для выполнения условий в кромке ледяного покрова используется преобразование Фурье, однако способ получения решения отличается от предложенных в [21–23].

1. ПОСТАНОВКА ЗАДАЧИ

Ледяной покров моделируется упругой полубесконечной пластиной постоянной толщины $h$. Жидкость полагается идеальной несжимаемой, имеющей глубину H. Рассматриваются колебания жидкости и пластины при заданных колебаниях погруженного цилиндра с заданной частотой $\omega $. Задача решается в линейном приближении и двумерной постановке. Введем декартову систему координат $Oxy$ с центром $O$ на верхней границе жидкости, осью $Ox$, перпендикулярной стенке, осью $Oy$, направленной вдоль стенки вертикально вниз. Пластина занимает область x > 0. Цилиндр радиуса $a$ с центром в точке $({{x}_{0}},{{y}_{0}})$, $a < {{x}_{0}},a < {{y}_{0}}$ совершает поступательные колебания с амплитудами ${{A}_{j}}$, $j = 1,2$ вдоль декартовых осей. Введем также цилиндрические координаты $(r,\theta )$

$x = {{x}_{0}} + rsin\theta ,\quad y = {{y}_{0}} + rcos\theta ,\quad r = \sqrt {{{{(x - {{x}_{0}})}}^{2}} + {{{(y - {{y}_{0}})}}^{2}}} $

Потенциал течения жидкости $\varphi (x,y,t)$ удовлетворяет уравнению Лапласа

(1.1)

$\frac{{{{\partial }^{2}}\varphi }}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}\varphi }}{{\partial {{y}^{2}}}} = 0$

Колебания пластины описываются уравнениями изгиба тонких упругих пластин Кирхгофа–Лява

(1.2)

$D\frac{{{{\partial }^{4}}w}}{{\partial {{x}^{4}}}} + {{\rho }_{0}}h\frac{{{{\partial }^{2}}w}}{{\partial {{t}^{2}}}} = - p,\quad D = \frac{{E{{h}^{3}}}}{{12(1 - {{\nu }^{2}})}}$

(1.3)

$p = - \rho ({{\varphi }_{t}} - gw)$

где $w(x)$ – нормальный прогиб пластины, ${{\rho }_{0}}$, $\rho $ – плотности льда и жидкости, $p$ – гидродинамическое давление, $g$ – ускорение свободного падения, $D$ – цилиндрическая жесткость пластины, $E$ – модуль Юнга, $\nu $ – коэффициент Пуассона, $t$ – время.

Осадка пластины в воду не учитывается. Граничные условия на верхней границе жидкости сносятся на плоскость $y = 0$. Предполагается, что вся нижняя поверхность пластины находится в контакте с жидкостью, отрыва не происходит. Тогда выполнено кинематическое соотношение

(1.4)

${{w}_{t}} = \partial \varphi {\text{/}}\partial y\quad (y = 0)$

Потенциал течения жидкости можно представить в виде суммы по степеням свободы

$\varphi (x,y,t) = {\text{Re}}\left( { - i\omega a\sum\limits_{j = 1}^2 \,{{A}_{j}}{{\varphi }_{j}}(x,y)exp( - i\omega t)} \right)$

где каждый потенциал ${{\varphi }_{j}}$ удовлетворяет уравнению Лапласа (1.1). Введем также безразмерные переменные и параметры

$(x{\text{'}},y{\text{'}},a{\text{'}},x_{0}^{'},y_{0}^{'},H{\text{'}}) = (x,y,a,{{x}_{0}},{{y}_{0}},H){\text{/}}a,\quad \beta = \frac{D}{{\rho g{{a}^{4}}}},\quad \lambda = \omega \sqrt {a{\text{/}}g} ,\quad \delta = \frac{{{{\rho }_{0}}h{{\omega }^{2}}}}{{\rho g}}$

Штрихи далее будем опускать. Из (1.2)–(1.4) получаем для каждого потенциала ${{\varphi }_{j}}$ условие на верхней границе в виде

(1.5)

$\left( {\beta \frac{{{{\partial }^{4}}}}{{\partial {{x}^{4}}}} + 1 - \delta } \right)\frac{{\partial {{\varphi }_{j}}}}{{\partial y}} + {{\lambda }^{2}}{{\varphi }_{j}} = 0$

На дне, на стенке и цилиндре ставятся условия непротекания

(1.6)

$\partial {{\varphi }_{j}}{\text{/}}\partial y = 0\quad (y = H),\quad \partial {{\varphi }_{j}}{\text{/}}\partial x = 0\quad (x = 0)$

(1.7)

$\frac{{\partial {{\varphi }_{j}}}}{{\partial r}} = {{n}_{j}}\quad (r = 1)$

где $({{n}_{1}},{{n}_{2}}) = ({{n}_{x}},{{n}_{y}}) = (sin\theta ,cos\theta )$. Граничные условия на кромке пластины в случае свободного края имеют вид

(1.8)

$\frac{{{{\partial }^{3}}{{\varphi }_{j}}}}{{\partial {{x}^{2}}\partial y}}(0,0) = \frac{{{{\partial }^{4}}{{\varphi }_{j}}}}{{\partial {{x}^{3}}\partial y}}(0,0) = 0$

в случае защемленного края

(1.9)

$\frac{{\partial {{\varphi }_{j}}}}{{\partial y}}(0,0) = \frac{{{{\partial }^{2}}{{\varphi }_{j}}}}{{\partial x\partial y}}(0,0) = 0$

На бесконечности ставится условие излучения (условие отсутствия приходящих волн).

2. МЕТОД РЕШЕНИЯ

Для построения решения будем использовать метод отражения. Вводим еще один цилиндр с центром в точке $( - {{x}_{0}},{{y}_{0}})$, который колеблется таким образом, что его центр находится на одинаковом расстоянии от стенки, что и исходный цилиндр. Таким образом, отраженный цилиндр колеблется с амплитудами $ - {{A}_{1}}$, ${{A}_{2}}$ по осям x, y. Вводим цилиндрические координаты $({{r}_{1}},{{\theta }_{1}})$, связанные с этим цилиндром,

$x = - {{x}_{0}} + {{r}_{1}}sin{{\theta }_{1}},\quad y = {{y}_{0}} + {{r}_{1}}cos{{\theta }_{1}},\quad {{r}_{1}} = \sqrt {{{{(x + {{x}_{0}})}}^{2}} + {{{(y - {{y}_{0}})}}^{2}}} $

Используя результаты работ [1, 7, 24], каждый из потенциалов ${{\phi }_{j}}$ можно записать в виде разложения по мультиполям – функциям, которые удовлетворяют уравнению Лапласа и всем граничным условиям, кроме условия (1.7) на поверхности цилиндра. Для кругового цилиндра с центром в точке $({{x}_{0}},{{y}_{0}})$ в жидкости под бесконечным ледяным покровом в отсутствие стенки мультиполи имеют вид

$\phi _{n}^{c} = \frac{{cos(n\theta )}}{{{{r}^{n}}}} + \frac{1}{{(n - 1)!}}\int\limits_0^\infty \,[A(k){\text{sh}}(ky) + {{B}_{c}}(k){\text{ch}}(k(H - y))]{{k}^{{n - 1}}}cos(k(x - {{x}_{0}}))dk$

$\phi _{n}^{s} = \frac{{sin(n\theta )}}{{{{r}^{n}}}} + \frac{1}{{(n - 1)!}}\int\limits_0^\infty \,[A(k){\text{sh}}(ky) + {{B}_{s}}(k){\text{ch}}(k(H - y))]{{k}^{{n - 1}}}sin(k(x - {{x}_{0}}))dk$

$\begin{gathered} A(k) = \frac{{exp(k({{y}_{0}} - H))}}{{{\text{ch}}(kH)}}, \\ {{B}_{c}}(k) = \frac{{(\beta {{k}^{4}} + 1 - \delta )kexp(k({{y}_{0}} - H)){\text{/ch}}(kH)}}{{(\beta {{k}^{4}} + 1 - \delta )k{\text{sh}}(kH) - {{\lambda }^{2}}{\text{ch}}(kH)}} + \frac{{{{{( - 1)}}^{n}}((\beta {{k}^{4}} + 1 - \delta )k + {{\lambda }^{2}})exp( - k{{y}_{0}})}}{{(\beta {{k}^{4}} + 1 - \delta )k{\text{sh}}(kH) - {{\lambda }^{2}}{\text{ch}}(kH)}} \\ \end{gathered} $

${{B}_{s}}(k) = \frac{{(\beta {{k}^{4}} + 1 - \delta )kexp(k({{y}_{0}} - H)){\text{/ch}}(kH)}}{{(\beta {{k}^{4}} + 1 - \delta )k{\text{sh}}(kH) - {{\lambda }^{2}}{\text{ch}}(kH)}} - \frac{{{{{( - 1)}}^{n}}((\beta {{k}^{4}} + 1 - \delta )k + {{\lambda }^{2}})exp( - k{{y}_{0}})}}{{(\beta {{k}^{4}} + 1 - \delta )k{\text{sh}}(kH) - {{\lambda }^{2}}{\text{ch}}(kH)}}$

Функции $\phi _{n}^{c}$, $\phi _{n}^{s}$ удовлетворяют уравнению (1.1), условию (1.5) и первому из условий (1.6). Второе из условий (1.6) будет удовлетворяться с помощью метода отражения. Для удовлетворения условий на кромке пластины нужно к этим потенциалам добавить дополнительные потенциалы $\psi _{n}^{c}$, $\psi _{n}^{s}$. Используя симметрию относительно оси $Ox$, представим каждый из потенциалов ${{\varphi }_{j}}$ в виде

${{\varphi }_{j}} = \sum\limits_{n = 1}^\infty \,[{{a}_{n}}(\varphi _{n}^{c} + \psi _{n}^{c}) + {{b}_{n}}(\varphi _{n}^{s} + \psi _{n}^{s})]$

$\begin{gathered} \varphi _{n}^{c} = \frac{{cos(n\theta )}}{{{{r}^{n}}}} + \frac{{cos(n{{\theta }_{1}})}}{{r_{1}^{n}}} + \\ \, + \frac{1}{{(n - 1)!}}\int\limits_0^\infty \,[A(k){\text{sh}}(ky) + {{B}_{c}}(k){\text{ch}}(k(H - y))]{{k}^{{n - 1}}}[cos(k(x - {{x}_{0}})) + cos(k(x + {{x}_{0}}))]dk \\ \end{gathered} $

$\begin{gathered} \varphi _{n}^{s} = \frac{{sin(n\theta )}}{{{{r}^{n}}}} - \frac{{sin(n{{\theta }_{1}})}}{{r_{1}^{n}}} + \\ \, + \frac{1}{{(n - 1)!}}\int\limits_0^\infty \,[A(k){\text{sh}}(ky) + {{B}_{s}}(k){\text{ch}}(k(H - y))]{{k}^{{n - 1}}}[sin(k(x - {{x}_{0}})) - sin(k(x + {{x}_{0}}))]dk \\ \end{gathered} $

Здесь ${{a}_{n}}$, ${{b}_{n}}$ – коэффициенты разложения, которые необходимо найти из условия (1.7).

Потенциалы $\psi _{n}^{c}$, $\psi _{n}^{s}$ должны удовлетворять уравнению (1.1), условиям (1.5), (1.6) и вместе с функциями $\varphi _{n}^{c}$, $\varphi _{n}^{s}$ условиям в кромке пластины (1.8) или (1.9). Приведем далее построение дополнительных потенциалов, опуская для краткости индексы. Применяем преобразование Фурье

$\Psi (k,y) = \int\limits_{ - \infty }^\infty \,exp( - ikx)\psi (x,y)dx$

Из уравнения (1.1) и первого условия (1.6) следует

$\Psi (k,y) = C(k){\text{ch}}(k(H - y)){\text{/ch}}(kH)$

Для функции

(2.1)

$u(x) = \partial \psi {\text{/}}\partial y(x,0)$

справедливо уравнение

(2.2)

$\left( {\beta \frac{{{{\partial }^{4}}}}{{\partial {{x}^{4}}}} + 1 - \delta } \right)u = - {{\lambda }^{2}}\psi (x,0)$

Общее решение этого уравнения имеет вид

(2.3)

$u(x) = {{C}_{1}}exp(i{{\kappa }_{1}}x) + {{C}_{2}}exp(i{{\kappa }_{2}}x) + {{u}_{0}}(x)$

Здесь первые два члена представляют решение однородного уравнения, ${{\kappa }_{1}}$ и ${{\kappa }_{2}}$ являются корнями уравнения

$\beta {{\kappa }^{4}} + 1 - \delta = 0$

лежащими в верхней полуплоскости, ${{\kappa }_{2}} = - {{\bar {\kappa }}_{1}}$, ${{u}_{0}}(x)$ – частное решение уравнения (2.2). Для образа Фурье ${{U}_{0}}(k)$ функции ${{u}_{0}}(x)$ из уравнения (2.2) получаем

(2.4)

$(\beta {{k}^{4}} + 1 - \delta ){{U}_{0}}(k) = - {{\lambda }^{2}}C(k),\quad {{U}_{0}}(k) = - \frac{{{{\lambda }^{2}}C(k)}}{{\beta {{k}^{4}} + 1 - \delta }}$

Из уравнений (2.1), (2.3), (2.4) находим

${{C}_{1}}\frac{{2i{{\kappa }_{1}}}}{{\kappa _{1}^{2} - {{k}^{2}}}} + {{C}_{2}}\frac{{2i{{\kappa }_{2}}}}{{\kappa _{2}^{2} - {{k}^{2}}}} - \frac{{{{\lambda }^{2}}C(k)}}{{\beta {{k}^{4}} + 1 - \delta }} = - C(k)k{\text{th}}(kH)$

Отсюда

$C(k) = 2\frac{{\beta {{k}^{4}} + 1 - \delta }}{{K(k)}}\left( {{{C}_{1}}\frac{{i{{\kappa }_{1}}}}{{{{k}^{2}} - \kappa _{1}^{2}}} + {{C}_{2}}\frac{{i{{\kappa }_{2}}}}{{{{k}^{2}} - \kappa _{2}^{2}}}} \right)$

${{U}_{0}}(k) = - \frac{{2{{\lambda }^{2}}}}{{K(k)}}\left( {{{C}_{1}}\frac{{i{{\kappa }_{1}}}}{{{{k}^{2}} - \kappa _{1}^{2}}} + {{C}_{2}}\frac{{i{{\kappa }_{2}}}}{{{{k}^{2}} - \kappa _{2}^{2}}}} \right)$

$K(k)$ – дисперсионная функция изгибно-гравитационных волн в жидкости под пластиной

$K(k) = (\beta {{k}^{4}} + 1 - \delta )k{\text{th}}(kH) - {{\lambda }^{2}}$

Известно, что она имеет два действительных корня $ \pm {{k}_{0}}$, четыре комплексных корня $ \pm {{k}_{{ - 1}}}$, $ \pm {{k}_{{ - 2}}}$, ${{k}_{{ - 2}}} = - {{\bar {k}}_{{ - 1}}}$ и счетное множество мнимых корней $ \pm {{k}_{j}}$, $j = 1,2,...$ . Применяя обратное преобразование Фурье, находим с помощью метода вычетов

(2.5)

$\begin{gathered} {{u}_{0}}(x) = 2{{\lambda }^{2}}\sum\limits_{j = - 2}^\infty \,\frac{{exp(i{{k}_{j}}x)}}{{K{\kern 1pt} {\text{'}}({{k}_{j}})}}\left( {{{C}_{1}}\frac{{{{\kappa }_{1}}}}{{k_{j}^{2} - \kappa _{1}^{2}}} + {{C}_{2}}\frac{{{{\kappa }_{2}}}}{{k_{j}^{2} - \kappa _{2}^{2}}}} \right) - {{C}_{1}}exp(i{{\kappa }_{1}}x) - {{C}_{2}}exp(i{{\kappa }_{2}}x) \\ u(x) = 2{{\lambda }^{2}}\sum\limits_{j = - 2}^\infty \,\frac{{exp(i{{k}_{j}}x)}}{{K{\kern 1pt} {\text{'}}({{k}_{j}})}}\left( {{{C}_{1}}\frac{{{{\kappa }_{1}}}}{{k_{j}^{2} - \kappa _{1}^{2}}} + {{C}_{2}}\frac{{{{\kappa }_{2}}}}{{k_{j}^{2} - \kappa _{2}^{2}}}} \right) \\ \end{gathered} $

Подставляем выражение (2.5) в условия на кромке и получаем систему уравнений для определения коэффициентов C₁, C₂

(2.6)

$\sum\limits_{j = 1}^2 \,{{A}_{{ij}}}{{C}_{j}} = {{B}_{i}}$

В случае закрепленного края коэффициенты матрицы системы и правой части имеют вид

$\begin{gathered} {{A}_{{11}}} = 2{{\lambda }^{2}}{{\kappa }_{1}}\sum\limits_{j = - 2}^\infty \,\frac{1}{{K{\kern 1pt} {\text{'}}({{k}_{j}})(k_{j}^{2} - \kappa _{1}^{2})}},\quad {{A}_{{12}}} = 2{{\lambda }^{2}}{{\kappa }_{2}}\sum\limits_{j = - 2}^\infty \,\frac{1}{{K{\kern 1pt} {\text{'}}({{k}_{j}})(k_{j}^{2} - \kappa _{2}^{2})}} \\ {{A}_{{21}}} = 2{{\lambda }^{2}}{{\kappa }_{1}}\sum\limits_{j = - 2}^\infty \,\frac{{{{k}_{j}}}}{{K{\kern 1pt} {\text{'}}({{k}_{j}})(k_{j}^{2} - \kappa _{1}^{2})}},\quad {{A}_{{22}}} = 2{{\lambda }^{2}}{{\kappa }_{2}}\sum\limits_{j = - 2}^\infty \,\frac{{{{k}_{j}}}}{{K{\kern 1pt} {\text{'}}({{k}_{j}})(k_{j}^{2} - \kappa _{2}^{2})}} \\ {{B}_{1}} = - \partial \varphi {\text{/}}\partial y(0,0),\quad {{B}_{2}} = 0 \\ \end{gathered} $

Для пластины со свободным краем

$\begin{gathered} {{A}_{{11}}} = - 2{{\lambda }^{2}}{{\kappa }_{1}}\sum\limits_{j = - 2}^\infty \,\frac{{k_{j}^{2}}}{{K{\kern 1pt} {\text{'}}({{k}_{j}})(k_{j}^{2} - \kappa _{1}^{2})}},\quad {{A}_{{12}}} = - 2{{\lambda }^{2}}{{\kappa }_{2}}\sum\limits_{j = - 2}^\infty \,\frac{{k_{j}^{2}}}{{K{\kern 1pt} {\text{'}}({{k}_{j}})(k_{j}^{2} - \kappa _{2}^{2})}} \\ {{A}_{{21}}} = 2{{\lambda }^{2}}{{\kappa }_{1}}\sum\limits_{j = - 2}^\infty \,\frac{{k_{j}^{3}}}{{K{\kern 1pt} {\text{'}}({{k}_{j}})(k_{j}^{2} - \kappa _{1}^{2})}},\quad {{A}_{{22}}} = 2{{\lambda }^{2}}{{\kappa }_{2}}\sum\limits_{j = - 2}^\infty \,\frac{{k_{j}^{3}}}{{K{\kern 1pt} {\text{'}}({{k}_{j}})(k_{j}^{2} - \kappa _{2}^{2})}} \\ {{B}_{1}} = - \frac{{{{\partial }^{3}}\varphi }}{{\partial {{x}^{2}}\partial y}}(0,0),\quad {{B}_{2}} = 0 \\ \end{gathered} $

Коэффициенты A₂₁ и A₂₂ можно вычислить точно, применяя прием, который использовался ранее в работе [25]. Используя теорию вычетов, запишем ряд в виде интеграла. Затем замыкая его сначала в верхней, затем в нижней полуплоскости, преобразуем ряд через вычеты в точках, соответствующих корням полинома, стоящего в знаменателе. В случае закрепленной пластины

$\sum\limits_{j = - 2}^\infty \,\frac{{{{k}_{j}}}}{{K{\kern 1pt} {\text{'}}({{k}_{j}})(k_{j}^{2} - \kappa _{1}^{2})}} = \frac{1}{{2\pi i}}\int\limits_{ - \infty }^\infty \,\frac{{kdk}}{{K(k)({{k}^{2}} - \kappa _{1}^{2})}} + \frac{1}{{2{{\lambda }^{2}}}} = - \sum\limits_{j = - 2}^\infty \,\frac{{{{k}_{j}}}}{{K{\kern 1pt} {\text{'}}({{k}_{j}})(k_{j}^{2} - \kappa _{1}^{2})}} + \frac{1}{{{{\lambda }^{2}}}}$

Отсюда находим

$\sum\limits_{j = - 2}^\infty \,\frac{{{{k}_{j}}}}{{K{\kern 1pt} {\text{'}}({{k}_{j}})(k_{j}^{2} - \kappa _{1}^{2})}} = \frac{1}{{2{{\lambda }^{2}}}},\quad {{A}_{{21}}} = {{\kappa }_{1}},\quad {{A}_{{22}}} = {{\kappa }_{2}},\quad {{C}_{1}}{{\kappa }_{1}} + {{C}_{2}}{{\kappa }_{2}} = 0$

Таким образом, система (2.6) решается явно. После преобразований находим

${{C}_{1}}{{\kappa }_{1}}4i{{\lambda }^{2}}\sqrt {\beta (1 - \delta )} Q = {{B}_{1}},\quad Q = \sum\limits_{j = - 2}^\infty \,\frac{1}{{K{\kern 1pt} {\text{'}}({{k}_{j}})(\beta k_{j}^{4} + 1 - \delta )}}$

$\psi (x,y) = \frac{1}{{2\pi }}\int\limits_{ - \infty }^\infty \,\frac{{exp(ikx)C(k){\text{ch}}(k(H - y))dk}}{{{\text{ch}}(kH)}} = \frac{{\partial \varphi }}{{\partial y}}(0,0)\frac{1}{{{{\lambda }^{2}}Q}}\sum\limits_{j = - 2}^\infty \,\frac{{exp(i{{k}_{j}}x){\text{ch}}{{k}_{j}}(H - y)}}{{K{\kern 1pt} '({{k}_{j}}){\text{ch}}({{k}_{j}}H)}}$

В случае пластины со свободным краем находим

$\sum\limits_{j = - 2}^\infty \,\frac{{k_{j}^{3}}}{{K{\kern 1pt} {\text{'}}({{k}_{j}})(k_{j}^{2} - \kappa _{1}^{2})}} = \frac{{\kappa _{1}^{2}}}{{2{{\lambda }^{2}}}},\quad {{A}_{{21}}} = \kappa _{1}^{3},\quad {{A}_{{22}}} = \kappa _{2}^{3},\quad {{C}_{1}}\kappa _{1}^{3} + {{C}_{2}}\kappa _{2}^{3} = 0$

Из первого уравнения системы получаем

$ - 4{{\beta }^{{3/4}}}{{(1 - \delta )}^{{1/4}}}{{\lambda }^{2}}{{C}_{1}}exp(i\pi {\text{/}}4){{Q}_{1}} = {{B}_{1}},\quad {{Q}_{1}} = \sum\limits_{j = - 2}^\infty \,\frac{{k_{j}^{4}}}{{K{\kern 1pt} {\text{'}}({{k}_{j}})(\beta k_{j}^{4} + 1 - \delta )}}$

$\psi (x,y) = \frac{1}{{2\pi }}\int\limits_{ - \infty }^\infty \,\frac{{exp(ikx)C(k){\text{ch}}(k(H - y))dk}}{{{\text{ch}}(kH)}} = - \frac{{{{\varphi }_{{xxy}}}(0,0)}}{{{{\lambda }^{2}}{{Q}_{1}}}}\sum\limits_{j = - 2}^\infty \,\frac{{exp(i{{k}_{j}}x){\text{ch}}{{k}_{j}}(H - y)}}{{K{\kern 1pt} {\text{'}}({{k}_{j}}){\text{ch}}({{k}_{j}}H)}}$

В силу симметрии на стенке при $x = 0$, $y = 0$ имеем

$r = {{r}_{1}} = {{r}_{*}} = \sqrt {x_{0}^{2} + y_{0}^{2}} ,\quad \theta = {{\theta }_{*}} = \pi + {\text{arctg}}({{x}_{0}}{\text{/}}{{y}_{0}}),\quad {{\theta }_{1}} = 2\pi - {{\theta }_{*}}$

$\frac{{\partial \varphi _{n}^{c}}}{{\partial y}}(0,0) = - 2n\frac{{cos(n + 1){{\theta }_{*}}}}{{r_{*}^{{n + 1}}}} + \frac{2}{{(n - 1)!}}\int\limits_0^\infty \,[A(k) - {{B}_{c}}(k){\text{sh}}(kH)]{{k}^{n}}cos(k{{x}_{0}})dk$

$\frac{{\partial \varphi _{n}^{s}}}{{\partial y}}(0,0) = - 2n\frac{{sin(n + 1){{\theta }_{*}}}}{{r_{*}^{{n + 1}}}} - \frac{2}{{(n - 1)!}}\int\limits_0^\infty \,[A(k) - {{B}_{s}}(k){\text{sh}}(kH)]{{k}^{n}}sin(k{{x}_{0}})dk$

$\frac{{{{\partial }^{3}}\varphi _{n}^{c}}}{{\partial {{x}^{2}}\partial y}}(0,0) = 2n(n + 1)(n + 2)\frac{{cos(n + 3){{\theta }_{*}}}}{{r_{*}^{{n + 3}}}} - \frac{2}{{(n - 1)!}}\int\limits_0^\infty \,[A(k) - {{B}_{c}}(k){\text{sh}}(kH)]{{k}^{{n + 2}}}cos(k{{x}_{0}})dk$

$\frac{{{{\partial }^{3}}\varphi _{n}^{s}}}{{\partial {{x}^{2}}\partial y}}(0,0) = 2n(n + 1)(n + 2)\frac{{sin(n + 3){{\theta }_{*}}}}{{r_{*}^{{n + 3}}}} + \frac{2}{{(n - 1)!}}\int\limits_0^\infty \,[A(k) - {{B}_{s}}(k){\text{sh}}(kH)]{{k}^{{n + 2}}}sin(k{{x}_{0}})dk$

Чтобы удовлетворить условию (1.7), необходимо все функции выразить в цилиндрических координатах исходного цилиндра. Имеем

$cosk(x + {{x}_{0}}) = cosk(x - {{x}_{0}})cos2k{{x}_{0}} - sink(x - {{x}_{0}})sin2k{{x}_{0}}$

$sink(x + {{x}_{0}}) = sink(x - {{x}_{0}})cos2k{{x}_{0}} + cosk(x - {{x}_{0}})sin2k{{x}_{0}}$

Аналогично тому, как изложено в [1], преобразуем выражения и раскладываем в ряд Тейлора

$exp( \pm k(y - {{y}_{0}}))cosk(x - {{x}_{0}}) = {\text{Re}}exp( \pm krexp( \pm i\theta )) = \sum\limits_{m = 0}^\infty \,\frac{{{{{( \pm kr)}}^{m}}cosm\theta }}{{m!}}$

$exp( \pm k(y - {{y}_{0}}))sink(x - {{x}_{0}}) = {\text{Im}}exp( \pm krexp( \pm i\theta )) = {\text{Im}}\sum\limits_{m = 0}^\infty \,\frac{{{{{( \pm kr)}}^{m}}exp( \pm im\theta )}}{{m!}} = \pm \sum\limits_{m = 0}^\infty \,\frac{{{{{( \pm kr)}}^{m}}sinm\theta }}{{m!}}$

Введем комплексную переменную $z = x + iy$

$z = {{z}_{0}} + rexp(i(\pi {\text{/}}2 - \theta )) = {{z}_{1}} + {{r}_{1}}exp(i(\pi {\text{/}}2 - {{\theta }_{1}}))$

Рассмотрим аналитическую функцию

${{f}_{n}}(z) = \frac{{{{i}^{n}}}}{{{{{(z - {{z}_{1}})}}^{n}}}} = \frac{{exp(in{{\theta }_{1}})}}{{r_{1}^{n}}}$

Представим ее в виде разложения в ряд Тейлора в окрестности точки z₀

${{f}_{n}}(z) = {{\left. {\sum\limits_{m = 0}^\infty \,\frac{{{{d}^{m}}{{f}_{n}}}}{{d{{z}^{m}}}}} \right|}_{{z = {{z}_{0}}}}}\frac{{{{{(z - {{z}_{0}})}}^{m}}}}{{m!}} = \sum\limits_{m = 0}^\infty \,\frac{{{{{( - 1)}}^{m}}(n + m - 1)!}}{{m!(n - 1)!{{{(2{{x}_{0}})}}^{{n + m}}}}}{{r}^{m}}exp(i(n + m)\pi {\text{/}}2 - m\theta )$

Отсюда находим

$\frac{{cosn{{\theta }_{1}}}}{{r_{1}^{n}}} = \sum\limits_{m = 0}^\infty \,\frac{{{{{( - 1)}}^{m}}(n + m - 1)!}}{{m!(n - 1)!{{{(2{{x}_{0}})}}^{{n + m}}}}}{{r}^{m}}cos((n + m)\pi {\text{/}}2 - m\theta )$

$\frac{{sinn{{\theta }_{1}}}}{{r_{1}^{n}}} = \sum\limits_{m = 0}^\infty \,\frac{{{{{( - 1)}}^{m}}(n + m - 1)!}}{{m!(n - 1)!{{{(2{{x}_{0}})}}^{{n + m}}}}}{{r}^{m}}sin((n + m)\pi {\text{/}}2 - m\theta )$

Таким образом, для каждого из потенциалов ${{\varphi }_{j}}$ получаем выражение

$\begin{gathered} {{\varphi }_{j}} = \sum\limits_{n = 1}^\infty \,\left\{ {{{a}_{n}}\left[ {\frac{{cosn\theta }}{{{{r}^{n}}}} + \sum\limits_{m = 0}^\infty \,\frac{{{{{( - 1)}}^{m}}(n + m - 1)!{{r}^{m}}}}{{m!(n - 1)!{{{(2{{x}_{0}})}}^{{n + m}}}}}cos((n + m)\pi {\text{/}}2 - m\theta ) + } \right.} \right. \\ \, + \frac{1}{{2(n - 1)!}}\sum\limits_{m = 0}^\infty \,\frac{{{{r}^{m}}cosm\theta }}{{m!}}\int\limits_0^\infty \,(1 + cos2k{{x}_{0}})[A(k)(exp(k{{y}_{0}}) - {{( - 1)}^{m}}exp( - k{{y}_{0}})) + \\ \end{gathered} $

$\begin{gathered} \, + {{B}_{c}}(k)(exp(k(H - {{y}_{0}})){{( - 1)}^{m}} + exp(k({{y}_{0}} - H)))]{{k}^{{n + m - 1}}}dk - \\ \, - \frac{1}{{2(n - 1)!}}\sum\limits_{m = 0}^\infty \,\frac{{{{r}^{m}}sinm\theta }}{{m!}}\int\limits_0^\infty \,sin2k{{x}_{0}}[A(k)(exp(k{{y}_{0}}) + {{( - 1)}^{m}}exp( - k{{y}_{0}})) + \\ \end{gathered} $

$\begin{gathered} \left. {\mathop {\, + {{B}_{c}}(k)(exp(k({{y}_{0}} - H)) - {{{( - 1)}}^{m}}exp(k(H - {{y}_{0}})))]{{k}^{{n + m - 1}}}dk + \psi _{n}^{c}}\limits_{}^{} } \right] + \\ \, + {{b}_{n}}\left[ {\frac{{sinn\theta }}{{{{r}^{n}}}} - \sum\limits_{m = 0}^\infty \,\frac{{{{{( - 1)}}^{m}}(n + m - 1)!{{r}^{m}}}}{{m!(n - 1)!{{{(2{{x}_{0}})}}^{{n + m}}}}}sin((n + m)\pi {\text{/}}2 - m\theta ) + } \right. \\ \end{gathered} $

$\begin{gathered} \, + \frac{1}{{2(n - 1)!}}\sum\limits_{m = 0}^\infty \,\frac{{{{r}^{m}}sinm\theta }}{{m!}}\int\limits_0^\infty \,(1 - cos2k{{x}_{0}})[A(k)(exp(k{{y}_{0}}) + {{( - 1)}^{m}}exp( - k{{y}_{0}})) + \\ \, + {{B}_{s}}(k)(exp(k({{y}_{0}} - H)) - {{( - 1)}^{m}}exp(k(H - {{y}_{0}})))]{{k}^{{n + m - 1}}}dk - \\ \end{gathered} $

(2.7)

$\begin{gathered} \, - \frac{1}{{2(n - 1)!}}\sum\limits_{m = 0}^\infty \,\frac{{{{r}^{m}}cosm\theta }}{{m!}}\int\limits_0^\infty \,sin2k{{x}_{0}}[A(k)(exp(k{{y}_{0}}) - {{( - 1)}^{m}}exp( - k{{y}_{0}})) + \\ \left. {\left. {\mathop {\, + {{B}_{s}}(k)(exp(k({{y}_{0}} - H)) + {{{( - 1)}}^{m}}exp(k(H - {{y}_{0}})))]{{k}^{{n + m - 1}}}dk + \psi _{n}^{s}}\limits_{}^{} } \right]} \right\} \\ \end{gathered} $

В случае закрепленной пластины (опуская верхние индексы)

(2.8)

$\begin{gathered} {{\psi }_{n}} = \frac{{\partial {{\varphi }_{n}}}}{{\partial y}}(0,0)\frac{1}{{2Q{{\lambda }^{2}}}}\sum\limits_{j = - 2}^\infty \,\frac{{exp(i{{k}_{j}}{{x}_{0}})}}{{K{\text{'}}({{k}_{j}}){\text{ch}}{{k}_{j}}H}}\left[ {exp({{k}_{j}}(H - {{y}_{0}}))\sum\limits_{m = 0}^\infty \,\frac{{{{{( - {{k}_{j}}r)}}^{m}}exp( - im\theta )}}{{m!}}} \right. + \\ \,\left. { + exp({{k}_{j}}({{y}_{0}} - H))\sum\limits_{m = 0}^\infty \,\frac{{{{{({{k}_{j}}r)}}^{m}}exp(im\theta )}}{{m!}}} \right] \\ \end{gathered} $

В случае пластины со свободным краем

(2.9)

$\begin{gathered} {{\psi }_{n}} = - \frac{{{{\partial }^{3}}{{\varphi }_{n}}}}{{\partial {{x}^{2}}\partial y}}(0,0)\frac{1}{{2{{Q}_{1}}{{\lambda }^{2}}}}\sum\limits_{j = - 2}^\infty \,\frac{{k_{j}^{2}exp(i{{k}_{j}}{{x}_{0}})}}{{K{\kern 1pt} {\text{'}}({{k}_{j}}){\text{ch}}{{k}_{j}}H}}\left[ {exp({{k}_{j}}(H - {{y}_{0}}))\sum\limits_{m = 0}^\infty \,\frac{{{{{( - {{k}_{j}}r)}}^{m}}exp( - im\theta )}}{{m!}} + } \right. \\ \left. {\, + exp({{k}_{j}}({{y}_{0}} - H))\sum\limits_{m = 0}^\infty \,\frac{{{{{({{k}_{j}}r)}}^{m}}exp(im\theta )}}{{m!}}} \right] \\ \end{gathered} $

Подставляем выражения (2.7)–(2.9) в уравнение (1.7), умножая на функции $cos(l\theta )$, $sin(l\theta )$ и интегрируя по $\theta $, получим бесконечную систему линейных алгебраических уравнений для определения коэффициентов a_n, b_n. Для случаев вертикальных и горизонтальных колебаний цилиндра матрица системы одна и та же, отличается только правая часть. Система решалась методом редукции.

После решения системы находим гидродинамические силы, действующие на колеблющийся цилиндр

(2.10)

$\begin{gathered} {{F}_{i}} = \int\limits_S \,p{{n}_{i}}ds = - \rho \int\limits_S \,{{\varphi }_{t}}{{n}_{i}}ds = \rho {{\omega }^{2}}{{a}^{2}}\sum\limits_{j = 1}^2 \,{{\tau }_{{ij}}}{{A}_{j}},\quad i = 1,2 \\ {{\tau }_{{ij}}} = \int\limits_0^{2\pi } \,{{\varphi }_{j}}{{n}_{i}}d\theta = {{\mu }_{{ij}}} + \frac{i}{\omega }{{\sigma }_{{ij}}} \\ \end{gathered} $

где S – поверхность цилиндра, ${{\mu }_{{ij}}}$, ${{\sigma }_{{ij}}}$ – коэффициенты присоединенных масс и демпфирования. Учитывая уравнения системы при l = 1, получаем

${{\tau }_{{11}}} = \pi (2{{b}_{1}}{\text{/}}a - a),\quad {{\tau }_{{12}}} = 2\pi {{b}_{1}}{\text{/}}a,\quad {{\tau }_{{21}}} = 2\pi {{a}_{1}}{\text{/}}a,\quad {{\tau }_{{22}}} = \pi (2{{a}_{1}}{\text{/}}a - a)$

Для коэффициентов демпфирования справедливы соотношения эквивалентности, связывающие их с амплитудами генерируемых волн в дальнем поле. Имеем в силу условий (1.7)

(2.11)

${{\tau }_{{ij}}} - {{\tau }_{{ji}}} = \int\limits_S \,\left( {{{\varphi }_{j}}\frac{{\partial {{\varphi }_{i}}}}{{\partial n}} - {{\varphi }_{i}}\frac{{\partial {{\varphi }_{j}}}}{{\partial n}}} \right)ds$

где S – поверхность цилиндра. С помощью тождества Грина интеграл по поверхности тела можно преобразовать в интеграл по всей остальной поверхности, ограничивающей жидкость. При этом интегралы по дну и по стенке обращаются в нуль в силу условий непротекания, на верхней границе из условий (1.5), (1.8), (1.9). При $x \to \infty $ потенциалы можно представить в виде

(2.12)

$\mathop {lim}\limits_{x \to \infty } {{\varphi }_{j}} = {{R}_{j}}exp(i{{k}_{0}}x)\frac{{{\text{ch}}{{k}_{0}}(H - y)}}{{{\text{ch}}{{k}_{0}}H}}$

(2.13)

$\begin{gathered} {{R}_{j}} = \frac{{2i\pi {{\lambda }^{2}}}}{{{\text{sh}}({{k}_{0}}H)K{\kern 1pt} {\text{'}}({{k}_{0}})}}\sum\limits_{n = 1}^\infty \,\frac{{k_{0}^{{n - 1}}}}{{(n - 1)!}}[{{a}_{n}}cos({{k}_{0}}{{x}_{0}})(exp({{k}_{0}}({{y}_{0}} - H)) + {{( - 1)}^{n}}exp({{k}_{0}}(H - {{y}_{0}}))) - \\ \, - {{b}_{n}}sin({{k}_{0}}{{x}_{0}})(exp({{k}_{0}}({{y}_{0}} - H)) - {{( - 1)}^{n}}exp({{k}_{0}}(H - {{y}_{0}})))] + {{R}_{{j1}}},\quad j = 1,2 \\ \end{gathered} $

В случае закрепленной пластины

(2.14)

${{R}_{{j1}}} = \frac{1}{{Q{{\lambda }^{2}}K{\kern 1pt} {\text{'}}({{k}_{0}})}}\sum\limits_{n = 1}^\infty \,\frac{1}{{(n - 1)!}}\left( {{{a}_{n}}\frac{{\partial \varphi _{n}^{c}}}{{\partial y}}(0,0) + {{b}_{n}}\frac{{\partial \varphi _{n}^{s}}}{{\partial y}}(0,0)} \right)$

в случае пластины со свободным краем

(2.15)

${{R}_{{j1}}} = - \frac{{k_{0}^{2}}}{{{{Q}_{1}}{{\lambda }^{2}}K{\kern 1pt} {\text{'}}({{k}_{0}})}}\sum\limits_{n = 1}^\infty \,\frac{1}{{(n - 1)!}}\left( {{{a}_{n}}\frac{{{{\partial }^{3}}\varphi _{n}^{c}}}{{\partial {{x}^{2}}\partial y}}(0,0) + {{b}_{n}}\frac{{\partial \varphi _{n}^{s}}}{{\partial {{x}^{2}}\partial y}}(0,0)} \right)$

В формулах (2.13)–(2.15) коэффициенты ${{a}_{n}}$ и ${{b}_{n}}$ получены при правой части, соответствующей моде колебаний с номером j. Интегралы (2.11) по вертикальным линиям $x = {\text{const}}$ обращаются в нуль при $x \to \infty $ в силу формул (2.12). Отсюда следует, что

${{\tau }_{{ij}}} = {{\tau }_{{ji}}},\quad {{\mu }_{{ij}}} = {{\mu }_{{ji}}},\quad {{\sigma }_{{ij}}} = {{\sigma }_{{ji}}}$

Для коэффициентов демпфирования из (2.10) получаем

$2i\frac{{{{\sigma }_{{ij}}}}}{\omega } = \int\limits_S \,\left( {{{\varphi }_{j}}\frac{{\partial {{{\bar {\varphi }}}_{i}}}}{{\partial n}} - {{{\bar {\varphi }}}_{i}}\frac{{\partial {{\varphi }_{j}}}}{{\partial n}}} \right)ds$

где черта означает комплексное сопряжение. Преобразуя интегрирование в силу тождества Грина на оставшуюся часть границы жидкости, находим

(2.16)

$2i\frac{{{{\sigma }_{{ij}}}}}{\omega } = \int\limits_0^\infty \,\left( {{{{\bar {\varphi }}}_{i}}\frac{{\partial {{\varphi }_{j}}}}{{\partial y}} - {{\varphi }_{j}}\frac{{\partial {{{\bar {\varphi }}}_{i}}}}{{\partial y}}} \right)dx - \mathop {lim}\limits_{x \to \infty } \int\limits_0^H \,\left( {{{\varphi }_{j}}\frac{{\partial {{{\bar {\varphi }}}_{i}}}}{{\partial x}} - {{{\bar {\varphi }}}_{i}}\frac{{\partial {{\varphi }_{j}}}}{{\partial x}}} \right)dy$

Первый интеграл в (2.16) вычисляем по частям, с учетом формулы (2.12) находим

(2.17)

$2\frac{{{{\sigma }_{{ij}}}}}{\omega } = {{R}_{j}}{{\bar {R}}_{i}}{{k}_{0}}\left[ {\frac{{4\beta k_{0}^{4}{\text{t}}{{{\text{h}}}^{2}}{{k}_{0}}H}}{{{{\lambda }^{2}}}} + \frac{1}{{{\text{c}}{{{\text{h}}}^{2}}{{k}_{0}}H}}\left( {1 + \frac{{{\text{sh}}2{{k}_{0}}H}}{{2{{k}_{0}}}}} \right)} \right]$

Эта формула может служить проверкой правильности проведенных вычислений.

Прогиб ледяной пластины определяется формулой (1.4). Деформации пластины имеют вид

$\varepsilon (x) = \frac{{hA}}{{2{{a}^{2}}}}\sum\limits_{n = 1}^\infty \,\left[ {{{a}_{n}}\left( {\frac{{{{\partial }^{3}}\varphi _{n}^{c}}}{{\partial {{x}^{2}}\partial y}} + \frac{{{{\partial }^{3}}\psi _{n}^{c}}}{{\partial {{x}^{2}}\partial y}}} \right)(x,0) + {{b}_{n}}\left( {\frac{{{{\partial }^{3}}\varphi _{n}^{s}}}{{\partial {{x}^{2}}\partial y}} + \frac{{{{\partial }^{3}}\psi _{n}^{s}}}{{\partial {{x}^{2}}\partial y}}} \right)(x,0)} \right]$

В линейной теории упругости напряжения и деформации связаны линейной зависимостью. Необходимо, чтобы деформации и напряжения не превышали предельных значений, при которых начинаются пластические деформации и разрушение. Экспериментально полученные в работе [26] критические значения максимальных деформаций для льда составляют $4.4 \times {{10}^{{ - 5}}}{\kern 1pt} - {\kern 1pt} 8.5$ × × 10^–5. В работе [22] использовалось критическое значение максимальных деформаций ${{\varepsilon }_{*}} = 8$ × × 10^–5. В данной работе также использyетcя это значение.

На стенку действует горизонтальная сила со стороны жидкости

${{F}_{h}} = \int\limits_0^H \,p(0,y)dy = - \rho \int\limits_0^H \,( - gy + {{\varphi }_{t}})dy = \rho g{{H}^{2}}{\text{/}}2 + \rho {{\omega }^{2}}A{{a}^{2}}\int\limits_0^H \,\varphi (0,y)dy$

Первый член в последней формуле представляет гидростатическую силу, а второй член – динамическую составляющую. В случае закрепленной пластины на стенку действует также вертикальная сила, равная перерезывающей силе в кромке, которая определяется формулой

${{F}_{v}} = - \frac{{DA}}{{{{a}^{3}}}}\frac{{{{\partial }^{3}}w}}{{\partial {{x}^{3}}}}(0,0)$

3. РЕЗУЛЬТАТЫ ЧИСЛЕННЫХ РАСЧЕТОВ

Проводились численные расчеты для ледяного покрова и цилиндра при следующих входных параметрах: E = 5 ГПа, $\rho = 1025$ кг/м³, ${{\rho }_{0}} = 922.5$ кг/м³, $\nu = 0.3$, $a = 5$ м, H = 100 м. Толщина пластины менялась в диапазоне $h = 0.5 \div 2$ м, глубина погружения цилиндра ${{y}_{0}} = 6{\kern 1pt} - {\kern 1pt} 10$ м, менялись также частота колебаний $\omega $ и расстояние ${{x}_{0}}$ от центра цилиндра до стенки.

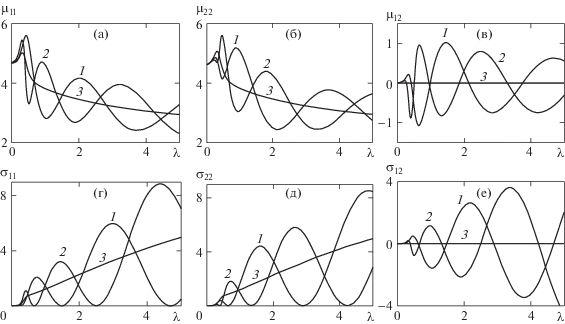
На рис. 1 представлены графики зависимости безразмерных коэффициентов присоединенных масс ${{\mu }_{{ij}}}$ и демпфирования ${{\sigma }_{{ij}}}$ от безразмерной частоты $\lambda $ для случаев закрепленной пластины и со свободным краем при h = 1 м, ${{x}_{0}} = 50$ м, ${{y}_{0}} = 6$ м вблизи вертикальной стенки, а также для цилиндра под бесконечным ледяным покровом в отсутствие стенки. Видно, что наличие стенки приводит к тому, что коэффициенты присоединенных масс и демпфирования осциллируют относительно кривых, которые соответствуют колебаниям цилиндра под бесконечным ледяным покровом в отсутствие стенки. При этом коэффициенты демпфирования обращаются в нуль при некоторых значениях частоты. Из формулы (2.17) следует, что при этих значениях частоты соответствующие амплитуды потенциала на бесконечности ${{R}_{j}}$ равны нулю, т.е. нет излучения волн на бесконечность. Коэффициенты ${{\mu }_{{ij}}}$ и ${{\sigma }_{{ij}}}$ для случаев закрепленной пластины и со свободным краем сдвинуты по фазе: если в случае закрепленной пластины достигается максимум при некоторой частоте, то в случае пластины со свободным краем этот коэффициент близок к минимуму и наоборот. Аналогичный эффект наблюдается для вертикальных и горизонтальных колебаний: если коэффициенты ${{\mu }_{{11}}}$ или ${{\sigma }_{{11}}}$ достигают максимума, то коэффициенты ${{\mu }_{{22}}}$ или ${{\sigma }_{{22}}}$ близки к минимуму.

Рис. 1.

Зависимость коэффициентов присоединенных масс и демпфирования от частоты при ${{x}_{0}} = $ 50 м, ${{y}_{0}} = $ 6 м, h = 1 м: 1 – закрепленная пластина, 2 – пластина со свободным краем, 3 – под бесконечным ледяным покровом в отсутствие стенки.

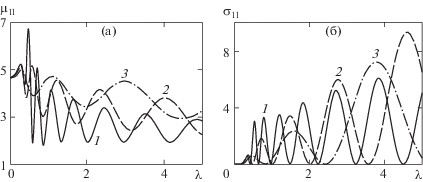
В работе [5] показано, что в случае цилиндра под бесконечным ледяным покровом в отсутствие стенки при увеличении толщины ледяного покрова при малых частотах коэффициенты присоединенных масс и демпфирования уменьшаются, а при высоких частотах увеличиваются. Аналогичный эффект влияния толщины ледяного покрова наблюдается и при наличии стенки. На рис. 2 приведены для сравнения зависимости коэффициентов ${{\mu }_{{11}}}$ и ${{\sigma }_{{11}}}$ от безразмерной частоты $\lambda $ для случаев толщины пластины $h = 0.5$, 1 и 2 м, ${{x}_{0}} = 100$ м, ${{y}_{0}} = 6$ м. Такое же влияние толщины ледяного покрова проявляется на остальные коэффициенты присоединенных масс и демпфирования.

Рис. 2.

Влияние толщины ледяного покрова на коэффициенты присоединенных масс и демпфирования ${{\mu }_{{11}}}$, ${{\sigma }_{{11}}}$: ${{x}_{0}} = $ 100 м, ${{y}_{0}} = $ 6 м, 1 – h = 0.5 м, 2 – h = 1 м, 3 – h = 2 м.

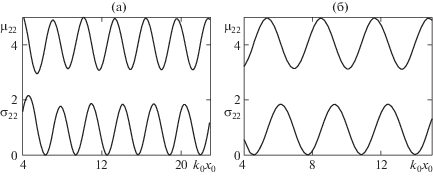
При уменьшении расстояния цилиндра от стенки период осцилляции коэффициентов ${{\mu }_{{ij}}}$ и ${{\sigma }_{{ij}}}$ увеличивается. Это можно увидеть из сравнения графиков на рис. 1 и 2 . Из формулы (2.13) следует, что амплитуда потенциала ${{R}_{j}}$ складывается из членов, периодических по параметру ${{x}_{0}}$, и членов, убывающих при ${{x}_{0}} \to \infty $. На рис. 3 изображены зависимости коэффициентов присоединенных масс и демпфирования ${{\mu }_{{22}}}$, ${{\sigma }_{{22}}}$ от произведения ${{k}_{0}}{{x}_{0}}$ в случаях закрепленной пластины толщиной h = 1 м и со свободным краем при ${{\lambda }^{2}} = 0.5$, ${{y}_{0}} = 6$ м. Видно, что в случае свободного края достаточно быстро при ${{k}_{0}}{{x}_{0}} > 4$ достигается периодическая зависимость, а в случае закрепленной пластины гораздо позже, при ${{k}_{0}}{{x}_{0}} > 11$. Остальные коэффициенты присоединенных масс и демпфирования зависят от расстояния от стенки аналогичным образом, а также при других значениях частоты колебаний.

Рис. 3.

Зависимость коэффициентов присоединенных масс и демпфирования ${{\mu }_{{22}}}$, ${{\sigma }_{{22}}}$ от расстояния до стенки ${{x}_{0}}$ в случае закрепленной пластины (а) и со свободным краем (б) при h = 1 м, ${{\lambda }^{2}} = 0.5$.

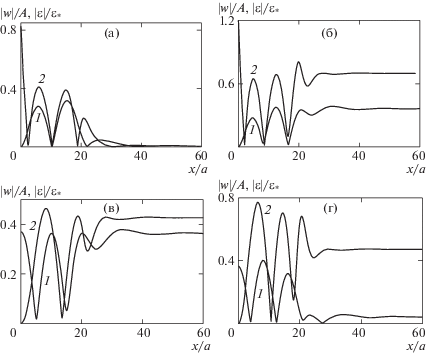
На рис. 4 представлены распределения по координате $x$ амплитуд безразмерного прогиба пластины ${\text{|}}w{\text{|/}}A$, отнесенных к амплитуде колебаний цилиндра A, и деформаций, вычисленных при значении A = 0.05 м и отнесенных к критическому значению ${{\varepsilon }_{ * }}$, при вертикальных колебаниях цилиндра в случаях закрепленной пластины и со свободным краем при значениях ${{\lambda }^{2}} = 0.5$ и 1, $h = 1$ м, ${{x}_{0}} = 100$ м, ${{y}_{0}} = 6$ м. Видно, что при ${{\lambda }^{2}} = 0.5$ в случае закрепленной пластины при $x \to \infty $ амплитуды прогиба пластины и деформаций стремятся к нулю, а при λ² = 1 близки к максимальным. В случае пластины со свободным краем, наоборот, при λ² = 0.5 амплитуды прогиба и деформаций максимальны при $x \to \infty $, а при λ² = 1 значительно меньше. В случае закрепленной пластины максимальные деформации достигаются в кромке и при λ² = 1 превышают критическое значение, ожидается разрушение пластины вблизи кромки. Однако если амплитуда колебаний цилиндра меньше, например $A = 0.03$ м, то максимальные деформации не превышают критическое значение, разрушение пластины не ожидается.

Рис. 4.

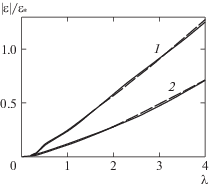
Зависимости безразмерных амплитуд прогиба пластины (1) и деформаций (2) от координаты x при вертикальных колебаниях цилиндра для закрепленной пластины (а, б) и со свободным краем (в, г) при ${{\lambda }^{2}} = $ 0.5 (а, в) и ${{\lambda }^{2}} = $ 1 (б, г), А = 0.05 м.

На рис. 5 показана зависимость амплитуды максимальных деформаций в кромке от частоты для закрепленных пластин толщиной h = 1 и 2 м при вертикальных и горизонтальных колебаниях при ${{x}_{0}} = 100$ м и $A = 0.01$ м. Видно, что деформации тонкой пластины значительно больше, однако изгибающий момент для толстой пластины больше, чем для тонкой. В силу линейности задачи по этому графику можно оценить применимость данной модели, найти параметры, при которых разрушение ледяного покрова не ожидается.

Рис. 5.

Зависимость амплитуды максимальных деформаций в кромке закрепленной пластины с толщиной h = 1 м (1) и 2 м (2) от безразмерной частоты λ при вертикальных (сплошные кривые) и горизонтальных колебаниях (штриховые кривые), x₀ = 100 м, A = 0.01 м.

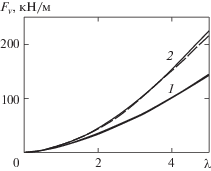
На рис. 6 приведены зависимости от частоты амплитуды вертикальной силы, действующей на стенку, при горизонтальных и вертикальных колебаниях цилиндра для закрепленной пластины толщиной h = 1 и 2 м, ${{x}_{0}} = 100$ м, ${{y}_{0}} = 6$ м, $A = 0.05$ м. Кривые для горизонтальных и вертикальных колебаний цилиндра практически сливаются, только при больших частотах в случае пластины толщиной h = 2 м заметно различие.

Рис. 6.

Сравнение амплитуды вертикальной силы, действующей на стенку, при вертикальных (сплошные кривые) и горизонтальных (штриховые кривые) колебаниях цилиндра и различных толщинах закрепленной пластины: h = 1 м (1) и 2 м (2), A = 0.05 м.

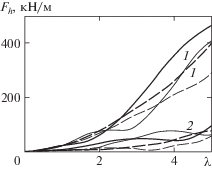
На рис. 7 показаны зависимости от частоты амплитуды динамической составляющей горизонтальной силы, действующей на стенку, при горизонтальных и вертикальных колебаниях цилиндра для закрепленной пластины и со свободным краем с толщиной h = 1 и 2 м, ${{x}_{0}} = 100$ м, ${{y}_{0}} = 6$ м. Видно, что в случае закрепленной пластины значение силы значительно выше, чем в случае свободного края. В случае закрепленной пластины увеличение толщины приводит к увеличению силы при больших частотах.

Рис. 7.

Сравнение амплитуды горизонтальной динамической силы, действующей на стенку, при вертикальных (сплошные кривые) и горизонтальных (штриховые кривые) колебаниях цилиндра в случаях закрепленной пластины (1) и со свободными краями (2) и различных толщинах пластины: h = 1 м (тонкие кривые) и 2 м (толстые кривые), A = 0.05 м.

При увеличении глубины погружения цилиндра все исследованные характеристики: коэффициенты присоединенных масс и демпфирования, прогиб и деформации ледяного покрова, действующие на стенку силы уменьшаются.

ЗАКЛЮЧЕНИЕ

Построено решение задачи о колебаниях цилиндра в жидкости под ледяным покровом вблизи вертикальной стенки. Исследованы зависимости присоединенных масс и коэффициентов демпфирования, прогиба и деформаций пластины, вертикальных и горизонтальных сил, действующих на стенку, от частоты и входных параметров задачи: толщины ледяного покрова, расстояния цилиндра от стенки и глубины его погружения.

Наличие стенки приводит к тому, что кривые зависимости коэффициентов присоединенных масс и демпфирования от частоты осциллируют относительно кривых, которые соответствуют колебаниям цилиндра под бесконечным ледяным покровом в отсутствие стенки. При уменьшении расстояния цилиндра от стенки период их осцилляции увеличивается. Коэффициенты демпфирования обращаются в нуль при некоторых значениях частоты, что означает отсутствие излучения волн на бесконечность. При увеличении толщины ледяного покрова при малых частотах коэффициенты присоединенных масс и демпфирования уменьшаются, а при больших частотах увеличиваются. Амплитуда вертикальной силы, действующей на стенку в случае примороженного края ледяного покрова, увеличивается при увеличении толщины льда. Амплитуда динамической составляющей горизонтальной силы при больших частотах значительно больше в случае закрепленной пластины, чем в случае свободного края.

Автор выражает благодарность И.В. Стуровой за внимание к работе и полезное обсуждение результатов.

Список литературы

Linton C.M., McIver P. Handbook of mathematical techniques for wave/structure interactions. 2001. Chapman & Hall/CRC, Boca Raton.
Sturova I.V. Unsteady three-dimensional sources in deep water with an elastic cover and their applications // J. Fluid Mech. 2013. V. 730. P. 794–418. https://doi.org/10.1017/jfm.2013.303
Das D., Thakur N. Water wave scattering by a sphere submerged in uniform finite depth water with an ice-cover // J. Mar. Struct. 2013. V. 30. P. 63–73.
Das D., Thakur N. Wave scattering by a sphere submerged in a two-layer fluid with an ice-cover // Int. J. Appl. Math. Eng. Sci. 2014. V. 8. P. 45–632.
Das D., Sahu M. Wave radiation by a horizontal circular cylinder submerged in deep water with ice-cover // J. of Ocean Engng and Science. 2019. V.4. P. 49–54.
Thakur N., Das D. Hydrodynamic forces on a submerged horizontal circular cylinder in water with an ice cover // Iran J. Sci. Technol. Trans. Sci. 2017. V. 41. P. 837–842.
Thorne R.C. Multipole expansions in the theory of surface waves // Proc. Camb. Philos. Soc. 1953. V. 49. P. 707–716.
Савин А.А., Савин А.С. Пространственная задача о возмущении ледяного покрова движущимся в жидкости диполем // Изв. РАН. МЖГ. 2015. № 5. С. 16–23.
Ильичев А.Т., Савин А.С. Процесс установления системы плоских волн на ледовом покрове над диполем, равномерно движущимся в толще идеальной жидкости // Теор. и матем. физика. 2017. Т. 193. № 3. С. 455–465.
Pogorelova A.V., Zemlyak V.L., Kozin V.M. Moving of a submarine under an ice cover in fluid of finite depth // J. Hydrodynamics. 2018. doi.org/https://doi.org/10.1007/s42241-018-0143-1
Стурова И.В. Генерация волн колеблющимся погруженным цилиндром при наличии плавающей полубесконечной упругой пластины // Изв. РАН, МЖГ. 2014. № 4. С. 98–108.
Стурова И.В. Влияние трещины в ледяном покрове на гидродинамические характеристики погруженного колеблющегося цилиндра // ПММ. 2015. Т. 79. Вып. 2. С. 251–263.
Sturova I.V. Radiation of waves by a cylinder submerged in water with ice floe or polynya // J. Fluid Mech. 2015. V. 784. P. 373–395.
Ткачева Л.А. Колебания цилиндрического тела, погруженного в жидкость, при наличии ледяного покрова // ПМТФ. 2015. Т. 56. № 6. С. 173–186.
Ren K., Wu G.X., Thomas G.A. Wave excited motion of a body floating on water confined between two semi-infinite ice sheets // Phys. Fluids. 2016. V. 28. P. 127101.
Li Z.F., Shi Y.Y., Wu G.X. Interaction of waves with a body floating on polynya between two semi-infinite ice sheets // J. Fluids and Structures. 2018. V. 78. P. 86–108.
Li Z.F., Shi Y.Y., Wu G.X. Interaction of wave with a body floating on a wide polynya // Phys. Fluids. 2017. V. 29(9). P. 097104.
Li Z.F., Wu G.X., Ji C.Y. Wave radiation and diffraction by a circular cylinder submerged below an ice sheet with a crack // J. Fluid Mech. 2018. V. 845. P. 682–712.
Li Z.F., Wu G.X., Ji C.Y. Interaction of wave with a body submerged below an ice sheet with multiple arbitrary spaced cracks // Phys. Fluids. 2018. V.30. P. 057107.
Li Z.F., Shi Y.Y., Wu G.X. Large amplitude motions of a submerged circular cylinder in water with an ice cover // Eur. J. Mech. (B/Fluids) 2017. V. 65. P. 141–159.
Chakrabarti A., Ahluwalia D.S., Manam S.R. Surface water waves involving a vertical barrier in the presence of an ice-cover // Intern. J. of Engng Science. 2003. V. 41. P. 1145–1162.
Brocklehurst P., Korobkin A., Parau E. Interaction of hydro-elastic waves with a vertical wall // J. Eng. Math., 2010. V. 68. P. 215–231.
Bhattacharjee J., Guedes Soares C. Flexural gravity wave over a floating ice sheet near a vertical wall // J. Engng Math. 2012. V. 75. P. 29–48. https://doi.org/10.1007/s10665-011-9511-3
Das D., Mandal B.N. Oblique wave scattering by a circular cylinder submerged beneath an ice-cover. Intl J. Engng Sci. 2006. 44 (3–4), 166–179.
Ткачева Л.А. Поведение полубесконечного ледяного покрова при периодическом динамическом воздействии // ПМТФ. 2017. Т. 58. № 4. С. 82–94.
Squire V., Martin S. A field study of the physical properties, response to swell, and subsequent fracture of a single ice floe in the winter Bering sea: Tech. report/ Univ. of Washington; Washington, N 18. 1980.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика жидкости и газа

Архивы выпусков Информация о журнале Отправить рукопись в журнал