Известия РАН. Механика жидкости и газа, 2022, № 1, стр. 14-31

1. БЛИЖНИЙ СЛЕД ОТ ЦИЛИНДРОВ В РАМКАХ ОДНОМЕРНЫХ МОДЕЛЕЙ

Нас здесь интересуют не все мыслимые свойства следовых течений, но условия катастрофической перестройки течения следа от пары цилиндров с одной крупномасштабной моды на другую, скажем не желательную по тем или иным соображениям. Можно ожидать, что такой феномен может быть более или менее успешно описан в рамках обобщения простой динамической модели ближнего следа от цилиндра в крупном масштабе – развивающейся вихревой дорожки Кармана. Известны два типа таких наипростейших – одномерных моделей ближнего следа от цилиндрических тел. Это модель Стюарта–Ландау (С-Л) [6], и Ван дер Поля (ВдП) [7]. Модель Л.Д. Ландау (1944 г.) создавалась для описания ламинарно-турбулентного перехода во внутренних течениях [8]. В современной общей теории динамических систем модель Ландау это – модель суперкритической бифуркации Андронова–Хопфа, и как таковая применима для подходящих систем в более или менее широкой закритической области перехода. Было показано [9], что для дорожки Кармана за одиночным цилиндром эта модель, называемая в данном случае моделью Стюарта–Ландау, количественно хорошо применима, по крайней мере, для режима двумерного квазиламинарного следа. Математическая форма модели С-Л – это эволюционное уравнение для “управляющего параметра модели” – комплексной величины A [9]:

В уравнении (1.1) ${{\varepsilon }_{L}}$ – вещественный, а ${{\lambda }_{L}}$ и ${{\mu }_{L}}$ – комплексные параметры модели. Предполагается, что основные физические величины, представляющие интерес в рассматриваемой задаче, могут быть выражены через этот управляющий параметр A. В применении к течению следа управляющий параметр A модели С-Л отождествляют с медленно эволюционирующей комплексной (включающей фазу) амплитудой осцилляций поперечной составляющей скорости в характерной точке дорожки Кармана за цилиндром. Соответственно, пространственное распределение амплитуды и фазы осцилляций скорости ${{V}_{ \bot }}$ в следе считается фиксированным, заданным посредством комплексной функции $f\left( {\mathbf{r}} \right)$:

В рамках уравнения (1.2) учтены установившиеся осцилляции скорости на базовой частоте ${{\omega }_{0}}$, тогда амплитудный сомножитель $A\left( t \right)$ позволяет учесть медленную динамику следа – модуляцию этих колебаний в переходных режимах течения. Пространственное распределение амплитуды и фазы осцилляций – функцию $f\left( {\mathbf{r}} \right)$ в соотношении (1.2) требуется оценивать независимо от модели С-Л, по экспериментальным данным или по результатам численных расчетов соответствующей краевой задачи для уравнений Навье–Стокса.

Теоретическое доказательство справедливости модели С-Л [9] заключается в обращении к решению соответствующей двумерной краевой задачи в форме (1.2). Это решение строится в виде разложения по малому параметру ${{\varepsilon }_{L}} = \operatorname{Re} _{*}^{{ - 1}} - {{\operatorname{Re} }^{{ - 1}}}$ надкритичности течения, поскольку известно, что для достаточно малых чисел Рейнольдса течения $\operatorname{Re} < 180$ трехмерные возмущения не возникают. Тогда уравнение С-Л (1.1) получается как условие существования первого приближения для решения краевой задачи в форме (1.2). Фигурирующее в расчетах [9], число Рейнольдса $\operatorname{Re} $ определяется по невозмущенной скорости набегающего потока и диаметру цилиндра, тогда критическое число Рейнольдса для бифуркации к течению дорожки Кармана за одиночным цилиндром ${{\operatorname{Re} }_{*}} = 46$ [10]. В целях верификации модели С-Л в [9] проведено сравнение расчетных и экспериментально измеренных характеристик следа. Расчетная оценка коэффициентов уравнения (1.1) получена прямым численным решением двумерной краевой задачи для системы уравнений Навье–Стокса при слегка закритическом числе Рейнольдса $\operatorname{Re} = {{\operatorname{Re} }_{*}}\, + 0.6$. Экспериментальная оценка получена из наблюдений переходных режимов следа в аналогичных условиях. Оказалось, что эти две оценки коэффициентов уравнения (1.1) при малом уровне надкритичности течения хорошо согласуются между собой. Более того, модель С-Л (1.1) с так фиксированными коэффициентами хорошо применима, по крайней мере, в диапазоне чисел Рейнольдса $46 < \operatorname{Re} < 180$, т.е. для квазидвумерного квазиламинарного режима обтекания достаточно коротких цилиндров. В частности, в случае $\operatorname{Re} \approx {{\operatorname{Re} }_{*}}$, экспериментальная и расчетная оценки установившейся частоты осцилляций в дорожке Кармана совпадают и составляют величину ${{\omega }^{{LC}}} = 0.74$ (в обозначениях [9]), а при увеличении числа Рейнольдса расчетная оценка дает несколько завышенное значение частоты, но на качественном уровне повторяет ход экспериментальной кривой. Так, в случае Re = 120 расчетная оценка (по формуле (2.34) или (2.44) статьи [9]) дает значение частоты установившихся осцилляций ${{\omega }^{{LC}}} = 1.20$ при экспериментальном значении ${{\omega }^{{LC}}} = 1.10$ [11]. Здесь следует иметь в виду, что штриховая кривая, иллюстрирующая расчетную зависимость $\omega _{{(\operatorname{Re} )}}^{{LC}}$, приведенная на рис. 1a в [9] для сравнения с нанесенными на этот график экспериментальными данными, может вводить в заблуждение относительно погрешности свойственной модели С-Л. Эта кривая рассчитана по формуле (2.34) в [9], но не для параметра малости модели ${{\varepsilon }_{L}} = \operatorname{Re} _{*}^{{ - 1}} - {{\operatorname{Re} }^{{ - 1}}}$, как указано в статье, а для линеаризованного параметра малости $\varepsilon _{L}^{*} = ({\text{Re}}{\kern 1pt} - {\kern 1pt} {\text{Re*}}){\text{/}}{{({\text{Re*}})}^{2}}$, что элементарно проверяется по подробным численным данным, приведенным в [9]. Обсуждая особенности модели С-Л, отметим ограничение, заложенное еще Л.Д. Ландау при ее формулировке, это – медленная скорость эволюции управляющего параметра (амплитуды осцилляций A поперечной составляющей скорости) в масштабах периода осцилляций. Математически это ограничение выражается неравенством

Рис. 1.

Области существования глобальных мод следа от двух цилиндров на плоскости параметров модели $\lambda $, $l$. На каждом сегменте плоскости нанесены номера мод, реализующихся в пределах данного сегмента.

В сравнении с моделью С-Л, модель ВдП (автогенератора с “мягким” возбуждением колебаний) давно и широко применяется в различных областях науки и техники [7, 12]. При изучении следовых течений модель ВдП широко используется для решения задач типа ветрового резонанса конструкций. Вещественное уравнение для управляющего параметра модели ВдП – $X$ имеет вид

В уравнении (1.4) время обезразмерено на период осцилляций $T$ в дорожке Кармана t = = $2\pi {{t}_{{phys}}}{\text{/}}T$, так, чтобы базовая частота установившихся осцилляций была единичной $\omega = 1$. Аналогично модели С-Л, управляющий параметр модели ВдП $X$ отождествляется либо с поперечной составляющей скорости в характерной точке следа, либо с поперечной составляющей силы, приложенной к цилиндру от обтекающей его жидкости. В первом варианте отождествления управляющего параметра пространственное распределение относительной амплитуды и фазы осцилляций скорости ${{V}_{ \bot }}\left( {{\mathbf{r}},t} \right)$, также как и в модели С-Л, следует считать фиксированным, определяемым теперь соотношением (1.5) вместо (1.2).

Здесь $g\left( {\mathbf{r}} \right)$ – некоторая вещественная функция. Она определяется независимо от модели ВдП, аналогично функции $f\left( {\mathbf{r}} \right)$ в модели С-Л. Определяющее относительную фазу колебаний в данной точке r течения, время задержки $\tau $ зависит от положения точки в поле следа. Соотношение (1.5) можно рассматривать как интерпретацию известной гипотезы “замороженной турбулентности” Джеффри Тейлора. Соответственно, можно оценить время задержки $\tau $ как отношение расстояния между текущей точкой и некоторой опорной точкой течения, расположенной выше по течению, к средней продольной скорости (сноса) в этой области следа. Здесь можно отметить работу [13], в которой, в том числе, изучалась корреляция сигналов поперечной составляющей скорости в поле за цилиндром.

Уравнение (1.4) содержит единственный действительный параметр $\varepsilon $, определяющий скорость эволюции осцилляций, который в общей модели ВдП может быть произвольным числом. Тем самым допускается весь спектр колебаний от квазигармонических до релаксационных [12], затухающих и не затухающих. В применении к следовым течениям типа дорожки Кармана интерес представляет случай квазигармонических колебаний скорости. Согласно методологии Ван дер Поля-Крылова-Боголюбова [14], это случай не слишком больших значений параметра $0 < \varepsilon < 1$, когда решение (1.4) в первом приближении по малой величине $\varepsilon $ имеет форму колебаний ${{V}_{ \bot }} = X = \rho \cos (t + P)$ на основной (несущей) частоте $\omega = 1$ с медленно изменяющейся амплитудой $\rho $. Соответствующая система осредненных по быстрым осцилляциям уравнений первого приближения по малой $\varepsilon $ следующая:

Здесь (1.7) необходимо отметить, что в рамках стандартной модели ВдП (1.4) [7, 12] не учитывается дрейф фазы P(t) колебаний скорости течения в переходных режимах следа. В то же время эта экспериментально наблюдаемая зависимость учтена (посредством коэффициента $\operatorname{Im} \mu \ne 0$) в модели С-Л, что легко продемонстрировать, представив решение уравнения (1.1) в аналогичной форме $A = {{\rho }_{L}}\exp (i{{P}_{L}})$. Тогда имеем эквивалентную (1.1) систему уравнений (1.8), (1.9).

Чтобы достигнуть совпадения двух систем уравнений (1.6), (1.7) и (1.8), (1.9), достаточно обобщить модель ВдП (1.4) до вида (1.10) (“совпадения” с учетом отличия в постоянных коэффициентах уравнений, вызванного несколько различающимся способом обезразмеривания уравнений в моделях ВдП и С-Л).

В результате такого обобщения система уравнений первого приближения модели ВдП по малым величинам $\varepsilon ,\;{\text{|}}\Delta {\text{|}}$ примет вид (1.6), (1.11).

Сопоставление моделей позволяет теоретически обосновать ВдП модель следа от уединенного цилиндра как соответствующей обоснованной модели С-Л, работоспособной, по крайней мере, в диапазоне чисел Рейнольдса $46 < \operatorname{Re} < 180$. Система уравнений первого приближения (1.6), (1.11) модели ВдП наглядна и позволяет дать физическую интерпретацию параметров модели. Так, параметр $\varepsilon $ определяет скорость эволюции амплитуды осцилляций, а параметр $\Delta $ – скорость дрейфа фазы, причем оба процесса медленные в меру малости этих величин $\varepsilon $, $\left| \Delta \right| < 1$. Соответственно, оба параметра определяют слабый ангармонизм колебаний в следе.

Согласно проведенному сопоставлению моделей, уравнения С-Л можно рассматривать как осредненные по быстрым осцилляциям уравнения первого приближения по малым параметрам $\varepsilon $, |Δ| для решения обобщенного уравнения ВдП (1.10). Тем самым обнаруживается следующее преимущество модели ВдП в форме (1.10) в сравнении с моделью С-Л: при таком подходе метод Крылова–Боголюбова позволяет систематически уточнять результат, строя высшие приближения по малым величинам $\varepsilon $, $\left| \Delta \right| < 1$, тем самым ослабляя требование малости этих параметров. Кроме того, модель ВдП имеет преимущество по простоте – компактности, она содержит всего два действительных параметра, тогда как модель С-Л – три, два из которых – комплексные.

Обе одномерные модели С-Л и ВдП следа способны непосредственно описать только эволюцию крупномасштабной когерентной структуры этого течения – динамику параметров дорожек Кармана. Мелкомасштабная, высокочастотная структура течения находится вне рамок рассмотрения. Этот недостаток простых моделей следа является в то же время их достоинством, поскольку допускает принципиальную возможность применения моделей в широком диапазоне чисел Рейнольдса, включающем существенно-турбулентные режимы течения, лишь бы крупномасшабная, низкочастотная, квазидвумерная структура дорожки Кармана была четко выражена. В подкрепление этого тезиса, помимо экспериментальных наблюдений следов, уместно привести один из основополагающих выводов теории динамических систем. Динамика низкочастотных степеней свободы системы (дорожек Кармана) самодавлеющая, определяющая эволюцию высокочастотных степеней свободы (мелкомасштабной турбулентности, формирующейся в прямом каскаде турбулентности). Обратное влияние мелкомасштабной турбулентности на дорожку Кармана в грубом приближении можно учесть перенормировкой коэффициента вязкости среды. В соответствии с указанными воззрениями, квазиламинарные модели обтекания цилиндра типа ВдП давно и широко применяют при решении задач гидроаэроупругости, в целях моделирования сил, действующих на погруженные в поток цилиндрические тела, т.е. при типичных числах Рейнольдса течения $\operatorname{Re} \approx {{10}^{4}}{\kern 1pt} - {\kern 1pt} 10{}^{5}$. Соответствующая методика расчетов отражена в профильной монографии [15], пример современной публикации [16].

В сравнении со случаем следа от одиночного цилиндра течение за парой параллельных цилиндров исследовано существенно менее подробно, вероятно, ввиду большего числа определяющих параметров в задаче. В случае одинаковых цилиндров кроме числа Рейнольдса необходимо дополнительно учитывать расстояние между цилиндрами и угол между направлением невозмущенного течения и плоскостью содержащей оси цилиндров. Известно, что малые вариации любого из этих параметров в некоторых областях значений существенно меняют картину комплексного следа [1–4]. В настоящее время для моделировании следа от группы цилиндров в рамках обобщения моделей С-Л или ВдП рассматривается система уравнений этого типа, причем каждое уравнение моделирует парциальный след от индивидуального цилиндра. При этом уравнения системы модифицируют на учет взаимного влияния вихрей в процессе их формирования вблизи цилиндров. Видимо ввиду сложности задачи, многообразия наблюдаемых режимов комплексного следа, при модификации уравнений принято использовать простейшее – линейное приближение по управляющим параметрам при обобщении уравнений (1.1) или (1.4). Посредством подобных моделей, с линейной аппроксимацией взаимодействия парциальных дорожек, удается воспроизвести основные наблюдаемые моды комплексного следа, но не уверенно наблюдаемый режим перемежаемости между модой синфазно-синхронизованных парциальных дорожек и модой biased flow, как следует, например, из рис. 2, 3 в [6]. Однако, режимы перемежаемости следа представляют первостепенный интерес для задач оптимизации течения при сохранении его устойчивости.

Рис. 2.

Разрядная камера с вертикально расположенными цилиндрами-турбулизаторами потока: (а) – схематический вид камеры сверху; (б) – вид по направлению течения газа; (в) фото под углом 45 градусов к направлению втекающего слева направо в камеру газа (вид через смотровое окно в боковой стенке камеры). Хорошо различим горизонтальный медный катод, касающийся обоих кварцевых цилиндров.

Рис. 3.

Спектры поперечной составляющей скорости течения в следе от двух цилиндров (в относительных единицах): (а) – газовый след, безразмерная центральная частота ВЧ-пика ${{\omega }^{{HF}}} = \frac{{{{f}^{{HF}}}}}{{{{f}_{{sol}}}}} = \frac{{1.12\;{\text{kHz}}}}{{0.90\;{\text{kHz}}}} = 1.24$; (б) – плазменный след при плотности тока $J = 1.5$ А/м, частоты НЧ- и ВЧ-пиков ${{\omega }^{{LF}}} = \frac{{{{f}^{{LF}}}}}{{{{f}_{{sol}}}}} = \frac{{0.81\;{\text{kHz}}}}{{0.90\;{\text{kHz}}}} = 0.90$, ω^HF = $\frac{{{{f}^{{HF}}}}}{{{{f}_{{sol}}}}} = \frac{{1.12\;{\text{kHz}}}}{{0.90\;{\text{kHz}}}}$ = 1.24; (в) – плазменный след при плотности тока $J = 2$ А/м, частоты ω^LF = = $\frac{{{{f}^{{LF}}}}}{{{{f}_{{sol}}}}} = \frac{{0.80\;{\text{kHz}}}}{{0.90\;{\text{kHz}}}}$ = 0.89, ${{\omega }^{{HF}}} = \frac{{{{f}^{{HF}}}}}{{{{f}_{{sol}}}}} = \frac{{1.12\;{\text{kHz}}}}{{0.90\;{\text{kHz}}}} = 1.24$. Для сравнения: (г) – спектр скорости в плазменном следе от одиночного цилиндра при токе $J = 2$ А/м, ${{f}_{{sol}}} = 0.9$ кГц, ${{\omega }_{{\,sol}}} = 1$.

В качестве вывода из приведенного краткого обзора литературы по маломерному моделированию газовых и жидкостных следов отметим следующее. В отличие от течения за уединенным цилиндром, используемая методика моделирования комплексного следа от группы цилиндров еще недостаточно совершенна, а принятая – линейная форма обобщения уравнений на учет взаимодействия парциальных следов, на наш взгляд, не оптимальна и подлежит уточнению. Учитывая очерченную выше ситуацию с маломерным моделированием комплексных следовых течений, формулируем цель настоящей работы – построить максимально простую модель следа от двух цилиндров, воспроизводящую основные режимы такого течения, включая режимы перемежаемости между модами, равно пригодную как для нейтральных газовых течений, так и для течений плазмы в условиях тлеющего разряда. Подобная – достаточно универсальная, но одновременно достаточно простая модель позволит физически объяснить наблюдавшуюся перестройку в сравнительно сложной и малоустойчивой системе турбулентного течения в условиях тлеющего разряда [5].

2. НЕЛИНЕЙНОЕ ОБОБЩЕНИЕ ОДНОМЕРНЫХ МОДЕЛЕЙ СЛЕДОВ ОТ ГРУППЫ ЦИЛИНДРОВ

Рассматривается следующая основная конфигурация группы цилиндров – пара одинаковых параллельных цилиндров, установленных в плоскости, перпендикулярной набегающему потоку. Комплексный след от пары цилиндров рассматривается в стиле теории возмущений – как два взаимодействующих в области формирования вблизи цилиндров парциальных следа, которые трансформируются ниже области формирования в две дорожки Кармана от двух соседних цилиндров соответственно. Каждая дорожка моделируется обобщенным осциллятором типа ВдП (1.10) с целью достижения большей общности по допустимой скорости эволюции дорожек.

Управляющие параметры дорожек Кармана X_i отождествлены с поперечной составляющей скорости течения в характерных точках каждой дорожки. В соответствии с (1.5) имеем для двух дорожек

Характерные точки дорожек ${{{\mathbf{r}}}_{i}}$, где калибруется пространственное распределение амплитуды осцилляций скорости $g\left( {{{{\mathbf{r}}}_{i}}} \right)$, выбираются симметрично расположенными относительно плоскости геометрической симметрии задачи, т.е. так, что продольные координаты точек совпадают ${{x}_{1}} = {{x}_{2}}$, а поперечные координаты антисимметричны ${{y}_{1}} = - {{y}_{2}}$ (с учетом того, что начало оси $y$ лежит в плоскости симметрии задачи). Характерные точки удобно выбрать на внешних границах парциальных дорожек Кармана так, чтобы избежать перекрестного проникновения возмущений от одной дорожки в измеряемый сигнал другой дорожки.

Взаимодействие вихрей в области формирования дорожек Кармана учтено посредством обобщения коэффициента при первой производной управляющего параметра в его уравнении (1.10). Этот коэффициент $\varepsilon (1 - X_{i}^{2})$ обобщен в уравнениях (2.1), (2.2) до квадратичного многочлена общего вида от управляющих параметров обеих дорожек: $\varepsilon (1 - X_{i}^{2} - \lambda X_{j}^{2} - l{{X}_{i}}{{X}_{j}})$. Аргументом в пользу использования данной формы многочлена в рамках обобщения модели с использованием теории возмущений является квадратичная нелинейность уравнений Навье–Стокса. Проведенная модификация потребовала введения еще двух дополнительных параметров модели ВдП – $\lambda $ и $l$, имеющих прозрачный физический смысл. Они характеризуют интенсивность взаимодействия парциальных следов, причем с учетом относительной фазы осцилляций в них – $l$. Соответственно виду многочлена, амплитуда и фаза осцилляций в соседней дорожке непосредственно влияют на амплитуду и фазу пульсаций в первой дорожке. Это основная отличительная особенность модели следа с нелинейным представлением взаимодействия парциальных дорожек, предложенной в рамках работ по проекту РФФИ 13-01-00742 [17]. В формализме теории возмущений величина учтенного в уравнениях (2.1), (2.2) взаимодействия парциальных дорожек Кармана характеризуется двумя безразмерными параметрами: $\varepsilon \,\lambda $ и $\varepsilon \,l$. Априори, в соответствии с идеологией теории возмущений предполагаем эти величины малыми, ввиду малости параметра $\varepsilon < 1$.

Кроме обобщения на учет взаимодействия дорожек, однородные уравнения типа ВдП (1.10) для каждой парциальной дорожки обобщены до системы неоднородных уравнений (2.1), (2.2) с целью охвата области турбулентных режимов течения. Для этого, согласно теории случайных процессов, в правые части уравнений введены случайные “силы” Ланжевена $S{{t}_{i}}$, моделирующие возникновение стохастизации в следе. Они обеспечивают, в частности, перемежаемость между квазиламинарными модами следа. По физическому смыслу это форма учета воздействия большого количества сравнительно слабо возбужденных высокочастотных мод турбулентного течения на основную низкочастотную моду осцилляций в дорожке Кармана. В той же форме следует учитывать возмущение дорожек турбулентностью набегающего потока.

Первые два параметра модели, определяющие скорость эволюции дорожек Кармана, $\varepsilon ,\left| \Delta \right| < 1$ малы согласно расчетным и экспериментальным оценкам, например [9, 17, 18], для следа за одиночным цилиндром. Считая, что они не сильно изменяются при переходе от одного цилиндра к двум (в меру применимости теории возмущений), ищем решение системы (2.1), (2.2) по методу Ван дер Поля-Крылова-Боголюбова [14], в форме осцилляций на основной частоте $\omega = 1$ с медленно меняющимися амплитудами $\rho $ и фазами $P$

Соответственно преобразованные осредненные уравнения первого приближения модели по малым параметрам $\varepsilon ,\left| \Delta \right| < 1$ принимают вид уравнений для медленных амплитуд ${{\rho }_{i}}$ и фаз ${{P}_{i}}$ осцилляций в дорожках Кармана.

В силу проведенного в части 1 сопоставления моделей следа за одиночным цилиндром, систему уравнений (2.5)–(2.8) можно интерпретировать как обобщение модели С-Л на случай следа за парой цилиндров.

Предлагаемая модель следа (2.1), (2.2) выглядит на первый взгляд как чисто гидродинамическая, применимая только к течениям нейтральных флюидов, тем не менее, влияние разряда на след нашло отражение в модели посредством учета вариации параметров модели (прежде всего $\lambda $ и $l$) под действием разряда. Учет этого воздействия разряда на гидродинамику течения обсуждается в разд. 4.

3. РЕЖИМЫ СЛЕДА ОТ ПАРЫ ЦИЛИНДРОВ В РАМКАХ НЕЛИНЕЙНОЙ МОДЕЛИ

Анализ модели удобно вести, преобразовав систему уравнений (2.5)–(2.8) первого приближения к глобальным переменным, характеризующим комплексный след в целом [17]. Это суммарная интенсивность осцилляций ${{R}^{2}} = \rho _{1}^{2} + \rho _{2}^{2}$, асимметрия следа $N = {{(\rho _{1}^{2} - \rho _{2}^{2})} \mathord{\left/ {\vphantom {{(\rho _{1}^{2} - \rho _{2}^{2})} {2(\rho _{1}^{2} + \rho _{2}^{2})}}} \right. \kern-0em} {2(\rho _{1}^{2} + \rho _{2}^{2})}}$, и относительная фаза осцилляций в дорожках $P = {{P}_{1}} - {{P}_{2}}$.

Проведенное преобразование зависимых переменных позволило сократить число уравнений и неизвестных в “ведущей” системе на единицу. Затем с помощью преобразования независимой переменной ${{R}^{2}}dt = d\tau $ удается упростить задачу до ведущей системы из двух уравнений (для неизвестных N и P). Глобальные квазиламинарные моды следа находим как линейно-устойчивые стационарные точки или квазипериодические решения системы уравнений (3.1)–(3.3) (и соответствующей двумерной системы) при нулевых правых частях. Точка покоя ${{R}^{2}} = 0$ всегда существует, но неустойчива. Среди оставшихся точек покоя имеется три моды симметричного следа – состоящего из одинаковых дорожек Кармана $N = 0$

№ 1 Мода в виде двух одинаковых синфазно синхронизованных дорожек Кармана. Ее конфигурация, частота осцилляций скорости и область существования моды в пространстве параметров модели следующие:

№ 2 Мода следа, представляющая собой две одинаковых противофазно синхронизованных дорожки Кармана. Конфигурация моды, частота осцилляций скорости в дорожках и область существования моды

№ 3 Мода в форме двух одинаковых дорожек Кармана, синхронизованных на угол, отличный от 0 и $\pi $. Ее конфигурация, частота осцилляций и область существования моды суть

Помимо мод симметричного следа, в рамках модели существуют асимметричные моды:

№ 4 Асимметричная мода в форме дорожки Кармана за одним из цилиндров при полностью подавленной второй дорожке, ее параметры

№ 5 Помимо одночастотных (№ 1–4), численно была рассчитана двухчастотная асимметричная мода следа. Ее примерная конфигурация представляет собой две дорожки Кармана, различающиеся между собой как по частоте, так и по интенсивности установившихся осцилляций [18]. Аппроксимация области существования этой моды

На левой границе области существования этой квазипериодической моды (первое неравенство (3.8)) две частоты осцилляций сливаются в одну.

Для обеспечения полноты реализуемого спектра мод (без учета их устойчивости) следует упомянуть асимметричную моду № 6 в форме двух различающиеся по интенсивности дорожек Кармана, имеющих при этом одну частоту осцилляций. Мода существует в форме двух ветвей, располагающихся в I и в III, или во II и IV квадрантах изменения P. Конфигурация моды № 6 и область ее формального существования следующие:

Аналитически (с помощью критерия Рауса-Гурвица, примененного к характеристическому уравнению линеаризованной системы уравнений) доказывается, что мода № 6 линейно неустойчива всюду в области формального существования.

Для наглядности области существования устойчивых глобальных квазиламинарных мод следа проиллюстрированы в виде карты на плоскости параметров модели $\lambda $, $l$: рис. 1. Полученный результат интерпретируем в рамках теории возмущений. Включение взаимодействия $\lambda \ne 0$, $l \ne 0$ между дорожками Кармана приводит к возникновению пяти коллективных мод комплексного следа, причем вырождение по частоте осцилляций в состояниях этих мод можно считать снятым. Расщепление частот осцилляций $\omega $ по модам определяется масштабным параметром $\Delta $ модели, определяющим скорость дрейфа фазы осцилляций согласно уравнению (1.11), но также и параметрами $\lambda $, $l$, характеризующими интенсивность взаимодействия дорожек: (3.4)–(3.9).

Сопоставим полученный спектр мод течения с данными визуализации следа от пары цилиндров в нейтральных жидкостях и газах. При изменении расстояния между цилиндрами различают смену режимов течения в пределах широкого набора “экспериментальных мод” следа [1–4]. Ограничимся случаем следа от цилиндров, установленных в плоскости перпендикулярной скорости натекающего флюида. Весь набор экспериментальных мод в этом случае можно сгруппировать в три огрубленные моды. Это – две моды симметричного следа: в форме синфазно-синхронизованных шахматных дорожек Кармана, и в форме противофазно-синхронизованных дорожек соответственно. Третья огрубленная асимметричная мода следа представляет собой две дорожки Кармана, отличающиеся по ширине, амплитуде и частоте осцилляций, а также и по скорости затухания колебаний вниз по потоку. Эту моду принято называть “biased flow” – по характеру течения в зазоре между цилиндрами. Уместно отметить, что для всех трех мод каждая парциальная шахматная дорожка Кармана несколько искажается – теряет свою симметрию в результате и в меру взаимодействия областей их формирования, при этом увеличивается скорость ее затухания вниз по течению.

Эти три экспериментальные моды следа однозначно отождествляются с модельными модами № 1, 2, 5 соответственно. При этом, в полном соответствии с данными визуализации следов, мода асимметричного следа № 5 добавляется к паре симметричных мод только при превышении порогового значения параметра взаимодействия в модели – при выполнении левого неравенства (3.8). В эксперименте этому соответствует сближение цилиндров до расстояния $T{\text{/}}D < 2.1$. В рамках модели возможны все режимы перемежаемости между модами № 1, 2, 5 (в зависимости от значений параметров $\lambda $ и $l$ – рис. 1) при том, что экспериментаторы отмечают [1–4] наблюдение перемежаемости только между огрубленными модами № 1 и № 5. Иными словами, модель предоставляет более широкий набор режимов перемежаемого течения, чем реализуется в течениях нейтральных жидкостей и газов.

Отдельного комментария заслуживает модельная мода следа № 4. Комплексный след в состоянии этой моды представляет собой дорожку Кармана от одного из цилиндров при полностью подавленной шахматной дорожке от второго цилиндра, причем характеристики первой дорожки полностью совпадают с характеристиками следа от уединенного цилиндра. Расчетная мода № 4 может реализовываться только при достаточно сильном взаимодействии областей формирования дорожек, а именно при $\lambda > 0.5$. На первый взгляд, отмеченные свойства моды № 4 удачно коррелируют с наблюдениями комплексного следа в форме одной широкой дорожки Кармана за достаточно близко расположенными цилиндрами, при $T{\text{/}}D < 1.2$ [1–4]. Однако при более внимательном рассмотрении данных визуализации отмечаем, что перестройка комплексного следа в результате сближения цилиндров (от формы двух отличающихся дорожек Кармана к течению одной широкой дорожки) происходит непрерывно, монотонно, т.е. в рамках одной глобальной моды – типа № 5. Вначале при расстояниях $T{\text{/}}D > 1.5{\kern 1pt} - {\kern 1pt} 1.7$ в комплексном следе наблюдается и узкая высокочастотная, и широкая низкочастотная дорожки. При дальнейшем сближении цилиндров скорость затухания высокочастотной дорожки существенно увеличивается, и начиная с некоторого расстояния от цилиндров вниз по потоку наблюдается только одна широкая низкочастотная шахматная дорожка. (Процесс затухания дорожек параметризуется посредством функции $g(r)$ из (1.5).) При сближении цилиндров до расстояния $T{\text{/}}D \approx 1.2$ высокочастотная дорожка практически не обнаруживается уже вблизи цилиндров. Следовательно, мода № 4 оказалась избыточной в расчетном спектре мод следа, как и мода № 3. Чтобы отсечь эти не наблюдаемые расчетные моды № 3, 4 течения достаточно ограничить область изменения параметра взаимодействия дорожек в модели до интервала $0 < \lambda < 0.5$.

Сопоставление выводов модели с данными визуализации следов от пары цилиндров в нейтральных средах позволяет сделать следующее заключение. В рамках модели, построенной на основе теории возмущений, с нелинейным представлением взаимодействия парциальных дорожек Кармана удается воспроизвести, по крайней мере, на качественном уровне все три основные визуализированные моды комплексного следа: № 1, 2, 5, с учетом всех возможных режимов перемежаемости между ними. В целом можно надеяться на применимость сравнительно простой модели, допускающей аналитическое исследование, для физического моделирования следов от не слишком близко расположенных цилиндров благодаря вполне обозримому спектру потенциально воспроизводимых режимов течения, включая режимы перемежающегося следа.

4. ВЗАИМОДЕЙСТВИЕ СЛЕДА С ТЛЕЮЩИМ РАЗРЯДОМ В РАМКАХ МОДЕЛИ

В строгой постановке моделирование следа в условиях разряда потребовало бы решения краевой задачи для уравнений Навье–Стокса совместно с системой уравнений электродинамики и кинетических уравнений для плотности электронов и ионов. Получающаяся система нелинейных уравнений краевой задачи оказывается слишком сложной, связанной. Так, на движение ионов существенно влияет гидродинамика нейтральной компоненты плазмы, составляющей львиную долю частиц, при этом разряд оказывает (обратное) влияние на гидродинамику нейтралов через тепловыделение, а также и через силу Лоренца. Ввиду сложности такую задачу никогда не решают в полной постановке, а используют те или иные упрощения. Нас интересует случай тлеющего разряда, т.е. сравнительно низких плотностей тока, соответственно магнитогидродинамическим взаимодействием в плазме можно пренебречь. В условиях эксперимента [5] средняя плотность тока в объеме камеры не превышала 40 А/м², а на катоде – менее 200 А/м². Для случая тлеющего разряда в системе электродинамических уравнений краевой задачи можно ограничиться учетом уравнения Пуассона для потенциала электрического поля и уравнений переноса электронов и ионов с учетом процессов их рождения и гибели [19, 22]. Остается рассмотреть влияние тепловыделения в разряде на течение в рамках этой модели. Плотность диссипации энергии электрического поля $\sigma \,{{E}^{2}}$ высока там, где велико электрическое поле. Тлеющий разряд отличается высоким пространственным контрастом напряженности поля. В этом случае поле мало в области основного объема разряда – “анодного столба” и прилегающих областей и, напротив, велико в узкой области катодного падения потенциала, прилегающей к катоду (а также и в области анодного падения). Практически вся диссипируемая в катодном (и анодном) падении энергия сразу выделяется в форме тепла, сообщаемого газу нейтральных частиц. В случае расчета течения плазмы молекулярных газов следует учитывать и другой канал нагрева. В молекулярных газах значительная (иногда бóльшая) часть диссипируемой в анодном столбе энергии поступает непосредственно в колебательные степени свободы молекул, и лишь затем сравнительно медленно релаксирует в тепло. Поскольку фактически строится модель формирования ближнего следа в окрестности цилиндра порядка его диаметра, то отмеченным прогревом газа через канал колебательной релаксации молекул можно пренебречь в этом малом объеме, расположенном на входе колебательно невозбужденного газа в область разряда. Тем более нагревом плазмы в области цилиндров через канал колебательной релаксации можно пренебречь для таких медленно релаксирующих газов, как азот [19, 22]. Соответственно отмеченным особенностям тепловыделения, непосредственное влияние тлеющего разряда на след в рамках предлагаемой модели сводится к локальному нагреву и соответствующему расширению газа в области катодного падения потенциала, которая погружена в пограничный слой на катоде, либо примыкает к области пограничного слоя (вблизи передней точки торможения потока). Прогрев заторможенного газа и рост толщины пограничного слоя на катоде приводят к росту толщины пограничного слоя на цилиндрах-турбулизаторах, формируемого из этого уже нагретого и заторможенного газа (не по всей высоте цилиндров, но на середине высоты канала – в области следа катода: рис. 2б). Этот процесс естественно трактовать как некоторое эффективное сближение цилиндров, тогда в рамках модели, процесс локального прогрева плазмы следует рассматривать как некоторое увеличение параметров, характеризующих взаимодействие парциальных следов – $\lambda $ и $\left| l \right|$. Эффективное сближение цилиндров будем количественно характеризовать вариацией толщины пограничного слоя на них.

В рамках решения краевой задачи (для уравнений Навье–Стокса, уравнения Пуассона для потенциала электрического поля, и кинетических уравнений для плотности заряженных частиц) для случая тлеющего разряда можно рассмотреть и обратное влияние течения на характеристики разряда, например, ВАХ. Однако нас здесь интересует только тепловыделение в области катодного падения потенциала, определяемое током и самим катодным падением. В эксперименте [5] режим горения разряда на катоде был близок к нормальному, может быть с некоторым заходом в режим аномального разряда, поскольку катодное пятно покрывало большую часть поверхности катода при обсуждаемых токах $I = 1.5{\kern 1pt} - {\kern 1pt} 2.0$ A. Величина катодного падения потенциала была близка к величине нормального катодного падения в покоящейся плазме, поскольку скорости дрейфа ионов в области катодного падения потенциала были существенно выше, чем скорость течения плазмы – порядка 100 м/с в условиях [5]. Тогда получаем, что при фиксированном токе с катода тепловыделение в локальной области, примыкающей к катоду и одному из цилиндров, могло варьировать за счет перераспределения плотности тока вдоль катода. Перераспределение тока вдоль катода возможно в меру перераспределения оставшейся свободной от катодного пятна поверхности катода и в меру локального перехода пятна в режим аномального горения. Отмеченное перераспределение плотности тока вдоль катода может быть вызвано как неоднородностью прогрева плазмы в пограничном слое на катоде, так и процессами в объеме разрядной камеры – развитием ионизационно-перегревной неустойчивости при повышенных токах. На данном этапе построения модели выносим вопросы развития неустойчивости в объеме камеры за рамки рассмотрения.

Имея соответствующую модель объекта, можно приступить к анализу экспериментальных данных.

5. ЭФФЕКТ ТЛЕЮЩЕГО РАЗРЯДА В РАМКАХ МОДЕЛИ СЛЕДА

5.2. Оценка свободных параметров модели по данным эксперимента

Проведем сопоставление частот осцилляций по глобальным модам с экспериментальными данными по локализации ВЧП и НЧП: ${{\omega }^{{HF}}} = 1.24$, ${{\omega }^{{LF}}} = 0.89$. Для этого рассмотрим распределение расчетных частот осцилляций, проиллюстрированное на рис. 4 для случая $\Delta = - 0.1$; $\varepsilon \approx 0.1{\kern 1pt} - {\kern 1pt} 0.2$. Как отмечено в разд. 4, включению разряда и увеличению его тока соответствует движение изображающей точки по карте параметров модели – рис. 4 вниз-направо, в сторону увеличения модельных параметров $\lambda $, $\left| l \right|$, характеризующих взаимодействие парциальных дорожек Кармана. Такое движение изображающей точки означает приближение к границе области существования моды № 1, что влечет за собой уменьшение вероятности ее осуществления в пользу моды № 5 и/или № 2. Если точка пересекает границу области существования моды № 5, то реализуется и эта мода.

Рис. 4.

Иллюстрация (тонкими линиями уровня) зависимости частот осцилляций $\omega \left( {\lambda ,l} \right)$ по глобальным модам следа от параметров модели $\lambda $, $l$: (а) – для моды № 1; (б) – для моды № 2; для моды № 5 $\omega = 0.89$ на левой границе ее области существования. Жирные линии – границы областей существования мод. Здесь стоит отметить, что на рис. 4 приведен сильно растянутый по горизонтали малый фрагмент той широкой области параметров модели $\lambda $, $l$, что приведена на рис. 1.

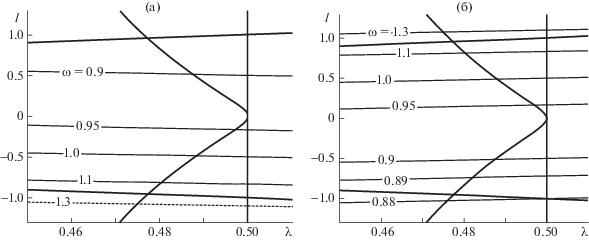
Допустим, что перестройка следа от моды № 1 в газе происходит сразу к двум модам в плазме: № 5 и № 2 (к той или к иной). В обоснование такой возможности отметим, что НЧ пик самый широкий среди наблюдавшихся – рис. 3а–г, что, по крайней мере, не противоречит возможности его отождествления с обеими модами № 5 и № 2. Тогда в точке перестройки следа к режиму трех перемежающихся мод (№ 1, 5, 2) должны быть выполнены три условия. Первое, параметр $\Delta = - 0.1$ с тем, чтобы частота возникающего в условиях разряда НЧП удовлетворяла условию = 0.89. Второе, аналогичное требование выставляем для моды № 2: . Третье условие – изображающая точка должна лежать на границе существования моды № 5: левая граница неравенства (3.8). Соответственно получаем оценку трех параметров модели, соответствующих точке перестройки от моды № 1 к двум модам № 5 и 2 сразу: $\Delta \approx - 0.1$; $\lambda \approx 0.48$; $l \approx - 0.77$. По результатам проведенного сопоставления расчетных и экспериментальных данных четвертый параметр модели остался несколько неопределенным, но он оценивался ранее экспериментально [17, 18]: $\varepsilon = 0.1{\kern 1pt} - {\kern 1pt} 0.2$.

Перестройка течения сразу к двум модам – это вырожденный случай. Теперь рассмотрим общий случай бифуркации к одной из мод № 5 или № 2. Перестройка только к моде № 5 соответствует пересечению границы ее существования (3.8) изображающей точкой (рис. 4) где-то выше уровня $\,l \approx - 0.77$. При этом значение параметра $\Delta \approx - 0.1$ остается фиксированным, чтобы частота осцилляций по моде № 5 соответствовала экспериментально наблюдаемому значению = 0.89.

Напротив, рассмотрим вариант перестройки течения к моде № 2 (без участия моды № 5); это случай $\Delta < - 0.1$. Трансформация следа происходит на линии уровня , где-то вблизи границы существования моды № 1, скажем, на пересечении с прямой $l \approx - 1.6\,\lambda $ (содержащей отмеченную выше точку $\lambda \approx 0.48$; $l \approx 0.77$ перестройки к режиму перемежаемости трех мод № 1, 2, 5). Соответственно, имеем оценку параметров модели в случае перестройки течения только к моде № 2: $\Delta < - 0.1$; $\lambda \approx 0.386{\text{/}}( - 18\Delta - 1)$; $l \approx - 1.6\lambda $.

Здесь уместно привести независимый аргумент в пользу перестройки течения под действием разряда в режим именно моды № 5 асимметричного следа. Рассматривая эффект тлеющего разряда, следует учитывать его имманентное свойство – ионизационно-перегревную неустойчивость. Вблизи катода режим разряда был близок к самостоятельному, поскольку катод располагался на входе нейтрального газа в разрядную камеру, причем область катода находилась практически вне области ионизующего поля. Соответственно самостоятельному режиму разряда, здесь и при умеренных токах вероятно развитие асимметрии токораспределения между двумя областями не секционированного катода, примыкающими к соседним цилиндрам рис. 2. Эта асимметрия токораспределения вдоль катода приводит к различию в нагреве пограничных слоев на цилиндрах, что в свою очередь индуцирует перестройку течения к гидродинамической моде асимметричного следа № 5 в условиях разряда.

Несмотря на некоторую неоднозначность полученного результата – неопределенности в идентификации НЧ-моды следа, проведенная оценка параметров модели для условий нашего эксперимента позволила продвинуться в обосновании предлагаемой модели комплексного следа. По результатам этой оценки, условия применимости теории возмущений оказались выполнены $\varepsilon \lambda \ll 1$, $\varepsilon \left| l \right| \ll 1$ для рассматриваемого случая [5]. Тем самым методика построения модели для системы слабо взаимодействующих парциальных дорожек Кармана на основании теории возмущений оказалась самосогласованной, по крайней мере, для области $L{\text{/}}D > 2$.

ЗАКЛЮЧЕНИЕ

Рассмотрены особенности и взаимосвязь известных одномерных моделей следов: типа Стюарта–Ландау и Ван дер Поля. На их основе, в стиле теории возмущений примененной к известной, обоснованной модели следа от уединенного цилиндра, построена простая динамическая модель турбулентного следа от пары не слишком близко расположенных цилиндров, установленных в плоскости, перпендикулярной набегающему потоку. Модель отличается учетом нелинейного характера взаимодействия между областями формирования парциальных дорожек Кармана от каждого цилиндра пары, при этом интенсивность взаимодействия дорожек считается малой, допускающей применение теории возмущений. Установлено, что в рамках развиваемой модели реализуется набор из трех огрубленных мод следа, визуализируемых при различных расстояниях между такими цилиндрами [1–4]. Это две симметричные одночастотные моды в форме синфазно- и противофазно-синхронизованных парциальных дорожек Кармана и асимметричная двухчастотная мода, представляющая собой две различающиеся дорожки. Все эти три расчетные моды реализуются, в том числе, в различных режимах перемежаемости между ними (при соответствующем выборе параметров взаимодействия $\lambda $ и $l$ модели); при том, что в экспериментах с нейтральными жидкостями и газами отмечается единственный режим перемежаемости (между модой синфазно-синхронизованных дорожек и асимметричной модой “biased flow”).

На основе сопоставления выводов модели с результатами наших измерений частот осцилляций скорости течения в следе и литературных данных визуализации нейтральных следов подтверждена первоначальная интерпретация эффекта разряда – перестройка от одномодового течения к режиму перемежаемости глобальных мод. Установлено, что эталонный газовый след находился в состоянии глобальной моды в форме двух синфазно-синхронизованных дорожек Кармана. С включением разряда происходила бифуркация следа к режиму перемежаемости между указанной выше модой и модой асимметричного следа (и/или модой в форме противофазно-синхронизованных дорожек). Более того, в рамках сопоставления модельных и экспериментальных результатов удалось выполнить количественные оценки параметров модели следа для окрестности точки перестройки следа в условиях нашего эксперимента. Эти оценки позволили обосновать правомерность использования теории возмущений в целях построения модели комплексного следа от пары не слишком близко расположенных цилиндров.

Успешное решение задачи интерпретации позволило исследовать механизм наблюдавшегося эффекта. Для этого проведена оценка прогрева плазмы при включении разряда. Тлеющий разряд в азоте приводит к прогреву плазмы, прежде всего, в слое катодного падения потенциала. Из этой нагретой плазмы формируются пограничные слои на цилиндрах, расположенных вплотную за катодом. С ростом тока разряда растет толщина пограничного слоя на цилиндрах, и тем самым усиливается гидродинамическое взаимодействие областей формирования парциальных дорожек Кармана. В рамках модели усиление взаимодействия выражается в увеличении соответствующих параметров модели – $\lambda $, $\left| l \right|$. Вариация параметров модели в окрестности их бифуркационных значений с необходимостью приводит к перестройке течения следа. В соответствии с установленной в рамках модели картой режимов следа, наблюдается бифуркация от одномодового режима (синфазно синхронизованных дорожек) к режиму перемежающегося турбулентного течения.

Тема исследования турбулентных следовых течений в условиях тлеющего разряда давно привлекает наше внимание, и мы неоднократно публиковались по этой тематике. Настоящая статья может рассматриваться как обзорная по нашим исследованиям следа от пары цилиндров, поэтому не лишним представляется отметить новые, не опубликованные нами ранее материалы:

1. Выполнен краткий обзор известных одномерных моделей нейтральных следовых течений. На основе выводов по обзору сформулирована задача построения простой модели комплексных следов от группы цилиндров, воспроизводящей свойство перемежаемости следа, и пригодной для моделирования течения, в том числе, в условиях тлеющего разряда.

2. Рассматриваемый вариант такой модели был предложен нами ранее [17, 18]. В данной публикации подробно прописаны конфигурация и область существования всего спектра глобальных мод следа, существующих в рамках этой модели, приведено распределение частот осцилляций по модам. В частности, впервые представлены характеристики всюду линейно-неустойчивой моды № 6.

3. Впервые проведенное подробное сопоставление результатов модели с литературными данными визуализации нейтральных следов и с нашими данными по осцилляциям скорости позволило сделать вывод о пригодности модели в целом для случая сравнительно далеко отстоящих цилиндров, т.е. для сравнительно слабо взаимодействующих парциальных следов в рамках модели. В области слабого взаимодействия модель оказалась самосогласованной и работоспособной, по крайней мере, для условий нашего эксперимента: $T{\text{/}}D = 2.2$. Для этих условий экспериментальные оценки параметров малости теории возмущений, использованной при построении модели, оказались благоприятными: $\varepsilon \lambda $, $\varepsilon \left| l \right| \ll 1$.

4. Отмечаются простота и наглядность модели. Так, впервые показано, что четырехмерная система уравнений модели может быть сведена к системе двух ведущих уравнений. Параметры модели имеют прозрачный физический смысл, который впервые подробно прописан в статье. Влияние разряда учтено простейшим способом – посредством вариации параметров модели. Простота модели, в совокупности с впервые проведенной минимальной оценкой утолщения пограничного слоя на цилиндрах в условиях разряда позволили дать элементарное объяснение эффекта разряда. Наблюдалась перестройка глобальной моды течения в результате индуцированного разрядом роста толщины пограничного слоя на цилиндрах, что нашло выражение в дрейфе управляющих параметров $\lambda $, $\left| l \right|$ модели следа в области их бифуркационных значений. Минимальность проведенной оценки роста пограничного слоя обоснована, в том числе, с учетом впервые публикуемого спектра скорости при промежуточном значении плотности тока J = = 1.5 A/m – рис. 3б.

Статья составлена по материалам, представленным на конференции “Нелинейные задачи теории гидродинамической устойчивости и турбулентность-2020” и на “Конференцию по прикладной математике и механике в аэрокосмической отрасли AMMAI-2020”.

Работа выполнена с использованием средств государственного бюджета по госзаданию № АААА-А20-120011690135-5. Авторы признательны Эдуарду Владимировичу Теодоровичу за внимание к работе и дискуссию.