Микроэлектроника, 2022, T. 51, № 2, стр. 140-147

Математическая модель работы адиабатических калориметрических измерителей потоков энергии пучков частиц в динамическом режиме

В. П. Кудря^*

Физико-технологический институт им. К.А. Валиева Российской академии наук
117218 Москва, Нахимовский проспект, 36, корп. 1, Россия

^* E-mail: kvp@ftian.ru

Поступила в редакцию 02.06.2021
После доработки 24.07.2021
Принята к публикации 24.07.2021

EDN: AUUIWV
DOI: 10.31857/S0544126922010070

Полный текст (PDF)

Аннотация

Представлен подробный анализ математической модели адиабатического калориметра. Приведено нестационарное решение соответствующего уравнения теплопроводности и рассмотрены его особенности. Предложены два определения времени отклика адиабатического калориметра, работающего, вообще говоря, в нестационарном режиме. Рассмотрен вопрос об определении чувствительности адиабатического калориметра. Основываясь на этих определениях, предложено решение проблемы оптимального выбора материала приемной пластины по соотношению чувствительности и времени отклика. Проведены сравнения с некоторыми опубликованными экспериментальными и теоретическими результатами. Полученные в работе результаты могут быть использованы при разработке и проектировании калориметрических систем диагностики пучков быстрых нейтральных частиц.

Ключевые слова: адиабатический калориметр, чувствительность калориметра, время отклика калориметра, диагностика потоков быстрых нейтральных частиц

1. ВВЕДЕНИЕ

Калориметрический метод измерения мощности потоков энергии является универсальным, поскольку измерения можно проводить и с потоками фотонов (в диапазоне от СВЧ до рентгеновского излучения), и с потоками быстрых частиц, как заряженных (ионы, электроны), так и нейтральных (атомы, радикалы, молекулы). Наш интерес к этому методу обусловлен необходимостью разработки методов диагностики пучков быстрых нейтральных частиц (БНЧ). Исследования в этой области являются частью большого научного направления, которое развивается в лаборатории ионно-лучевых технологий Физико-технологического института им. К.А. Валиева РАН и которое может быть сформулировано как “Технология пучков быстрых нейтральных частиц: источники, диагностика, применение”. Настоящая работа продолжает серию наших публикаций [1–3], посвященных различным методам диагностики пучков БНЧ.

В общем случае, калориметрический измеритель мощности потоков энергии, который для краткости далее будем называть калориметром, состоит из: 1) приемной пластины, в которой происходит преобразование энергии падающих частиц в тепловую энергию, 2) специальных элементов конструкции, через которые тепло отводится от приемной пластины, и 3) одного или нескольких термодатчиков, которые используются для измерения температуры пластины и, в некоторых случаях, элементов конструкции. В качестве термодатчиков могут использоваться термопары, терморезисторы, пироэлектрики. Отметим, что в общем случае тепло отводится также через соединительные провода термодатчиков, излучением в пространство, а при работе калориметра в атмосфере, еще и конвекцией. При измерении небольших потоков энергии калориметр может быть помещен в корпус, который экранирует элементы конструкции от паразитного теплового излучения, а также внешних электрических полей. В этом случае поток энергии поступает на приемную пластину через входную апертуру. В некоторых случаях в качестве приемной пластины может использоваться непосредственно сам термодатчик.

Частным случаем калориметров с одним термодатчиком являются так называемые адиабатические калориметры, у которых потери тепла, полученного приемной пластиной, сведены к минимуму. Такие калориметры могут работать только в импульсном режиме, поэтому они используются для измерения энергии пучков, генерируемых импульсными источниками [4–7]. Адиабатические калориметры весьма чувствительны, имеют относительно простую конструкцию и обеспечивают достаточно точную абсолютную калибровку, не требующую экспериментального проведения калибровочных измерений.

Как правило, для описания работы адиабатических калориметров используют простое соотношения, в котором повышение температуры приемной пластины определяется как энергия, поглощенная этой пластиной, деленная на ее теплоемкость. Это соотношение справедливо при выполнении двух условий. Во-первых, паразитные потери тепла не должны изменять температуру приемной пластины в течение времени измерения. Во-вторых, к моменту начала измерения во всем объеме пластины должна установиться одинаковая (равновесная) температура. Эти условия накладывают взаимно противоречивые требования на время измерения, поэтому на практике часто используют динамический режим, при котором измеряется и анализируется поведение временной производной температуры в некоторой точке приемной пластины. Отметим, что математическое описание функционирования калориметров этого типа в динамическом режиме весьма неполно и разбросано по литературе.

Настоящая работа посвящена последовательному изложению математической модели работы калориметров адиабатического типа в динамическом режиме, анализу аналитических решений, исследованию времени отклика и чувствительности, решению проблемы оптимального выбора материала приемной пластины. Проводятся сравнения с опубликованными экспериментальными и теоретическими результатами. Отметим, что эффективность преобразования энергии падающих частиц в тепловую энергию приемной пластины рассматривалась в работе [3], а в настоящей работе рассматривается только тепловая задача.

2. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ АДИАБАТИЧЕСКОГО КАЛОРИМЕТРА

Моделью адиабатического калориметра может служить теплоизолированная приемная пластина толщиной d и площадью фронтальной поверхности A. Для простоты ограничимся случаем сравнительно небольшого изменения температуры пластины, когда можно считать постоянными величины коэффициента теплопроводности λ, удельной теплоемкости c и плотности ρ материала пластины, а также пренебречь радиационными потерями. В этом случае математическая модель адиабатического калориметра в условиях полного поглощения падающего на его фронтальную поверхность потока мощности F, допускает аналитическое решение в виде ряда с умеренной сходимостью (см., например, классическую книгу [8]). Обозначим через κ = λ/(cρ) коэффициент температуропроводности материала пластины, а через T – величину превышения температуры над ее начальным значением, и перейдем к нормированным величинам времени, координаты по толщине и температуры:

$t{\kern 1pt} ' = \frac{{\kappa t}}{{{{d}^{2}}}};\,\,\,\,x{\kern 1pt} ' = \frac{x}{d};\,\,\,\,T{\kern 1pt} ' = \frac{\lambda }{{Fd}}T.$

В этих переменных уравнение теплопроводности вместе с начальным и граничными условиями запишется в виде:

(1)

$\frac{{\partial T{\kern 1pt} '}}{{\partial t{\kern 1pt} '}} = \frac{{{{\partial }^{2}}T{\kern 1pt} '}}{{\partial x{\kern 1pt} {{'}^{2}}}};\,\,\,\,T{\kern 1pt} '(x{\kern 1pt} ',0) = 0;\,\,\,\,{{\left. {\frac{{\partial T{\kern 1pt} '}}{{\partial x{\kern 1pt} '}}} \right|}_{{x{\kern 1pt} ' = 0}}} = 0;\,\,\,\,{{\left. {\frac{{\partial T{\kern 1pt} '}}{{\partial x{\kern 1pt} '}}} \right|}_{{x{\kern 1pt} ' = 1}}} = 1,$

где x' = 0 соответствует тыльной поверхности приемной пластины.

Решение уравнения (1) дается выражением

(2)

$T{\kern 1pt} '(x{\kern 1pt} ',t{\kern 1pt} ') = t{\kern 1pt} ' + \frac{{x{\kern 1pt} {{'}^{2}}}}{2} - \frac{1}{6} - \frac{2}{{{{\pi }^{2}}}}\sum\limits_{n = 1}^\infty {\frac{{{{{( - 1)}}^{n}}}}{{{{n}^{2}}}}\exp ( - {{n}^{2}}{{\pi }^{2}}t{\kern 1pt} ')\cos (n\pi x{\kern 1pt} ')} ;\,\,\,\,0 \leqslant x{\kern 1pt} ' \leqslant 1.$

Характерной особенностью этого решения является его асимптотический выход на линейную зависимость

(3)

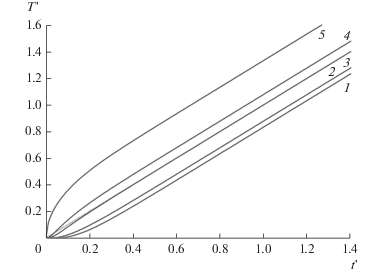
$\mathop {\lim }\limits_{t' \to \infty } T{\kern 1pt} '(x{\kern 1pt} ',t{\kern 1pt} ') = t{\kern 1pt} ' + \frac{1}{2}\left( {x{\kern 1pt} {{'}^{2}} - \frac{1}{3}} \right);\,\,\,\,0 \leqslant x{\kern 1pt} ' \leqslant 1.$

По координате x' эта зависимость является квадратичной, что соответствует линейному падению теплового потока в пластине от единичного значения на фронтальной поверхности приемной пластины до нулевого значения на тыльной поверхности. На рис. 1 показано семейство решений (2) для нескольких значений x'.

Рис. 1.

Семейство решений (2) для нескольких значений x' :1 – 0; 2 – 0.3; 3 – $x_{{{\text{eq}}}}^{'}$; 4 – 0.7; 5 – 1.0; пунктирная линия – T ' = t'.

Отметим, что в абсолютных единицах асимптотическое поведение описывается линейной зависимостью

(4)

$\mathop {\lim }\limits_{t \to \infty } T(x,t) = \frac{F}{{\rho cd}}t + \frac{{Fd}}{{2\lambda }}\left[ {{{{\left( {\frac{x}{d}} \right)}}^{2}} - \frac{1}{3}} \right].$

Следовательно, аппроксимировав асимптотическую часть экспериментальной зависимости T(t) прямой линией и определив ее коэффициент наклона k, можно определить плотность падающей мощности

$F = k\rho cd.$

Для достаточно тонких приемных пластин, выполненных из материала с высокой теплопроводность, линейная зависимость (4) очень мало отличается от прямо пропорциональной зависимости. Следовательно, в этом случае можно использовать соотношение

(5)

$T(t) = \frac{F}{{\rho cd}}t = \frac{{W(t)}}{C},$

где W(t) = FAt – энергия, поглощенная приемной пластиной за время t; C – теплоемкость приемной пластины. Действительно, соотношение (5) широко используется для приемных пластин, выполненных из металлической фольги (см., например, [6, 7, 9]). Отметим, что температура (5) соответствует так называемой равновесной температуре T_eq, т. е. такой температуре, которая в каждый момент времени устанавливалась бы по всей толщине пластины при условии, что вся полученная ею тепловая энергия W(t) мгновенно и однородно распределяется по всей пластине.

Среди семейства решений (3) выделяется одно, которое получается при $x{\kern 1pt} ' = x_{{{\text{eq}}}}^{'} = 1{\text{/}}\sqrt 3 \approx 0.577$. Его асимптотика представляет собой прямо пропорциональную зависимость $T{\kern 1pt} '(x_{{{\text{eq}}}}^{'},t{\kern 1pt} ') = T_{{{\text{eq}}}}^{'}(t{\kern 1pt} ') = t{\kern 1pt} '$ (рис. 1, кривая 3). Таким образом, установка термодатчика на указанном расстоянии от тыльной стороны приемной пластины позволяет использовать наиболее простую однопараметрическую процедуру определения наклона асимптотической части экспериментальной зависимости T(t). Именно на таком оптимальном расстоянии были установлены термодатчики, описанные в работах [10, 11]. Отметим, что авторы работы [11] утверждали, что для получения достаточно точной зависимости от времени достаточно учесть четыре слагаемых в сумме (2). Это утверждение вполне подтверждается нашими расчетами, хотя оно никак не связано с асимптотическим прямо пропорциональным поведением решения. Кроме того, авторы работы [11], по-видимому, ошиблись в знаке при расчетах вклада слагаемых, стоящих под знаком суммы, так как полученный ими график расположен зеркально относительно прямой $T{\kern 1pt} '(x{\kern 1pt} ',t{\kern 1pt} ') = t{\kern 1pt} '$, т. е. выше нее.

Отметим еще одно свойство решения, которое имеет место при x' = 1, т.е. на фронтальной поверхности приемной пластины. Для этого запишем общее решение уравнения (1) в другом виде [8]:

(6)

$T{\kern 1pt} '(x{\kern 1pt} ',t{\kern 1pt} ') = 2\sqrt {t{\kern 1pt} '} \sum\limits_{n = 0}^\infty {\left[ {{{{\text{i}}}^{1}}{\text{erfc}}\left( {\frac{{(2n + 1) - x{\kern 1pt} '}}{{2\sqrt {t{\kern 1pt} '} }}} \right) + {{{\text{i}}}^{1}}{\text{erfc}}\left( {\frac{{(2n + 1) + x{\kern 1pt} '}}{{2\sqrt {t{\kern 1pt} '} }}} \right)} \right]} ;\,\,\,\,0 \leqslant x{\kern 1pt} ' \leqslant 1,$

где функция i¹erfc(x) (кратный интеграл вероятности) определяется формулой

${{{\text{i}}}^{{\text{1}}}}{\text{erfc}}(x) = \int\limits_x^\infty {{\text{erfc}}(z){\text{d}}z} .$

Эта функция быстро падает при увеличении значения аргумента, поэтому при x' = 1 и малых значениях t ' в сумме (6) можно оставить только первое слагаемое, что приводит к простой зависимости

(7)

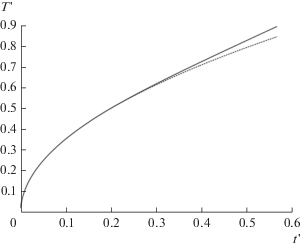
$T{\kern 1pt} '(1,t{\kern 1pt} ') = 2\sqrt {t{\kern 1pt} '} {{{\text{i}}}^{{\text{1}}}}{\text{erfc}}(0) = 2\sqrt {t{\kern 1pt} '{\text{/}}\pi } \approx 1.1284\sqrt {t{\kern 1pt} '} .$

Непосредственная проверка показывает хорошее совпадение точного и приближенного решения до времен t' порядка 0.3. Отметим, что решение (7) описывает температуру поверхности полубесконечного тела, на которое падает поток единичной плотности. Таким образом, на временах t' < 0.3 температура фронтальной поверхности приемной пластина ведет себя так, как будто эта пластина очень толстая (практически полубесконечная).

В абсолютных единицах формула (7) принимает вид

(8)

$T(t) = 1.1284F\sqrt {\frac{t}{{\lambda \rho c}}} .$

Формула (8) использовалась в работах [12, 13] для описания функционирования “толстого” адиабатического калориметра. Отметим, что для используемой в указанных работах медной пластины (κ = 1.2 × 10^–4 м²/с) толщиной 19 мм безразмерная величина t' = 0.3, в пределах которой справедливо приближенное решение (7), соответствует времени t = 0.9 с, что с хорошим запасом превышает длительность импульсов t_p = 0.5 с, с которыми имели дело в указанных работах.

3. ЧУВСТВИТЕЛЬНОСТЬ АДИАБАТИЧЕСКОГО КАЛОРИМЕТРА

В качестве определения удельной (на единицу площади) чувствительности калориметра естественно взять величину производной температуры по времени, деленную на величину поглощаемого при этом потока мощности. В общем случае в нормированных переменных производная температуры по времени определяется выражением

(9)

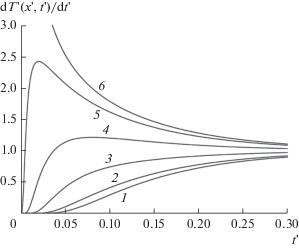
$\frac{{{\text{d}}T{\kern 1pt} '(x{\kern 1pt} ',t{\kern 1pt} ')}}{{{\text{d}}t{\kern 1pt} '}} = 1 + 2\sum\limits_{n = 1}^\infty {{{{( - 1)}}^{n}}\exp ( - {{n}^{2}}{{\pi }^{2}}t{\kern 1pt} ')\cos (n\pi x{\kern 1pt} ')} ;\,\,\,\,0 \leqslant x{\kern 1pt} ' \leqslant 1.$

Зависимость этой величины от времени при нескольких значениях x' показана на рис. 2. Видно, что производная (9), вообще говоря, немонотонно зависит от времени, поэтому для определения чувствительности целесообразно использовать ее асимптотическое (по t') значение, которое при всех x' равно 1. Таким образом, в абсолютных величинах чувствительность определяется следующим образом:

(10)

${{S}_{F}} = {{\left( {\frac{1}{F}\frac{{{\text{d}}T}}{{{\text{d}}t}}} \right)}_{{t \to \infty }}} = \frac{1}{{c\rho d}}.$

Рис. 2.

Зависимость производной (9) при нескольких значениях x':1 – 0; 2 – 0.2; 3 – 0.4; 4 – 0.6; 5 – 0.8; 6 – 1.0.

Размерность этой величины равна К/(Дж/м²) или °С/(Дж/м²). Видно, что так определенная чувствительность калориметра обратно пропорциональна теплоемкости приемной пластины единичной площади.

Для характеристики конкретного конструктивного решения калориметра удобно использовать чувствительность относительно всей падающей мощности W = FA, которая определяется выражением

(11)

${{S}_{W}} = {{\left( {\frac{1}{W}\frac{{{\text{d}}T}}{{{\text{d}}t}}} \right)}_{{t \to \infty }}} = \frac{{{{S}_{F}}}}{A} = \frac{1}{C}.$

Таким образом, чувствительность S_W обратно пропорциональна теплоемкости приемной пластины и имеет размерность К/Дж или °С/Дж. Отметим, что в работе [14] было введено понятие чувствительности калориметра, похожее на (10), но при ошибочном условии t → 0.

4. ВРЕМЯ ОТКЛИКА АДИАБАТИЧЕСКОГО КАЛОРИМЕТРА

Так как при действии потока энергии адиабатический калориметр все время находится в нестационарном состоянии, то для определения времени отклика необходимо воспользоваться величиной, которая со временем все же приходит к некоторому стационарному значению. Тогда время установления стационарного значения этой величины и целесообразно принять за время отклика калориметра. Очевидно, что можно предложить, по крайней мере, две такие величины. Во-первых, это разность температур фронтальной и тыльной поверхностей калориметра, а, во-вторых, уже упоминавшаяся производная температуры по времени.

Рассмотрим сначала первую величину. В безразмерных переменных разность температур на фронтальной и тыльной поверхностях пластины описывается формулой:

(12)

$\Delta T{\kern 1pt} '(t{\kern 1pt} ') = T{\kern 1pt} '(1,t{\kern 1pt} ') - T{\kern 1pt} '(0,t{\kern 1pt} ') = \frac{1}{2} - \frac{4}{{{{\pi }^{2}}}}\sum\limits_{n = 1,\,3,\,...}^\infty {\frac{1}{{{{n}^{2}}}}\exp \left( { - {{n}^{2}}{{\pi }^{2}}t{\kern 1pt} '} \right)} .$

Видно, что асимптотическое значение этой разности составляет 0.5. Пусть действие потока энергии прекращается в момент времени $t_{0}^{'}$, при котором распределение температуры по глубине пластины можно с хорошей точностью описать асимптотическим выражением (3). Тогда, решая уравнение теплопроводности (1) с начальным условием (3) и нулевыми граничными условиями второго рода, можно получить решение для t' ≥ $t_{0}^{'}$:

$T{\kern 1pt} '(x{\kern 1pt} ',t{\kern 1pt} ') = t_{0}^{'} + \frac{2}{{{{\pi }^{2}}}}\sum\limits_{n = 1}^\infty {\frac{{{{{( - 1)}}^{n}}}}{{{{n}^{2}}}}\exp \left[ { - {{n}^{2}}{{\pi }^{2}}(t{\kern 1pt} ' - t_{0}^{'})} \right]\cos (n\pi x{\kern 1pt} ')} ;\,\,\,\,0 \leqslant x{\kern 1pt} ' \leqslant 1.$

Отсюда получаем выражение для разности температур на фронтальной и тыльной поверхностях пластины после прекращения действия потока энергии

(13)

$\Delta T{\kern 1pt} '(t{\kern 1pt} ') = \frac{4}{{{{\pi }^{2}}}}\sum\limits_{n = 1,\,3,\,...}^\infty {\frac{1}{{{{n}^{2}}}}\exp \left[ { - {{n}^{2}}{{\pi }^{2}}(t{\kern 1pt} ' - t_{0}^{'})} \right]} .$

Как и должно быть, в момент времени t' = $t_{0}^{'}$ эта разность составляет 0.5. График зависимости ΔT'(t') при длительности импульсного воздействия $t_{0}^{'}$ = 1, показан на рис. 3.

Рис. 3.

Зависимость разности температур фронтальной и тыльной поверхностей приемной пластины от времени при длительности импульса $t_{0}^{'}$ = 1.0.

Непосредственными расчетами можно убедиться в практически экспоненциальном характере роста и спада этой функции, причем постоянная времени с очень хорошей точностью определяется первым слагаемым в суммах формул (12) и (13):

(14)

$\tau {\kern 1pt} ' = \frac{1}{{{{\pi }^{2}}}} \approx 0.10.$

В абсолютных единицах получаем

(15)

$\tau = \frac{{{{d}^{2}}\rho c}}{{{{\pi }^{2}}\lambda }} \approx 0.1\frac{{{{d}^{2}}\rho c}}{\lambda } = 0.1\frac{{{{d}^{2}}}}{\kappa }.$

Видно, что так определенная величина времени отклика калориметра уменьшается при увеличении коэффициента температуропроводности материала пластины и квадратично растет с ростом ее толщины.

Поведение производной температуры по времени до выхода на асимптотическое значение имеет более сложный характер и зависит от значения x' (рис. 4). Эта функция является монотонно возрастающей по t' в диапазоне значений 0 ≤ x' ≤ 0.5. В области 0.5 < x' < 1.0 эта функция сначала пересекает уровень своего асимптотического значения (равного единице), достигает некоторого максимума, а затем монотонно уменьшается до асимптотического значения. Ни в одном из указанных случаев поведение производной не может быть аппроксимировано выражением типа 1 – exp(–t'/τ'), что не позволяет корректно ввести постоянную времени аналогично формуле (14). (Отметим, что такая некорректная попытка была сделана в работе [14].)

Рис. 4.

Зависимость времени отклика $\tau _{\Delta }^{'}$ от глубины расположения термодатчика x′ при различных значениях Δ-окрестности: 1 – 0.01; 2 – 0.1; 3 – 0.2; 4 – 0.3; 5 – 1/e ≈ 0.37.

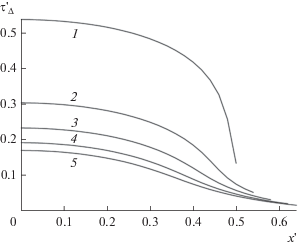
С другой стороны вполне практичным может оказаться использование в качестве времени отклика значения времени $\tau _{\Delta }^{'}$, начиная с которого значение производной остается в пределах 1 ± Δ (т. е. в ±Δ-окрестности асимптотического значения, равного единице). Графики зависимостей момента пересечения $\tau _{\Delta }^{'}$ с уровнем 1 – Δ (при условии последующего непересечения с уровнем 1 + Δ, т. е. невыхода из полосы значений 1 ± Δ) от значения координаты x' для различных значений Δ показаны на рис. 5. Видно, что оптимальная с точки зрения времени отклика глубина расположения термодатчика находится в диапазоне x' = 0.5–0.6. При этом выигрыш во времени отклика по сравнению с положением термодатчика x'' = 0 получается в 4–7 раз.

Рис. 5.

Относительные значения чувствительности S и времени отклика τ для некоторых материалов при фиксированной толщине приемной пластины.

5. ВЫБОР МАТЕРИАЛА ПРИЕМНОЙ ПЛАСТИНЫ

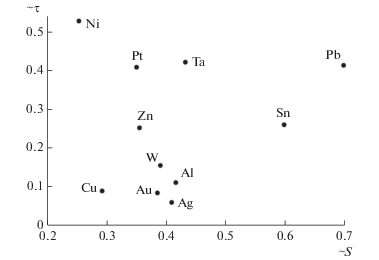
Рассмотрим проблему выбора материала для приемной пластины. Понятно, что это многофакторная проблема, которая включает в себя, в частности, экономические аспекты (стоимость материала), технологические аспекты (легкость обработки материала), эксплуатационные аспекты (температура плавления, коэффициенты распыления ионами и/или быстрыми атомами). Поэтому ограничимся двумя функциональными критериями: время отклика и чувствительность. Так как при заданной толщине пластины чувствительность S обратно пропорциональна объемной теплоемкости материала cρ, а время отклика τ обратно пропорционально его температуропроводности, то естественно выбирать материал с минимальным значением cρ и максимальным значением κ.

На рис. 5 представлено расположение некоторых материалов на диаграмме в соответствующих координатах. Видно, что наибольшую чувствительность обеспечивают Pb и Sn, а наименьшую – Ni и Cu. С другой стороны, такие материалы как Ag, Au, Cu, Al, W обеспечивают наименьшее время отклика адиабатического калориметра. Худшими с точки зрения рассматриваемых критериев материалами для изготовления приемной пластины являются Ni, Pt, Zn и Ta.

Выражения для чувствительности (10) и времени отклика (15) показывают, что эти величины связаны между собой через параметры материала приемной пластины и ее толщину:

(16)

${{S}_{F}} = \frac{1}{{\pi \sqrt {c\rho \lambda \tau } }}.$

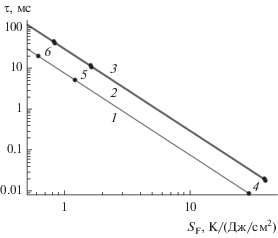
На рис. 6 показаны зависимости τ(S_F) для трех материалов; в логарифмическом масштабе они представляют собой прямые линии, причем толщина уменьшается слева направо. Таким образом, при уменьшении толщины приемной пластины увеличивается чувствительность адиабатического калориметра и уменьшается его время отклика. Отметим довольно близкое расположение прямых, соответствующих таким, казалось бы, разным в теплофизическом отношении материалам как молибден и дюралюминий. Дело в том, что, согласно формуле (16), связь величин S_F и τ определяется произведением cρλ, которое у указанных материалов оказалось приблизительно одинаковым.

Рис. 6.

Зависимости времени отклика τ от чувствительности S для Cu – 1, Mo – 2 и дюралюминий 3; точками обозначены значения толщины приемной пластины: 4 – 0.1 , 5 – 1 и 6 – 10 мм.

ЗАКЛЮЧЕНИЕ

В настоящей работе представлен подробный анализ математической модели адиабатического калориметра. Рассмотрены нестационарные решения соответствующего уравнения теплопроводности, предложены корректные определения времени отклика и чувствительности адиабатического калориметра. Основываясь на этих определениях, предложено решение проблемы оптимального выбора материала приемной пластины. Проведены сравнения с некоторыми опубликованными экспериментальными и теоретическими результатами. Полученные в работе результаты могут быть полезны при разработке и проектировании калориметрических систем диагностики пучков энергии.

Работа выполнена в рамках Государственного задания ФТИАН им. К.А. Валиева РАН Минобрнауки России по теме № 0066-2019-0004.

Список литературы

Kudrya V.P., Maishev Yu.P. Fundamentals of the fast neutral beams diagnostics // Proc. SPIE. 2016. V. 10224. P. 10224-2C. P. 1–12. https://doi.org/10.1117/12.2266889
Кудря В.П., Маишев Ю.П. Физические принципы диагностики пучков быстрых нейтральных частиц. I. Определение состава пучка и энергетических характеристик его компонент // Труды ФТИАН. М.: Наука. 2017. Т. 26. С. 103–116. ISBN 978-5-02-039983-9
Кудря В.П., Маишев Ю.П. Физические принципы диагностики пучков быстрых нейтральных частиц. II. Методы определения полного потока частиц в пучке // Труды ФТИАН. М.: Наука. 2018. Т. 27. С. 89–98. ISBN 978-5-02-040089-4
Barr W.L. A Pulsed Source of Fast Hydrogen Atoms // J. Appl. Phys. 1971. V. 42. № 13. P. 5411–5417. https://doi.org/10.1063/1.1659958
Christodoulides C.E., Freeman J.H. Ion beam studies. Part II: A calorimetric method for ion beam studies // Nucl. Instr. Meth. 1976. V. 135. № 1. P. 13–19. https://doi.org/10.1016/0029-554X(76)90819-3
Mizutani T., Nishimatsu S. Sputtering yield and radiation damage by neutral beam bombardment // J. Vac. Sci. Technol. A. 1988. V. 6. № 3. P. 1417–1420. https://doi.org/10.1116/1.575717
Shimokawa F., Nagai K. A low-energy fast-atom source // Nucl. Instr. Meth. Phys. Res. B. 1988. V. 33. № 1–4. P. 867–870. https://doi.org/10.1016/0168-583X(88)90701-X
Карслоу Г., Егер Д. Теплопроводность твердых тел. М.: Наука, 1964. (Carslaw H., Jaeger J. Conduction of Heat in Solids. 2nd edition. Oxford: Clarendon Press, 1959.)
Росляков Г.В., Фиксель Г.И. Источник атомов водорода низкой энергии // Физика плазмы. 1986. Т. 12. № 2. С. 232–236. (Roslyakov G.V., Fiksel G.I. Source of Low-Energy Hydrogen Atoms // Sov. J. Plasma Phys. 1986. V. 12. № 2. P. 136–139.)
Burrell C.F., Cooper W.S., Steele W.F., Smith R.R. Calorimetric and Optical Beam Diagnostics of the LBL 120‑keV Neutral Beam Test Facility // Lawrence Berkeley Laboratory (Berkeley, CA, USA). Preprint LBL-6383. 1977. https://escholarship.org/uc/item/ 5hf1q80t
Watkins J.G., Lasnier C.J., Whyte D.G., Stangeby P.C., Ulrickson M.A. Calorimeter probe for the DIII-D divertor // Rev. Sci. Instr. 2003. V. 74. № 3. P. 1574–1577. https://doi.org/10.1063/1.1527241
LBL/LLL CTR Staff. TFTR Neutral Beam Injection System Conceptual Design // Lawrence Berkeley Laboratory (Berkeley, CA, USA). Preprint LBL-3296. 1975. https://escholarship.org/uc/item/7j253360
Haughian J.M., Cooper W.S., Paterson J.A. The design and development of multi-megawatt beam dumps // Lawrence Berkeley Laboratory (Berkeley, CA, USA). Preprint LBL-5901. 1976. https://escholarship.org/ uc/item/3jt946zn
Broido A., Willoughby A.B. Measurement of Intense Beams of Thermal Radiation // J. Opt. Soc. Amer. 1958. V. 48. № 5. P. 344–350. https://doi.org/10.1364/JOSA.48.000344

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Микроэлектроника

Архивы выпусков Информация о журнале Отправить рукопись в журнал