Микроэлектроника, 2022, T. 51, № 2, стр. 148-154

Зависимость магнитной индукции внутри тонкой цилиндрической проволоки из металла от механизма поверхностного рассеяния электронов

Э. В. Завитаев^a, *, О. В. Русаков^a, А. И. Уткин^a, К. Е. Харитонов^a

^a Государственный гуманитарно-технологический университет
142611 Московская область, Орехово-Зуево, ул. Зеленая, 22, Россия

^* E-mail: EduardZavitaev@yandex.ru

Поступила в редакцию 13.05.2021
После доработки 30.06.2021
Принята к публикации 02.07.2021

EDN: CSZIHK
DOI: 10.31857/S0544126922020090

Полный текст (PDF)

Аннотация

Выполнен расчет магнитной индукции внутри прямой металлической проволоки круглого сечения. Рассмотрен общий случай, когда отношение длины свободного пробега электронов к радиусу проволоки может принимать произвольные значения. В качестве граничных условий задачи принято условие, учитывающее зависимость коэффициента зеркальности от дефектов поверхности и угла падения электронов на внутреннюю поверхность проволоки. Рассмотрен предельный случай и проведено обсуждение полученных результатов.

Ключевые слова: тонкая проволока, плотность тока, магнитная индукция

1. ВВЕДЕНИЕ

В настоящее время в микроэлектронике наблюдается растущий интерес к электромагнитным свойствам малых проводящих объектов, включающих в себя металлические проволоки малого радиуса [1–5]. Электромагнитные свойства данных малых проводящих объектов определяются такими свойствами проволок как электропроводность и индукция. Для металлических проволок, радиус которых существенно превышает длину свободного пробега электронов внутри объемного образца, эти характеристики могут быть найдены с использованием макроскопической электродинамики [6].

В то же время электрические и магнитные свойства металлических проволок, радиус которых сравним с длиной свободного пробега электронов $\Lambda $, существенно отличаются от свойств “массивных” проволок [7–9].

Вопросы, касающиеся расчета электрической проводимости тонких цилиндрических проволок из металла, обсуждались в работах [7, 8]. Магнитная индукция внутри такой проволоки при условии зеркально-диффузного отражения электронов от внутренней поверхности определялась в работе [9]. В упомянутых работах применяется подход, основанный на решении кинетического уравнения Больцмана для электронов в металле.

В настоящей работе применяется рассчитанная кинетическим методом функция распределения, которая описывает линейный отклик электронов в цилиндрической проволоке из металла на переменное электрическое поле, ориентированное вдоль ее оси симметрии. С помощью данной функции распределения удается рассчитать зависимость магнитной индукции внутри проволоки как функцию от дефектов поверхности и угла падения электронов на внутреннюю поверхность проволоки.

2. ПОСТАНОВКА ЗАДАЧИ

Рассматривается цилиндрическая проволока из немагнитного металла (относительная магнитная проницаемость $\mu $ = 1) радиуса $R$ и длины $L$ (считаем, что $L \gg R$), к концам которой приложено переменное электрическое напряжение частоты $\omega $. Принимается, что направление электрического поля совпадает с осью цилиндра. Скин-эффект не учитывается (предполагается, что $R < \gamma $ – глубины скин-слоя).

Однородное периодическое по времени электрическое поле, вектор напряженности которого

(1)

${\mathbf{E}} = {{{\mathbf{E}}}_{0}}\exp \left( { - i\omega t} \right),~$

воздействует на электроны проводимости внутри проволоки и вызывает появление внутри нее высокочастотного тока с плотностью ${\mathbf{j}}$.

Связь между$~{\mathbf{E}}$ и ${\mathbf{j}}~$ в случае, когда радиус проволоки $R$ сравним с длиной свободного пробега электронов в металле $\Lambda $ или меньше ее: $R < \Lambda $, оказывается существенно нелокальной. Для описания этой связи применим кинетическое уравнение (в приближении времени релаксации) к вырожденному ферми-газу электронов находящемуся внутри проволоки.

Для достаточно слабых внешних полей это уравнение можно линеаризовать по внешнему полю ${\mathbf{E}}$ и по малым отклонениям ${{f}_{1}}\left( {{\mathbf{r}},{\mathbf{v}}} \right)$ от равновесной фермиевской функции распределения ${{f}_{0}}\left( \varepsilon \right)$ [10–12]:

(2)

$ - i\omega {{f}_{1}} + {\mathbf{v}}\frac{{\partial {{f}_{1}}}}{{\partial {\mathbf{r}}}} + e\left( {{\mathbf{vE}}} \right)\frac{{\partial {{f}_{0}}}}{{\partial \varepsilon }} = - \frac{{{{f}_{1}}}}{\tau },$

Здесь $e$ и ${\mathbf{v}}$ – соответственно, заряд и скорость электронов; $\tau $ – электронное время релаксации.

Далее рассматривается квадратичная зависимость энергии электронов $\varepsilon $ от скорости: $\varepsilon = {{m{{{\mathbf{v}}}^{2}}} \mathord{\left/ {\vphantom {{m{{{\mathbf{v}}}^{2}}} 2}} \right. \kern-0em} 2}$ ($m$– эффективная масса электрона) и используется ступенчатая аппроксимация для равновесной функции распределения электронов по энергиям [10]:

${{f}_{0}}\left( \varepsilon \right) = \theta \left( {{{\varepsilon }_{{\text{F}}}} - \varepsilon } \right) = \left\{ \begin{gathered} 1,\,\,\,\,~0 \leqslant \varepsilon \leqslant {{\varepsilon }_{{\text{F}}}} \hfill \\ 0,\,\,\,\,~{{\varepsilon }_{{\text{F}}}} < \varepsilon ~~~~~~~~ \hfill \\ \end{gathered} \right.,$

где ${{\varepsilon }_{{\text{F}}}} = {{m{\mathbf{v}}_{{\text{F}}}^{2}} \mathord{\left/ {\vphantom {{m{\mathbf{v}}_{{\text{F}}}^{2}} 2}} \right. \kern-0em} 2}$ – энергия Ферми (${{{\mathbf{v}}}_{{\text{F}}}}$ – скорость Ферми). Предполагается, что поверхность Ферми имеет сферическую форму.

Функция распределения электронов

$f\left( {{\mathbf{r}},{\mathbf{v}}} \right) = {{f}_{0}}\left( \varepsilon \right) + {{f}_{1}}\left( {{\mathbf{r}},{\mathbf{v}}} \right).$

Отклонение ${{f}_{1}}\left( {{\mathbf{r}},{\mathbf{v}}} \right)$ функции распределения электронов $f\left( {{\mathbf{r}},{\mathbf{v}}} \right)$ от равновесного значения ${{f}_{0}}\left( \varepsilon \right)$, возникающее под действием электрического поля (1), позволяет рассчитать плотность высокочастотного тока внутри проволоки

(3)

${\mathbf{j}} = en\left\langle {\mathbf{v}} \right\rangle = en{{\left( {\int {{{f}_{0}}{{d}^{3}}} v} \right)}^{{ - 1}}}\int {{{f}_{1}}{\mathbf{v}}{{d}^{3}}v} .$

Концентрация электронов $n$ в проволоке определяется по стандартной формуле, согласно которой

(4)

$n = 2\frac{{{{m}^{3}}}}{{{{h}^{3}}}}\int {} {{f}_{0}}{{d}^{3}}v = 2\frac{{{{m}^{3}}}}{{{{h}^{3}}}}\frac{{4\pi v_{{\text{F}}}^{3}}}{3},~$

где $h$ – постоянная Планка.

Применив формулу (4), выражение для плотности тока (3) можно записать в виде:

(5)

${\mathbf{j}} = \frac{3}{4}\frac{{ne}}{{\pi {\mathbf{v}}_{{\text{F}}}^{3}}}\int {{\mathbf{v}}{{f}_{1}}{{d}^{3}}v} .~~~$

Взяв в уравнении (2) поле ${\mathbf{E}}$ в виде (1), найдем ${{f}_{1}}\left( {{\mathbf{r}},{\mathbf{v}}} \right)$ как решение этого уравнения. Затем, используя выражение (3), определим плотность тока и стандартным образом рассчитаем магнитную индукцию внутри проволоки.

Однозначное решение поставленной задачи возможно при выборе граничного условия для неизвестной функции ${{f}_{1}}\left( {{\mathbf{r}},{\mathbf{v}}} \right)$ на цилиндрической поверхности металлической проволоки. В качестве такового принимаем условие, которое учитывает зависимость коэффициента зеркальности $q$ от дефектов поверхности – параметра шероховатости поверхности $H$ и угла падения электронов $\theta $ на внутреннюю поверхность проволоки (модель Соффера): [8, 13]

(6)

$\begin{gathered} {{f}_{1}}\left( {{{{\mathbf{r}}}_{ \bot }},{{{\mathbf{v}}}_{ \bot }},{{{\mathbf{v}}}_{{\text{z}}}}} \right) = q\left( {H,\cos {\kern 1pt} \theta } \right){{f}_{1}}\left( {{{{\mathbf{r}}}_{ \bot }},{\mathbf{v}}_{ \bot }^{'},{{{\mathbf{v}}}_{{\text{z}}}}} \right)~\,\,\,\,{\text{при}}~\,\,\,\,\left\{ {\begin{array}{*{20}{c}} {\left| {{{{\mathbf{r}}}_{ \bot }}} \right| = R,~~~} \\ {{{{\mathbf{r}}}_{ \bot }}{{{\mathbf{v}}}_{ \bot }} < 0,~} \end{array}} \right.~ \\ q\left( {H,\cos {\kern 1pt} \theta } \right) = \exp \left( { - {{{\left( {4\pi H\cos {\kern 1pt} \theta } \right)}}^{2}}} \right),~\,\,\,\,H = \frac{{{{h}_{S}}}}{{{{\lambda }_{{\text{F}}}}}}, \\ \end{gathered} $

где ${{{\mathbf{r}}}_{ \bot }}$ и ${{{\mathbf{v}}}_{ \bot }}$ – соответственно, компоненты радиус-вектора электрона ${\mathbf{r}}$ и его скорости ${\mathbf{v}}$ в плоскости перпендикулярной оси симметрии проволоки, ${\mathbf{v}}_{ \bot }^{{\text{'}}} = {{{\mathbf{v}}}_{ \bot }} - {{\left( {2{{{\mathbf{r}}}_{ \bot }}\left( {{{{\mathbf{r}}}_{ \bot }} \cdot {{{\mathbf{v}}}_{ \bot }}} \right)} \right)} \mathord{\left/ {\vphantom {{\left( {2{{{\mathbf{r}}}_{ \bot }}\left( {{{{\mathbf{r}}}_{ \bot }} \cdot {{{\mathbf{v}}}_{ \bot }}} \right)} \right)} {{{R}^{2}}}}} \right. \kern-0em} {{{R}^{2}}}}$ – вектор скорости, который при зеркальном отражении от внутренней поверхности проволоки в точке ${{{\mathbf{r}}}_{ \bot }}$($\left| {{{{\mathbf{r}}}_{ \bot }}} \right| = R$) переходит в вектор ${{{\mathbf{v}}}_{ \bot }}$; ${{{\mathbf{v}}}_{{\text{z}}}}$ – составляющая скорости электрона вдоль оси симметрии проволоки; ${{h}_{S}}$ – среднеквадратичная высота поверхностного рельефа, ${{\lambda }_{{\text{F}}}}$ – длина волны де-Бройля электрона на поверхности Ферми.

3. РАСЧЕТ МАГНИТНОЙ ИНДУКЦИИ

Решение кинетического уравнения (2) и расчет плотности тока (5) проведены в работе [7].

При вычислении плотности тока (5) и расчете магнитной индукции удобно перейти к цилиндрическим координатам как в пространстве координат (${{r}_{ \bot }}$, $\varphi $, $z$; полярная ось – ось $Z$; вектор ${{E}_{0}}$ параллелен оси $Z$), так и в пространстве скоростей ${{v}_{ \bot }}$, $\alpha $, ${{v}_{z}}$; полярная ось – ось ${{v}_{z}}$). Ось симметрии проволоки совпадает с осью $Z$.

Поле (1) в цилиндрических координатах имеет лишь $z$-компоненту:

$E = {{E}_{z}}{{e}_{z}},~\,\,\,\,{{E}_{z}} = {{E}_{{\text{0}}}}{\kern 1pt} {\text{exp}}\left( { - i\omega t} \right).$

Соответственно, и плотность тока (5) обладает лишь $z$-компонентой (линии тока являются прямыми параллельными оси Z) и вычисляется по формуле [7] c учетом граничного условия (6):

${{j}_{z}} = \frac{{3n{{e}^{2}}R{{E}_{z}}}}{{\pi {{v}_{{\text{F}}}}m}}\int\limits_0^1 {\int\limits_0^\pi {\frac{{\rho \sqrt {1 - {{\rho }^{2}}} }}{z}} } \left( {\frac{{\left( {q\left( {H,\cos {\kern 1pt} \theta } \right) - 1} \right)\exp \left( {{{ - z\eta } \mathord{\left/ {\vphantom {{ - z\eta } \rho }} \right. \kern-0em} \rho }} \right)}}{{\left( {1 - q\left( {H,\cos {\kern 1pt} \theta } \right)\exp \left( {{{ - z{{\eta }_{0}}} \mathord{\left/ {\vphantom {{ - z{{\eta }_{0}}} \rho }} \right. \kern-0em} \rho }} \right)} \right)}} + 1} \right)d\rho d\alpha ,~$

где

$\rho = \frac{{{{v}_{ \bot }}}}{{{{v}_{{\text{F}}}}}},~\,\,\,\,z = \left( {\frac{1}{\tau } - i\omega } \right)\frac{R}{{{{v}_{{\text{F}}}}}},\,\,\,\,~\xi = \frac{{{{r}_{ \bot }}}}{R},$

$\eta = \xi {\kern 1pt} \cos {\kern 1pt} \alpha + \sqrt {1 - {{\xi }^{2}}{\kern 1pt} {{{\sin }}^{2}}{\kern 1pt} \alpha } ,\,\,\,\,{{\eta }_{0}} = 2\sqrt {1 - {{\xi }^{2}}{\kern 1pt} {{{\sin }}^{2}}{\kern 1pt} \alpha } .$

Для расчета вектора магнитной индукции ${\mathbf{B}}$ внутри тонкой цилиндрической проволоки будем применять теорему о циркуляции с учетом того факта, что распределение тока по поперечному сечению является неоднородным (линии индукции являются замкнутыми окружностями, лежащими в плоскостях, перпендикулярных к оси симметрии проволоки, поэтому ${\mathbf{B}} = {{B}_{\varphi }}{{e}_{\varphi }}$):

$\oint\limits_L {{{B}_{\varphi }}dl} = {{\mu }_{0}}\int\limits_S {{{j}_{z}}dS} ,$

где ${{\mu }_{0}}$ – магнитная постоянная вакуума.

После применения теоремы к контуру в виде окружности, получаем:

(8)

${{B}_{\varphi }} = \frac{{{{\mu }_{0}}}}{{{{r}_{{ \bot ,B}}}}}\int\limits_0^{{{r}_{{ \bot ,B}}}} {{{j}_{z}}{{r}_{ \bot }}d{{r}_{ \bot }}} .$

Для дальнейших вычислений и анализа результатов, введем новые переменные

$\delta = \frac{{{{r}_{{ \bot ,B}}}}}{R},\,\,\,\,~x = \frac{R}{{\tau {{v}_{{\text{F}}}}}} = \frac{R}{{{\Lambda }}},\,\,\,\,~y = ~\omega \frac{R}{{{{v}_{{\text{F}}}}}},$

где $\delta $ – “безразмерный радиус индукции”, $x$ – безразмерная обратная длина свободного пробега электронов, $y$ – безразмерная частота электрического поля.

Тогда магнитную индукцию (8) можно рассчитать по формуле

${{B}_{\varphi }} = \frac{{{{\mu }_{0}}R}}{\delta }\mathop \smallint \limits_0^\delta {{j}_{z}}\xi d\xi ,$

или, с учетом формулы (7) и граничного условия (6),

(9)

${{B}_{\varphi }} = \frac{{3{{\mu }_{0}}n{{e}^{2}}{{R}^{2}}{{E}_{z}}}}{{\pi {{v}_{{\text{F}}}}m}}\mathop \smallint \limits_0^\delta \mathop \smallint \limits_0^1 \mathop \smallint \limits_0^\pi \frac{{\rho \sqrt {1 - {{\rho }^{2}}} }}{{z\delta }}\left( {\frac{{\left( {\exp \left( { - {{{\left( {4\pi H\rho {\kern 1pt} \cos {\kern 1pt} \alpha } \right)}}^{2}}} \right) - 1} \right)\exp \left( {{{ - z\eta } \mathord{\left/ {\vphantom {{ - z\eta } \rho }} \right. \kern-0em} \rho }} \right)}}{{\left( {1 - \exp \left( { - {{{\left( {4\pi H\rho {\kern 1pt} \cos {\kern 1pt} \alpha } \right)}}^{2}}} \right)\exp \left( {{{ - z{{\eta }_{0}}} \mathord{\left/ {\vphantom {{ - z{{\eta }_{0}}} \rho }} \right. \kern-0em} \rho }} \right)} \right)}} + 1} \right)\xi d\xi d\rho d\alpha .~$

Магнитную индукцию (9), которая является комплексной величиной, представим в виде

(10)

${{B}_{\varphi }} = {{B}_{0}}N\left( {\delta ,x,y,H} \right),$

где

(11)

$\begin{gathered} {{B}_{0}} = \frac{{3{{\mu }_{0}}n{{e}^{2}}{{R}^{2}}{{E}_{z}}}}{{\pi {{v}_{{\text{F}}}}m}}, \\ N\left( {\delta ,x,y,H} \right) = \mathop \smallint \limits_0^\delta \mathop \smallint \limits_0^1 \mathop \smallint \limits_0^\pi \frac{{\rho \sqrt {1 - {{\rho }^{2}}} }}{{z\delta }}\left( {\frac{{\left( {\exp \left( { - {{{\left( {4\pi H\rho {\kern 1pt} \cos {\kern 1pt} \alpha } \right)}}^{2}}} \right) - 1} \right)\exp \left( {{{ - z\eta } \mathord{\left/ {\vphantom {{ - z\eta } \rho }} \right. \kern-0em} \rho }} \right)}}{{\left( {1 - \exp \left( { - {{{\left( {4\pi H\rho {\kern 1pt} \cos {\kern 1pt} \alpha } \right)}}^{2}}} \right)\exp \left( {{{ - z{{\eta }_{0}}} \mathord{\left/ {\vphantom {{ - z{{\eta }_{0}}} \rho }} \right. \kern-0em} \rho }} \right)} \right)}} + 1} \right)\xi d\xi d\rho d\alpha .~~ \\ \end{gathered} $

Численный расчет модуля $M\left( {\delta ,x,y,H} \right)$ и аргумента $A\left( {\delta ,x,y,H} \right)$ (фазы) безразмерной магнитной индукции $N\left( {\delta ,x,y,H} \right)$ вытянутой цилиндрической проволоки представлен на рисунках ниже.

4. ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ

В пределе абсолютно гладкой поверхности тонкой металлической проволоки ($H = 0$) для расчета магнитной индукции получаем выражение:

${{B}_{{{\text{мак}}}}} = \frac{{{{\mu }_{0}}n{{e}^{2}}{{R}^{2}}{{E}_{z}}\delta }}{{2{{v}_{{\text{F}}}}mz}}.~$(12)

Выражение (12) соответствует классическому макроскопическому результату для цилиндрической проволоки, когда при расчете магнитной индукции применяется локальный закон Ома, в котором удельная проводимость проволоки определяется по формуле Друде [7]. Это связано с тем, что при $H = 0$ граница проволоки не оказывает влияния на функцию распределения электронов $f\left( {{{r}_{ \bot }},{{v}_{ \bot }},{{v}_{z}}} \right)$. Высокочастотный ток внутри металлической проволоки с абсолютно гладкой поверхностью удовлетворяет локальному закону Ома при любом соотношении между радиусом проволоки $R$ и длиной свободного пробега электронов $\Lambda $. Таким образом, при наличии границы проволоки по свойствам близкой к идеальной, отсутствуют нелокальные (поверхностные) эффекты.

Независимо от характера отражения электронов на границе (при любых $H$) с ростом размера проволоки (при $x \gg 1$) (в этом случае в формуле (11) можно пренебречь членами с экспонентами в виду их быстрого затухания) также имеет место макроскопическая асимптотика (12).

На рис. 1 приведено сравнение результатов численного расчета магнитной индукции внутри тонкой цилиндрической проволоки, выполненного с применением кинетического (11) и макроскопического (12) подходов.

Рис. 1.

Зависимость отношения модуля магнитной индукции ${{B}_{\varphi }}\left( \delta \right)$ к модулю магнитной индукции ${{B}_{{{\text{мак}}}}}\left( \delta \right)$ от “безразмерного радиуса индукции” $\delta $ при постоянных значениях безразмерной обратной длины свободного пробега электронов $x$, безразмерной частоты электрического поля $y$ и параметра шероховатости поверхности $H$: ($x$ = 1, $y$ = 0.1, $H$ = 1).

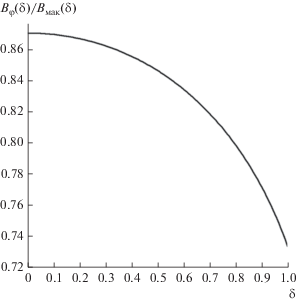
Отношение модуля магнитной индукции ${{B}_{\varphi }}\left( \delta \right)$, вычисленной с помощью кинетической модели, к модулю магнитной индукции ${{B}_{{{\text{мак}}}}}\left( \delta \right)$, вычисленной в рамках классической электродинамики, определялось при постоянных значениях безразмерной обратной длины свободного пробега электронов $x$, безразмерной частоты электрического поля $y$ и параметра шероховатости поверхности $H$. Из анализа хода кривой можно сделать вывод о том, что отличие модуля магнитной индукции, рассчитанной с использованием кинетической модели, и модуля магнитной индукции, рассчитанной в рамках классической электродинамики, при фиксированных значениях параметров расчета составляет от 13 до 26%.

Это обстоятельство подтверждает существенное влияние на абсолютную величину магнитной индукции вклада поверхностных механизмов рассеяния в случае, когда радиус проволоки будет одного порядка с длиной свободного пробега электронов.

На рис. 2 приведено сравнение результатов численного расчета магнитной индукции внутри тонкой цилиндрической проволоки, выполненного с применением кинетических подходов с различными граничными условиями: Соффера (см. [11]) и Фукса (см. [9]).

Рис. 2.

Зависимость отношения модуля магнитной индукции ${{B}_{\varphi }}\left( H \right)$ к модулю магнитной индукции ${{B}_{\varphi }}\left( q \right)$ от параметра шероховатости поверхности $H$ ($q = 1 - H)$ при постоянных значениях “безразмерного радиуса индукции” $\delta $, безразмерной обратной длины свободного пробега электронов $x$ и безразмерной частоты электрического поля $y$: ($\delta $ = 0.99, $x$ = 0.1, $y$ = 0.1).

Отношение модуля магнитной индукции ${{B}_{\varphi }}\left( H \right)$, вычисленной с помощью кинетической модели с граничными условиями Соффера, к модулю магнитной индукции ${{B}_{\varphi }}\left( q \right)$, вычисленной с помощью кинетической модели с граничными условиями Фукса, также определялось при постоянных значениях безразмерной обратной длины свободного пробега электронов $x$ и безразмерной частоты электрического поля $y$. Из анализа хода кривой можно сделать вывод о том, что данное отношение имеет нетривиальный характер из-за наличия вырождения, когда результаты расчета магнитной индукции внутри проволоки совпадают при двух значениях параметра шероховатости $H$ поверхности (или двух значениях коэффициента зеркальности $q$).

На рис. 3 построены графики зависимости модуля $M\left( \delta \right)$ безразмерной магнитной индукции цилиндрической проволоки $N\left( {\delta ,x,y,H} \right)$ от “безразмерного радиуса индукции” δ для случая, когда все кривые построены при одинаковом значении безразмерной частоты электрического поля $y$ и параметра шероховатости поверхности $H$. Безразмерная обратная длина свободного пробега электронов $x$ варьируется для каждой кривой.

Рис. 3.

Зависимость модуля $M\left( \delta \right)$ безразмерной магнитной индукции от “безразмерного радиуса индукции” $\delta $ при фиксированном значении безразмерной обратной длины свободного пробега электронов $x$ и постоянных значениях безразмерной частоты электрического поля $y$ и параметра шероховатости поверхности $H$: 1 – ($x$ = 0.1, $y$ = 1, $H$ = 0.5), 2 – ($x$ = 1, $y$ = 1, $H$ = 0.5), 3 – ($x$ = 5, $y$ = 1, $H$ = 0.5).

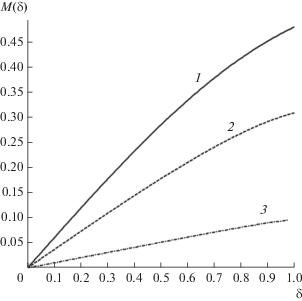
Из хода кривых на рисунке видно, что модуль безразмерной магнитной индукции в значительной степени зависит от текущего расстояния, отсчитываемого от оси симметрии проволоки(интересно, что на аргумент (фазу) безразмерной индукции этот параметр практически не влияет).

На рис. 4 построены графики зависимости модуля $~M\left( H \right)$ безразмерной магнитной индукции цилиндрической проволоки $N\left( {\delta ,x,y,H} \right)$ от параметра шероховатости поверхности $H$ для случая, когда все кривые построены при одинаковом значении безразмерной частоты электрического поля $y$ и безразмерной обратной длины свободного пробега электронов $x$, а “безразмерный радиус индукции” $\delta $ варьируется для каждой кривой.

Рис. 4.

Зависимость модуля $M\left( H \right)$ безразмерной магнитной индукции от параметра шероховатости поверхности $H$ при фиксированном значении “безразмерного радиуса индукции” $\delta $ и постоянных значениях безразмерной обратной длины свободного пробега электронов $x$ и безразмерной частоты электрического поля $y$: 1 – ($\delta $ = 0.1, $x$ = 0.1, $y$ = 0.1), 2 – ($\delta $ = 0.5, $x$ = 0.1, $y$ = 0.1), 3 – ($\delta $ = 1, $x$ = 0.1, $y$ = 0.1).

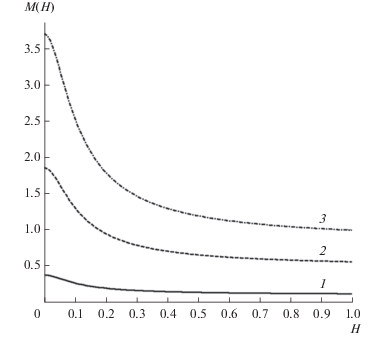
Из хода кривых на рисунке видно, что модуль безразмерной магнитной индукции по мере увеличения параметра шероховатости поверхности $H$ монотонно убывает по всему поперечному сечению проволоки. Причем для каждой кривой, начиная с определенного значения $H$, имеет место выход индукции на постоянные значения.

На рис. 5 построены графики зависимости аргумента $~A\left( \delta \right)$ (фазы) безразмерной магнитной индукции цилиндрической проволоки $N\left( {\delta ,x,y,H} \right)$ от “безразмерного радиуса индукции” $\delta $ для случая, когда все кривые построены при одинаковом значении безразмерной частоты электрического поля $y$ и безразмерной обратной длины свободного пробега электронов $x$. Параметр шероховатости поверхности $H$ варьируется для каждой кривой.

Рис. 5.

Зависимость аргумента $A\left( \delta \right)$ (фазы) безразмерной магнитной индукции от “безразмерного радиуса индукции” $\delta $ при фиксированном значении параметра шероховатости поверхности $H$ и постоянных значениях безразмерной обратной длины свободного пробега электронов $x$ и безразмерной частоты электрического поля$y$: 1 – ($H$ = 0.1, $x$ = 0.1, $y$ = 5), 2 – ($H$ = 0.2, $x$ = 0.1, $y$ = 5), 3 – ($H$ = 0.5, $x$ = 0.1, $y$ = 5).

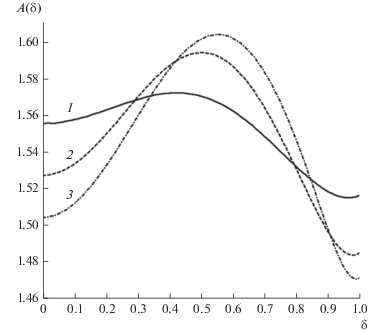
Из хода кривых на рисунке видно, что аргумент (фаза) безразмерной магнитной индукции имеет локальный максимум, который зависит от параметра шероховатости и смещается в направлении к поверхности проволоки по мере его увеличения (пока не будут достигнуты значения соответствующие практически диффузному отражению электронов).

Список литературы

Op‘t Root W.P.E.M., Brussaard G.J.H., Smorenburg P.W., Luiten O.J. Single-cycle surface plasmonpolaritons on bare metal wire excited by relativistic electrons // Nat. Commun. 2016. 7:13769.
Yang J., Cao Q., Zhou C. Explicit formula for metal wire plasmon of terahertz wave // Opt. Express. 2009. V. 17. № 23. P. 20806–20815.
Maier S.A., Andrews S.R., Martin-Moreno L., Garcia-Vidal F.J. Terahertz Surface Plasmon-Polariton Propagation and Focusing on Periodically Corrugated Metal Wires // Phys. Rev. Lett. 2006. V. 97. P. 176805 (1–4).
Manjavacas A., Garcia de Abajo F.J. Coupling of gap plasmons in multi-wire waveguides // Opt. Express. 2009. V. 17. № 22. P. 19401–19413.
Neubrech F., Kolb T., Lovrincic R., Fahsold G., Pucci A., Aizpurua J., Cornelius T.W., Toimil-Molares M.E., Neumann R., Karim S. Resonances of individual metal nanowires in the infrared // Appl. Phys. Lett. 2006. V. 89. P. 253104 (1–3).
Ландау Л.Д., Лифшиц Е.М. Электродинамика сплошных сред. М.: Физмат-лит, 2016. 656 с.
Завитаев Э.В., Юшканов А.А. Высокочастотная проводимость тонкой цилиндрической проволоки из металла // Микроэлектроника. 2008. Т. 37. № 6. С. 429–438.
Кузнецова И.А., Чапкин А.В., Юшканов А.А. Влияние механизма поверхностного рассеяния электронов на высокочастотную проводимость тонкой металлической проволоки // Микроэлектроника. 2011. Т. 40. № 1. С. 45–51.
Завитаев Э.В., Русаков О.В., Харитонов К.Е. Расчет магнитной индукции внутри тонкой цилиндрической проволоки из металла // Вестник МГОУ. Серия Физика-Математика. 2016. № 2. С. 74–84.
Харрисон У. Теория твердого тела. М.: Мир, 1972. 616 с.
Займан Дж. Электроны и фононы. М.: ИЛ, 1962. 488 с.
Лифшиц И.М., Азбель М.Я., Каганов М.И. Электронная теория металлов. М.: Наука, 1971. 415 с.
Завитаев Э.В., Русаков О.В., Харитонов К.Е. К вопросу о расчете плотности тока внутри тонкой цилиндрической проволоки из металла в продольном магнитном поле // Вестник МГОУ. Серия Физика-Математика. 2016. № 3. С. 72–83.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Микроэлектроника

Архивы выпусков Информация о журнале Отправить рукопись в журнал