Российские нанотехнологии, 2021, T. 16, № 2, стр. 269-277

ВВЕДЕНИЕ

Благодаря результатам многолетнего развития микроэлектроники и активной разработке нейросетевых алгоритмов в различные сферы человеческой деятельности внедряется все большее количество систем сенсорного искусственного интеллекта (ССИИ): от распознавания объектов окружающей среды, текста и речи [1–3] до автономных систем управления транспортными средствами [4–7]. Несмотря на оптимизацию существующих архитектур традиционных ЭВМ (CPU) и графических ускорителей (GPU), ССИИ на их основе отличаются крайне высоким уровнем потребляемой энергии в сравнении с биологическими прототипами при решении задач с высокой степенью параллелизма. Имеются значительные трудности, связанные с масштабированием КМОП-структур (комплементарная структура металл–оксид–полупроводник) [8], наблюдается снижение темпов роста производительности микропроцессорных устройств (от 50%/год в 1980-х и 90-х годах, до 3–4%/год в 2010-х) [9] и при этом непрерывное усложнение нейросетевых алгоритмов, являющихся основой развития ССИИ и требующих для своей работы все большего количества энергии и более продвинутых вычислительных средств. Эти факторы привели к созданию специализированных цифровых и аналого-цифровых аппаратных средств ускорения нейросетевых алгоритмов, ориентированных на работу в режиме сверхнизкого потребления энергии с различными типами нейронных сетей (НС) [10–14]. Одним из наиболее перспективных решений в данной области являются аппаратные НС, основанные на мемристорах – наноразмерных сопротивлениях с эффектом памяти резистивных состояний. Их способность изменять проводимость при определенном внешнем воздействии (эффект резистивного переключения) позволяет исследователям рассматривать мемристоры как аналог биологических синапсов [14–16]. В [17, 18] было продемонстрировано, что НС-вычисления на основе мемристоров с точки зрения энергоэффективности на несколько порядков превосходят существующие решения на основе GPU и минимум в 5 раз – решения на основе специализированных тензорных процессоров.

В то же время у рассматриваемого подхода имеется ряд неразрешенных недостатков: разброс характеристик мемристивных структур как аналоговых элементов, ограничения в архитектуре нейросинаптических ядер и, как следствие, в вычислениях и передаче данных между ними, малоизученные подходы к созданию хотя бы частично самоoбучаемых НС. Последнее является особенно важным, поскольку на данный момент главным образом изучаются так называемые глубокие НС, состоящие из нескольких слоев нейронов и обучение в которых происходит по методу обратного распространения ошибки [19]. В таких сетях для их настройки (обучения) необходимо рассчитать требуемое изменение для каждого синаптического весового коэффициента, зависящее от ошибок для всех нейронов в более глубоких слоях НС, и затем последовательно осуществить данное изменение путем операции записи (подачей напряжения на каждый мемристивный элемент). Из-за этого в лучшем случае возрастают лишь затраты энергии и занимаемая на кристалле площадь под дополнительные схемы памяти и логики (для выполнения глобальных операций), а в худшем – также снижается производительность системы в целом (например, число обрабатываемых сетью кадров в секунду). Импульсные, или спайковые, НС (СНС), в свою очередь, основываются на локальных принципах, т.е. на данных об активности соседних нейронов, соединенных синаптическими весами, благодаря чему отпадает необходимость в дополнительных блоках расчетов для обучения сети. Одним из перспективных локальных правил изменения веса является STDP (от англ. “Spike-Timing-Dependent Plasticity” – пластичность, зависящая от интервалов между импульсами (спайками)). Правила STDP основаны на принципах причинности, их истоки происходят из знаний о функционировании биологических НС, а реализация их аналогов была продемонстрирована на различных типах мемристорных устройств [20–22].

Отметим, что не каждая схема нейрона подойдет для аппаратной реализации СНС. К примеру, большой класс нейроно-подобных устройств [23], моделирующих динамику, наблюдаемую в биологических нервных системах, не сможет обеспечить работу по локальным правилам STDP из-за поддержки генерации только однополярных по напряжению импульсов. В то же время в любой реализации мемристивного STDP требуется наличие импульсов обеих полярностей с целью обеспечения возможности как увеличения, так и уменьшения проводимости мемристора. Помимо этого, сами алгоритмы обучения по локальным правилам имеют узкие диапазоны сходимости с точки зрения параметров кривых STDP [24], что делает систему тонкой настройки формы спайков одной из ключевых в схеме их генерации.

Обучение с подкреплением представляет собой [25–27] способ самообучения интеллектуальных систем (агентов), основанный на их взаимодействии со средой и получении (ожидании) условной награды после выполнения каких-либо действий. Таким образом, обучение агента происходит в рамках универсального ценностно-ориентированного подхода, что наделяет его возможностью переобучения и адаптивностью отклика в изменяющихся условиях среды. В биологических системах подкрепление опосредовано нейромедиатором дофамином. Для реализации обучения импульсных НС-алгоритмов с подкреплением по аналогии с дофаминовой модуляцией в биологической нервной системе [28] необходимо дополнительно к перечисленным выше требованиям к искусственному нейрону иметь возможность изменения амплитуд спайка независимо друг от друга и в полном диапазоне двухполярного напряжения питания схемы, что не предусмотрено в существующих реализациях схем нейронов для STDP [29–31].

Настоящее исследование посвящено разработке и моделированию работоспособности электрической схемы нейрона с возможностью на аппаратном уровне дофаминоподобного обучения мемристивных синаптических связей СНС. Предлагаемая схема поддерживает двунаправленную генерацию спайков для обновления весов на входном и выходном слоях сети относительно нейрона, а также реализует две настраиваемые формы импульсов: бипрямоугольную и битреугольную. Также показано влияние параметров напряжения переключения мемристоров на особенности аппаратной реализации локальных правил STDP.

МОДЕЛЬ НЕЙРОНА И ЕГО ЭЛЕКТРИЧЕСКАЯ СХЕМА

Для реализации дофаминоподобного обучения СНС аппаратный нейрон должен обладать следующими характеристиками: поддержка двунаправленной генерации спайков для изменения весов на предыдущих и последующих слоях сети; поддержка генерации импульсов битреугольной и бипрямоугольной форм, что дает широкие возможности по настройке локальных правил обучения; поддержка независимой настройки амплитуд и длительностей импульсов. Для соответствия каждому из критериев предложена общая схема нейрона, представленная на рис. 1а. Она состоит из четырех связанных друг с другом блоков: интегратора-повторителя, который отвечает за обработку входных сигналов и реализацию двунаправленной передачи импульсов, двух блоков генерации спайков различной формы и цифрового блока управления, который содержит всю логику работы схемы нейрона. Рассмотрим подробнее каждый из них.

Рис. 1.

Общая схема импульсного нейрона с поддержкой генерации бипрямоугольных и битреугольных импульсов. Сплошные линии – сигналы управления состоянием нейрона, пунктирные линии – сигналы, по которым распространяются спайки для реализации двунаправленной передачи импульсов (а), граф состояний нейрона (б).

Цифровой блок управления. Основным назначением данной схемы является контроль работы импульсного нейрона в рамках модели конечного автомата с набором из трех состояний (рис. 1б). В первом из них, или начальном состоянии, нейрон накапливает заряд на мембране путем интегрирования всех входящих сигналов. При этом как только будет достигнут порог срабатывания, цифровая логика сгенерирует сигнал “Старт”, сигнализирующий остальным блокам схемы о начале генерации спайка. Этот процесс представляет собой два отдельных этапа: генерация первой половины импульса и второй, окончание которых оповещается сигналами “Половина” и “Конец” соответственно. По завершении процесса генерации нейрон возвращается в исходное состояние.

Интегратор-повторитель. Как было указано выше, схема данного блока (рис. 2) реализует интегрирование входящих сигналов на начальном этапе работы нейрона, а также реализует передачу спайка с выходов генераторов на вход нейрона. Эта функциональность достигается благодаря использованию двух наборов ключей, управляемых сигналом “Старт”, в связке с операционным усилителем DA₁, который обеспечивает необходимый запас по току при подключении к нейрону большого числа мемристоров:

Рис. 2.

Схема входного контура импульсного нейрона, осуществляющая интегрирование всех входных сигналов, а по достижению на мембране порога по напряжению U_th схема переходит в режим повторителя сигнала с выхода генератора импульсов.

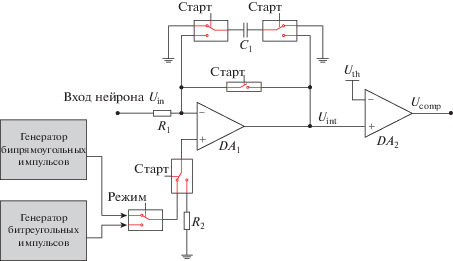
− при “Старт”, равном по уровню напряжения логическому нулю, операционный усилитель DA₁ включен по схеме интегратора напряжения с постоянной времени, определяемой сопротивлением R₁ (задается мемристорами, подключенными ко входу нейрона) и емкостью C₁. В этом состоянии достижение выходного напряжения интегратором U_int заданного порогового напряже-ния U_th контролируется с помощью компаратора DA₂ и его выходного сигнала U_comp, который анализируется блоком управления.

− при “Старт”, равном по уровню напряжения логической единице, операционный усилитель переключается в режим повторителя напряжения с его неинвертирующего входа, который, в свою очередь, замыкается на один из двух генераторов импульсов. Емкость С₁ при этом мгновенно разряжается, подготавливая схему интегратора для работы из начального состояния. Выбор генератора определяется уровнем сигнала “Режим”, который формируется на основе данных, записанных в конфигурационный регистр нейрона перед началом работы. Отметим, что после завершения процесса интегрирования всех входящих сигналов и начала двунаправленной генерации спайка этот процесс не может быть прерван. Новый спайк генерируется схемой нейрона только после завершения формирования предыдущего и с учетом повторного накопления на мембране достаточного количества заряда.

Генератор битреугольных импульсов. Данный блок во многом является продолжением и развитием идей, заложенных в предыдущей версии импульсного нейрона [32], при этом были учтены и устранены некоторые недостатки предыдущей модели:

− первый из них связан с формированием амплитуды отрицательной части импульса через напряжение смещения, что приводило к неработоспособности схемы из-за перехода одного из операционных усилителей в режим насыщения;

− второй недостаток заключался в невозможности перехода нейрона из возбуждающего в тормозный режим работы (и наоборот) без замены компонентов блока управления на печатной плате;

− третий недостаток связан с необходимостью использования подстроечных резисторов для настройки параметров нейрона.

Разработанная электрическая схема генератора битреугольных импульсов с учетом устранения описанных выше недостатков представлена на рис. 3. Как и в предыдущей версии нейрона, формирование конечного сигнала осуществляется с помощью интеграторов напряжения на операционных усилителях, однако в новой реализации входные напряжения схемы задаются с помощью цифро-аналогового преобразователя (ЦАП). Благодаря этому возможно выполнение тонкой настройки амплитуды положительной и отрицательной частей спайка, а также быстрого и простого перехода из возбуждающего режима работы в тормозный. Работа через ЦАП также позволяет обеспечить подстройку формы битреугольного спайка для обеспечения дофаминоподобного обучения импульсного НС-алгоритма [32].

Рис. 3.

Схема генерации битреугольного импульса: через ЦАП задаются параметры U_A и U_K1 – амплитуда и наклон первой части спайка, U_B и U_K2 – амплитуда и наклон второй части спайка. Начало генерации импульса осуществляется по сигналу “Старт”, а переключение между этапами генерации первой и второй частей спайка по сигналу “Половина”.

В разработанной схеме ЦАП нейрона формируются пять значений напряжения, определяющих следующие параметры: U_th – пороговое значение напряжения на мембране; U_K1 – коэффициент наклона первой части спайка; U_A – амплитуда первой части спайка; U_K2 – коэффициент наклона второй части спайка; U_B – амплитуда второй части спайка.

Формирование первой половины спайка с заданным через напряжение U_K1 коэффициентом наклона проводится через связку повторителя напряжения (DA₁) и интегратора (DA₄). Как только напряжение на интеграторе достигает заданного значения амплитуды U_A, компаратор (DA₇) сообщает блоку управления о необходимости перехода к генерации второй части импульса, и по сигналу “Половина” выход нейрона подключается к соответствующей схеме.

Формирование второй половины спайка также происходит с помощью связки повторителя напряжения (DA₂), интегратора (DA₅), параметра U_K2 и отдельной схемы сумматора на операционном усилителе (DA₆), через который задается амплитуда U_B. Окончание генерации спайка контролируется компаратором (DA₈): как только значение на сумматоре становится равным нулю, блок управления сигналом “Конец” возвращает схему нейрона в исходное состояние.

Генератор бипрямоугольных импульсов представляет собой связку блока формирования амплитуд импульса и блока контроля его длительности. Первый из них состоит из связки ЦАП, который формирует амплитуды спайка U_A и U_B, с двумя повторителями напряжения, обеспечивающими запас по току, необходимый при работе с несколькими мемристорами на входе или выходе нейрона. Выходы повторителей подключаются к мультиплексору, через который блок управления по сигналу “Половина” формирует бипрямоугольный импульс с заданными амплитудами.

В то же время задача второго блока заключается в обеспечении заданной длительности первой и второй частей спайка. Это достигается благодаря схеме, представленной на рис. 4.

Рис. 4.

Схема контроля длительности бипрямоугольного спайка; внешняя система управления записывает 16-битное значение в конфигурационный регистр, биты с Q0 по Q11 используются для определения длительности первой или второй частей спайка (одна единица равна 100 мкс), бит Q12 определяет выбор формы генерируемого спайка: битреугольную или бипрямоугольную.

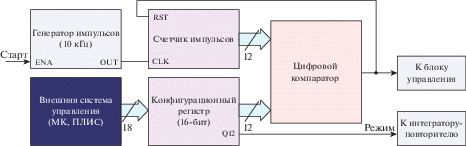
Основная идея здесь заключается в переопределении длительности спайка, генерируемого нейроном, в определенное количество тактов генератора заданной частоты: необходимая длительность, кратная в данном случае 100 мкс при частоте источника 10 кГц, записывается в виде 12-битного числа в конфигурационный регистр. После преодоления порога по напряжению на мембране нейрона и старта генерации импульса начинается подсчет тактов высокочастотного генератора до тех пор, пока цифровой компаратор не зафиксирует равенство между заданным и пройденным числом тактов, после чего блок управления по сигналу “Половина” приступит к генерации второй половины спайка с повторным использованием схемы подсчета длительности.

Так как используемые в [28, 29] спайки имеют длительность порядка десятков миллисекунд, кратность в 100 мкс не внесет каких-либо значительных искажений в процесс обучения импульсных НС-алгоритмов. В то же время 12-битное значение при тактовой частоте генератора 10 кГц позволяет задавать длительности отдельных частей спайка (первой или второй) до 400 мс, чего с запасом хватает при работе с мемристорами.

Отметим, что конфигурационный регистр определяет выбор формы генерируемого нейроном импульса путем записанного в бит Q12 значения.

ПОЛУЧЕННЫЕ РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ

Моделирование аппаратной реализации нейрона. Модели представленных принципиальных электрических схем блоков нейрона реализованы в системе автоматизированного проектирования, и проведено электрофизическое моделирование их работы. Полученные временные диаграммы процессов генерации битреугольных и бипрямоугольных импульсов представлены на рис. 5.

Рис. 5.

Временные диаграммы генерации спайков битреугольной (а) и бипрямоугольной форм (б), на которых U_int – выходное напряжение интегратора нейрона (определяет напряжение на мембране нейрона), “Старт” – сигнал начала генерации импульса, U₁ – выходное напряжение генератора первой половины спайка, “Половина” – сигнал переключения между частями спайка, U₂ – выходное напряжение генератора второй половины спайка, U_out – напряжение на выходе нейрона.

Поскольку в обоих случаях на вход схемы подавался постоянный сигнал величиной 1 В, на мембране нейрона происходило накопление заряда, что сопровождалось изменением напряжения на выходе интегратора схемы мембраны. В момент достижения порога срабатывания U_th блок управления генерировал сигнал “Старт”, сигнализируя другим блокам схемы о начале генерации импульса: в случае битреугольного спайка конечный результат складывался из двух изменяющихся во времени напряжений U₁ и U₂ (задаваемых схемой рис. 3), определяющих первую и вторую части спайка соответственно. Переключение между “частями” происходило по сигналу “Половина”, через который фиксировалось достижение заданной амплитуды U_A. Аналогичным образом происходила генерация бипрямоугольного спайка, за тем исключением, что напряжения U₁ и U₂ в данном случае являлись константами и определяли амплитуды импульса U_A и U_B. Сами импульсы формируются на входе и выходе нейрона, которые обозначены как U_int и U_out соответственно. Отметим, что в момент начала генерации спайка наблюдается переходный процесс, связанный с изменением состояния аналогового ключа. Из-за малой длительности и уровня напряжения, не превышающего значительно амплитуду полезного импульса, данные скачки не могут вызвать заметного изменения проводимости мемристора и тем самым оказать влияние на процесс обучения ИНС, что было показано при реализации хеббовского обучения на основе схемы нейрона с аналогичными коммутационными выбросами [36].

Кривые STDP для различных пар нейронов. С помощью метода измерения кривых окна STDP (зависимость изменения веса от межспайковых интервалов), описанного в [33], и модели мемристора VTEAM [34] проведено моделирование взаимодействия различных пар (рис. 6а) импульсных нейронов: “возбуждающий–возбуждающий”, “тормозный–тормозный”, “возбуждающий–тормозный”, “тормозный–возбуждающий”. Полученные результаты для первых двух пар (рис. 6б, 6в) хорошо соотносятся с данными [22, 24]: сохранение причинно-следственной связи, т.е. когда преспайк вызывает генерацию постспайка (Δt > 0), ведет к потенциации проводимости мемристора, а ее нарушение ведет к уменьшению синаптического веса сети.

Рис. 6.

Пара импульсных нейронов с синаптической связью в виде мемристора (а). Семейства кривых STDP для битреугольного типа спайков, измеренные из различных начальных состояний мемристора для пар нейронов “возбуждающий–возбуждающий” (б) и “тормозный–тормозный” (в). Синаптический вес W определяется по формуле (G₀ – G_min)/(G_max – G_min), где G₀ – проводимость мемристора в начальный момент времени, G_min и G_max – минимальная и максимальная проводимости мемристора.

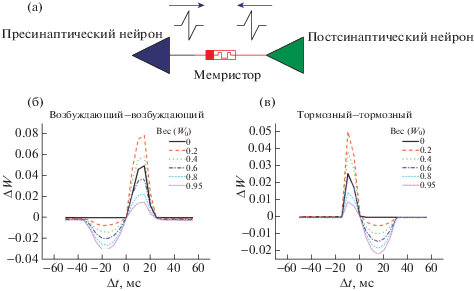
В то же время для пар “тормозный–возбуждающий” и “возбуждающий–тормозный” было получено два набора идентичных кривых, неполностью согласующихся с проведенным ранее исследованием по влиянию форм спайков на вид кривых STDP: согласно [28, 31] кривые STDP для битреугольных спайков имеют колоколообразную форму и располагаются в квадрантах 1–2 для пары “тормозный–возбуждающий” и 3–4 для пары “возбуждающий–тормозный”, т.е. являются симметричными относительно оси абсцисс. С другой стороны, полученные в ходе данной работы кривые располагаются во всех четырех квадрантах: в 1–2 для начальных весов W₀ от 0 до 0.4 и в 3–4 для весов от 0.6 до 0.95.

Для объяснения данного несоответствия достаточно рассмотреть разницу пре- и постсинаптических спайков в момент времени Δt = 0 (рис. 7а) совместно с возможностью разброса параметров мемристивной структуры: пороговых напряжений и динамики переключения в низкоомное и высокоомное состояния. С целью упрощения анализа взяты два симметричных импульса с одинаковыми длительностями и разными амплитудами: B₁ и B₂, T₁ и T₂ для спайков возбуждающего (В) и тормозного (Т) нейронов соответственно. Два разностных сигнала (В–Т и Т–В), полученные в результате перекрытия импульсов и представленные в нижней части рис. 7а, демонстрируют, что площади S₁ и S₂ зависят от пороговых напряжений переключения V₊ и V_–. В модели мемристора VTEAM скорость переключения структуры в каждый момент времени определяется выражениями типа ${{K}_{{{\text{on}}}}}{{(V - {{V}_{ + }})}^{{{{\alpha }_{{{\text{on}}}}}}}}$ для потенциации и ${{K}_{{{\text{off}}}}}{{({\text{|}}V - {{V}_{ + }}{\text{|}})}^{{{{\alpha }_{{{\text{off}}}}}}}}$ для депрессии. Очевидно, параметры K_on, K_off, α_on, α_off явно не зависят от прикладываемых к мемристивной структуре напряжений (хотя косвенно могут определяться ими, например, через степень локального джоулева разогрева) и регулируют динамику переключения наряду со значениями пороговых напряжений V₊ и V_–. Для удобства интерпретации разделим вклады явного влияния уровня напряжений (через V₊ и V_–) от неявной и прочей зависимости, обозначив вклады параметров K_on, α_on и K_off, α_off посредством D₊ и D_– соответственно. При этом условимся обозначать общие вклады потенциации и депрессии через S₁ × D₊ и S₂ × D_– (рис. 7). Тогда в случае, когда параметры, определяющие динамику переключения мемристора, одинаковы для потенциации и депрессии (D₊ = D_–), неравнозначность площадей S₁ и S₂ определяется различными по величине пороговыми напряжениями переключения V₊ и V_– (в случае симметричных спайков, т.е. при В₁ = |В₂|). В свою очередь, это неравенство площадей будет определять одну из колоколообразных кривых STDP (рис. 7б): в случае S₁ > S₂ преобладает потенциация, и кривая STDP имеет колоколообразную форму; в случае S₁ < S₂ конечным результатом процесса наложения импульсов будет, наоборот, уменьшение проводимости мемристора, и кривая STDP становится анти-колоколообразной. Аналогичные выводы можно сделать при различных параметрах динамики переключения D₊ и D_– в случае равенства площадей S₁ и S₂.

Рис. 7.

Результирующие спайки для пар нейронов “возбуждающий–тормозный” и “тормозный–возбуждающий” в момент времени Δt = 0 (а), зависимость кривой STDP для начального состояния W₀= 0.4 от произведения площадей S₁ и S₂, определяемых пороговыми напряжениями мемристора V₊ и V_–, и параметров динамики переключения мемристора D₊ и D_– (б).

Таким образом, для пар импульсных нейронов “тормозный–возбуждающий” и “возбуждающий–тормозный” кривая STDP в большей степени зависит от формы спайков и соотношений параметров мемристивной структуры, а именно пороговых напряжений переключения и скоростей изменения проводимости.

ЗАКЛЮЧЕНИЕ

Разработана принципиальная электрическая схема нейрона, которая обеспечивает поддержку дофаминоподобного обучения мемристивных синаптических весов в импульсной нейронной сети путем независимой подстройки параметров формы импульсов непосредственно в процессе работы сети. Путем моделирования функционирования аппаратной реализации нейрона продемонстрирована способность изменять амплитуды и длительности генерируемых импульсов независимо друг от друга под действием управляющих дофаминоподобных сигналов. Показано, что параметры мемристивных структур, в частности напряжения переключения и скорости потенциации/депрессии, оказывают значительное влияние на процесс аппаратного исполнения локальных правил обучения в парах с тормозными нейронами. Таким образом, допустимый разброс статических и динамических характеристик мемристивных структур наряду с их временной стабильностью [36] являются критически важными физико-техническими условиями для создания эффективных аппаратных ускорителей вычислений на основе импульсных нейросетевых алгоритмов. Удовлетворение данным требованиям возможно с использованием продвинутых нанотехнологических методов инженерии дефектов и структуры пленок мемристивных устройств [37]. В то же время принципиальное аппаратное исполнение биологически правдоподобного обучения с подкреплением представляется достижимым на базе предлагаемого решения в виде адаптивного, дофаминоподобного генератора импульсов.

Работа выполнена при финансовой поддержке Российского научного фонда (грант № 20-79-10185).