Российские нанотехнологии, 2021, T. 16, № 3, стр. 418-423

ВВЕДЕНИЕ

За счет реализации физических эффектов Зеебека и Пельтье термоэлектрические материалы и устройства используются для преобразования тепловой энергии в электрическую или наоборот [1]. Эффективность преобразования определяется безразмерной величиной термоэлектрической добротности zT = S²T/ρκ, где S – коэффициент Зеебека, ρ – удельное электросопротивление, κ = = κ_L + κ_E – общая теплопроводность, κ_L – решеточная теплопроводность, κ_E – электронная теплопроводность, T – температура [2]. Существуют две основные стратегии увеличения добротности zT. Первая заключается в повышении коэффициента мощности (PF = S ²/ρ) за счет создания примесных уровней в запрещенной зоне [3], инженерии дефектов [4, 5] и энергетической фильтрации зарядов [6]. Вторая стратегия заключается в понижении общей теплопроводности за счет ограничения фононного транспорта вследствие создания дополнительных центров их рассеяния [7].

Оксид цинка известен как полупроводник n-типа проводимости с шириной запрещенной зоны ~3.5 эВ. Среди термоэлектрических материалов ZnO выделяется высоким коэффициентом Зеебека, термической стабильностью, невысокой стоимостью и нетоксичностью. Однако высокие значения электрического сопротивления и теплопроводности ограничивают возможность существенного повышения значения zT. Недавние исследования показывают, что термоэлектрическая добротность может быть повышена путем замещения Zn²⁺ ионами Al³⁺ [8–12], Ga³⁺ [13, 14], In³⁺ [15, 16], Bi³⁺ [16], Ni²⁺ [17, 18] в основном за счет снижения удельного электросопротивления вследствие роста концентрации носителей заряда. Двойное легирование ZnO ионами Al и Ga позволило достичь максимального значения zT при 1273 К, равного 0.64 [8].

В настоящее время большинство исследований термоэлектрических материалов на основе оксидов металлов направлено на ограничение фононного транспорта и, как следствие, снижение решеточной теплопроводности за счет их наноструктурирования (путем внедрения наночастиц, создания наноразмерных дефектов, уменьшения размера зерна) [19]. В [15, 20, 21] показано, что внедрение In₂O₃ в ZnO приводит к образованию двумерных дефектов путем внутренней диффузии, что приводит к снижению теплопроводности до 0.8 Вт м^–1 К^–1 при 1000 К и, соответственно, к увеличению добротности zT до 0.4.

В данной работе исследовано влияние внедрения наночастиц NiO в матрицу ZnO в нанокомпозитах номинальных составов (ZnO)_{1 –x}(NiO)_x, где x = 0, 0.01, 0.03, 0.06.

ОБРАЗЦЫ И МЕТОДЫ ИССЛЕДОВАНИЙ

В качестве прекурсоров для получения нанокомпозитов (ZnO)_{1 –x}(NiO)_х, где x = 0, 0.01, 0.03, 0.06, использовали химические соединения Zn(NO₃)₂ ⋅ 6H₂O, Ni(NO₃)₂ ⋅ 6H₂O и NaOH чистотой 99.99% (АО “Вектон”, Россия). Химическое осаждение проводили при постоянной pH = 13 для синтеза Zn(OH)₂, pH = 11 для Ni(OH)₂, с использованием 10%-ного раствора гидроксида натрия и 10%-ных водных растворов солей нитратов Zn(NO₃)₂ ⋅ 6H₂O, Ni(NO₃)₂ ⋅ 6H₂O. В этом случае уравнения реакции со стехиометрическими коэффициентами для получения гидроксида цинка и гидроксида никеля имеют вид:

Образованные в результате реакции гелеобразные осадки промывали дистиллированной водой методом декантации с последующим центрифугированием на установке Rotanta 460 apparatus (Hettich, Германия). Полученный осадок прокаливали при температуре 973 K до получения оксидов ZnO и NiO. Полученные оксиды смешивали в атмосфере вакуума в стехиометрическом соотношении в планетарной мельнице Pulverisette 7 premium line (Fritsch, Германия) с циркониевыми размольными шарами (Ø = 5 мм) и стаканами (45 мл) при скорости 500 об./мин в течение 120 мин с массовым соотношением порошка и размольных тел 1: 20 для получения смесей порошков состава (ZnO)_{1 –x}(NiO)_x (x = 0, 0.01, 0.03, 0.06). Консолидацию порошковых смесей проводили с помощью отжига после предварительного прессования порошков при температуре 1673 К в атмосфере воздуха.

Фазовый состав консолидированных керамических образцов определяли методом рентгеновской дифракции на дифрактометре MiniFlex 600 (Rigaku, Япония) с излучением CuK_α. Плотности образцов измеряли методом гидростатического взвешивания (методом Архимеда). Исследования морфологии структуры и элементного состава образцов проводили методом сканирующей электронной микроскопии (СЭМ) и энергодисперсионной рентгеновской спектроскопии на приборе Vega 3 SB (Tescan, Республика Чехия) с использованием детектора X-Act (Oxford Instruments, Англия). Теплопроводность измеряли с помощью двух анализаторов температуропроводности LFA 467 (Netzch, Германия) и TC-1000 (Ulvac-Riko, Япония) методом лазерной вспышки и рассчитывали по формуле ${{\kappa }} = {{\lambda }}{{C}_{p}}d$, где λ – коэффициент температуропроводности [м² с^–1], C_p – удельная теплоемкость [Дж K^–1 кг^–1], которую измеряли на LFA 467 (Netzch, Германия) методом сравнения, d – плотность [кг м^–3]. Электрофизические свойства для всех полученных образцов в диапазоне температур от 400 до 1000 К измеряли одновременно на параллелепипедах размером 1 × 3 × 12 мм³ с использованием лабораторной измерительной системы (ООО Криотэл, Россия).

РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЙ

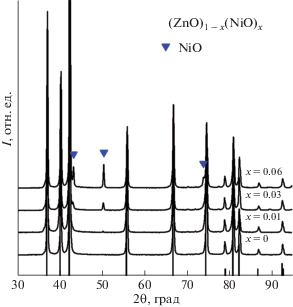
Плотность консолидированных образцов составила не менее 97% от кристаллографической. Зависимости изменения плотности от концентрации NiO обнаружено не было. Результаты рентгенофазового анализа для всех консолидированных образцов (ZnO)_{1 –x}(NiO)_x (x = 0, 0.01, 0.03, 0.06) представлены на рис. 1. Самые интенсивные пики соответствуют фазе ZnO со структурой типа вюрцита (PDF № 00-036-1451). Увеличение номинального количества фазы NiO приводит к возникновению соответствующих ей пиков (PDF № 03‑065‑2901).

Из  СЭМ-изображений  для  образцов (ZnO)_{1 –x}(NiO)_x (рис. 2) были рассчитаны средние размеры зерен по методу, представленному в [22], которые составили 10.5, 0.6, 0.5 и 0.4 мкм для х = 0, 0.01, 0.03, 0.06 соответственно. Размер включений NiO для всех образцов не превышал 100 нм. Уменьшение размеров зерен для концентраций х > 0 может быть обусловлено преимущественным распределением фазы NiO по границам зерен, что ограничивает рост зерна матрицы ZnO во время спекания. Это, в свою очередь, подтверждается результатами анализа распределения элементов в образцах (рис. 2в–2д).

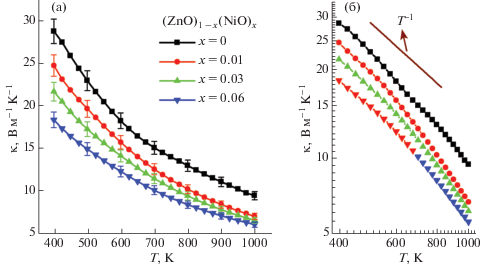
На рис. 3 представлены температурные зависимости полной (κ) и решеточной (κ_L) теплопроводности в диапазоне 400 < Т < 1000 К для образцов нелегированного оксида цинка и нанокомпозитов (ZnO)_{1 –x}(NiO)_x с разной концентрацией наночастиц NiO. Решеточную составляющую теплопроводности определяли как κ_L = κ – κ_E, где значения κ_E рассчитывали в соответствии с законом Видемана–Франца:

Число Лоренца L в (3) вычисляли из эмпирического соотношения

предложенного в [23]. Число Лоренца L в соотношении (4) имеет размерность Вт Ом К^–2, а коэффициент Зеебека S – мкВ/К.

Как видно из рис. 3а, максимальное различие значений полной теплопроводности в ZnO и нанокомпозитах (ZnO)_{1 –x}(NiO)_x наблюдается при низких температурах. Согласно рис. 3б решеточная составляющая теплопроводности для нелегированного ZnO падает с ростом температуры по закону, близкому к зависимости κ_L ~ Т^–1. Следовательно, у исходного ZnO основным механизмом рассеяния является фонон-фононное взаимодействие. Однако более крутой ход зависимостей κ_L(Т) в двойных логарифмических координатах в образцах (ZnO)_{1 –x}(NiO)_x (x = 0.01, 0.03, 0.06) указывает на то, что температурный ход решеточного вклада в теплопроводность близок к закону κ_L ~ Т^–1.5. Последнее может свидетельствовать о том, что в керамических образцах интенсивность рассеяния фононов увеличивается за счет роста концентрации статических несовершенств (дефектов) кристаллической решетки (границ зерен, межфазных границ и точечных дефектов) [23, 25].

По-видимому, увеличение концентрации NiO приводит к снижению κ_L за счет нескольких механизмов: увеличения рассеяния фононов на межзеренных границах вследствие уменьшения размера зерна (роста площади границ зерен) при x > 0, увеличения рассеяния фононов на точечных дефектах и межфазных границах.

На рис. 4 представлены температурные зависимости удельного электросопротивления (ρ), коэффициента Зеебека (S), взвешенной подвижности носителей заряда (µ_w) и фактора мощности (PF) в диапазоне температур от 400 до 1000 К для серии  консолидированных образцов (ZnO)_{1 – x}(NiO)_x (x = 0, 0.01, 0.03, 0.06). Как видно, увеличение концентрации наночастиц NiO приводит к снижению ρ во всем диапазоне температур. При этом все изученные образцы демонстрируют полупроводниковый характер зависимостей ρ(Т).

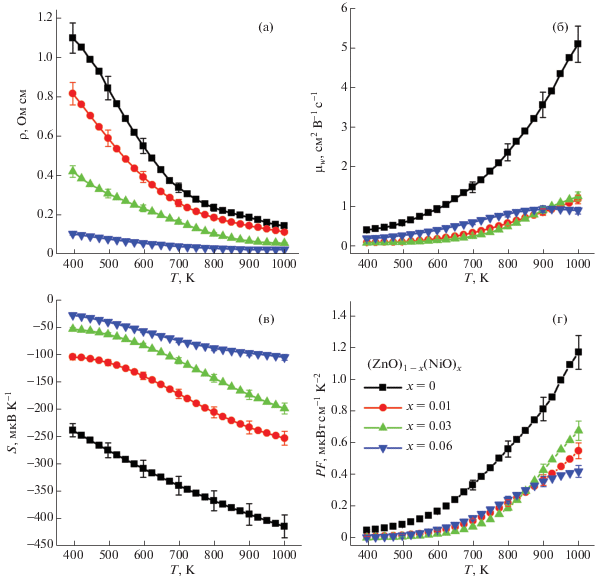
Согласно рис. 4б отрицательные значения S во всем диапазоне температур указывают на n-тип проводимости. Добавление NiO существенно снижает абсолютные значения S, вплоть до –30 мкВ/К при 400 К для композита с наибольшим содержанием NiO, х = 0.06.

Основываясь на формуле $\rho = 1{\text{/}}en\mu $ (е – заряд электрона, n – концентрация носителей заряда, μ – подвижность носителей заряда), можно выделить два фактора, ответственных за изменения электросопротивления с увеличением температуры: повышение концентрации (n) и увеличение подвижности (μ) носителей заряда.

Для определения вклада от μ была рассчитана температурная зависимость так называемой “взвешенной” подвижности носителей заряда (μ_w), которая в общем виде может быть записана как ${{\mu }_{w}} = \mu {{\left( {\frac{{m{\kern 1pt} *}}{{{{m}_{e}}}}} \right)}^{{3{\text{/}}2}}}$, где m* – эффективная масса, m_e – масса электрона. Используя соотношение, предложенное в [25], данный параметр можно рассчитать с помощью измерений ρ(Т) и S(Т) (рис. 4 в). В композиционных образцах с NiO значения μ_w ниже, чем у ZnO, и слабо зависят от концентрации х, что можно объяснить более высокой концентрацией дефектов в нанокомпозитах, препятствующих электронному транспорту. Таким образом, падение электросопротивления оксида цинка при добавлении оксида никеля невозможно объяснить изменением подвижности основных носителей заряда.

Для косвенного определения изменений концентрации носителей заряда был проведен анализ полученных экспериментальных температурных зависимостей коэффициента Зеебека. В рамках двухзонной модели запрещенной зоны [26] коэффициент Зеебека для невырожденных полупроводников n-типа может быть записан следующим образом:

где n – концентрация носителей заряда, N_c – эффективная плотность состояний в валентной зоне, А – константа. Как указывалось ранее, внедрение наночастиц NiO в оксид цинка повышает концентрацию носителей заряда, что приводит к снижению значений S. Таким образом, снижение электросопротивления преимущественно обусловлено повышением концентрации носителей заряда.

Температурные зависимости коэффициента мощности PF = S ²/ρ исследованных нанокомпозитов представлены на рис. 4г. Максимальные значения PF наблюдаются у нелегированного ZnO, что в основном обусловлено его более высокими значениями S. В образцах (ZnO)_{1 –x}(NiO)_x с ростом x величина ρ существенно снижается, однако вместе с тем снижаются значения S. D итоге это приводит к уменьшению фактора мощности композитов (ZnO)_{1 –x}(NiO)_x с увеличением содержания NiO.

ВЫВОДЫ

Исследовано влияние внедрения наночастиц NiO на электрофизические и тепловые свойства композитов cоставов (ZnO)_{1 –x}(NiO)_x (x = 0, 0.01, 0.03, 0.06). Исходные порошки ZnO и NiO были получены методом химического осаждения. Установлено, что вместе с увеличением концентрации NiO происходит уменьшение размеров зерен в спеченных композитах, обусловленное распределением NiO по границам зерен и, как следствие, торможением роста зерен матрицы ZnO при спекании. Последнее приводит к уменьшению теплопроводности за счет увеличения рассеяния на формируемой системе несовершенств кристаллической решетки вюрцитной фазы оксида цинка, а именно на межзеренных и межфазных границах, а также точечных дефектах. Достигнуты значения общей теплопроводности, равные 4.5 Вт м^–1 К^–1 при 1000 К для образца (ZnO)_0.94(NiO)_0.06, что примерно на 40% ниже значений для нелегированного ZnO при той же температуре. Однако, несмотря на относительно низкое удельное электросопротивление, коэффициент мощности для композиционных образцов (ZnO)_{1 –x}(NiO)_x не превышал 0.7 мкВт см^–1 К^–2, что на 35% ниже значений ZnO. Последнее обусловлено понижением абсолютных значений коэффициента Зеебека с ростом концентрации NiO ввиду увеличения концентрации носителей заряда.

Работа выполнена при поддержке Минобрнауки России в рамках государственного задания (код проекта 0718-2020-0037), а также при частичной поддержке Государственной программы научных исследований Республики Беларусь “ФизМатТех. Новые материалы и технологии” (задание 1.15.1) (А. Федотов).