Российские нанотехнологии, 2021, T. 16, № 6, стр. 799-809
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ АНАЛОГОВОЙ САМООБУЧАЮЩЕЙСЯ НЕЙРОННОЙ СЕТИ НА ОСНОВЕ МЕМРИСТИВНЫХ ЭЛЕМЕНТОВ С УЧЕТОМ СТОХАСТИЧЕСКОЙ ДИНАМИКИ ПЕРЕКЛЮЧЕНИЯ
А. Ю. Морозов 1, 2, *, К. К. Абгарян 1, 2, Д. Л. Ревизников 1, 2
1 Федеральный исследовательский центр “Информатика и управление” Российской академии наук
Москва, Россия
2 Московский авиационный институт (Национальный исследовательский университет)
Москва, Россия
* E-mail: morozov@infway.ru
Поступила в редакцию 15.07.2021
После доработки 28.07.2021
Принята к публикации 28.07.2021
Аннотация
Рассмотрены вопросы моделирования аналоговой самообучающейся импульсной нейронной сети на основе мемристивных элементов. Одним из важных свойств мемристора является стохастическая динамика переключения, обусловленная главным образом случайными процессами генерации/рекомбинации и перемещения ионов (или кислородных вакансий) в диэлектрической пленке под действием электрического поля. Учет стохастических особенностей выполняется за счет добавления в уравнение состояния мемристора слагаемого, отвечающего за аддитивный (гауссовский) шум. На примере динамической модели мемристора демонстрируется влияние шума на процесс функционирования элемента. Показано, что переключение мемристора из высокоомного состояния в низкоомное и обратно происходит от цикла к циклу по-разному, что соответствует экспериментальным данным. Формулируется стохастическая модель, описывающая аппаратную аналоговую реализацию импульсной нейронной сети с мемристивными элементами в качестве синаптических весов и механизмом обучения на основе метода STDP. Выполнено моделирование работы двух нейронных сетей, состоящих из одного нейрона с 64 синапсами и двух нейронов со 128 синапсами соответственно. Осуществлено распознавание изображений размером 8 × 8. Показано, что стохастическая составляющая в модели мемристоров сказывается на том, что шаблоны от реализации к реализации распределяются по нейронам по-разному и адаптация весов (обучение сети) происходит с различной скоростью. В обоих случаях сеть успешно обучается распознавать заданные изображения.
ВВЕДЕНИЕ
Вопрос ускорения вычислений является актуальным в любое время. Сначала производители увеличивали частоту работы процессора, потом увеличивали количество ядер в одном процессоре, далее адаптировали графические процессоры для вычислений общего характера, а в настоящее время перспективным представляется переход от цифровых вычислений к аналоговым, так как они выполняются на порядки быстрее [1]. При разработке аналоговых вычислительных устройств часто используется относительно новый электрический элемент – мемристор [2, 3], представляющий собой резистор, проводимость которого зависит от суммарного протекшего через него электрического заряда. Одним из способов применения этих элементов для ускорения вычислений является объединение их в матрицу (кроссбар), что позволяет эффективно реализовать аналоговое произведение матрицы на вектор [4, 5]. Помимо этого, за счет определенного сходства свойств данных элементов со свойствами биологических синапсов имеется возможность использовать мемристоры для создания аналоговых самообучающихся импульсных нейронных сетей (ИНС) [6].
Импульсные нейронные сети являются третьим поколением нейронных сетей. В данном виде сетей обмен информацией осуществляется в виде импульсов, что в наибольшей степени соответствует физиологии биологического мозга. Обучение ИНС основывается на локальных правилах изменения весов. Существуют аппаратные реализации ИНС на полупроводниковых элементах, в частности проект TrueNorth [7]. Мемристивные элементы используются не только в ИНС, но и в глубоких нейронных сетях [8], однако зачастую в этом случае задействуются алгоритмы обратного распространения ошибок, обладающие нелокальным характером и большими вычислительными сложностями.
Существует ряд работ, посвященных вопросам реализации ИНС на основе мемристоров. В частности, работа [9] направлена на изучение экспериментальных и теоретических подходов к поиску эффективных правил обучения. В [10] представлен подход к моделированию нейронных сетей, основанный на реализации металлооксидных гетероструктур с энергонезависимой памятью и многоуровневым резистивным переключением. В [11] экспериментально демонстрируется протокол обучения, который является не чувствительным к начальному состоянию мемристоров, а также к их различиям в рамках одной сети.
Обучение ИНС на аппаратном уровне традиционно основывается на правиле Хебба и синаптической пластичности. Используется метод Spike Timing Dependent Plasticity (STDP), согласно которому изменение весов синапсов нейрона зависит от разницы во времени между входным и выходным импульсом [12–14]. Те синаптические связи, которые вызвали активацию нейрона, усиливаются, а другие ослабляются. Со схемотехнической позиции метод STDP реализуется за счет 1T1R-кроссбар-архитектуры, в которой каждому мемристору соответствует один транзистор, отвечающий за изменение проводимости, и наличия обратной связи у каждого нейрона со всеми синапсами. В [15] была предложена математическая модель ИНС. Наличие такой модели позволяет осуществлять подбор параметров ИНС и проводить имитационное моделирование работы сети в различных режимах.
Согласно экспериментальным данным по мемристивным элементам характер их функционирования является отчасти стохастическим [16]. Как правило, процесс переключения мемристора из низкоомного состояния в высокоомное и наоборот происходит от цикла к циклу по-разному [17]. В частности, это связано со случайными процессами, происходящими в кристаллической решетке [18–20]. Математические модели мемристоров обычно формулируются в виде динамических систем относительно параметра состояния мемристора, характеризующего уровень проводимости элемента. На практике учет вероятностного поведения элементов можно выполнять, используя вместо детерминированного уравнения состояния стохастическое. Один из вариантов получения такого уравнения заключается во введении добавки в виде аддитивного белого (гауссовского) шума [21].
В настоящей работе исследовано влияние стохастических свойств мемристоров на работу нейроморфной сети. Практический интерес представляет вопрос использования значений параметров сети, определенных с помощью детерминированной модели, в условиях стохастической динамики мемристивных элементов. Другими словами, возможно ли выполнять настройку сети только на детерминированной модели. Кроме этого, важным представляется понимание того, как уровень шума будет влиять на скорость обучения и при каком уровне аддитивного шума нейронная сеть не сможет нормально функционировать.
СТОХАСТИЧЕСКАЯ МОДЕЛЬ МЕМРИСТОРА
Можно выделить несколько групп математических моделей мемристоров: модели линейного [22] и нелинейного дрейфа [23], модель, основанная на барьере Симмонса [24], модели, использующие специальные функции окна для ограничения переменной состояния [25–27], модели, учитывающие уровни напряжений, при которых начинается процесс переключения в виде пороговых условий [28–31].
Важной особенностью мемристоров является их стохастическое поведение. От цикла к циклу переключение мемристора из низкорезистивного состояния в высокорезистивное может происходить по-разному [16, 17]. Природа такого поведения связана со случайными процессами, происходящими на уровне перемещения кислородных вакансий в диэлектрической пленке мемристивного элемента [18–20]. В [32, 33] эффекты, связанные с влиянием шума на процесс переключения, рассмотрены с общих позиций нелинейных релаксационных явлений в метастабильных системах под действием шума [32, 33].
В настоящей работе учет стохастических особенностей выполняется за счет введения в дифференциальное уравнение состояния мемристора стохастической добавки в виде аддитивного белого (гауссовского) шума. Такой подход был успешно апробирован в [21].
Рассмотрим модель с нелинейной зависимостью от напряжения. В общем виде уравнение, описывающее состояние мемристора с аддитивным белым шумом, может быть представлено следующим образом:
где $x \in [0,1]$ – переменная состояния, $a$ – постоянная, определяемая свойствами материала, $V$ – текущее значение напряжения, $s$ – нечетное целое число, $f(x)$ – функция окна, используемая для приблизительного представления нелинейных эффектов ионного дрейфа и ограничения границ, η – коэффициент, характеризующий интенсивность шума, $W$ – винеровский процесс. Часто применяется оконная функция Biolek [26]:В настоящей работе использована модель мемристора данного класса [34] с учетом шума:
(1)
$\begin{gathered} dx = {{\eta }}dW + \\ \, + a{{V}^{s}}\left\{ \begin{gathered} \left[ {1 - {{{(1 - x)}}^{{2round\left( {\frac{b}{{|V| + c}}} \right)}}}} \right]dt,\quad V \leqslant - {{v}_{{thr}}}, \hfill \\ 0,\; - {{v}_{{thr}}} < V \leqslant {{v}_{{thr}}}, \hfill \\ \left[ {1 - {{{(x)}}^{{2round\left( {\frac{b}{{|V| + c}}} \right)}}}} \right]dt,\quad V > {{v}_{{thr}}}, \hfill \\ \end{gathered} \right. \\ I = {{x}^{n}}\beta \sinh \left( {{{\alpha }_{M}}V} \right) + {{\chi }}[\exp (\gamma V) - 1],\quad R = \frac{V}{I}, \\ \end{gathered} $Моделирование работы мемристора выполнено при следующих значениях параметров: $n = 5$, ${{\beta }} = 7.069 \times {{10}^{{ - 5}}}$ А, ${{\alpha }_{M}} = 1.8$ В–1, ${{\chi }} = 1.946 \times {{10}^{{ - 4}}}$ А, $\gamma = 0.15$ В–1, $a = 1$ B–5, $s = 5$, $b = 15$ В, $c = 2$ В, ${{v}_{{thr}}} = 1$ В, $x(0) = 0$, $V(t)$ – рис. 1а. Часть значений (${{\alpha }_{M}}$, γ, $a$, $s$, $b$, $c$, ${{v}_{{thr}}}$) соответствует значениям, приведенным в исходной работе [34], а часть (β, χ) подобрана для наилучшего соответствия экспериментальным данным [34] по оксиду гафния (HfO2) в рамках детерминированной модели (η = 0).
Рис. 1.
Зависимость напряжения от времени (a), ВАХ при значении коэффициента шума η = 0.05 (б), 0.10 (в) и 0.15 (г).
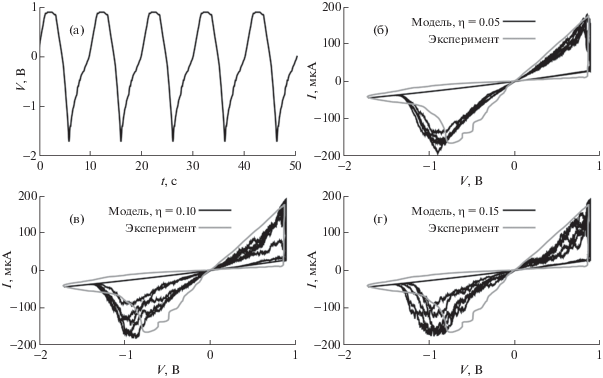
На рис. 1б–1г показано сравнение модельной вольт-амперной характеристики (ВАХ) при различных значениях коэффициента шума с экспериментальной кривой из работы [34].
На графиках ВАХ присутствуют несколько случайных траекторий, каждая из которых соответствует определенному циклу переключения мемристора. Отметим, что полученный разброс в ВАХ на разных циклах согласуется с экспериментальными данными [16] для оксида гафния.
Наличие шума в модели мемристора приводит к тому, что все параметры приобретают стохастические свойства. В частности, при η = 0.05 оценка математического ожидания минимального сопротивления мемристора $M[{{R}_{{{\text{on}}}}}] \approx 6.77$ кОм, а дисперсии $D[{{R}_{{{\text{on}}}}}] \approx 1$ кОм2. На другие параметры, такие как максимальное значение сопротивления и напряжения переключения, аддитивный шум сказывается в меньшей степени. Ясно, что с увеличением значения коэффициента шума разброс параметров будет также увеличиваться.
Без ограничения общности предположим, что мемристорную модель можно представить в виде двух уравнений:
Первое уравнение определяет зависимость скорости изменения состояния мемристора от приложенного напряжения ($V$) и состояния ($x$), а второе определяет значение сопротивления мемристора.
СТОХАСТИЧЕСКАЯ МАТЕМАТИЧЕСКАЯ МОДЕЛЬ НЕЙРОМОРФНОЙ СЕТИ
В [15, 35–39] рассмотрены вопросы моделирования схемотехнических решений нейроморфных сетей, в том числе использования метода обучения STDP. В настоящей работе метод STDP реализуется за счет использования 1T1R-кроссбар-архитектуры и наличия обратной связи в соответствии с [15]. В момент активации нейрона по каналу обратной связи с задержками поступают два противоположных по знаку импульса. Если на синапсе есть активность и пришел положительный импульс обратной связи, то значение сопротивления соответствующего мемристора уменьшается, а если пришел отрицательный импульс обратной связи, то сопротивление мемристора увеличивается.
Схемотехническая модель нейрона представляет параллельную RC-цепь и абстрактный генератор импульсов. При превышении значения потенциала на конденсаторе некоторого порога его потенциал сбрасывается, и генератор импульсов выдает выходной сигнал и сигнал обратной связи. Дополнительно в момент активации нейрона происходит подавление других нейронов (принудительно уменьшается накопленный ими потенциал пропорционально определенному коэффициенту).
Обучение сети происходит следующим образом: в начальный момент времени синаптические веса инициализируются случайным образом, а далее многократно на вход в сеть с равной вероятностью подается или произвольный шум, или заранее определенные шаблоны. Спустя некоторое время сеть адаптируется к распознаванию шаблонов. Под одной эпохой обучения подразумевается то время, на протяжении которого сети демонстрируется образец или случайный шум. Распределение шаблонов по нейронам происходит в процессе обучения.
В [15] приведена ранее разработанная математическая модель нейроморфной сети без учета стохастической динамики переключения мемристора. Учет соответствующих свойств мемристивных элементов заключается в замене уравнений (3) в [15] на:
В результате использования стохастических уравнений состояния мемристоров вся модель нейроморфной сети становится также стохастической.
Отметим, что все мемристоры и нейронные сети в данной работе являются модельными, физическая реализация является предметом будущих исследований.
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ НЕЙРОМОРФНОЙ СЕТИ С УЧЕТОМ СТОХАСТИЧЕСКИХ ОСОБЕННОСТЕЙ МЕМРИСТИВНЫХ ЭЛЕМЕНТОВ
Рассмотрим сеть, состоящую из одного нейрона ($m = 1$, поэтому индекс $j$ в дальнейшем опускается) с 64 синапсами. Значения параметров: $n = 64$, ${{R}_{{{\text{int}}}}} = \;1\;кОм$, ${{C}_{{{\text{int}}}}} = 45\;мкФ$, $V_{{te}}^{ + } = 1.5\;В$, $V_{{te}}^{ - } = - 1.6\;В$, $V_{{te}}^{0} = 10\;мВ$, $V_{{{\text{out}}}}^{ + } = 2\;В$, ${{V}_{{th}}} = 3\;мВ$, ${{{{\tau }}}_{r}} = 20\;мс$, ${{{{\tau }}}_{s}} = 2\;мс$, ${{{{\tau }}}_{{{\text{out}}}}} = 10\;мс$. Данные значения получены в [15] на основе детерминированной модели нейроморфной сети. Параметры $V_{{te}}^{ + }$, $V_{{te}}^{ - }$, $V_{{te}}^{0}$, ${{{{\tau }}}_{r}}$, ${{{{\tau }}}_{s}}$ определяют амплитуды, продолжительность и задержку между импульсами в обратной связи, благодаря которым происходит обучение согласно методу STDP.
В процессе моделирования в каждой эпохе (равной τr/2 с) вектор входных сигналов ${{{\mathbf{V}}}_{{\mathbf{g}}}}(t)$ соответствует распознаваемому шаблону (рис. 2) или задается случайно (элементы вектора имеют дискретное распределение: $V_{g}^{i} = 0$ В с вероятностью $0.81$ и $V_{g}^{i} = 2В$ с вероятностью $0.19$). Для наглядности вектор ${{{\mathbf{V}}}_{{\mathbf{g}}}}$, соответствующий шаблону, запишем в виде матрицы:
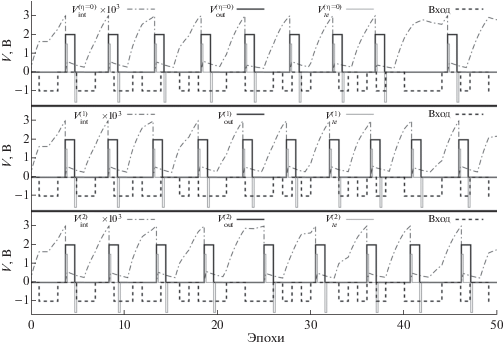
На рис. 3, 4 приведены графики поведения характерных напряжений нейронной сети в зависимости от времени. Верхние графики соответствуют нулевому значению коэффициента, характеризующего интенсивность шума, т.е. фактически детерминированной модели мемристора, а нижние графики – двум разным реализациям при значении η = 0.05. Пунктирной линией показано, какой сигнал в каждую конкретную эпоху подавался на вход нейронной сети. Значению –1 соответствует шум, а значению 0 – распознаваемый шаблон. Пунктирная линия с точкой отражает значение напряжения на конденсаторе нейрона, сплошная серая тонкая линия – значение напряжения в обратной связи. Сплошная толстая линия соответствует напряжению на выходе сети. Как только напряжение на конденсаторе достигает определенного порога, происходит активация нейрона: появляются импульс на выходе и серия импульсов в обратной связи.
Рис. 4.
Сравнение поведения основных параметров нейронной сети в конце обучения при η = 0 (верхний график) и при η = 0.05 (нижние графики).
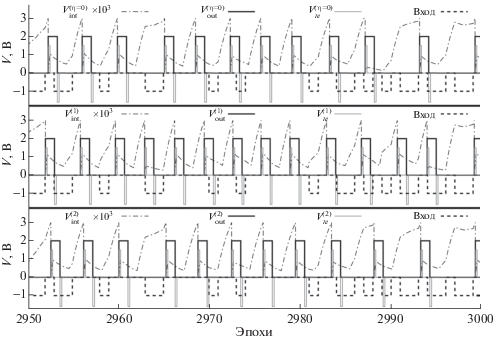
Во всех случаях начальные условия и процесс обучения были зафиксированы (на вход в сеть подавалась одна и та же последовательность значений). По графикам видно, что сеть успешно обучилась, при этом за счет наличия стохастического члена в модели мемристора активации нейрона происходят с некоторыми случайными смещениями во времени. На рис. 5 показан процесс изменения переменных состояний мемристоров для пяти различных реализаций. Здесь видим, что стохастическая добавка в модель мемристора приводит к различной скорости адаптации весов: в частности, в первой реализации распознаваемый шаблон начинает просматриваться уже с 1500-й эпохи, а в остальных реализациях – только с 2000-й эпохи.
Далее рассмотрим задачу распознавания двух образцов (рис. 6) [15]. Параметры модели нейроморфной сети остаются прежними, за исключением ${{V}_{{th}}} = 4\;мВ$. Так как здесь происходит взаимодействие между нейронами, дополнительно задается коэффициент подавления α = 0.1 (в момент активации одного нейрона потенциал другого нейрона сбрасывается в соответствии с коэффициентом подавления).
Как и ранее, в каждой эпохе вектор входных сигналов ${{{\mathbf{V}}}_{{\mathbf{g}}}}(t)$ соответствует распознаваемым шаблонам (рис. 6) или задается случайно (элементы вектора имеют дискретное распределение: $V_{g}^{i} = 0В$ с вероятностью $0.8$ и $V_{g}^{i} = 2В$ с вероятностью $0.2$).
На рис. 7, 8 приведены графики зависимости напряжений от времени в начале и в конце процесса обучения для двух различных реализаций. На рис. 9 продемонстрировано изменение переменных состояний мемристоров для пяти реализаций.
Рис. 7.
Сравнение поведения основных параметров нейронной сети в начале обучения в двух разных реализациях.
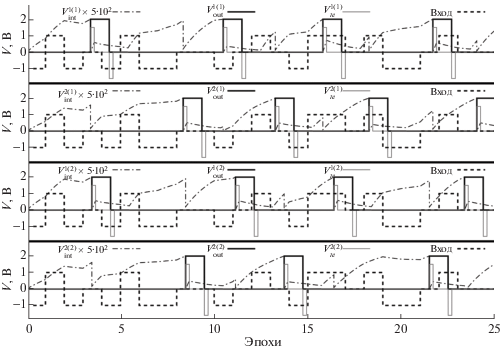
Рис. 8.
Сравнение поведения основных параметров нейронной сети в конце обучения в двух разных реализациях.
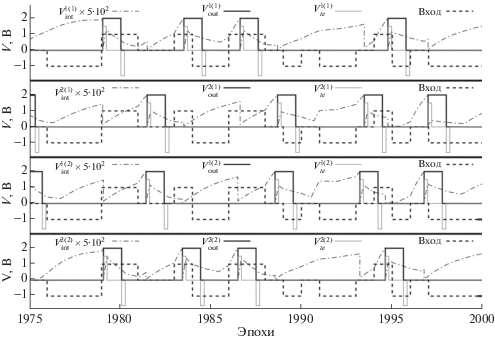
Пунктирной линией показано, что в каждую конкретную эпоху подавалось на вход нейронной сети. Значению –1 соответствует шум, значению 0 – первый распознаваемый шаблон, значению 1 – второй распознаваемый шаблон.
Здесь видим, что шаблоны распределились по нейронам по-разному, но при этом различия в функционировании сети являются незначительными: как и в предыдущем примере, присутствуют небольшие смещения во времени выходных импульсов.
Во всех случаях сеть успешно обучилась распознавать заданные изображения. Однако стохастическая составляющая в модели мемристоров повлияла на то, что шаблоны от реализации к реализации распределяются по нейронам по-разному и адаптация весов происходит с различной скоростью.
ОБСУЖДЕНИЕ
В результате имитационного моделирования работы нейроморфной сети получено, что сеть успешно обучилась распознавать заданные шаблоны при значениях параметров, подобранных в рамках детерминированной модели. Это говорит о том, что настройку сети возможно выполнять без учета стохастической природы мемристивных элементов. В первую очередь, аддитивный шум влияет на то, каким образом шаблоны распределяются по нейронам, и в меньшей степени на задержки в выходных импульсах.
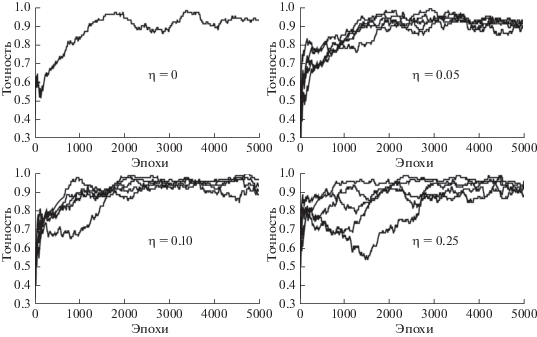
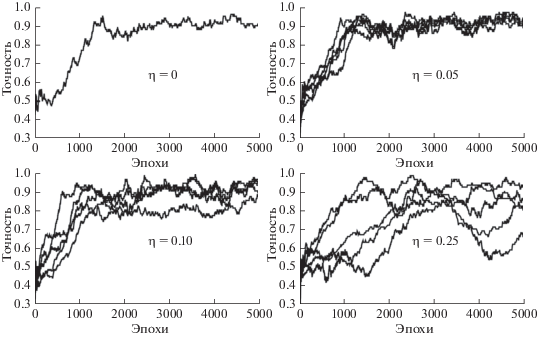
Главной характеристикой любой нейронной сети является точность. Обычно для ее оценки в сеть подается на вход тестовый набор данных и определяется процент правильных ответов. Отличительной особенностью рассматриваемой в работе сети является наличие внутреннего состояния, которое изменяется в процессе функционирования, поэтому классический подход тестирования не совсем корректен. В связи с этим для оценки точности выполнено усреднение по некоторому временному окну в процессе обучения сети: подсчитано, сколько раз сеть правильно отреагировала на входные данные. Используемый размер окна – 100 эпох. Также вопрос вызывает то, что шаблоны в процессе обучения случайным образом могут перераспределяться по нейронам, поэтому заранее перед процессом обучения определить, какой из нейронов будет отвечать за какой шаблон, нельзя. Для решения этого вопроса на каждой эпохе проверяется, к какому нейрону больше всего подходит шаблон: максимизируется скалярное произведение между входным вектором и текущим вектором значений синаптических весов каждого нейрона.
На рис. 10, 11 показаны зависимости точности от номера эпохи для двух рассмотренных ранее сетей. Кривые, соответствующие нулевому значению коэффициента шума, фактически получены с использованием детерминированной модели. Для ненулевых значений коэффициента шума на графиках приведено по пять разных кривых, соответствующих разным реализациям. Видно, что при небольшом значении η сеть в ряде реализаций обучается быстрее, чем при отсутствии шума. Однако с увеличением η процесс обучения теряет стабильность и перестает сходиться, о чем свидетельствует сильный разброс в графиках при η = 0.25.
ЗАКЛЮЧЕНИЕ
Представлено математическое моделирование самообучающейся нейроморфной сети, основанной на мемристивных элементах, с учетом стохастичности протекающих процессов. Реализована динамическая модель мемристора с аддитивным шумом. ВАХ оксида гафния, полученные в результате моделирования, согласуются с экспериментальными данными. Сформулирована комплексная стохастическая математическая модель импульсной нейроморфной сети с механизмом обучения согласно правилу STDP. На примере распознавания образов с использованием нейроморфных сетей с одним и двумя нейронами показано, что скорость адаптации весов сети к распознаваемым шаблонам, а также распределение шаблонов по нейронам зависят от стохастических особенностей мемристивных элементов. При этом настройка параметров сети может проводиться без учета стохастической динамики переключения мемристоров. При относительно невысоком уровне шума нейронные сети с параметрами, подобранными с помощью детерминированной математической модели, успешно обучаются распознавать заданные шаблоны.
Работа выполнена при поддержке Российского фонда фундаментальных исследований (грант № 19-29-03051 мк).
Список литературы
Chatterji B.N. // IETE J. Education. 1993. V. 34 № 1. P. 27. https://doi.org/10.1080/09747338.1993.11436397
Wong H.-S.P., Lee H.-Y., Yu S. et al. // Proc. IEEE. 2012. V. 100. № 6. P. 1951. https://doi.org/10.1109/JPROC.2012.2190369
Yang J.J., Strukov D.B., Stewart D.R. // Nature Nanotechnology. 2013. V. 8. № 1. P. 13. https://doi.org/10.1038/nnano.2012.240
Li C., Hu M., Li Y. et al. // Nature Electronics. 2017. V. 1. № 1. P. 52. https://doi.org/10.1038/s41928-017-0002-z
Hu M., Graves C.E., Li C. et al. // Adv. Mater. 2018. V. 30. № 9. P. 1705914. https://doi.org/10.1002/adma.201705914
Морозов А.Ю., Ревизников Д.Л., Абгарян К.К. // Изв. вузов. Материалы электронной техники. 2019. Т. 22. № 4. С. 272. https://doi.org/10.17073/1609-3577-2019-4-272-278
Merolla P.A., Arthur J.V., Alvarez-Icaza R. et al. // Science. 2014. V. 345. № 6197. P. 668. https://doi.org/10.1126/science.1254642
Emelyanov A.V., Lapkin D.A., Demin V.A. et al. // AIP Adv. 2016. V.6 № 11. P. 111301. https://doi.org/10.1063/1.4966257
Demin V.A., Nekhaev D.V., Surazhevsky I.A. et al. // Neural Netw. 2021. V. 134. P. 64. https://doi.org/10.1016/j.neunet.2020.11.005
Andreeva N.V., Ryndin E.A., Gerasimova M.I. // BioNanoSci. 2020. V. 10. P. 824. https://doi.org/10.1007/s12668-020-00778-2
Emelyanov A.V., Nikiruy K.E., Serenko A.V. et al. // Nanotechnology. 2019. V. 31. № 4. P. 045201. https://doi.org/10.1088/1361-6528/ab4a6d
Diehl P., Cook M. // Frontiers in Computational Neuroscience. 2015. V. 9. Art. 99. P. 9. https://doi.org/10.3389/fncom.2015.00099
Guo Y., Wu H., Gao B., Qian H. // Front Neurosci. 2019. V. 13. Art. 812. https://doi.org/10.3389/fnins.2019.00812
Milo V., Ielmini D., Chicca E. // 2017 IEEE International Electron Devices Meeting (IEDM). San Francisco. CA. 2017. P. 11.2.1. https://doi.org/10.1109/IEDM.2017.8268369
Morozov A.Yu., Abgaryan K.K., Reviznikov D.L. // Chaos, Solitons Fractals. 2021. V. 143. P. 110548. https://doi.org/10.1016/j.chaos.2020.110548
Rodriguez-Fernandez A., Cagli C., Perniola L. et al. // Microelectron. Eng. 2018. V. 195. P. 101. https://doi.org/10.1016/j.mee.2018.04.006
Теплов Г.С., Горнев Е.С. // Микроэлектроника. 2019. Т. 48. № 3. С. 163. https://doi.org/10.1134/S0544126919030104
Agudov N.V., Safonov A.V., Krichigin A.V. et al. // J. Stat. Mech: Theory Exp. 2020. P. 024003. https://doi.org/10.1088/1742-5468/ab684a
Mikhaylov A.N., Gryaznov E.G., Belov A.I. et al. // Phys. Status Solidi. C. 2016. V. 13. P. 870 https://doi.org/10.1002/pssc.201600083
Filatov D.O., Vrzheshch D.V., Tabakov O.V. et al. // J. Stat. Mec.: Theory Exp. 2019. № 12. P. 124026. https://doi.org/10.1088/1742-5468/ab5704
Васильев А., Чернов П.С. // Матем. моделирование. 2014. Т. 26. № 1. С. 122.
Strukov D.B., Snider G.S., Stewart D.R. et al. // Nature. 2008. № 453. P. 80. https://doi.org/10.1038/nature06932
Yang J.J., Pickett M.D., Xuema L. et al. // Nature Nanotechnology. 2008. V. 3. № 7. P. 429. https://doi.org/10.1038/nnano.2008.160
Pickett M.D., Stukov D.B., Borghetti J.L. et al. // J. Appl. Phys. 2009. V. 106. № 7. P. 074508. https://doi.org/10.1063/1.3236506
Joglekar Y.N., Wolf S.J. // Eur. J. Phys. 2009. V. 30. № 4. P. 661. https://doi.org/10.1088/0143-0807/30/4/001
Biolek Z., Biolek D., Biolkova V. // Radioengineering. 2009. V. 18. № 2. P. 210.
Zha J., Huang H., Liu Y. // IEEE Transactions on Circuits and Systems II: Express Briefs. 2015. V. 63. № 5. P. 423. https://doi.org/10.1109/TCSII.2015.2505959
Kvatinsky S., Friedman E.G., Kolodny A., Weiser U.C. // IEEE Transactions on Circuits and Systems I: Regular Papers. 2012. V. 60. № 1. P. 211. https://doi.org/10.1109/TCSI.2012.2215714
Kvatinsky S., Ramadan M., Friedman E.G., Kolodny A. // IEEE Transactions on Circuits and Systems II: Express Briefs. 2015. V. 62. № 8. P. 786. https://doi.org/10.1109/TCSII.2015.2433536
Yakopcic C., Taha T.M., Subramanyam G. et al. // IEEE Electron Device Lett. 2011. V. 32. № 10. P. 1436. https://doi.org/10.1109/LED.2011.2163292
Zheng G., Mohanty S.P., Kougianos E., Okobiah O. // 2013 IEEE 56th International Midwest Symposium on Circuits and Systems (MWSCAS). Columbus. OH. 2013. P. 916. https://doi.org/10.1109/MWSCAS.2013.6674799
Spagnolo B., Valenti D., Guarcello C. et al. // Chaos, Solitons Fractals. 2015. (81). P. 412. https://doi.org/10.1016/j.chaos.2015.07.023
Spagnolo B., Guarcello C., Magazzù L. et al. // Entropy. 2017. V. 19. № 1. P. 20. https://doi.org/10.3390/e19010020
Mladenov V. // Electronics. 2019. V. 8. № 4. P. 16. https://doi.org/10.3390/electronics8040383
Ielmini D., Ambrogio S., Milo V. et al. // 2016 IEEE International Symposium on Circuits and Systems (ISCAS). Montreal. QC. 2016. P. 1386. https://doi.org/10.1109/ISCAS.2016.7527508
Milo V., Pedretti G., Carboni R. et al. // 2016 IEEE International Electron Devices Meeting (IEDM). San Francisco. CA. 2016. P. 16.8.1. https://doi.org/10.1109/IEDM.2016.7838435
Ambrogio S., Balatti S., Milo V. et al. // 2016 IEEE Symposium on VLSI Technology. Honolulu. HI. 2016. P. 1. https://doi.org/10.1109/VLSIT.2016.7573432
Wenger C., Zahari F., Mahadevaiah M.K. et al. // IEEE Electron Device Lett. 2019. V. 40. № 4. P. 639. https://doi.org/10.1109/LED.2019.2900867
Морозов А.Ю., Абгарян К.К., Ревизников Д.Л. // Изв. вузов. Материалы электронной техники. 2020. Т. 23. № 3. С. 186. https://doi.org/10.17073/1609-3577-2020-3-186-195
Дополнительные материалы отсутствуют.
Инструменты
Российские нанотехнологии