Российские нанотехнологии, 2022, T. 17, № 3, стр. 400-404

ВВЕДЕНИЕ

В жидкостях могут происходить структурные переходы изотропная фаза–изотропная фаза, однако до настоящего времени они остаются слабо изученным явлением. Тенденцией последних лет было наблюдение данных переходов при экстремально высоких давлениях и температурах в расплавах простых веществ, таких как сера [1], а также в расплавах бинарных соединений [2–5]. Было показано, что изменение ближнего порядка в расплавах может происходить под влиянием внешних условий не только постепенно, но и резко. При этом изменение структуры может сопровождаться изменением ряда физических свойств аналогично фазовым переходам первого рода в кристаллических веществах, а число изотропно-жидких состояний у одного вещества может достигать трех [2]. Вместе с тем даже при нормальном давлении в изотропно-жидкой фазе таких сложных веществ, как полимеры, могут происходить сильные изменения структуры и ближнего порядка при изменении температуры. Для их наблюдения с успехом используется метод электрического двойного лучепреломления (ЭДЛ, или эффект Керра) [6]. С его помощью был обнаружен переход между двумя изотропно-жидкими состояниями в расплаве полиметакрилата с хиральными боковыми мезогенными группами, подтвержденный методами калориметрии и широкоуглового рентгеновского рассеяния [7]. Фазовый переход первого рода, связанный с микрофазовой сегрегацией мезогенных и кислотных боковых групп, наблюдался в изотропном расплаве статистических гребнеобразных сополимеров [8, 9]. Наконец, у многих гибкоцепных полимеров с помощью различных экспериментальных методов исследовалось явление, названное переходом жидкость–жидкость (LL-переход) [10–14]. Оно проявлялось как в равновесных, так и в динамических свойствах. Переход был объяснен тем, что при нагреве и достижении температуры LL-перехода уменьшается кооперативность движения мономерных звеньев цепи, сегментальное движение пропадает, а основной кинетической единицей становится мономерное звено макромолекулы. Этот переход исследовался также в полистироле [10, 12, 14]. Результаты настоящей работы показывают, что такого рода переход в полистироле приводит к появлению аномальной температурной зависимости ЭДЛ в расплаве полистирола при высокой температуре, связанной с увеличением ближнего ориентационного порядка в системе фенильных циклов.

РЕЗУЛЬТАТЫ

Были исследованы электрооптические свойства расплавов четырех фракций полистирола, в том числе олигомера P-5 с массой M_W = 504 и трех полимеров P-25, P-45 и P-88 с массами 2.63 × 10³, 4.65 × 10³ и 9.1 × 10³ соответственно. Обозначение вида P-n указывает на число мономерных звеньев в цепи (рис. 1), где n = 5, 25, 45 или 88. Полимеры произведены фирмой Tosoh Corp. (Japan) методом анионной полимеризации и обладают узким распределением молекулярных масс, коэффициент полидисперсности M_W/M_N находится в интервале от 1.02 до 1.14.

Рис. 1.

Структура мономерного звена полистирола. Фенильные кольца атактического полистирола распределены статистически по обе стороны цепи.

Использовалась экспериментальная методика, применявшаяся ранее при работе с расплавами полимеров [6–9, 15]. Электрическое двойное лучепреломление Δn измерялось в импульсном электрическом поле с напряженностью Е до 2.5 × × 10³ В/см при длительности импульсов до 100 мс. Длительность прямоугольных импульсов выбиралась такой, чтобы она была достаточна для установления равновесного электрооптического эффекта. Постоянную Керра K рассчитывали из соотношения K = Δn/Е². Закон Керра выполнялся во всех случаях, относительная погрешность измерений не превышала 10%. Для измерений применялись поворотный эллиптический компенсатор, модулятор эллиптической поляризации света [15] и электрооптическая ячейка с длиной оптического пути 10 мм и объемом 10 мм³. Измерения выполнены в интервале от температуры стеклования Т_g  до 200°С. Систематическое исследование электрооптических свойств расплавов ряда фракций полистирола в зависимости от длины макромолекулы было выполнено впервые.

Результаты измерений представлены на рис. 2. Отметим, во-первых, существенную зависимость средней величины K от числа мономерных звеньев в полимере и, во-вторых, существование двух принципиально разных видов температурной зависимости К, что ранее было выявлено у одной из фракций [16]. Там же на графике приведены постоянные Керра бензола C₆H₆ и толуола C₆H₅CH₃ при температуре 20°С. Строение этих молекул сходно со строением мономерных звеньев полистирола.

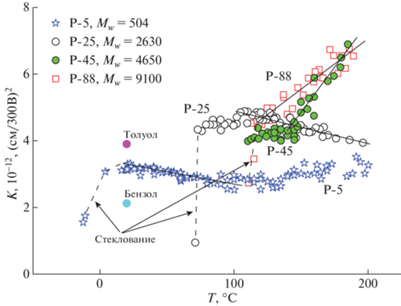
Рис. 2.

Температурные зависимости постоянной Керра K(T) в расплаве олигомера P-5 и полимеров P-25, P-45, P-88. Сплошные линии на графиках демонстрируют преобладающую температурную зависимость вида K ∝ (1/T) у образцов P-5 и P-25 и вида K ∝ T у образцов P-45 и P-88. Пунктирными линиями отмечено падение величины электрооптической постоянной в области стеклования. Отмечены значения K для бензола и толуола при 20°С.

Полимерный расплав является конденсированной фазой. Полимерные цепи в плотно упакованной молекулярной системе взаимно переплетены. Вместе с тем они обладают индивидуальными характеристиками, такими как размер клубка и жесткость цепи, которые могут оказывать влияние на физические свойства среды в целом. На это обстоятельство прямо указывает обнаруженная в работе сильная зависимость электрооптических свойств от числа мономерных звеньев в макромолекуле. У полистирола, как и у других гибкоцепных полимеров, при изменении количества звеньев в цепи от нескольких единиц до десятков n происходит формирование полимерного клубка. Способность макромолекулы образовывать клубок зависит от жесткости цепи, мерой которой является сегмент Куна – кинетически независимый участок цепи, состоящий из нескольких мономерных звеньев. Чем больше мономерных звеньев входит в состав одного сегмента, тем цепь жестче и поэтому такая цепь менее свернута. Для полистирола величина сегмента Куна соответствует восьми мономерным звеньям [17]. Поэтому состоящая из пяти звеньев молекула олигомера P-5 меньше сегмента Куна и имеет форму палочки, а молекула полимера P-25 является слабоизогнутой палочкой. Формирование клубка происходит у полимеров P-45 и P-88. Как следует из полученных данных, изменение конформации цепи сопровождается изменением величины K. У полимера P-25 постоянная Керра больше, чем у олигомера P-5, в 1.5 раза, а у P-45 и P-88 – уже более чем в 2 раза.

Постоянная Керра в теории Ланжевена–Борна выражается через молекулярные параметры вещества следующим образом:

Здесь Δb и Δα – анизотропии оптической и электрической поляризуемостей, μ – дипольный момент, β – угол между дипольным моментом и продольной осью молекулы, k – постоянная Больцмана, T – температура, A – численный коэффициент. Мономерное звено полистирола состоит из неполярного фенильного цикла с большой электрической и оптической анизотропиями, а также групп –CH₂– и –CH– с дипольным моментом μ < 0.2D. Поэтому при 20°С постоянная K олигомера, равная 3.3 × 10^–12 (см/300В)², оказывается между значениями K = 2.1 × 10^–12 (см/300В)² бензола с нулевым дипольным моментом и K = = 3.9 × 10^–12 (см/300В)² толуола с μ = 0.37D, рис. 2. Таким образом, электрооптический эффект полистирола определяется наличием как анизотропных циклов, так и слабополярных групп.

Фенильные циклы обладают способностью взаимного упорядочения благодаря ароматическому π–π-взаимодействию между ними [18]. Существуют несколько основных конфигураций, в которых могут находиться кольца в условиях плотной упаковки [18, 19]. Расположение колец в T-конфигурации (рис. 3a), которая энергетически наиболее выгодна, ведет к минимизации локальной оптической и электрической анизотропии. Поэтому в случае T-конфигурации постоянная Керра будет минимальна. В двух других вариантах, изображенных на рис. 3б и 3в, создается большая локальная анизотропия, что существенно увеличивает постоянную K расплава.

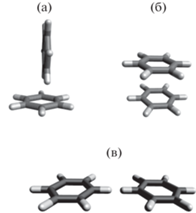
Рис. 3.

Возможные конфигурации взаимного расположения молекул в жидком бензоле: a – Т-конфигурация; б – “сэндвич”-конфигурация; в – планарная конфигурация.

Для того чтобы определить, каким конфигурациям в большей мере соответствуют полученные экспериментальные данные, было выполнено моделирование жидкого бензола как аналога фенильных циклов полистирола. Использовался метод молекулярной динамики в программе AKMD [20]. При этом ограничивались температурой 20°С, при которой экспериментальные значения K для бензола и полистирола могут быть сопоставлены. Из графика на рис. 2 видно, что добавление к молекуле бензола дипольного момента, соответствующего мономерному звену полистирола, должно приводить к хорошему соответствию величин K двух веществ. Следовательно, их близость дает основание полагать, что в этих условиях результат моделирования бензола можно переносить на ближний порядок для колец в одном из исследованных образцов – в олигомере P-5.

При моделировании использовалась полноатомная модель молекулы с параметрами атом-атомного взаимодействия OPLS-AA [20]. Моделирование выполнялось в ансамбле NpT с использованием термостата-баростата Нозе с периодическими граничными условиями и использованием метода Эвальда для вычисления электростатических взаимодействий. Для поддержания длины химических связей неизменной использовался алгоритм SHAKE, при этом шаг моделирования составлял 2 фс. В системе было 2700 молекул. Время уравновешивания систем составляло 4 нс, а время анализа траектории – 1 нс, что было достаточно для получения равновесных распределений молекул друг относительно друга. В результате расчетов было получено распределение центров масс молекул бензола как функция цилиндрического распределения [22] вокруг центральной молекулы, рис. 4.

Рис. 4.

Функция цилиндрического распределения центров масс молекул бензола. Ось цилиндрической системы координат направлена вверх и совпадает с осью симметрии молекулы C₆. Центр масс (начало координат) отмечено крестом. В центре распределения показано положение атомов углерода и водорода центральной молекулы. На шкале плотности вероятности и масштаба изображения серый цвет соответствует средней плотности молекул бензола, белый показывает исключенный объем молекулы.

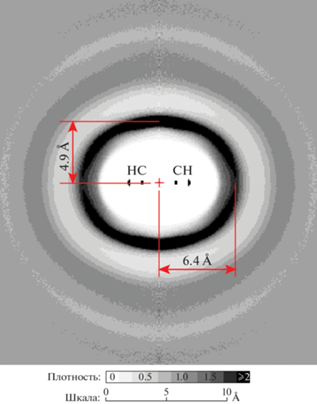
Оказалось, что расстояние до максимума плотности распределения центров масс окружающих молекул над плоскостью центральной молекулы составляет 4.9 Å, что близко к расстоянию 5.1  Å между центрами масс молекул в Т-конфигурации. Плотность вероятности планарной конфигурации молекул получилась заметно меньше. В “сэндвич”-конфигурации, для которой расстояние между центрами масс должно составлять 4.0 Å, находится еще мѐньшая доля молекул. Следовательно, большинство бензольных колец находится в Т-конфигурации, которая частично размывается тепловым движением молекул. Расчет, выполненный методом Монте-Карло [23], и эксперимент по рентгеновскому рассеянию [24] также показали присутствие всех конфигураций в жидком бензоле, однако среди них преобладала Т-конфигурация. В чистом виде конфигурация T‑типа реализуется в кристаллическом бензоле [25, 26], в условиях максимального координационного и ориентационного порядков.

Основываясь на полученных данных, связь между длиной цепи и поведением ЭДЛ расплава можно представить следующим образом. Постоянная Керра K для олигомера P-5 имеет наименьшее среднее значение среди измеренных образцов и при комнатной температуре близка к постоянной K бензола. В этих условиях величины ориентационного порядка для фенильных циклов в олигомере P-5 и для молекул бензола сопоставимы, а доля фенильных колец, находящихся в T-конфигурации у обоих веществ, достаточна для того, чтобы сохранить величины Δb и Δα на низком уровне. Формирование клубка у полимера P-25 ведет к тому, что полимерная цепь начинает ограничивать свободу ориентации колец из-за стерических взаимодействий. В результате распределение колец по возможным конфигурациям изменяется, и доля колец, находящихся в Т-конфигурации, уменьшается за счет тех колец, которые приобрели “сэндвич” и планарную конфигурации. Поэтому локальная анизотропия у полимера P-25 возрастает, и средняя величина K становится в 1.5 раза больше, чем у олигомера. При этом у образцов P-5 и P-25 температурная зависимость сохраняет классический вид K ∝ (1/T). А вот у образцов P-45 и P-88, у которых сформировалась конформация клубка, при T >120°С наблюдается смена температурной зависимости на противоположную, а именно, на зависимость K ∝ T. Это может быть результатом “плавления” полимерной цепи при переходе изотропная фаза–изотропная фаза [13]. В результате с повышением температуры возрастает свобода поворотов мономерных звеньев вокруг соединяющих их простых (одиночных) связей основной цепи. Микроброуновское тепловое движение мономерных звеньев усиливается и усредняет вероятности различных конфигураций для фенильных циклов. Вследствие этого вклад преобладающей T-конфигурации непрерывно уменьшается с ростом температуры, тогда как вклад “сэндвич” и планарной конфигураций растет. Это приводит к росту локальной оптической и электрической анизотропий и, соответственно, возникновению аномальной (инверсной) температурной зависимости постоянной Керра K.

ЗАКЛЮЧЕНИЕ

Наблюдавшееся в работе наноструктурирование полистирола, которое проявлялось в резком нарастании локальной анизотропии при высокой температуре, обусловлено сочетанием нескольких факторов. Наиболее важные из них: ароматическое π–π-взаимодействие между фенильными кольцами, сильное влияние полимерной цепи на ориентацию колец и происходящий при повышенных температурах переход изотропная фаза–изотропная фаза, в результате которого нарастает микроброуновское движение звеньев полимерной цепи.

Авторы выражают благодарность профессору Н.В. Цветкову за ценные рекомендации, данные им при обсуждении данной работы.