Российские нанотехнологии, 2023, T. 18, № 6, стр. 817-822

ВВЕДЕНИЕ

В последнее десятилетие произошел значительный прогресс в области машинного обучения для решения так называемых когнитивных задач [1, 2]. Отмечены значительные достижения, включая коммерческие решения, в сфере сенсорного интеллекта, направленного на распознавание текстов, речи, естественного языка [3]. Тем не менее большинство недавних разработок основаны на программных искусственных нейронных сетях, испытывающих трудности из-за сложности алгоритмов и высокого энергопотребления. Это связано с тем, что традиционная бинарная компьютерная архитектура фон Неймана сильно отличается от принципов работы мозга. Создание аппаратных нейроморфных вычислительных систем (НВС) может помочь решить эти и другие проблемы.

Одним из стимулов их развития стало появление мемристоров (резисторов с памятью) [4], которые могут эффективно моделировать синаптические связи в НВС [5]. Ключевым фактором в выборе мемристоров для использования в качестве весов НВС является их пластичность – способность устанавливать и удерживать различные уровни проводимости [6].

В настоящее время на аппаратном уровне реализовано множество мемристивных НВС, таких как сети с долгосрочной и краткосрочной памятью [7, 8], импульсные [9–14] и более сложные системы [15–17]. При этом демонстрируются высокий уровень разработки алгоритмов и возможность их применения на мемристивных устройствах в задачах обучения с учителем и без учителя. В то же время НВС с алгоритмами оперантного обучения и контроля, которые обеспечивают реакцию искусственного интеллектуального агента на основе оценки состояния среды, недостаточно разработаны. Такое обучение с подкреплением [18] основано на взаимодействии между агентом и его окружением с целью получения агентом максимальной награды.

Формальные нейронные сети с подкреплением, которые показали значительный успех в решении задач в игровых средах (например, в играх Atari [19]), обладают разнообразным набором реакций и были реализованы на мемристорах [20]. В то же время основные проблемы формальных сетей с подкреплением связаны с высокой сложностью обучения агентов с большим количеством степеней свободы, переобучением и неуниверсальностью обучения. Последнее означает, что система, обученная в одной среде, не сможет корректно работать в другой [21], в том числе из-за так называемой проблемы катастрофического забывания [22].

Таким образом, необходима разработка новых методик аппаратного обучения с подкреплением. Мемристивные НВС на базе импульсных, или спайковых, нейронных сетей представляются в этом плане наиболее перспективными, так как они приспособлены к решению задач в системах с биоподобной архитектурой, произвольной топологией связей и в режиме реального времени. Есть надежда, что функциональный переход к биоподобным архитектурам сетей сможет частично снизить значимость указанных выше проблем обучения с подкреплением. Кроме того, биоинспирированные архитектуры НВС характеризуются повышенной производительностью и меньшим энергопотреблением [1].

В этой связи ведется поиск альтернативных методов разработки и обучения НВС с подкреплением, которые, с одной стороны, обладают богатой вариативностью и адаптивностью, а с другой стороны, способны к универсальному ценностно-ориентированному обучению. Перспективным подходом является изучение биоподобных систем с подкреплением, опосредованным аналогом дофамина – основным медиатором вознаграждения в нервной системе животных [23]. Выработка дофамина в мозге связана с ощущением субъективного удовольствия, его отсутствие – с наказанием [24]. Дофамин помогает формировать наборы значений “стимул–реакция”, определяющие поведение животного. Отметим, что сравнительно недавно был подробно раскрыт механизм влияния дофамина на синаптическую пластичность, зависящую от времени прихода импульсов, или STDP (spike-timing-dependent plasticity) [25], что открывает возможность моделирования этого правила обучения с подкреплением как программно, так и аппаратно.

Таким образом, мемристоры, изменяющие свою проводимость по правилам STDP, являются перспективными для аппаратной реализации обучения с подкреплением. Например, в [26] показано, что простая пара нейронов, соединенных через мемристор на основе парилена, успешно может изменять мемристивный вес в соответствии с такими правилами дофамин-модулированного STDP. Перспективные результаты были получены и для неорганических мемристоров на основе нанокомпозитов (НК) (Co–Fe–B)_x(LiNbO₃)_100–x [27]. Согласно [27–29], мемристоры на основе НК обладают характеристиками, необходимыми для их использования в качестве синапсов аппаратных НВС. В данной работе расширим предыдущие исследования и продемонстрируем возможность реализации дофамин-модулированного мемристивного STDP на массивах НК-мемристоров с низкой вариабельностью окна STDP как от цикла к циклу (C2C), так и от устройства к устройству (D2D). Кроме того, полученные здесь результаты несут важный методический характер: показано, что более высокий D2D-разброс характеристик по сравнению с разбросом C2C требует повышенного внимания при проектировании НВС на основе данных устройств. Результаты могут помочь в реализации аппаратных нейронных сетей на базе НК-мемристоров, способных к обучению с подкреплением.

ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ

Изучены мемристоры на основе нанокомпозита (Co–Fe–B)_x(LiNbO₃)_100–x вида металл/НК/металл (М/НК/М) [28]. В качестве верхнего электрода выступала медь, в качестве нижнего – Cr/Cu/Cr. Массивы мемристивных структур M/НК/M в конденсаторной геометрии синтезировали методом ионно-лучевого распыления на оригинальной установке, позволяющей напылять слои различного состава в едином цикле. Толщина слоя НК составила ~1 мкм, верхние электроды наносили через теневую маску с размером отверстий 0.2 × 0.5 мм².

Электрофизические измерения проводили с помощью четырехканального источника-измерителя PXIe-4140 (National Instruments). Вольт-амперные характеристики (ВАХ) измеряли со скоростью развертки по напряжению 2 В/с, длительность каждого импульса напряжения – 50 мс, шаг дискретизации – 0.1 В. Напряжение U_set определяли как напряжение, при котором впервые достигается ограничение по току в положительной области, напряжение U_reset – как напряжение, на котором происходит перегиб графика ВАХ. Изучение возможности изменения резистивного состояния мемристоров по правилам STDP проводили путем подачи программно сложенных пре- и постсинаптических импульсов, умноженных на коэффициенты K_pre и K_post соответственно, для осуществления дофаминоподобной модуляции окна STDP [27].

РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЯ И ИХ ОБСУЖДЕНИЕ

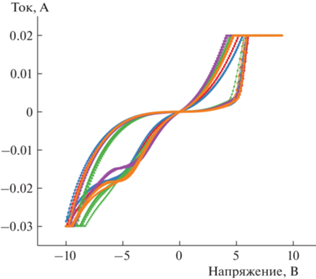
На рис. 1 представлены типичные ВАХ М/НК/М для пяти мемристоров, полученные для пяти циклов резистивного переключения (РП). Структуры демонстрируют эффект РП с отношением сопротивлений R_off/R_on ~ 10. Кривые ВАХ практически не различаются от цикла к циклу и имеют малые вариации от устройства к устройству. Среднее значение напряжения U_set для пяти мемристоров составило U_set = 5.9 ± 0.1 В (коэффициент D2D вариации 1.7%), U_reset = –5.8 ± 0.5 В (коэффициент D2D вариации 9%). Можно оценить разброс тех же параметров и для C2C. Для этого рассчитывали стандартные отклонения напряжений U_set и U_reset по пяти циклам РП для каждого мемристора по отдельности. Средние значения полученных отклонений составили 0.08 В для U_set и 0.21 В для U_reset. Таким образом, разброс D2D напряжений РП существенно превышает разброс C2C. Это обстоятельство свидетельствует о том, что для оценки работоспособности массивов таких мемристоров необходимо исследовать большое количество мемристоров массива и основной вклад в разброс их характеристик вносят отклонения D2D, а не C2C. В связи с этим интересно было выяснить, выполняются ли аналогичные соотношения для других мемристивных характеристик. Для этого оценивали возможность изменения проводимости мемристоров по локальным биоподобным правилам STDP – важное свойство для их применения в импульсных НВС.

Рис. 1.

Типичные ВАХ мемристивных структур М/НК/М. Для каждого из пяти мемристоров ВАХ получены для пяти циклов РП.

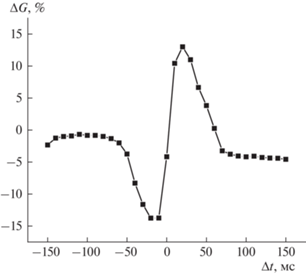
Для изучения возможности изменения проводимости НК-мемристоров по правилам STDP на один из электродов мемристора подавали пресинаптический, а на другой – постсинаптический спайк (импульс), которые генерировались программными нейронами. При этом интервал Δt между спайками варьировался. Параметры спайков были выбраны так, чтобы по отдельности они не изменяли сопротивление мемристора: их амплитуды в положительной и отрицательной части составляли +3 и –4 В соответственно, а длительность – 100 мс. Было измерено так называемое окно STDP (рис. 2): зависимость от Δt относительного изменения проводимости ΔG из промежуточного состояния (0.5 мСм) после подачи пары спайковых импульсов. Проводимость в 0.5 мСм была выбрана в качестве начальной, поскольку она находится примерно посередине окна проводимостей исследуемых мемристоров, что позволяет ожидать достаточно симметричные (по амплитуде ΔG в положительной и отрицательной части) окна STDP. Из полученной зависимости видно, что мемристивные веса структур могут изменяться согласно правилам STDP, а следовательно, изучаемые мемристоры могут быть использованы в реализации НВС, способных, в том числе, к обучению с дофаминоподобным подкреплением.

Рис. 2.

Типичный вид окна STDP мемристоров М/НК/М. Начальное состояние G₀ = 0.5 мСм.

Для изучения особенностей изменения проводимости мемристоров по правилам дофамин-модулированного STDP амплитуды пре- и постсинаптических спайков (генерируемых программными нейронами) умножали на коэффициенты K, равные 1 или –1. В [27, 30] было показано, что четыре возможные комбинации K_pre и K_post соответствуют четырем типам окна STDP: (1, 1) – классическое STDP по Хеббу, (–1, –1) – “anti-STDP”, (–1, 1) – колоколообразное STDP (“bell”), (1, –1) – анти-колоколообразное STDP (“anti-bell”).

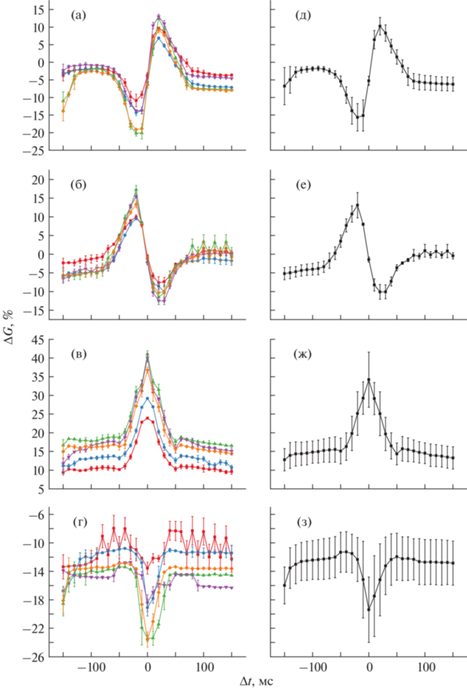
На рис. 3 приведены кривые окна дофамин-модулированного STDP образцов М/НК/М для четырех возможных случаев, сверху вниз: “STDP”, “anti-STDP”, “bell” и “anti-bell”. В левом столбце (рис. 3а–3г) показаны соответствующие кривые для пяти мемристоров по отдельности. Каждая точка кривой показывает изменение проводимости мемристора из начального состояния G₀ = 0.5 мСм при подаче пары импульсов с заданной задержкой. При этом каждый такой эксперимент для отдельного устройства проводили 5 раз, а из полученных значений ΔG затем выбирали медианное для каждого Δt. Планки погрешностей отражают разброс C2C. В правом столбце (рис. 3 д–3з) построены кривые для оценки разброса от устройства к устройству. Каждая точка кривых представляет собой среднее значение по экспериментам на пяти различных мемристорах (по тем же экспериментальным результатам, что показаны в левом столбце), т.е. планки погрешностей демонстрируют вариации от устройства к устройству (D2D). Видно, что мемристоры М/НК/М способны изменять свою проводимость по правилам дофамин-модулированного STDP: форма окна STDP изменяется от обычной Хеббовской (K_pre = K_post = 1, рис. 3а, 3д) к “anti-STDP” (рис. 3б, 3е) при инвертировании обоих коэффициентов (K_pre = K_post = –1). Инвертирование только одного коэффициента приводит к колоколообразной форме окна типа “bell” (K_pre = –1, K_post = 1, рис. 3в, 3ж) или типа “anti-bell” (K_pre = 1, K_post = –1, рис. 3г, 3з).

Рис. 3.

Изменение проводимости мемристоров М/НК/М по правилам дофамин-модулированного STDP, значения для пяти устройств по отдельности: а – STDP по Хеббу (K_pre = 1, K_post = 1), б – anti-STDP (K_pre = –1, K_post = –1), в ‒ колоколообразное STDP, “bell” (K_pre = –1, K_post = 1), г – анти-колоколообразное STDP, “anti-bell” (K_pre = 1, K_post = –1). Cредние значения для пяти устройств (вариация от устройства к устройству, D2D): д – STDP, е – anti-STDP, ж – “bell”, з – “anti-bell”. Исходное состояние G₀ = 0.5 мСм.

Данные вариации окна STDP могут моделировать биологическое STDP в различных участках головного мозга млекопитающих. Например, в гиппокампе присутствие дофамина в синаптической щели в процессе STDP изменяет форму окна STDP от классической хеббовской в форму типа “bell” [31]. Тем самым обучение переходит из режима пластичности по Хеббу в режим долговременного ассоциативного запоминания значимых стимулов (уровень значимости кодируется концентрацией дофамина). Похожие процессы моделирования синаптической пластичности под действием дофамина имеют место в других структурах головного мозга, таких как базальные ганглии, вентральная область покрышки, некоторые структуры лимбического и среднего мозга и др. [24].

Согласно исследованиям [24] изменение K_post от –1 до 1 при K_pre = 1 можно рассматривать как увеличение концентрации дофамина в синаптической щели с рецепторами D1-типа на мембране постсинаптического нейрона. В свою очередь, изменение K_pre от –1 до 1 при K_post = 1 является аналогом увеличения концентрации дофамина с рецепторами D2-типа. Это позволяет рассматривать данные коэффициенты как индикаторы концентрации дофамина в нервной системе. Дофамин кодирует актуальные потребности и обеспечивает как постановку цели, так и принятие решения, т.е. активацию специфической связи “состояние—действие” [24]. D2-рецептор обычно действует как антагонист в этом процессе, что приводит к тонкому балансу возбуждающих и тормозных стимулов, опосредованных дофамином. Кроме того, дофамин опосредует эффективное оперантное обусловливание [32], что приводит к запоминанию и воспроизведению наиболее успешных моделей поведения.

Описанная выше аналогия, а также различные формы полученных STDP-окон могут быть использованы в будущем для задания связей между различными типами нейронов (например, возбуждающими или тормозными), а также для моделирования различных импульсных НВС, способных к обучению с подкреплением. Отметим, что такая модуляция потенциально может быть реализована аппаратно с помощью специальных аппаратных нейронов с поддержкой независимой регулировки амплитуды и длительности спайков непосредственно во время работы сети [14]. Таким образом, мемристоры, способные изменять свою проводимость посредством правил дофамин-модулированного STDP, могут моделировать синаптическую пластичность при различных концентрациях дофамина – основного нейромедиатора “награды”, напрямую участвующего в процессах обучения с подкреплением и являющегося основным медиатором формирования системы ценностей интеллектуального агента.

В то же время при проектировании систем с таким обучением необходимо иметь в виду, что разброс изменений проводимости ΔG от устройства к устройству существенно превышает разброс от цикла к циклу. Так, средние D2D-разбросы для каждого из четырех видов дофамин-модулированного STDP составляют: 2.1, 1.4, 3.6 и 3.3% для STDP-, anti-STDP-, bell- и anti-bell-окон соответственно. Аналогичные значения для С2С-отклонений равны 0.6, 0.8, 0.6 и 0.6%. Результаты (рис. 3) показывают, что при использовании локальных правил STDP изменения проводимости мемристоров разброс ΔG для разных устройств при подаче спайков с одинаковой задержкой оказывается больше разброса ΔG от цикла к циклу (для одного мемристора). Аналогичное верно при использовании обучения по правилам дофаминоподбной модуляции пластичности: anti-STDP, bell и anti-bell.

ЗАКЛЮЧЕНИЕ

Продемонстрированы основные синаптические свойства устройств массива мемристоров М/НК/М на основе нанокомпозита (Co–Fe–B)_x(LiNbO₃)_100–x, показана возможность изменения их проводимости по биоподобным правилам STDP, в том числе с использованием дофаминоподобной модуляции спайков. Показано, что такое изменение проводимости возможно для всех исследованных мемристоров массива. Оценены разбросы характеристик: U_set, U_reset и изменения проводимости ΔG при измерении окна STDP для всего массива (разброс D2D) и для каждого устройства по отдельности (разброс C2C). Показано, что первый существенно превышает последний для всех изученных характеристик. Полученные результаты могут быть полезны при построении НВС на основе массивов мемристоров.

Исследование выполнено при поддержке Российского научного фонда (грант № 20-79-10185). Измерения выполнены на оборудовании ресурсных центров НИЦ “Курчатовский институт”.