Неорганические материалы, 2019, T. 55, № 3, стр. 231-235

ВВЕДЕНИЕ

Научная значимость и перспективность масштабного практического использования полупроводниковых твердых растворов ставят технологические задачи по выращиванию их объемных монокристаллов в разряд приоритетных. Это обстоятельство мотивирует исследования, направленные на совершенствование и модификацию существующих методов, а также на создание новых методов выращивания и легирования монокристаллов твердых растворов [1–10].

В настоящей работе представлены концепция и теоретическая основа выращивания монокристаллов полупроводниковых твердых растворов новым модифицированным методом зонной плавки с использованием затравок составных компонентов, а также результаты математического моделирования концентрационного распределения компонентов в кристаллах системы InAs–GaAs, выращенных этим методом при различных технологических параметрах.

Цель работы – создание модели модифицированного метода зонной плавки твердых растворов с использованием затравок составных компонентов для выращивания монокристаллов с заданными однородным и градиентным составами.

КОНЦЕПЦИЯ И ТЕОРЕТИЧЕСКИЙ АНАЛИЗ

Для примера рассмотрим известную систему твердых растворов InAs–GaAs. Составные компоненты этой системы растворяются друг в друге при любых соотношениях. На рис. 1 представлены концептуальные схемы выращивания кристаллов InAs–GaAs c использованием затравок из InAs (А) и GaAs (В). В обоих случаях в тигель цилиндрической формы закладываются предварительно изготовленные стержни с соответствующими составами и размерами. В случае с монокристаллической затравкой из менее тугоплавкого компонента InAs (рис. 1А, а) в тигле над затравкой последовательно размещаются стержень из поликристаллического InAs и предварительно изготовленный макрооднородный подпитывающий стержень из (1–х)InAs ⋅ хGaAs с заданным х. В условиях вакуума проводится расплавление стержня из InAs, расположенного непосредственно над затравкой (рис. 1А, б). Рост кристалла идет на затравке с момента включения механизма перемещения нагревателя относительно тигля и продолжается до полной перекристаллизации подпитывающего стержня (1 – х)InAs ⋅ хGaAs. Длина зоны расплава Z, до момента образования конечной расплавленной зоны (рис. 1А, в), поддерживается постоянной. Заметим, что в отличие от традиционного метода зонной плавки здесь стартовый материал расплавленной зоны идентичен с таковым затравки. Это обстоятельство решает проблему затравки, необходимой для получения монокристаллов InAs–GaAs с различным составом путем использования затравки из InAs.

Рис. 1.

Схемы выращивания кристаллов InAs–GaAs модифицированным методом зонной плавки c использованием затравок из InAs (А) и GaAs (В): а – порядок загрузки тигля стержнями исходных материалов, б – предстартовый момент кристаллизации первичной расплавленной зоны длиной Z, в – момент образования финальной расплавленной зоны длиной Z; 1, 1* – затравки из InAs и GaAs соответственно; 2, 2* – InAs- и GaAs-стержни cоответственно; 3, 3* – стержни (1–х)InAs ⋅ хGaAs; 4, 4* – стартовые расплавленные зоны из InAs и (1–х*)InAs ⋅ х*GaAs соответственно; 5, 5* – растущие монокристаллы InAs–GaAs; 6, 6* – финальные расплавленные зоны длиной Z.

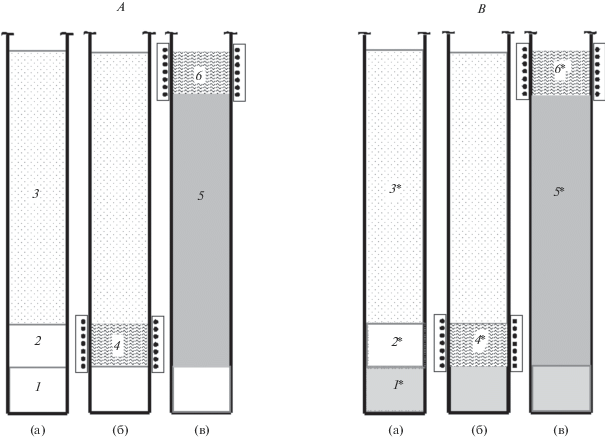
Для выращивания монокристаллов InAs–GaAs с использованием затравки из более тугоплавкого компонента GaAs (рис. 1В, а) в тигель над затравкой закладываются макрооднородные стержни с составами (1–х*)InAs ⋅ х*GaAs и (1 – х)InAs ⋅ · хGaAs. Стержень, размещенный непосредственно над затравкой, служит для создания начальной расплавленной зоны длиной Z (рис. 1В, б). Его состав х* определяем из диаграммы равновесного фазового состояния системы InAs–GaAs, который равен составу расплава, находящегося в фазовом равновесии с верхним подпитывающим стержнем с заданным х. В стартовый момент кристаллизации расплава температура на границах расплава с затравкой и верхним стержнем равна температуре ликвидуса твердого раствора (1 – х*)InAs ⋅ х*GaAs. Как и в случае с использованием затравки из InAs, длина зоны расплава в процессе перекристаллизации верхнего стержня поддерживается неизменной вплоть до образования финальной расплавленной зоны (рис. 1В, в).

Отметим, что в работе [9] с использованием затравки из более тугоплавкого компонента были успешно выращены монокристаллы Ge–Si переменного состава из расплавов с различным содержанием Si.

Задачу аксиального распределения компонентов в кристаллах твердых растворов, выращенных модифицированным методом зонной плавки, решали в приближении полностью размешанного расплава [11].

Введем следующие обозначения: L – общая длина исходных стержней над затравкой; Z, $\ell $ – длины расплавленной зоны и перекристаллизированной части материала от затравки соответственно; $V_{m}^{0}$ и ${{V}_{m}}$ – объемы расплавленной зоны в начальный и текущий моменты; $C$ – общая концентрационная доля молекул второго компонента (GaAs) в расплаве; $C_{m}^{0}$ – концентрационная доля GaAs в расплавленной зоне в начальный момент; ${{C}_{c}},$ ${{C}_{i}},$ ${{C}_{m}}$ – концентрационные доли атомов GaAs в растущем кристалле, подпитывающем стержне (рис. 1) и в расплавленной зоне соответственно; ${{V}_{c}}$ – объем расплава кристаллизующийся в единицу времени; ${{V}_{i}}$ – объем подпитывающего стержня, расплавляющийся в единицу времени; $K = {{{{C}_{c}}} \mathord{\left/ {\vphantom {{{{C}_{c}}} {{{C}_{m}}}}} \right. \kern-0em} {{{C}_{m}}}}$ – равновесный коэффициент сегрегации GaAs.

В принятых обозначениях имеем:

По условию задачи считаем, что до момента образования финальной расплавленной зоны значения параметров Z и ${{V}_{i}}$ остаются неизменными; в процессе всего технологического цикла перекристаллизации материала ${{V}_{c}}$ не зависит от времени. В этом случае на участке длиной L–Z при использовании затравки из InAs (рис. 1А) справедливы следующие уравнения:

Учитывая уравнения (2), из (1) после ряда преобразований и интегрирования имеем:

Для случая с использованием затравки из GaAs (рис. 1В) до момента образования конечной расплавленной зоны

Здесь K* – коэффициент сегрегации GaAs, соответствующий исходному составу расплава с $C_{m}^{0} = x{\text{*}}.$ Согласно уравнению (4), до начала образования конечной расплавленной зоны имеет место рост полностью однородного кристалла InAs–GaAs с составом, аналогичным составу исходного подпитывающего слитка.

С момента образования конечной расплавленной зоны при использовании затравки как из первого, так и из второго компонентов системы InAs–GaAs имеем:

С учетом (5) из (1) после ряда преобразований и интегрирования получим

Здесь $C_{{mf}}^{0}$ – концентрационная доля InAs в расплаве в момент образования финальной расплавленной зоны длиной Z. Обозначив длину и долю закристаллизованной части расплава конечной зоны (${{{{V}_{c}}\tau } \mathord{\left/ {\vphantom {{{{V}_{c}}\tau } {V_{m}^{0}}}} \right. \kern-0em} {V_{m}^{0}}}$) в момент τ соответственно символами $l{\text{*}}$ и $\gamma ,$ запишем (6) в следующем виде:

Пары уравнений (3), (7) и (4), (7) определяют аксиальное концентрационное распределение компонентов в кристаллах InAs–GaAs, выращенных модифицированным методом зонной плавки с использованием затравок из первого и второго компонентов соответственно.

МОДЕЛИРОВАНИЕ КОНЦЕНТРАЦИОННОГО ПРОФИЛЯ КОМПОНЕНТОВ В ТВЕРДЫХ РАСТВОРАХ InAs–GaAs И УСЛОВИЯ РОСТА ИХ МОНОКРИСТАЛЛОВ

Расчет концентрационного распределения компонентов по длине кристаллов требует решения интегралов в уравнениях (3) и (7), в которые входит коэффициент сегрегации K, зависящий от ${{C}_{m}}.$ В рассматриваемой системе K изменяется с составом расплава сложным образом и в широких пределах: от ~20.4 при ${{C}_{m}} \to 1$ до ~1 при ${{C}_{m}} \to 0$ [12]. В этом случае интегралы в (3) и (7) вычисляются путем определения сопряженных значений K в соответствующих интервалах изменения ${{C}_{m}}$ по данным диаграммы равновесного фазового состояния системы.

На рис. 2 представлены характерные кривые концентрационного распределения GaAs по длине кристаллов InAs–GaAs, выращенных модифицированным методом зонной плавки с использованием затравок из InAs и GaAs. Расчеты проведены для пяти различных значений С_i исходного подпитывающего стержня InAs–GaAs при длине расплавленной зоны Z = 0.1L. Кривые, относящиеся к использованию затравки из InAs (рис. 2а), рассчитаны из уравнений (3) и (7) с учетом соотношения ${{C}_{c}} = {{C}_{m}}K.$ Как видно из рис. 2а, в начальной части всех кристаллов имеет место резкое возрастание аксиальной концентрации GaAs, затем, по мере дальнейшего роста кристалла, достигается насыщение, при котором ${{C}_{c}} \approx {{C}_{i}}.$ Протяженность начального участка с растущей концентрацией GaAs зависит от состава исходного подпитывающего слитка ${{C}_{i}},$ значения K и скорости его изменения с составом расплавленной зоны. Стоит обратить внимание на достаточно быстрый переход кривых 1–3 в область плато, свидетельствующий о росте однородных кристаллов InAs–GaAs на достаточно большой длине.

Рис. 2.

Расчетные кривые концентрационного распределения GaAs по длине кристаллов InAs–GaAs, выращенных с использованием затравок из InAs (а) и GaAs (б) при Z = 0.1L: кривые 1–5 отвечают значениям С_i = 0.1, 0.3, 0.5, 0.7 и 0.9 соответственно.

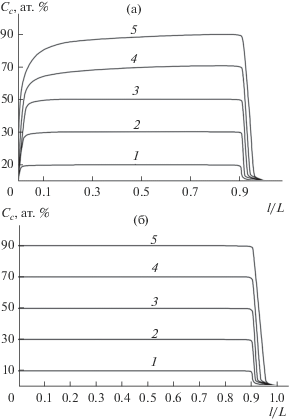
Кривые для случая с GaAs-затравкой (рис. 2б) рассчитаны из уравнений (4) и (7) для участков от затравки до конечной расплавленной зоны и после ее образования соответственно. Как видно, здесь для всех пяти значений С_i, с момента начала кристаллизации до образования финальной расплавленной зоны, идет рост полностью однородных кристаллов с концентрацией GaAs, равной соответствующему значению С_i.

Концентрационное распределение GaAs в конечной зоне при использовании затравок как из InAs, так и из GaAs для рассмотренных случаев идентично для соответствующих значений С_i подпитывающих стержней. На этом участке все кривые демонстрируют крутой спад концентрации GaAs по длине кристалла от ${{C}_{c}} \approx {{C}_{i}}$ до ${{C}_{c}} \approx 0.$

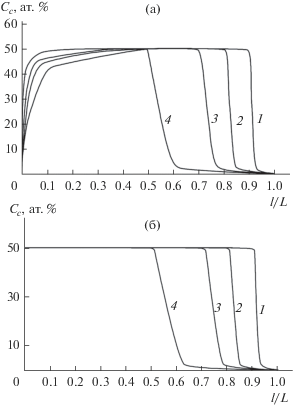
На рис. 3 представлены расчетные кривые концентрационного распределения молекул GaAs вдоль кристаллов InAs–GaAs, выращенных с использованием затравок из InAs (а) и GaAs (б) при четырех различных значениях длины расплавленной зоны Z. Для примера, в расчетах состав всех подпитывающих слитков принят С_i = 0.5. Как видно из рис. 3, операционный параметр Z существенно влияет на перераспределение компонентов при зонной перекристаллизации исходного стержня InAs–GaAs заданного состава. При этом длины как однородной, так и неоднородной по составу частей слитка определяются величиной Z расплавленной зоны.

Рис. 3.

Концентрационные профили GaAs в кристаллах InAs–GaAs, выращенных с использованием затравок из InAs (а) и GaAs (б) при С_i = 0.5: кривые 1–4 соответственно для Z = 0.1, 0.2, 0.3 и 0.5L.

Семейства кривых на рис. 2 и 3 наглядно демонстрируют потенциал модифицированного метода зонной плавки с использованием затравок составных компонентов для получения монокристаллов InAs–GaAs с требуемыми однородным и переменным составами во всем ряду непрерывных твердых растворов. При этом целенаправленное математическое моделирование концентрационных профилей компонентов в кристаллах дает возможность оценить оптимальные технологические параметры (Z, C_i, материал затравки InAs/GaAs) для получения твердых растворов с конкретными параметрами.

Задачи по определению условий и режимов кристаллизации расплава, обеспечивающих рост монокристаллов твердых растворов, решаются следующим образом. Известно, что специфической особенностью технологии твердых растворов является то, что их монокристалличность обеспечивается только при достаточно малых скоростях роста кристалла [1, 7]. Например, для концентрированных твердых растворов Ge–Si скорость роста монокристаллов более чем на два порядка ниже скорости роста их составных компонентов [7]. Связано это с явлением концентрационного переохлаждения расплава вблизи зоны основного фронта кристаллизации. Возникает оно в результате существенной сегрегации компонентов в процессе кристаллизации расплава и является причиной нарушения монокристалличности растущего твердого раствора. Критическая скорость ${{\nu }_{c}},$ выше значения которой происходит поликристаллизация растущего кристалла, может быть оценена с помощью следующей известной формулы Тиллера, заимствованной из [5]:

Здесь $\nabla \Theta $ – аксиальный градиент температуры в расплаве; $\nabla {{T}_{\ell }}$ – наклон кривой ликвидуса при соответствующем составе расплава, $D$ – коэффициент диффузии GaAs в расплаве, k – коэффициент сегрегации GaAs, x – доля GaAs в кристалле. Согласно (8), для любой заданной системы технологическим параметром, определяющим критическую скорость ${{\nu }_{c}}$, является аксиальный градиент температуры в расплаве $\nabla \Theta $ у фронта кристаллизации. Увеличивая этот параметр, удается преодолеть концентрационное переохлаждение при практически приемлемых скоростях роста монокристаллов, удовлетворяющих условию $\nu < {{\nu }_{c}}.$ Для обеспечения монокристалличности твердых растворов InAs–GaAs, выращенных рассмотренным методом, необходимо применение таких технологических режимов, при которых в процессе выращивания кристалла скорость его роста на участках как с переменным, так и с однородным составами (рис. 2 и 3) не будет превышать соответствующие значения ${{\nu }_{c}}$, оцениваемые по (8).

ЗАКЛЮЧЕНИЕ

Результаты анализа данных математического моделирования концентрационных профилей компонентов в кристаллах системы InAs–GaAs, выращенных новым модифицированным методом зонной плавки, определяют оптимальные условия для получения монокристаллов с заданными однородным и градиентным составами во всем ряду непрерывных твердых растворов InAs–GaAs и указывают на перспективность метода для выращивания монокристаллов полупроводниковых твердых растворов с заданными свойствами.