Неорганические материалы, 2019, T. 55, № 3, стр. 236-248
Магнитные свойства твердых растворов на основе FеCr2S4 в системе FeCr2S4–CdCr2S4
Т. Г. Аминов 1, *, Г. Г. Шабунина 1, Н. Н. Ефимов 1, Е. В. Бушева 1, В. М. Новоторцев 1
1 Институт общей и неорганической химии им. Н.С. Курнакова Российской академии наук
119991 Москва, Ленинский пр., 31, Россия
* E-mail: aminov@igic.ras.ru
Поступила в редакцию 16.05.2018
После доработки 15.10.2018
Принята к публикации 13.09.2018
Аннотация
Изучены магнитные свойства твердых растворов Cd1 – xFexCr2S4 в системе FeCr2S4–CdCr2S4 в области 0.6 ≤ x < 1. Измерения проводили в температурном интервале 5–300 K в постоянном (до 7960 А/м) и переменном (10, 100 и 1000 Гц) магнитных полях амплитудой 79.60 А/м. Во всех образцах обнаружены низкотемпературные магнитные аномалии как результат влияния орбитального упорядочения (ОУ) в базовом компоненте FeCr2S4 при ТОУ = 10 K.
ВВЕДЕНИЕ
В [1] изучены магнитные свойства твердых растворов на основе ферромагнетика CdCr2S4 в системе FeCr2S4–CdCr2S4. Настоящая работа посвящена изучению твердых растворов на основе ферримагнетика FeCr2S4в той же системе. Многочисленными исследованиями установлено, что FeCr2S4 обладает уникальными свойствами типа колоссального магнитосопротивления, гигантского вращения Керра, обнаруживает ряд аномалий или необычное магнитное поведение, которое может быть классифицировано как сложное орбитальное состояние [2–5].
Орбитальным степеням свободы в формировании физических свойств коррелированных электронных систем сейчас уделяется большое внимание. Сильная связь “орбиты” со спиновой, зарядовой и решеточной степенями свободы нередко приводит к новым интересным эффектам и явлениям. Шпинель FeCr2S4 – типичный пример такого соединения, которому свойственны вышеназванные взаимодействия [6–8].
С точки зрения целей настоящей работы наиболее актуальны сведения по низкотемпературным магнитным аномалиям в FeCr2S4. Согласно [4, 9], в интервале температур от точки Кюри (ТС = 170 K) до Т = 100 K действительная и мнимая части динамической восприимчивости в FeCr2S4 слабо зависят от частоты, но ниже Т = 90 K действительная часть динамической восприимчивости начинает резко уменьшаться и обнаруживает выраженную частотную зависимость. Мнимая часть динамической восприимчивости проявляет такие же свойства в интервале температур от 90 до 20 K. Точка перегиба на этой зависимости с увеличением частоты измерения сдвигается в сторону более высоких температур подобно тому, как это наблюдается в случае кластерных спиновых стекол. В пользу спиновых стекол свидетельствуют: пик при Т ≈ 75 K на температурной зависимости мнимой части динамической восприимчивости FeCr2S4, различный ход кривых статической магнитной восприимчивости χ(Т)ZFC и χ(Т)FC, явления магнитной необратимости [10–16].
В работах [6, 7, 15] с целью получения более полных сведений путем измерений структурных, магнитных и термодинамических свойств FeCr2S4 изучены явление орбитального упорядочения (ОУ) при температурах, близких к 10 K, магнитный переход при Т ≈ 60 K и некоторые другие. Низкотемпературный рентгеновский анализ с высоким разрешением показал для FeCr2S4 факт уширения всех брэгговских рефлексов. Начало этого уширения совпало со спин-ориентационным переходом при Т ≈ 60 K, а максимум уширения был близок к Т = 10 K, отвечающей орбитальному переходу. Данная структурная аномалия при температуре ОУ говорит о сжатии кристаллической решетки FeCr2S4 в соответствии с JT-антиферродисторсионным расположением FeS4-тетраэдров в основном состоянии [17, 18].
О переходе FeCr2S4 в ОУ-состояние свидетельствует также λ-аномалия на температурной зависимости удельной теплоемкости вблизи Т = 10 K. Важно, что при Т ≈ 60 K подобная аномалия не обнаружена, т.е. при этой температуре не существует перехода типа порядок–беспорядок. Однако возможно, что вблизи Т ≈ 60 K ОУ, начинающееся как ближний порядок, разрушает существующее при этой температуре спиновое упорядочение c дальним порядком, вызывая уменьшение намагниченности образца.
Внешнее поле напряженностью до 3.98 × 106 А/м не оказывает заметного влияния на λ-аномалию в FeCr2S4, что говорит об инертности ОУ по отношению к магнитному полю [19]. С другой стороны, ОУ оказалось весьма чувствительным к изменению давления, что свидетельствует о его связи с кристаллической решеткой, ее сжатием. Результатом этого сжатия может быть изменение магнитокристаллической симметрии, ответственной в FeCr2S4 за смещение доменных границ и ориентацию спинов.
Исследование FeCr2S4 с помощью метода спиновой релаксации положительных мюонов (μSR) поставило вопрос о существовании соединения при Т = 50 K в виде несоизмеримой модулированной неколлинеарной спиновой структуры, сходной с геликоидальной спиновой структурой. По [19], выше Т = 50 K спектры μSR совместимы с коллинеарным ферримагнетизмом, в котором имеется существенный спиновый беспорядок на протяжении нескольких постоянных решетки. Размеры этих областей с искаженной спиновой решеткой особенно возрастают при Т = 150 K, здесь магнитное состояние материала можно представить в виде быстро флуктуирующих ферронов – микрообластей ближнего порядка с упорядоченными спинами.
ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ
Для исследования были синтезированы твердые растворы Cd1 – xFexCr2S4 в области (0.6 ≤ x < 1) базового соединения – тиохромита железа FеCr2S4. Исходными веществами для получения твердых растворов Cd1 – xFexCr2S4 служили элементы: S (99.999%), Fe (99.9%), порошкообразный Cr (99.8%) производства Koch Light и CdS (“ос. ч.”). Синтез проводили методом твердофазных реакций в кварцевых ампулах, откачанных до 10–2 Па, при температуре 900°С в течение 7–10 дней. Рентгенофазовый анализ показал, что все образцы однофазны. Зависимость параметра решетки от состава a(x) подчинялась закону Вегарда. В соответствии с соотношением радиусов ${{r}_{{{\text{C}}{{{\text{d}}}^{{2 + }}}}}}$ > ${{r}_{{{\text{F}}{{{\text{e}}}^{{2 + }}}}}}$ значение a закономерно уменьшалось при увеличении в твердом растворе концентрации железа.
Магнитные измерения проводили на приборе Quantum Design PPMS-9 в температурном интервале 5–300 K в постоянном (3980 А/м) и/или переменном (10, 100, 1000 и 10 000 Гц) магнитных полях амплитудой 79.6 А/м. В первом случае – ZFC – охлаждение проводили до температуры жидкого гелия в отсутствие магнитного поля, а затем включали небольшое измерительное поле напряженностью не выше 7960 А/м и медленно поднимали температуру, регистрируя значения намагниченности. Во втором случае – FC – после охлаждения до температуры жидкого гелия измеряли динамическую восприимчивость образцов при различных частотах переменного магнитного поля напряженностью 79.6 А/м. Изотермы намагниченности измеряли вплоть до значений напряженности магнитного поля Н = 3.98 × 106 А/м.
РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ
На рис. 1а показаны температурные зависимости намагниченности σ(Т)ZFC и σ(Т)FC твердого раствора Cd0.4Fe0.6Cr2S4 (х = 0.6) в интервале от комнатной до гелиевой температуры в слабом магнитном поле Н = 3980 А/м, а на вставке к рис. 1а – температурные зависимости разности намагниченностей σ(Т)FC и σ(Т)ZFC, пропорциональные, как предполагается, константе магнитокристаллической анизотропии образца. Согласно рис. 1а, твердый раствор Cd0.4Fe0.6Cr2S4 характеризуется температурой перехода из парамагнитного в ферримагнитное состояние, равной ТС = 144 K, и температурой необратимости (ТН) кривых σ(Т)ZFC и σ(Т)FC, которая в данном случае практически совпадает с температурой Кюри образца. В отличие от ТС температура необратимости не является характеристическим параметром материала, и ее величина может зависеть от многих трудно прогнозируемых причин. Например, по [6], она зависит от степени стехиометричности материала, его дисперсности (моно- или поликристалл), наличия или отсутствия неконтролируемых примесей. Поскольку во всех образцах, исследованных в данной работе, значения ТС и ТН очень близки и практически совпадают друг с другом, можно предположить, что это явление имеет общие причины. Наиболее вероятными из них являются значение константы магнитокристаллической анизотропии K1 и пининг магнитных доменных стенок.
Рис. 1.
Температурные зависимости намагниченности σ(Т)ZFC и σ(Т)FC твердого раствора Cd0.4Fe0.6Cr2S4 (х = 0.6) в интервале от комнатной до гелиевой температуры в слабом магнитном поле Н = 3980 А/м; на вставке – температурные зависимости разности намагниченностей σ(Т)FC и σ(Т)ZFC (а) и полевые зависимости намагниченности этого же образца (б).
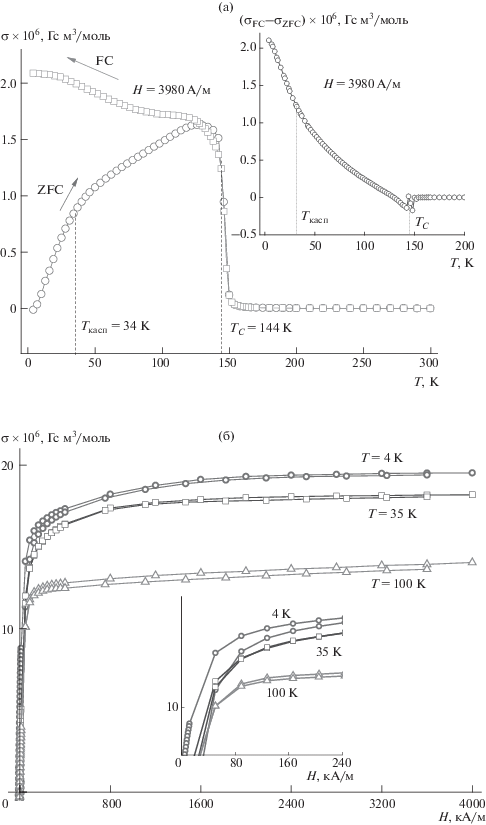
Первое предположение базируется на том, что для FeCr2S4 величина K1 является одной из самых больших среди шпинелей. Согласно [16], она в магнитно упорядоченном соединении имеет положительный знак и при Т = 4.2 K составляет K1 = = (3–6) × 106 эрг/см3 [20]. С этим фактом также связывают то, что кривые намагниченности FeCr2S4 насыщаются лишь в больших полях (Н ≈ ≈ 1.1 × 107 А/м) и при низких температурах (Т = = 4.2 и 20 K) [9, 18]. Необходимость сильных полей для насыщения намагниченности объясняют быстрым возрастанием при низких температурах магнитокристаллической анизотропии соединения [5].
Подтверждением сказанного могут служить кривые намагничивания для х = 0.6–1.0, показанные на рис. 1б, 2б, 3б и 4б. Здесь до резкого возрастания константы анизотропии со снижением температуры (при Т < 60 K) полевые зависимости намагниченности, например при Т = 100 K, идут почти параллельно оси абсцисс (т.е. близки к насыщению) по сравнению с аналогичными зависимостями при температуре жидкого гелия. При максимальных напряженностях магнитного поля Н = 1.1 × 107 А/м все кривые σ(Н) достигают технического насыщения.
На рис. 2а представлены температурные зависимости намагниченности σ(Т)ZFC и σ(Т)FC твердого раствора Cd0.3Fe0.7Cr2S4 (х = 0.7) в интервале от комнатной до гелиевой температуры в слабом магнитном поле Н = 3980 А/м, а на вставке к рис. 2а – температурные зависимости разности намагниченностей σ(Т)FC и σ(Т)ZFC. Как видно, рис. 1а и 2а внешне похожи друг на друга, хотя в последнем случае температура перехода образца из парамагнитного в ферримагнитное состояние увеличилась от ТС = 144 до ТС = 155 K, что говорит об укрупнении в образце ферромагнитных кластеров. Сходство кривых на рис. 1а и 2а проистекает в первую очередь из близкого хода кривых σ(Т) в низкотемпературной области, где обычно по каспу на ZFC-зависимости считывается температура спин-стекольного перехода. Однако в данном случае этот подход нельзя считать правильным, так как гладкий ход кривых σ(Т) со снижением температуры, скорее всего, обусловлен пинингом доменных стенок немагнитными ионами кадмия.
Рис. 2.
Температурные зависимости намагниченности σ(Т)ZFC и σ(Т)FC твердого раствора Cd0.3Fe0.7Cr2S4 (х = 0.7) в интервале от комнатной до гелиевой температуры в слабом магнитном поле Н = 3980 А/м; на вставке – температурные зависимости разности намагниченностей σ(Т)FC и σ(Т)ZFC (а) и полевые зависимости намагниченности этого же образца (б).
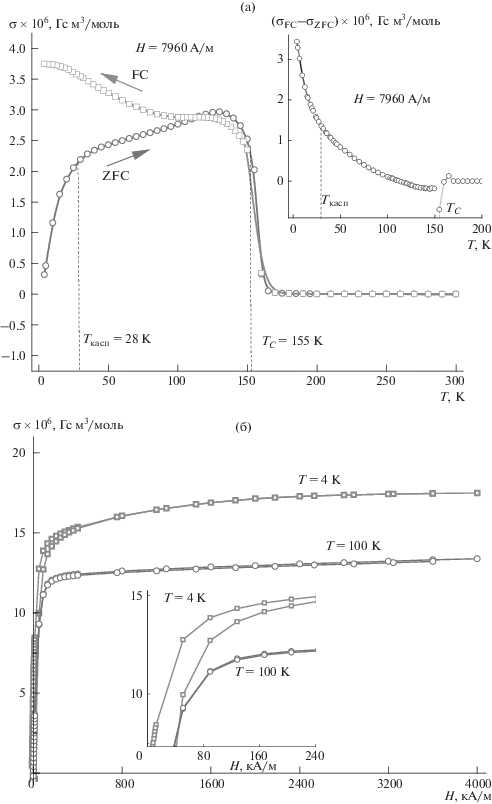
Наряду с магнитной анизотропией коэрцитивная сила материала преимущественно определяется пинингом магнитных доменных стенок. Хотя в случае FeCr2S4 доминирует магнитокристаллическая анизотропия, введение в шпинель немагнитных ионов кадмия может создавать для доменных стенок новые пининговые центры, которые уширяют магнитный переход, вызванный низкотемпературным скачком константы K1.
На рис. 3а приведены температурные зависимости намагниченности σ(Т)ZFC и σ(Т)FC твердого раствора Cd0.2Fe0.8Cr2S4 (х = 0.8) в интервале от комнатной до гелиевой температуры в слабом магнитном поле Н = 3980 А/м, а на вставке – температурные зависимости разности намагниченностей σ(Т)FC и σ(Т)ZFC. Переход в этом образце из парамагнитного в ферримагнитное состояние происходит при ТС = 162 K. Рис. 3а отличается от предыдущих тем, что в данном случае при Т = 32 K на кривой σ(Т)ZFC наблюдается касп, возникновение которого, согласно вставке к рис. 3а, тесно корреллирует с резким ростом температурной зависимости разности намагниченностей σ(Т)FC и σ(Т)ZFC, пропорциональной, как предполагается, константе магнитокристаллической анизотропии образца.
Рис. 3.
Температурные зависимости намагниченности σ(Т)ZFC и σ(Т)FC твердого раствора Cd0.2Fe0.8Cr2S4 (х = 0.8) в интервале от комнатной до гелиевой температуры в слабом магнитном поле Н = 3980 А/м; на вставке – температурные зависимости разности намагниченностей σ(Т)FC и σ(Т)ZFC (а) и полевые зависимости намагниченности этого же образца (б).
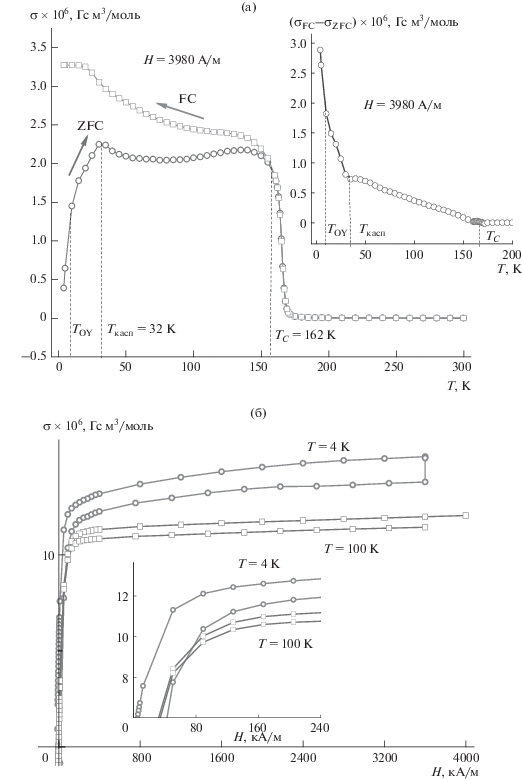
Происхождение каспа на рис. 3а можно объяснить следующим образом. При охлаждении образца в нулевом магнитном поле его домены ориентируются произвольным образом в соответствии с направлениями осей легкого намагничивания зерен, образующих поликристалл. Если к такому образцу, охлажденному от комнатной до гелиевой температуры, приложить слабое магнитное поле, то его результирующая намагниченность будет очень малой из-за сильно возросшей коэрцитивной силы и связанной с этим малой подвижностью доменных стенок. С другой стороны, при нагреве образца, сопровождающемся резким уменьшением коэрцитивной силы, движение доменов в данной температурной области значительно ускорится. Измеряемая намагниченность будет быстро расти, обнаруживая касп при Т = 32 K.
Отсутствие каспа на рис. 1а и 2а обусловлено тем, что здесь, наряду с магнитной анизотропией, коэрцитивная сила материала определяется пинингом магнитных доменных стенок: введение в FeCr2S4 немагнитных ионов кадмия создает во всей области температур дополнительные пининговые центры, которые уширяют магнитный переход, обусловленный резким низкотемпературным ростом магнитокристаллической анизотропии.
На рис. 4а показаны температурные зависимости намагниченности σ(Т)ZFC и σ(Т)FC твердого раствора Cd0.1Fe0.9Cr2S4 (х = 0.9) в интервале от комнатной до гелиевой температуры в слабом магнитном поле Н = 3980 А/м, а на вставке – температурные зависимости разности намагниченностей σ(Т)FC и σ(Т)ZFC. Как и на всех предыдущих рисунках, здесь в первую очередь обращает на себя внимание необратимый ход намагниченностей σ(Т)ZFC и σ(Т)FC начиная от температуры ферримагнитного перехода ТС. По [3], вышеуказанное полное расхождение зависимостей σ(Т)ZFC и σ(Т)FC считается характерным для поликристаллических образцов, а в случае монокристаллов расхождение, аналогично спиновым стеклам, начинается в конце демагнетизационного плато.
Рис. 4.
Температурные зависимости намагниченности σ(Т)ZFC и σ(Т)FC твердого раствора Cd0.1Fe0.9Cr2S4 (х = 0.9) в интервале от комнатной до гелиевой температуры в слабом магнитном поле Н = 3980 А/м; на вставке – температурные зависимости разности намагниченностей σ(Т)FC и σ(Т)ZFC (а) и полевые зависимости намагниченности этого же образца (б).
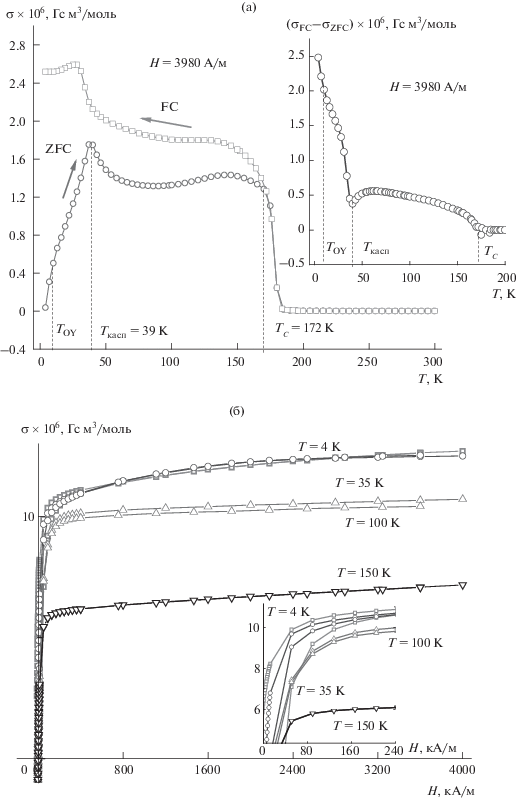
Согласно [21], для магнитных наночастиц зависимости σ(Т)ZFC и σ(Т)FC, совпадая при повышенных температурах, расщепляются ниже температуры необратимости ТН. При этом кривая σ(Т)ZFC часто характеризуется максимумом типа каспа, а кривая σ(Т)FC монотонно возрастает вплоть до самых низких температур. Отметим, что подобные различия между кривыми σ(Т)ZFC и σ(Т)FC наблюдаются также в макроскопических магнетиках с элементами неупорядоченности (фрустрацией обменных связей, топологическим беспорядком, дефектами структуры) и даже в упорядоченных магнетиках со значительной магнитной анизотропией [20].
Как видно из рис. 4а, с уменьшением температуры ниже точки Кюри в образце Cd0.1Fe0.9Cr2S4 сразу наблюдается необратимое поведение кривых намагниченностей ZFC и FC, затем при Т ≈ 39 K возникает аномалия в виде каспа, вызванная резким ростом магнитной анизотропии и связанной с этим спиновой переориентацией доменов. При дальнейшем снижении температуры образца обнаруживается еще одна аномалия. А именно, при Т ≈10 K происходит ступенчатый переход – спад (ZFC) или подъем (FC) намагниченностей, связанный с началом ОУ при температуре ТОУ.
Последняя магнитная аномалия FeCr2S4 первоначально была установлена при низкотемпературных измерениях удельной теплоемкости и эффекта Мессбауэра [7, 16, 22]. В согласии со ступенчатым ходом намагниченности в нулевом поле удельная теплоемкость при Т = 10 K показывает четкую аномалию λ-типа, которую считают признаком перехода к ОУ. Магнитное поле силой до 3.98 × 106 А/м практически не влияет на наблюдаемую λ-аномалию. Будучи инертным в отношении магнитного поля, ОУ чувствительно к изменениям внешнего давления, возрастая вместе с ним. Это означает, что ОУ больше связано со структурой кристалла, так как решетка под давлением претерпевает сжатие, а микроструктура зависит от давления [14].
Согласно рентгеновским исследованиям на синхротроне, при Т = ТОУ брэгговские рефлексы максимально уширены из-за структурной аномалии, связанной с переходом к орбитальному порядку. Понижение геометрической симметрии влечет за собой изменение магнитокристаллической симметрии. Последняя влияет на движение доменных стенок и ориентацию спинов, т.е. намагниченность [7].
На рис. 5–8 представлены температурные зависимости действительной (χ') и мнимой (χ'') частей динамической магнитной восприимчивости твердых растворов Cd1 – xFexCr2S4 (x = 0.6, 0.7, 0.8 и 0.9) при частотах 10, 100, 1000 и 10 000 Гц переменного магнитного поля напряженностью Н = = 79.6 А/м. На вставках в увеличенном виде показаны участки кривых χ'(Т) и χ''(Т) в области магнитного фазового перехода. Все зависимости на рис. 5–8 сходны друг с другом в том отношении, что они имеют близкую частотную зависимость, наиболее выраженную в районе температуры Кюри. По этой причине при обсуждении результатов иногда говорят о совпадении температур ферримагнитного и спин-стекольного переходов. Кроме простой констатации, это утверждение не содержит какого-либо физического смысла хотя бы потому, что само существование в образцах Cd1 – xFexCr2S4 спиновых стекол в общепринятом значении не очевидно.
Рис. 5.
Температурные зависимости действительной (χ') (а) и мнимой (χ'') части (б) магнитной восприимчивости твердого раствора Cd0.4Fe0.6Cr2S4 (х = 0.6) при частотах 10, 100 и 1000 Гц переменного магнитного поля напряженностью Н = 79.6 А/м; на вставке – участок кривой в области магнитного фазового перехода в увеличенном виде.
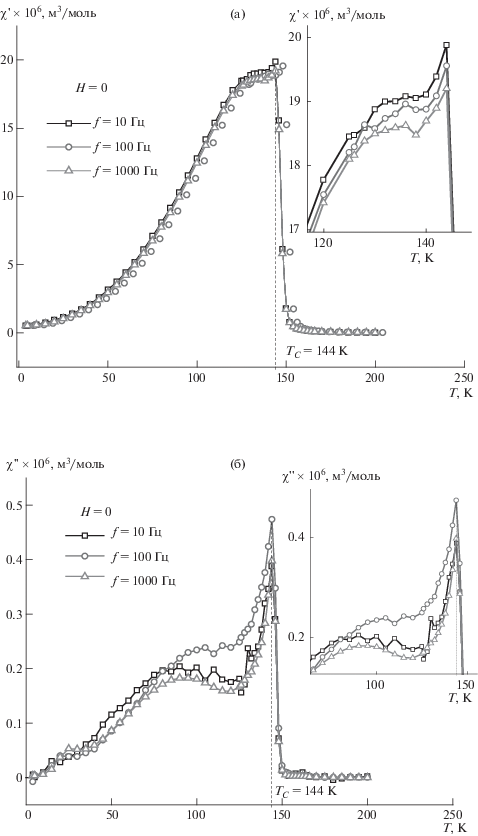
Рис. 6.
Температурные зависимости действительной (χ') (а) и мнимой (χ'') части (б) магнитной восприимчивости твердого раствора Cd0.3Fe0.7Cr2S4 (х = 0.7) при частотах 10, 100, 1000 и 10 000 Гц переменного магнитного поля напряженностью Н = 79.6 А/м; на вставке – участок кривой в области магнитного фазового перехода в увеличенном виде.
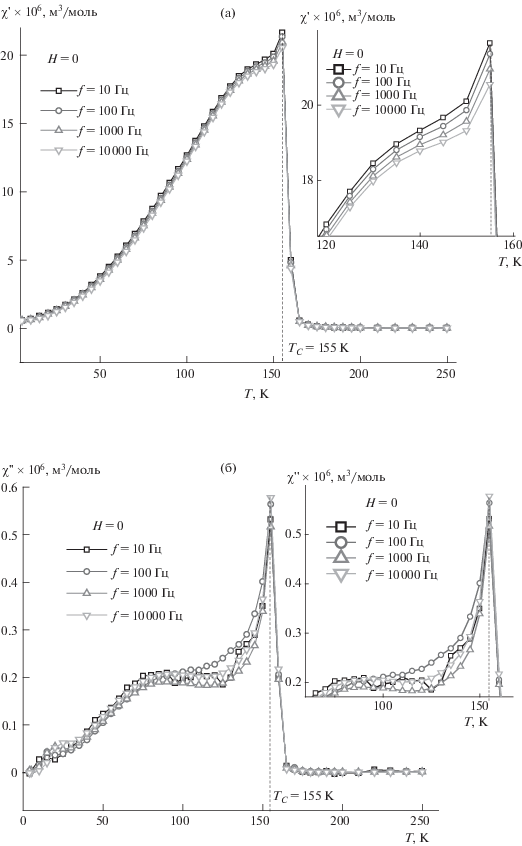
Рис. 7.
Температурные зависимости действительной (χ') (а) и мнимой (χ'') части (б) магнитной восприимчивости твердого раствора Cd0.2Fe0.8Cr2S4 (х = 0.8) при частотах 10, 100, 1000 и 10 000 Гц переменного магнитного поля напряженностью Н = 79.6 А/м; на вставке – участок кривой в области магнитного фазового перехода в увеличенном виде.
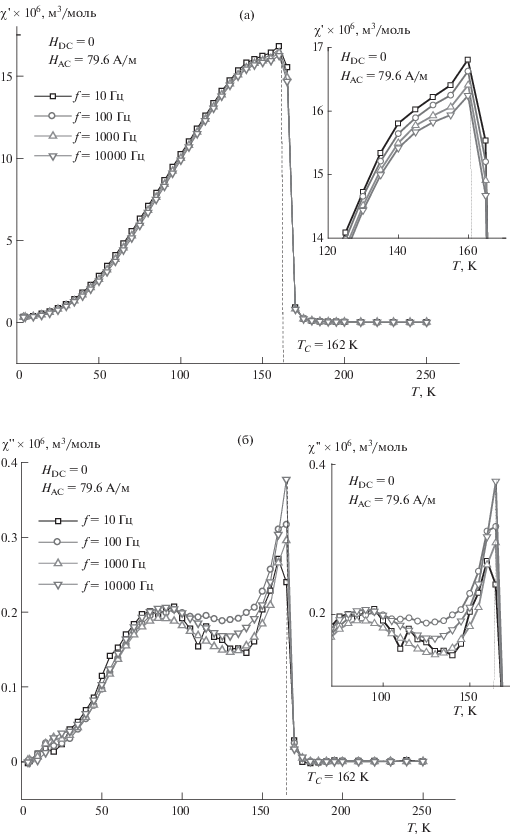
Рис. 8.
Температурные зависимости действительной (χ') (а) и мнимой (χ'') части (б) магнитной восприимчивости твердого раствора Cd0.1Fe0.9Cr2S4 (х = 0.9) при частотах 10, 100 и 1000 Гц переменного магнитного поля напряженностью Н = 79.6 А/м; на вставке – участок кривой в области магнитного фазового перехода в увеличенном виде.
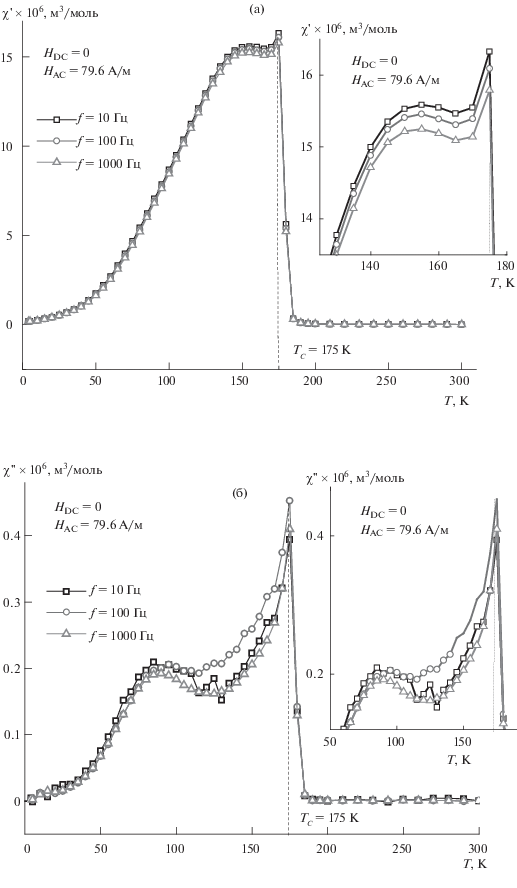
Вместе с тем, как факт можно отметить, что протяженность областей частотной зависимости не является одинаковой для монокристаллического и поликристаллического образцов FeCr2S4 [1, 4]. К примеру, для поликристаллов Cd1 – xFexCr2S4 этот интервал, начавшись вблизи точки Кюри, заканчивается при неопределенной температуре из-за размытости конца кривой χ'(Т). В то же время о монокристаллическом образце FeCr2S4 известно следующее [4]: восприимчивости χ'(Т) и χ''(Т) в интервале температур от ТС до 100 K очень слабо зависят от частоты. Однако ниже 90 K, когда действительная часть восприимчивости χ'(Т) начинает резко уменьшаться с понижением температуры, образец проявляет четкую частотную зависимость вплоть Т = 20 K. Далее χ'(Т) опять не зависит от частоты. Аналогичное поведение показывает и мнимая часть χ''(Т) магнитной восприимчивости соединения.
Наиболее вероятным объяснением [4] упомянутой выше частотной зависимости χ'(Т) и χ''(Т) для FeCr2S4 является то, что ОУ вблизи каспа Т ≈ ≈ 60 К, начинающееся как ближний порядок, разрушает существующее при этой температуре спиновое упорядочение c дальним порядком, вызывая уменьшение намагниченности образца. В случае твердых растворов Cd1 – xFexCr2S4 представляется логичным данную модель ближнего порядка распространить на весь температурный интервал вплоть до точки Кюри.
В [19] исследование FeCr2S4 с помощью метода спиновой релаксации положительных мюонов (μSR) поставило вопрос о существовании соединения при Т = 50 К в виде несоизмеримой модулированной неколлинеарной спиновой структуры. Это важный результат для осмысления, тем более что речь идет о той самой области температур, где, как говорилось выше, образец FeCr2S4 проявляет выраженную частотную зависимость, свидетельствуя о наличии ближнего спинового порядка, напоминающего спиновое стекло. Выбор в пользу того или иного варианта из этих двух возможностей определяется характером магнитных взаимодействий в образце, вернее, наличием или отсутствием таких взаимодействий. Вообще, в случае, когда магнитные частицы располагаются нерегулярно, взаимодействия между ними при некоторой температуре должны перевести систему в состояние спинового стекла [20, 21]. Однако проблема состоит в том, что ZFC- и FC-кривые температурных зависимостей намагниченности для системы как невзаимодействующих, так и для взаимодействующих частиц (спиновых стекол) сходны, потому однозначное определение природы магнитного перехода представляет собой непростую задачу.
ЗАКЛЮЧЕНИЕ
Изучены магнитные свойства твердых растворов Cd1 – xFexCr2S4 на основе соединения FeCr2S4, которое отличает сильная связь “орбиты” со спиновой, зарядовой и решеточной степенями свободы, обусловливающая новые интересные эффекты и явления. Магнитные аномалии, выявленные при исследовании полученных образцов, обсуждаются на основе модели, учитывающей доминирующее влияние на их свойства орбитального упорядочения в базовом компоненте FeCr2S4 при ТОУ = 10 K.
БЛАГОДАРНОСТЬ
Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований, проект № 17-03-01114, а также при поддержке Программы фундаментальных научных исследований Президиума Российской академии наук № 35 “Научные основы создания новых функциональных материалов”.
Часть работы выполнена в рамках государственного задания № 0088-2014-0003 ИОНХ РАН в области фундаментальных научных исследований.
Список литературы
Аминов Т.Г., Шабунина Г.Г., Ефимов Н.Н., Бушева Е.В., Новоторцев В.М. Магнитные свойства твердых растворов Cd1 – xFexCr2S4 (x = 0.5–0.8) // Неорган. материалы. 2017. Т. 53. № 11. С. 1173–1180.
Ramirez A.P., Cava R.J., Krajewski J. Colossal Magnetoresistance in Cr-based Chalcogenide Spinels // Nature.1997. V. 386. P. 156–159.
Tokura Y., Tomioka Y. Colossal Magnetoresistive Manganites // J. Magn. Magn. Mater. 1999. V. 200. P. 1–23.
Tsurkan V., Hemberger J., Klem M., Klim S., Loidl A., Horn S., Tidecks R. Ac Susceptibility Studies of Ferrimagnetic FeCr2S4 Single Crystals // J. Appl. Phys. 2001.V. 90. № 9. P. 4636–4644.
Tsurkan V., Baran M., Szymczak R., Szymczak H., Tidecks R. Spin-Glass-Like States in the Ferrimagnet FeCr2S4 // Physica . 2001. V. 296. P. 301–305.
Tsurkan V., Zaharko O., Schrettle F., Kant Ch., Deisenhofer J., Krug von Nidda et al. Structural Anomalies and the Orbital Ground State in FeCr2S4 // Phys. Rev. B. 2010. V. 81. P. 184426.
Shen C., Yang Z., Tong R., Li G., Wang B., Y. Sun Y. et al. Magnetic Anomaly around Orbital Ordering in FeCr2S4 // J. Appl. Phys. 2011. V. 109. P. 07E144.
Fichtl R., Fritsch V., Krug von Nidda H.-A., Scheiht E-W., Tsurkan V. et al. Orbital Freezing and Orbital Glass State in FeCr2S4 // Phys. Rev. Lett. 2005. V. 94. P. 027601.
Suguru Kitani, Makoto Tashibana, Hidoshi Rawaji. Spin-Glass-Like Behavior in Ferromagnetic Phase of CdCr2S4 // Solid State Commun. 2014. V. 179. P. 16–19.
Yang, Z., Tan S. Magnetic Polaron Conductivity in FeCr2S4 with the Colossal Magnetoresistance Effect // Phys. Rev. B: Condens. Mater. Phys. 2000. V. 62. № 21. P. 13872–13875.
Aminov T.G., Kirdyankin D.I., Shabunina G.G., Novotortsev V.M. The Study of Magnetic Phase Diagram of Fe1 – xZnxCr2S4 Solid Solutions // J. Solid State Chem. 2013. V. 204. P. 123–127.
Аминов Т.Г., Кирдянкин Д.И., Шабунина Г.Г., Новоторцев В.М. Магнитные свойства твердых растворов на основе Cu0.5Fe0.5Cr2S4 // Неорган. материалы. 2012. Т. 48. № 2. С. 136–143.
Andrianov A.V., Saveleva O.A., Lyubutin I.S., Aminov T.G. A Simple Phenomenological Model Formagnetoresistive Properties of FeCr2S4 and Related Compounds // J. Magn. Magn. Mater. 2007. V. 310. № 2. P. 1984–1985.
Bertinshow J., Ulrich C., Gunther A., Schrettle F., Wohlauer M., Krohns S.et al. FeCr2S4 in Magnetic Fields: Possible Evidence for a Multyferroic Ground State // Sci. Rep. 2014. 4: 6079. doi 10.1038/srep06079
Magnetic Nanoparticles / Ed. Gubin S. Weinheim: Wiley–VCH, 2009. P. 197–254.
Spender M.S., Morrish L.E. Mossbauer Study of the Ferrimagnetic Spinel FeCr2S4 // Can. J. Phys. 1972. V. 50. № 1. P. 1125–1138.
Van Diepen A.M., Van Stapele R.P. Ordered Local Distortions in Cubic FeCr2S4 // Solid. State Common. 1973. V. 13. № 10. P. I65I–I653.
Ito M., Nagi Y., Kado N., Urakawa S. et al. Magnetic Properties of Spinel FeCr2S4 in High Magnetic Field // J. Magn. Magn. Mater. 2011. V. 323. P. 3290–3293.
Kalvius G.M., Krimmel A., Hartmann O., Wapping R. Low Temperature Incommensurately Modulated and Noncollinear Spin Structure in FeCr2S4 // J. Phys.: Condens. Matter. 2010. V. 22. P. 052205.
Krupicka S. Physik der Ferrite und der Verwandten Magnetishen Oxide. Prague: Academia, 1973.
Коренблит И.Я., Шендер Е.Ф. Спиновые стекла и неэргодичность // Успехи физ. наук. 1989. Т. 157. № 2. С. 267–310.
Tsurkan V., Fritsch V., Hemberger J., Krug von Nidda H.A. et al. Orbital Fluctuations and Orbital Order in FeCr2S4 // J. Phys. Chem. Solids. 2005. V. 66. P. 2036–2039.
Дополнительные материалы отсутствуют.
Инструменты
Неорганические материалы


