Неорганические материалы, 2020, T. 56, № 9, стр. 931-942
Магнитная диаграмма твердых растворов Fex(Cu0.5In0.5)1 – xCr2S4
Т. Г. Аминов 1, *, Г. Г. Шабунина 1, Е. В. Бушева 1, Н. Н. Ефимов 1
1 Институт общей и неорганической химии им. Н.С. Курнакова Российской академии наук
119991 Москва, Ленинский пр., 31, Россия
* E-mail: aminov@igic.ras.ru
Поступила в редакцию 28.02.2020
После доработки 26.03.2020
Принята к публикации 11.04.2020
Аннотация
Синтезированы твердые растворы Fex(Cu0.5In0.5)1– xCr2S4 и изучены температурные зависимости их намагниченности и динамической восприимчивости в интервале от комнатной до гелиевой температуры в слабом магнитном поле Н = 100 Э и Н~ = 1 Э при частотах 10, 100, 1000 и 10000 Гц. На основании полученных данных построена магнитная диаграмма системы FeCr2S4–(Cu0.5In0.5)Cr2S4. Наибольшую площадь на диаграмме занимает поле ферримагнетика FeCr2S4 (х = 0.28–1), в котором существуют два типа возвратных спиновых стекол – RSG1 и RSG2. Следующую по размеру площадь на диаграмме занимает спиновое стекло SG1 (х ≈ 0.03–0.28). Наименьшая площадь на диаграмме принадлежит составам на основе антиферромагнетика (х = 0–0.2).
ВВЕДЕНИЕ
В работе изучены магнитные свойства твердых растворов шпинелей Fex(Cu0.5In0.5)1– xCr2S4, образованных между ферримагнетиком FeCr2S4 (TC = = 170 K) и антиферромагнетиком Cu0.5In0.5Cr2S4 (TN = 28 K) во всем интервале составов.
Среди соединений ${\text{A}}_{{0.5}}^{ + }$${\text{A}}_{{0.5}}^{{3 + }}$Cr2X4 (A+ = Li+, Cu+, Ag+; А3+ = Al3+, Ga3+, In3+) наиболее подробно изучен сульфид Cu0.5In0.5Cr2S4 [1–7], ограничивающий изучаемую систему Cu0.5In0.5Cr2S4–FeCr2S4. Магнитная структура соединения соизмерима с его кристаллической структурой и характеризуется четырьмя магнитными подрешетками, намагниченности которых направлены вдоль пространственных диагоналей куба из ионов Сr3+, при этом магнитные моменты ионов Сr3+ в четырех В-узлах одного октанта Cu0.5In0.5Cr2S4 принадлежат разным магнитным подрешеткам. По данным нейтронной дифракции дальний антиферромагнитный порядок в Cu0.5In0.5Cr2S4 исчезает при ТN = 35 К, но вплоть до температуры Т = 85 К все еще сохраняется ближний магнитный порядок, для которого характерно существование магнитных состояний, сходных со спин-стекольным. Для соединения Cu0.5In0.5Cr2S4 достаточно часто используют температуру Нееля ТN = 35 К. Но при этом нужно отметить, что максимуму отражения 100 на нейтронограмме отвечает температура ТN = 29 К.
Соединение FeCr2S4 имеет структуру шпинели, его отличают такие уникальные свойства, как колоссальное магнитосопротивление [8], мультиферроичность, сильные эффекты спин-фононной связи [9–14].
FeCr2S4 является коллинеарным ферримагнетиком с антиферромагнитно выстроенными ферромагнитными Fe- и Cr-подрешетками. При понижении температуры от Ткасп = 70 К намагниченность σ(Т) в FeCr2S4 начинает уменьшаться, обнаруживая при этом явления необратимости, сходные со спин-стекольным состоянием. Кроме того, около Тоо = 9 К удельная теплоемкость соединения показывает четкий пик λ-аномалии – перехода, связанного с орбитальным упорядочением. Мессбауровские данные говорят о структурной трансформации шпинели при Т = 10 К. Кроме этого, просвечивающая электронная микроскопия выявила при Т ~ 60 К переход от кубической к триклинной симметрии. При той же температуре Т ≈ 60 К в FeCr2S4 наблюдался касп на кривых температурной зависимости намагниченности, что могло быть следствием возвратного спин-стекольного состояния.
В данной работе изучение магнитной диаграммы твердых растворов Fex(Cu0.5In0.5)1 – xCr2S4 проводили в три этапа с учетом особенностей составляющих ее компонентов – вначале измеряли свойства образцов, которые прилегают к граничным соединениям: антиферромагнетику Cu0.5In0.5Cr2S4 (составы 0 > x > 0.3) [15] и ферримагнетику FeCr2S4 (составы 0.6 < x < 1) [16].
В антиферромагнитной области образцы Fex(Cu0.5In0.5)1 –xCr2S4 (х = 0.05, 0.1 и 0.15) при Т = = 4 К суперпарамагнитны. Поэтому было предположено, что причиной наблюдаемого хода намагниченности может быть неоднородность магнитных наночастиц, обусловленная собственным разупорядочением или неравномерным распределением ферримагнитной присадки в однородной антиферромагнитной матрице Cu0.5In0.5Cr2S4.
Повышенные температуры Кюри ТC = 66 К (х = 0.05), 53 К (х = 0.1), 51 К (х = 0.15), присущие крупным ферромагнитным кластерам в Fex(Cu0.5In0.5)1 – xCr2S4, свидетельствуют о неоднородности в синтезированных образцах; их значения уменьшались с ростом концентрации FeCr2S4 до х = 0.2. При дальнейшем росте х проблема равномерного распределения в матрице легирующей добавки лишается смысла, так как при указанной критической концентрации происходит разрушение антиферромагнетика Cu0.5In0.5Cr2S4. В результате начиная с состава х ≈ 0.2 в системе отсутствуют в качестве бесконечного кластера как ферримагнетик FeCr2S4, так и антиферромагнетик Cu0.5In0.5Cr2S4, игравший роль его разбавителя. Возникает и существует вплоть до х ≈ 0.3 новая магнитоактивная фаза – идеальное спиновое стекло. Для этой новой фазы наблюдалась отчетливая частотная зависимость линейной магнитной восприимчивости, что является характерным признаком спиновых стекол, образованных магнитными кластерами.
На втором этапе были изучены магнитные свойства твердых растворов Fex(Cu0.5In0.5)1 – xCr2S4 (составы 0.6 < x < 1) со стороны шпинели FeCr2S4 [16]. Были определены: температура Кюри для этих образцов, которая росла с увеличением концентрации железа от 144 К (x = 0.6) до 185 K (x = 1), а также температура каспа, колеблющаяся около 50 К. Появление каспа для этих концентраций связано с проявлением ближнего порядка новой кристаллической фазы, существующей при температуре орбитального упорядочения Тоо = 10 К.
Задачами данного исследования на третьем этапе являлись изучение магнитных свойств ранее не изученных средних концентраций Fex(Cu0.5In0.5)1 – xCr2S4 (0.3 > x > 0.6); уточнение магнитного состояния части образцов, прилегающих к Cu0.5In0.5Cr2S4 (x = 0.05–0.15) после третьего отжига, позволившего более равномерно распределить малые присадки тиохромита железа в матрице Cu0.5In0.5Cr2S4 и, следовательно, уточнить состав первой трикритической точки парамагнетик–спиновое стекло–антиферромагнетик. А также на основании всей суммы магнитных свойств построить магнитную фазовую диаграмму твердых растворов Fex(Cu0.5In0.5)1 – xCr2S4 в системе FeCr2S4– Cu0.5In0.5Cr2S4.
ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ
Исходными веществами для получения твердых растворов Fex(Cu0.5In0.5)1 –xCr2S4 служили элементы: In-000 (99.999%), S (“ос. ч.”) с содержанием серы не менее 99.999%, порошкообразные Fe (99.99%), Cu (99.99%) и Cr (99.8%) производства Koch Light. Образцы получали методом твердофазных реакций. Навеска составляла 3 г. Вещества помещали в кварцевые ампулы, откачивали до остаточного давления 10–2 Па. Чтобы избежать разрушения ампул из-за резкого повышения давления паров серы, температуру в течение 2–3 суток медленно поднимали до 600°С, выдерживали 1–2 суток, затем ее так же медленно повышали до 900°С и выдерживали в течение 7–10 суток до полного протекания твердофазной реакции. Далее температуру снижали до 550–600°С в течение 2–3 суток. Заключительное охлаждение вели в режиме выключенной печи. Ампулы вскрывали, образцы перетирали, откачивали и повторно отжигали по вышеизложенной схеме. Для получения однофазных образцов требовалось провести две серии отжигов. Для малых присадок железа потребовался третий дополнительный отжиг.
Рентгенограммы снимали на дифрактометре Bruker D8 ADVANCE (CuKα-излучение, в диапазоне 2θ = 10°–100° с шагом 0.02°) в Центре коллективного пользования ИОНХ РАН. Полученные данные сравнивали со спектрами из базы данных картотеки JCPDS для подтверждения фазового состава. Обсчет спектров однофазных образцов проводили с помощью программы ORIGIN. Параметр решетки для кубической сингонии определяли методом наименьших квадратов при помощи специальной программы с точностью ±0.001 Å.
Магнитные измерения проводили на приборе Quantum Design PPMS-9 в температурном интервале 5–300 К в постоянном магнитном поле 0.1–40 кЭ. Для этого образец охлаждали до температуры жидкого гелия в отсутствие магнитного поля, а затем включали небольшое измерительное поле напряженностью 100 Э и медленно поднимали температуру, регистрируя значения намагниченности. Изотермы намагниченности измеряли вплоть до значений напряженности магнитного поля Н = 40 кЭ. Динамическую восприимчивость измеряли при различных частотах переменного магнитного поля напряженностью 1 Э. Температуру замораживания спинов находили по максимуму на температурной зависимости начальной намагниченности образцов, охлажденных в нулевом поле, а также по каспу на температурной зависимости действительной части динамической магнитной восприимчивости.
РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ
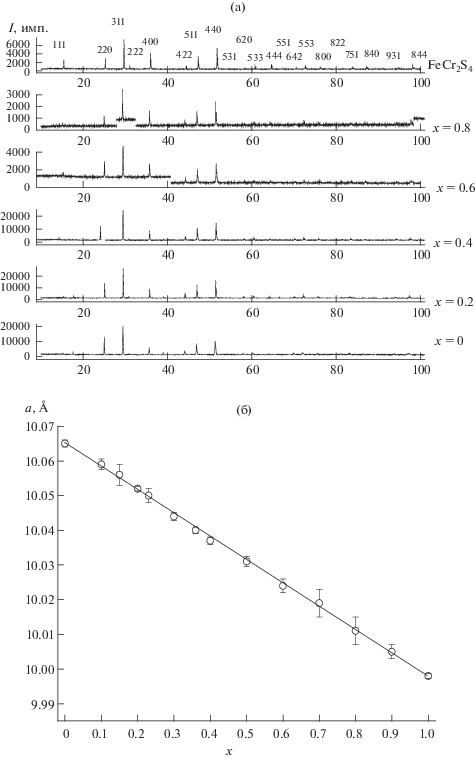
Были синтезированы образцы Fex(Cu0.5In0.5)1 – xCr2S4 составов: х = 0, 0.05, 0.10, 0.15, 0.2, 0.23, 0.3, 0.36, 0.40, 0.5, 0.6, 0.7, 0.8, 0.9 и 1. Все они, по данным РФА, являлись однофазными (рис. 1а). С ростом концентрации железа параметр элементарной ячейки уменьшался от 10.065 Å (х = 0) до 9.995 (x = 1), подчиняясь правилу Вегарда (рис. 1б).
Рис. 1.
Дифрактограммы (а) и концентрационная зависимость параметра решетки (б) образцов Fex(Cu0.5In0.5)1 –xCr2S4.
Для более однородного распределения малых присадок железа в (Cu0.5In0.5)Cr2S4 проводили дополнительный (третий) отжиг образцов в условиях, идентичных первым двум. В результате, как будет показано ниже, на кривых σ(Т)ZFC размытые максимумы переходили в острые пики Tf = 24 K (x = 0.05), 25 K (x = 0.1) и 30 K (x = 0.15), отвечающие состоянию спинового стекла (рис. 2, 3а). Соответственно, сильное поле их подавляло, формируя антиферромагнитные максимумы (рис. 3б) при температурах: ТN = 13 К (x = 0.05), 11 К (x = 0.1), 9 К (x = 0.15).
Рис. 2.
Температурные зависимости намагниченности σ(T)ZFC образцов (Cu0.5In0.5)0.95Fe0.05Cr2S4 (а), (Cu0.5In0.5)0.90Fe0.10Cr2S4 (б) в слабом магнитном поле Н = 100 Э: 1 – после синтеза, 2 – после дополнительного отжига; на вставках – полевые зависимости намагниченности образцов.
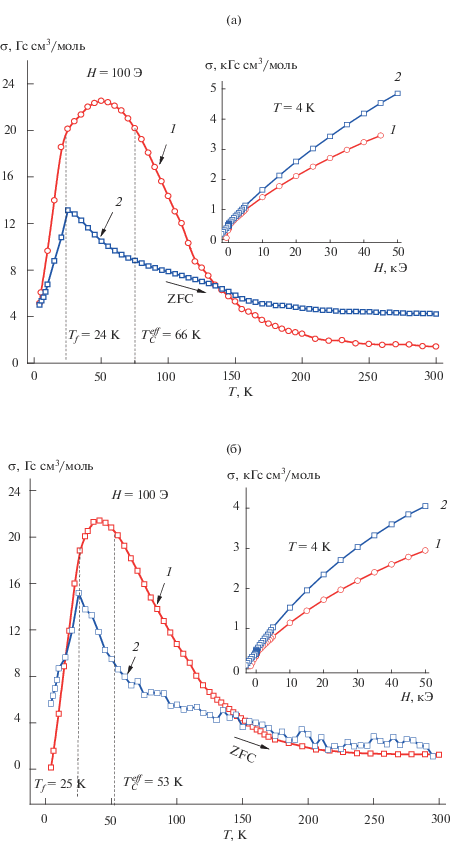
Рис. 3.
Температурные зависимости намагниченности σ(T)ZFC образца (Cu0.5In0.5)0.85Fe0.15Cr2S4 в слабом магнитном поле Н = 100 Э: 1 – после синтеза, 2 – после дополнительного отжига; на вставке – полевые зависимости намагниченности этого образца (а), а также намагниченности σ(T) образцов (Cu0.5In0.5)1 –xFexCr2S4 с x = 0.05 (1), 0.10 (2), 0.15 (3) в сильном магнитном поле Н = 40 кЭ.
На рис. 2 и 3а показаны температурные зависимости намагниченности σ(T)ZFC твердых растворов Fex(Cu0.5In0.5)1 –xCr2S4 c х = 0.05, 0.10 и 0.15 в интервале от комнатной до гелиевой температуры в слабом магнитном поле Н = 100 Э, снятые после проведения синтеза (кривые 1) и после дополнительного отжига (кривые 2). Образец с х = 0.05 наиболее близок по свойствам к нелегированной шпинели Cu0.5In0.5Cr2S4, которая была изучена рядом авторов [2–7]. Нами она изучалась в условиях, указанных выше. Речь идет прежде всего о кривой 1, характеризующейся значительной степенью размытости. Определить точно температуру магнитного перехода образца в таких случаях бывает трудно, хотя само наличие перехода не вызывает сомнений. Обычно поступают следующим образом: более высокую температуру Кюри определяют по правому крылу кривой 1, а более низкую температуру точку замораживания спинов находят по левому крылу той же кривой 1. Применение этого правила в случае образца с х = 0.05 дало эффективную температуру Кюри ТС = 66 К (рис. 2а). Напомним, что для нелегированного Cu0.5In0.5Cr2S4 эффективная температура Кюри ТС = 67 К [15]. И, наконец, в случае образца с х = 0.10 получили эффективную температуру Кюри ТС = 53 К (рис. 2б). Тот факт, что для состава х = 0.15 эффективная температура Кюри оказалась равной 56 К (рис. 3а), будет рассмотрен ниже.
Прежде чем приступить к анализу полученных результатов, следует обсудить ситуацию с нелегированным соединением Cu0.5In0.5Cr2S4. Надо уточнить, каким образом оно стало вдруг проявлять парамагнетизм и даже ферромагнетизм, будучи изначально однородным антиферромагнетиком. Конечно, можно предположить, что дело в наличии неконтролируемых примесей по преимуществу ферромагнитного характера. Но если в образцах присутствуют неконтролируемые примеси, тогда возникает вопрос, почему они ведут себя одинаково в образцах всех составов, рассмотренных выше (табл. 1, колонка 3). Такую одинаковость можно получить лишь в случае контролируемых примесей, и ее невозможно получить для неконтролируемых примесей. Чтобы дополнительно убедиться в одинаковом поведении примесей для образцов с х = 0.05 и 0.1, достаточно взглянуть на значения их максимальной намагниченности, которые практически одинаковы: 446 и 450 Гс см3/моль (табл. 1, колонка 3). Более того, даже в случае совсем другого антиферромагнитного соединения Cu0.5Ga0.5Cr2S4 [17–20] наблюдается сходная картина.
Таблица 1.
Магнитные данные образцов (Cu0.5In0.5)1 –xFexCr2S4
| x | a, Å | σнас, Гс см3/моль | TN, K | Tf,K | $T_{C}^{{eff}},$ K | Tкасп, K | Tоо, K | μs, μB | Тип магнитного упорядочения |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 0 | 10.065 | 0 | 28 | 67 | 0 | AF | |||
| 0.05 | 10.060 | 446 | 13 | 24 | 66 | 0.08 | AF + SG1 | ||
| 0.1 | 10.059 | 450 | 11 | 25 | 53 | 0.08 | AF + SG1 | ||
| 0.15 | 10.056 | 670 | 9 | 32 | 56 | 0.12 | AF + SG1 | ||
| 0.2 | 10.052 | 2350 | 35 | 0.42 | SG1 | ||||
| 0.23 | 10.050 | 2800 | 35 | 0.50 | SG1 | ||||
| 0.3 | 10.044 | 3560 | 35 | 68 | 0.637 | FiM + RSG1 | |||
| 0.36 | 10.040 | 5010 | 36 | 91 | 0.897 | FiM + RSG1 | |||
| 0.4 | 10.037 | 5305 | 39 | 102 | 0.950 | FiM + RSG1 | |||
| 0.5 | 10.029 | 8825 | 30 | 128 | 1.58 | FiM + RSG1 | |||
| 0.6 | 10.024 | 9500 | 144 | 7 | 1.7 | FiM + RSG2 | |||
| 0.7 | 10.019 | 12570 | 155 | 55 | 8 | 2.25 | FiM + RSG2 | ||
| 0.8 | 10.011 | 12120 | 165 | 55 | 7 | 2.17 | FiM + RSG2 | ||
| 0.9 | 10.005 | 11530 | 175 | 45 | 7 | 2.065 | FiM + RSG2 | ||
| 1.0 | 9.995 | 10500 | 185 | 50 | 10 | 1.88 | FiM |
Объяснение данному явлению, известному как раскомпенсация спинов, было дано Неелем и другими авторами [21–26]. Согласно [21, 22], наночастицам антиферромагнетика размером ~5 нм свойственно нарушение полной компенсации спинов магнитных подрешеток. Поэтому они проявляют особые магнитные свойства, а именно: начинают вести себя как ферромагнитные частицы, находящиеся в суперпарамагнитном состоянии. Аналогично ведут себя и более крупные антиферромагнитные частицы (кластеры) размером ~10 нм, если их магнитная структура характеризуется нечетным числом ферромагнитных плоскостей.
Зависимости σ(Т) для Cu0.5In0.5Cr2S4 в слабом поле H = 100 Э свидетельствуют о наличии в данном образце нестехиометрии или раскомпенсации спинов, образующих небольшое количество локального спинового стекла возвратного типа. По своим магнитным параметрам составы с х = 0 и х = 0.05 почти неотличимы друг от друга. Это свидетельствует о том, что введение FeCr2S4 (х = = 0.05) в соединение Cu0.5In0.5Cr2S4 практически никак не отражается на его магнитных свойствах. Этого нельзя сказать про образец с х = 0.15, где начавшееся изменение величин ТС и Тf отражает влияние новых типов кластеров, связанных не только с нарушением стехиометрии, но и с введением в антиферромагнитную матрицу ферримагнитного компонента.
Рассмотрим подробнее эффективные температуры Кюри в образцах с х = 0, 0.05, 0.10, равные соответственно 67, 66 и 53 К. Эти температуры принадлежат наиболее крупным ферромагнитным кластерам, присутствующим в образце. При этом чем крупнее кластер, тем менее регулярно распределена примесь в матрице, и наоборот. Сказанное относится не только к вводимым внешним присадкам, но и к собственным, или автодефектам, возникающим в результате деструкции образца по тем или иным причинам, например по модели Нееля [21, 22].
Априорно нерегулярное распределение примесей в матрице представляется наиболее убедительным в случае внешних присадок, но в случае автодефектов оно не кажется справедливым. Напротив, в последнем случае вполне допустимо регулярное распределение примесей в таком однородном магнетике, каким является исходный антиферромагнетик Cu0.5In0.5Cr2S4. В нашем случае для выяснения был использован повторный отжиг синтезированных образцов. Как известно, отжиг помогает гомогенизировать образцы, достичь большей их однородности по составу, получить нормальное распределение кластеров по размерам в объеме имеющегося вещества.
Результаты проведенных дополнительных отжигов образцов с х = 0.05, 0.10 и 0.15 представлены на рис. 2 и 3а. Они демонстрируют то большое влияние, которое оказал дополнительный отжиг на температурный ход намагниченности материала. Остановим внимание на образце с х = 0.05 (рис. 2а), содержащем минимальное количество тиохромита железа и потому наиболее близкого по составу к однородному антиферромагнетику Cu0.5In0.5Cr2S4. Как видно, предположение об изначально регулярном распределении ферромагнитных кластеров по Неелю здесь не оправдывается: после отжига размытая кривая 1 переходит в более равновесную кривую 2. При этом возвратный спин-стекольный переход, определяемый ранее по левому крылу кривой 1, замещается кривой 2 с острым максимумом при той же температуре замораживания спинов Tf = 24 K.
При переходе к следующему составу твердого раствора х = 0.10 (рис. 2) в образце уменьшается относительное количество тиохромита меди-индия и увеличивается содержание тиохромита железа. Это приводит к тому, что эффективная температура Кюри уменьшается до ТС = 53 К при сохранении того же значения Tf = 25 K возвратного спин-стекольного перехода. Уменьшение эффективной температуры Кюри при переходе от образца с х = 0.05 к образцу с х = 0.10 (табл. 1, колонка 6) говорит об уменьшении размеров ферромагнитных кластеров. К такому же результату приводит дополнительный отжиг образцов: от ТС = 66 К до Tf = 24 К (х = 0.05), от ТС = 53 К до Tf = 25 K (х = 0.10), от ТС = 56 К до Tf = 32 K (х = = 0.15). Эти результаты, представленные в табл. 1 (колонки 5 и 6), позволяют приблизительно оценить относительное уменьшение размеров кластеров, которое происходит при дополнительном отжиге. Для этого можно использовать уравнение Аррениуса в виде 25kT = KvV где k – константа Больцмана, Kv – константа магнитокристаллической анизотропии, V – объем магнитной наночастицы. Взяв в качестве температуры найденные значения ТС и Tf, мы установили, что при отжиге относительный диаметр ферромагнитной наночастицы уменьшился в 1.4 раза (х = 0.05), 1.28 раза (х =0.10) и 1.19 раза (х = 0.15). Полученные значения уменьшаются синхронно с ТС при возрастании х, что говорит об уменьшении размеров кластеров и в этом направлении. Следует отметить, что представленные выше закономерности справедливы лишь для составов, лежащих в области существования антиферромагнетика Cu0.5In0.5Cr2S4. Рост температур до ТС = 56 К и Tf = 32 К в случае х = 0.15 говорит о появлении в системе новых кластеров на основе тиохромита железа, что также подтверждается ростом намагниченности образца (табл. 1, колонка 3).
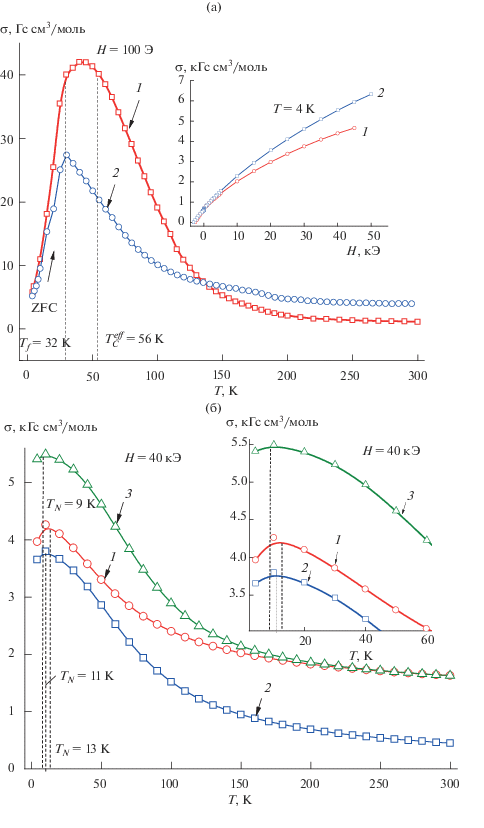
На рис. 4а представлены температурные зависимости намагниченности σ(T)ZFC твердых растворов (Cu0.5In0.5)0.77Fe0.23Cr2S4 (кривая 1) и (Cu0.5In0.5)0.70Fe0.30Cr2S4 (кривая 2) в интервале от комнатной до гелиевой температуры в слабом магнитном поле Н = 100 Э. В отличие от предыдущих составов в случае образца c х = 0.23 на графике присутствует лишь один спин-стекольный пик с температурой Tf = 35 К. Это свидетельствует о том, что данный состав (так же как и ранее измеренный для x = 0.2 в [15]) располагается в области идеального спинового стекла. В подтверждение сказанному на рис. 4б приводятся температурные зависимости действительной (χ') части магнитной восприимчивости образца с х = 0.23 при частотах 10, 100, 1000 и 10000 Гц переменного магнитного поля силой 1 Э, а на вставке – область пика кривой χ' показана в увеличенном виде. Как и должно быть в случае кластерного спинового стекла, с возрастанием частоты измерения максимум χ' сдвигается вниз и смещается к более высоким частотам. Образец с х = 0.30 на рис. 4а, с более высоким содержанием тиохромита железа, демонстрирует быстрое возрастание намагниченности и, по-видимому, располагается близко к границе между спин-стекольной и ферримагнитной фазами.
Рис. 4.
Температурные зависимости намагниченности σ(T)ZFC твердых растворов (Cu0.5In0.5)0.77Fe0.23Cr2S4 (1) и (Cu0.5In0.5)0.70Fe0.30Cr2S4 (2) в слабом магнитном поле Н = 100 Э; на вставке – полевые зависимости намагниченности этих образцов (а), а также действительной части (χ') магнитной восприимчивости образца (Cu0.5In0.5)0.77Fe0.23Cr2S4 при частотах 10, 100, 1000 и 10 000 Гц переменного магнитного поля; на вставке – участок в увеличенном виде (б).
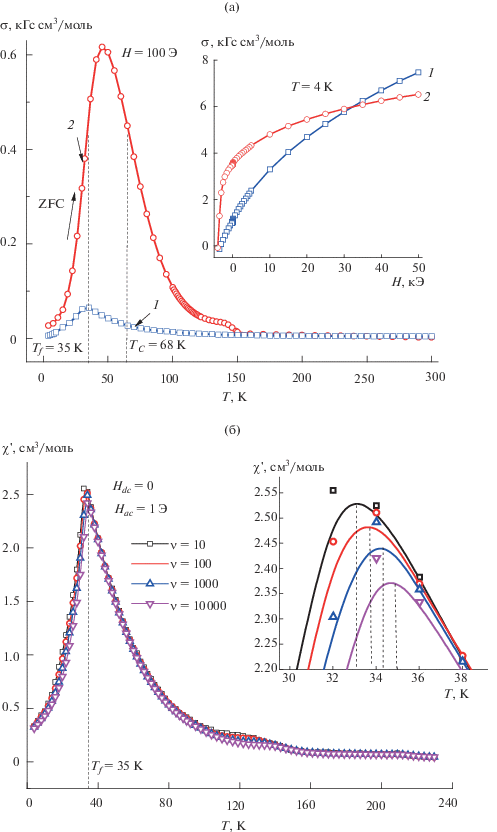
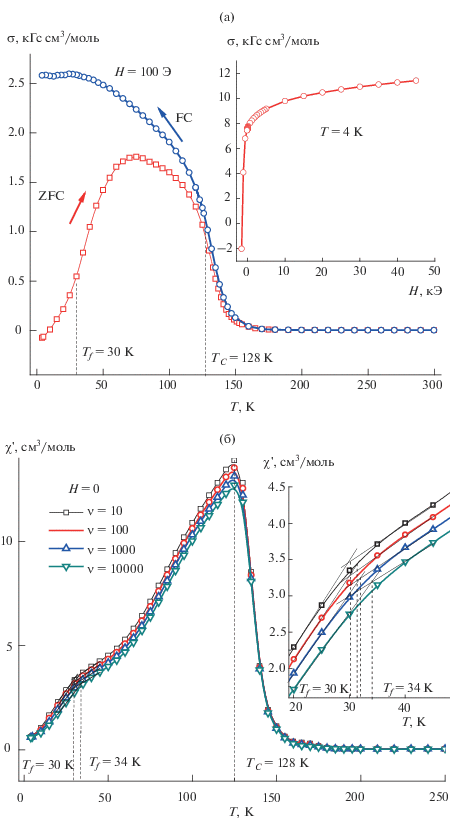
На рис. 5 показаны температурные зависимости намагниченности σ(T)ZFC и σ(Т)FC твердого раствора (Cu0.5In0.5)0.50Fe0.50Cr2S4 в интервале от комнатной до гелиевой температуры в слабом магнитном поле Н = 100 Э и температурные зависимости действительной части (χ') магнитной восприимчивости этого же образца при частотах 10, 100, 1000 и 10 000 Гц переменного магнитного поля напряженностью 1 Э. Кривая σ(T)ZFC в этом случае сильно размыта из-за присутствия различных магнитных кластеров в образовавшемся бесконечном кластере FeCr2S4. Температура ферримагнитного перехода, найденная по правому крылу кривой σ(T)ZFC, в этом случае составила ТС = 128 К, а температура возвратного спин-стекольного перехода Tf = 30 К. Температурная зависимость действительной (χ') части магнитной восприимчивости образца (рис. 4б) однозначно свидетельствует о кластерной природе возвратного спинового стекла с Tf ~ 32 К, существующего в бесконечном кластере FeCr2S4.
Рис. 5.
Температурные зависимости намагниченности σ(T)ZFC и σ(Т)FC образца (Cu0.5In0.5)0.50Fe0.50Cr2S4 в слабом магнитном поле Н = 100 Э; на вставке – полевые зависимости намагниченности этого образца (а), а также действительной части (χ') магнитной восприимчивости этого образца при частотах 10, 100, 1000 и 10 000 Гц переменного магнитного поля; на вставке – участок в увеличенном виде (б).
В образцах с x = 0.36 и x = 0.4 зависимости намагниченности σ(T)ZFC и σ(Т)FC твердых растворов Fex(Cu0.5In0.5)1 – xCr2S4 в интервале от комнатной до гелиевой температуры в слабом магнитном поле Н = 100 Э и температурные зависимости χ'(T) при частотах 10–10 000 Гц переменного магнитного поля напряженностью 1 Э имеют вид, сходный с аналогичными зависимостями для образца с x = 0.5. Температуры переходов для них сведены в табл. 1.
Магнитные данные для Fex(Cu0.5In0.5)1 – xCr2S4, приведенные в табл. 1, помимо построения соответствующей диаграммы, позволяют сделать некоторые обобщения. Так, можно уверенно сказать, что завершением эволюции составов, прилегающих к антиферромагнетику Cu0.5In0.5Cr2S4, можно считать твердый раствор Cu0.4In0.4Fe0.2Cr2S4, для которого на кривой намагниченности σ(Т)ZFC отсутствуют пики, отвечающие переходам парамагнетик–ферримагнетик с соответствующими эффективными температурами Кюри, характерные для крупных и особо крупных ферромагнитных кластеров в антиферромагнитной матрице Cu0.5In0.5Cr2S4. То есть при концентрации FeCr2S4х ≈ 0.2 в твердом растворе Fex(Cu0.5In0.5)1 – xCr2S4 не только достигается равномерное распределение в матрице легирующей добавки, но и отсутствует сама антиферромагнитная матрица, которая разрушилась по достижении критической концентрации х ≈ 0.2 с образованием спинового стекла.
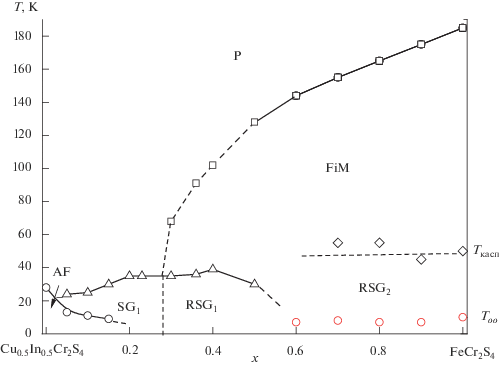
На участке магнитной фазовой диаграммы 0 < < x < 0.28 сосуществуют три магнитные фазы: парамагнитная, антиферромагнитная и спиновое стекло. При этом переход парамагнетик–антиферромагнетик наблюдался лишь в узкой, до x ≈ 0.03, области концентраций. С дальнейшим увеличением концентрации железа до x ≈ 0.20 при понижении температуры проявлялся возвратный переход спиновое стекло–антиферромагнетик. Трикритическая точка парамагнетик–антиферромагнетик–спиновое стекло лежит при x ≈ 0.03. Вторая трикритическая точка парамагнетик–спиновое стекло–ферримагнетик находится при x ≈ 0.28.
Матрицей в этом случае является сама спин-стекольная фаза, в которой размещаются ферро- или антиферромагнитные кластеры различного состава в зависимости от величины х, являющейся параметром пространственных флуктуаций системы.
При увеличении х будет происходить рост числа и размеров ферромагнитных кластеров в бесконечном спин-стекольном кластере до достижения второй критической концентрации и протекания ферримагнитной жидкости со сменой типа матрицы от спин-стекольной до ферримагнитной. Начало этого процесса регистрируется при спин-стекольной фазе Cu0.36In0.36Fe0.28Cr2S4 (вторая трикритическая точка).
Итак, при х > 0.3 (с состава x = 0.36) начинается новый этап исследуемой системы. Он заключается в том, что возникает новая ферримагнитная фаза на основе FeCr2S4 с дальним магнитным порядком, которая вначале проявляется уширением или размытием пика на кривой σ(Т). Для образцов с x = 0.36, 0.4 и 0.5 точки Кюри изменяются от 76 К (x = 0.36) и 100 К (x = 0.4) до 125 K (x = 0.5). При этом с понижением температуры ниже ТС они проявляют свойства возвратного ферримагнетика, обнаруживая переход к спиновому стеклу. При x > 0.6, для образцов с x = 0.7, 0.8, 0.9 и 1, изученных нами ранее [16], кривые σ(Т)ZFC приобретают демагнетизационный вид, а образец с x = 0.8 характеризовался наличием каспа, связанного с ближним порядком новой кристаллической фазы, существующей при температуре орбитального упорядочения Тоо = 10 К [24]. Ткасп – это температура магнитного перехода из коллинеарной феримагнитной фазы в неколлинеарную несоизмеримую магнитную фазу спирального типа [25]. Температура Кюри для этих образцов растет с увеличением концентрации железа от 144 К (x = 0.6) до 185 K (x = 1). Температура каспа, которую мы связываем с условным спиновым стеклом, колеблется в районе 50 К.
На рис. 6 показана магнитная фазовая диаграмма системы FeCr2S4–Cu0.5In0.5Cr2S4, построенная на основании измеренных магнитных свойств, сведенных в табл. 1. На диаграмме представлены следующие области: парамагнитная, ферримагнитная, антиферромагнитная, область чисто спинового стекла (SG1) и две области возвратного спинового стекла. При этом одна, прилежащая к чисто спиновому стеклу (RSG1), является возвратным спиновым стеклом, и ее температура с увеличением концентрации железа уменьшается, а другая (RSG2) по сути лишь условно является возвратным спиновым стеклом, и ее температура колеблется около Ткасп нелегированного тиохромита FeCr2S4, ответственного за этот переход.
Наибольшую площадь (0.28 < х < 1) на диаграмме после парамагнитной области занимают твердые растворы на основе ферримагнитного FeCr2S4 (ТС = 185 K). В этой области концентраций, где существует бесконечный ферримагнитный кластер, также имеются “бесконечные” спин-стекольные кластеры, называемые возвратными, или локальными, спиновыми стеклами. Они образуются при перколяции спин-стекольной жидкости по достижении пороговой концентрации (x = = 0.28) в пределах бесконечного ферримагнитного кластера в области, граничащей с чисто спиновым стеклом, возникшим из парамагнитной области диаграммы при понижении температуры.
Кроме “бесконечных” спин-стекольных кластеров в бесконечном ферримагнитном кластере, в интервале составов, примыкающих к FeCr2S4, располагаются конечные антиферромагнитные и спин-стекольные кластеры среднего и малого размеров, не оказывающие заметного влияния на баланс разграниченных фаз магнитной диаграммы. Эти антиферромагнитные и спин-стекольные кластеры непрерывно переходят друг в друга, растут или даже деградируют. При уменьшении размеров они смещаются по оси составов в сторону FeCr2S4, в то время как при росте размеров они смещаются в сторону границы с истинным спиновым стеклом (при х = 0.28). Возможность перехода в чисто спин-стекольное состояние существует как через перколяционную стадию, так и при понижении температуры образца соответствующего состава. Для антиферромагнитной фазы на основе шпинели Cu0.5In0.5Cr2S4 (расположенной в интервале составов 0 < x < 0.20) также существуют при понижении температуры два варианта магнитного перехода: при 0.03 < x < 0.20 из чистого спин-стекольного состояния и при x < 0.03 из парамагнитной области.
Список литературы
Talanov V.M. Structural Mechanisms of Ion Ordering in Tetrahedral Sites Spinel // Zh. Strukt. Khim. 1986. V. 31. № 2. P. 172–176.
Plumier R., Lotgering F.K., van Stapele R.P. Magnetic Properties of Cu0.5In0.5Cr2S4 and Some Related Compounds // J. Phys. 1971. V. C1-52. Suppl. au № 2–3. P. 324–325.
Nauciel-Bloch M., Plumier R. Magnetic structures in spinel B-site lattices with ordered diamagnetic ions at the A-site. // J. Solid. State Commun. 1971. V. 9. P. 223–226.
Plumier R., Sougi M., Lecomte M. Observation of an Unusual Short Range Magnetic Ordering in Spinel Cu0.5In0.5Cr2S4 // Phys. Lett. A. 1977. V. 60. № 4. P. 341–344.
Plumier R., Sougi.M., Lecomte M., Miedan-Gros A. High Magnetic Field Study of Sulphur Spinel Cu0.5In0.5Cr2S4 // Z. Phys. B. 1980. V. 40. P. 227–231.
Gobel H., Pink H., Treitinger L., Unger W.K. Magnetic and Crystallographic Properties of Fe1 – x(Cu0.5In0.5)xCr2S4 Spinels // Mater. Res. Bull. 1975. V. 10. P. 783–786.
Treitinger L., Pink H., Mews H., Kopl R. The Influence of Iron Substitution on the Properties of Magnetic Semiconducting Thiospinels // J. Magn. Magn. Mater. 1976. V. 3. P. 184–188.
Ramirez A.P., Cava R.J., Krajewski J. Colossal Magnetoresistance in Cr-Based Chalcogeenide Spinels // Nature. 1997. V. 386. P. 156–159.
Tsurkan V., Zaharko O., Schrettle F., Kant Ch., Deisenhofer J. et al. Structural Anomalies and the Orbital Ground State in FeCr2S4 // Phys. Rev. B. 2010. V. 81. P. 184426.
Tsurkan V., Hemberger J., Klemm M., Klimm S., Loidl A. et al. Ac Susceptibility Studies of Ferrimagnrtic FeCr2S4 Single Crystals // J. Appl. Phys. 2001. V. 90. № 9. P. 4639–4644.
Ito M., Nagi Y., Kado N., Urakawa S. et al. Magnetic Properties of Spinel FeCr2S4 in High Magnetic Field. // J. Magn. Magn. Mater. 2011. V. 323. P. 3290–3293.
Van Diepen A.M., Van Stapele R.P. Ordered Local Distortions in Cubic FeCr2S4 // Solid. State Commun. 1973. V. 13. № 10. P. I65I–I653.
Fichtl R., Tsurkan V., Lunkenheimer P., Hemberger J. et al. Orbital Freezing and Orbital Glass State in FeCr2S4 // Phys. Rev. Lett. 2005. V. 94. P. 027601.
Kalvius A., Krimmel O., Hartmann R., Wappling F., Wagner E. et al. Low Temperature Incommensurately Modulated and Noncollinear Spin Structure in FeCr2S4 // J. Phys.: Condens. Matter. 2010. V. 22. P. 052205.
Аминов Т.Г., Бушева Е.В., Шабунина Г.Г., Ефимов Н.Н. Магнитные свойства твердых растворов Fex(Cu0.5In0.5)1 – xCr2S4 (x = 0–0.3) // Неорган. материалы. 2018. Т. 54. № 10. С. 1055–1065.
Аминов Т.Г., Бушева Е.В., Шабунина Г.Г. Магнитные свойства шпинели FeCr2S4, легированной медью и индием // Неорган. материалы. 2019. Т. 64. № 12. С. 1340–1348.
Wilkinson C., Knapp B.M., Forsyth J.B. The Magnetic Structure of Cu0.5Ga0.5Cr2S4 // J. Phys. C: Solid State Phys. 1976. V. 9. № 21. P. 4021.
Аминов Т.Г., Кирдянкин Д.И., Шабунина Г.Г., Новоторцев В.М. Магнитные свойства твердых растворов Cu0.5Fe0.5 – xGaxCr2S4 // ЖНХ. 2012. Т. 57. № 7. С. 991–997.
Аминов Т.Г., Шабунина Г.Г., Новоторцев В.М. Магнитные свойства твердых растворов (Cu0.5Ga0.5)1 – xFexCr2S4// ЖНХ. 2014. Т. 59. № 11. С. 1557–1569.
Аминов Т.Г., Бушева Е.В., Шабунина Г.Г., Новоторцев В.М. Магнитная фазовая диаграмма твердых растворов в системе CoCr2S4–Cu0.5Ga0.5Cr2S4 // ЖНХ. 2018. Т. 63. № 4. С. 487–494.
Neel L. Superparamagnétisme des grains très fins antiferromagnétiques // C. R. Acad. Sci. 1961. V. 252. P. 4075–4080.
Neel. L. Influence of Thermal Fluctuations on the Magnetization of Ferromagnetic Small Particles // C. R. Acad. Sci. 1949. V. 228. P. 664–668.
Крупичка С. Физика ферритов и родственных магнитных окислов. М.: Мир, 1976. Т. 1. 353 с.
Королева Л.И. Магнитные полупроводники. М.: Изд-во МГУ, 2003. 312 с.
Вонсовский С.В. Магнетизм. М.: Наука, 1972. 1032 с.
Боровик Е.С., Еременко В.В., Мильнер А.С. Лекции по магнетизму. М.: Физматлит, 2005. 510 с.
Дополнительные материалы отсутствуют.
Инструменты
Неорганические материалы