Неорганические материалы, 2022, T. 58, № 6, стр. 684-696
Размерные объемные и поверхностные характеристики кристаллов типа KDP, рассчитанные в модели решеточного газа с многочастичным потенциалом взаимодействия
Е. С. Зайцева 1, *, Т. Ю. Михайлова 1, С. П. Долин 1, Ю. К. Товбин 1
1 Институт общей и неорганической химии им. Н.С. Курнакова Российской академии наук
119991 Москва, Ленинский пр., 31, Россия
* E-mail: zaya261011@gmail.com
Поступила в редакцию 09.01.2022
После доработки 30.03.2022
Принята к публикации 04.04.2022
- EDN: DBIOQA
- DOI: 10.31857/S0002337X2206015X
Аннотация
Сформулирован подход к расчету размерных объемных и поверхностных характеристик многодоменного кристалла типа KDP на основе модели решеточного газа (МРГ). Энергетические состояния разных конфигураций протонов, ответственных за возникновение спонтанной поляризации кристалла при понижении температуры, рассчитываются неэмпирически. С использованием статистической эквивалентности между ориентациями псевдоспинов кристалла KDP и состояниями занятости узлов МРГ компонентами бинарной смеси A + B получены уравнения, описывающие размерные зависимости критической температуры упорядочения, межфазного и поверхностного натяжений. Расчеты проведены в квазихимическом приближении с учетом прямых корреляций между соседними компонентами А и В. Критическая температура упорядочения, межфазное (МН) и поверхностное (ПН) натяжения рассмотрены как функции линейного размера L кубического домена, когда вклад поверхности в термодинамические функции вещества становится существенным. Расчет размерной зависимости величины МН выполнен для 180-градусной ориентации соседних фаз. Установлено, что все три размерные зависимости критической температуры упорядочения, МН и ПН в безразмерном виде, нормированном на соответствующую величину для макрообразца, уменьшаются при уменьшении линейного размера домена L.
ВВЕДЕНИЕ
Объемные свойства сегнетоэлектриков (СЭ) изучаются более семидесяти лет [1–7]. При понижении температуры СЭ переходят в состояние спонтанной поляризации, которое связано с процессами упорядочения ионов в решетках многоатомных кристаллов, состоящих из двух и более сортов ионов. В зависимости от механизма формирования упорядоченного состояния выделяют СЭ типа смещения (смещение мягких подрешеток в поле потенциала жестких подрешеток) и СЭ типа порядок-беспорядок (перераспределение отдельных ионов между эквивалентными положениями вблизи других подрешеток).
Поверхностные свойства и размерные зависимости СЭ изучаются порядка тридцати лет. Процессы появления спонтанной поляризации изучались в полимерных пленках [8, 9], в различных наноструктурах СЭ типа смещения: пленках [10, 11], проводящих монокристаллах, проводящих композитах, в т. ч. на основе пористых металлических матриц с внедренными СЭ типа KNO3, NaNO2 и др. (см., например, [12–19]).
Аналогичных данных по композитам в пористых матрицах для СЭ типа порядок-беспорядок гораздо меньше (см., например, [20–31]). В них исследуются закономерности поведения критической температуры упорядочения триглицинсульфата (ТГС) и его модифицированных аналогов в пористых оксидах алюминия и кремния, в матрице NO2 и других пористых материалах в зависимости от геометрии кристаллов и свойств нанокомпозитов (которые важны для разных прикладных применений). Кристалл ТГС активно исследуется экспериментально (фазовый переход (ФП) при температуре около 50°С) [6]. У него есть два типа водородных связей и три симметрически неэквивалентных группы ионов глицина. Механизм перехода считается связанным с упорядочением порядок-беспорядок не только протонов на двух разных типах водородных связей (OHO, NHO), но и одного из типов ионов глицина.
Другим общеизвестным примером СЭ типа порядок-беспорядок являются кристаллы дигидрофосфата калия KH2PO4 (KDP) и его модификаций [1–6]. Выбор KDP в данной работе обусловлен тем, что, видимо, это самая простая система СЭ типа порядок–беспорядок. В ней реализуется перераспределение протонов вдоль водородной связи между двумя соседними ионами кислорода (KН2РО4). Она значительно проще системы ТГС, для которой применение псевдоспиновой модели, да и само квантовохимическое моделирование с помощью малых молекулярных кластеров неочевидно.
Как правило, все эксперименты для СЭ трактуются [32–43] с позиции феноменологической теории Ландау [44–49], в которой не учитываются эффекты корреляции взаимодействующих частиц. Для СЭ типа порядок-беспорядок часто используются более точные методы статфизики, основанные на модели Изинга [3, 50, 51], которые традиционно применяются для других упорядоченных систем (сплавов, растворов, адсорбированных частиц и т.д.) [52–55]. Модель Изинга эквивалентна модели решеточного газа (МРГ) [49, 50, 56].
С помощью МРГ впервые исследовано влияние размера ограниченного по объему домена на величину критической температуры Tcr упорядочения бинарного сплава АВ стехиометрического состава А : В = 1 : 1 [57, 58]. Согласно этой эквивалентности, результаты по влиянию размеров домена на Tcr [57, 58] также относятся к исследованию на микроскопическом уровне влияния размера домена в СЭ типа порядок–беспорядок на величину критической температуры Tcr(L), где L – сторона кубического домена. Было установлено, что при уменьшении размера домена уменьшается Tcr, а также исследовано влияние внешнего поля, ограничивающего размер домена, и учета эффекта непрямых корреляций на значения Tcr. Привлечение МРГ впервые позволило вывести анализ размерных эффектов в СЭ типа порядок-беспорядок с фазовым структурным переходом второго рода на уровень микроскопического анализа фазовых переходов первого рода [59].
Традиционно межионные взаимодействия описываются с помощью эффективных парных потенциалов [1–6] или потенциалов электростатического [7] взаимодействия. При этом часто вводят представления, уменьшающие энергию кулоновского потенциала. С этой целью используют понятия о долях ковалентности связей в ионных кристаллах ([2], стр. 9) или о долях энергии деполяризации [2, 60] при формировании доменов: этот путь дает уменьшение энергии деполяризации на два–три порядка ([2], стр. 100). В последнее время для определения параметров межионного взаимодействия привлекают квантовохимические подходы. Эти методы оказались достаточно удачными для ряда СЭ типа порядок–беспорядок (K(Н/D)2РО4) [61–63], что позволило обсуждать энергетику не только объемных состояний, но и межфазных границ кристаллов, которые обычно трактуются на основе более грубых оценок [64, 65]. В результате, система K(Н/D)2РО4 практически единственная, которая имеет квантовохимическое описание энергии локальных кластеров, хорошо коррелирующее с экспериментальными данными, поэтому микроскопические изменения рассчитываемых энергий кластеров в данной системе могут быть отражены только с помощью микроскопических статистических подходов.
В данном исследовании разработана статистическая модель доменных границ в СЭ типа кристаллов KDP как для открытой поверхности (вакуум), так и для межфазной границы 180-градусной доменной структуры, а также методика расчетов поверхностного натяжения (ПН) на границе с вакуумом и межфазного натяжения (МН) для многодоменной структуры. Решение этой задачи связано с обсуждением вопроса о проблемах расчета ПН на границе раздела фаз с многочастичными потенциалами в МРГ.
Напомним, что термодинамическое понятие фазы, введенное Гиббсом, автоматически подразумевает наличие границы, которая характеризуется ПН [66]. Если есть фаза, то должно быть ПН, и наоборот. Понятие ПН доменной стенки было хорошо известно создателям феноменологической теории еще до ее формулировки (оно использовалось в работах 1935 г. (стр. 212) и 1934 г. (стр. 216) [67]), где также дано определение понятия ПН доменной стенки как межфазной границы. Однако со временем понятие ПН уходит из литературы по фазовым переходам в СЭ, оно заменяется на удельную поверхностную энергию стенки ([6], стр. 138). С точки зрения термодинамики Гиббса эта замена не является эквивалентной, особенно для искривленных границ и малых систем, т.к., помимо введения самой разности свободных энергий, должно быть сформулировано и условие на положение разделяющей поверхности, к которой относится данное ПН. В итоге, понятие ПН для ФП 2-го рода неявно перенесено в граничные условия. В то же время для ФП 1-го рода понятие ПН сохраняется, и более чем 70 лет размерная зависимость ПН является основным объектом теории и эксперимента. Работы по ФП 1-го рода ориентировались на расслаивающиеся системы, что много проще, чем ФП 2-го рода в многоатомных кристаллах со сложными потенциальными взаимодействиями. Это позволило значительно продвинуться в анализе размерных эффектов для ФП 1-го рода [59].
В данной работе демонстрируется, что общие термодинамические принципы работают и в случае твердофазных систем. Это утверждение позволило не только впервые представить МН и ПН как функции размера домена, но и связать энергию локального кластера с этой размерной зависимостью. Это открывает потенциальную возможность для связи наблюдаемых характеристик с локальными энергиями между ионами в объемной фазе и на границе доменов.
КВАНТОВОХИМИЧЕСКИЕ РАСЧЕТЫ
Квантовохимическое моделирование СЭ рассматривает небольшие молекулярные кластеры с геометрией, отвечающей экспериментальным данным о кристалле. В рамках однодоменного приближения даже малые модельные кластеры хорошо воспроизводят критическую температуру СЭФП, особенно если задача решается с учетом туннелирования и дальнодействия [63, 68]. Увеличение размера кластера, необходимое для рассмотрения доменных эффектов, требует увеличения вычислительных затрат, при этом выбор модельного кластера существенно ограничен, так как оказывается критически важным максимально полный учет не только параметров водородных связей, но и симметрии образца. Для ряда модельных кластеров с числом элементарных РО4-тетраэдров от трех до семи показано [68, 69], что лишь высокосимметричные модели способны верно передать основные характеристики СЭФП. Так, расчет для крестовидного пентатетраэдрического кластера, рассмотренного отдельно или расширенного вдоль одной из осей (до 6 или 7 тетраэдров), качественно верно воспроизводит основное СЭ-состояние и дает разумную оценку для критической температуры СЭФП. При этом для кластеров с тем же числом элементарных тетраэдров, но другой формы – линейных, угловых, Т-образных – в расчетах основным оказывается состояние, отвечающее не СЭ-, но антисегнетоэлектрическому (АСЭ) упорядочению. Различие в энергиях между АСЭ- и СЭ-состояниями в таких моделях падает с ростом размера кластера, но этот рост ограничен возможностями неэмпирического расчета. Поэтому логичным оказывается учет доменных эффектов с помощью статистических методов на базе результатов квантовохимического расчета для кластера разумного размера.
Расчет. Для выбранного кластера осуществляется расчет (B3LYP/6-311+G**) всех 16 энергий, отвечающих всевозможным значениям четырех псевдоспинов в центральном тетраэдре.
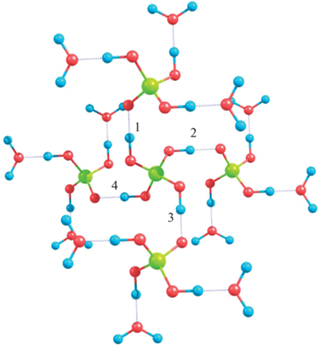
Схема кластера показана на рис. 1. В табл. 1 показаны различия между энергиями 16 конфигураций для четырех протонов, находящихся вокруг катиона фосфора. Расположение протонов отвечает конфигурации 1K2K3K4K, где порядковое число означает номер протона, а символ К (D) означает короткую (длинную) связь относительно центрального иона фосфора.
Таблица 1.
Относительные энергии полного списка конфигураций ближайших протонов вблизи центрального иона фосфора
| № | Конфигурация | Δε, эВ | |||
|---|---|---|---|---|---|
| D | E | F | G | ||
| 1 | 1D2D3D4D | 2.125 | 2.100 | 2.056 | 2.042 |
| 2 | 1K2D3D4D | 1.443 | 1.534 | 1.585 | 1.648 |
| 3 | 1D2D3K4D | 1.443 | 1.404 | 1.339 | 1.301 |
| 4 | 1K2D3K4D | 0.847 | 0.922 | 0.954 | 0.993 |
| 5 | 1D2K3D4D | 1.443 | 1.419 | 1.347 | 1.315 |
| 6 | 1K2K3D4D | 0.863 | 0.954 | 0.979 | 1.025 |
| 7 | 1D2K3K4D | 0.863 | 0.822 | 0.729 | 0.673 |
| 8 | 1K2K3K4D | 0.374 | 0.449 | 0.453 | 0.475 |
| 9 | 1D2D3D4K | 1.443 | 1.346 | 1.297 | 1.261 |
| 10 | 1K2D3D4K | 0.863 | 0.881 | 0.928 | 0.970 |
| 11 | 1D2D3K4K | 0.863 | 0.748 | 0.679 | 0.618 |
| 12 | 1K2D3K4K | 0.374 | 0.375 | 0.402 | 0.420 |
| 13 | 1D2K3D4K | 0.847 | 0.749 | 0.673 | 0.619 |
| 14 | 1K2K3D4K | 0.374 | 0.393 | 0.413 | 0.438 |
| 15 | 1D2K3K4K | 0.374 | 0.258 | 0.161 | 0.081 |
| 16 | 1K2K3K4K | 0.000 | 0.000 | 0.000 | 0.000 |
Рассчитанные разности энергии по отношению к конфигурации 16 относятся к полной энергии взаимодействия между протонами со всеми окружающими их электронами и ионами KDP. Эти разности наглядно демонстрируют обсуждаемую корреляцию между энергиями конфигураций псевдоспинов системы и энергиями компонентов А и В в МРГ. Энергия с четырьмя короткими связями принята за нулевую. По мере увеличения числа длинных связей различие в энергиях конфигураций увеличивается, максимальная величина энергетических отличий относится к четырем длинным связям. Простейшее отнесение изменения энергии конфигурации к числу ее длинных связей указывает на их пропорциональность (которая, однако, несколько отличается от линейной зависимости).
Коэффициент пропорциональности между энергиями псевдоспинов и энергиями конфигураций МРГ не может быть однозначно определен без детального анализа всех вкладов в эти энергии от взаимодействий с электронами и ионами системы (в силу необходимости уточнения этих вкладов в алгоритме расчета). Поэтому выделение вкладов взаимодействий между отдельными протонами практически невозможно, можно только обсуждать их соответствие другим версиям записи энергии системы.
Ниже обсудим три варианта соответствия между энергиями из квантовохимических расчетов и эффективным парным параметром латерального взаимодействия ω в МРГ, используемым для расчета размерных эффектов. Простейший случай относится к использованию средней энергии взаимодействия между протонами. Эта средняя энергия может быть напрямую соотнесена с параметром взаимодействия ω. Тогда непосредственное применение уравнений МРГ дает возможность получить размерные зависимости ${{T}_{{cr}}}$ и поверхностных характеристик – МН и ПН (см ниже).
Более точным является учет отклонений изменений энергий между конфигурациями в зависимости от числа длинных связей – это определяет второй способ соответствия, учитывающий многочастичный характер взаимодействий в квантовохимических расчетах.
Оба соответствия основаны на данных об энергиях для однородной фазы СЭ-кристалла. В них наличие границ не влияет на значения энергетических параметров, что является определенным приближением, т.к. прямой квантовохимический расчет указывает на влияние изменения энергий тех же самых 16 конфигураций под действием соседних протонов, влияющих на их энергетику (см. табл. 1). В этом случае квантовая химия оценивает влияние структуры границы на энергии псевдоспинов внутри объема и на границе, а МРГ одновременно учитывает изменения энергий за счет границы и отражает размерные эффекты.
Отметим, что в работах [62, 63, 68] удачное согласие с экспериментом было получено за счет использования статистической части теории для СЭ типа порядок-беспорядок Вакса [3]. Данная оценка исходит из использования энергий для четырех связанных псевдоспинов (в виде квадрата) (табл. 1). С точки зрения Займана [70], статическая часть задачи описания СЭ типа порядок– беспорядок в рамках теории молекулярного поля достаточна точная для качественных оценок по сравнению с проблемой расчета квантовохимических энергий конфигураций. Здесь под термином “молекулярное поле” понимается весь класс приближенных кластерных методов (так, квадраты псевдоспинов обеспечивают ~7% от точного значения ${{T}_{{cr}}}$, а простейший кластер из двух псевдоспинов – ~20%). Ниже для описания размерных эффектов ограничимся использованием кластера из двух псевдоспинов – это т.н. квазихимическое приближение (КХП) учета прямых корреляций.
Данные по учету влияния границы на энергии тех же конфигураций протонов представлены в табл. 1. В столбце D приведены энергии для всех 16 возможных конфигураций псевдоспинов в полносимметричном окружении. Следующие столбцы иллюстрируют приближение деформирующей границы: в соседнем с центральным элементарном тетраэдре, ближайшем к границе, протоны из его внешнего окружения смещаются по направлению от центра – сначала один (столбец E), затем два (F) и, наконец, все три периферических протона (G). Видно, что наличие границы незначительно, но уменьшает весь диапазон энергий 16 возможных псевдоспиновых конфигураций, при этом снимается вырождение тех из них, что были вырождены в полносимметричном случае, и расщепление этих состояний выражено тем сильнее, чем больше влияние границы, которая модулирует среднее молекулярное поле, создаваемое для четырех центральных псевдоспинов их окружением.
Ниже рассмотрены три ситуации, для которых строятся уравнения МРГ: 1) квантовая химия дает одну среднюю оценку энергии взаимодействия между псевдоспинами, тогда МРГ дает для нее размерные оценки; 2) квантовая химия дает средние оценки энергий взаимодействия для типовых конфигураций протонов, тогда МРГ должна учесть более детальное описание энергии и дать размерные оценки; 3) квантовая химия оценивает влияние границы на энергии псевдоспинов внутри объема и на границе, тогда МРГ учитывает изменение энергий за счет границы и дает размерные эффекты.
ОСНОВЫ МОДЕЛИ РЕШЕТОЧНОГО ГАЗА
При понижении температуры в кристаллах типа KDP возникает спонтанная поляризация, связанная с характером распределения протонов по водородным связям, формирующих разное количество длинных и коротких связей относительно ионов фосфора. С этой физической картиной в рамках МРГ сопоставляются распределения частиц А и В внутри своих ячеек, в которых происходит замена одной из частиц А или В на другую В или А [3, 50–56]. То есть число относительно смещенных протонов заменяется на число измененных состояний занятости узлов МРГ компонентами смеси А + В. Этот путь с привлечением понятия о бинарной смеси А + В стехиометрического состава А : В = 1 : 1 оказался эффективным для исследования термодинамики упорядоченных систем, в т.ч. поверхностных и размерных эффектов [57, 58].
Энергия частиц бинарной смеси А + В задается парными эффективными потенциалами взаимодействия εij (i, j = A, B), которые отвечают за упорядочение компонентов в решетке с числом ближайших соседей z [57]. В нашем случае система состоит из двух взаимопроникающих подрешеток в простой кубической решетке (z = 6). Первую подрешетку, узлы которой преимущественно заняты частицами А, обозначим через α, вторую подрешетку, узлы которой преимущественно заняты частицами В, обозначим через β. Каждый узел α-подрешетки окружен узлами β‑подрешетки, и наоборот. Это позволяет задать упорядоченное состояние частиц с помощью введенных в [55] функций распределения узлов разного типа: fα= fβ= 1/2, zαβ= zβα= z.
Обозначим через $\theta _{f}^{{\text{A}}}$ вероятность заполнения узлов типа f частицами А. Уравнения [55, 57] в КХП локальных заполнений узлов разного типа в однородной объемной фазе (внутренние степени свободы частиц и их парные потенциалы взаимодействия, аппроксимируемые параметрами ω = = εАА + εВВ – 2εАВ, не зависят от типа узла подрешетки) и в переходной области на границе домена в зависимости от $a_{f}^{i}P_{f}^{i}$, где $P_{f}^{i}$ и $a_{f}^{i}$ – локальное давление и локальная константа Генри компонента i, запишутся как
(1)
$\frac{{a_{f}^{{\text{A}}}P_{f}^{{\text{A}}}}}{{a_{f}^{{\text{B}}}P_{f}^{{\text{B}}}}} = \frac{{\theta _{f}^{{\text{A}}}}}{{1 - \theta _{f}^{A}}}{{\prod\limits_{g \in G\left( f \right)} {\left[ {t_{{fg}}^{{{\text{AB}}}}\exp \left\{ {\beta \left( {{{\varepsilon }^{{{\text{BB}}}}} - {{\varepsilon }^{{{\text{BA}}}}}} \right)} \right\} + t_{{fg}}^{{{\text{AA}}}}\exp \left\{ {\beta \left( {{{\varepsilon }^{{{\text{AB}}}}} - {{\varepsilon }^{{{\text{AA}}}}}} \right)} \right\}} \right]} }^{{{{z}_{{fg}}}}}},$Условная вероятность нахождения частиц АА в соседних узлах fg определяется как $t_{{fg}}^{{{\text{AA}}}} = \theta _{{fg}}^{{{\text{AA}}}}{\text{/}}\theta _{f}^{{\text{A}}}$, $\theta _{{fg}}^{{{\text{AA}}}} = 2\theta _{f}^{{\text{A}}}\theta _{g}^{{\text{A}}}{\text{/}}(\delta + b)$, δ = 1 + x × × $(1 - \theta _{f}^{{\text{A}}} - \theta _{g}^{{\text{A}}})$, $b = {{\left( {{{\delta }^{2}} + 4x\theta _{f}^{{\text{A}}}\theta _{g}^{{\text{A}}}} \right)}^{{1/2}}}$. Также выполняются нормировки: $\sum\nolimits_j {t_{{fg}}^{{ij}}} = 1$ и $\sum\nolimits_j {\theta _{{fg}}^{{ij}}} = \theta _{f}^{i}$.
Средняя мольная плотность компонента А смеси задается как ${{\theta }^{{\text{A}}}} = \sum\nolimits_f {{{f}_{f}}\theta _{f}^{{\text{A}}}} $, где ff – доля узлов типа f от всех узлов домена.
Уравнение (1) дает размерные оценки при одной средней оценке энергии взаимодействия между псевдоспинами ω, представляемой квантовой химией (первая ситуация).
Уравнения с учетом эффективных многочастичных взаимодействий строятся аналогичным образом [55]:
(2)
$\begin{gathered} \frac{{a_{f}^{{\text{A}}}P_{f}^{{\text{A}}}}}{{a_{f}^{{\text{B}}}P_{f}^{{\text{B}}}}} = \frac{{\theta _{f}^{{\text{A}}}}}{{\theta _{f}^{{\text{B}}}}}\sum\limits_{{{{\{ {{k}_{{fg}}}\} }}_{g}}} {\exp \left\{ {\beta \left( {{{E}^{{\text{B}}}}\left( {{{k}_{f}}} \right) - {{E}^{{\text{A}}}}\left( {{{k}_{f}}} \right)} \right)} \right\}} \times \\ \times \,\,\prod\limits_{g \in G\left( f \right)} {C_{{{{z}_{{fg}}}}}^{{{{k}_{{fg}}}}}{{{\left( {t_{{fg}}^{{{\text{AA}}}}} \right)}}^{{{{k}_{{fg}}}}}}{{{\left( {t_{{fg}}^{{{\text{AB}}}}} \right)}}^{{{{z}_{{fg}}} - {{k}_{{fg}}}}}}} , \\ \end{gathered} $(3)
$\begin{gathered} {{E}^{i}}\left( {{{k}_{f}}} \right) = {{\varepsilon }_{{i{\text{A}}}}}{{k}_{f}}\left( {1 + ({{k}_{f}} - 1)\Delta {{\varepsilon }_{{i{\text{A}}}}}} \right) + \\ + \,\,{{\varepsilon }_{{i{\text{B}}}}}\left( {z - {{k}_{f}}} \right)\left( {1 + ({{k}_{f}} - 1)\Delta {{\varepsilon }_{{i{\text{B}}}}}} \right), \\ \end{gathered} $Парные функции $t_{{fg}}^{{{\text{AA}}}}$ определяются через решение системы уравнений:
(4)
$\begin{gathered} \frac{{a_{f}^{{\text{A}}}P_{f}^{{\text{A}}}}}{{a_{f}^{{\text{B}}}P_{f}^{{\text{B}}}}} = \frac{{\theta _{{fh}}^{{{\text{AA}}}}}}{{\theta _{h}^{{\text{A}}} - \theta _{{fh}}^{{{\text{AA}}}}}}\sum\limits_{\{ {{k}_{{fg}}}\} _{g}^{*}} {С_{{{{z}_{{fh}}}}}^{{{{k}_{{fh}}} + 1}}{{{\left( {t_{{fh}}^{{{\text{AA}}}}} \right)}}^{{{{k}_{{fh}}}}}}{{{\left( {t_{{fh}}^{{{\text{AB}}}}} \right)}}^{{{{z}_{{fh}}} - 1 - {{k}_{{fh}}}}}}} \times \\ \times \,\,\exp \left\{ {\beta \left( {{{E}^{{\text{B}}}}\left( {{{k}_{f}} + 1} \right) - {{E}^{{\text{A}}}}\left( {{{k}_{f}} + 1} \right)} \right)} \right\} \times \\ \times \,\,\prod\limits_{g \ne h} {С_{{{{z}_{{fg}}}}}^{{{{k}_{{fg}}}}}t_{{fg}}^{{{{k}_{{fg}}}}}{{{\left( {1 - {{t}_{{fg}}}} \right)}}^{{{{z}_{{fg}}} - {{k}_{{fg}}}}}}} . \\ \end{gathered} $Для неоднородных ситуаций на границе локальные изотермы при варьировании способов расстановки kfg частиц по zfg узлам (конфигурации σfg) выражается как
(5)
$\begin{gathered} \frac{{a_{f}^{{\text{A}}}P_{f}^{{\text{A}}}}}{{a_{f}^{{\text{B}}}P_{f}^{{\text{B}}}}} = \frac{{\theta _{f}^{{\text{A}}}}}{{\theta _{f}^{{\text{B}}}}}\sum\limits_{{{{\{ {{k}_{{fg}}}\} }}_{g}}} {\sum\limits_{\left\{ {{{\sigma }_{{fg}}}\left( {{{k}_{{fg}}}} \right)} \right\}} {\exp \left\{ {\beta \left( {E_{f}^{{\text{B}}}\left( {\left\{ {{{k}_{{fg}}}} \right\},\left\{ {{{\sigma }_{{fg}}}} \right\}} \right) - E_{f}^{{\text{A}}}\left( {\left\{ {{{k}_{{fg}}}} \right\},\left\{ {{{\sigma }_{{fg}}}} \right\}} \right)} \right)} \right\} \times } } \\ \times \,\,\prod\limits_{g \in G\left( f \right)} {{{{\left( {t_{{fg}}^{{{\text{AA}}}}} \right)}}^{{{{k}_{{fg}}}}}}{{{\left( {t_{{fg}}^{{{\text{AB}}}}} \right)}}^{{{{z}_{{fg}}} - {{k}_{{fg}}}}}}b_{{{{\sigma }_{{fg}}}\left( {{{k}_{{fg}}}} \right)}}^{{{{\sigma }_{{fg}}}\left( 0 \right)}}} . \\ \end{gathered} $Аналогичное уравнение для парной функции $\theta _{{fh}}^{{{\text{AA}}}}$ имеет вид:
(6)
$\begin{gathered} \frac{{a_{f}^{{\text{A}}}P_{f}^{{\text{A}}}}}{{a_{f}^{{\text{B}}}P_{f}^{{\text{B}}}}} = \frac{{\theta _{{fh}}^{{{\text{AA}}}}}}{{\theta _{h}^{{\text{A}}} - \theta _{{fh}}^{{{\text{AA}}}}}}\sum\limits_{\{ {{k}_{{fg}}}\} _{g}^{*}} {\sum\limits_{\left\{ {{{\sigma }_{{fg}}}\left( {{{k}_{{fg}}}} \right)} \right\}} {{{{\left( {t_{{fh}}^{{{\text{AA}}}}} \right)}}^{{{{k}_{{fh}}}}}}{{{\left( {t_{{fh}}^{{{\text{AB}}}}} \right)}}^{{{{z}_{{fh}}} - 1 - {{k}_{{fh}}}}}}} b_{{{{\sigma }_{{fh}}}\left( {{{k}_{{fh}}} + 1} \right)}}^{{{{\sigma }_{{fh}}}\left( 1 \right)}}} \times \\ \times \,\,\exp \left\{ {\beta \left( {E_{f}^{{\text{B}}}\left( {{{k}_{{fh}}} + 1,\left\{ {{{k}_{{fg \ne h}}}} \right\},\left\{ {{{\sigma }_{{fg}}}} \right\}} \right) - E_{f}^{{\text{A}}}\left( {{{k}_{{fh}}} + 1,\left\{ {{{k}_{{fg \ne h}}}} \right\},\left\{ {{{\sigma }_{{fg}}}} \right\}} \right)} \right)} \right\} \times \\ \times \,\,\prod\limits_{g \ne h} {t_{{fg}}^{{{{k}_{{fg}}}}}{{{\left( {1 - {{t}_{{fg}}}} \right)}}^{{{{z}_{{fg}}} - {{k}_{{fg}}}}}}b_{{{{\sigma }_{{fg}}}\left( {{{k}_{{fg}}}} \right)}}^{{{{\sigma }_{{fg}}}\left( 0 \right)}}} . \\ \end{gathered} $Здесь f, g и h – типы узлов, причем в каждый тип входят узлы с одинаковым окружением, так что все числа связей zfg целочисленные. В уравнении (5) для каждых заданных чисел частиц {kfg}, Σgkfg = kf, kf – число частиц А в соседних узлах вокруг узла типа f, с заданными конфигурациями {σfg(kfg)} рассчитывается функция неидеальности, в которую входят энергия $E_{f}^{i}\left( {\left\{ {{{k}_{{fg}}}} \right\},\left\{ {{{\sigma }_{{fg}}}} \right\}} \right)$ кластера со всеми соседями центрального узла заданной конфигурации и число перестановок $b_{{{{\sigma }_{{fg}}}\left( {{{k}_{{fg}}}} \right)}}^{{{{\sigma }_{{fg}}}\left( 0 \right)}}$ заданных конфигураций {σfg(kfg)} заданных частиц {kfg}.
Уравнение (6) построено при условии, что один узел типа h априори занят частицей, поэтому в первой сумме по {kfg}* значение kfh варьируется от 0 до (zfh – 1), а остальные значения kfg, g ≠ h – от 0 до zfg, где zfh и zfg – числа пар заданного типа. Это также отражено в числе перестановок $b_{{{{\sigma }_{{fh}}}\left( {{{k}_{{fh}}} + 1} \right)}}^{{{{\sigma }_{{fh}}}\left( 1 \right)}}$ для fh и в энергии кластера $E_{f}^{i}\left( {{{k}_{{fh}}} + 1,\left\{ {{{k}_{{fg \ne h}}}} \right\},\left\{ {{{\sigma }_{{fg}}}} \right\}} \right)$.
Решение системы уравнений (5) и (6) позволяет получить оценки размерных эффектов при учете влияния границы на энергии псевдоспинов как внутри объема домена, так и на его границе (ситуация 3).
Система уравнений (1)—(6) решается итерационным методом Ньютона при заданном соотношении плотности компонентов в системе θА : θB = 1 : 1 при отсутствии вакансий, т.е. ${{\theta }^{{\text{А}}}} = 0.5$ и ${{\theta }^{{\text{B}}}} = 0.5$. Также выполняется условие: ${{\theta }^{i}} = \left( {\theta _{\alpha }^{i} + \theta _{\beta }^{i}} \right){\text{/}}2$, i = = А и В.
Для получения эффективных энергий $\tilde {\varepsilon }_{{fh}}^{{{\text{AA}}}}$, $\tilde {\varepsilon }_{{fh}}^{{{\text{BB}}}}$ и $\tilde {\varepsilon }_{{fh}}^{{{\text{AB}}}}$ для пар fh решается система уравнений, полученных из условия равенства выражений (2)–(4) и
(7)
$\begin{gathered} \frac{{a_{f}^{{\text{A}}}P_{f}^{{\text{A}}}}}{{a_{f}^{{\text{B}}}P_{f}^{{\text{B}}}}} = \frac{{\theta _{{fh}}^{{{\text{AA}}}}}}{{\theta _{h}^{{\text{A}}} - \theta _{{fh}}^{{{\text{AA}}}}}}\exp \left\{ { - \beta \tilde {\varepsilon }_{{fh}}^{{{\text{AA}}}}} \right\}t_{{fh}}^{{{\text{AA}}}} \times \\ \times \,\,\prod\limits_g {{{{\left( {t_{{fg}}^{{{\text{AB}}}}\exp \left\{ {\beta ({{{\tilde {\varepsilon }}}^{{{\text{BB}}}}} - {{{\tilde {\varepsilon }}}^{{{\text{BA}}}}})} \right\} + t_{{fg}}^{{{\text{AA}}}}\exp \left\{ {\beta ({{{\tilde {\varepsilon }}}^{{{\text{AB}}}}} - {{{\tilde {\varepsilon }}}^{{{\text{AA}}}}}} \right\}} \right)}}^{{{{z}_{{fg}}} - {{\Delta }_{{gh}}}}}}} , \\ \end{gathered} $включая аналогичные выражения для пар частиц ВВ и АВ в узлах fh. Выражение (7) построено через биномиальный ряд с эффективными энергиями $\tilde {\varepsilon }_{{fh}}^{{{\text{AA}}}}$, $\tilde {\varepsilon }_{{fh}}^{{{\text{BB}}}}$ и $\tilde {\varepsilon }_{{fh}}^{{{\text{AB}}}}$. Точно так же строятся эффективные парные потенциалы и в случае ситуации 3.
Через найденный профиль локальных плотностей в узлах подрешеток α и β в переходной области на границе домена рассчитывается химический потенциал в КХП $\mu _{f}^{i}$ компонента i в узлах f:
(8)
$\beta \mu _{f}^{i} = \ln {\kern 1pt} \theta _{f}^{i} + \frac{{kT}}{2}\sum\limits_{g \in G\left( f \right)} {\ln \left[ {*\theta _{{fg}}^{{ii}}{\text{/}}(\theta _{f}^{i}\theta _{g}^{i})} \right]} ,$МН на границе между доменами с разной ориентацией псевдоспинов и ПН на границе домена и вакуума рассчитываются как суммарный избыточный химический потенциал в монослоях переходной области, $\mu _{f}^{i}$ по сравнению с химическим потенциалом в фазе домена на соответствующей подрешетке $\mu _{{\alpha /\beta }}^{i}$ [59, 71]:
где A – площадь единичной поверхности (площадь ячейки), f * – вес реперного монослоя.ОБЪЕМНАЯ ФАЗА
Важнейшей характеристикой объемной фазы СЭ является величина критической температуры, ниже которой появляется спонтанная поляризация образца. Очевидно, что квантовохимический расчет дает энергии состояний системы, многократно превышающие энергию взаимодействия изолированных протонов [1–7, 60]. Так, среднее значение различий в энергиях 16 конфигураций (табл. 1, колонка D) равно 0.284 эВ, что чуть меньше чем на два порядка превышает тепловую энергию, отвечающую экспериментальному значению Тcr = 122К для кристалла KDP [72]. Для наших целей главная задача заключается в анализе поверхностных и размерных характеристик кристалла, поэтому конкретное значение средней энергии не является принципиальным (в работах [62, 63, 68] ориентация на экспериментальное значение Тcr обеспечивалась использованием статистической части теории для СЭ [3]). Формально считаем, что существует коэффициент пересчета квантовохимических величин на область экспериментально измеряемых величин Тcr, тогда различие распределений энергий для разных длин связей будет характеризовать фактор многочастичных взаимодействий в рассматриваемой системе (табл. 1, колонка D) (в зависимости от числа длинных связей kd = 0 (0), 0.258 (1), 0.291 (2), 0.361 (3), 0.531 (4) эВ). Аналогично колонка G в табл. 1 характеризует влияние границы на энергетическое состояние тех же четырех протонов (в зависимости от числа длинных связей kd = 0 (0), 0.257 (1), 0.307 (2), 0.345 (3), 0.510 (4) эВ). Это позволяет рассматривать влияние указанных факторов в безразмерных величинах Тcr(L)/Тcr(bulk), исключающих точное значение коэффициента пересчета.
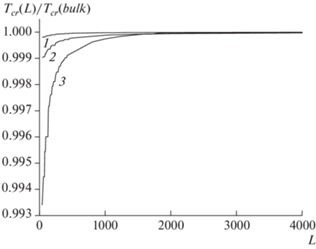
На рис. 2 показана размерная зависимость Тcr(L)/Тcr(bulk) для трех ситуаций с соответствующими номерами кривых. Наблюдается уменьшение критической температуры с уменьшением линейного размера домена во всех случаях. Этот результат соответствует полученным ранее результатам [57, 58] для такого же типа упорядочения, а также результатам для ФП 1-го рода [59]. Из рис. 2 следует, что более точный характер учета межчастичных взаимодействий влияет на диапазон размерных отклонений критической температуры упорядочения от своего объемного значения. Следует отметить, что степень отклонения упорядочения Tcr(L) невелика и не менее чем на порядок меньше, чем в случае ФП 1-го рода. Этот факт обусловлен спецификой СЭ типа порядок–беспорядок, отмеченной выше: энергетические изменения разных конфигураций протонов реализуются в поле остальных практически неизменных по своему состоянию ионов кристалла KDP. Эти изменения значительно меньше энергий связи ионов, поэтому ФП в подсистеме протонов слабо влияют на общее состояние кристалла.
ГРАНИЦА РАЗДЕЛА ФАЗ
Для учета размерных эффектов необходимо рассчитать распределение компонентов А и В на границах раздела фаз при учете взаимного влияния границ раздела фаз от разных ориентаций границ. Размерные эффекты в данной системе анализировались в работе [57]. Был рассмотрен домен в форме куба со стороной L на объемной решетке z = 6 с шестью гранями. Всего в домене находится L3 узлов. На границе домена происходит изменение состояния упорядоченной фазы: это либо межфазная граница, либо граница образца с вакуумом. (В работе [57] присутствовала стенка поры, ограничивающая домен, с внешним потенциалом Qw).
Аналогичный подход использован в данной работе. На рис. 3а показана схема поперечного центрального сечения домена со стороной L. Граница домена отмечена двойной линией. Фаза в домене имеет сторону Lph и ее ячейки отмечены белым цветом. Переходная область имеет ширину Ltr и ее ячейки отмечены светло-серым цветом. Темно-серые ячейки относятся к угловым ячейкам, связующим смежные стороны домена.
Рис. 3.
Схемы домена со стороной L (выделена область влияния границы величиной Ltr) (а) и переходной области на границе двух соседних доменов (б).
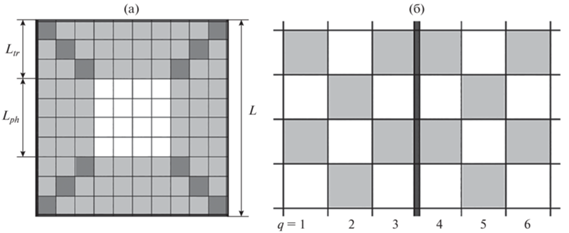
На рис. 3б показана схема переходной области на границе двух соседних доменов, где монослои 1 ≤ q ≤ 3 относятся к переходной области первого домена, а монослои 4 ≤ q ≤ 6 – к переходной области соседнего домена. Белым отмечены ячейки подрешетки α, серым – подрешетки β. Граница между доменами отмечена жирной линией. Домен обладает центральной симметрией относительно центра куба, и противоположные стенки кубического домена находятся в одинаковом состоянии, что позволяет сократить число типов узлов и понизить размерность задачи. Схема границы раздела фаз представлена на рис. 3а. На границе реализуется сдвиг по фазе на 180° в ориентациях упорядочения за счет повтора расположения подрешеток соседних доменов по отношению друг к другу (рис. 3б). Согласно схеме на рис. 3б, узлы в граничных монослоях перпендикулярно границе оказываются по соседству с одноименными узлами, что нарушает общую упорядоченность системы. В работе рассмотрены два состояния монослоев, примыкающих к границе между доменами: а – в граничном монослое рассчитываются локальные плотности на обеих подрешетках (α и β), что позволяет внутри самой задачи получить наличие или отсутствие упорядочения в монослое; б – в граничном монослое фиксируется равенство локальных плотностей на обеих подрешетках (α и β), что априори в задаче задает разупорядоченное состояние в монослое. Эти две модели границы по-разному отражают способ построения разделяющей поверхности для кубических доменов, необходимой с позиции классической термодинамики [66], связанной с отсутствием упорядочения на границе упорядоченных фаз.
Принцип влияния границы домена остается без изменения при любом радиусе ее влияния, обусловленном взаимодействиями частиц по обе стороны границы шириной Ltr (в числах монослоев). На граничных узлах домена на состояния внутренних узлов могут действовать одновременно частицы из соседних доменов. Их максимальное число равно ns (0 ≤ ns ≤ 3). Учет упорядочения компонентов А и В и неоднородность в распределениях частиц описываются функциями узлов разного типа [55, 57]. Доля узлов в вершинах куба равна: ${{f}_{v}} = 8L_{{tr}}^{3}{\text{/}}{{L}^{3}}$. В вершинах имеется $L_{{tr}}^{3}$ узлов α- и β‑решетки. Доля узлов отдельного типа в вершинах fq = 4/L3. Доля узлов на ребрах куба равна ${{f}_{e}} = 4L_{{tr}}^{2}{{L}_{{ph}}}{\text{/}}{{L}^{3}}$. В ребрах имеется $L_{{tr}}^{2}$ типов узлов α-решетки и столько же типов узлов β-решетки. Доля узлов отдельного типа в ребрах fq = 2(L – ‒ 2Ltr)/L3. Доля узлов на гранях куба равна ${{f}_{e}} = 2{{r}_{s}}L_{{ph}}^{2}{\text{/}}{{L}^{3}}$. Здесь также доля узлов отдельного типа на гранях ${{f}_{q}} = L_{{ph}}^{2}{\text{/}}{{L}^{3}}$. В целом доля узлов внутри куба равна: ${{f}_{e}} = L_{{ph}}^{3}{\text{/}}{{L}^{3}}$. Как и в объеме, здесь имеются два типа узлов на решетках α и β. Доля узлов в центре куба ${{f}_{q}} = L_{{ph}}^{3}{\text{/2}}{{L}^{3}}$.
Таким образом, доля узлов в домене заданного типа q, которому соответствует определенное число ns, равна: ${{f}_{q}}\left( {{{n}_{s}}} \right)$ = $\frac{{{{2}^{{{{n}_{s}}}}}{{{\left( {L - 2{{L}_{{tr}}}} \right)}}^{{3 - {{n}_{s}}}}}}}{{2{{L}^{3}}}}$, где двойка в знаменателе связана с тем, что имеются две подрешетки – α и β, ${{2}^{{{{n}_{s}}}}}$ – множитель, связанный с тем, что типы узлов у противоположных стенок совпадают, данный множитель отражает свойство симметрии и повышает вес типов узлов, считаемых идентичными в силу симметрии. С данной функцией распределения были проведены расчеты для разных значений стороны домена L. Ширина переходной области границы Ltr определяется из минимума свободной энергии системы и ищется итерационным способом, как и в задаче c переходной областью жидкость–пар [57, 59].
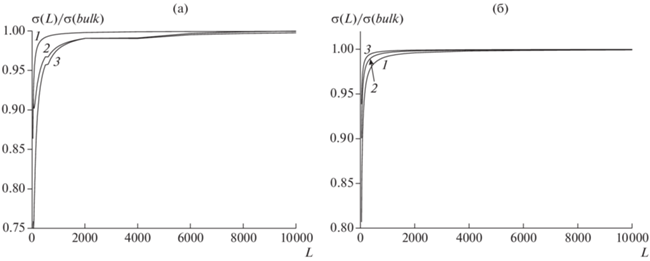
На рис. 4 показаны размерные зависимости МН на границе двух доменов соответственно для трех ситуаций с соответствующими номерами кривых для вариантов границ а и б (4а и 4б соответственно). Значения МН σ(L) нормированы на соответствующие значения в макросистеме σ(bulk), когда отсутствует размерный эффект. Нижний предел рассмотренного интервала размеров домена ограничен оценкой в 29 параметров решетки (здесь число монослоев) [59], выше которой обосновано применение термодинамики границ раздела фаз.
Получено уменьшение МН с уменьшением линейного размера домена во всех случаях. Наибольшее влияние размера домена наблюдается для кривой 1 – учет эффективных парных взаимодействий (эта величина определяется максимальным диапазоном значений энергий из квантовой химии, что дает оценку средней энергии взаимодействия между псевдоспинами). По мере уточнения влияния локальных распределений электронов размерный эффект уменьшается. Для кривой 2 учитывается отклонение локальной энергии от парного потенциала в объеме, а для кривой 3 – и в объеме, и на границе. МРГ учитывает эти изменения энергий за счет межфазной границы и отражает общий размерный эффект.
Хотя для всех трех вариантов описания локальных энергий получено уменьшение величин МН с уменьшением линейного размера домена, однако модель границы влияет на взаимное расположение размерных зависимостей МН. Для варианта границы а самый малый размерный эффект наблюдается для ситуации 1, а самый большой размерный эффект – для ситуации 3. Для варианта границы б, наоборот, самый малый размерный эффект наблюдается для ситуации 3, а самый большой размерный эффект – для ситуации 1.
Обнаруженный фактор влияния модели границы требует дальнейшего анализа, т.к. традиционные методы выделения разделяющей поверхности в термодинамике ориентированы на простейшую геометрию системы [66]. В данном случае разделяющая поверхность, к которой относится рассчитываемая величина МН, имеет сложную форму, включающую в себя как число узлов переходной области Ltr на сторонах середины куба, так и угловые области домена, в которых существует влияние взаимодействия частиц со стороны соседних граней куба. Формально, следует отметить влияние модели границы на величину Тcr(L) для малых размеров доменов (влияние границы отсутствует для макрофаз). Проведенный анализ показал, что в рассмотренном диапазоне величин L модель разупорядоченной границы б дает несколько более сильную размерную зависимость Тcr(L) в области нижних величин L, чем модель границы а, для всех видов потенциальных зависимостей. Однако это отличие незначительно (менее 1%), поэтому форма кривых на рис. 2 практически не меняется. Причина незначительности влияния модели границы на Тcr(L) заключается в том, что нижний предел L соответствует области применимости термодинамики [59].
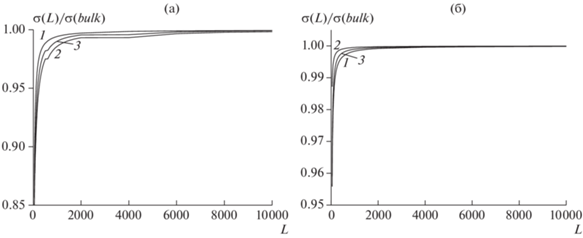
На рис. 5 показаны размерные зависимости ПН на границе домена с вакуумом соответственно для трех ситуаций с соответствующими номерами кривых для вариантов границ а и б (5а и 5б соответственно). Значения ПН σ(L) нормированы на соответствующие значения в макросистеме σ(bulk), когда отсутствует размерный эффект. Нижний предел рассмотренного интервала размеров изолированного домена ограничен оценкой в 40 параметров решетки (здесь монослоев) [59], выше которой обосновано применение термодинамики границ раздела фаз. Эта величина отличается от аналогичной величины для объемных фаз, т.к. относится к двумерной геометрии поверхности [59].
Как и выше, установлено уменьшение ПН с уменьшением линейного размера домена для трех вариантов описания локальных энергий. Для варианта границы а самый малый размерный эффект наблюдается для ситуации 1, а самый большой размерный эффект – для ситуации 2. Для варианта границы б, наоборот, самый малый размерный эффект наблюдается для ситуации 2, а самый большой размерный эффект – для ситуации 1.
Полученные размерные кривые для ПН носят оценочный характер, т.к. граница с вакуумом означает наличие разрывов связей для всех ионов твердого тела, а не только для протонов. Этот фактор сейчас не учитывается. Для количественного описания характеристик границы СЭ–вакуум необходимо перейти к более детальной модели приповерхностной области, включающей в себя как разрыв наружных связей всех ионов, так и наличие в твердом теле вакансий. В случае ПН также наблюдается зависимость от модели границы.
ЗАКЛЮЧЕНИЕ
Выполнен первый микроскопический расчет МН и ПН для СЭ типа порядок-беспорядок на основе известной эквивалентности модели Изинга как для спиновых систем, так и для МРГ [50, 51, 56]. Расчет зависимостей Тcr(L), МН и ПН от L проведен в квазихимическом приближении в МРГ с учетом прямых корреляций распределения соседних компонентов бинарной смеси А + В. Обнаружено влияние модели границы на рассчитываемые величины поверхностных характеристик МН и ПН, что обусловлено сложной формой разделяющей поверхности для доменов в виде ограниченного куба.
Модель является феноменологической: она использует эффективные энергетические парные параметры, соответствующие величине критической температуры упорядочения в объемной фазе, а также более точному распределению энергий в рассматриваемых кластерах квантовохимическими методами с помощью эффективных многочастичных потенциалов. Модель позволяет оценивать поверхностные и размерные вклады в характеристики СЭ типа KDP.
С помощью этой модели можно проводить широкий спектр численных исследований характеристик неоднородных СЭ типа KDP. Простейшие примеры расчета МН и ПН, наряду с расчетами Тcr(L), приведенные в данной работе, демонстрируют ее возможности. Таким образом, в дополнение к существующим подходам по описанию свойств СЭ в рамках феноменологической теории [44–49] и ее современных вариантов [32–43] предложен альтернативный микроскопический подход в строгом соответствии с понятиями термодинамики [66].
Полученные результаты для локальных микроскопических систем указывают на необходимость построения более конкретной модели границ раздела упорядоченных фаз и границ твердая фаза–пар, как и совместного включения разных факторов (неоднородности системы, деформаций решетки и т.д.), для выхода на реальный эксперимент. Однако уже приведенные примеры указывают на перспективность нового подхода.
Список литературы
Иона Ф., Ширане Д. Сегнетоэлектрические кристаллы. М.: Мир, 1965. 556 с.
Сонин А.С., Струков Б.А. Введение в сегнетоэлектричество. М.: Высшая школа, 1970. 272 с.
Вакс В.Г. Введение в микроскопическую теорию сегнетоэлектриков. М.: Наука, 1973. 327 с.
Блинц Р. Сегнетоэлектрики и антисегнетоэлектрики. Динамика решетки. М.: Мир, 1975. 398 с.
Лайнс М., Гласс А. Сегнетоэлектрики и родственные им материалы. М.: Мир, 1981. 735 с.
Струков Б.А., Леванюк А.П. Физические основы сегнетоэлектрических явлений в кристаллах. М.: Наука, 1983. 240 с.
Веневцев Ю.Н., Политова Е.Д., Иванов С.А. Сегнето- и антисегнетоэлектрики семейства титаната бария. М.: Химия, 1985. 256 с.
Блинов Л.М., Фридкин В.М., Палто С.П., Буне А.В., Даубен П.А., Дюшарм С. Двумерные сегнетоэлектрики // УФН. 2000. Т. 170. № 3. С. 247–262. https://doi.org/10.3367/UFNr.0170.200003b.0247
Кочервинский B.В. Электрофизические свойства сверхтонких пленок сегнетоэлектрических полимеров // Высокомолекулярные соединения. Серия Б. 2005. Т. 47. № 3. С. 542–576.
Фридкин В.М. Критический размер в сегнетоэлектрических наноструктурах // УФН. 2006. Т. 176. № 2. С. 203–212.
Фридкин В.М., Дюшарм С. Сегнетоэлектричество в наноразмерной области // УФН. 2014. Т. 184. № 6. С. 645–651. https://doi.org/10.3367/UFNr.0184.201406d.0645
Барышников С.В., Чарная Е.В., Меределина Т.А., Милинский А.Ю., Гойхман А.Ю., Максимова К.Ю. Линейные и нелинейные диэлектрические свойства пленочных гетероструктур BaTiO3/Si, полученных методом импульсного лазерного осаждения // ФТТ. 2015. Т. 57. № 2. С. 375–379.
Меределина Т.А., Барышников С.В., Стукова Е.В. Вклад свободных носителей заряда в диэлектрический отклик кристаллов ниобата калия // Изв. РАН. Сер. физ. 2016. Т. 80. № 9. С. 1297–1300.
Stukova E.V., Astapova E.S., Vanina E.A. Size Effects in Solid Solutions Na(NO3)x(NO2)1–x // Rare Met. 2009. V. 28. P. 637–639.
Baryshnikov S.V., Tien C., Charnaya E.V., Lee M.K., Michel D., Böhlmann W., Stukova E.V. Dielectric Properties of Mesoporous Sieves Filled with NaNO2 // Ferroelectrics. 2008. V. 363. P. 177–186. https://doi.org/10.1080/00150190802026127
Emelianov N.A. Structure and Dielectric Properties of Composite Material Based on Surface-Modified BaTiO3 Nanoparticles in Polystyrene // Eur. Phys. J. Appl. Phys. 2015. V. 69. № 1. P. 10401–10405. https://doi.org/10.1051/epjap/2014140343
Семенов А.А., Дедык А.И., Мыльников И.Л., Пахомов О.В., Богачев Ю.В., Князев М.Н., Павлова Ю.В., Белявский П.Ю. Исследование сегнетоэлектрических многослойных структур со свойствами мультиферроиков на основе пленок титаната бария-стронция // ФТТ. 2015. Т. 57. № 3 С. 523–530.
Tumarkin A., Gagarin A., Altynnikov A., Gaidukov M., Odinets A., Razumov., Kozyrev A. Effect of Annealing in Oxygen Atmosphere on Structure and Microwave Properties of Multilayered Tunable (Ba, Sr)TiO3 Capacitors // Thin Solid Films. 2015. V. 593. P. 189–192. https://doi.org/10.1016/j.tsf.2015.09.057
Shaw T.M., Trolier-McKinstry S., McIntyre P.C. The Properties of Ferroelectric Films at Small Dimensions // Ann. Rev. Mater. Sci. 2000. V. 30. P. 263–298. https://doi.org/10.1146/annurev.matsci.30.1.263
Барышников С.В., Чарная Е.В., Стукова Е.В., Милинский А.Ю., Tien C. Диэлектрические исследования нанопористых пленок оксида алюминия, заполненных сегнетовой солью // ФТТ. 2010. Т. 52. № 7. С. 1347–1350.
Трюхан Т.А., Стукова Е.В., Барышников С.В. Диэлектрические свойства триглицинсульфата в пористых матрицах // Изв. Самарского научного центра Российской академии наук. Физика и электроника. 2010. Т. 12. № 4. С. 97–99.
Colla E.V., Koroleva E.Yu., Kumzerov W.A., Savenko B.N., Vakhrushev S.B. Ferroelectric Phase Transitions in Materials Embedded in Porous Media // Ferroelectric Lett. 1996. V. 20. P. 143–147. https://doi.org/10.1080/07315179608204732
Домашевская Э.П., Терехов В.А., Кашкаров В.М., Мануковский Э.Ю., Турищев С.Ю., Молодцов С.Л., Вялых Д.В., Хохлов А.Ф., Машин А.И., Шенгуров В.Г., Светлов С.П., Чалков В.Ю. Синхротронные исследования особенностей электронно-энергетического спектра кремниевых наноструктур // ФТТ. 2004. Т. 46. С. 335–340.
Рогазинская О.В., Миловидова С.Д., Сидоркин А.С., Чернышев В.В., Бабичева Н.Г. Свойства нанопористого оксида алюминия с включениями триглицинсульфата и сегнетовой соли // ФТТ. 2009. Т. 51. № 7. С. 1430–1432.
Голицына О.М., Дрождин С.Н., Гриднев А.Е., Чернышев В.В., Занин И.Е. Диэлектрические свойства пористого оксида алюминия с включениями триглицинсульфата и сегнетовой соли // Изв. РАН. Сер. физ. 2010. Т. 74. № 9. С. 1347–1350.
Барышников С.В., Чарная Е.В., Шацкая Ю.А., Милинский А.Ю., Самойлович М.И., Michel D., Tien C. Влияние ограниченной геометрии на линейные и нелинейные диэлектрические свойства триглицинсульфата вблизи фазового перехода // ФТТ. 2011. Т. 53. № 6. С. 1146–1149.
Kinka M., Banys Ju., Naberezhnov A. Dielectric Properties of Sodium Nitrite Confined in Porous Glass // Ferroelectrics. 2007. V. 348. P. 67–74. https://doi.org/10.1080/00150190701196161
Поправко Н.Г., Тучина Ю.С. Структура и электрические свойства нанокомпозитов с включениями ТГС // Вестн. ТГТУ. 2012. Т. 18. С. 731–736.
Борисов В.С., Щербаченко Л.А. Особенности состояния термодинамического равновесия тонкой водной пленки, находящейся в электрическом поле активных центров поверхности кристалла слюды // ФТТ. 2009. Т. 51. С. 2394–2399.
Голицына О.М., Дрождин С.Н. Диэлектрические свойства пленочных материалов на основе полиэтилентерефталата и поликарбоната с сегнетоэлектрическими включениями // ФТТ. 2012. Т. 54. № 8. С. 1503–1506.
Голицына О.М., Дрождин С.Н., Нечаев В.Н., Висковатых А.В., Кашкаров В.М., Гриднев А.Е., Чернышев В.В. Диэлектрические свойства пористых оксидов алюминия и кремния с включениями триглицинсульфата и его модифицированных аналогов // ФТТ. 2013. Т. 55. № 3. С. 479–484.
Bratkovsky A.M., Levanyuk A.P. Abrupt Appearance of the Domain Pattern and Fatigue of Thin Ferroelectric Films // Phys. Rev. Lett. 2000. V. 84. P. 3177. https://doi.org/10.1063/1.1324458
Bratkovsky A.M., Levanyuk A.P. Very Large Dielectric Response of Thin Ferroelectric Films with the Dead Layers // Phys. Rev. B. 2001. V. 63. P. 132103. https://doi.org/10.1103/PhysRevB.63.132103
Bratkovsky A.M., Levanyuk A.P. Formation and Rapid Evolution of Domain Structure at Phase Transitions in Slightly Inhomogeneous Ferroelectrics and Ferroelastics // Phys. Rev. B. 2002. V. 66. P. 184109. https://doi.org/10.1103/PhysRevB.66.184109
Bratkovsky A.M., Levanyuk A.P. Smearing of Phase Transition due to a Surface Effect or a Bulk Inhomogeneity in Ferroelectric Nanostructures // Phys. Rev. Lett. 2005. V. 94. P. 107601. https://doi.org/10.1103/PhysRevLett.94.107601
Bratkovsky A.M., Levanyuk A.P. Phase Transitions and Ferroelectricity in Very Thin Films: Homogeneous and Inhomogeneous (Domains) States // Integr. Ferroelectrics. 2006. V. 84. P. 3–21. https://doi.org/10.1080/10584580601077831
Нечаев В.Н., Висковатых А.В. Об изменении механизма фазового перехода в сегнетоэлектрическом включении нанокомпозита сегнетоэлектрик−диэлектрик в зависимости от его размеров // ФТТ. 2015. Т. 57. № 4. С. 704–709.
Нечаев В.Н., Шуба А.В. О возможном механизме повышения температуры фазового перехода в композите сегнетоэлектрик–диэлектрик // ФТТ. 2014. Т. 56. № 5. С. 949–952.
Нечаев В.Н., Висковатых А.В. Влияние температурных напряжений на температуру фазового перехода в нанокомпозите сегнетоэлектрик-диэлектрик // ФТТ. 2014. Т. 56. № 10. С. 1930–1933.
Нечаев В.Н., Висковатых А.В. О механизме повышения температуры фазового перехода в сегнетоактивных нанокомпозитах // ФТТ. 2016. Т. 58. № 12. С. 2377–2379. https://doi.org/10.21883/ftt.2016.12.43859.466
Нечаев В.Н., Шуба А.В. О неоднородных поляризованных состояниях вблизи точки фазового перехода в тонкой сегнетоэлектрической пленке // ФТТ. 2018. Т. 60. № 7. С. 1322–1327.
Чандра П., Литтлвуд П.Б. // Физика сегнетоэлектриков. Современный взгляд / Под ред. Рабе К.М. и др. М: БИНОМ. Лаборатория знаний, 2015. С. 84–134.
Лихтенштейгер С., Даубер М., Трискон Ж.-М. Физика сегнетоэлектриков. Современный взгляд / Под редакцией Рабе К.М. и др. М.: БИНОМ. Лаборатория знаний, 2015. С. 346.
Ландау Л.Д. Сб. науч. тр. М.: Наука, 1969. Т. 1. С. 97.
Ландау Л.Д. Сб. науч. тр. М.: Наука, 1969. Т. 1. С. 123.
Ландау Л.Д. Сб. науч. тр. М.: Наука, 1969. Т. 1. С. 234.
Ландау Л.Д., Лифшиц Е.М. Сб. науч. тр. М.: Наука, 1969. Т. 1. С. 128.
Гуфан Ю.М. Структурные фазовые переходы. М.: Наука, 1982. 304 с.
Толедано Ж.-К., Толедано П. Теория Ландау фазовых переходов. М.: Мир, 1994. 462 с.
Хилл Т. Статистическая механика. М.: Изд-во иностр. лит., 1960. 485 с.
Хуанг К. Статистическая механика. М.: Мир, 1966. 520 с.
Кривоглаз А.М., Смирнов А.А. Теория упорядочивающихся сплавов. М.: ГИФМЛ, 1958. 388 с.
Мозольков А.Е., Федянин В.К. Дифракция медленных электронов поверхностью. М.: Энергоиздат, 1982. 144 с.
Товбин Ю.К. Кинетика и равновесие в упорядоченных системах // ДАН СССР. 1984. Т. 277. № 4. С. 917–921.
Товбин Ю.К. Тeория физико-химичeских процессов на границe газ–твeрдоe тeло. М.: Наука, 1990. 288 с.
Кубо Р. Статистическая механика. М.: Мир, 1967. 452 с.
Зайцева Е.С., Товбин Ю.К. Влияние ограниченности объема системы на критическую температуру упорядочения бинарной системы А0.5В0.5 в модели решеточного газа // ЖФХ. 2020. Т. 94. № 6. С. 951–955. https://doi.org/10.31857/S0044453720060345
Зайцева Е.С., Товбин Ю.К. Влияние непрямых корреляций на критическую температуру упорядочения бинарной системы А0.5В0.5 в объемной фазе и ограниченных кубических доменах // ЖФХ. 2021. Т. 95. № 10. С. 1481–1489. https://doi.org/10.31857/S0044453721100320
Товбин Ю.К. Малые системы и основы термодинамики. М.: Физматлит, 2018. 404 с.
Жирнов В.А. К теории доменных стенок в сегнетоэлектриках // ЖЭТФ. 1958. Т. 38. С. 1175–1180.
Levin A.A., Dolin S.P. Direct and Indirect Proton–Proton Coupling in Quantum-Chemical Theory of H‑Bonded Materials // J. Mol. Struct. 2000. V. 552. P. 39–44. https://doi.org/10.1016/S0022-2860(00)00457-9
Dolin S.P., Mikhailova T.Yu., Breslavskaya N.N. et al. On the Possibility of Quantum-Chemical Cluster Approach to the Description of Structural Phase Transition in H-Bonded Materials on the Example of KDP // Int. J. Quant. Chem. 2016. V. 116. № 3. P. 202–210. https://doi.org/10.1002/qua.25037
Долин С.П., Михайлова Т.Ю., Бреславская Н.Н. О влиянии расширения модельного кластера на результаты микроскопического описания свойств Н‑связанных сегнетоэлектриков семейства KDP // Журн. неорган. химии. 2020. Т. 65. № 4. С. 522–527. https://doi.org/10.31857/S0044457X20040224
Хуберт А. Теория доменных стенок в упорядоченных средах. М.: Мир, 1977. 308 с.
Сидоркин А.С. Доменная структура в сегнетоэлектриках и родственных материалах. М.: Физматлит, 2000. 240 с.
Гиббс Дж.В. Термодинамика. Статистическая механика. М.: Наука. 1982. 584 с.
Ландау Л.Д., Лифшиц Е.М. Теоретическая физика. Т. 8. Электродинамика сплошных сред. М.: Наука, 1982. 623 с.
Долин С.П., Михайлова Т.Ю., Бреславская Н.Н. Возможности упрощенных схем изучения особенностей структурных фазовых переходов в Н-связанных сегнетоэлектриках с помощью квантово-химических расчетов // Журн. неорган. химии. 2021. Т. 65. № 5. С. 615–622. https://doi.org/10.31857/S0044457X21050044
Долин С.П., Михайлова Т.Ю., Бреславская Н.Н. Возможности квантовохимического моделирования доменных границ в кластерном приближении модели Изинга для материалов семейства KDP // Журн. неорган. химии. 2022. Т. 67. № 8.
Займан Дж. Модели беспорядка. М.: Мир, 1972. 592 с.
Оно С., Кондо С. Молекулярная теория поверхностного натяжения. М.: Изд-во иностр. лит., 1963. 292 с.
Grindlay J., ter Haar D. On the Ferroelectric Behaviour of Potassium Dihydrogen Phosphate // Proc. Royal Soc. London, A. 1959. V. 250. P. 266–285. https://doi.org/10.1098/rspa.1959.0063
Дополнительные материалы отсутствуют.
Инструменты
Неорганические материалы