Журнал неорганической химии, 2019, T. 64, № 3, стр. 314-317
Расчет фазовой диаграммы системы NaCl–RaCl2 на основании анализа систем NaCl–MCl2 (M = Ca, Sr, Ba) с использованием уравнения Шредера–Ле Шателье
И. К. Гаркушин 1, *, А. В. Бурчаков 1, У. А. Емельянова 1
1 Самарский государственный технический университет,
443100 Самара, ул. Молодогвардейская, 244, Россия
* E-mail: uliana_sergeeva@bk.ru
Поступила в редакцию 06.03.2018
После доработки 28.03.2018
Принята к публикации 15.08.2018
Аннотация
Выполнен прогноз фазовых равновесий в двухкомпонентной системе NaCl–RaCl2 на основе двойных систем NaCl–MCl2 (M = Ca, Sr, Ba). Все рассматриваемые системы эвтектического типа. Проведена обработка экспериментальных данных и получены функциональные зависимости Te/Z = f(Z) и Te/r = f(r), где Te – температура плавления эвтектики в двухкомпонентных системах NaCl–CaCl2, NaCl–SrCl2 и NaCl–BaCl2, Z – порядковый номер, а r – ионный радиус элементов Ca, Sr и Ba. Дальнейшими расчетами с помощью этих функций определена температура плавления эвтектики в системе NaCl–RaCl2. С помощью уравнения Шредера–Ле Шателье рассчитан состав двухкомпонентной эвтектики в прогнозируемой системе, молярная энтальпия плавления RaCl2, а также построены ветви ликвидуса системы.
ВВЕДЕНИЕ
Большое значение в неорганической и физической химии имеет прогнозирование и расчет свойств элементов, простых веществ, соединений и смесей в группах Периодической системы Д.И. Менделеева. В работах [1–3] приводятся аналитические и графические зависимости свойств от различных параметров: порядковых номеров s1-элементов, ионных радиусов, отношения ионных радиусов, энергий связи, энергий кристаллических решеток, ионного потенциала и т.д. Использование различных методов прогноза и моделирования фазовых равновесий многокомпонентных систем актуально в современном физико-химическом анализе [1–17].
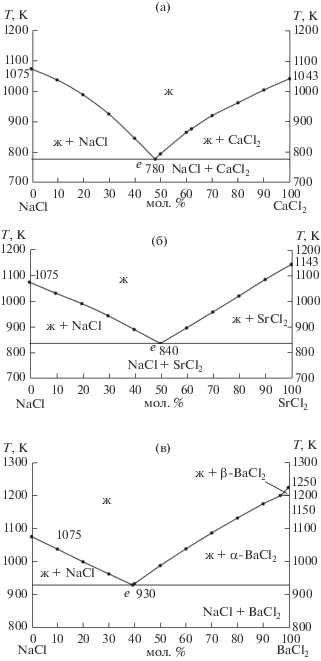
В настоящей работе изложены результаты прогноза состава и температуры плавления эвтектики, образующейся в двухкомпонентной системе NaCl–RaCl2, аналитическим методом, описанным в [1]. Прогнозирование фазовой диаграммы двойной системы NaCl–RaCl2 состоит из нескольких этапов. На первом этапе проведен литературный обзор термических свойств индивидуальных веществ [18–20] и фазовых равновесий в двойных системах NaCl–MCl2 (M = Ca, Sr, Ba) [21, 22]. На втором этапе изучены системы NaCl–MCl2, где M = Ca, Sr, Ba – щелочноземельные металлы (рис. 1). Все они относятся к эвтектическому типу [21, 22]. Поскольку топология фазовых диаграмм рассматриваемых систем одинакова, можно предположить, что система NaCl–RaCl2 также относится к эвтектическому типу.
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
На следующем этапе выполнено построение графиков функций Te/Z = f(Z) и Te/r = f(r) по трем точкам, которым соответствуют значения температур плавления эвтектик для систем NaCl–MCl2 (M = Ca, Sr, Ba), значения порядкового номера Z и ионного радиуса r металлов Ca, Sr, Ba (рис. 2, 3). Данные для построения представлены в табл. 1 и 2. Определены искомые функциональные зависимости с помощью инструментов MO Excel:
(1)
${{{{T}_{e}}} \mathord{\left/ {\vphantom {{{{T}_{e}}} Z}} \right. \kern-0em} Z} = {\text{471}}{\text{.35}}{{Z}^{{ - 0.835}}};R = {\text{0}}{\text{.9988; }}\sigma = {\text{0}}{\text{.39;}}$(2)
$\begin{gathered} {{{{T}_{e}}} \mathord{\left/ {\vphantom {{{{T}_{e}}} r}} \right. \kern-0em} r} = 507{\kern 1pt} 579{{r}^{2}} - 145{\kern 1pt} 211r + 17{\kern 1pt} 112; \\ R = 1;\,\,\,\,\sigma = {\text{0}}{\text{.17;}} \\ \end{gathered} $Рис. 2.
Зависимость отношения Te/Z от порядкового номера щелочноземельного металла (Z), звездочкой отмечена прогнозируемая система.
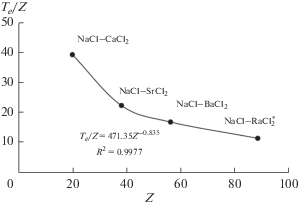
Рис. 3.
Зависимость отношения Te/r от ионного радиуса металла (r), звездочкой отмечена прогнозируемая система.
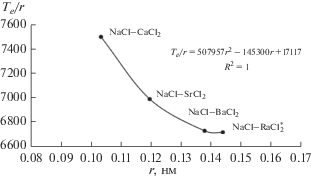
Таблица 2.
Данные [23] для построения зависимости Te/r от ионного радиуса металла (r) для систем NaCl–MCl2 (M = Ca, Sr, Ba)
| r, нм | Te, K | Te/r |
|---|---|---|
| 0.104 | 780 | 39 |
| 0.120 | 839 | 22.09 |
| 0.138 | 930 | 16.6 |
Экстраполяцией функций (1) и (2) для Z = 88 и r = 0.144 нм, относящихся к хлориду радия, выявлены два значения температур плавления эвтектики в системе NaCl–RaCl2: Te1 = 987 и Te2 = 969 K соответственно.
С помощью уравнения Шредера–Ле Шателье [23] проведен расчет мольной доли NaCl в двойной эвтектике системы NaCl–RaCl2:
(3)
$\ln x({\text{NaCl}}) = \frac{{{{\Delta }_{m}}H({\text{NaCl)(}}{{T}_{e}} - {{T}_{m}}({\text{NaCl}}))}}{{R{{T}_{m}}({\text{NaCl}}){{T}_{e}}}},$Определена мольная доля NaCl в двойной эвтектике для двух значений температур Te1 и Te2: x1(NaCl) = 0.757 и x2(NaCl) = 0.709 и рассчитана мольная доля RaCl2 в двойной эвтектике в соответствии с результатами предыдущего расчета: х1(RaCl2) = 0.243; х2(RaCl2) = 0.291.
На основании уравнения Шредера–Ле Шателье для RaCl2:
(4)
$\ln x({\text{RaC}}{{{\text{l}}}_{{\text{2}}}}) = \frac{{{{\Delta }_{m}}H({\text{RaC}}{{{\text{l}}}_{{\text{2}}}}{\text{)(}}{{T}_{e}} - {{T}_{m}}({\text{RaC}}{{{\text{l}}}_{{\text{2}}}}))}}{{R{{T}_{m}}({\text{RaC}}{{{\text{l}}}_{{\text{2}}}}){{T}_{e}}}}$На последнем этапе построены ветви кристаллизации ж ⇄ NaCl и ж ⇄ RaCl2 по уравнению Шредера–Ле Шателье:
(5)
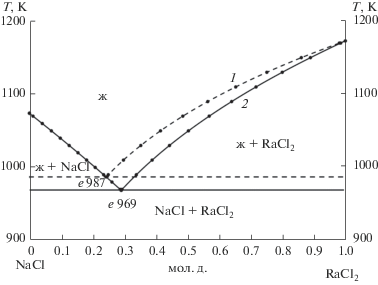
$\ln x{{(k)}_{i}} = \frac{{{{\Delta }_{m}}{{H}_{k}}({{T}_{i}} - {{T}_{m}}(k))}}{{R{{T}_{m}}(k){{T}_{i}}}},$На рис. 4 представлены рассчитанные фазовые диаграммы системы NaCl–RaCl2, построенные по двум значениям температуры плавления эвтектики, в одной системе координат: 1 – Te1 = 987, 2 – Te2 = 969 K.
АНАЛИЗ РЕЗУЛЬТАТОВ ИССЛЕДОВАНИЯ
Расчетные значения температуры и состава в точках на линиях ликвидуса, по которым проводилось построение фазовых диаграмм (рис. 4), представлены в табл. 3 и 4. Анализируя значения R и δ (уравнения (1) и (2)), приходим к выводу, что второй расчет (по экстраполяции функции Te/r = f(r)) дает более надежные результаты. Следовательно, прогнозируемая эвтектика имеет следующие характеристики: Te2 = 969 K и состав x2(NaCl) = 0.709 и х2(RaCl2) = 0.291 (в мол. д.).
Таблица 3.
Температура ликвидуса и состав эвтектики в точках на линиях ликвидуса в прогнозируемой системе NaCl–RaCl2. Te/Z = f(Z)
| Состав эвтектики, мол. д. | Температура ликвидуса, K | |
|---|---|---|
| NaCl | RaCl2 | |
| Ветвь кристаллизации NaCl | ||
| 0.757 0.765 0.792 0.819 0.846 0.874 0.902 0.930 0.959 0.988 1.000 | 0.243 0.235 0.208 0.181 0.154 0.126 0.098 0.070 0.041 0.012 0.000 | 987 990 1000 1010 1020 1030 1040 1050 1060 1070 1074 |
| Ветвь кристаллизации RaCl2 | ||
| 0.755 0.748 0.700 0.645 0.583 0.513 0.434 0.345 0.247 0.139 0.019 0.000 | 0.245 0.252 0.300 0.355 0.417 0.487 0.566 0.655 0.753 0.861 0.981 1.000 | 987 990 1010 1030 1050 1070 1090 1110 1130 1150 1170 1173 |
Таблица 4.
Температура ликвидуса и состав эвтектики в точках на линиях ликвидуса в прогнозируемой системе NaCl–RaCl2. Te/r = f(r)
| Состав эвтектики, мол. д. | Температура ликвидуса, K | |
|---|---|---|
| NaCl | RaCl2 | |
| Ветвь кристаллизации NaCl | ||
| 0.709 0.713 0.739 0.765 0.792 0.819 0.846 0.874 0.902 0.930 0.959 1.000 | 0.291 0.287 0.261 0.235 0.208 0.181 0.154 0.126 0.098 0.070 0.041 0.000 | 968.6
970 980 990 1000 1010 1020 1030 1040 1050 1060 1074 |
| Ветвь кристаллизации RaCl2 | ||
| 0.709 0.706 0.661 0.611 0.557 0.496 0.431 0.360 0.283 0.200 0.111 0.015 0.000 | 0.291 0.294 0.339 0.389 0.443 0.504 0.569 0.640 0.717 0.800 0.889 0.985 1.000 | 968.6
970
990 1010 1030 1050 1070 1090 1110 1130 1150 1170 1173 |
Рассчитанные значения температуры плавления и состава двойной эвтектики дают возможность оптимизировать экспериментальное изучение системы NaCl–RaCl2 и поиск эвтектической точки.
Список литературы
Замалдинова Г.И., Парфенова С.Н., Гаркушин А.И. и др. Свойства s1-элементов, простых веществ, галогенидов и их смесей: аналитическое описание, расчет и взаимосвязь. Самара: Самар. гос. техн. ун-т, 2010. 202 с.
Замалдинова Г.И., Гаркушин А.И., Парфенова С.Н., Гаркушин И.К. // Бутлеровские сообщения. 2012. Т. 31. № 7. С. 104.
Замалдинова Г.И., Гаркушин А.И., Парфенова С.Н., Гаркушин И.К. // Бутлеровские сообщения. 2012. Т. 31. № 7. С. 108.
Burchakov A.V., Dvoryanova E.M., Kondratyuk I.M., Moshchenskii Yu.V. // Russ. J. Inorg. Chem. 2017. V. 62. № 5. P. 563. [Бурчаков А.В., Дворянова Е.М., Кондратюк И.М., Мощенский Ю.В. // Журн. неорган. химии. Т. 62. № 5. 2017. С. 564.]
Wang S.L., Su X.H., Li S.S. et al. // Calphad. 2018. V. 60. P. 214.
Chenyang Zhou, Jiaxin Cui, Cuiping Guo et al. // Calphad. 2017. V. 58. P. 138.
Yanhui Zhang, Peter Franke, Hans Jürgen Seifert // Calphad. 2017. V. 59. P. 142.
Tazuddin, Hemantkumar N. Aiyer, Amit Chatterjee // Calphad. 2018. V. 60. P. 116.
Berche A., Tédenac J.C., Jund P. // Calphad. 2016. V. 125. P. 271.
Claire A. Utton, Ioannis Papadimitriou, Hajime Kinoshita, Panos Tsakiropoulos // J. Alloys Compd. 2017. V. 717. P. 303.
Belmonte D., Ottonello G., Vetuschi Zuccolini M. // Calphad. 2017. V. 59. P. 12.
Zlomanov V.P., Zavrazhnov A.J., Davydov A.V. // Intermetallics. 2003. V. 11. P. 1287.
Bożena Pilarek, Beata Salamon, Jan Kapałaa // Calphad. 2014. V. 47. P. 211.
Lutsyk V., Zelenaya A. // Solid State Sciences. 2012. V. 14. № 11–12. P. 1604.
Lutsyk V.I., Vorob’eva V.P., Zyryanov A.M., Shodorova S.Ya. // IFAC Proceedings Volumes. 2013. V. 46. Issue 16. P. 371.
Lutsyk V.I., Vorob’eva V.P., Sumkina O.G., Tsyngeev B.V. // IFAC Proceedings Volumes. 2013. V. 46. Issue 16. P. 365.
Кондратюк И.М. // Изв. Самарск. научн. центра РАН. Проблемы нефти и газа. 2003. Т. 1. С. 206.
Термические константы веществ: Справочник / Под ред. Глушко В.П. М.: ВИНИТИ, 1981. Вып. X. Ч. 1. 299 с.
Термические константы веществ: Справочник / Под ред. Глушко В.П. М.: ВИНИТИ, 1979. Вып. IX. 574 с.
Термические константы веществ. База данных. Институт теплофизики экстремальных состояний РАН Объединенного института высоких температур РАН. Химический факультет Московского государственного университета им. М.В. Ломоносова. [Электронный ресурс] URL: http://www.chem.msu.su/cgi-bin/tkv.pl?show=welcom.html (Дата обращения 24.02.18).
Barin Ihsan. Thermochemical data of pure substances / In collab. with Gregor Platzki. Weinheim, N.Y., Base1, Cambridge, Tokyo: VCH, 1995.
Hattori T., Ikezawa H., Hirano R., Mochinaga J. // Nippon Kagaku Kaishi. 1982. № 6. P. 925.
Ефимов А.И., Белорукова Л.В., Василькова И.В., Чечев В.П. Свойства неорганических соединений. Л.: Химия, 1983. С. 82, 83.
Гаркушин И.К., Дворянова Е.М., Бурчаков А.В. Моделирование фазовых систем и фазовых равновесий. Самара: Самар. гос. техн. ун-т, 2015. Ч. 1. 176 с.
Дополнительные материалы отсутствуют.
Инструменты
Журнал неорганической химии