1. На главную
  2. Электронные версии
  3. Журнал неорганической химии
  4. T. 64, № 9, 2019

Журнал неорганической химии, 2019, T. 64, № 9, стр. 1006-1010

Моделирование коэффициентов активности в водных растворах солей алюминия с помощью обобщенной теории Дебая–Хюккеля

И. Ю. Шилов 1, *, А. К. Лященко 2, **

1 Московский государственный университет им. М.В. Ломоносова, Химический факультет
119991 Москва, Россия

2 Институт общей и неорганической химии им. Н.С. Курнакова РАН
119991 Москва, Ленинский пр-т, 31, Россия

* E-mail: ignatshilov@mail.ru
** E-mail: aklyas@mail.ru

Поступила в редакцию 05.05.2019
После доработки 03.06.2019
Принята к публикации 17.06.2019

Полный текст (PDF)

Аннотация

Проведен расчет коэффициентов активности в водных растворах хлорида и сульфата алюминия при 298 K по обобщенной теории Дебая–Хюккеля с использованием экспериментальных концентрационных зависимостей статической диэлектрической проницаемости. Получено полуколичественное согласие с экспериментальными данными, в том числе воспроизведена немонотонная зависимость коэффициентов активности от концентрации. Показано, что обобщенная теория Дебая–Хюккеля применима к описанию термодинамических свойств растворов 3,1- и 3,2-валентных электролитов.

Ключевые слова: растворы электролитов, хлорид алюминия, сульфат алюминия, диэлектрическая проницаемость, сольватация

ВВЕДЕНИЕ

Обобщенная теория Дебая–Хюккеля (ОТДХ), учитывающая концентрационную зависимость статической диэлектрической проницаемости растворов электролитов, расширяет область применимости формализма Дебая–Хюккеля на три порядка по концентрации с выходом в область концентрированных растворов по крайней мере на качественном уровне, а в некоторых случаях достигается количественное согласие с экспериментальными данными по коэффициентам активности до концентрации 6–7 моль/кг [1–4]. При этом описание проводится без оптимизации параметров модели, т.е. носит априорный характер. Это означает, что в расчетах используются экспериментальные данные по статической диэлектрической проницаемости, полученные методами диэлектрической спектроскопии [5, 6], а параметры, относящиеся к размерам ионов, однозначно оцениваются на основе кристаллографических радиусов ионов.

ОТДХ позволяет количественно проанализировать взаимосвязь диэлектрических и термодинамических свойств растворов электролитов, а также интерпретировать поведение коэффициентов активности как результат конкуренции межионных взаимодействий и взаимодействий ион–вода. Кроме того, анализ отклонений расчетных результатов от экспериментальных данных позволяет судить о степени ионной ассоциации растворов электролитов и ее изменении в рядах солей с изменением катиона или аниона. Эти результаты были получены ранее при анализе растворов 1,1-валентных электролитов, главным образом галогенидов щелочных металлов [1–4].

В настоящей работе в рамках ОТДХ проанализированы коэффициенты активности в растворах хлорида и сульфата алюминия при 298 K. Ион алюминия Al3+ известен как сильно гидратированный: по результатам дифракционных методов, в его водном окружении выделяются по крайней мере две гидратные сферы [7, 8]. В отношении ион-ионных корреляций строение растворов AlCl3 и Al2(SO4)3 существенно различается. Так, в диэлектрических спектрах 0.4 М раствора AlCl3 не наблюдается низкочастотных вкладов [9], тогда как в 0.15 М растворе Al2(SO4)3 обнаруживается область низкочастотной релаксации ионных пар [9, 10], из-за которой статическая диэлектрическая проницаемость растворов сульфата оказывается больше, чем у чистой воды. В работе [11], авторы которой исследовали водные растворы Al2(SO4)3 в интервале концентраций 0.012–0.65 моль/л, эту область удалось разделить на три вклада, отвечающих ионным парам трех видов (контактные, связанные и разделенные растворителем), и рассчитать их распределение. В спектрах КР растворов AlCl3 (0.21–3.14 моль/л) не наблюдаются ионные пары, тогда как фрагмент Al–O–SO3 явно проявляется в растворе Al2(SO4)3 [12].

Таким образом, в данной работе ОТДХ впервые применяется к описанию коэффициентов активности компонентов растворов солей с многозарядными ионами, проявляющих существенно разные степени ионной ассоциации.

МОДЕЛЬ

Обобщенная теория Дебая–Хюккеля, развитая в работе [1], основана на классических подходах, связанных с применением линеаризованного уравнения Пуассона–Больцмана и процедуры заряжения по Дебаю [13, 14], но учитывает изменение диэлектрической проницаемости раствора с концентрацией. Концентрационная зависимость диэлектрической проницаемости $\varepsilon $ описывается с помощью функции f(κ0):

(1)
$\varepsilon = {{\varepsilon }_{0}}f({{\kappa }_{0}}),$
где ε0 – диэлектрическая проницаемость чистого растворителя, κ0 – обычным образом определенная обратная длина Дебая:

(2)
$\kappa _{0}^{2} = \frac{{4\pi e_{0}^{2}}}{{{{\varepsilon }_{0}}kTV}}\sum\limits_i {{{N}_{i}}z_{i}^{2}} .$

В уравнении (2) e0 – элементарный заряд, k – постоянная Больцмана, T – температура, V – объем раствора, Ni – число частиц i-го типа, zi – зарядовое число иона.

Коэффициент активности воды γw и рациональный среднеионный коэффициент активности γ± полностью диссоциированного электролита $C_{{{{\nu }_{ + }}}}^{{{{z}_{ + }}}}A_{{{{\nu }_{ - }}}}^{{{{z}_{ - }}}}$ состоят из двух вкладов, отвечающих ион-ионым взаимодействиям (индекс 1) и взаимодействиям ион–вода (сольватация, индекс 2):

(3)
$\ln {{\gamma }_{w}} = \ln {{\gamma }_{{w,1}}} + \ln {{\gamma }_{{w,2}}},$
(4)
$\ln {{\gamma }_{ \pm }} = \ln {{\gamma }_{{ \pm ,1}}} + \ln {{\gamma }_{{ \pm ,2}}}.$

Вклады для коэффициента активности воды определяются по формулам:

(5)
$\ln {{\gamma }_{{w,1}}} = \frac{{{{{\overline V }}_{w}}\kappa _{0}^{3}{{\sigma }_{1}}({{\kappa }_{0}},a)}}{{24\pi \,{{N}_{A}}\,}},$
(6)
$\ln {{\gamma }_{{w,2}}} = - \frac{{{{{\overline V }}_{w}}\kappa _{0}^{2}{{\sigma }_{2}}({{\kappa }_{0}})}}{{16\pi {{N}_{A}}{{R}_{ \pm }}}},$
где ${{\overline V }_{w}}$ – парциальный мольный объем воды, NA – число Авогадро, a – расстояние наибольшего сближения ионов, R± – средний ионный радиус. Функции σ1(κ0, a) и σ2(κ0) выражаются с помощью интегралов, конкретный вид которых приведен в [1–4].

Вклады в рациональный среднеионный коэффициент активности γ± равны:

(7)
$\ln {{\gamma }_{{ \pm ,1}}} = - \frac{{\left| {{{z}_{ + }}{{z}_{ - }}} \right|e_{0}^{2}{{\kappa }_{0}}{{\chi }_{1}}({{\kappa }_{0}},a)}}{{3kT{{\varepsilon }_{0}}}} + \frac{{{{{\overline V }}_{ \pm }}\kappa _{0}^{3}{{\sigma }_{1}}({{\kappa }_{0}},a)}}{{24\pi {{N}_{A}}}},$
(8)
$\ln {{\gamma }_{{ \pm ,2}}} = \frac{{\left| {{{z}_{ + }}{{z}_{ - }}} \right|e_{0}^{2}}}{{2{{R}_{ \pm }}kT}}\left( {\frac{1}{\varepsilon } - \frac{1}{{{{\varepsilon }_{0}}}}} \right) - \frac{{{{{\overline V }}_{ \pm }}\kappa _{0}^{2}{{\sigma }_{2}}({{\kappa }_{0}})}}{{16\pi {{N}_{A}}{{R}_{ \pm }}}},$
где ${{\overline V }_{ \pm }}$ – среднеионный парциальный объем, а функция χ1(κ0, a) выражается с помощью интеграла, явный вид которого приведен в работах [1–4].

Для сравнения результатов расчета с экспериментальными данными рациональные коэффициенты активности γ±, рассчитанные по уравнениям (4), (7) и (8), конвертировали в моляльную шкалу, используя стандартную формулу [15]. Далее под величиной γ± будет пониматься моляльный коэффициент активности.

АНАЛИЗ ДАННЫХ И РЕЗУЛЬТАТЫ МОДЕЛИРОВАНИЯ

Экспериментальные значения коэффициентов активности в водных растворах AlCl3 и Al2(SO4)3 при 298 K взяты из [15]. Плотности растворов, необходимые для перехода между различными концентрационными шкалами взяты из [16, 17].

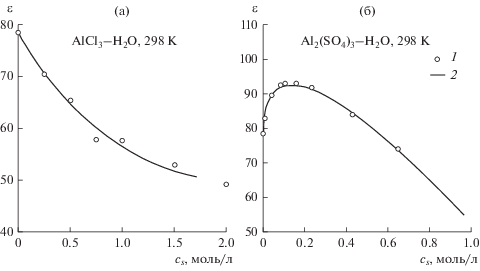
Экспериментальные значения статической диэлектрической проницаемости растворов AlCl3 заимствованы из работы [18], а Al2(SO4)3 – из работы [11]. Для диэлектрической проницаемости чистой воды использовано значение из [19]. Данные по статической диэлектрической проницаемости растворов солей алюминия были аппроксимированы выражениями, приведенными в табл. 1. Зависимости диэлектрической проницаемости растворов от концентрации показаны на рис. 1. Следует отметить, что диэлектрическая проницаемость растворов AlCl3 определяется водной подсистемой, тогда как диэлектрическая проницаемость растворов Al2(SO4)3 учитывает также вклады контактных, связанных и разделенных растворителем ионных пар.

Таблица 1.

Концентрационная зависимость статической диэлектрической проницаемости ε растворов солей алюминия при 298 K, ε0 = 78.36 [19], cs – молярная концентрация соли (моль/л), cs,max, ms,max – максимальная молярная концентрация и моляльность соли в экспериментальных данных по ε, Δν – интервал частот, в котором измерена комплексная диэлектрическая проницаемость раствора, использованная для определения статической диэлектрической проницаемости, модель означает уравнение, использованное для экстраполяции комплексной диэлектрической проницаемости к нулевой частоте: CC (выражение Коула–Коула), 5D (пять функций Дебая)

Соль Зависимость ε(cs) cs,max, моль/л ms,max, моль/кг Δν, ГГц Модель Ссылка
AlCl3 $\varepsilon = {{\varepsilon }_{0}}{\text{ }} - 40.4{{с}_{s}} + 18.5с_{s}^{{3/2}}$ 2.0 2.1 13–25 СС [18]
Al2(SO4)3 $\varepsilon = {{\varepsilon }_{0}}{\text{ }} + 75.6\sqrt {{{c}_{s}}} - 101{{c}_{s}}$   0.65   0.66 0.2–89 5D [11]
Рис. 1.

Статическая диэлектрическая проницаемость водных растворов AlCl3 (а) и Al2(SO4)3 (б) при 298 K: 1 – экспериментальные данные [18, 11 ], 2 – расчет по уравнениям из табл. 1, cs – молярная концентрация соли.

Параметр наибольшего сближения ионов a и средний ионный радиус R± рассчитывали по формулам:

(9)
$a = {{R}_{ + }} + {{R}_{ - }},\,\,\,\,{{R}_{ \pm }} = \frac{{{{R}_{ + }} + {{R}_{ - }}}}{2},$
где R+ и R– – радиусы катиона и аниона. Для оценки размеров ионов Al3+ и Cl– использовали радиусы Полинга [20], а для иона $SO_{4}^{{2 - }}$ – радиус Маркуса [21]. Значения этих радиусов приведены в табл. 2.

Таблица 2.  

Ионные радиусы Полинга (RP) [20] и Маркуса (RM) [21]

Ион RP, Å RM, Å
Al3+ 0.5  0.53
Cl–  1.81 1.81
$SO_{4}^{{2 - }}$ – 2.3

Имеющиеся специфические для данных систем экспериментальные функции (плотность и диэлектрическая проницаемость) и однозначно рассчитанные параметры (a, R±) позволяют провести прогнозирование коэффициентов активности компонентов растворов солей алюминия по уравнениям (3)–(8), т.е. расчет с заранее установленными значениями параметров модели.

Результаты расчета коэффициента активности воды и среднеионного коэффициента активности в растворах AlCl3 и Al2(SO4)3 изображены на рис. 2 и 3 по сравнению с экспериментальными данными [15]. Расчет качественно воспроизводит концентрационную зависимость коэффициента активности воды и среднеионного коэффициента активности, при этом немонотонный характер этой зависимости интерпретируется как следствие изменяющегося с концентрацией баланса вкладов ион-ионного взаимодействия и сольватации. Для растворов AlCl3 модель занижает среднеионный коэффициент активности по всей исследованной области концентраций, а для Al2(SO4)3 – до концентрации 0.8 моль/л.

Рис. 2.

Коэффициент активности воды (а) и среднеионный коэффициент активности (б) в водных растворах хлорида алюминия при 298 K: 1 – расчет по обобщенной теории Дебая–Хюккеля, 2 – экспериментальные данные [15], ms – моляльность соли.

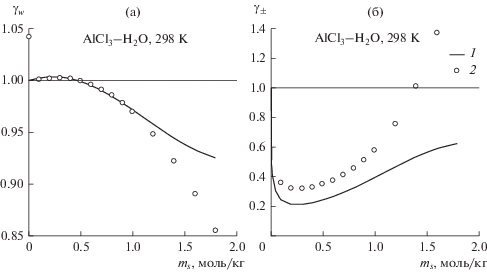
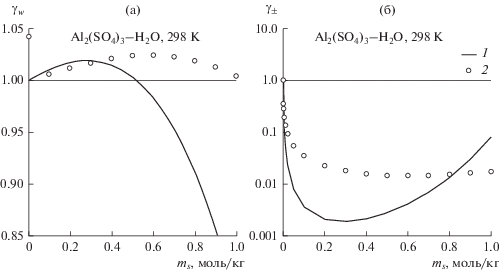
Рис. 3.

Коэффициент активности воды (а) и среднеионный коэффициент активности (б) в водных растворах сульфата алюминия при 298 K: 1 – расчет по обобщенной теории Дебая–Хюккеля, 2 – экспериментальные данные [15], ms – моляльность соли.

В целом различия в стехиометрии и структуре двух растворов мало отражаются на качестве описания их коэффициентов активности в рамках ОТДХ. Вероятно, это является следствием способности формализма Дебая–Хюккеля к взаимной компенсации эффектов различных факторов строения и взаимодействия в растворах электролитов. При этом в случае растворов Al2(SO4)3 неявно (через экспериментальную диэлектрическую проницаемость) учитывается влияние ионной ассоциации на термодинамические свойства.

ЗАКЛЮЧЕНИЕ

Показано, что обобщенная теория Дебая–Хюккеля позволяет полуколичественно прогнозировать коэффициенты активности в растворах 3,1- и 3,2-валентных электролитов на основе их диэлектрических свойств.

Список литературы

  1. Shilov I.Yu., Lyashchenko A.K. // J. Phys. Chem. B. 2015. V. 119. № 31. P. 10087.

  2. Shilov I.Yu., Lyashchenko A.K. // J. Mol. Liq. 2017. V. 240. P. 172.

  3. Shilov I.Yu., Lyashchenko A.K. // J. Solution Chem. 2019. V. 48. № 2. P. 234.

  4. Shilov I.Yu., Lyashchenko A.K. // Fluid Phase Equilib. 2019. V. 485. P. 248.

  5. Buchner R., Hefter G. // Phys. Chem. Chem. Phys. 2009. V. 11. № 40. P. 8984.

  6. Lyashchenko A., Lileev A. // J. Chem. Eng. Data. 2010. V. 55. № 5. P. 2008.

  7. Ohtaki H., Radnai T. // Chem. Rev. 1993. V. 93. № 3. P. 1157.

  8. Смирнов П.Р., Тростин В.Н. // Журн. общ. химии. 2013. Т. 83. № 1. С. 18.

  9. Kaatze U. // Z. Phys. Chem. N. F. 1983. B. 135. S. 51.

  10. Kaatze U., Giese K. // J. Mol. Liq. 1987. V. 36. P. 15.

  11. Schrödle S., Rudolph W.W., Hefter G. et al. // Geochim. Cosmochim. Acta. 2007. V. 71. № 22. P. 5287.

  12. Rudolph W.W., Mason R., Pye C.C. // Phys. Chem. Chem. Phys. 2000. V. 2. № 22. P. 5030.

  13. Debye P., Hückel E. // Phys. Z. 1923. B. 24. S. 185.

  14. Debye P. // Phys. Z. 1924. B. 25. S. 97.

  15. Робинсон Р., Стокс Р. Растворы электролитов. М.: Иностранная литература, 1963. 646 с.

  16. Mason C.M. // J. Am. Chem. Soc. 1938. V. 60. № 7. P. 1638.

  17. Зайцев И.Д., Асеев Г.Г. Физико-химические свойства бинарных и многокомпонентных растворов неорганических веществ. Справ. изд. М.: Химия, 1988. 416 с.

  18. Лященко А.К., Балакаева И.В., Шебалкова А.Ю. и др. // Журн. неорган. химии. 2018. Т. 63. № 8. С. 1073. https://doi.org/10.1134/S0036023618080144

  19. Kaatze U. // J. Chem. Eng. Data. 1989. V. 34. № 4. P. 371.

  20. Pauling L. // J. Am. Chem. Soc. 1927. V. 49. № 3. P. 765.

  21. Marcus Y. Ions in Solution and their Solvation. New Jersey: Wiley, Hoboken, 2015.

Дополнительные материалы отсутствуют.

Инструменты

предыдущая статья выпуска содержание выпуска

Журнал неорганической химии

Архивы выпусков Информация о журнале Отправить рукопись в журнал